3D成像和测量技术广泛应用于工业，娱乐，文物保护，医药等领域。然而就传统的3D测量技术而言，已经越来越难以满足市场的需求，因此，寻找快速有效的3D成像和测量方法成为趋势，也成为了当前研究的热门话题。在众多方法之中，基于光场原理的成像技术具有结构简单，成像速度快的优点，它通过分析不同视角等图像之间的冗余视差信息，获得完整的场景三维点云数据^[1-4]。这些优点符合三维测量领域的需求，因此，受到国内外学者的广泛关注。目前，关于利用光场成像原理进行三维测量的研究很多。首先，利用记录的4D光场的数据，可以通过堆栈估计场景深度的信息，即清晰成像中的点的对应聚焦堆栈是该点的深度信息。其中主要的计算方法包括傅里叶层析成像和数字重聚焦^[5]。此外，还可以通过使用对象点的视差来获得场景深度的信息^[6-9]。例如，在多目系统中，通过多个摄像机的有序排布获得不同视角的图像，并且通过多视角的像素匹配来获得视差信息^[10]。再例如，在分析光场数据的极线平面图像时，根据极坐标曲线的性质，对象点对应的像素会呈线性分布在极坐标图上，通过计算极坐标图中拟合直线的斜率信息来估计视差信息^[11]。

在文中的方法中，笔者将结构光投影技术和光场成像相结合，并提出了一种灵活的3D测量过程。首先，笔者通过投影一系列编码条纹图像对测量物体的表面进行编码的标记，利用摄像机在特定方向上的有序移动，模拟相机阵列采集光场数据的方式，来记录具有编码信息的物体图像。其次，通过处理图像序列来求解相位，同时建立4D相位光场图像。在光场理论中，从同一点发出的每条光线，其对应的相位值是恒定的。4D相位光场图像中的像素可以用来表征光线，因此构成具有相同相位的这些像素，分别对应于物体表面的同一个点所发出的光线。所以空间中所有点的3D坐标可以利用每个点各自所对应的光线进行计算。与以前的方法相比，该方法可以通过利用编码条纹标记物体的方式，简单快速地获取3D数据，具有较高的精度和稳定性。与此同时，所提出的方法使用来自各种视角的信息来计算场景深度，有效地弥补了在传统的结构光测量方法当中阴影、遮挡或过度曝光的问题。实验结果证明了该方法的可靠性。

光场的本质是空间中所有光线向各个方向传播的光辐射函数的总体，这可以通过全光函数完全描述。但是当光线在光场中传输时，只考虑由射线携带的二维位置信息（u，v）和二维方向信息（θ，φ）。在这种情况下，光场数据可以利用两个平行平面进行参数化描述。如图1所示，光线分别与透镜平面（u，v）和传感器平面（s，t）相交与两点，构成4D光场函数L（u，v，s，t）。其中透镜平面和传感器平面之间的距离是d，透镜平面与传感器平面之间的关系用于描述光线的传播方向，并且光线的强度由传感器获得。在这种情况下，光线的强度和方向就由光线和两个平面的交叉点的坐标表示。

图  1  两平面参数化表征

Figure 1.  Parameterized representation of two planes

在文中，主要利用极平面分析法估算场景的深度信息，因此，下面就极平面分法的原理进行描述。通过单点采样模型来描述3D场景，并且将4D光场的平面参数化模型转换为几何图像进行分析。在图2（a）中，从空间中的点P（px，py，pz）发散出的光线与两个平面（u，v），（s，t）分别相交与两个点并且在两个平面之间的距离为d。

图  2  (a) 两平面参数化描述的几何表示；(b) u-s面几何分析的示意图

Figure 2.  (a) Geometric representation of two plane parameterized; (b) Schematic diagram of geometric analysis of u-s plane

值得注意的是，相机在实验中获得的光场图像由不同视角下的图像组成，其中u和v表示相机在空间坐标系中特定移动的相对物理位置，例如（u₁，v₁）表示第1行第1列的摄像机采集到的一组子图象，s和t描述了对应的子图像中像素的位置分布。由于各自表示的单位不同，因此在计算时，要将单位进行统一，例如将s，t的单位转换为物理尺寸。

如图2（b）所示，当只考虑单向的数据时，例如u，s，分析如下。首先，根据三角形相似的原理，p点坐标之间的u，s对应关系如下：

然后，直线的斜率$ \dfrac{{\Delta {\rm{u}}}}{{\Delta {\rm{s}}}}$可以表示为：

类似地，也可以得到关于点p的坐标在v和t之间的关系。

通常来说，u和s分别可以由r_u和r_s代替，(同理v和t也可以），然后可以将两组方程(u, v和s, t)重新整合为一个方程，由点p所表示的4D射线空间的子集可以描述为：

其中，P_x和P_y可以通过公式变换可得，并且都可以用P_z来表示，如公式(6)所示：

当物距远大于像距时，可以将d的值近似看作焦距值，因此，可以通过校准相机来准确地确定d的值。当然，考虑到相机镜头的失真，在校准过程中进行了失真的校正。经过u-s平面的分析可以看出，由于空间中的点p在多个子图像上成像，并且这些像素可以拟合成直线，因此，p点的深度值与所拟合成的直线的斜率成比例关系。同理，对于v-t平面，同样满足。

目前，有很多方法可以收集4D光场的数据，最常见的两种采集方法是基于相机阵列和微透镜阵列^[12-13]。对于4D光场数据中的每个子图像，如果以相机阵列的形式获取，则可以将其视为使用不同相机采集的数据，但是微透镜阵列可以视为子成像系统由主透镜组和用于收集的微透镜组成。两者之间有一些相似之处，但每种都有各自的优缺点。在文中，笔者使用基于相机阵列的光场采集来获得不同位置的场景视差图，将图像数据转换为4D光场数据。摄像机之间的位置关系可以通过平移矩阵进行变换。因此，可以从多视图图像估计场景3D信息。该4D光场数据采集具有更宽的视场，并且从每个视图获取的图像具有相机分辨率，即高分辨率微图像阵列。相邻相机之间的串扰很小，可以应用于具有不同参数的成像系统。如图3所示，笔者设计了一个系统，用于对由相机阵列收集的光场数据进行3D测量，包括相机，投影仪和物体。

图  3  系统结构图

Figure 3.  Schematic diagram of system

在提出的方法中，利用结合了四步相移和格雷码的编码条纹，来求解连续相位值和所对应的相位标记^[14-16]。一旦获得连续相位，具有相同相位值的点是物体上的一点在不同视角下成像的结果，因此，4D光场数据中直线的斜率可以快速求解，物体的深度通过这种标记特征点的方法进行估算。在整个过程中，需要校准单个摄像机并确定摄像机移动的精确的相对位置关系，但无需校准投影机和摄像机之间的位置关系。

在实验中，使用基于结构光标记的灵活光场3D成像系统来验证所提出的方法的有效性。其中相机的型号是PointGray的FL2G-13S2M-C，分辨率为1 280×960像素，单像素尺寸为3.75×3.75 μm。使用了计算机公司的镜头，DLP4500的投影机型号，分辨率为800×600像素，一个电动平移台，被测对象是人的石膏模型。笔者在水平方向上收集了15组条纹图案，并通过求解代码得到每个对象的绝对相图。其中，将第一个视图的位置定义为1 mm，每次移动之间的距离为1 mm。因此，u和v的单位是mm，s和t的单位是像素。当然，在计算数据时，要对单位进行归一化。

根据光场成像原理，首先将收集的光场数据转换为u-s坐标系进行分析，如图4（a）所示，表示u=1,5,10,15四个视角下的相位图，当t=460,600时，u-s平面图像分别如图4（b）和4（c）所示。可以看出，具有相同相位值的点是从不同视角对物体上的同一点进行成像的结果，换句话说，这些像素点拟合成的直线的斜率对应于该点的深度。

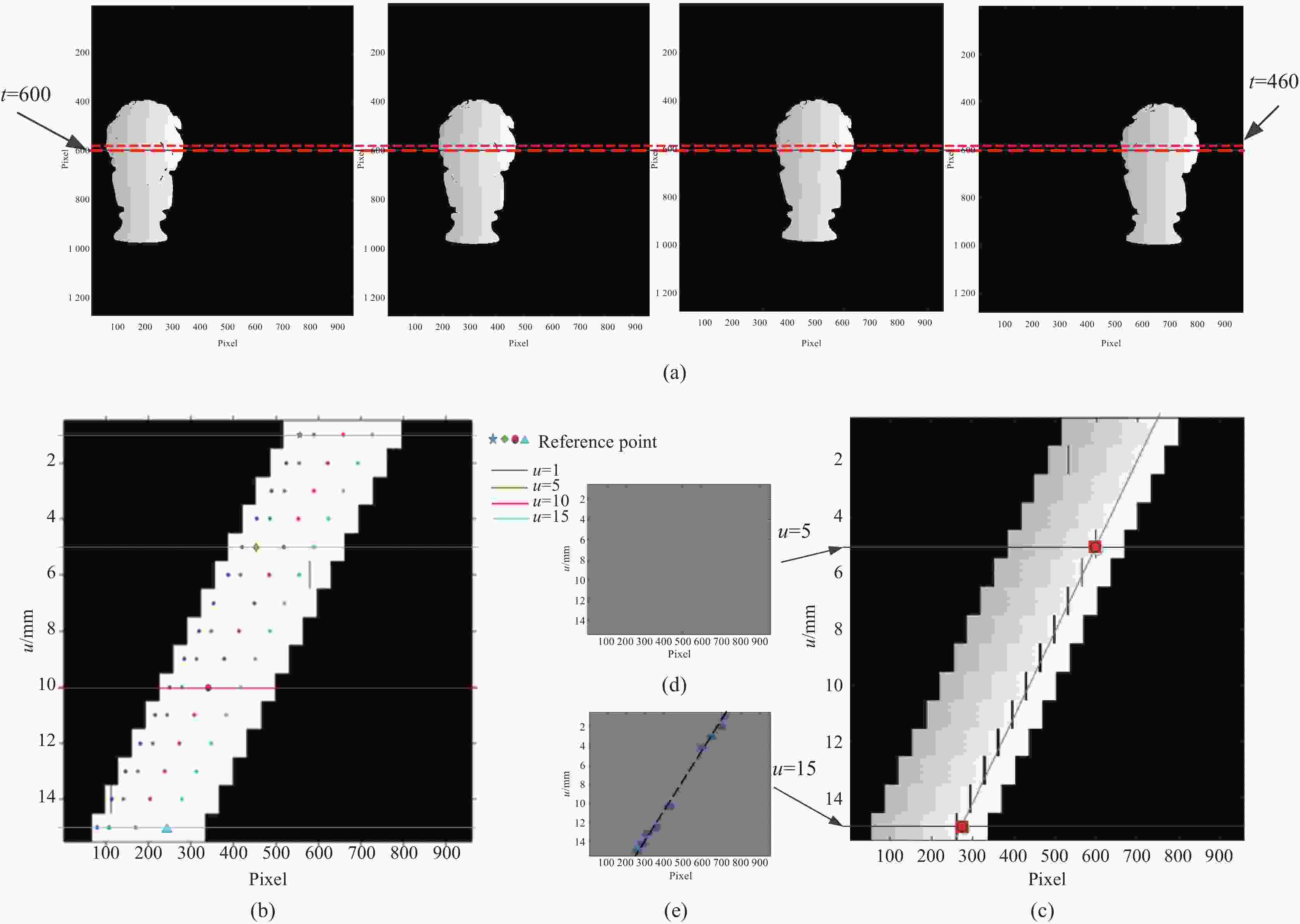
图  4  (a) 相位图；（b）、（c） t=460，t=600时的u-s平面图；（d）、（e）当u=5，u=15时，相位值的插值描述值的插值描述

Figure 4.  (a) Unwraped phase image; (b), (c) Unwraped phase image of u-s plane at t=460 and t=600; (d), (e) Interpolation diagram when u=5 and u=15

事实上，由于视角的变化，采样位置也发生了稍许变化，因此，笔者得到的相位值并不是绝对准确的。为了提高查找的准确性，笔者使用三次样条插值方法，以某一个视角下的相位值为基准，插值查找该值在其他视角下的分布情况，可想而知由于光场的特性，每个视角下都有成像且具有不同部分上相位数据，因此，视角与视角之间可以进行相位值的交替插值查找，即使由于单个透镜的视场有限而导致图像中某些区域存在遮挡和阴影，只要保证在整个视场中能获取它的相位值，总能从某一个视角下求解得到对应的深度值。值得说明的是，由于直线的拟合至少需要两个点，所以要确定一个点至少在两个视角下有对应的相位值。如图4（b）～（e）所示，通过数据进行了说明。

对石膏模型进行测量，将得到的数据导入到Geomagic软件中，当在全局坐标系中显示时，有效地获得了完整的3D点云数据。图5（a）显示了从单一视角获得的3D点云数据。图5（b）是笔者计算的最终完整的3D点云数据。圆形区域的比较表明，该方法大大提高了物体的重建精度和空间分辨率，获得了复杂物体的完整点云数据。它还为解决由于物体表面上的遮挡或过度曝光而导致物体无法获得完整的脸部形状的问题提供了基础。

图  5  （a）从单一角度获得的3D点云数据；（b）最终的完整3D点云数据

Figure 5.  (a) 3D point cloud data from one single perspective; (b) Complete 3D point cloud data

为了验证笔者的方法是否可以解决部分高光的问题，笔者测量了金属板。如图6（a），图6（b）所示，它们在单个透视图中表示条纹图像和得到的相位图。从图中笔者可以看出：金属板的部分表面区域存在高光，使得该区域的相位值为0，该部分的点云数据是重建不出来的。但是通过笔者的方法利用多次查找和所有视角下的点云数据进行数据补偿的方式，求解得到了高光区域完整的三维点云数据，如图6（d）所示。

图  6  （a）金属板的条纹图；（b）对应的相位图；（c）金属板的实物图；（d）重建得到的点云数据图

Figure 6.  (a) Image of fringe pattern on metal plate; (b) Corresponding phase diagram; (c) Image of metal plates; (d) Reconstructed 3D point cloud

最后，笔者测量了标准方块（60 mm×60 mm×60 mm），对笔者方法的测量精度进行定量分析。其中，使用最小二乘法进行平面拟合并分析相关误差系数，如图7（a）所示。通过分析，标准平面方程为0.682 7X + 0.035 2Y + −0.729 9Z + −0.007 6=0，其中最大平面偏差为0.004 127 mm，平均偏差为0.000 3 mm，标准偏差为0.000 4 mm。最后，对平面的夹角进行了评估，计算出的角度为89.739 2，如图7（b）所示。可以看出测量精度达到了微米数量级，符合笔者的测量要求，并且证明了所提出方法的有效性。

图  7  （a）平面点云数据的颜色矢量图；（b）角度评估图

Figure 7.  (a) Color vector diagram of plane point cloud; (b) Angle between two planes

提出了一种基于结构光标记的光场三维成像系统，能够以高精度和稳定性轻松快速地获取三维物体坐标。所提出的方法解决了难以确定哪些光线包含有效3D数据信息的问题，并且在存在阴影、遮挡或过度曝光表面的情况下提供高质量的3D数据重建。通过实验验证了所提方法的可行性。