光学干涉仪由于具有高精度和非接触式全场测量特点，在光学元件的面形检测中得到了极其广泛的应用。针对处于加工阶段的光学元件而言，通常需要同时测得其不同空间频率范围内的面形信息，进而对其表面加工特性进行评价反馈。针对不同空间频率范围的干涉检测需要，可采用激光干涉仪和干涉显微镜来分别获取低频和中高频范围面形信息。其中激光干涉仪包括Fizeau型^[1]、Twyman-Green型以及点衍射干涉仪^[2-3]等，它可用于实现低频段宏观面形误差的检测；干涉显微镜^[4]可实现微观轮廓（表面粗糙度）测量。现有商业干涉仪由于系统体积和抗干扰能力的限制一般只能用于实验室环境的离线式测量，因而只能将被测元件从车削机床上拆卸下来进行检测，这也对其复位到车削平台的安装调整精度提出了很高的要求，整个测量过程费时费力且效率低。尤其是在加工前的对刀阶段，需要对对中工具的整体面形以及微观加工刀痕进行反复检测，在此基础上对刀具进行调整，因而极其需要可直接在线测量的检测仪器。

针对加工在线检测需要，学者们对紧凑型干涉仪^[5]、共焦显微测头^[6]、立体视觉测量技术^[7]和光学偏折术^[8-10]等方法和装置进行了研究，并开发了相应的应用装置。但干涉仪在内各种的现有测量仪器，都只能实现单一工作模式，即宏观面形或面形粗糙度的测量，而无法同时实现两种测量模式。这也导致需要同时用多个测量仪器组合才能实现加工过程中光学元件面形信息的全面评价。针对此问题，美国亚利桑那大学提出了一种双测量模式干涉系统^[11]，可同时用于宏观面形和面形粗糙度的在线测量。该系统将两种测量模式下的两路光路集成到一个系统中，光路较为复杂，同时实际测量中需要对系统元件进行安装或移除才能实现测量模式的切换，因而给实际应用带来了一定的不便。

针对光学元件加工阶段在线检测需要，文中提出了一种紧凑型的多测量模式干涉仪，可分别实现单波长激光干涉、多波长激光干涉以及LED干涉显微测量等多种工作模式。针对多工作模式下的高精度在线检测要求，对所涉及的关键系统元件选择、布局设计以及主要误差因素进行了分析。为了验证所以提出的可用于在线检测的紧凑型多测量模式干涉仪的可行性，利用所搭建的原理样机在金刚石车削机床上进行了在线检测，并与Zygo干涉仪和Zygo光学轮廓仪测量结果进行了比对；同时也利用该系统对金刚石车削自由曲面进行了在线检测。

用于在线检测的紧凑型多测量模式干涉仪系统光路布局如图1所示，其中光源系统包含波长分别为632.8 nm和543 nm的气体激光器以及470 nm LED光源，并且三个波长光束可进行切换开启。来自光源系统的光经光纤耦合接入干涉系统的光纤准直器后变为准直光束，再经一个线偏振片得到某一方向的线偏振光。为了缩短系统尺寸，采用折光反射镜对光路进行90°转折。线偏振光分别经过分光棱镜（BS）和偏振分光棱镜（PBS）后分为透射p偏振光和反射s偏振光，其中p偏振光作为检测光，先后经长波通过滤光片（F1）（三波长光束均透射）和显微物镜1后入射到待测元件表面并沿原路反射回来；s偏振光作为参考光，其中632.8 nm和543 nm波长激光束被短波长通过滤光片（F2）第一个面反射回来，470 nm波长LED光束透射短波长通过滤光片（F2）后经显微物镜2入射到位于焦平面上的参考反射镜并沿原路返回。p偏振检测光和s偏振参考光沿原路返回并在偏振分光棱镜（PBS）透射、反射汇合后，分别经分光棱镜（BS）反射和宽波段消色差1/4波片（AQWP）透射后，变为两个旋向相反的圆偏振光。两束圆偏振光经成像透镜在偏振相机上可同时得到相移量为π/2的四个通道移相干涉条纹，利用四步移相算法即可计算得到与待测元件表面信息相对应的瞬态波前分布，进而实现待测元件表面的瞬态检测。

图  1  紧凑型多测量模式干涉仪系统布局

Figure 1.  System layout for compact multi-measurement mode interferometer

为了满足不同工作波长应用要求，系统中光纤准直器采用了离轴抛物线反射式光纤准直器，分光棱镜（BS）、偏振分光棱镜（PBS）和1/4波片（AQWP）都为宽工作波段。针对在线检测中环境扰动影响问题，系统采用了偏振相机来实现波前的四步偏振移相瞬态检测，以最大程度提高系统的抗干扰能力。偏振相机是在传统的象元面阵前加入了由2×2微偏振器（透光轴方向分别为0°、45°、90°和135°）为超像素单元所组成的偏振面阵（图1），因而可实现一帧图像同时获取四个偏振方向对应四个通道图像信息^[12]。

为了利用单一光路来实现不同测量模式的切换，系统采用短波长通过滤光片（F2，截止波长：500 nm，反射波段：512~715 nm，透射波段：300~490 nm）实现激光光束的反射和LED光束的透射，同时利用长波通过滤光片（F1，截止波长：350 nm，反射波段：200~340 nm，透射波段：358~1 600 nm）来补偿光程。在单波长或多波长激光干涉测量模式中，可采用512~715 nm范围激光器作为光源，该模式下滤光片（F2）的第一入射面的反射光作为参考光；在干涉显微测量模式中，可采用358~490 nm中心波长范围的LED作为光源，该模式下参考反射镜的反射光作为参考光。

在单波长激光干涉测量模式或者LED显微测量模式中，利用偏振相机单帧采集得到四通道π/2移相条纹，设0°、45°、90°和135°透光轴方向对应的干涉图强度分布为${I_j}$(j=1, …, 4)，可得对应的待测波前光程差为:

式中：$\lambda $为光波长。

在单波长干涉检测中，其表面相邻两个采样点可测高度差最大值为λ/4，即对应632.8 nm光波长为0.158 2 μm）。为了满足实际加工中到自由曲面等大动态范围面形测量需要，可采用多波长干涉技术来扩展干涉检测系统的测量范围。对于${\lambda _1}$和${\lambda _2}$两个波长组合情况，其表面相邻两点可测高度差最大值为Λ/4，其中等效波长$\varLambda = {{{\lambda _1}{\lambda _2}}/{({\lambda _1} - {\lambda _2})}}$。对应两个波长为632.8 nm和543 nm的激光波长，其组合对应的等效波长为Λ=3.826 4 μm，若采用两个更为接近的波长则可得到更大的等效波长。

图1所示紧凑型多测量模式干涉仪中，主要误差因素包括滤光片面形误差、1/4波片相位延迟误差、偏振相机视场误差和多波长干涉误差等。

在宏观面形干涉检测中，滤光片（F1）的透射像差和滤光片（F2）的入射面（为参考面）会对检测结果引入误差；微观干涉显微测量中，滤光片（F1）和滤光片（F2）的透射像差会对检测结果引入误差。为了最大程度减小滤光片对测量结果的影响，系统中滤光片玻璃基底选用面形精度较高的平板玻璃。实际系统中滤光片面形误差均方根（RMS）约为10 nm量级，测量中可利用高精度干涉仪测得滤光片面形误差并作为系统误差，在最后被测结果中加以校正消除。

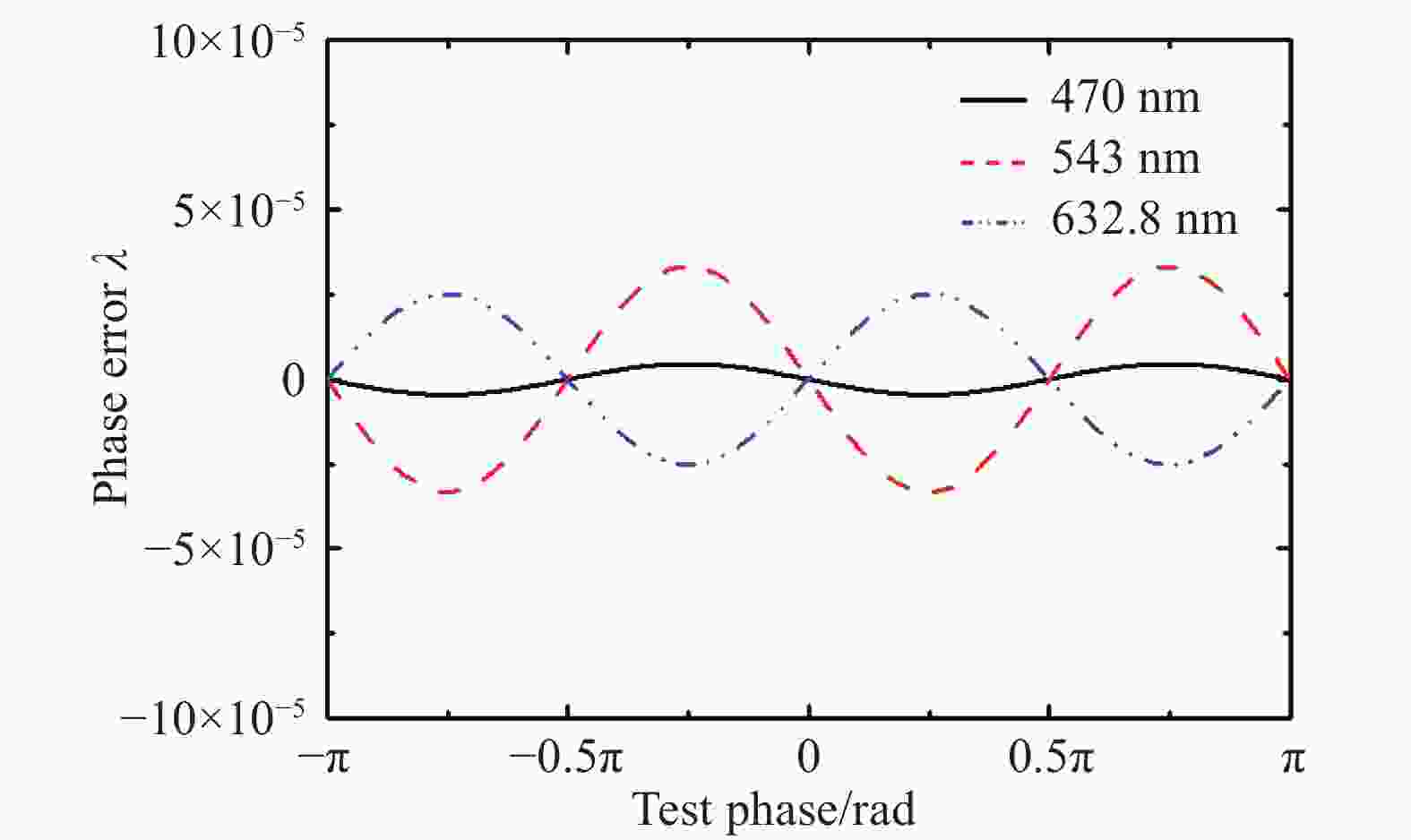
干涉系统利用1/4波片（AQWP）将振动方向相互垂直的两个线偏振测量光和参考光转换为旋向相反的圆偏振光。针对不同光波长应用要求，采用宽波段消色差1/4波片（AQWP），其对应470 、543 、和632.8 nm光波长的相位延迟量分别为0.251 7λ、0.245 4λ和0.246 0λ，而非理想情况下的λ/4。1/4波片对不同相位所引入的波前误差分布曲线如图2所示，对应470 、543 、632.8 nm光波长的波前测量误差峰谷（PV）值分别仅为0.9×10⁻⁵λ、6.6×10⁻⁵λ和5.0×10⁻⁵λ，因而可忽略其对测量结果的影响。

图  2  1/4波片引入波前测量误差

Figure 2.  Wavefront measurement error introduced by quarter-wave plate

在对偏振相机所采集的单帧图像提取四个通道移相干涉条纹并根据式(1)进行相位或光程差求解时，近似认为同一超像素单元（对应2×2 pixel）内的相位分布保持不变，而该近似处理对测量结果会一定的测量误差，即偏振相机视场误差。偏振相机视场误差的大小与入射波前斜率有关，可利用相邻像素相位值的加权平均线性插值方法^[13]，对该误差因素实现有效的校正。图3所示为不同波前斜率对应偏振相机视场误差以及采用3×3相邻像元加权平均线性插值方法校正后引入的波前误差PV值。以图3所示的3×3相邻像元相位加权平均线性插值校正为例，各个通道的强度${I_j}$(j=1, …, 4，分别对应0°、45°、90°和135°透光轴方向)计算公式为：

图  3  偏振相机视场误差影响

Figure 3.  Error of field of view in polarization camera

根据图3可知，偏振相机视场误差会随着波前斜率的增大而快速增大，对应0.02λ/pixel的波前斜率，其引入的波前误差PV值为0.251 7λ；利用相邻像元相位加权平均线性插值法可实现偏振相机视场误差的有效校正，校正后对应0.02λ/pixel的波前斜率引入的波前误差PV值仅约为5.0×10⁻⁵λ。

在多波长波前干涉检测中，通过等效波长概念可实现测量范围的有效放大，但其对应的相位噪声（如透射元件对不同波长的色散作用）也同时会按波长同等放大倍数被放大，进而会对最后测量结果引入误差，即多波长干涉误差。可采用条纹级次法^[14-15]来校正多波长干涉误差，令两组${\lambda _1}$和${\lambda _2}$不同光波长测得波面相位分别为${\varphi _1}$和${\varphi _2}$，则待测光程差$W$对应等效波长Λ的等效相位为$\psi = {\varphi _1} - {\varphi _2}$：

由此可将其转换为单波长${\lambda _1}$对应测得光程差${W_1}：$

式中：INT表示取整函数。当波长组数大于2时，可根据公式(4)类推。根据条纹级次法可以使多波长干涉测量获得与单波长测量相同的测量精度。

为了验证所提出用于在线检测的紧凑型多测量模式瞬态干涉仪的可行性，根据图1搭建了相应的系统样机，并将其用于Moore Nanotech 350FG DTM金刚石车削机床在线检测，如图4所示。所采用的偏振相机象元尺寸为3.45 μm×3.45 μm，像素数为2 448×2 048；光源系统包含了632.8 nm和543 nm的气体激光器以及470 nm LED光源，可分别用于单、多波长宏观面形干涉测量和单波长干涉显微测量。所搭建的系统样机整体尺寸仅为195 mm×160 mm×65 mm，结构的紧凑性使其能很好的满足在线检测的安装要求。利用所搭建的系统样机，分别对加工机床对中工具和自由曲面元件进行了在线检测。

图  4  系统样机照片

Figure 4.  Photo of system device

在车削机床对刀阶段，需要同时测量对中工具表面宏观面形和微观轮廓，作为车削刀具状态的判断和调整依据。利用所搭建的系统样机，对机床的对中工具表面进行了在线检测，同时利用Zygo Verifire系列激光干涉仪和NewView 8300型白光轮廓仪分别对其宏观面形和微观轮廓进行比对测量。被测对中工具表面为一凸球面，对应口径和曲率半径分别为12.7 mm和19.990 mm。

利用本系统（632.8 nm波长激光束）对对中工具进行宏观面形测量时，从偏振相机四个偏振通道提取的四幅π/2移相干涉图如图5(a)所示。图5(b)为利用该系统和Zygo激光干涉仪测得面形结果，其中本系统测得面形PV和RMS值分别为0.141 6 μm和0.022 6 μm，Zygo干涉仪测得面形PV和RMS值分别为0.116 5 μm和0.020 5 μm，二者对应PV和RMS值的差值为0.025 1 μm和0.001 1 μm。

图  5  宏观面形测量结果

Figure 5.  Measurement results of surface

利用本系统（采用470 nm波长LED光源）对对中工具进行微观轮廓测量时，从偏振相机四个偏振通道提出的四幅π/2移相干涉图（对应的视场大小约为0.6 mm×0.6 mm）如图6(a)所示。图6(b)为利用该系统和Zygo白光轮廓仪所测得微观轮廓结果，其中本系统测得面形PV、RMS和Ra值分别为0.209 0 μm、0.005 4 μm和0.003 5 μm，Zygo干涉仪测得面形PV、RMS和Ra值分别为0.173 1 μm、0.005 5 μm和0.004 1 μm，二者对应PV、RMS和Ra值的差值为0.035 9 μm、0.000 1 μm和0.000 6 μm。由于在线检测中被测元件表面个别位置存在车削残余碎屑，使得本系统的检测结果PV值相对较大。

图  6  面形粗糙度测量结果

Figure 6.  Measurement results of surface roughness

由测量结果如图5和图6所示的对中工具宏观面形和微观轮廓在线检测结果可知，利用所搭建的干涉仪在面形形状分布和量值上均实现了较高的检测精度，尤其是系统的结构紧凑性和瞬态波前检测特性，使其可很好的满足在线检测要求。

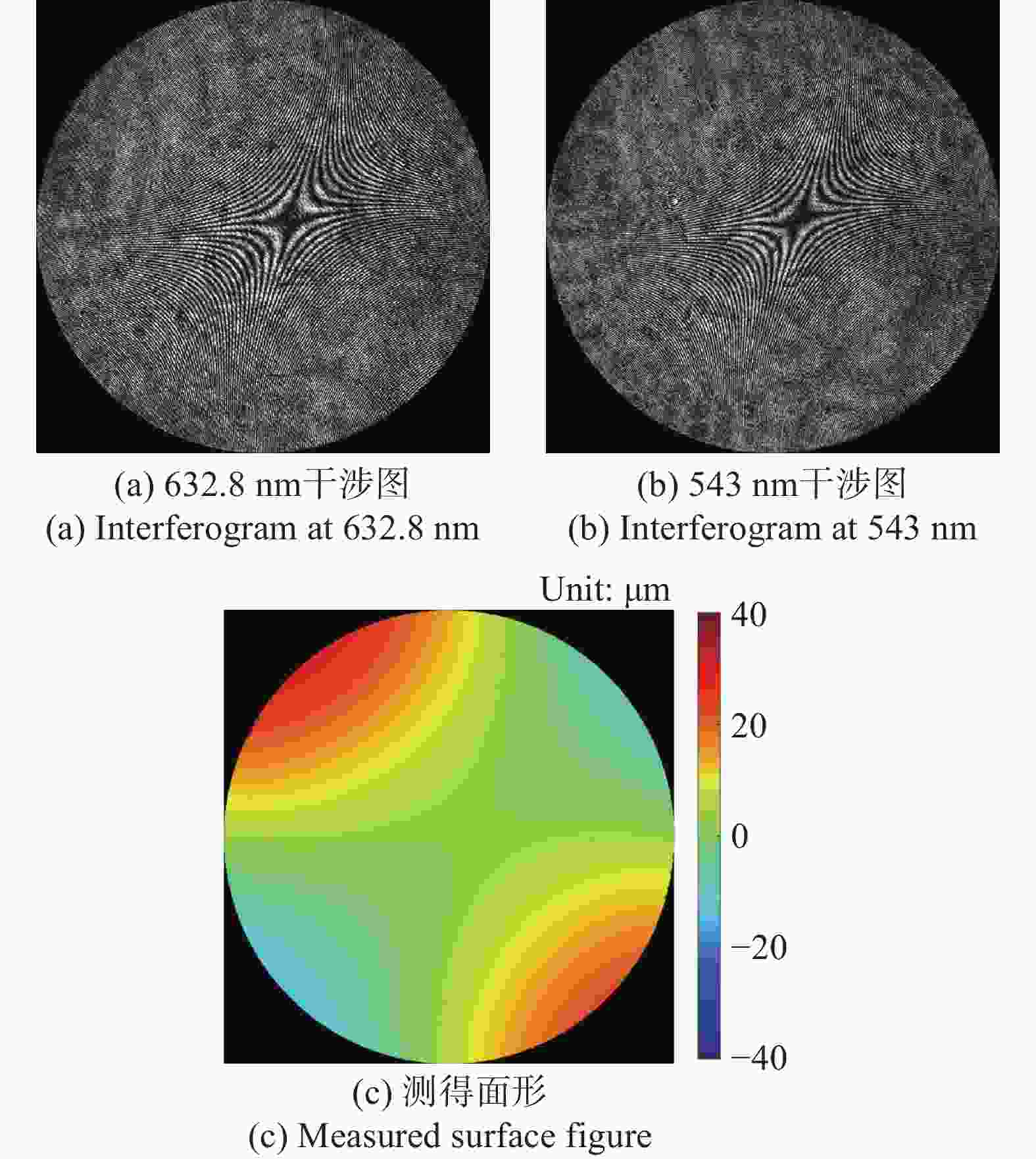
为验证本系统在自由曲面检测中的可行性，基于多波长技术，利用所搭建的系统样机对一个口径为25.4 mm、x方向圆锥系数和曲率半径分别为−2和23.5 mm、y方向圆锥系数和曲率半径分别为−1和26 mm的金刚石车削反射自由曲面进行了在线检测，其测量结果如图7所示。图7(a)和图7(b)分别为632.8 nm和543 nm激光波长所对应采集提取的干涉图，由于条纹过密，无法直接利用单波长干涉解调得到连续波面。在此基础上，利用多波长技术和条纹干涉级次法，可计算得到连续的干涉波前如图7(c)所示，其PV和RMS值分别为45.388 0 μm和7.628 1 μm，因而实现了大动态范围波前的测量。基于所测得波前信息，可在进一步消除光线回程误差基础上，实现自由曲面面形的有效测量。

图  7  多波长干涉面形测量结果

Figure 7.  Measurement results about surface figure with multi-wavelength method

文中针对光学元件在线检测需要，提出了一种紧凑型多测量模式瞬态干涉仪，利用不同工作光源的切换，可在单一系统光路基础上，实现单波长激光干涉和多波长干涉测量以及LED干涉显微测量等多种工作模式。定量分析了系统测量误差因素及其影响，并给出了相应的校正方法。所提出的干涉系统结构紧凑，可满足在线安装和测量应用要求。在对金刚石车削机床对刀阶段的对中工具在线检测中，同时实现了对其宏观面形和微观轮廓的高精度测量，且相对Zygo激光干涉仪和Zygo白光轮廓仪的面形RMS值偏差分别达到了0.001 1 μm和0.000 1 μm。在基于所提出干涉仪多波长技术的由曲自面测量中，实现对PV值达到45 μm的大动态范围波前的有效测量，同时也为自由曲面面形的进一步评价提供了可行的检测手段。由于该系统基于瞬态波前检测，对环境扰动不敏感，在机床对中工具在线调整以及加工元件等在线检测中具有广泛应用。