-
在大型激光系统的运行过程中,由于光学元件的加工误差、外界环境的振动、空气扰动等不可避免的客观因素的存在,对输出的激光光束产生明显的相位调制,形成光束波前的相位畸变[1-3]。相位畸变最直接的影响是降低光束质量,使其聚焦特性受到影响。因此,为了在远场能够获得均匀的焦斑分布,必须在系统中采用束匀滑技术,尽量避免激光焦斑不均匀对物理应用的影响[4-6]。目前,在光路中加入连续位相板(CPP)是实现束匀滑的一种行之有效的技术途径[7]。如何评价CPP的束匀滑性能是指导元件设计、优化应用光路的前提,因此,有必要从CPP的工作机理出发,对其匀滑特性进行系统的分析。
众所周知,CPP元件设计的出发点,是要在激光系统中实现匀滑、散斑和整形等效果。其中的匀滑效果,是指能降低远场光强的中高频分量(散斑除外),使焦斑包络更均匀。为了得到更好的应用效果,束匀滑效应需要给出确切的理论解释。目前,国内外关于CPP的研究主要集中在束匀滑方案选择[8-10]和束匀滑实验[11- 12]方面,而关于其匀滑机理方面的理论分析方面则没有见到系统的分析。文中从统计的角度出发,利用几何光学理论对CPP的匀滑机理和特性分析进行详细讨论。
-
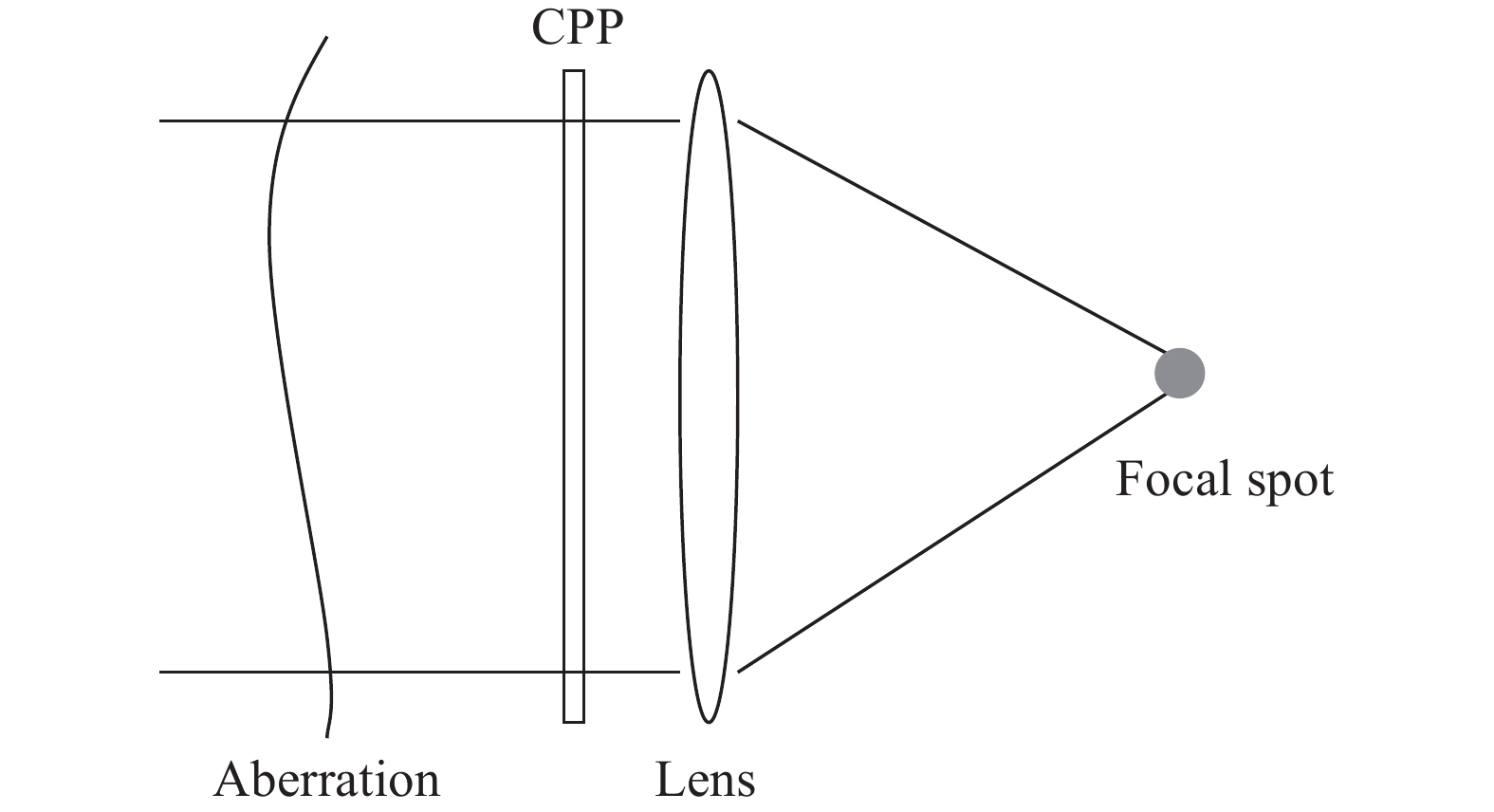
研究CPP的匀滑特性,实际上就是分析畸变波前与CPP面形之间的相位叠加。如图1所示,在光路中,在聚焦透镜前放置CPP,从而实现改善焦斑质量的目的。
在标量衍射理论下,相位叠加后的远场满足傅里叶变换关系。设畸变波前相位为
${\phi _1}$ ,CPP面形相位为${\phi _2}$ ,叠加后的波前位相是$\phi $ ,则有:$$\phi = {\phi _1} + {\phi _2}$$ (1) $${E_\phi } = F\{ \exp [ - j\phi ]\} = {E_{\phi 1}}*{E_{\phi 2}}$$ (2) $${I_\phi } = {\left| {{E_\phi }} \right|^2}$$ (3) 式中:E为远场光振幅;
${I_\phi }$ 为远场光强;F{}为傅里叶变换;*为卷积。从公式上看,复振幅的卷积看上去像是匀滑,实际上,干涉散斑也包含在公式(2)中,而散斑既不均匀也不平滑,所以不能根据卷积运算来解释CPP的匀滑机理。这里笔者利用梯度直方图来对这一现象进行解释,梯度直方图可以认为是几何光学描述下的角谱,CPP面型梯度方向对应角谱方向,直方图则对应角谱的相对强度[13]:
$${I_\phi } = hist(\nabla \phi )$$ (4) 式中:hist( )为直方图计算;
$\nabla $ 为梯度计算,在一维情况下实际上计算的是斜率;${I_\phi }$ 为CPP的角谱,也可以认为是焦斑光强。注意到公式(4)中的焦斑光强${I_\phi }$ 与公式(3)中的不完全一致,实际上描述的是公式(3)的包络,或者说低通滤波结果。这是由于几何光学方法忽略了光学位相,因此,不含干涉效应。 -
根据大数定律可知,在足够多独立实验的情况下,概率密度函数等于实验直方图。由于CPP的孔径尺寸远大于随机面型的自相关长度,在物理上是满足大数定律的。可以将CPP面形函数的概率密度与其远场直方图之间的关系表示为:
$$hist(\xi ) = PDF(\xi )$$ (5) 式中:
$\xi $ 为一个随机函数,表示了CPP的面形。另外两个独立随机变量${\xi _1}$ 与${\xi _2}$ 之和的概率密度等于各自概率密度的卷积,可以写为:$$PDF({\xi _1} + {\xi _2}) = PDF({\xi _1})*PDF({\xi _2})$$ (6) 虽然CPP的面型具有随机分布的特性,但一个已经加工好的元件其表面数据是确定的,因此,可以将任意一个CPP看做随机函数的一个实例。
如果笔者把公式(4)中的
$\phi $ 及$\nabla \phi $ 看作随机变量,可以令$\nabla \phi = \xi $ 。此外,${\phi _1}$ 和${\phi _2}$ 分别代表CPP和其他输入(比如加工误差)面型,注意到${\phi _1}$ 和${\phi _2}$ 是完全独立无关的随机量,满足公式(5)的条件,于是根据公式(1)、(4)~(6)可以推得:$$hist(\nabla \phi ) = hist(\nabla {\phi _1})*hist(\nabla {\phi _2})$$ (7) 公式的物理意义是叠加后的焦斑包络等于叠加前焦斑包络的卷积。注意到卷积就是匀滑,就是低通滤波。这意味着通过CPP的畸变光束,其远场光强将被去掉很多中高频成分。这样,最终得到了CPP匀滑的数学解释。
与公式(2)的形式相比较,公式(7)描述的是光强包络的卷积而非振幅卷积。在大小相当的情况下,具有平顶焦斑的CPP和具有高斯焦斑的CPP比较,后者的匀滑能力要更强,因为前者对应到频谱空间是一个sinc函数的滤波器,有一些残留高频部分,而后者是高斯函数滤波器,基本没有残留的高频部分。
应用统计几何光学方法分析CPP,与常规的标量衍射方法相比,简化了焦斑计算,降低了波前叠加分析的困难,得到了关于CPP匀滑的数学公式。这对匀滑特性的物理图像有一个更清晰的描述和解释。
-
为了直观地给出公式(7)所表述的结论,利用数值运算对CPP的束匀滑特性进行了模拟。
首先计算一维CPP的特性,利用随机函数生成一个短相关长度的一维CPP面型
$\phi $ ,如图2(a)所示,另外,再生成两个长相关长度的随机波前畸变,图3(a)是一个畸变深度较大的波前A,将其标识为${\phi _A}$ ,图4(a)则给出了一个畸变深度较小的波前B,将其标识为${\phi _B}$ 。对应图2(b),图3(b),图4(b),则是利用公式(4)计算的3个面型的远场焦斑分布,也就是光强角谱。其中符号$\nabla \phi $ 是面型梯度,它刚好对应角谱的方向。CPP的焦斑非常接近高斯函数,这是由面型的统计特性决定的。由图可见,畸变波前对应的焦斑其分布非常不稳定的,而且随着畸变深度的增大,焦斑的畸变也越严重,因此需要加入CPP对其进行束匀滑处理。
利用公式(4)可以计算得到畸变波前经过CPP后的焦斑分布。首先将CPP面型与畸变A直接叠加,然后计算其远场,结果如图5(a)所示;另外分别对CPP和畸变波前A的焦斑进行计算,然后再将两个焦斑进行卷积,计算结果如图5(b)所示。

图 5 畸变A通过CPP的焦斑。(a)
$hist(\nabla \phi + \nabla {\phi _A})$ 计算结果;(b)$hist(\nabla \phi )*hist(\nabla {\phi _A})$ 计算结果Figure 5. Focal spot of distortion A passing through CPP. (a) Calculation result of
$hist(\nabla \phi + \nabla {\phi _A})$ ; (b) Calculation result of$hist(\nabla \phi )*hist(\nabla {\phi _A})$ 同样,畸变B经过CPP匀滑后的远场焦斑计算结果如图6所示。从计算结果可看出,两者的确非常相似,包括形状相似,宽度相当。这就验证了公式(7)的正确性。

图 6 畸变B通过CPP的焦斑。(a)
$hist(\nabla \phi + \nabla {\phi _B})$ 计算结果;(b)$hist(\nabla \phi )*hist(\nabla {\phi _B})$ 计算结果Figure 6. Focal spot of distortion B passing through CPP. (a) Calculation result of
$hist(\nabla \phi + \nabla {\phi _B})$ ; (b) Calculation result of$hist(\nabla \phi )*hist(\nabla {\phi _B})$ 由于畸变A的深度比较大,其原始焦斑也紊乱程度也更为严重,焦斑的实际分布范围更大,通过CPP后虽然也实现了焦斑的匀滑,但相比畸变B的匀滑效果,其焦斑中仍保留了较多低频畸变成份。而畸变B的深度较小,原始焦斑的大小与CPP焦斑大小相当,这种情况下,CPP实现了较为明显的匀滑效果,非常接近高斯分布。比较图5与图6可知,随着入射畸变波前的深度增加,同一个CPP的匀滑效果会变差。如果CPP的相关长度越短,其面形的随机性就越突出,这样在位相叠加过程中,对畸变波前的处理能力就会越强[14]。因此,在设计CPP时,可以通过减小空间尺度的方法来扩大入射畸变深度的适用范围。
利用一维CPP对公式(7)进行验证后,用一个实际的二维CPP和畸变波前做一个数值模拟。
图7给出了一个典型的二维CPP的面型,图8则是一个随机二维波前畸变。从图中可以看出,两个位相分布都具有明显的随机特性,但是CPP的相关长度远远小于波前畸变。长相干长度的波前畸变对应的焦斑具有相当混乱的光强分布,因此实际应用中必须对其进行匀滑处理。当畸变波前经过CPP后,在远场获得的焦斑分布如图9所示。

图 9 二维畸变通过CPP的焦斑。(a)
$hist(\nabla {\phi _{CPP}} + \nabla {\phi _{abb}})$ 计算结果;(b)$hist(\nabla {\phi _{CPP}})*hist(\nabla {\phi _{abb}})$ 计算结果Figure 9. Focal spot of 2D distortion passing through CPP. (a) Calculation result of
$hist(\nabla {\phi _{CPP}} + \nabla {\phi _{abb}})$ ; (b) Calculation result of$hist(\nabla {\phi _{CPP}})*hist$ ($\nabla {\phi _{abb}}$ )对比图8中的焦斑分布,畸变波前经过CPP后,焦斑光强分布得到了显著的匀滑。两种计算方法得到的结果从形状、尺寸上是相似的。但图9的计算及结果含有更多细碎成份,也就是高频分量,这一点与前面一维情况是相同,但是二维情况由于显示的原因更突出。这种差别也体现了公式(7)的近似程度,因此,直接使用直方图这种几何统计方法得到的结果还是存在近似性。虽然用直方图统计在CPP匀滑过程分析中是一种近似的方法,但是其理论模型更直接,分析过程明晰,能够对CPP的束匀滑机理、特性进行更加直观和简洁的说明。
-
文中在几何光学基础上,应用统计方法(即直方图)分析了CPP的束匀滑特性。与常规的标量衍射方法相比,简化了焦斑计算,降低了波前叠加分析的困难。使用梯度直方图进行统计,可以直接描述面型或者波前的远场角谱。由于这种方法并不考虑光的相干性,而CPP实际应用又恰好是其去相干作用,因此,该方法在分析CPP的束匀滑机理时是非常适合的,同时又避免了衍射积分过程的复杂推导和计算。
根据物理图像和数学推导,得到了CPP束匀滑分析的统计解析表达式。CPP的面型作用与畸变波前后,两个相位叠加后的远场光强包络等于各自远场光强包络的卷积。而卷积在数学上的意义就是匀滑性,在物理上对应着低通滤波的能力,这就对CPP的匀滑机理进行了解释。数值计算还表明,针对相关长度确定的CPP,如果畸变和它对应的焦斑都非常大,其匀滑性能将会下降。
Influence of phase additive effect on beam smoothing character of continuous phase plate
-
摘要: 在大型激光系统的运行过程中,为了对相位畸变导致的焦斑分布不均匀进行改善,在光路通常会使用连续位相板(CPP) 来进行远场束匀滑。根据CPP 面型的随机特性,利用统计的方法对位相板与畸变波前相位的叠加特性进行了计算,系统研究了连续位相板对光束波前分布实现控制的机理。从CPP面形的概率密度与远场直方图之间的关系出发,推导了畸变波前通过CPP 后远场光强分布的表达式,从理论上解释了这种束匀滑器件的工作原理及特性。通过数值模拟计算了不同畸变光束经过CPP后的远场直方图,对结果进行比较并分析了不同面型特性对最终束匀滑效果的影响。结果证明:位相板能在焦斑光强上起到卷积滤波的作用,从而实现光束匀滑效果。从原理上解释了CPP 在具有小相关长度时具有更高匀滑效果这一特性,为实际面型设计和优化提供理论基础。另外,应用统计几何光学方法进行分析,可有效降低波前叠加分析的难度。Abstract: During the operational process of high power laser system, the uniformity of focal spot will impact the experiment and application seriously. To improve the focal spot quality, a continuous phase plate (CPP) should be used in the light path for far field beam smoothing. As a phase element CPP has different functions, such as decoherece and beam shaping. In this paper the smoothing performance of CPP was concerned. Good performance of beam smoothing depended on a reasonable surface figure distribution. According to the random characteristic of phase plate surface, the statistical method was employed to study the beam smoothing mechanism. According to the relationship between the probability density and far field histogram of the surface of CPP, the expression of the superposition intensity envelope of distorted beam and CPP surface figure was deduced. The formula proved that the function of a CPP for focal spot was just a convolution filtering. So the mathematical explanation on the beam smoothing mechanism was achieved. Furthermore, using this analysis model the reason that the CPP with short correlation length will have the capability of better beam smoothing was explained theoretically. Numerical simulations were done to show the beam smoothing performance of CPP. The far field histograms with different distorted beams are calculated and compared. The results show that after the phase additive of the distorted beam and CPP a new wavefront was generated. If the law of large numbers is satisfied, when the correlation length and the gradient of the wavefront is small, the light focus spot distribution is smooth and uniform. The statistical geometrical optical method used in this paper can reduce the analysis difficulty on the phase additive effectively.
-
Key words:
- continuous phase plate /
- statistics character /
- phase additive /
- beam smoothing
-
图 5 畸变A通过CPP的焦斑。(a)
$hist(\nabla \phi + \nabla {\phi _A})$ 计算结果;(b)$hist(\nabla \phi )*hist(\nabla {\phi _A})$ 计算结果Figure 5. Focal spot of distortion A passing through CPP. (a) Calculation result of
$hist(\nabla \phi + \nabla {\phi _A})$ ; (b) Calculation result of$hist(\nabla \phi )*hist(\nabla {\phi _A})$ 图 6 畸变B通过CPP的焦斑。(a)
$hist(\nabla \phi + \nabla {\phi _B})$ 计算结果;(b)$hist(\nabla \phi )*hist(\nabla {\phi _B})$ 计算结果Figure 6. Focal spot of distortion B passing through CPP. (a) Calculation result of
$hist(\nabla \phi + \nabla {\phi _B})$ ; (b) Calculation result of$hist(\nabla \phi )*hist(\nabla {\phi _B})$ 图 9 二维畸变通过CPP的焦斑。(a)
$hist(\nabla {\phi _{CPP}} + \nabla {\phi _{abb}})$ 计算结果;(b)$hist(\nabla {\phi _{CPP}})*hist(\nabla {\phi _{abb}})$ 计算结果Figure 9. Focal spot of 2D distortion passing through CPP. (a) Calculation result of
$hist(\nabla {\phi _{CPP}} + \nabla {\phi _{abb}})$ ; (b) Calculation result of$hist(\nabla {\phi _{CPP}})*hist$ ($\nabla {\phi _{abb}}$ ) -
[1] 黄金勇, 赵恒, 胡庆, 等. 大口径平面光学元件波前梯度数控抛光[J]. 光学 精密工程, 2019, 27(7): 1473-1480. doi: 10.3788/OPE.20192707.1473 Huang Jinyong , Zhao Heng, Hu Qing, et al. Large aperture optical element wavefront gradient controlled by computer numerical controlled polishing [J]. Optics and Precision Engineering, 2019, 27(7): 1473-1480. (in Chinese) doi: 10.3788/OPE.20192707.1473 [2] 杨勋, 徐抒岩, 马宏财, 等. 径向温度梯度对轻量化反射镜面形精度的影响[J]. 光学 精密工程, 2019, 27(7): 1553-1560. Yang Xun, Xu Shuyan, Ma Hongcai, et al. Influence of radial temperature gradient on surface figure of lightweight reflective mirror [J]. Optics and Precision Engineering, 2019, 27(7): 1553-1560. (in Chinese) [3] 张博文, 王小勇, 赵野, 等. 天基大口径反射镜支撑技术的发展[J]. 红外与激光工程, 2018, 47(11): 1113001. doi: 10.3788/IRLA201847.1113001 Zhang Bowen, Wang Xiaoyong, Zhao Ye, et al. Progress of support technique of space-based large aperture mirror [J]. Infrared and Laser Engineering, 2018, 47(11): 1113001. (in Chinese) doi: 10.3788/IRLA201847.1113001 [4] Kato Y, Mima K, Miyanaga N, et al. Random phasing of high-power lasers for uniform target acceleration and plasma-instability suppression [J]. Phys Revi Letts, 1984, 53(11): 1057-1060. doi: 10.1103/PhysRevLett.53.1057 [5] 王震, 付文静, 张蓉竹. 飞秒激光多脉冲烧蚀金属铁的数值模拟[J]. 红外与激光工程, 2019, 48(7): 0706002. doi: 10.3788/IRLA201948.0706002 Wang Zhen, Fu Wenjing, Zhang Rongzhu. Numerical simulation of femtosecond laser multi-pulse ablation of metal iron [J]. Infrared and Laser Engineering, 2019, 48(7): 0706002. (in Chinese) doi: 10.3788/IRLA201948.0706002 [6] 刘克俭, 苗锡奎, 徐晨阳, 等. 半主动激光制导能量传输与模拟技术[J]. 中国光学, 2019, 12(2): 256-264. doi: 10.3788/co.20191202.0256 Liu Kejian, Miao Xikui, Xu Chenyang, et al. Semi-active laser-guided energy transmission and simulation technology [J]. Chinese Optics, 2019, 12(2): 256-264. (in Chinese) doi: 10.3788/co.20191202.0256 [7] Néauport J, Ribeyre X, Daurios J, et al. Design and optical characterization of a large continuous phase plate for laser integration line and laser Megajoule facilities [J]. Appl Opt, 2003, 32(14): 2377-2382. [8] Yang Chunlin, Yan Hao, Wang Jian, et al. A novel design method for continuous-phase plate [J]. Opt Express, 2013, 21(9): 11171-11180. doi: 10.1364/OE.21.011171 [9] Arieli Y. Continuous phase plate for non-uniform illumination beam shaping using the inverse phase contrast method [J]. Opt Comm, 2000, 180(4): 239-245. [10] Zhang Dazhi, Wan Yongjian, Zhang Rongzhu, et al. Surface statistical characteristics and smoothing analysis of continuous phase plate [J]. Optik, 2012, 123(22): 2062-2067. doi: 10.1016/j.ijleo.2011.09.032 [11] 陈波, 王菡子, 韦辉, 等. 用于惯性约束聚变束匀滑的完全连续相位板设计方法[J]. 光学学报, 2001, 21(4): 480-484. doi: 10.3321/j.issn:0253-2239.2001.04.024 Chen Bo, Wang Hanzi, Wei Hui, et al. , Desigen of fully continuous phase plates for beam smoothing in ICF [J]. Acta Optica Sinica, 2001, 21(4): 480-484. (in Chinese) doi: 10.3321/j.issn:0253-2239.2001.04.024 [12] Marozas John A. Fourier transform–based continuous phase-plate design technique: a high-pass phase-plate design as an application for OMEGA and the National Ignition Facility [J]. J Opt Soc Am A, 2007, 24(1): 74-83. doi: 10.1364/JOSAA.24.000074 [13] Yang Chunlin. Using the gradient histogram to analyze the continuous phase plate [J]. Opt Laser Tech, 2015, 65: 137-141. doi: 10.1016/j.optlastec.2014.07.018 [14] Yang Chunlin. Analysis on the focal spot characteristics of random Gauss phase plate [J]. Optik, 2017, 130: 601-607. doi: 10.1016/j.ijleo.2016.10.084 -







 下载:
下载: