-
南极内陆的冰穹A是世界上视宁度最好的地面天文台址[1]。但在冰穹A建造望远镜面临很多困难:望远镜运输路途遥远,沿途遍布冰裂缝、冰坝等地形,振动剧烈;每年只有两三个星期时间能进行望远镜装调;内陆科考队规模小,人手和设备严重不足。在面临诸多困难前提下,我国在冰宆A成功放置多架小型光学望远镜,在南极望远镜的运输、装调方面积累了初步经验和数据[2-3]。但是对于南极天文台主镜口径2.5 m的大型光学红外望远镜[4],现场装调时间、人手和设备的不足对项目的影响要大得多。南极大型光学望远镜结构复杂,常规装调的工作量很大,但受冰穹A条件限制,望远镜现场装调量不能多,从而要求南极大型光学望远镜尽量以调试好的大型装配体的形式进行整体运输,并在运输时保证装配状态不变,这样才能有效减少现场装调量。所以,研究满足南极大型光学望远镜关键结构整体运输需求的抗振缓冲系统是一件很有意义的事情。
文中以南极天文台的暗宇宙巡天望远镜(Kunlun Dark Universe Survey Telescope, KDUST)口径2.5 m的主镜的运输抗振缓冲系统为研究目标,为南极大型望远镜的关键脆弱结构的运输抗振缓冲系统方案提供参考。
-
隔振器一般采用柔性结构以满足良好的振动隔离要求。理想的振动隔离器要求隔振系统的柔性为无穷大,这样只要冲击的位移小于许用值,隔振系统就能提供无限的振动隔离。但理想隔振器不存储能量,所以它不能隔离冲击。
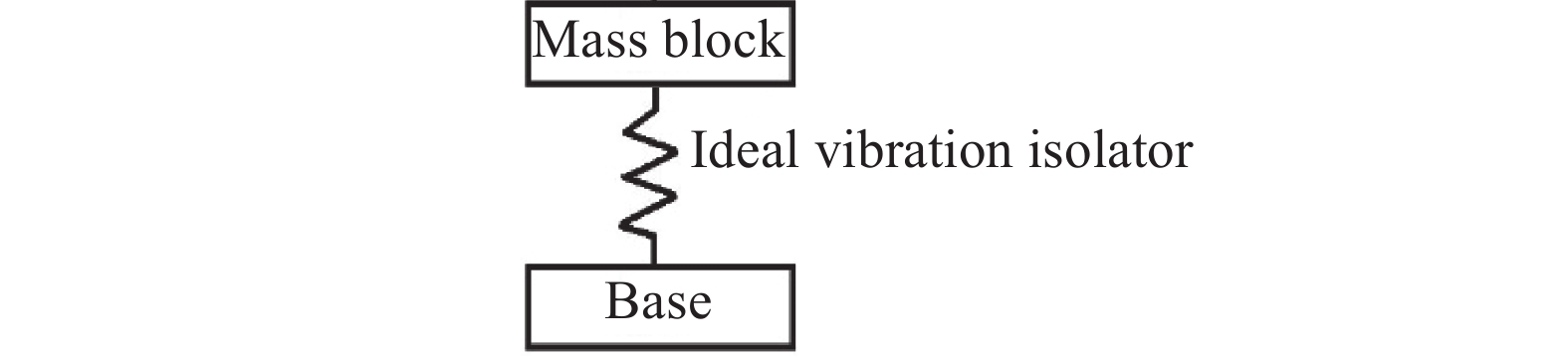
建立理想隔振器理论模型:质量块m与底座M之间用理想隔振器K连接(图1),设质量块在上方,底座在下方,理想隔振器传递给质量块与底座的力的大小都等于质量块重力的大小mg。无论是质量块所引起振动的主动隔离还是底座所引起振动的被动隔离,只要振源位移小于许用值h0,理想隔振器凭借足够大的柔度都能将传递给质量块与底座的力的大小维持于质量块重力的大小。
假设底座受到竖直向上冲击I,冲击结束后底座获得向上运动速度v,具备动能Ek
,由于理想隔振器的刚度为0,底座向上运动时其动能不能转化为隔振器的弹性势能,只能存储为重力势能Ep =Mgh,其最大值Epmax=Mgh0。当冲击后动能Ek大于Epmax时,理想隔振器将失效,底座与质量块发生碰撞。单纯提高隔振器的位移许用值h0对于提高抗冲能力的效率非常低,更重要的是,需要应用隔振器的场合一般都有限制振动位移的需求。 针对理想隔振器的问题,提出了在最短行程内吸收、存储最大能量的理想缓冲器(图2):对于所有大于零的挠度δ,理想缓冲器的出力一直等于被保护体所能承受的最大力Fmax,从运动学角度描述是:在所有大于零的位移处,被保护体的加速度等于所能承受的最大加速度vmax。
理想缓冲器的模型给出了实际缓冲减振系统的关于缓冲距离的下限,反映了缓冲器的储能性能。理想隔振器的模型给出了实际缓冲减振系统的隔振效率上限,反映了缓冲器的隔振性能。南极望远镜的运输隔振缓冲系统应当在性能上逼近理想缓冲器,尽量减少缓冲距离。
-
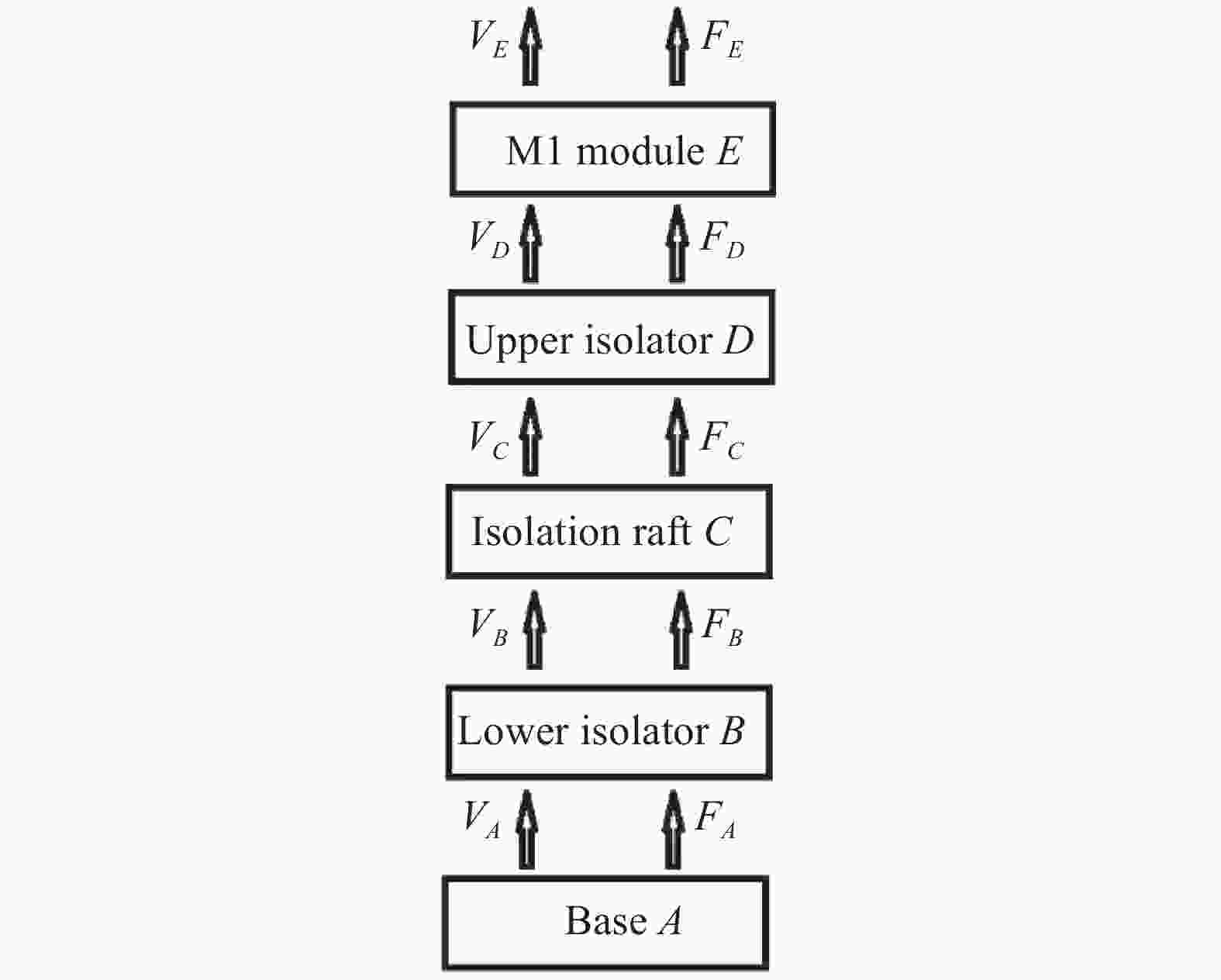
大量工程实践和文献[5-6]表明,单层隔振系统很少能提供大于20 dB的衰减,而在动力机械隔振中常用的双层隔振系统能提供更优良的隔振效果。因此,文中建立了大型望远镜主镜运输的双层抗振缓冲系统理论模型(图3)。
根据功率流四端参数法[7],对下层隔振器有:
$$\left[ {\begin{array}{*{20}{c}} {{F_A}}\\ {{V_A}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ {\dfrac{{i\omega }}{{{K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{F_B}}\\ {{V_B}} \end{array}} \right]$$ (1) 对筏体有:
$$\left[ {\begin{array}{*{20}{c}} {{{{F}}_B}}\\ {{V_B}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{{{i}}{M_C}\omega }\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_C}}\\ {{V_C}} \end{array}} \right]$$ (2) 对上层隔振器有:
$$\left[ {\begin{array}{*{20}{c}} {{{{F}}_C}}\\ {{V_C}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ {\dfrac{{i\omega }}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right)}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{F_D}}\\ {{V_D}} \end{array}} \right]$$ (3) 对主镜室模块有:
$$\left[ {\begin{array}{*{20}{c}} {{F_D}}\\ {{V_D}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{{{i}}{M_E}\omega }\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_E}}\\ {{V_E}} \end{array}} \right]$$ (4) 式中:Fi、Vi(i=A、B、C、D、E)为各子系统力和速度;MC、ME分别为筏体和主镜室模块的质量;KB、CB、KD、CD分别为上层隔振器和下层隔振器的刚度和阻尼。文中的隔振系统属于消极隔振系统。
根据四端参数法原理有:
$$\begin{split} \left[ {\begin{array}{*{20}{c}} {{F_A}}\\ {{V_A}} \end{array}} \right] =\; & \left[ {\begin{array}{*{20}{c}} 1&0\\ {\dfrac{{i\omega }}{{{K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&{{{i}}{M_C}\omega }\\ 0&1 \end{array}} \right]\\ &\left[ {\begin{array}{*{20}{c}} 1&0\\ {\dfrac{{i\omega }}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right)}}}&1 \end{array}} \right] \left[ {\begin{array}{*{20}{c}} 1&{{{i}}{M_E}\omega }\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_E}}\\ {{V_E}} \end{array}} \right] \end{split}$$ (5) 可简写成
$$\left[ {\begin{array}{*{20}{c}} {{F_A}}\\ {{V_A}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\alpha _{11}}}&{{\alpha _{12}}}\\ {{\alpha _{21}}}&{{\alpha _{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{F}}_E}}\\ {{V_E}} \end{array}} \right]$$ (6) 其中
$${\alpha _{11}} = {\rm{}}1 - \frac{{{M_C}{\omega ^2}}}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right)}}$$ (7) $${\alpha _{12}} = {{i}}{M_E}\omega + {{i}}{M_C}\omega - \frac{{i{M_C}{M_E}{\omega ^3}}}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right)}}$$ (8) $$\begin{split} {\alpha _{21}} =\; & \dfrac{{i\omega }}{{{K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)}} + \dfrac{{i\omega }}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right)}} - \\ &\dfrac{{i{M_C}{\omega ^3}}}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right){K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)}}\end{split}$$ (9) $$ \begin{split} {\alpha _{22}} =\; & 1 -\dfrac{{{M_E}{\omega ^2}}}{{{K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)}} - \dfrac{{{M_C}{\omega ^2}}}{{{K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)}} -\\ & \dfrac{{{M_E}{\omega ^2}}}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right)}} + \dfrac{{{M_E}{M_C}{\omega ^4}}}{{{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right){K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)}}\end{split}$$ (10) 隔振效果可用速度传递率表示,对于主镜室模块,有FE=0,定义速度传递率为:
$$T = \frac{{{V_E}}}{{{V_A}}}$$ (11) 由公式(6)有:
$${{T = }}\frac{{{V_E}}}{{{V_A}}} = \frac{1}{{{\alpha _{22}}}}$$ (12) 将公式(10)代入公式(12)得:
$${{T = }}\frac{{{\varPhi _B}{\varPhi _D}}}{{{\varPhi _B}{\varPhi _D} - \left( {{M_E} + {M_C}} \right){\omega ^2}{\varPhi _D} - {M_E}{\omega ^2}{\varPhi _B} + {M_E}{M_C}{\omega ^4}}}$$ (13) 式中:
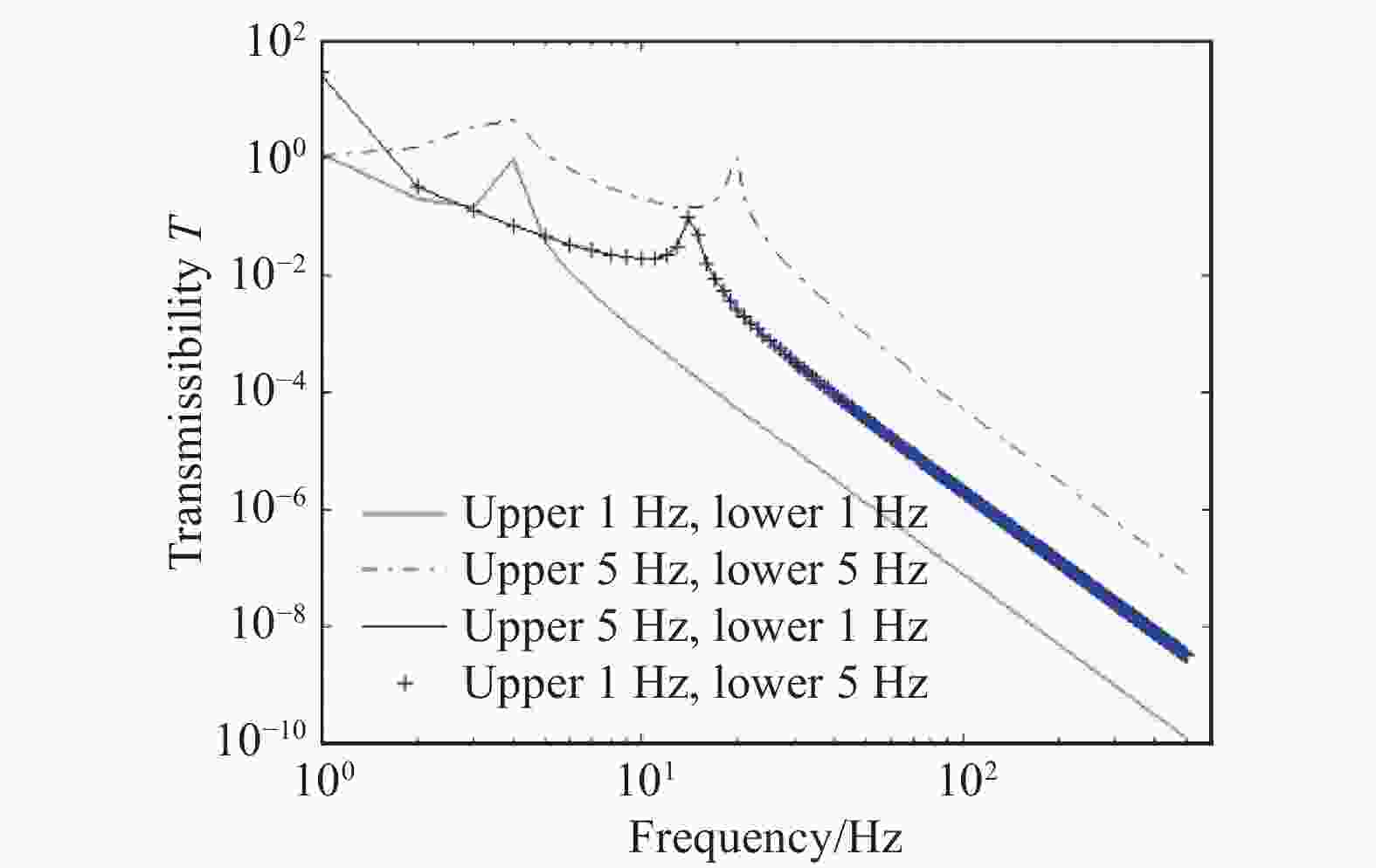
${\varPhi _B} = {K_B}\left( {1 + \dfrac{{i{C_B}\omega }}{{{K_B}}}} \right)$ ,${\varPhi _D} = {\rm{}}{K_D}\left( {1 + \dfrac{{i{C_D}\omega }}{{{K_D}}}} \right)$ ,分别为上层隔振器和下层隔振器的复刚度。研究KDUST主镜抗振缓冲系统初始方案的算例:主镜室模块质量ME=3 500 kg,运输模块总质量M=4 000 kg,频率f=1~500 Hz,上层隔振器刚度KD=1.38×105 N/m(对应固有频率1 Hz)、3.45×106 N/m(对应固有频率5 Hz)阻尼系数CD=1 N·s/m,下层隔振器刚度KB=1.57×105 N/m(对应固有频率1 Hz)、3.95×106 N/m(对应固有频率5 Hz),阻尼系数CB=1 N·s/m。计算传递率曲线如图4所示。图4表明,在满足承载能力的前提下,为了让传递率尽量小,隔振器的刚度需要尽量低。
-
聚乙烯泡沫塑料常用于运输包装领域,最低使用温度可达−50 ℃,可用于南极望远镜的运输包装。聚乙烯泡沫塑料的本构模型具有渐硬型特征,可用公式(14)表示[8-10]:
$$ {\rm{\sigma }} = {\rm{A}} + {\rm{B\varepsilon }} + {\rm{C}}{\varepsilon ^{2.5}} + {\rm{D}}{\varepsilon ^3} $$ (14) 式中:系数A、B、C和D与聚乙烯泡沫塑料的具体牌号有关。采用聚乙烯泡沫塑料制作缓冲结构,一方面利用材料的非线性提高对共振的抑制能力,另一方面利用材料的渐硬特征降低缓冲距离,有利于实现对理想缓冲器的逼近。
-
根据2007年以来,南京天文光学技术研究所在南极科考时实测的运输振动加速度数据,望远镜在公路阶段和雪龙号阶段的加速度幅值相对小,而雪橇阶段的加速度幅值相对前两个阶段大得多[4],所以南极望远镜的隔振缓冲系统以隔离雪橇阶段的振动为主要目标。
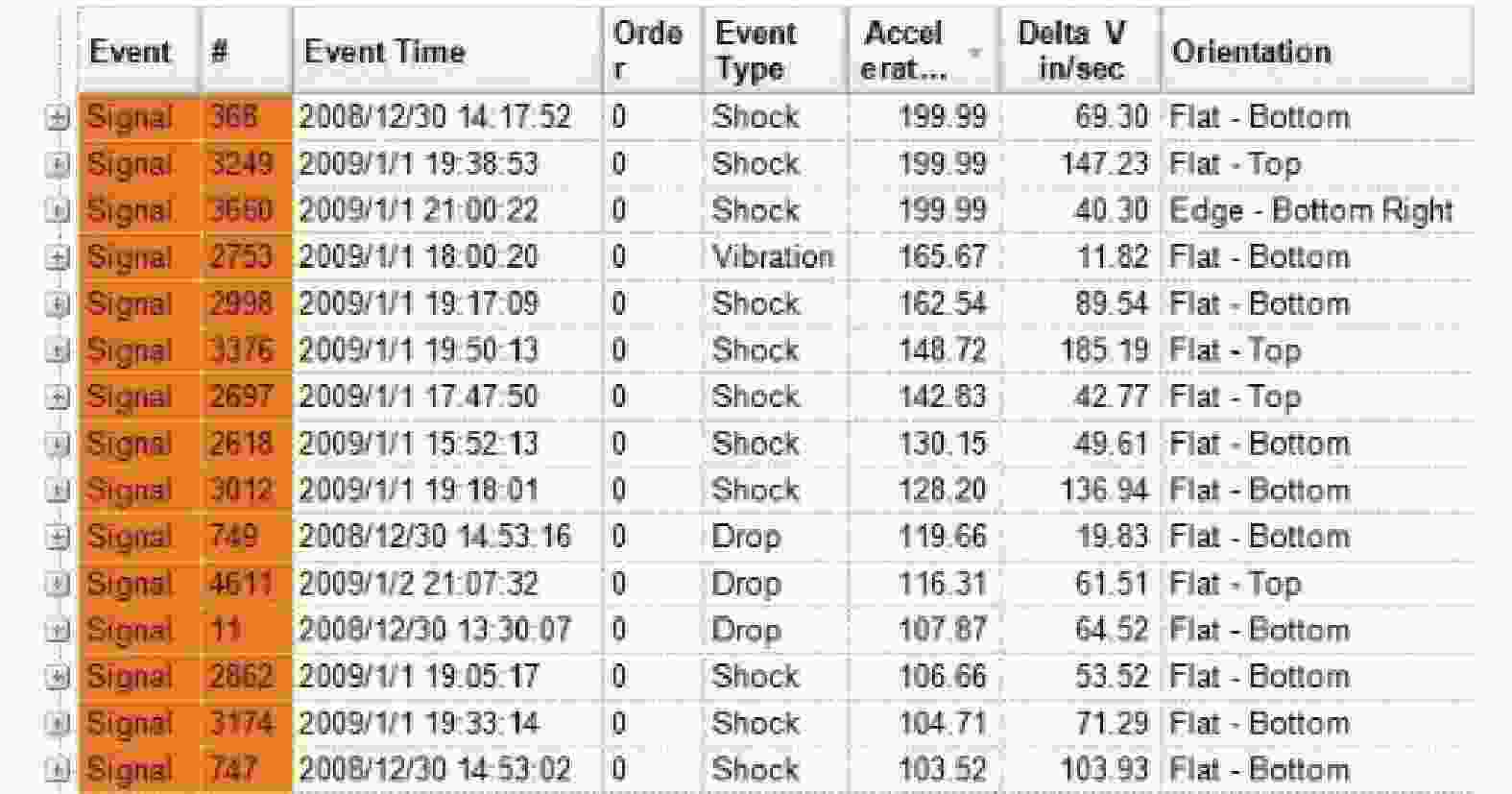
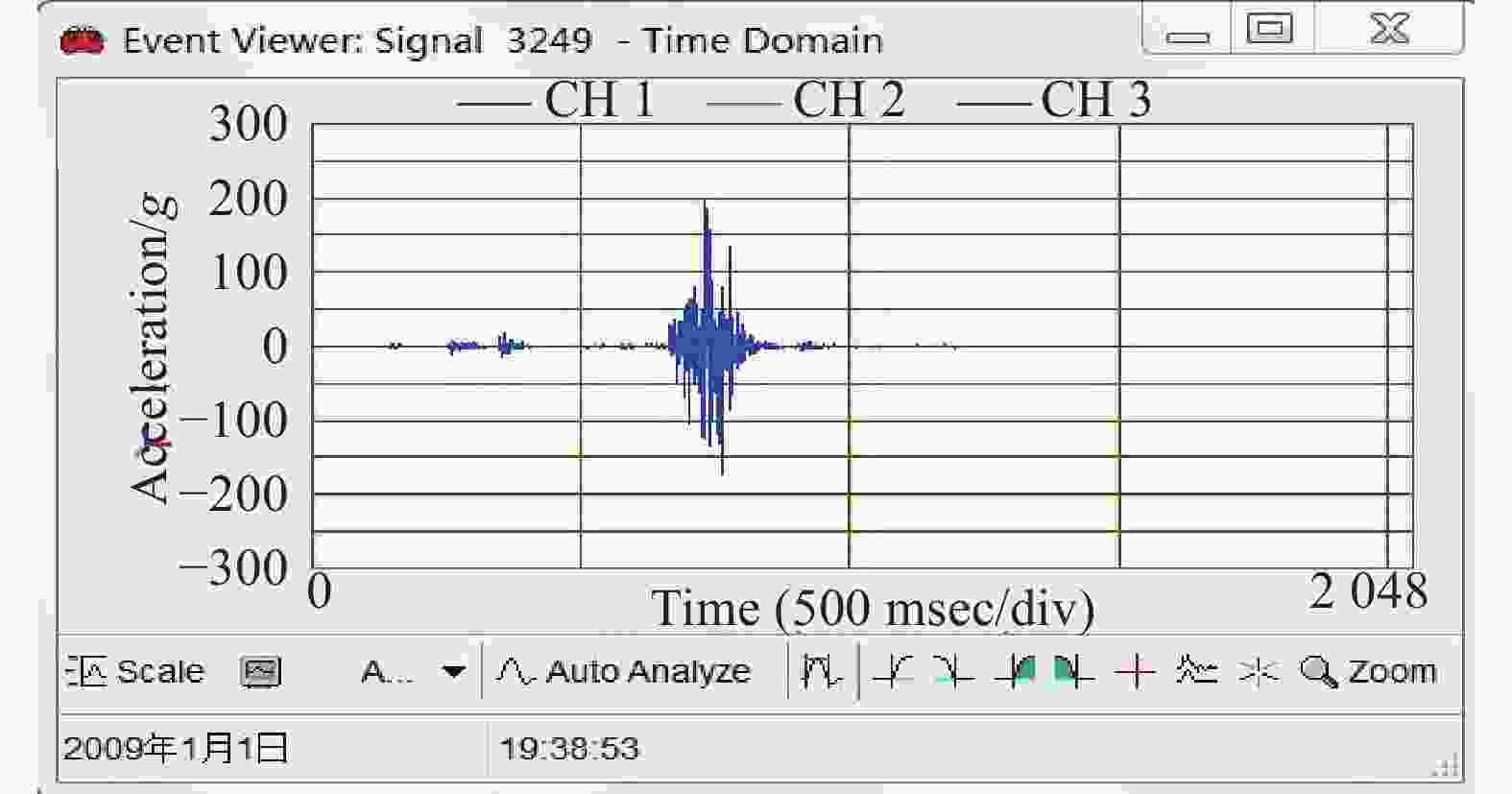
据南极内陆队实测数据,2008年12月30日13:28:40到2009年1月2日22:38:17,行程约300 km,测得加速度峰值大于10 g的冲击和振动信号4 713次,其中50~100 g的78次,100 g以上的15次。图5是安装于集装箱底部附近的美国蓝氏Lansmont振动测试仪记录的加速度峰值大于100 g的振动信号数据。图6~图8是单轴瞬态加速度最大的3个信号。
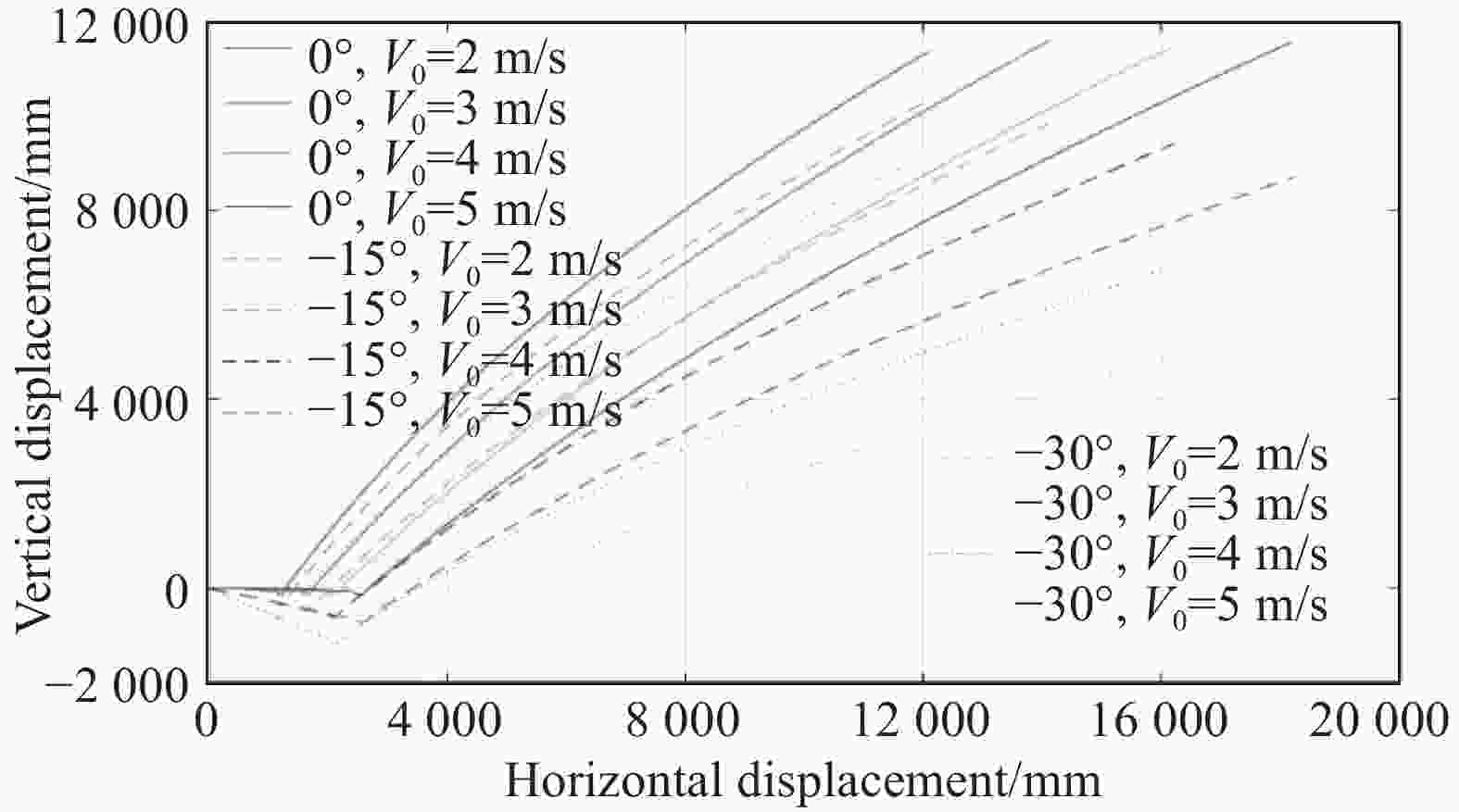
3660#信号是此批数据中冲击严苛程度最大的信号。图9是3660#信号的冲击响应谱,图10是加速度功率谱密度。在零初始条件下,3660#信号在高度方向(Z向)的速度增量7.6 m/s,按能量原理折合成等效跌落高度达2.8 m,对缓冲系统的缓冲性能提出很高要求。对3660#信号的加速度进行二次积分,综合得到此信号发生时的运动轨迹(图11)。
3660#信号的运动轨迹族显示:载有望远镜的雪橇在牵引力的作用下在运动轨迹底部发生剧烈冲击从而产生峰值加速度,随后雪橇在牵引力的继续作用下加速上升,此冲击过程符合科考队员的体验。
-
南极暗宇宙巡天望远镜(KDUST)初始方案的主镜室模块(图12)长3 000 mm,宽3 000 mm,高1 483 mm,重量3 500 kg,其中主镜是主镜室模块中的脆弱部件,重量880 kg,材料是低膨胀系数微晶玻璃,许用应力为15 MPa。
在运输时将主镜镜面的姿态设置为指向天顶,定义力比为此状态下底部60个支承点所受的最大力与平均力之比。在运输振动时,以主镜的应力小于微晶玻璃的许用应力为条件,进行瞬态动力学分析,提取力比与许用加速度的关系如图13所示。

图 13 不同力比时的M1主镜最大许用加速度
Figure 13. Maximum allowable transient acceleration of the M1 mirror with different force ratios
图13显示,力比增加,许用加速度减少。力比越大,对缓冲系统的要求越高。反之,力比越小,主镜底支承的最大力越接近平均力,对主镜底支承装配精度的要求越高。文中以力比为7.5,许用加速度为5 g进行缓冲系统的研究,当实际装配精度更高时,实际许用加速度可以更大,而较小的实际加速度能让运输的安全性更好。
-
文中提出一种包含杠杆式缓冲结构和聚乙烯泡沫塑料结构的双层隔振缓冲系统(图14),建立了虚拟样机模型[11](图15)。

图 14 暗宇宙巡天望远镜(KDUST)M1主镜部套运输的两级缓冲系统
Figure 14. Two-stage vibration isolation system for M1 module transport of KDUST
文中的隔振缓冲系统的外层缓冲结构采用主缓冲器、辅助缓冲器相结合的方式,主缓冲器采用杠杆结构,其中横臂与框架结构之间用旋转副连接,横臂与竖臂之间用球面副连接,竖臂与中间框体之间用球面副连接,这是一种欠约束并联机构,通过欠约束设计降低了系统结构的复杂程度。主缓冲器的储能元件布置于横臂与框架结构之间,通过杠杆原理放大储能元件的运动范围。所提出方案的突出优点是:主缓冲器的弹簧和阻尼器的速度和行程不需要很大,从而能使用小型阻尼器。辅助缓冲器采用线性弹簧。实测严苛冲击都来自竖直方向,主缓冲器主要吸收竖直方向的冲击,辅助缓冲器增加侧向冲击时的稳定性。
以实测最严苛冲击信号3660#为输入条件对缓冲系统进行优化(图16~图18)。

图 16 横臂、竖臂的长度与最大加速度的关系
Figure 16. Relationship between the length of the horizontal arm and the vertical arm and the maximum acceleration
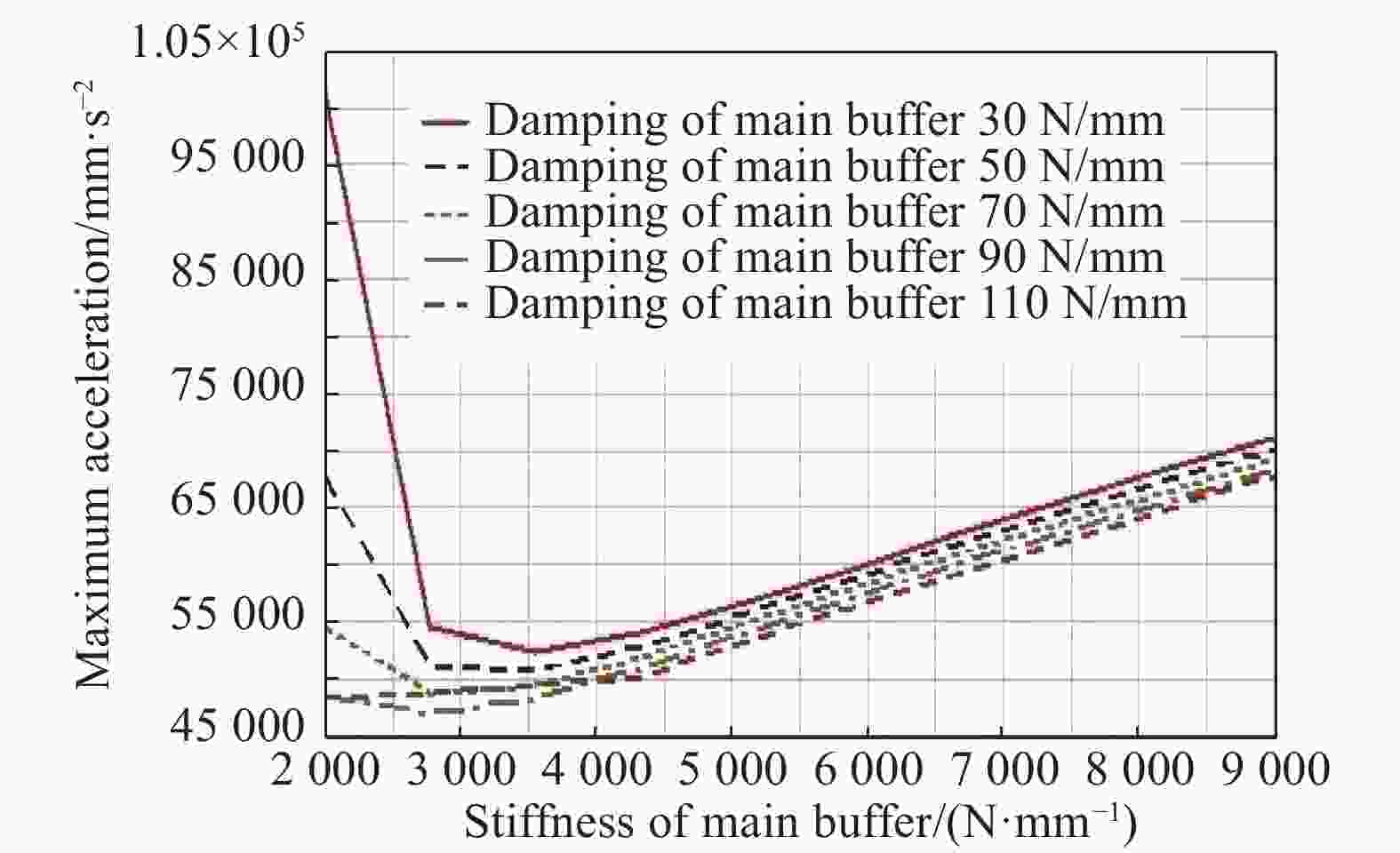
图 17 主缓冲器的刚度、阻尼与最大加速度的关系
Figure 17. Relationship between the stiffness and damping and the maximum acceleration of the main buffer
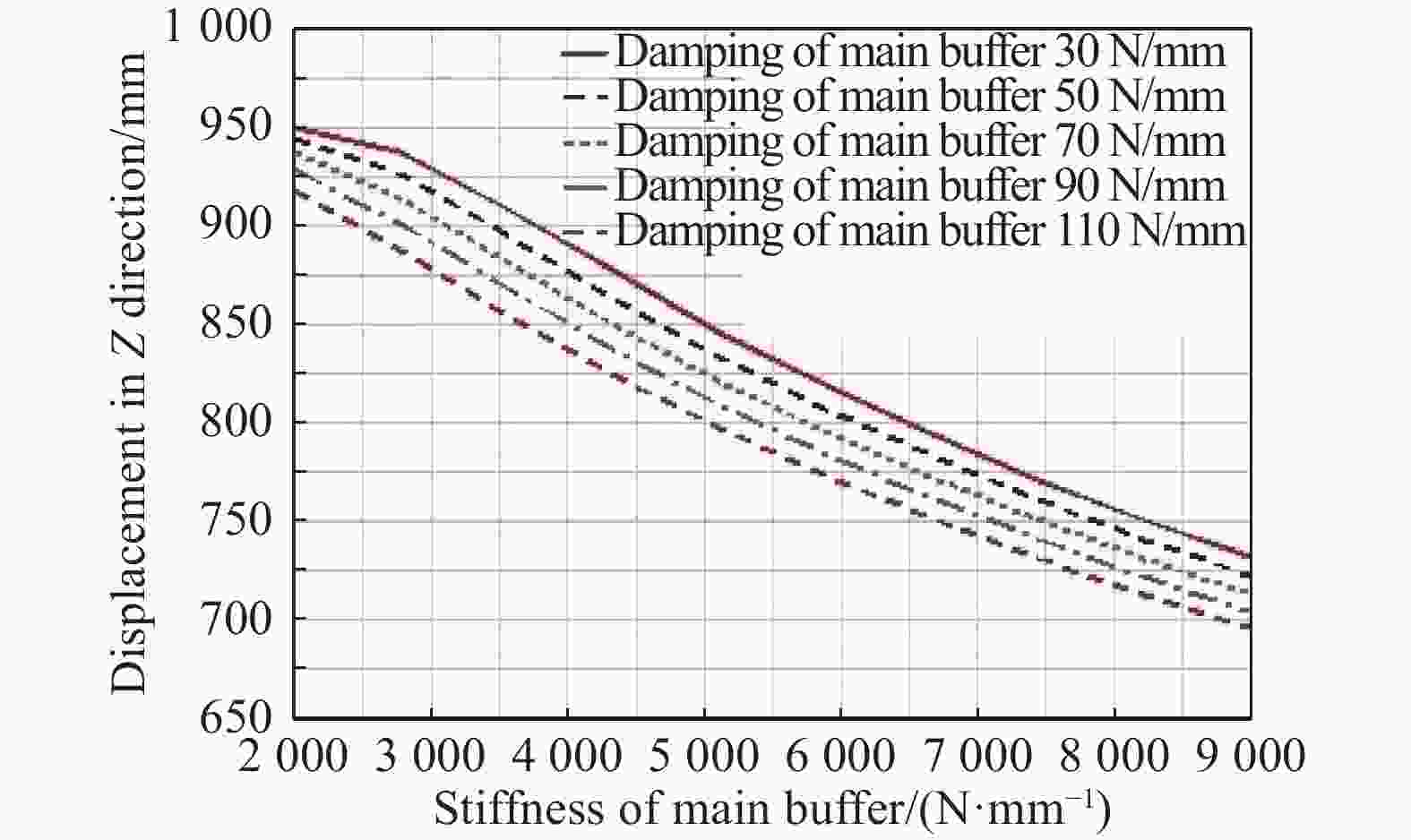
图 18 主缓冲器的刚度、阻尼与Z向最大位移的关系
Figure 18. Relationship between the stiffness and damping of the main buffer and the maximum displacement in Z direction
图16显示,较大的横臂与竖臂长度有利于降低最大加速度。图17显示,主缓冲器的刚度在2 700~4 000 N/mm时,比较容易保证最大加速度小于5 g,而较低的外层主缓冲器阻尼有利于降低最大加速度。图18显示,主镜模块Z向最大位移随外层主缓冲器阻尼与刚度的增加而降低。经综合比较,得到外层缓冲系统的横臂长度为1.19 m,竖臂长度为0.98 m,主缓冲器的刚度为3 000 N/mm,阻尼为100 N·s/mm,横臂的杠杆放大比例为10,外层缓冲系统折合到系统的刚度为1.2×105 N/m,对应固有频率0.93 Hz。
所提到的隔振缓冲系统的内层缓冲结构采用聚乙烯泡沫塑料制作。内层缓冲系统在平衡位置附近的刚度3.45×106 N/m,对应固有频率5 Hz。
根据隔振缓冲系统模型理论,文中隔振缓冲系统对大于2 Hz的振动信号有隔振效果,对大于20 Hz的振动信号的隔振效率大于99%。
根据理想缓冲器模型理论,在3660#信号的作用下,主镜模块峰值加速度小于5 g时需要的Z向位移量0.563 m,实际缓冲系统的Z向位移量不小于此值,当以纯线性弹簧作为缓冲元件时,Z向总位移约4.8 m。
运输振动的强烈程度与路面条件、车速和车辆减震缓冲条件等因素有关。南极大陆边沿的中山站到南极内陆昆仑站的1 300 km路面基本被冰雪覆盖,每年内陆队的雪橇车驶过的车辙与车速都不相同,因此实测数据的重复性不佳。筛选出实测数据中的极端冲击信号作为缓冲系统的动力学边界条件可以提高缓冲系统的可靠性,而且当针对极端冲击信号设计的缓冲系统的成本相对增加不大时,更有以极端冲击信号作为缓冲系统的动力学边界条件的合理性,这也是文中不将极端冲击信号作为传感器误差予以排除的原因。
-
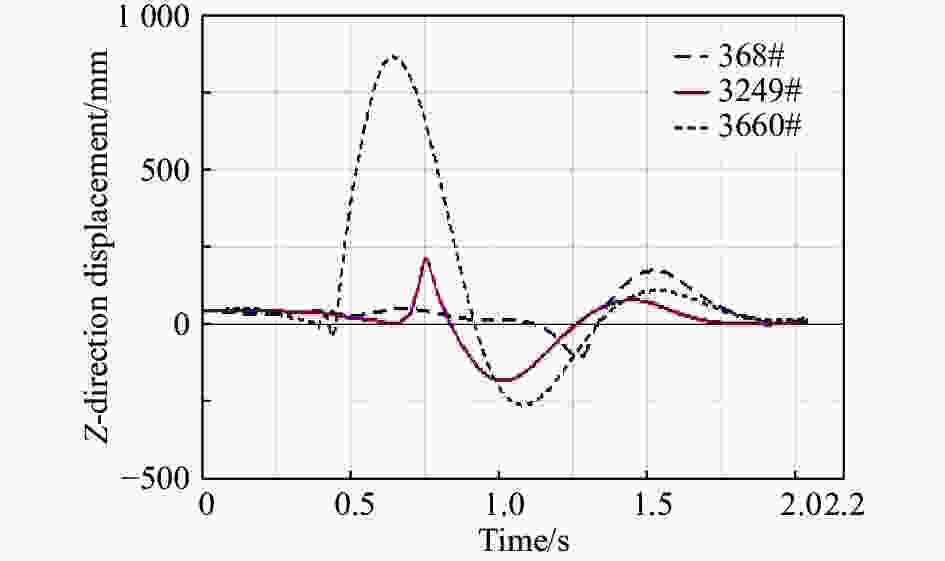
以南极实测峰值加速度达200 g的3个极端信号368#、249#和3660#为输入,在虚拟样机模型中对文中提出的隔振缓冲系统的性能进行分析,提取主镜的瞬态加速度(图19)和Z向位移(图20)。
图19显示,主镜模块最大瞬态加速度约4.8 g,出现于3660#信号作用期间;在3249#信号作用下的最大瞬态加速度约3 g;在368#信号作用下的最大瞬态加速度约1.7 g。说明以实测最严苛冲击信号3660#为条件进行优化,提高了缓冲系统的可靠性。
图20显示,主镜模块在3660#信号作用下Z向最大下沉量0.87 m,Z向回升时超调量0.31 m,即主镜模块的Z向运动总距离约1.2 m,远低于采用纯线性弹簧作为缓冲元件时,Z向总位移4.8 m,说明以理想缓冲器理论指导缓冲系统的设计是合适的。
在3249#信号作用下主镜模块的Z向运动总距离约0.4 m,在368#信号作用下主镜模块的Z向运动总距离约0.28 m。再次说明以实测最严苛冲击信号3660#为条件进行优化,提高了缓冲系统的可靠性。
所提出的缓冲系统的虚拟样机模型的仿真结果与理论模型的预测能相互验证。文中提出的缓冲系统对南极2.5 m望远镜主镜整体运输具有应用价值。
-
(1) 以最严苛的冲击信号3660#作为缓冲系统优化的输入条件,提高了缓冲系统的可靠性。
(2) 提出的缓冲系统可以充分发挥杠杆式结构和聚乙烯泡沫塑料的性能特点,在杠杆结构上能使用相对易获得的小型阻尼器,在整体性能上较好地逼近理想缓冲系统,从而在确保加速度合规的前提下尽量缩短缓冲距离。
(3) 提出的缓冲系统在实测的最极端冲击信号的作用下可以满足主镜模块最大加速度不大于5 g的要求,此时主镜模块的Z向运动范围约1.2 m。该缓冲系统可以在南极2.5 m望远镜主镜的整体运输中使用,为南极大型望远镜的其他关键脆弱结构的运输抗振缓冲系统方案提供参考。
Vibration isolation system for transportation of main mirror of a large Antarctic telescope
-
摘要: 我国南极天文台规划有一台主镜口径2.5 m的光学红外望远镜。这台望远镜在国内制造,以大型装配体的形式运输到南极天文台,从南极边沿的中山站到南极内陆的昆仑站需要用雪橇车运输。雪橇车在一些路段振动剧烈。文中以这台望远镜主镜运输的抗振缓冲系统为研究目标,首先研究了隔振系统理论模型,用四端参数法分析了双层隔振系统的传输特性,然后研究了南极内陆科考队在雪橇运输中测得的振动数据,分析了考虑底支承力不均匀时主镜运输的许用动力学条件,提出了一种包含杠杆式缓冲结构和聚乙烯泡沫塑料结构的双层隔振系统,最后对这种隔振系统的性能进行了有限元分析与多体动力学研究。结果表明:所提出的抗振缓冲系统在南极实测得到的最极端冲击信号的作用下可以满足主镜模块最大加速度不大于5 g的要求,此时主镜模块的 Z 向运动范围约1.2 m,该缓冲系统具有实用价值,可以在南极2.5 m望远镜主镜的整体运输中使用。所提出的方法对其他脆弱结构的缓冲系统设计有参考价值。Abstract: The Antarctic Observatory of China contains an optical/infrared telescope with a diameter of 2.5 m primary mirror. The telescope is made in China and needs to be transported to the Antarctic Observatory in the form of large assembly. From Zhongshan Station in the edge of the Antarctic continent to Kunlun Station in the interior of the continent, the telescope needs to be transported by sled, which vibrates violently in some regions. In this paper, the vibration isolation system of the telescope's 2.5 m primary mirror module for transportation was researched. Firstly, the theoretical model of vibration isolation system was established and the performance of two-stage vibration isolation system was analyzed by the four-terminal parametric method. Secondly, the historical data from the Antarctic inland expedition team in the sled transportation was studied and the allowable dynamic condition of the primary mirror module was calculated by finite element method(FEM) considering the non-uniformity of the bottom supporting force. Thirdly, a two-stage vibration isolation system consisting of a leverage buffer structure and a polyethylene foam structure was proposed. Finally, the performance of this vibration isolation system was researched with FEM simulation and multi-body system simulation. The results show that the vibration isolation system proposed in this paper can meet the requirement of the mirror's transportation. In the finite element model, when the most extreme impact signal is loaded which is acquired by the Antarctic inland expedition team form the sled transportation, the maximum acceleration of the primary mirror module is less than 5 times acceleration of gravity which is a security value coming from the dynamic analysis of primary mirror module, and the Z-direction moving range of the module is about 1.2 m. So the vibration isolation system has practical value. This system can be used in the transport of the primary mirror module of the 2.5 m telescope to the Antarctic inland. The vibration isolation system proposed in this paper is valuable for transportation of other fragile structures.
-
-
[1] 张唯诚. 南极天文学的“中国篇章”[J]. 百科知识, 2013(2): 11-14. Zhang Weicheng. The "Chinese Chapter" of Antarctic astronomy [J]. Encyclopedic Knowledge, 2013(2): 11-14. (in Chinese) [2] Wen Haikun, Gong Xuefei, Zhang Ru, et al. The package cushioning design of the first AST3 and its dynamics analysis[C]//Larry M Stepp, Roberto Gilmozzi, Helen J Hall. Proc of SPIE, Ground-based and Airborne Telescopes IV, 2012, 8444: 84445F. [3] 温海焜, 宫雪非, 杜福嘉, 等. 南极内陆精密仪器运输减振设计与测试[J]. 振动与冲击, 2015, 34(24): 98-103. Wen Haikun, Gong Xuefei, Du Fujia, et al. Vibration attenuation design and test for precise instruments during antarctic inland transport [J]. Journal of Vibration and Shock, 2015, 34(24): 98-103. (in Chinese) [4] 方成. 关于我国未来天文大设备的一点战略思考[J]. 中国科学: 物理学力学天文学, 2012, 12: 1265-1273. Fang Cheng. Some thinking on the development stratagem of future large facilities in Chinese astronomy (in Chinese) [J]. Sci Sin-Phys Mech Astron, 2012, 12: 1265-1273. (in Chinese) [5] 孙玉华, 董大伟, 闫兵, 等. 双层隔振系统隔振效果实验分析[J]. 振动、测试与诊断, 2015, 35(3): 547-552, 596. Sun Yuhua, Dong Dawei, Yan Bing, et al. Experimental isolation effect analysis of two-stage vibration isolation system [J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 547-552, 596. (in Chinese) [6] 王真, 赵志高, 刘芳. 全柔性浮筏隔振系统建模与隔振性能分析[J]. 振动、测试与诊断, 2017, 37(1): 70-75, 200. Wang Zhen, Zhao Zhigao, Liu Fang. Modeling and vibration isolation performance analysis of fully flexible floating raft vibration isolation system [J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(1): 70-75, 200. (in Chinese) [7] Snowdon J C. Mechanical four pole parameters and their application [J]. Journal Sound and Vibration, 1971, 15(3): 307-323. doi: 10.1016/0022-460X(71)90427-5 [8] 卢子兴, 王仁, 黄筑平, 等. 泡沫塑料力学性能研究综述[J]. 力学进展, 1996, 26(3): 306-323. doi: 10.3321/j.issn:1000-0992.1996.03.002 Lu Zixing, Wang Ren, Huang Zhuping, et al. A review of studies on the mechanical properties of foam plastics [J]. Advances in Mechanics, 1996, 26(3): 306-323. (in Chinese) doi: 10.3321/j.issn:1000-0992.1996.03.002 [9] 奚德昌, 高德. 缓冲包装材料的本构建模研究进展[J]. 包装工程, 2011, 32(1): 1-4, 53. Xi Dechang, Gao De. The review on constitutive modeling of cushion packaging materials [J]. Packaging Engineering, 2011, 32(1): 1-4, 53. (in Chinese) [10] Rusch K C. Load-compression behavior of flexible foams [J]. Journal of Applied Polymer Science, 1969(13): 2297-2311. [11] 于殿勇, 钱玉进. 基于ADAMS动力学仿真参数设置的研究[J]. 计算机仿真, 2006, 23(9): 103-107. doi: 10.3969/j.issn.1006-9348.2006.09.028 Yu Dianyong, Qian Yujin. Parameter-settings for the Dynamic simulation Based on ADAMS [J]. Computer Simulation, 2006, 23(9): 103-107. (in Chinese) doi: 10.3969/j.issn.1006-9348.2006.09.028 -






 下载:
下载: