下载:
-
准分子激光器是目前紫外波段输出功率最大的激光器，其短波长和高功率特性使得它广泛应用于工业、医疗和科研等领域[1-3]。特别是稀有气体卤化物准分子激光器，由于其输出激光峰值功率高、脉冲能量大、波长在紫外区的特点，发展迅速并得到了广泛的应用[4-5]，是目前半导体光刻行业最主要的光刻光源[6-7]。其中能量特性是光刻用准分子激光器的三大关键指标（能量、线宽、波长）之一[8]，直接决定了加工的精度，产率和关键尺寸。目前我国国内对准分子激光器能量特性控制的研究还很少。
改善准分子激光器的能量特性的方法有很多，如优化放电腔的结构，改变工作气体成分，抑制腔体内放电时产生的放电冲击波[9]，实时控制放电高压[10-11]等。由于放电气体温度、气体消耗或更新、以及运行时间等因素的影响，准分子激光器总会出现单脉冲能量的波动，平均脉冲能量的漂移和单脉冲能量的超调，为解决这些问题，实时控制激光器的放电高压更加及时和有效。参考文献[12]实现对于准分子激光器剂量精度的控制，而没有考虑到单脉冲能量稳定性。参考文献[13]改善了准分子激光器的单脉冲稳定性，但是该控制方法是在准分子激光器工作在5 Hz的重频下进行的，离准分子激光器的高重频应用[14]还有较大的差距。参考文献[15]针对高重频的准分子激光器设计了基于比例积分的控制算法，该方法通过仿真验证效果较好，但是该方法只针对于准分子激光器工作在连续模式下，没考虑在半导体光刻中的Burst模式（突发模式）。
文中针对准分子激光器的能量特性进行了分析，在分析的基础上建立了激光器出光能量仿真模型。设计了能量稳定性控制算法，基于PID的双闭环控制算法和基于决策算法的能量控制算法，旨在同时控制准分子激光器的能量稳定性和剂量精度。通过将所设计的控制算法在文中建立的激光器出光模型上实验，分析各算法的控制效果，筛选出基于决策的能量控制算法。文中设计的基于决策的能量控制算法通过在一台4 kHz的KrF准分子激光器上进行实验验证，实现在光刻用到的目标能量范围和工作重频范围内，能量稳定性的3σ小于5%，剂量精度小于0.4%，满足160 nm节点以上半导体光刻的要求。
-
对于准分子激光器出光能量进行建模和设计控制算法的首要条件是对于准分子激光器能量特性有充分的认识。
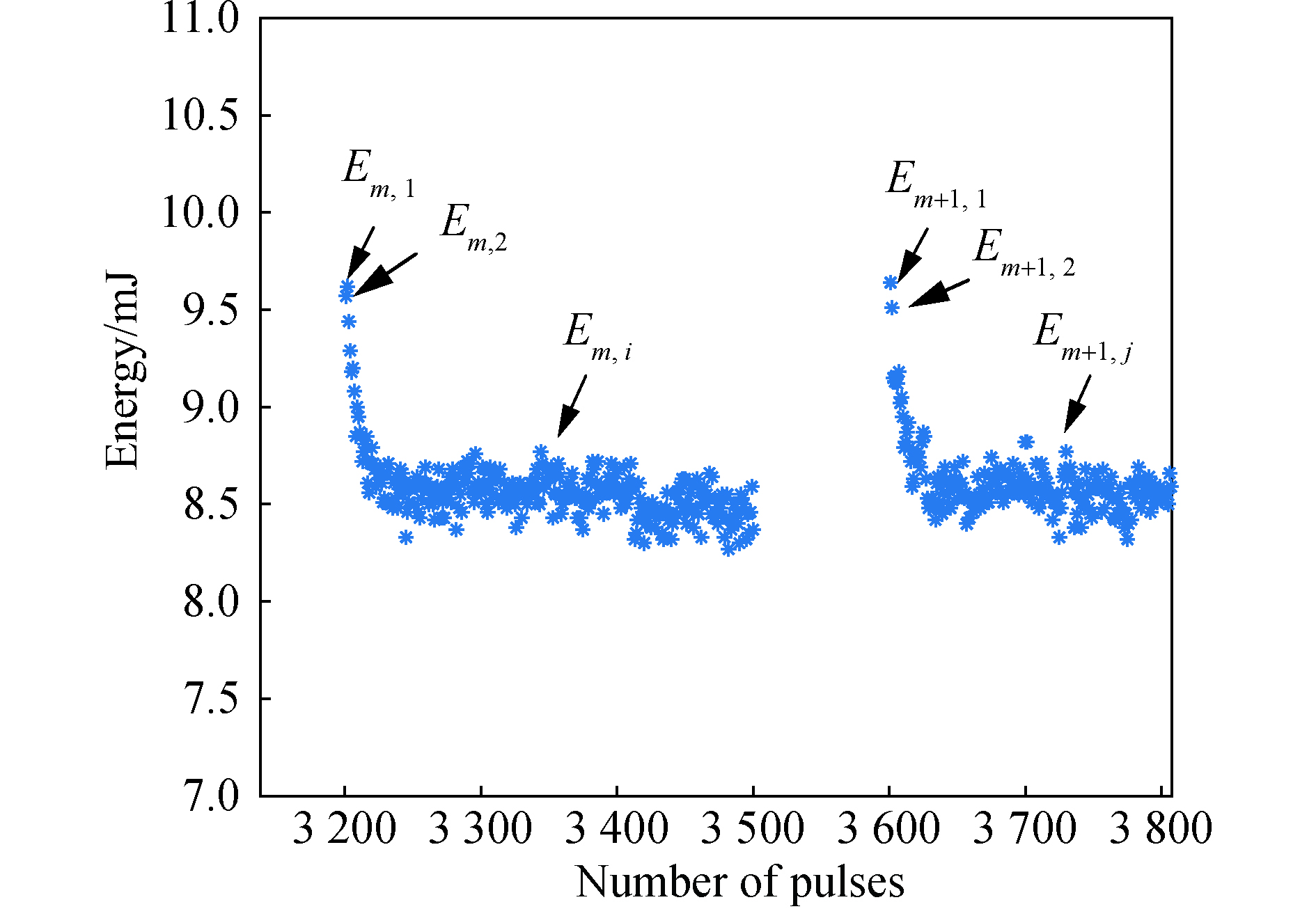
激光器在半导体光刻的应用场景下是工作在Burst模式下的，即激光器输出一个序列的激光脉冲后，有一个停止出光的时间间隔，然后继续输出一个序列的脉冲激光，以此类推。Burst激光器脉冲能量序列如图1所示。从图中可以看到在每一个Burst的前几十个脉冲能量都会比后面的脉冲能量高很多，将其定义为“超调”，并且在Burst中的激光脉冲能量也有波动。
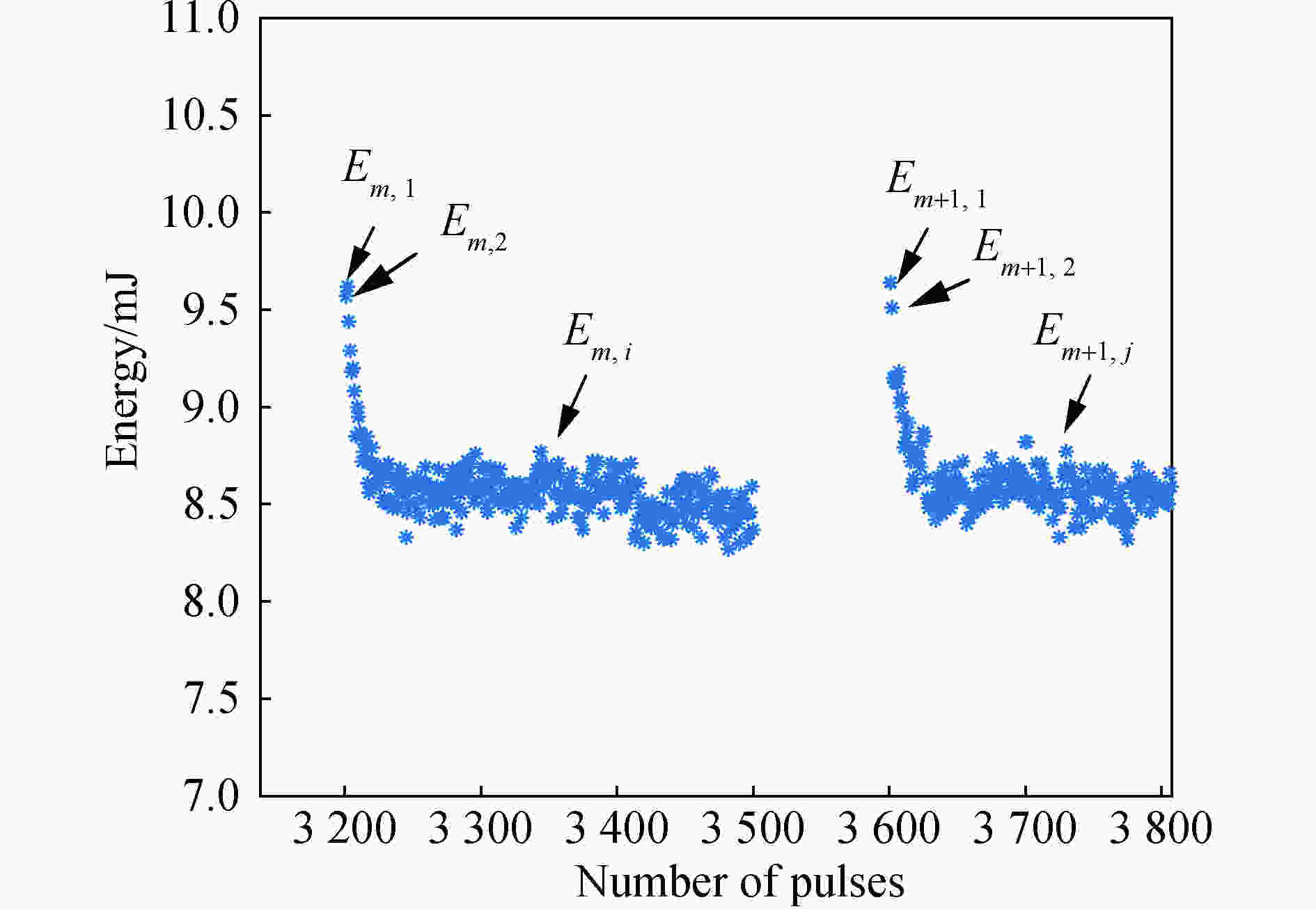
图 1 恒高压工作模式下单脉冲能量变化规律图
Figure 1. Single pulse energy variation law in excimer laser constant voltage operation mode
由于Burst中单脉冲激光的能量与脉冲所处Burst的位置有很大关系，所以在分析激光单脉冲能量特性时，选取不同Burst中的同一位置的单脉冲能量进行了分析。
在准分子激光器的激光能量Burst序列中，单脉冲的能量由于夹杂噪声，在分析Burst中能量变化规律时，采用平均滤波方法，即对于Burst序列中所处位置相同的激光脉冲能量取均值，如公式(1)所示：
$${\bar E_i} = \frac{{\displaystyle\sum\limits_{m = 1}^N {{E_{m,i}}} }}{N}$$ (1) 式中：
${\bar E_i}$ 表示在Burst序列中第i个脉冲的能量均值；${E_{m,i}}$ 表示第m个Burst中的第i个脉冲的能量。针对于准分子激光器在恒高压1500 V时，Burst中脉冲数为300的模式下，在激光器工作重频设定为1 kHz，2 kHz，3 kHz和4 kHz情况下，各采集100个Burst的单脉冲能量，对数据分别进行平均滤波处理，得出的Burst中激光脉冲能量变化规律如图2(a)所示。从图中可以看出，在不同工作重频下，Burst的前几十个脉冲能量会出现超调，不同之处在于超调的大小不同。在不同工作重频下，Burst的前几个脉冲能量几乎相等，Burst中的脉冲能量达到稳态时，重频越高能量越低。
图 2 激光器单脉冲能量特性分析结果图。(a) 恒高压模式下不同重频Burst脉冲能量变化规律；(b) 恒高压模式下不同重频Burst脉冲能量的标准差变化规律；(c) 恒高压工况下Burst序列中相同位置激光脉冲能量的直方图
Figure 2. Analysis results of laser single pulse energy characteristics. (a) Energy variation of pulses in Burst with different repetition frequency under constant high voltage mode; (b) Standard deviation of pulse energy in Burst with different repetition frequency under constant high voltage mode; (c) Histogram of laser pulse energy at the same position in Burst sequence under constant high voltage mode
对于在Burst中同一位置上的激光脉冲能量取标准差，如公式(2)所示：
$$st{d_i} = \sqrt {\frac{{\displaystyle\sum\limits_{j = 1}^N {({E_{m,i}}} - {{\bar E}_i}{)^2}}}{N}} $$ (2) 式中：
$st{d_i}$ 表示在Burst序列中第i个脉冲的标准差；N表示一共有N个Burst脉冲序列。得出的分析结果如图2(b)所示。在图中可以看出工作重频从1 kHz到4 kHz的脉冲能量标准差会随频率的升高而恶化。Burst中前几个脉冲的标准差比激光能量达到稳态时的标准差要小。对于激光器的单脉冲能量，除了与放电高压、气体状态以及在Burst序列中所处的位置有关外，单脉冲能量还有一定的随机性。为分析其随机性的变化规律，针对激光器重频4 kHz的Burst序列中同一位置上的脉冲进行统计分析，其直方图如图2(c)所示。从图2（c）中可以看出，在放电高压和气体状态不变的情况下，Burst序列中相同位置的激光脉冲能量值接近于正态分布。
通过以上分析，可以得出以下关于激光器单脉冲能量特性的结论：
(1)放电高压相同的情况下，不同工作重频的Burst序列中的前几个激光脉冲的能量值接近；
(2)放电高压相同的情况下，不同工作重频的Burst序列中的常态脉冲能量会随重频的增加而降低；
(3)在相同的放电高压的情况下，不同工作重频的Burst序列中相同位置上的激光脉冲能量的标准差随工作重频的增加略有恶化；
(4)在Burst的能量脉冲序列中，处于Burst序列的前几个激光脉冲能量的标准差较小，即稳定性高；
(5)在放电高压和气体状态不变的情况下，在Burst序列中相同位置的激光脉冲能量值成正态分布。
-
根据对激光器单脉冲能量特性的分析，建立了一个从经验上接近于激光器单脉冲能量特性的仿真模型。
根据激光脉冲能量的数理统计特性，假设每个激光脉冲的能量值成正态分布，其表达形式如公式(3)所示：
$${E_{m,i}} \sim N({\bar E_i},st{d_i}^{\rm{2}})$$ (3) 式中：
${E_{m,i}}$ 表示第m个Burst中的第i个脉冲的能量；${\bar E_i}$ 表示在Burst中第i个脉冲的能量均值；$st{d_i}$ 表示在Burst中第i个脉冲的能量标准差。下面需要确定的是${\bar E_i}$ 的模型。根据对于准分子激光器单脉冲能量的分析，可以推断激光器的出光能量和激光脉冲能量间的时间间隔有关系，时间间隔越长，这种能力恢复的越好。基于这种思想，可以建立如图3所示的准分子激光器单脉冲能量模型。该模型以激光器的出光能力为核心，当激光器发出一个脉冲的激光能量时，激光器的出光能力会有相应的下降，出光能力会随放电脉冲的间隔时间而有所恢复，在计算下一个脉冲的出光能量前，根据脉冲间隔时间更新出光能力值，然后根据放电高压和当前的出光能力，计算出所发出激光脉冲的能量。
图 3 准分子激光器单脉冲能量仿真模型示意图
Figure 3. Schematic of single pulse energy simulation model of excimer laser
通过放电高压计算能量需要一个基准的放电高压和能量的关系。在相同条件下，激光器的放电高压越大能量越高，但会出现饱和的现象，所以建立一个基准激光脉冲能量和放电高压的关系如公式(4)所示：
$$\left\{ \begin{gathered} {{{E}}_{{b}}}{{(n + 1) = }}{{{E}}_{{b}}}{{(n) + }}\Delta {{{E}}_{{b}}}{{(n + 1)}} \hfill \\ \Delta {{{E}}_{{b}}}{{(n + 1)}} = {{ k(HV)\cdot}}\Delta {{HV(n + 1)}} \hfill \cdots \cdots\\ {{k(HV) = }}\frac{{{{R\cdot(H}}{{{V}}_{{{\rm{h}}}}}{{ - HV)}}}}{{{{H}}{{{V}}_{{{\rm{h}}}}}{{ - H}}{{{V}}_{{{\rm{l}}}}}}} \hfill \\ \end{gathered} \right.$$ (4) 式中：
$H{V_{\rm{h}}}$ 为放电高压的上限；$H{V_{\rm{l}}}$ 为放电高压的下限；$HV$ 为放电高压；$R$ 为比例常数；$k(HV)$ 为当放电高压为HV时的$\Delta {E_{\rm{b}}}/\Delta HV$ ；${E_{\rm{b}}}(n + 1)$ 为放电高压$HV(n + 1)$ 对应的基准能量。将一个激光器出光能量模型的出光的初始能力定义为在对应设定放电高压的基准能量，如公式(5)所示：
$$Abilit{y_{{\rm{init}}}} = {\rm{1}}$$ (5) 式中：
$Abilit{y_{{\rm{init}}}}$ 表示激光器出光能力的初始值。出光能力一定的条件下，激光器的出光能量的期望表示为公式(6)：
$$\bar E = Abilit{y_{{\rm{New}}}}{E_{\rm{b}}}(HV)$$ (6) 式中：
$\bar E$ 表示激光器可出能量的期望；$Abilit{y_{{\rm{New}}}}$ 表示为激光器最新的出光能力。当激光器每发出一个脉冲的激光后，其出光能力需要更新，更新方程定义为公式(7)：
$$\begin{array}{*{20}{c}} {Abilit{y_{{\rm{old}}}} = \alpha \cdot Ablit{y_{{\rm{New}}}}}&{0 < \alpha < 1} \end{array}$$ (7) 式中：
$Abilit{y_{{\rm{old}}}}$ 表示激光器出光后的出光能力。激光器进行下一个激光脉冲出光时，由于脉冲间的时间间隔，激光器的出光能力得到更新，其表示为一个与脉冲间的时间间隔相关的函数，如公式(8)所示：
$$Abilit{y_{{\rm{new}}}} = \left\{ {\begin{array}{*{20}{c}} {Abilit{y_{{\rm{old}}}} + a + \dfrac{b}{T}}&{Abilit{y_{{\rm{new}}}} < Abilit{y_{{\rm{init}}}}} \\ {Abilit{y_{{\rm{init}}}}}&{Abilit{y_{{\rm{new}}}} \geqslant Abilit{y_{{\rm{init}}}}} \end{array}} \right.$$ (8) 式中：
$T$ 为出光脉冲时间间隔；a，b分别为合适的参数。利用该模型产生恒高压条件下4 kHz重频的工况下的一个Burst的单脉冲能量。分别从时域和频域上与实际测得的相同工况下的一个Burst的单脉冲能量进行对比，其结果如图4所示。从图4中可以看出，模型产生的模拟Burst脉冲能量的频域特性和实际测量的Burst脉冲能量的频域特性相似度很大。
图 4 实测和模型产生一个Burst的脉冲能量变化对比图。(a) 时域；(b) 频域
Figure 4. Comparison of actual and simulated Burst pulse energy changes. (a) Time domain; (b) Frequency domain
-
准分子激光器单脉冲能量的变化与激光器的放电高压和工作气体状态有直接关系，通过调节放电高压能够瞬间控制单脉冲能量，即实现能量的单脉冲可控，所以能量稳定性和剂量精度控制通过调节放电高压来实现。
激光器单脉冲能量的变化量和放电高压的调节量之间在短时间内为线性关系，其关系如公式(9)所示：
$$\Delta E = k\Delta V$$ (9) 式中：
$\Delta E$ 为激光单脉冲能量变化量；$\Delta V$ 为产生该脉冲能量的放电高压调节量；$k$ 为激光单脉冲能量变化量和放电高压调节量之间的比例系数，该系数会随激光器工作气体的老化而衰减。当激光器工作在Burst模式下，这个系数也会随激光脉冲在一个Burst中的不同位置而有差异。 -
能量稳定性
$\sigma $ 的定义如公式(10)所示：$$\sigma {\rm{ = }}\frac{{\sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^N {{{({E_{{\rm{average}}}} - {E_i})}^2}} }}{{N - 1}}} }}{{{E_{{\rm{average}}}}}} \times 100\% $$ (10) 式中：
$N$ 表示一系列激光的脉冲数量；${E_i}$ 表示某一个激光脉冲的能量值；${E_{{\rm{average}}}}$ 表示$N$ 个激光脉冲能量的平均值。通常单脉冲能量稳定性采用3$\sigma $ 来衡量。激光器
${N_{{\rm{slit}}}}$ 个脉冲的剂量定义如公式(11)所示：$$Dos{e_j} = \sum\limits_{i = j}^{{N_{{\rm{slit}}}} + j - 1} {{E_i}} $$ (11) 这个公式表示的是从第
$j$ 个脉冲到第$({N_{{\rm{slit}}}} +$ $ j - 1)$ 个脉冲的${N_{{\rm{slit}}}}$ 个脉冲的能量和。激光器脉冲剂量精度
${H_j}$ 的定义如公式(12)所示：$${H_j} = \frac{{Dos{e_j} - Dos{e_t}}}{{Dos{e_t}}} \times {\rm{100\% }}$$ (12) 式中：
$Dos{e_t}$ 为${N_{{\rm{slit}}}}$ 个脉冲的目标剂量值。衡量剂量精度的方法为：计算Burst序列中每个脉冲（脉冲所在位置序列号大于等于${N_{{\rm{slit}}}}$ ）发出后的剂量精度，每个Burst的剂量精度用每个Burst中的剂量精度的最大值和最小值来衡量。当计算能量稳定性用到的
$N$ 和计算剂量稳定性用到的${N_{{\rm{slit}}}}$ 相等时，激光器单脉冲能量稳定性和剂量稳定性的关系经过推导可表示为公式(13)所示形式：$$H_j^2 = \frac{1}{{{N_{{\rm{slit}}}}}}{\sigma ^2} + \frac{{{{({N_{{\rm{slit}}}} - 1)}^2}}}{{N_{{\rm{slit}}}^2}}Cov({\varepsilon _l}{\varepsilon _k})$$ (13) 式中：
$\varepsilon $ 表示实际出光能量和目标出光能量的误差；$Cov({\varepsilon _l}{\varepsilon _k})$ 表示激光器各个脉冲出光能量和目标能量之间误差的协方差。通过该表达式可知，剂量稳定性的大小取决于能量稳定性的大小和$Cov({\varepsilon _l}{\varepsilon _k})$ 的大小。 -
通过分析能量稳定性和剂量精度的关系得知，控制的首要任务是控制能量稳定性。从图1中可以发现，Burst中的前几十个脉冲的能量相比于后面脉冲的能量高很多。说明Burst的前几十个脉冲对于放电高压的响应和Burst中后面的激光脉冲能量对于相同放电高压的响应有显著的不同，所以不能采用同一个控制算法。针对这个特点，文中设计了针对超调部分的脉冲能量的控制算法和针对于非超调部分脉冲能量的控制算法。通过观察，人为设定Burst中第g个脉冲前的部分为超调部分，第g个脉冲后的部分为非超调部分。
针对超调部分，控制率的作用周期是跨Burst的，以不同Burst间同一位置上的脉冲形成PI （比例积分）控制算法。例如，第m个Burst的第1个脉冲
${E_{m,1}}$ 与第m+1个Burst的第1个脉冲${E_{m + 1,1}}$ 形成控制序列。针对于超调部分的PI能量控制算法的表示如公式(14)所示：$$ H{V_E}_{m + 1,i} = {K_{Eo}}\left(\Delta {E_{m,i}} + \dfrac{{\displaystyle\sum\limits_{k = 1}^m {\Delta {E_{m,i}}} }}{{{I_{Eo}}}}\right)\;\;\;(i < g) $$ (14) 式中：
$H{V_E}_{m + 1,i}$ 表示通过反馈控制算法得出的产生第m+1个Burst中第i个激光脉冲所需要设定的放电高压值；${E_{m,i}}$ 表示第m个Burst的第i个激光脉冲的能量值；${K_{Eo}}$ 表示针对于能量超调部分的反馈控制算法的比例参数；${I_{Eo}}$ 表示针对于能量超调部分的反馈控制算法的积分参数；$\Delta {E_{m,i}}$ 表示${E_{m,i}}$ 和设定能量${E_t}$ 之间的误差，如公式(15)所示：$$ \Delta {E_{m,i}} = {E_{\rm{t}}} - {E_{m,i}}\;\;\;\;(i < g) $$ (15) 每个Burst中第g个激光脉冲为过渡脉冲，所需要设定的高压值，直接取产生这个Burst的第
$(g - 1)$ 个激光脉冲时所设定的放电高压值，其表达式如公式(16)所示：$$H{V_E}_{m,g} = H{V_E}_{m,g - 1}$$ (16) 针对于非超调部分，由于脉冲能量对于放电高压的响应基本一致，为消除激光脉冲间能量的波动，将同一Burst中相邻的激光脉冲能量形成控制序列。所设计的PI能量控制算法的表示如公式(17)所示：
$$ H{V_E}_{m,i} = {K_{Eu}}\left(\Delta {E_{m,i - 1}} + \frac{{\displaystyle\sum\limits_{k = g + 1}^i {\Delta {E_{m,k - 1}}} }}{{{I_{Eu}}}}\right)\;\;\;\;(i > g) $$ (17) 式中：
$H{V_E}_{m,i}$ 表示为产生第m个Burst中第i个激光脉冲能量所应该设定的放电高压值；${E_{m,i{\rm{ - 1}}}}$ 表示第m个Burst中第i−1个激光脉冲的能量值；${K_{Eu}}$ 表示针对于非超调部分所设计的反馈控制算法的比例参数；${I_{Eu}}$ 表示针对于非超调部分所设计的反馈控制算法的积分参数；$\Delta {E_{m,i - 1}}$ 表示第m个Burst中第i−1个激光脉冲能量的实际能量值和设定能量${E_{\rm{t}}}$ 之间的误差，其表达式如公式(18)所示：$$ \Delta {E_{m,i - 1}} = {E_{\rm{t}}} - {E_{m,i - 1}}\;\;\;\;(i > g) $$ (18) -
激光器单脉冲能量特性的好坏由单脉冲能量稳定性和剂量精度同时去衡量。其中剂量精度更加苛刻，也更加重要。容易想到的剂量精度控制算法原理框图如图5所示，图中展示的控制器为双闭环结构，内部闭环为单脉冲能量稳定性控制器，具体算法见3.3节；外部的闭环以剂量精度为控制目标，通过PI反馈控制算法，得出所需要的单脉冲能量的设定值
${E_t}$ 。图5中剂量精度控制器的控制算法采用的PI控制算法，其算法公式如公式(19)所示：
$${E_{\rm{t}}}(n + 1) = {K_D}\left(\Delta Dose(n) + \dfrac{{\displaystyle\sum\limits_{i = 1}^n {\Delta Dose(i)} }}{{{I_D}}}\right)$$ (19) 式中：
${E_{\rm{t}}}(n + 1)$ 为下一个脉冲需要设置的能量值；${K_D}$ 为PI算法的比例系数；$\Delta Dose(n)$ 为该次测量剂量稳定性的偏差；${I_D}$ 为PI算法的积分系数；$\displaystyle\sum\limits_{i = 1}^n {\Delta Dose(i)} $ 表示剂量历史偏差的累加。针对每个Burst，在每个Burst开始后重新开始计算，累计偏差清零。
图 5 双闭环剂量精度控制算法结构框图
Figure 5. Block diagram of double closed-loop dose precision control algorithm
针对于每个Burst的第一个脉冲，其能量设定值如公式(20)所示：
$${E_{\rm{t}}}(1) = \frac{{Dos{e_{\rm{t}}}}}{N}$$ (20) 图5中剂量计算器的算法如公式(21)所示：
$$Dose(n) = \left\{ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{k = 1}^n {{E_{m,k}}} + ({N_{{\rm{slit}}}} - n){E_{\rm{t}}}}&{n < {N_{{\rm{slit}}}}} \\ {\displaystyle\sum\limits_{k = n - {N_{{\rm{slit}}}} + 1}^n {{E_{m,k}}} }&{n \geqslant {N_{{\rm{slit}}}}} \end{array}} \right.$$ (21) 式中：
$Dose(n)$ 表示根据第m个Burst中第i个激光脉冲能量和其前面的$({N_{{\rm{slit}}}} - 1)$ 个激光脉冲能量计算出的剂量值。这个计算公式由两个部分组成，当$i < {N_{{\rm{slit}}}}$ 时，实际所积累的激光脉冲数不足${N_{{\rm{slit}}}}$ 个，不足以计算剂量值。为了有效利用这部分数据，形成剂量反馈控制，利用被控目标能量${E_{\rm{t}}}$ 将剩余激光脉冲补齐，从而计算出一个剂量值；当$i \geqslant {N_{{\rm{slit}}}}$ 时，利用最近的${N_{\rm{slit}}}$ 个激光脉冲能量计算剂量值。 -
基于决策控制的剂量精度控制算法的结构框图如图6所示。因为控制目标为能量稳定性和剂量精度两个指标，而可以控制的量只有放电高压，所以需要分别针对能量稳定性和剂量精度设计控制算法，从而分别得出放电高压的调节量，再用一个决策控制算法来平衡两个电压调节量，得出最终的放电高压设定量，达到能量稳定性和剂量精度同时满足指标的目的。
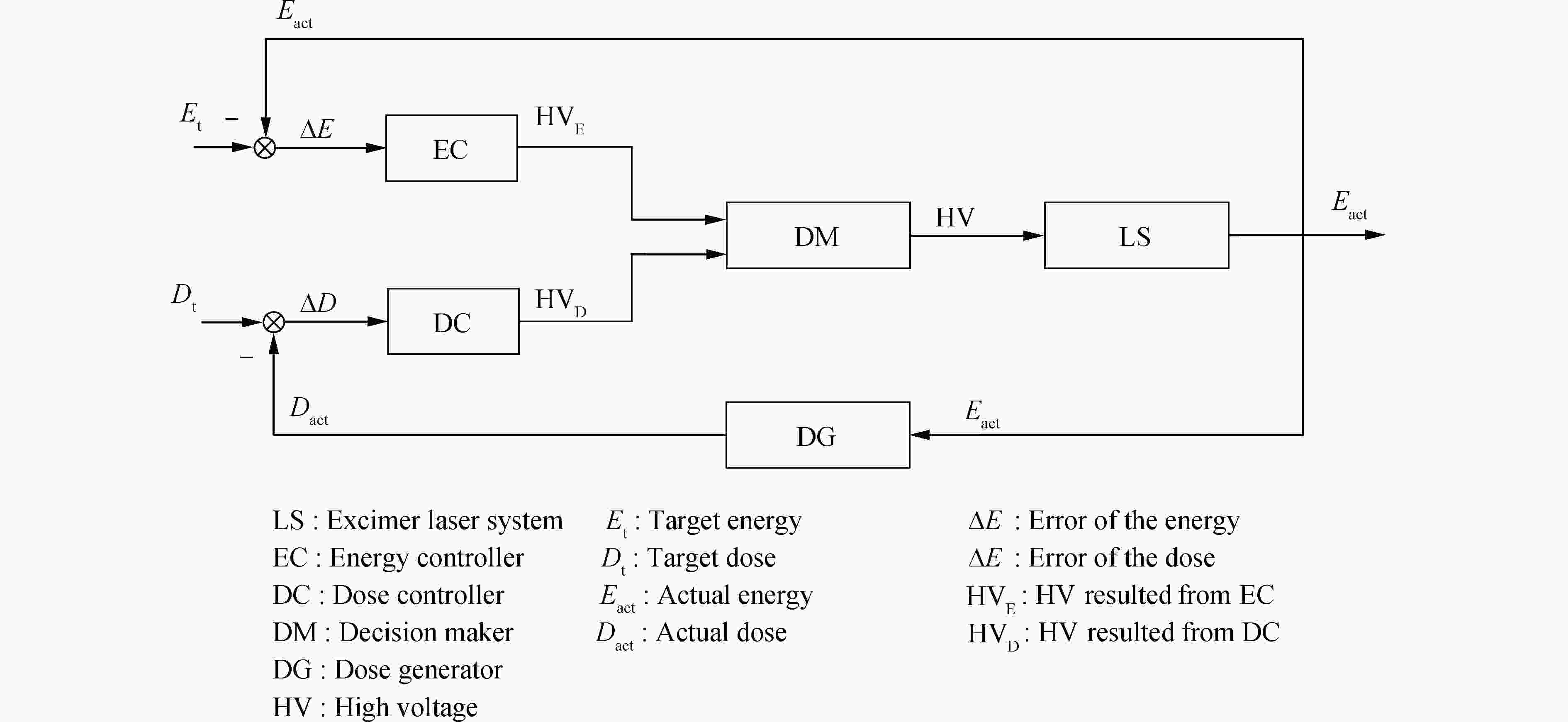
图 6 基于决策控制的剂量精度控制算法结构框图
Figure 6. Structural block diagram of dose accuracy control algorithm based on decision control
能量反馈控制算法(EC)采用方法和3.3节中的算法一致。
针对于剂量精度控制而设计的反馈控制的PI算法如公式(22)所示：
$$H{V_D}_{m,i} = {K_{Ed}}(\Delta Dos{e_{m,i - 1}} + \frac{{\displaystyle\sum\limits_{k = 2}^i {\Delta Dos{e_{m,k - 1}}} }}{{{I_{Ed}}}})$$ (22) 式中：
$H{V_D}_{m,i}$ 表示根据剂量反馈控制算法计算出的为产生第m个Burst的第i个激光脉冲能量所设定的放电高压值；${K_{Ed}}$ 表示剂量反馈PI控制算法的比例参数；${I_{Ed}}$ 表示剂量反馈PI控制算法的积分参数；$\Delta Dos{e_{m,i - 1}}$ 表示实际的剂量偏差，表示方法如公式(23)所示：$$\Delta Dos{e_{m,i - 1}} = Dos{e_{\rm{t}}} - Dos{e_{m,i - 1}}$$ (23) 式中：
$Dos{e_{\rm{t}}}$ 为目标剂量值。在决策控制器中，输入量为
$H{V_E}_{m,i}$ 和$H{V_D}_{m,i}$ ，经过决策算法计算得出最终的放电高压值$H{V_{m,i}}$ 。在该控制算法中，决策算法采用
$H{V_E}_{m,i}$ 和$H{V_D}_{m,i}$ 加权平均的方法，经过计算得到最终设定放电高压值$H{V_{m,i}}$ ，其决策算法如公式(24)所示：$$ H{V_{m,i}} = \alpha H{V_E}_{m,i} + (1 - \alpha )H{V_D}_{m,i}\;({\rm{0 < }}\alpha {\rm{ < 1)}} $$ (24) 式中：
$\alpha $ 为加权系数。通过能量稳定性和剂量精度控制的大量实验数据分析得出，在$\alpha {\rm{ = 0}}{\rm{.5}}$ 时控制效果最佳，即一般平均。 -
将该研究设计的基于PID的双闭环控制算法和基于决策的控制算法分别利用激光器能量仿真模型进行仿真实验验证。仿真实验结果如图7所示。
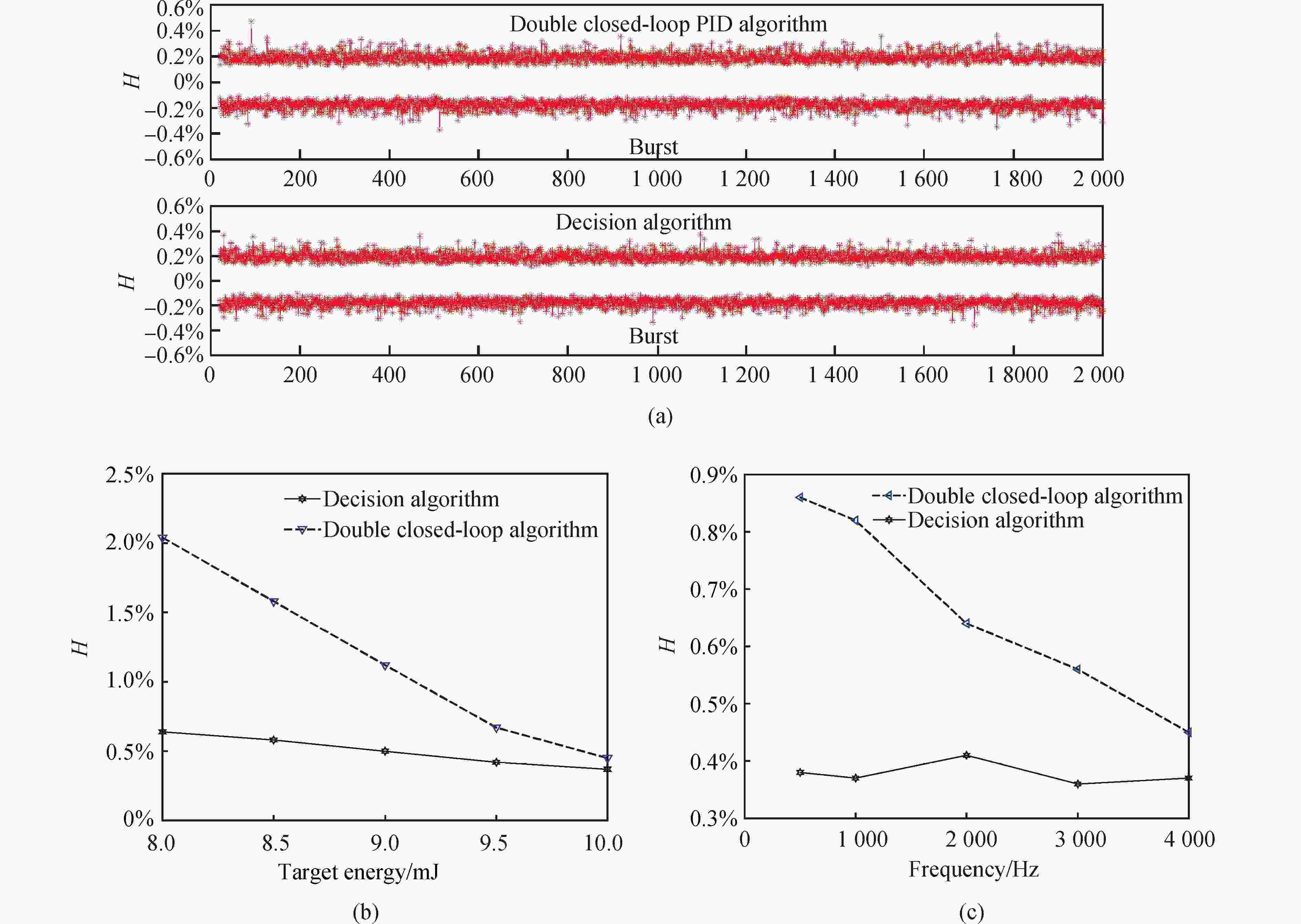
图 7 仿真实验结果：（a）仿真模型在重频4 kHz目标能量10 mJ工况下双闭环和决策算法剂量精度对比图; (b) 仿真条件下双闭环和决策控制算法对于目标能量的适应性对比图; (c) 仿真条件下双闭环和决策控制算法对于工作重频的适应性对比图
Figure 7. Simulation experiment results: (a) Comparison of dose accuracy of double closed-loop and decision algorithms of the simulation model under repeated 4 kHz target energy at 10 mJ; (b) Comparison of the adaptability of dual closed-loop and decision control algorithms to target energy under simulation conditions; (c) Comparison of the adaptability of dual closed-loop and decision-control algorithms for re-frequency operation under simulation conditions
激光器能量仿真模型的能量标准差设为0.1 mJ，模拟激光器重频为4 kHz工作在Burst模式的工况，将目标能量设定为10 mJ，经过参数调好的基于PID的双闭环的和基于决策控的控制算法控制后的各Burst的剂量精度对比如图7(a)所示。从图中可以看出，在基于PID的双闭环控制算法和基于决策的控制算法下，在4 kHz重频10 mJ目标能量工况下，各参数调整到最佳时，两种控制算法的剂量精度基本相同。
保持两个控制算法控制参数不变，在激光器出光模型模拟4 kHz重频Burst工况下，目标能量分别设为8 mJ，8.5 mJ，9 mJ，9.5 mJ和10 mJ，得到两个控制算法的剂量精度控制效果如图7(b)所示。由图7（b）可以看出，当目标能量发生变化时，在不调整两个控制算法控制参数的情况下，两种算法的控制剂量精度都会有变化，但基于决策算法的控制算法的控制精度要比基于PID的双闭环控制算法的控制精度变化小得多，即基于决策算法的控制算法对于设定值改变的适应性要比基于PID控制的控制算法的适应性更强。
保持两个控制算法控制参数不变，激光器出光模型模拟目标能量设定为10 mJ，变换工作重频1 kHz到4 kHz，得到的控制效果图如图7(c)所示。由图7（c）可以看出，当工作重频发生变化时，基于PID的双闭环控制算法的剂量控制精度变化很大，而基于决策算法的控制算法的剂量控制精度基本保持不变。由此可知，在重频发生变化时，基于决策算法的剂量精度控制算法适应性更强。
-
将文中所设计的基于决策的能量控制算法应用到一台工作最高重频为4 kHz的KrF准分子激光器上。实验中实现算法的反馈链路图如图8所示。
图 8 能量控制算法反馈链路图
Figure 8. Energy control algorithm feedback link diagram
在控制效果验证实验中，实验设定激光器的工作重频为4 kHz，出光模式为Burst模式。Burst中的脉冲数设为250个，Burst的时间间隔为50 ms。实验中在控制算法的控制下，即恒能量模式下，设定激光器的目标能量为10 mJ。同时设立对照组实验，工作参数与恒能量模式下相同，不同之处在于放电高压恒定，设定的放电高压为1 500 V。分别针对工作在有控制算法的恒能量模式下和没有算法控制的恒高压模式下的激光器，用能量计采集1 min的激光脉冲能量，并对其进行分析，实验结果如图9所示。
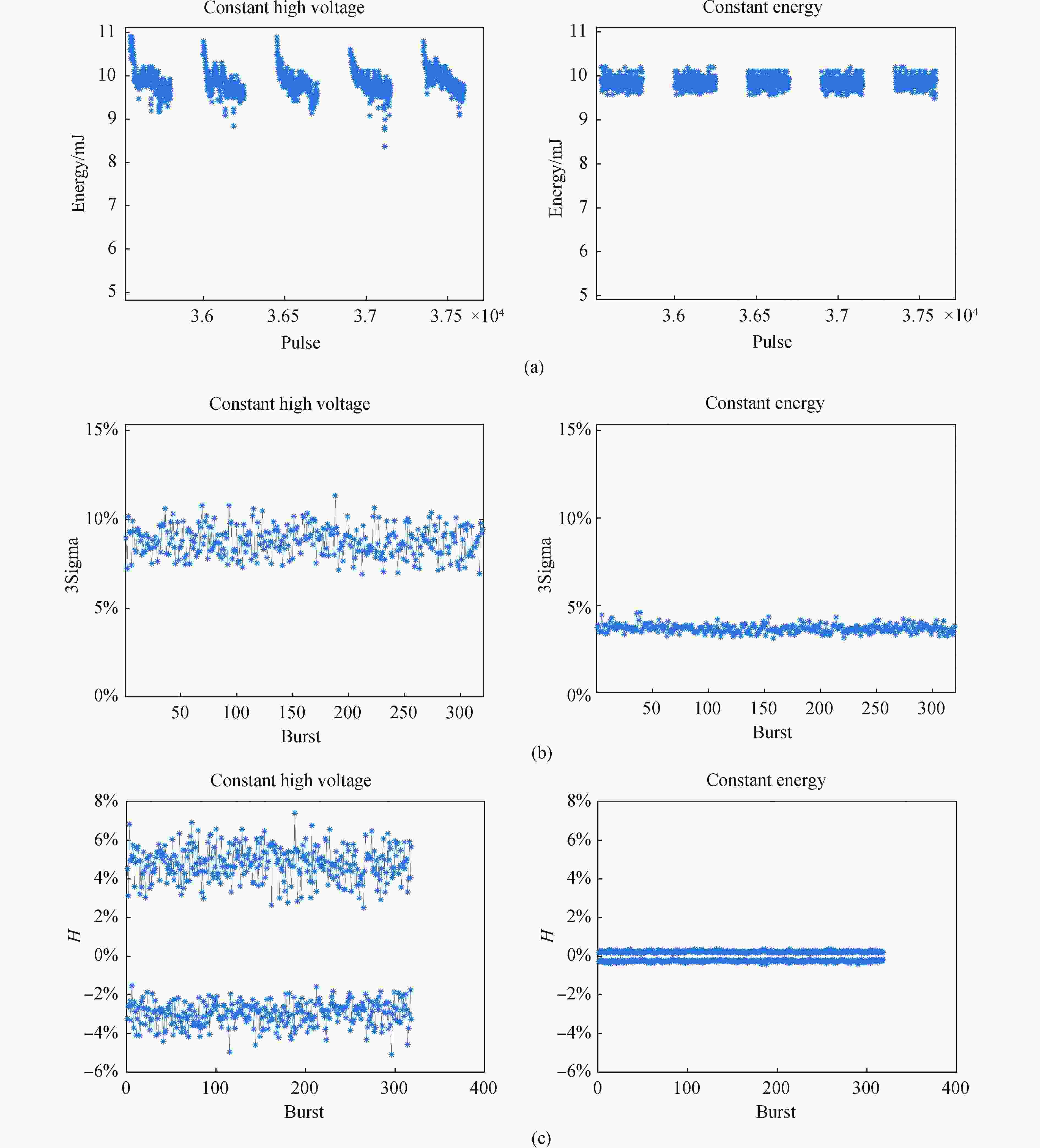
图 9 恒能量和恒高压模式实验结果对比：(a)恒能量和恒高压模式下单脉冲能量对比图; (b) 能量稳定性对比图; (c) 剂量精度对比图
Figure 9. Comparison of experimental results between constant energy and constant high voltage mode : (a) Comparison of pulse energy in constant energy and constant high voltage mode; (b) Comparison chart of energy stability; (c) Comparison of dose accuracy
单脉冲能量对比如图9(a)所示。从图9（a）中可以看出，经过文中设计的决策控制算法控制后的单脉冲能量已经消除了激光脉冲能量在中Burst的超调和随机波动。
针对采集到的数据，每个Burst分别计算能量稳定性，即计算3
$\sigma $ 。得到在文中设计的控制算法的恒能量模式下的能量稳定性和无控制算法的恒高压模式下的能量稳定性对比如图9(b)所示。从图中可以看出，在没有控制算法控制的恒高压模式下，计算得到的能量稳定性小于11%；在加入文中设计的决策控制算法后的恒能量模式下，计算得到的能量稳定性小于5%。可以看出经过控制算法控制后，激光器的能量稳定性有了很大提高。对采集到的数据，分别以
${N_{{\rm{slit}}}}$ 为30计算剂量精度，并用每个Burst中的剂量精度的最大值和最小值来表征该Burst的剂量精度，得到在决策控制算法作用下的恒能量模式下的剂量精度和无控制算法的恒高压模式下的剂量精度的对比如图9(c)所示。从图9（c）中可以看出，在恒高压模式下，激光器的剂量精度只有7%，而在经过决策控制算法控制后的恒能量模式下，剂量精度提高到了0.4%。可以看出，文中所设计的决策控制对于剂量精度的提升有很大帮助。在决策控制算法针对目标能量值适应性实验中，激光器工作在4 kHz的工况下，Burst参数与控制效果实验中的相同，分别改变激光器能量控制目标设定值（8~12 mJ）。每个能量目标设定值的情况下采集1 min的单脉冲能量数据，并分别计算剂量精度，以每组能量数据的剂量精度最大值作为该组数据的剂量精度。实验数据处理结果如图10(a)所示。从图10（a）中可以看出，在决策控制算法的控制下，设定目标能量在8 mJ到12 mJ的变化中，剂量精度始终在0.4%以下。
图 10 算法适应性实验结果：(a)决策控制算法在不同目标能量设定值下的剂量精度控制效果；(b) 决策控制算法在不同工作重频下的剂量精度控制效果
Figure 10. Algorithm adaptive experiment results : (a) Effect of decision control algorithm on dose accuracy control under different target energy; (b) Effect of decision control algorithm on dose accuracy control at different work frequency
在决策控制算法对于激光器工作重频的适应性实验中，激光器的目标能量值设定为10 mJ，Burst参数与控制效果实验中相同，分别设定激光器的工作重频为1、2 、3、4 kHz。在每个重频下采集1 min的单脉冲数据，分别以
${N_{{\rm{slit}}}}$ 为30计算剂量精度。实验处理结果如图10(b)所示。从图10（b）中可以看出，在决策控制算法的控制下，不同重频下剂量精度均小于0.4%。剂量控制精度会随频率的升高而恶化的原因是激光器本身的出光能量稳定性会随频率的升高而恶化。 -
文中针对高重频准分子激光器的出光特性提出了对于激光器出光脉冲序列的每个Burst的相同位置上的激光脉冲能量进行分析的分析方法。通过分析得出激光器单脉冲能量的能量变化规律和能量稳定性变化规律。基于单脉冲能量特性的分析建立了准分子激光器出光特性仿真模型，并与实际激光器产生的激光器脉冲能量序列进行了时域和频域的对比，证明了文中建立的激光器出光仿真模型的有效性。
根据准分子激光器的出光能量特性分别针对Burst中的能量超调和能量随机波动设计了能量稳定性控制器。针对剂量精度，提出了基于PID的双闭环控制算法和基于决策算法的控制算法。通过在文中建立的激光器出光仿真模型上的实验，证明了基于决策算法的控制算法适应性更强。通过在一台工作重频为4 kHz的KrF准分子激光器上的实验证明了基于决策算法的控制算法的有效性。最终实现该激光器在目标能量从8 mJ至12 mJ，工作重频从1 kHz至4 kHz，都能使能量稳定性达到
${\rm{3}}\sigma < {\rm{5\% }}$ ，剂量精度高达0.4%，比恒高压模式的能量稳定性的${\rm{3}}\sigma < {\rm{11}}{\rm{\% }}$ 和剂量精度的6%有了很大提高。特别是剂量精度有了质的飞跃。最终使得能量稳定性和剂量精度都满足半导体光刻的需求。
Energy characteristics control of high-repetition frequency KrF excimer laser
-
摘要: 能量稳定性和剂量精度是半导体光刻用高重频准分子激光器的重要指标，必须采用高精度的控制算法对其进行控制。针对准分子激光器，首先对准分子激光器的单脉冲能量特性进行了分析，并在分析的基础上建立了准分子激光器的出光能量仿真模型。然后，分别设计了能量稳定性控制算法，基于PID的双闭环剂量精度控制算法和基于决策算法的剂量精度控制算法，并通过在仿真模型上实验对于算法控制效果进行了分析，证明了基于决策算法的剂量精度控制算法的适应性更强。最后，将基于决策的控制算法在一台重频为4 kHz的KrF准分子激光器上进行了验证。该激光器在基于决策的控制算法的控制下，能量稳定性的3σ小于5%，剂量精度小于0.4%，满足半导体光刻的需求。在仿真实验和实际实验中都证明了研究中设计的能量特性控制算法的有效性。Abstract: Energy stability and dose accuracy are important indicators of high-repetition frequency excimer lasers for semiconductor lithography, which must be controlled by high-precision control algorithms. Firstly, the single-pulse energy characteristics of the excimer laser were analyzed. Based on the analysis, a simulation model of the output energy of the excimer laser was established and had been experimentally proven to be effective. Then, the energy stability control algorithm, the double closed-loop dose accuracy control algorithm based on PID and the dose accuracy control algorithm based on decision algorithm were designed respectively and the control effects of the algorithms were tested separately on the simulation model. The simulation analysis results showed that the dose accuracy control algorithm based on the decision algorithm is more adaptable. The algorithm based on decision was validated on a KrF excimer laser with a repetitive frequency of 4 kHz. Controlled by the algorithm, the 3σ of laser energy stability was less than 5% and the dose accuracy was less than 0.4%, which satisfied the requirements of semiconductor lithography. The effectiveness of the energy characteristic control algorithm in the research had been proved in both simulation and actual experiments.
-
Key words:
- energy control /
- dose control /
- excimer laser /
- decision control
-
图 1 恒高压工作模式下单脉冲能量变化规律图
Figure 1. Single pulse energy variation law in excimer laser constant voltage operation mode
图 2 激光器单脉冲能量特性分析结果图。(a) 恒高压模式下不同重频Burst脉冲能量变化规律；(b) 恒高压模式下不同重频Burst脉冲能量的标准差变化规律；(c) 恒高压工况下Burst序列中相同位置激光脉冲能量的直方图
Figure 2. Analysis results of laser single pulse energy characteristics. (a) Energy variation of pulses in Burst with different repetition frequency under constant high voltage mode; (b) Standard deviation of pulse energy in Burst with different repetition frequency under constant high voltage mode; (c) Histogram of laser pulse energy at the same position in Burst sequence under constant high voltage mode
图 3 准分子激光器单脉冲能量仿真模型示意图
Figure 3. Schematic of single pulse energy simulation model of excimer laser
图 4 实测和模型产生一个Burst的脉冲能量变化对比图。(a) 时域；(b) 频域
Figure 4. Comparison of actual and simulated Burst pulse energy changes. (a) Time domain; (b) Frequency domain
图 5 双闭环剂量精度控制算法结构框图
Figure 5. Block diagram of double closed-loop dose precision control algorithm
图 6 基于决策控制的剂量精度控制算法结构框图
Figure 6. Structural block diagram of dose accuracy control algorithm based on decision control
图 7 仿真实验结果：（a）仿真模型在重频4 kHz目标能量10 mJ工况下双闭环和决策算法剂量精度对比图; (b) 仿真条件下双闭环和决策控制算法对于目标能量的适应性对比图; (c) 仿真条件下双闭环和决策控制算法对于工作重频的适应性对比图
Figure 7. Simulation experiment results: (a) Comparison of dose accuracy of double closed-loop and decision algorithms of the simulation model under repeated 4 kHz target energy at 10 mJ; (b) Comparison of the adaptability of dual closed-loop and decision control algorithms to target energy under simulation conditions; (c) Comparison of the adaptability of dual closed-loop and decision-control algorithms for re-frequency operation under simulation conditions
图 9 恒能量和恒高压模式实验结果对比：(a)恒能量和恒高压模式下单脉冲能量对比图; (b) 能量稳定性对比图; (c) 剂量精度对比图
Figure 9. Comparison of experimental results between constant energy and constant high voltage mode : (a) Comparison of pulse energy in constant energy and constant high voltage mode; (b) Comparison chart of energy stability; (c) Comparison of dose accuracy
图 10 算法适应性实验结果：(a)决策控制算法在不同目标能量设定值下的剂量精度控制效果；(b) 决策控制算法在不同工作重频下的剂量精度控制效果
Figure 10. Algorithm adaptive experiment results : (a) Effect of decision control algorithm on dose accuracy control under different target energy; (b) Effect of decision control algorithm on dose accuracy control at different work frequency
-
[1] 潘宁, 梁勖, 林颖, 等. 准分子激光系统中模拟信号的传输方法[J]. 红外与激光工程, 2019, 48(9): 0905003. doi: 10.3788/IRLA201948.0905003 Pan Ning, Liang Xu, Lin Ying, et al. Transmission method of analog signal in excimer laser system [J]. Infrared and Laser Engineering, 2019, 48(9): 0905003. (in Chinese doi: 10.3788/IRLA201948.0905003 [2] 朱峰, 于力, 易爱平, 等. 内置标准具光栅腔XeF(C-A)准分子激光器的线宽压缩[J]. 光学 精密工程, 2018, 26(12): 2888-2893. doi: 10.3788/OPE.20182612.2888 Zhu Feng, Yu Li, Yi Aiping, et al. Spectral compression of XeF(C-A) excimer laser using grating resonator with an intra-acvity etalon [J]. Optics and Precision Engineering, 2018, 26(12): 2888-2893. (in Chinese doi: 10.3788/OPE.20182612.2888 [3] 周传清, 余雷, 陆培华, 等. 准分子屈光手术中非球面系数对球差以及切削深度的影响[J]. 光学 精密工程, 2007, 15(2): 167-172. doi: 10.3321/j.issn:1004-924X.2007.02.004 Zhou Chuanqing, Yu Lei, Lu Peihua, et al. Effect of asphericity parameter on Seidal aberration and ablation depth in laser refractive surgery [J]. Optics and Precision Engineering, 2007, 15(2): 167-172. (in Chinese doi: 10.3321/j.issn:1004-924X.2007.02.004 [4] 毕丹丹, 张立超, 时光. 浸没式光刻投影物镜光学薄膜[J]. 中国光学, 2018, 11(5): 745-764. doi: 10.3788/co.20181105.0745 Bi Dandan, Zhang Lichao, Shi Guang. Optical coatings for projection objective immersion lithography [J]. Chinese Journal of Optics, 2018, 11(5): 745-764. (in Chinese doi: 10.3788/co.20181105.0745 [5] Petrova T B, Petrov G M, Wolford M F, et al. Modeling of an electron-beam pumped arf excimer laser[C]//2017 IEEE International Conference on Plasma Science (ICOPS), 2017: 1-1. [6] Tsushima H, Fujimaki Y, Kiyota Y, et al. Extremely long life excimer laser chamber technology for multi-patterning lithography[C]//SPIE, 2019, 10961: 109610X. [7] Losev V F, Panchenko Y N, Dudarev V V, 等. 放电脉冲重频准分子激光器在不同应用领域的发展现状[J]. 中国光学, 2011, 4(1): 1-8. Losev V F, Panchenko Y N, Dudarev V V, et al. Development of discharge pulse repetition rate excimer lasers for different applications [J]. Chinese Journal of Optics, 2011, 4(1): 1-8. (in Chinese [8] 袁靖超, 赵江山, 李慧, 等. 基于准分子激光绝对波长校准的寻峰算法研究[J]. 中国激光, 2018, 45(7): 19-25. Yuan Jingchao, Zhao Jiangshan, Li Hui, et al. Research of peak-detection algorithm based on absolute wavelength calibration of excimer laser [J]. Chinese Journal of Lasers, 2018, 45(7): 19-25. (in Chinese [9] 刘斌, 丁金滨, 王魁波, 等. 高重复频率准分子激光器中放电冲击波特性的实验研究[J]. 中国激光, 2019, 46(12): 1201001. doi: 10.3788/CJL201946.1201001 Liu Bin, Ding Jinbin, Wang Kuibo, et al. Experimental study of characteristics of discharge shock waves in high-repetition-rate excimer lasers [J]. Chinese Journal of Lasers, 2019, 46(12): 1201001. (in Chinese doi: 10.3788/CJL201946.1201001 [10] 梁勖, 赵读亮, 林颖, 等. 基于可控LC串联谐振的高重频高精度脉冲充电电源[J]. 高电压技术, 2018, 44(9): 3022-3027. Liang Xu, Zhao Duliang, Lin Ying, et al. High repetition rate and high accuracy capacitor charging pulse power supply based on controllable LC series resonance [J]. High Voltage Engineering, 2018, 44(9): 3022-3027. (in Chinese [11] 周松青, 黄珂, 沈炎龙, 等. 电激励重频HF激光器非稳腔设计及实验研究[J]. 红外与激光工程, 2019, 48(10): 1005002. Zhou Songqing, Huang Ke, Shen Yanlong, et al. Design and experimental investigation of unstable resonator for discharge initiated repetitive-pulsed HF laser [J]. Infrared and Laser Engineering, 2019, 48(10): 1005002. (in Chinese [12] 来五星, 史铁林, 杨叔子. 嵌入式激光器能量实时控制系统的开发[J]. 半导体光电, 2006, 27(3): 328-330. doi: 10.3969/j.issn.1001-5868.2006.03.028 Lai W X, Shi T L, Yang S Z. Development of embedded laser energy real-time control system [J]. Semiconductor Optoelectronics, 2006, 27(3): 328-330. (in Chinese doi: 10.3969/j.issn.1001-5868.2006.03.028 [13] 梁勖, 游利兵, 王涛,等. 实时调节工作电压实现稳定准分子脉冲能量[J]. 中国激光, 2010, 37(2): 374-378. doi: 10.3788/CJL20103702.0374 Liang Xu, You Libing, Wang Tao, et al. Excimer pulse energy stabilization realized by charging voltage realtime adjusting [J]. Chinese Journal of Lasers, 2010, 37(2): 374-378. (in Chinese doi: 10.3788/CJL20103702.0374 [14] Ishida K, Ohta T, Miyamoto H, et al. The ArF laser for the next-generation multiple-patterning immersion lithography supporting green operations[C]//SPIE 2016, 9780: 978010. [15] 王效顺, 梁勖, 游利兵,等. 高重复频率ArF准分子激光器能量控制算法研究[J]. 激光技术, 2012, 36(6): 763-766. Wang Xiaoshun, Liang Xu, You Libing, et al. Study on energy control algorithm for high-repetition-rate ArF excimer lasers [J]. Laser Technology, 2012, 36(6): 763-766. (in Chinese -
点击查看大图
计量
- 文章访问数: 1304
- HTML全文浏览量: 675
- PDF下载量: 79
- 被引次数: 0
