-
获取真实世界中物体的三维模型一直是计算机视觉领域的研究重点。常见的主动式获取三维模型的方法有：结构光法[1, 2]、激光扫描法[3, 4]和飞行时间法[5]等。这些方法能在得到物体模型的同时解算出物体的深度信息，即重建的模型是具有真实尺寸的。但是，这些方法也具有相当多的局限性，如结构光法多用于室内重建，需要搭建相应的实验平台；激光扫描法需要昂贵的采集设备；飞行时间法涉及的传感器较贵且信息采集易受到环境因素的影响。
相比较而言，被动式重建中基于运动恢复结构（Structure from Motion, SfM）的重建方法因其简易的设备、方便的操作而应用前景广泛。SfM根据图像添加顺序的拓扑结构可分为增量式SfM、全局式SfM和混合式SfM三种，文中的主要研究对象是增量式SfM。经典增量式SfM通过求解透视n点（Perspective-n-Point, PnP）问题来进行图像配准，因此重建后的点云存在单目视觉的尺度不确定性缺陷。
针对上述问题，向奉卓等[6]在相机高度已知的基础上，通过图像区域稠密匹配，建立非线性优化模型求解尺度因子；周围[7]通过重建场景中的一个绝对尺度将度量重建恢复至欧式重建；Wang等[8]通过三角剖分方法将输入图像分割为多三角，确定道路区域后使用道路特征点计算道路模型，并利用相机高度信息来恢复尺度；Westoby等[9]通过手工定位点云中的控制点并计算相对坐标系到绝对坐标系的转换矩阵，使用绝对定向算法分解矩阵得到旋转矩阵、平移向量和尺度因子；陈朋等[10]通过引入惯性传感单元，将惯性传感单元获取的加速度和角速度与相机位姿进行时域和频域上的协同，从频域中获取单目相机的尺度信息；Micheletti等[11]将相机拍摄的图片进行SfM三维重建后形成点云，然后与地面激光扫描的数据配准获得尺度信息。
文中首先提出了一种新的增量式SfM重建拓扑结构——邻图配对式SfM重建拓扑结构，该拓扑结构将图像序列中相邻图像两两配对重建出多个点云；然后，以首张图像相机坐标系下的点云作为主点云，通过建立对应表关系寻找部分点云和主点云间的三维坐标点对；接着，在参考文献[12-13]的基础上，提出抗噪声的尺度迭代最近点法（Anti-Noise Scaling Iterative Closest Point, ANSICP）实现部分点云与主点云的配准，重建出目标物体的稀疏点云；最后，在重建的场景中布置地面控制点，并规定世界坐标系，确定控制点在首图相机坐标系下和世界坐标系下的三维坐标点对，根据ANSICP算法计算变换矩阵，对稀疏点云进行坐标系变换实现点云尺度信息的恢复。
-
传统的增量式SfM和文中改进的增量式SfM重建拓扑结构示意图分别如图1（a）、图1（b）所示。传统的增量式SfM首先选取两张图片重建初始点云，然后通过求解PnP问题恢复增添图片对应的相机位姿，最后将重建的点云添加到初始点云中去。但是该方法存在尺度上的缺陷。PnP问题要求拍摄的图片在同一尺度上，如果存在尺度变化，PnP算出的相机位姿就不准确，新建点云和初始点云不能重合，而且这个误差会随着图片的增加逐渐累积，最后导致光束平差法的结果不能收敛。文中提出的增量式SfM首先也是选取两张图片重建初始主点云，然后对添加的每一张图片，根据极线几何关系，将其结合前一张图片重建出新的点云，接着根据对应表关系找出主点云和新建点云中对应同一世界点的三维坐标点对，最后根据ANSICP算法配准点云。
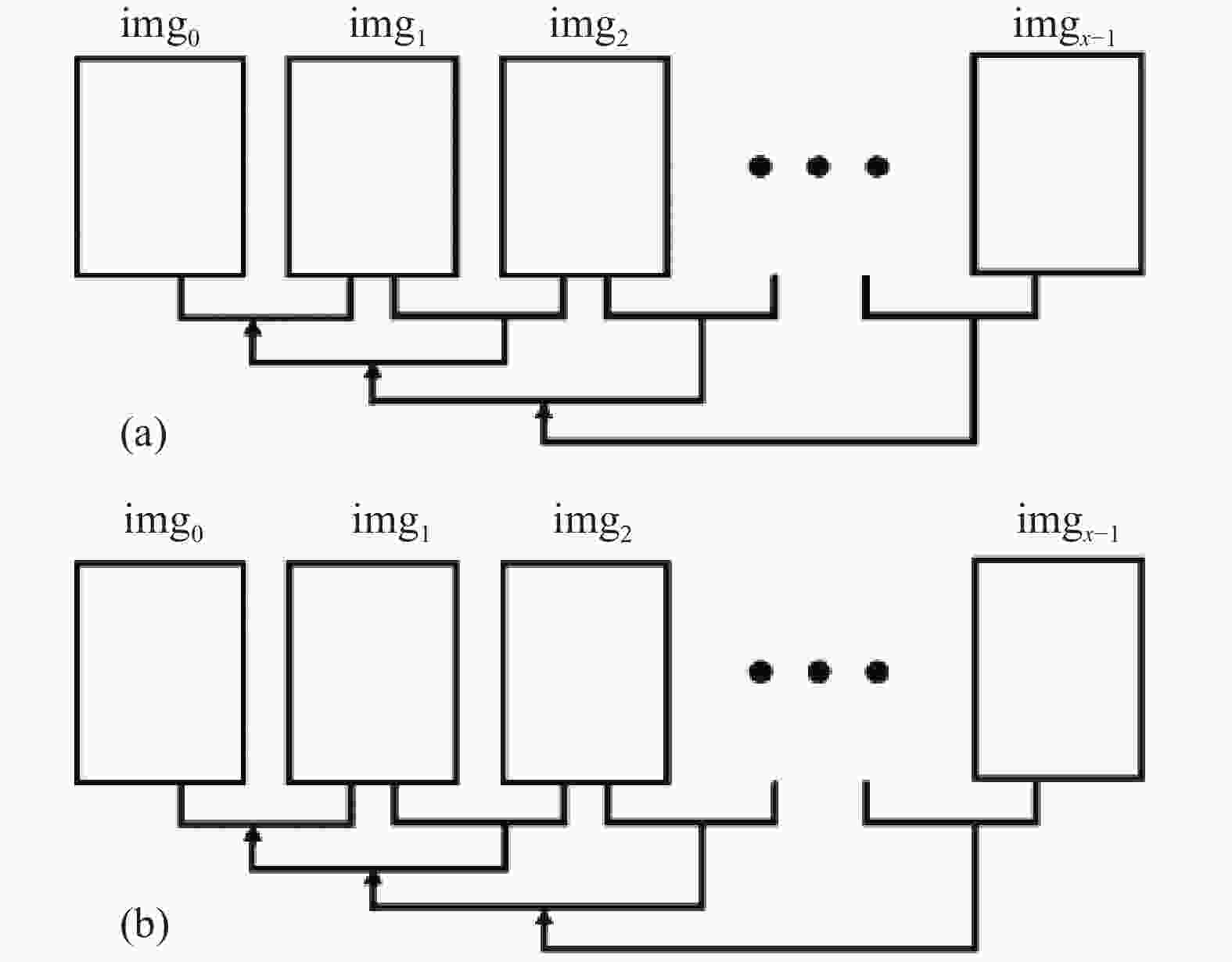
图 1 增量式SfM重建拓扑图。(a)传统增量式SfM重建拓扑结构图; (b)文中提出的增量式SfM重建拓扑结构图
Figure 1. Reconstruction topology of incremental SfM. (a) Reconstruction topology of traditional incremental SfM; (b) reconstruction topology of proposed incremental SfM
文中提出的增量式SfM不必要求拍摄的图片在同一尺度上。邻图配对式SfM重建拓扑结构中，通过序列图像配对重建可以将不同尺度的点云区分开，并根据对应表关系和提出的配准算法配准点云，使最终重建的稀疏点云不受尺度的影响，解决了各点云之间由于尺度不同导致的点云分层问题，使重建出的点云更精确。因此，文中提出的增量式SfM重建拓扑结构相较于传统的更有优势。
根据极线几何约束关系，两两相邻图像可以重建出点云。但是这些不同尺度的点云处在不同的世界坐标系中，需要根据对应的世界坐标点关系将点云统一到同一坐标系下，即点云配准问题。文中设计了对应表，旨在从不同点云中寻找到同一世界点的对应坐标，示意图如图2所示。示意图分为图像层、特征点层和查找表层三层。图像0，图像1，图像2是图像序列流中相邻的三张图像，
$m_{01}^0$ 、$m_{01}^1$ 是图像0和图像1匹配后的对应匹配点，$m_{12}^1$ 、$m_{12}^2$ 是图像1和图像2匹配后的对应匹配点。由$m_{ij}^i$ 和$m_{ij}^j$ （j>i≥0）建立查找表tij，查找表的索引是图像匹配点对应的特征点序号(ki，kj)，查找表的内容是图像匹配点对应的三维点坐标$w_{ij}^p$ 。对相邻的两张查找表，如t01、t12中含有相同的特征点序号k1，以特征点序号k1为索引，找到对应的三维点对($w_{01}^p$ ,$m_{12}^p$ )。在此基础上，利用ANSICP算法配准点云。
图 2 对应表示意图
Figure 2. Diagram of corresponding table
-
在图2中，若仅仅通过刚性变换（旋转+平移），图像0、图像1重建的点云和图像1、图像2重建的点云通常不能完全重合。原因是两片点云之间存在尺度变换，用公式表示如下：
$$\left[ {\begin{array}{*{20}{c}} {{{{p}}_i}} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{r}} {s{{R}}}&{{T}} \\ {{{{0}}^{\rm{T}}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{q}}_i}} \\ 1 \end{array}} \right] = {{S}}\left[ {\begin{array}{*{20}{c}} {{{{q}}_i}} \\ 1 \end{array}} \right],i \in \left[ {0,M - 1} \right]$$ (1) 式中：(pi，qi)是空间点在不同世界坐标系下的三维坐标点对；R、T分别表示刚性变换中的旋转矩阵和平移向量；s是两片点云之间的尺度变换因子。
实际情况中，公式（1）中的等号不能完全成立，配准算法主要用于求解一个非线性最小二乘问题：
$$\arg \min {{C}} \left( {{{R}},{{T}},s} \right) = \sum\limits_{i = 0}^{M - 1} {{{\left\| {{{{p}}_i} - s{{R}}{{{q}}_i} - {{T}}} \right\|}^2}} $$ (2) 公式（2）的常见解法包括基于SVD分解的（Scaling Iterative Closest Point, SICP）[12]算法、基于相似变换李代数（Similar Lie Algebra, SLA）的迭代算法以及基于光束平差（Bundle Adjustment, BA）的最小二乘算法三种。该文受参考文献[13]的启发，采用更鲁棒的核函数—Geman-McClure范数度量误差项，则公式（2）变为：
$$\arg \min {\rm{C}} \left( {{{R}},{{T}},s} \right) = \sum\limits_{i = 0}^{M - 1} {{\rm{\omega }}\left( {\left\| {{{{p}}_i} - s{{R}}{{{q}}_i} - {{T}}} \right\|} \right)} $$ (3) 式中：ω是Geman-McClure核函数，μ是函数惩罚项：
$${\rm{\omega }}\left( x \right) = \frac{{\mu {x^2}}}{{\mu + {x^2}}},$$ (4) 当误差项较大（x2>>μ）时，如遇到噪声点的情况，函数值趋于μ值，一定程度上抑制了噪声的影响；当误差项较小（x2<<μ）时，函数退化为二范数，不能起到抑制噪声的作用。因此，μ的取值对核函数影响较大，选择合适的μ值对公式（3）的优化至关重要。
根据参考文献[14]的建议，构造对应点对(pi, qi)的线过程L(pi, qi)：
$$L\left( {{{{p}}_i},{{{q}}_i}} \right) = {\left( {\frac{\mu }{{\mu + {{\left\| {{{{p}}_i} - s{{R}}{{{q}}_i} - {{T}}} \right\|}^2}}}} \right)^2}$$ (5) 则可构造公式（3）的等价优化式：
$$\begin{split}{{E}} \left( {L,{{R}},{{T}},s} \right) = & \sum\limits_{i = 0}^{M - 1} {\left( {L\left( {{{{p}}_i},{{{q}}_i}} \right){{\left\| {{{{p}}_i} - s{{R}}{{{q}}_i} - {{T}}} \right\|}^2}} \right)} + \\ & {\sum\limits_{i = 0}^{M - 1} {\mu {{\left( {\sqrt {L\left( {{{{p}}_i},{{{q}}_i}} \right)} - 1} \right)}^2}} } \end{split} $$ (6) 通过代入k步的s(k)、R(k)和T(k)到公式（5）中固定L(pi, qi)值后，公式（6）便成为常数项与平方误差项相乘后再加一个常数项的形式。令：
$$\left\{ {\begin{aligned} & {{\bar{{p}}} = \frac{{\sum\limits_{i = 0}^{M - 1} {\left( {L\left( {{{{p}}_i},{{{q}}_i}} \right){{{p}}_i}} \right)} }}{{\sum\limits_{i = 0}^{M - 1} {L\left( {{{{p}}_i},{{{q}}_i}} \right)} }}} \\ & {{\bar{{q}}} = \frac{{\sum\limits_{i = 0}^{M - 1} {\left( {L\left( {{{{p}}_i},{{{q}}_i}} \right){{{q}}_i}} \right)} }}{{\sum\limits_{i = 0}^{M - 1} {L\left( {{{{p}}_i},{{{q}}_i}} \right)} }}} \end{aligned}} \right.$$ (7) 以及：
$$\left\{ {\begin{aligned} & {{{\tilde {{p}}}_i} = \sqrt {L\left( {{{{p}}_i},{{{q}}_i}} \right)} \left( {{{{p}}_i} - {\bar{{p}}}} \right)} \\ & {{{\tilde {{q}}}_i} = \sqrt {L\left( {{{{p}}_i},{{{q}}_i}} \right)} \left( {{{{q}}_i} - {\bar{{q}}}} \right)} \end{aligned}} \right.$$ (8) 则公式（6）可化为平方误差项加常数项的形式：
$$ \begin{split} {{E}} \left( {L,{{R}},{{T}},s} \right) = \; & \sum\limits_{i = 0}^{M - 1} {{{\left\| {{{\tilde {{p}}}_i} - s{{R}}{{\tilde {{q}}}_i}} \right\|}^2}} + \\ &\sum\limits_{i = 0}^{M - 1} {\mu {{\left( {\sqrt {L\left( {{{{p}}_i},{{{q}}_i}} \right)} - 1} \right)}^2}} \end{split} $$ (9) 对公式（9）的非线性最小二乘问题，忽略常数项的影响。令：
$$\sum\limits_{i = 0}^{M - 1} {{{\tilde {{p}}}_i}} \tilde {{q}}_i^{\rm{T}} = {{UD}}{{{V}}^{\rm{T}} }$$ (10) 则旋转矩阵R、尺度因子s和平移向量T的求解公式如下：
$$\left\{ {\begin{aligned} & {{{R}} = {{U}}{{{V}}^{\rm{T}} }} \\ & {s = \frac{{\sum\limits_{i = 0}^{M - 1} {\tilde {{p}}_i^{\rm{T}} {{R}}{{\tilde {{q}}}_i}} }}{{\sum\limits_{i = 0}^{M - 1} {\tilde {{q}}_i^{\rm{T}} {{\tilde {{q}}}_i}} }}} \\ & {{{T}} = s{{R}}{\bar{{q}}} - {\bar{{p}}}} \end{aligned}} \right.$$ (11) ANSICP算法计算变换矩阵的步骤如下：
（1）输入含有噪声点的坐标点对集(pi, qi)，其中i∈[0, M-1]；
（2）初始化旋转矩阵R(0)为单位阵，平移向量T(0)为零向量，尺度因子s(0)为1.0，迭代终止阈值ε=0.01；
（3）迭代（第k次迭代）
1）将R(k)、T(k)及s(k)代入到公（5）中得L(pi, qi)；
2）根据公式（7）计算去中心化后点云对
$\left( {{{\tilde p}_i},{{\tilde q}_i}} \right)$ ，其中i∈[0, M-1]；3）根据公式（11）计算R(k+1)、s(k+1)和T(k+1)；
（4）迭代终止条件
1）根据公式（9）计算θ=1-E(k+1)/E(k)；
2）如果θ<ε成立，输出R(k+1)、s(k+1)和T(k+1)；
3）如果θ<ε不成立，令R(k)=R(k+1)、s(k)=s(k+1)和T(k)=T(k+1)，返回步骤（3）继续迭代过程。
-
对室外物体测量，文中首先设计了一种简单的控制点模式，然后在要重建的场景中布置多张控制点模式，如图3（a）所示；对室内物体测量，文中直接选用打印好的棋盘格，设置棋盘格上的角点为控制点，如图3（b）所示。
图 3 控制点模式布置场景图。(a)室外; (b) 室内
Figure 3. Scene graph of control point plot. (a) Outdoor; (b) indoor
选定坐标原点并建立右手坐标系，则各个控制点的三维世界坐标PW将确定。选择初始点云对应的两张图片，通过角点选择工具手动采集两张图片上控制点的像素坐标对
${{x}}(u,v,1)$ 和$x'(u',v',1)$ 。设
${{{A}}^{\rm{T}}} = \left( {{{a}}_1^{\rm{T}},{{a}}_2^{\rm{T}},{{a}}_3^{\rm{T}}} \right)$ 和${{\widetilde {{A}}}^{\rm{T}}} = \left( {{\widetilde {{a}}}_1^{\rm{T}},{\widetilde {{a}}}_2^{\rm{T}},{\widetilde {{a}}}_3^{\rm{T}}} \right)$ 分别是两张图片对应的投影矩阵，PC表示首图相机坐标系下控制点的三维坐标，λ、$\lambda '$ 表示未知的尺度参数。根据像素坐标对和投影矩阵可得公式（12）、（13）：$$\left\{ {\begin{aligned} & {\lambda u = {{a}}_1^{\rm{T}}{{{P}}_{\rm{C}}}} \\ & {\lambda v = {{a}}_2^{\rm{T}}{{{P}}_{\rm{C}}}} \\ & {\lambda = {{a}}_3^{\rm{T}}{{{P}}_{\rm{C}}}} \end{aligned}} \right.$$ (12) 和
$$\left\{ {\begin{aligned} & {\lambda 'u' = {\widetilde {{a}}}_1^{\rm{T}}{{{P}}_{\rm{C}}}} \\ & {\lambda 'v' = {\widetilde {{a}}}_2^{\rm{T}}{{{P}}_{\rm{C}}}} \\ & {\lambda ' = {\widetilde {{a}}}_3^{\rm{T}}{{{P}}_{\rm{C}}}} \end{aligned}} \right.$$ (13) 从公式（12）、公式（13）中消去λ、
$\lambda '$ 可以得到关于PC的线性方程组，如公式（14）所示：$$\left( {\begin{aligned} & {u{{a}}_3^{\rm{T}} - {{a}}_1^{\rm{T}}} \\ & {v{{a}}_3^{\rm{T}} - {{a}}_2^{\rm{T}}} \\ & {u'{\widetilde {{a}}}_3^{\rm{T}} - {\widetilde {{a}}}_1^{\rm{T}}} \\ & {v'{\widetilde {{a}}}_3^{\rm{T}} - {\widetilde {{a}}}_2^{\rm{T}}} \end{aligned}} \right){{{P}}_{\rm{C}}} = {\bf{0}}$$ (14) 求解公式（14）可得控制点在首图相机坐标系下的三维坐标。最后根据(PW, PC)和ANSICP算法可将重建的稀疏点云由首图相机坐标系转换到世界坐标系下，恢复出重建点云的尺度，实现目标物体的欧式重建。
-
文中在Intel® Core(TM) i7-5500 CPU的平台上，使用C++语言编程。依赖的开源库包括OpenCV，Ceres Solver和Sophus库，重建点云使用的序列图像集有Fountain-P11，Herzjesu-P8，People-P6以及Bottle-P7四种。点云重建中采用Difference of Gaussians检测图像特征点，并提取MCP二进制描述子[15]进行图像最近邻匹配，然后使用RANSAC算法提纯匹配结果，结合三角定位算法求解匹配点对对应的三维坐标点。
-
在ANSICP算法中，μ值的选取对迭代优化的结果影响很大。实验中选取Fountain、Herzjesu、People和Bottle点云研究配准时选取合适的μ值，点云对中加入占比50%，均值为0，标准差σ=1.0的高斯白噪声。实验结果如图4所示，图中横轴表示以10为对数底的μ值，纵轴表示均方根误差。
图 4 不同μ值下点云配准均方根误差曲线图
Figure 4. Root mean squared error of point registration for different μ
从图4可以看出，当μ值较小或较大时，均方根误差都比较大，这与公式（4）的讨论结果一致。μ值远小于误差项时，ω(x)为定值，迭代会陷入局部最小值而造成较大的误差；μ值远大于误差项时，ω(x)表现为二范数，也会陷入局部最小值造成较大的误差。大量实验表明，噪声点的平方误差是非噪声点的平方误差百倍以上，初始均方误差受噪声点的影响较大，通常和噪声点平方误差一个数量级。令：
$$e = {{\sum\limits_{i = 0}^{M - 1} {{{\left( {\left\| {{{{p}}_i} - {s^{\left( 0 \right)}}*{{{R}}^{\left( 0 \right)}}*{{{q}}_i} - {{{T}}^{\left( 0 \right)}}} \right\|} \right)}^2}} } / M}$$ (15) 根据公式（4）可知，当μ值取e/(20~50)时，对噪声数据x符合μ<<x2的情况，能很好地抑制噪声数据的影响，从而用公式（9）能较快地迭代至全局最小值。
为验证文中算法相对于其他算法在抗噪性上的表现，在Fountain点云三维坐标对应点集中选取不同百分比的数据加入均值为0，标准差σ=0.5的高斯白噪声。实验中核函数的μ=0.1，SICP算法、带Huber损失函数的BA算法和ANSICP算法的抗噪效果如图5所示。图5中横轴表示噪声点占总数据的百分比，图5（a）纵轴表示均方误差，图5（b）纵轴表示以10为对数底的时间变量。在均方误差曲线图中，曲线越往下，说明通过该算法计算的均方误差越小，算法的抗噪性越好；在时耗曲线图中，曲线越往下，说明该算法的耗时越短，算法的时间复杂度越低。从图5（a）可以看出，ANSICP算法对噪声有很好的抑制作用。但当噪声数据占比过小或过大时，改进算法的抗噪能力相较于常见算法的就没有那么明显。从图5（b）可以看出，ANSICP迭代算法的时间复杂度比较高，耗时比SICP的高出一个数量级。因此，当噪声数据较少时，应同时考虑算法的抗噪性和时间复杂度。
图 5 不同算法抗噪效果图。(a)不同算法配准点云后均方误差曲线图; (b)不同算法配准点云后时耗曲线图
Figure 5. Anti-noise effect of different methods. (a) Mean squared error of point registration by different methods; (b) time consumption of point registration by different methods
选取Fountain图像集中的11张图片，分别使用基于PnP的传统增量式SfM法、基于ICP、SICP和ANSICP的改进增量式SfM法重建点云，重建结果如图6所示。从图6中可以看出，基于PnP的传统增量式SfM算法重建的点云有明显的分层、不重叠现象，重建的点云效果较差；基于ICP的改进增量式SfM算法没有考虑尺度的影响，点云与点云之间也不能完全重合，点云也出现了分层现象；基于SICP的改进增量式SfM算法解决了点云配准上尺度的问题，缓解了点云分层现象，但是由于噪声点的存在，计算的变换矩阵不够准确，不同点云间未能完全重合；基于ANSICP的改进增量式SfM算法很好地克服了上述缺陷，点云重建效果最佳。
图 6 不同算法重建的Fountain点云图。(a) PnP; (b) ICP; (c) SICP; (d)提出方法
Figure 6. Reconstruction of Fountain by different methods. (a) PnP; (b) ICP; (c) SICP; (d) Proposed method
-
对室外场景，选择People图像集中含控制点模式的六张图像重建人物点云；对室内场景，选择Bottle图像集中含棋盘格的七张图像重建壶点云。实验中分别使用基于ICP、SICP和ANSICP的改进增量式SfM法重建点云，然后根据1.3节内容将重建点云恢复到世界坐标系下，实现点云的欧式重建。
实际情况中人物的身高、手臂和肩的测量值分别为176 cm，54.4 cm和45 cm，壶的高度、宽度分别为30 cm和18 cm。测量人物点云中身高和手臂、肩的长度，结果如表1所示；测量壶点云中高度和宽度，结果如表2所示。其中
$\widetilde d$ 、|Δd|分别表示点云中测量值和绝对误差值。表 1 人物点云长度测量
Table 1. Distance measurement of point cloud for people
Methods Height/cm Arm/cm Shoulder/cm $\widetilde d$ |Δd| $\widetilde d$ |Δd| $\widetilde d$ |Δd| ICP 162.50 13.5 50.17 4.23 41.68 3.32 SICP 159.86 16.14 48.84 5.56 40.80 4.20 ANSICP 178.47 2.47 53.35 1.05 46.01 1.01 表 2 壶点云长度测量
Table 2. Distance measurement of point cloud for bottle
Methods Height/cm Width/cm $\widetilde d$ |Δd| $\widetilde d$ |Δd| ICP 36.96 6.96 21.18 3.18 SICP 29.36 0.64 16.10 1.90 ANSICP 29.56 0.44 16.84 1.16 从表1、表2中可以看出，基于ANSICP的改进增量式SfM重建精度要明显好于其他两种方法的。但其测量误差随着测量物体长度的增长而增加，测量绝对误差百分比在1%~2%左右，测量精度较高。
-
针对传统增量式SfM重建的点云存在分层和不具有量纲的问题，文中提出了一种新的增量式SfM欧式重建方法。方法提出新的增量式SfM重建拓扑结构——邻图配对式拓扑结构，首先根据新提出的拓扑结构依次重建多个点云，初始点云作为主点云，然后根据拓扑结构建立对应表关系快速、准确地寻找部分点云和主点云中对应同一世界点的三维坐标点对，接着结合三维坐标点对，使用抗噪声的尺度迭代最近点方法求解点云之间的变换矩阵，并将部分点云配准到主点云，最后，通过设置控制点，恢复重建点云的尺度，实现目标物体的欧式三维重建。通过序列图像对的三维重建对比实验表明，基于ANSICP的改进增量式SfM重建方法重建的点云效果最优，同时，设置控制点方法恢复的点云尺度绝对误差百分比在1%~2%左右，测量精度较高。但是，文中欧式重建点云的精度难以满足大部分场景的应用，接下来的工作将使用带畸变参数的相机模型和更精确的控制点方式来提高测量精度。
Euclidean 3D reconstruction based on structure from motion of matching adjacent images
-
摘要:
传统增量式运动恢复结构重建易受到尺度变化的影响，重建出的点云存在分层现象，并且不存在量纲。通过改进重建拓扑结构和尺度迭代最近点算法，提出了一种新的欧式三维重建方法。首先，设计了两两相邻图片重建点云后并入主点云的重建拓扑结构；然后，建立了对应表，旨在找到同一世界点在新建点云和主点云下的对应三维点对；接着，结合Geman-McClure范数，提出了抗噪声的尺度迭代最近点求解算法；最后，设置地面控制点，为重建出的点云引入尺度。实验结果表明，提出方法重建出的点云比传统增量式运动恢复结构重建出的点云更精确，并且点云长度的测量绝对误差在1%~2%左右。提出方法适用于近场景物体较精确的欧式三维重建。
-
关键词:
- 邻图配对式运动恢复结构 /
- 对应表 /
- 抗噪声的尺度迭代最近点 /
- 欧式三维重建
Abstract:Traditional incremental structure from motion is susceptible to scale change, and the reconstructed point cloud is hierarchical and has no units. A new Euclidean 3D reconstruction method was proposed by improving the reconstruction topology and the scaling iterative closest point algorithm. First, a new reconstruction topology, reconstructing a point cloud from two adjacent pictures and then merging it into the main point cloud, was presented; then, corresponding tables were established aiming to find the corresponding 3D point pairs of a world point between the newly created point cloud and the main point cloud; subsequently, combining Geman-McClure norm, an anti-noise scaling iterative closest point method was proposed; finally, ground control points were set up to introduce scale for the reconstructed point cloud. Experiment results show that the point cloud reconstructed by proposed method is more accurate than that reconstructed by traditional incremental structure from motion, and the absolute error of length for the point cloud is about 1%-2%. The proposed method is suitable for precise Euclidean reconstruction of objects in close scene.
-
图 1 增量式SfM重建拓扑图。(a)传统增量式SfM重建拓扑结构图; (b)文中提出的增量式SfM重建拓扑结构图
Figure 1. Reconstruction topology of incremental SfM. (a) Reconstruction topology of traditional incremental SfM; (b) reconstruction topology of proposed incremental SfM
图 3 控制点模式布置场景图。(a)室外; (b) 室内
Figure 3. Scene graph of control point plot. (a) Outdoor; (b) indoor
图 4 不同μ值下点云配准均方根误差曲线图
Figure 4. Root mean squared error of point registration for different μ
图 5 不同算法抗噪效果图。(a)不同算法配准点云后均方误差曲线图; (b)不同算法配准点云后时耗曲线图
Figure 5. Anti-noise effect of different methods. (a) Mean squared error of point registration by different methods; (b) time consumption of point registration by different methods
图 6 不同算法重建的Fountain点云图。(a) PnP; (b) ICP; (c) SICP; (d)提出方法
Figure 6. Reconstruction of Fountain by different methods. (a) PnP; (b) ICP; (c) SICP; (d) Proposed method
表 1 人物点云长度测量
Table 1. Distance measurement of point cloud for people
Methods Height/cm Arm/cm Shoulder/cm $\widetilde d$ |Δd| $\widetilde d$ |Δd| $\widetilde d$ |Δd| ICP 162.50 13.5 50.17 4.23 41.68 3.32 SICP 159.86 16.14 48.84 5.56 40.80 4.20 ANSICP 178.47 2.47 53.35 1.05 46.01 1.01 
下载: 导出CSV
表 2 壶点云长度测量
Table 2. Distance measurement of point cloud for bottle
Methods Height/cm Width/cm $\widetilde d$ |Δd| $\widetilde d$ |Δd| ICP 36.96 6.96 21.18 3.18 SICP 29.36 0.64 16.10 1.90 ANSICP 29.56 0.44 16.84 1.16
下载: 导出CSV
-
[1] Zhang Qican, Wu Zhoujie. Three-dimensional imaging technique based on Gray-coded structured illumination [J]. Infrared and Laser Engineering, 2020, 49(3): 0303004. (in Chinese) [2] Zhu Xiang, Shao Shuangyun, Song Zhijun. A detection method based on line-structured light sensor for geometrical morphology of track slab [J]. Chinese Optics, 2018, 11(5): 841−850. (in Chinese) doi: 10.3788/co.20181105.0841 [3] Wang Kai, Ou Yi, Zeng Shiqiang, et al. Measurement of ball nut profile using laser sensors [J]. Optics and Precision Engineering, 2020, 28(1): 39−49. (in Chinese) doi: 10.3788/OPE.20202801.0039 [4] Bu Yuming, Du Xiaoping, Zeng Zhaoyang, et al. Research progress and trend analysis of non-scanning laser 3D imaging radar [J]. Chinese Optics, 2018, 11(5): 711−727. (in Chinese) doi: 10.3788/co.20181105.0711 [5] Lu Chunqing, Song Yuzhi, Wu Yanpeng, et al. 3D information acquisition and error analysis based on TOF computational imaging [J]. Infrared and Laser Engineering, 2018, 47(10): 1041004. (in Chinese) [6] Xiang Fengzhuo, Li Guangyun, Wang Li, et al. Monocular visual odometry with absolute scale recovery [J]. Journal of Geomatics Science and Technology, 2018, 35(5): 462−466. (in Chinese) [7] Zhou Wei. Monocular vision based motion estimation and structure reconstruction[D]. Hangzhou: Zhejiang University, 2007. (in Chinese). [8] Wang X W, Zhang H, Yin X C, et al. Monocular visual odometry scale recovery using geometrical constraint[C]//Proceedings of 2018 IEEE International Conference on Robotics and Automation, ICRA, 2018: 988-995. [9] Westoby M J, Brasington J, Glasser N F, et al. Structure from motion photogrammetry: A low cost, effective tool for geoscience applications [J]. Geomorphology, 2012, 179: 300−314. doi: 10.1016/j.geomorph.2012.08.021 [10] Chen Peng, Ren Jinjin, Wang Haixia, et al. Equal scale structure from motion method based on deep learning [J]. Opto-Electronic Engineering, 2019, 46(12): 190006. (in Chinese) [11] Micheletti N, Chandler J H, Lane S N. Investigating the geomorphological potential of freely available and accessible structure from motion photogrammetry using a smartphone [J]. Earth Surface Processes and Landforms, 2015, 40(4): 473−486. doi: 10.1002/esp.3648 [12] Zinber T, Schmidt J, Niemann H. Point set registration with integrated scale estimation[C]//Proceedings of International Conference on Pattern Recognition and Image Processing, PRIP, 2005: 116-119. [13] Zhou Q Y, Park J, Koltun V. Fast global registration[C]//Proceedings of European Conference on Computer Vision, ECCV, 2016: 766-782. [14] Black M J, Rangarajan A. On the unification of line processes, outlier rejection, and robust statistics with applications in early vision [J]. International Journal of Computer Vision, 1996, 19(1): 57−91. doi: 10.1007/BF00131148 [15] Liu Kai, Wang Kan, Yang Xiaomei, et al. DoG keypoint detection based fast binary descriptor [J]. Optics and Precision Engineering, 2020, 28(2): 485−496. (in Chinese) -
点击查看大图
计量
- 文章访问数: 329
- HTML全文浏览量: 126
- 被引次数: 0
