-
近几年环境污染问题日益严重,烟尘雾霾粒子与辐射之间的相互作用成为了研究热点。为了能够降低甚至解决不良气候环境对光传输造成的影响,需要发展更为真实且实用的传输模型,首先要获取烟雾环境粒子的偏振散射特性。研究者对退偏度与球形粒子的物理特性、光学特性之间的关系进行了分析,完善了退偏振理论方法[1-3]。北京航空航天大学进行了关于球形气溶胶散射光偏振特性的研究。但自然界中很多粒子不是球形,而且目前无论是理论计算还是工程应用,大多基于Mie散射球形理论来处理光在大气中传输的散射问题。有研究通过对黄沙粒子进行电镜扫描后发现,该粒子长短轴之比约为1.7[4],Hil对类似粒子进行测试的结果是2.0,因此沙尘粒子形状应为非球形[5]。所以采用假定为球形颗粒的方法在将散射介质假设为理想的均匀球型同性粒子的同时也忽略了真实散射介质的异常有用偏振信息。目前计算非球型粒子散射特性方法有有限差分时域法(Finite Difference Time Domain method,FDTD),离散偶极子近似法(Discrete Dipole Approxim,DDA),T矩阵法(T-Matrix Method),几何光学近似法(Geometric Anomalous Approxim,GOA)[6-8]。其中T矩阵算法可以计算各种均匀对称粒子,或者层状粒子等,而且可以实现较大粒子尺度参数的计算,当粒子尺度参数小于180时都可以使用该方法计算。西安理工大学采用T矩阵发现火星非球形粒子群的散射主要集中在前向40°以内,在前向散射大于60°时非球形的散射强度比球形粒子高[9]。近期,研究者利用T矩阵方法发现金纳米旋转椭球在波长1 310 nm处具有最大的散射特性[10]。江西理工大学采用T矩阵的方法对自然光入射到非球形粒子的后向散射光偏振度空间分布进行了分析[11]。
文中将T矩阵算法从粒子散射引入到粒子的偏振散射特性中,对偏振光入射到非球形粒子后的偏振散射特性进行了计算。建立了非球型粒子偏振特性模型,以球坐标为基准求得散射振幅矩阵,并考虑粒子尺度与形状,对椭球形粒子,圆柱形粒子以及且切比雪夫(Chebyshev)粒子粒子的偏振特性进行了模拟,获得了其偏振特性分布特点,分析了其不同横纵轴比与不同形状对偏振特性的影响。为非球型粒子的多重散射提供了理论基础,也适应了更实际的情况。
-
非球型粒子可以通过T矩阵的方法计算任意形状的旋转对称粒子,任意形状散射体的外接球以外的散射区域,可以用矢量球谐函数展开。
将入射场与散射场通过矢量球面波函数展开如下:
$${E^{inc}}\left( r \right) = \sum\limits_{n = 1}^\infty {\sum\limits_{m = - n}^n {\left[ {{a_{mn}}Rg{M_{mn}}\left( {{k_1}r} \right) + {b_{mn}}Rg{N_{mn}}\left( {{k_1}r} \right)} \right]} } $$ (1) $${E^{sca}}\left( r \right) = \sum\limits_{n = 1}^\infty {\sum\limits_{m = - n}^n {\left[ {{p_{mn}}{M_{mn}}\left( {{k_1}r} \right) + {q_{mn}}{N_{mn}}\left( {{k_1}r} \right)} \right]} } $$ (2) 式中:
$RgM$ 、$M$ 、$RgN$ 、$N$ 均为矢量球面谐波;${k_1}$ 为周围介质的波数;$r$ 为位置矢量;${r_ > }$ 为以坐标原点为中心的散射体最小外接球半径,$r > {r_ > }$ 如图1所示。其中入射平面波的展开系数为:
$${a_{mn}} = 4{\text{π}} {\left( { - 1} \right)^m}{i^n}{d_n}E_0^{inc} \cdot C_{mn}^*\left( {{\vartheta ^{inc}}} \right)\exp \left( { - im{\varphi ^{inc}}} \right)$$ (3) $${b_{mn}} = 4{\text{π}} {\left( { - 1} \right)^m}{i^{n - 1}}{d_n}E_0^{inc} \cdot B_{mn}^*\left( {{\vartheta ^{inc}}} \right)\exp \left( { - im{\varphi ^{inc}}} \right)$$ (4) 式中:
$E_0^{inc}$ 为入射场;$\varphi $ 、$\vartheta $ 为方位角;C*、B*为矢量球面变量的对称函数。散射场展开系数
${p_{mn}}$ 和${q_{mn}}$ 与入射场展开系数${a_{mn}}$ 和${b_{mn}}$ 之间的关系也必然是线性的,由T矩阵给出如下关系:$${p_{mn}} = \sum\limits_{n' = 1}^\infty {\sum\limits_{m' = - n'}^{n'} {\left( {T_{mnm'n'}^{11}{a_{m'n}} + T_{mnm'n'}^{12}{b_{m'n'}}} \right)} } $$ (5) $${q_{mn}} = \sum\limits_{n' = 1}^\infty {\sum\limits_{m' = - n'}^{n'} {\left( {T_{mnm'n'}^{21}{a_{m'n'}} + T_{mnm'n'}^{22}{b_{m'n'}}} \right)} } $$ (6) 采用矩阵符号,上述两式可写为:
$$\left[ {\begin{array}{*{20}{c}} p \\ q \end{array}} \right] = T\left[ {\begin{array}{*{20}{c}} a \\ b \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{T^{11}}}&{{T^{12}}} \\ {{T^{21}}}&{{T^{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} a \\ b \end{array}} \right]$$ (7) 这表明散射场展开系数的列矢量由T矩阵和入射场展开系数的列矢量相乘获得。公式(7)就是T矩阵计算的核心。事实上,如果T矩阵已知,则公式(3)~(6)就给出了散射场。
联立公式(3)~(6)可得:
$$\begin{split} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftrightarrow$}} \over A} \left( {{{\hat n}^{sca}},{{\hat n}^{inc}}} \right) =& \frac{{4{\text{π}} }}{k}\sum\limits_{mnn'm'} {{i^{n' - n - 1}}{{\left( { - 1} \right)}^{m + m'}}{d_n}{d_{n'}}\exp \left[ {i\left( {m{\phi ^{sca}} - m'{\phi ^{inc}}} \right)} \right]} \cdot \left\{ {\left[ {T_{mnm'n'}^{11}{C_{mn}}\left( {{\vartheta ^{sca}}} \right) + iT_{mnm'n'}^{21}{B_{mn}}\left( {{\vartheta ^{sca}}} \right)} \right] \otimes C_{m'n'}^*\left( {{\vartheta ^{inc}}} \right)} \right. + \hfill\\ & \left. {\left[ { - iT_{mnm'n'}^{12}{C_{mn}}\left( {{\vartheta ^{sca}}} \right) + T_{mnm'n'}^{22}{B_{mn}}\left( {{\vartheta ^{sca}}} \right)} \right] \otimes B_{m'n'}^*\left( {{\vartheta ^{sca}}} \right)} \right\} \hfill \\ \end{split}$$ (8) 散射振幅矩阵元素如下:
$$\begin{split} {S_{11}}\left( {{{\hat n}^{sca}},{{\hat n}^{inc}}} \right) =& \frac{1}{k}\sum\limits_{n = 1}^\infty {\sum\limits_{n' = 1}^\infty {\sum\limits_{m = - n}^n {\sum\limits_{m' = - n'}^{n'} {{\alpha _{mnm'n'}}} } } } \left[ {T_{mnm'n'}^{11}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{21}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + } \right. \hfill \\ & \left. {{\text{ }}T_{mnm'n'}^{12}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{22}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right){\text{ }}} \right]\exp \left[ {i\left( {m{\phi ^{sca}} - m'{\phi ^{inc}}} \right)} \right] \hfill \\ \end{split} $$ (9) $$\begin{split} {S_{12}}\left( {{{\hat n}^{sca}},{{\hat n}^{inc}}} \right) =& \frac{1}{{i{k_1}}}\sum\limits_{n = 1}^\infty {\sum\limits_{n' = 1}^\infty {\sum\limits_{m = - n}^n {\sum\limits_{m' = - n'}^{n'} {{\alpha _{mnm'n'}}} } } } \left[ {T_{mnm'n'}^{11}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{21}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right)} \right. + \hfill \\ & \left. {T_{mnm'n'}^{12}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{22}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right)} \right]\exp \left[ {i\left( {m{\phi ^{sca}} - m'{\phi ^{inc}}} \right)} \right] \hfill \\ \end{split} $$ (10) $$\begin{split} {S_{21}}\left( {{{\hat n}^{sca}},{{\hat n}^{inc}}} \right) = &\frac{i}{{{k_1}}}\sum\limits_{n = 1}^\infty {\sum\limits_{n' = 1}^\infty {\sum\limits_{m = - n}^n {\sum\limits_{m' = - n'}^{n'} {{\alpha _{mnm'n'}}} } } } \left[ {T_{mnm'n'}^{11}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{21}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + } \right. \hfill \\ & \left. {T_{mnm'n'}^{12}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{22}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right){\text{ }}} \right]\exp \left[ {i\left( {m{\phi ^{sca}} - m'{\phi ^{inc}}} \right)} \right] \hfill \\ \end{split}$$ (11) $$\begin{split} {S_{22}}\left( {{{\hat n}^{sca}},{{\hat n}^{inc}}} \right) =& \frac{1}{{{k_1}}}\sum\limits_{n = 1}^\infty {\sum\limits_{n' = 1}^\infty {\sum\limits_{m = - n}^n {\sum\limits_{m' = - n'}^{n'} {{\alpha _{mnm'n'}}} } } } \left[ {T_{mnm'n'}^{11}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{21}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\pi _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + } \right. \hfill \\ & \left. {T_{mnm'n'}^{12}{\pi _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right) + T_{mnm'n'}^{22}{\tau _{mn}}\left( {{\vartheta ^{sca}}} \right){\tau _{m'n'}}\left( {{\vartheta ^{inc}}} \right){\text{ }}} \right]\exp \left[ {i\left( {m{\phi ^{sca}} - m'{\phi ^{inc}}} \right)} \right] \hfill \\ \end{split}$$ (12) k是内部场介质波数。由公式(9)~(12)的振幅散射矩阵单元即可求得非球形粒子的消光矩阵等偏振散射特性参数。
-
文中以几种旋转对称粒子进行计算,分别为切比雪夫粒子(Chebyshev)、椭球形粒子,圆柱形粒子,通过改进T矩阵的算法,计算了三种波长条件下的非球形粒子的偏振散射情况,为粒子形貌对偏振传输影响做了理论工作。所以针对非球形粒子的研究计算成为热点,将T矩阵计算方法应用到非球形的偏振光散射中。
椭圆绕着其自身的长轴旋转就可以形成长球体,椭圆绕着其自身的短轴旋转就可以形成扁球体。对于球坐标系而言,长球体形状可以表示为[9]:
$$r\left( {\theta ,\phi } \right) = a{\left( {{{\sin }^2}\theta + \frac{a}{b}{{\cos }^2}\theta } \right)^{\frac{1}{2}}}$$ (13) 式中:
$\theta $ 为偏振角;$\varphi $ 为方位角;$\alpha $ 的取值是椭圆旋转轴平行方向的一半;$b$ 是旋转轴垂直方向的一半。$a$ 与$b$ 相等时就是球形粒子;长球体或者扁球体的形状可以用偏心率来表示,偏心率$\varepsilon = b/a$ ,粒子的尺度分布函数可以用对数分布,表示如下:$$n\left( r \right) = \frac{1}{{{{\left( {2{\text{π}} } \right)}^{1/2}}r\ln {\sigma _g}}}\exp \left[ { - \frac{{{{\left( {\ln r - \ln {r_g}} \right)}^2}}}{{2{{\ln }^2}{\sigma _g}}}} \right]$$ (14) 当
${\sigma _g} > 1$ ,$n(r) = \dfrac{{2{r_1}}}{{r_2^2 - r_1^2}}{r^{ - 3}}$ ,$ {r}_{2}\leqslant r \leqslant {r}_{1} $ 时,粒子的等效半径${r_{{\rm{eff}}}}$ 与有效方差${v_{{\rm{eff}}}}$ 可以按下式计算:$${r_{{\rm{eff}}}} = \frac{1}{G}\int_{{r_1}}^{{r_2}} {{\rm{d}}r{\text{π}} {r^3}n\left( r \right)} $$ (15) $${v_{{\rm{eff}}}} = \frac{1}{{Gr_{{\rm{eff}}}^2}}\int_{{r_1}}^{{r_2}} {{\rm{d}}rn(r){{\left( {r - {r_{{\rm{eff}}}}} \right)}^2}{\text{π}} {r^2}} $$ (16) 其中,
$$G = \int_{{r_1}}^{{r_2}} {{\rm{d}}r{\text{π}} {r^2}n\left( r \right)} $$ (17) 即可计算出非球形颗粒的散射相函数,得到相应的偏振变化情况。
-
设定椭球形粒子为偏心率
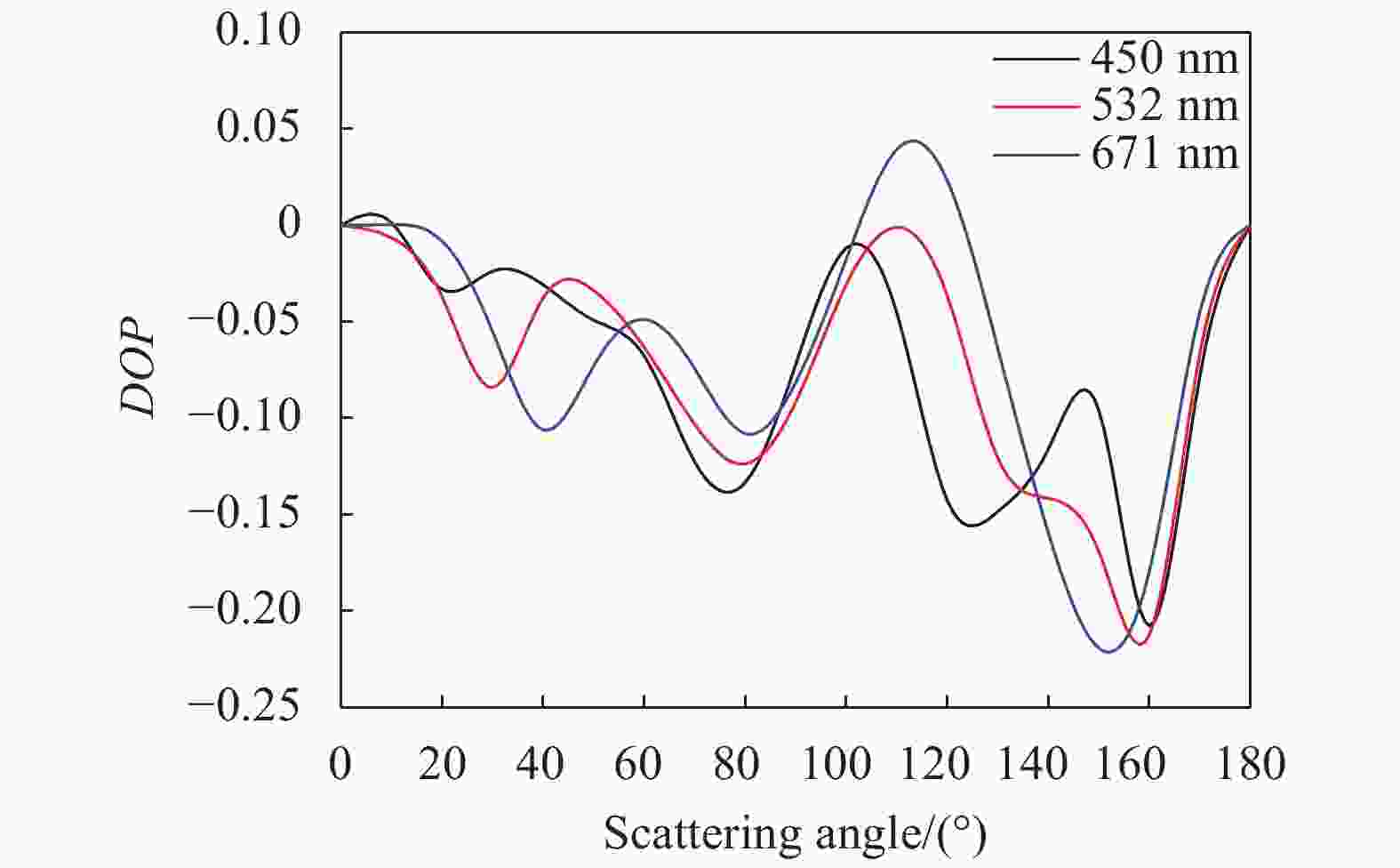
$\varepsilon = b/a$ =3的长椭球体。选取入射光的三种波长分别为450、532、671 nm,传输环境为吸湿性差的沙尘粒子,湿度20%,粒子折射率为0.150 5+0.006 9,半径为0.522 8 μm进行仿真,结果如下。从图2中可以看出,对于b/a=3的长椭球型粒子,偏振光的散射集中于侧向散射,在散射角为90°时,达到顶峰,当散射角为0°~20°,450 nm的偏振光散射后的偏振度大于其他两个波长,随着散射角的增加(散射角20°~90°),671 nm波长的偏振度高于450 nm与532 nm的偏振度;该类型粒子前向散射时(散射角为90°~130°)的偏振度以671 nm波长为最高。从图3中可以看出,对于b/a=2的长椭球型粒子,无论是前向散射还是后向散射都是波长越长偏振度越大,而且前向散射偏振度大于后向散射偏振度,但是部分散射角方向(50°~80°)时,532 nm的偏振度大于其他两个波长。

图 2 椭球形b/a=3的粒子散射角与偏振度关系
Figure 2. Relation between the scattering angle and the degree of polarization of ellipsoid b/a=3
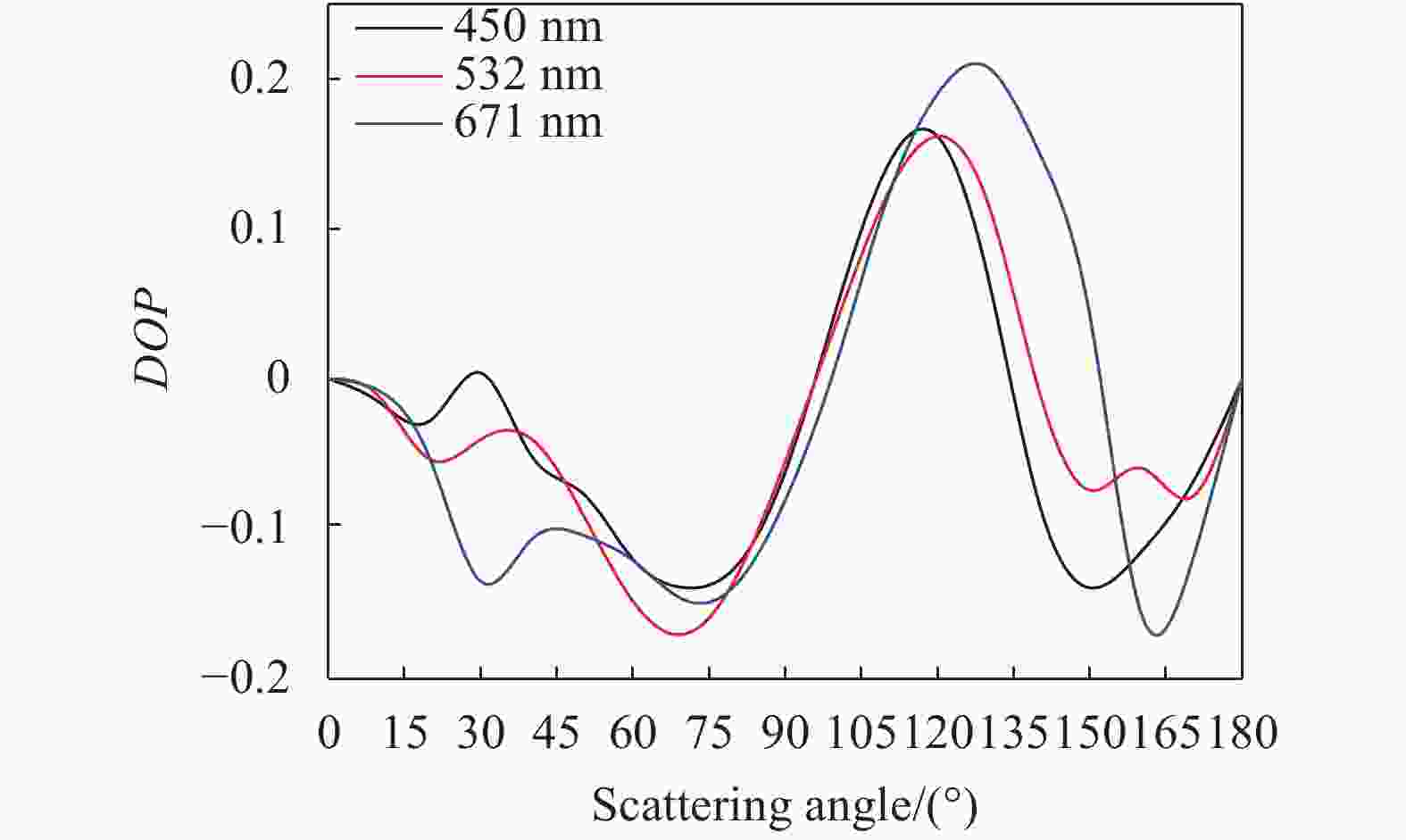
图 3 椭球形b/a=2的粒子散射角与偏振度关系
Figure 3. Relation between the scattering angle and the degree of polarization of ellipsoid b/a=2
从图4中可以看出,当偏心率为2时,三种波长的偏振度在散射角130°时达到最大,当偏心率为3时,三种波长的偏振度在散射角90°时达到最大,而且偏心率为3时的偏振度峰值高于偏心率为2时的峰值,450、532、671 nm的偏振度分别增加了50%、25%、24%。这说明随着椭球体的长短轴之比不断增大,前向散射逐渐变为侧向散射,并且长短轴之比增大意味着粒子形状变地尖锐,说明随着粒子形状变地尖锐,偏振度也增大了。
-
设定圆柱形粒子为偏心率(截面直径/长度)为0.5的圆柱体。选取入射光的3种波长分别为450、532、671 nm。传输环境为吸湿性差的沙尘粒子,湿度一定,粒子折射率为0.151+0.006 900,半径为0.523 μm,进行仿真结果如下。
从图5中可以看出,偏心率为0.5的扁圆柱粒子的偏振度在后向散射较为突出,当散射角达到150°~160°之间,偏振度最大;三种波长的偏振度随散射角震荡趋势几乎一致。图6中偏心率为2的长圆柱粒子在散射角为140°~160°时达到偏振度峰值,后向散射的偏振度高于前向散射;三种波长偏振度随散射角震荡趋势也是相同的。在散射角30°~90°之间,150°~170°之间,671 nm波长的偏振度要高于532 nm与450 nm的偏振度。
-
切比雪夫粒子的形状表示为:
$$r\left( {\theta ,\phi } \right) = {r_0}\left[ {1 + \xi {T_n}\left( {\cos \theta } \right)} \right],\left| \xi \right| < 1$$ (18) 式中:
${T_n}\left( {\cos \theta } \right)$ 代表的是颗粒的凹陷情况,选取了两种切比雪夫粒子进行计算,分别为$ {T}_{3}\left(-0.15\right) $ 、$ {T}_{8}\left(-0.1\right) $ ,n越大说明凹陷程度越大,仿真曲线如图7、图8所示。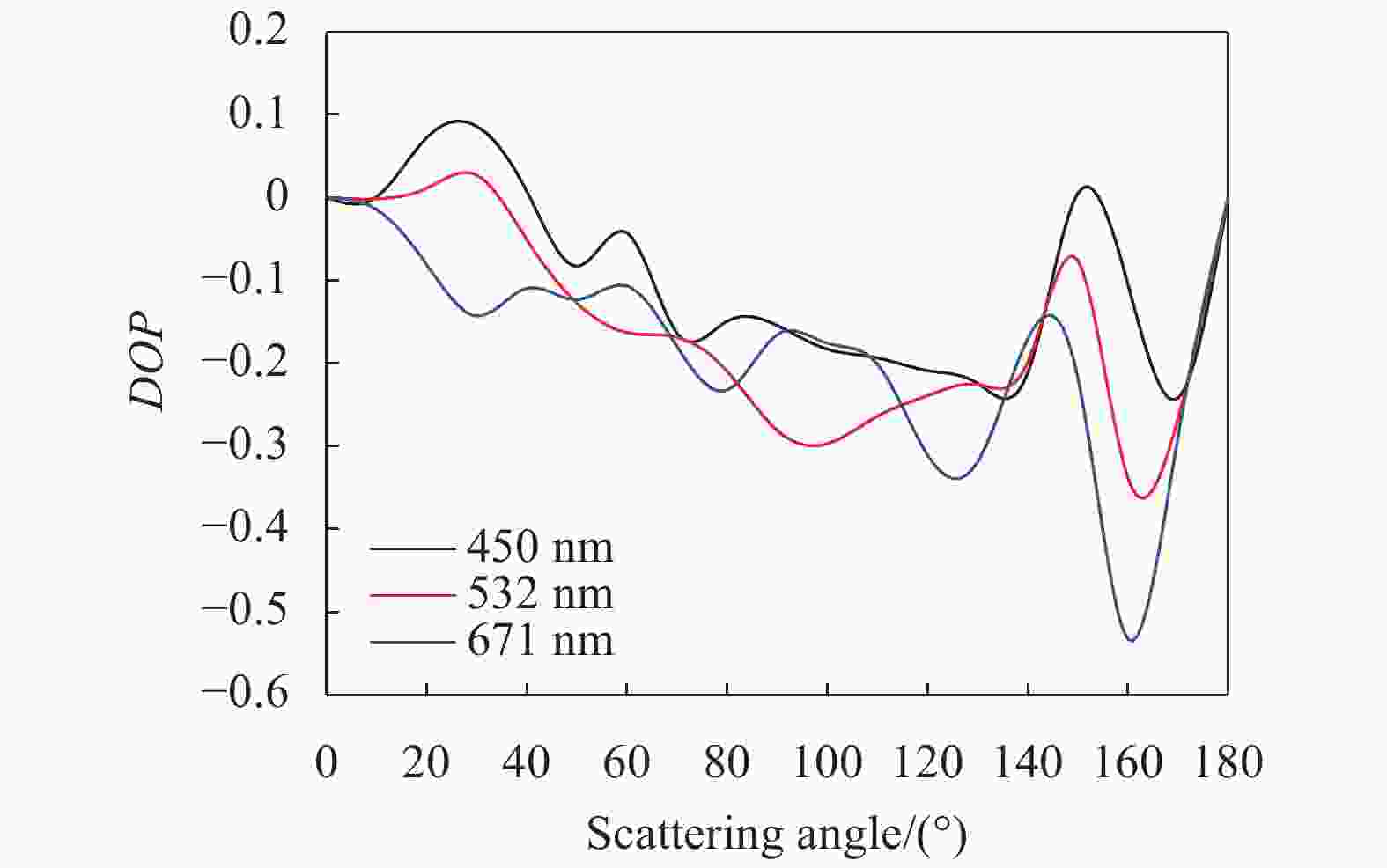
图 7
$ {T}_{8}\left(-0.1\right) $ 切比雪夫粒子偏振度随偏振角变化情况Figure 7. Polarization degree varies with the polarization angle of
${T_8}\left( { - 0.1} \right)$ Chebyshev particle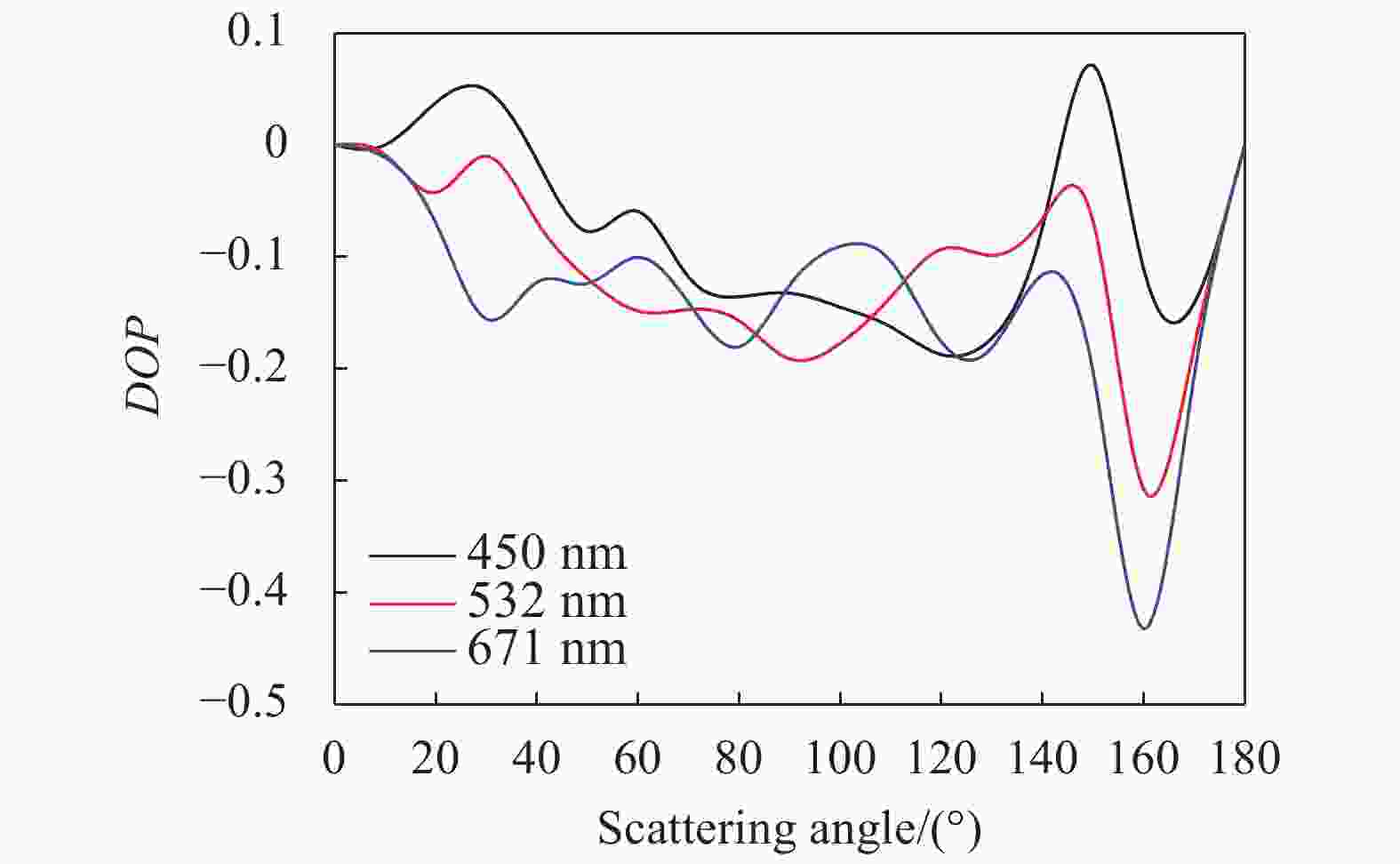
图 8
$ {T}_{3}\left(-0.15\right) $ 切比雪夫粒子偏振度随偏振角变化情况Figure 8. Polarization degree varies with the polarization angle of
${T_3}\left( { - 0.15} \right)$ Chebyshev particle通过图7与图8可以看出,如果散射粒子为切比雪夫粒子,那么偏振光的前向散射偏振度要高于后向散射偏振度,每种波长的偏振度最大值都在散射角160°~170°之间。在散射角为0°~50°与130°~170°时,随着波长的增加偏振度是增大的。而且
${T_8}\left( { - 0.1} \right)$ 型的切比雪夫粒子比$ T_{3}\left(-0.15\right) $ 型的切比雪夫粒子的偏振度高18%,而$ T_{8}\left(-0.1\right) $ 粒子表面的凹陷程度要大于$ T_{3}\left(-0.15\right) $ ,说明粒子表面的不规则度对偏振度是有影响的,随着凹陷程度增大,偏振度也变大。对于非球形粒子而言,随着椭球体的长短轴之比不断增大,前向散射逐渐变为侧向散射,并且随着粒子形状变得尖锐,偏振度也增大了。非球形粒子的长短轴如果互换,偏振特性几乎不发生改变。粒子表面的不规则度对偏振度是有影响的,随着凹陷程度增大,偏振度也变大。
-
基于T矩阵理论对非球型粒子的偏振传输特性进行了数学建模,计算了椭球形粒子,圆柱形粒子,以及切比雪夫粒子在450、532、671 nm三种波段下的偏振改变情况。当椭球形粒子偏心率为b/a=3时,偏振特性在散射角90°时最强。前向散射时,450 nm的偏振光散射后的偏振度大于其他2个波长;后向散射时偏振度以671 nm波长为最高。对于b/a=2的长椭球型粒子,无论是前向散射还是后向散射都是随着波长越长偏振度越大,而且前向散射偏振度大于后向散射偏振度,散射角方向为50°~80°时,532 nm的偏振度最大。随着椭球体的长短轴之比不断增大,前向散射逐渐变为侧向散射,并且随着粒子形状变得尖锐,偏振度也增大了。扁圆柱粒子的偏振度在前向散射较为突出,三种波长的偏振度随散射角震荡趋势几乎一致,可见粒子的长短轴如果互换的话,偏振特性几乎不发生改变。对于表面存在凹陷的且比夫雪粒子而言,偏振光的前向散射偏振度要高于后向散射偏振度,
${T_8}\left( { - 0.1} \right)$ 型粒子比${T_3}\left( { - 0.15} \right)$ 型粒子的偏振度高18%,随着粒子表面凹陷程度增大,偏振度也变大。研究结果为非球型粒子群的多次散射特性提供了理论基础,由于更加接近于真实非球形粒子, 所以具有更实际意义,为解决真实环境下与理想传输环境偏振传输特性之间存在差异提供了新思路。
Effect of aspheric particles on laser polarization characteristics
-
摘要: 球形粒子群的偏振散射特性已经通过研究获得,但是真实环境中粒子形状为非球形,非球型粒子的多次散射偏振特性规律尚未得到。基于T矩阵计算方法对非球型粒子散射模型进行了改进,获得了非球型粒子的散射振幅矩阵,对椭球形粒子,圆柱形粒子以及且切比雪夫粒子的偏振特性进行了模拟,分析了不同横纵轴比、形状、波长对粒子偏振特性的影响。研究结果表明:对于椭球形粒子而言,偏心率由2变为3后偏振度最大值从散射角130°变为90°,450、532、671 nm的偏振度分别增大了50%、25%、24%;圆柱粒子长短轴互换对于偏振度的改变影响不大。切比雪夫粒子表面的不规则度由3变为8后,偏振度增大了18%。研究结果为非球型粒子群的多次散射特性提供了理论基础,最终解决了真实环境与理想环境之间的偏振传输特性差异的问题。Abstract: The polarization scattering characteristics of spherical particle swarm have been studied, but in the real environment, the shape of particles is non-spherical, and the multiple scattering polarization characteristics of non-spherical particles have not been obtained. The aspheric particle scattering model was improved based on the T matrix calculation method to obtain the scattering amplitude matrix of aspheric particles. The influence of different horizontal and vertical axis ratios, shape and wavelength on the polarization characteristics of ellipsoidal particles, cylindrical particles and Chebyshev particles were analyzed by computer simulation. The results show that for ellipsoid particles, the maximum polarization degree changes from 130° to 90° after the eccentricity changes from 2 to 3, and the polarization degrees of 450 nm, 532 nm and 671 nm increases by 50%, 25% and 24% respectively. Cylindrical particle long and short axis interchange has little effect on the change of polarization. The surface irregularity of Chebyshev particles changes from 3 to 8, the polarization degree increases by 18%. The research results provide a theoretical basis for the multiple scattering characteristics of the aspheric particle group, finally solve the problem of the difference in polarization transmission characteristics between the real environment and the ideal environment.
-
Key words:
- aspheric /
- polarization characteristics /
- polarization degree /
- T-matrix /
- scattering characteristics
-
-
[1] Chandrasekhar S, Elbert D. The illumination and polarization of the sunlight sky on Rayleigh scattering [J]. Trans Am Phil, 1954, 44(6): 10.2307/1005777. [2] Dai Bing, Luo Xiangdong, Wang Yawei. Multiple light scattering of non-spherical particles with elliptical cross section [J]. Acta Physica Sinica, 2009, 58(6): 3864-3869. (in Chinese [3] Tang Meng, Zhang Yu. Research on polarization characteristics of micro-bubbles laser detection in wake [J]. Infrared and Laser Engineering, 2020, 49(1): 0105006. (in Chinese [4] Tian Jing, Bai Guangfu, Jiang Yang. Research of scattering Stokes parameters for ship wake bubbles [J]. Infrared and Laser Engineering, 2018, 47(2): 0206003. (in Chinese doi: 10.3788/IRLA201847.0206003 [5] Nakajima T, Tanaka M, Yamano M, et al. Aerosol optical characteristics in the yellow sand event sobserved in May, 1982 at Nagasaki, Ⅱ, Models [J]. J Meteorol, 1989, 65: 279-291. [6] Hill S C, Hill A C, Barber P W. Light scattering by size/shape distributions of soil particles and spheroids [J]. Opt Appl, 1984, 23(7): 1025-1031. doi: 10.1364/AO.23.001025 [7] Hu Shuai, Gao Taichang, Li Hao, et al. An analysis on the impact of non-spherical aerosol on polarized radiative transfer in near-infrared band and its equivalent-sphere errors [J]. J Infrared Millim Waves, 2017, 36(2): 235-245. (in Chinese [8] Clyde O, Kenneth H F, William J C. Aerosol size and relative humidity [J]. Journal of Colloid Science, 1958, 13: 472-482. doi: 10.1016/0095-8522(58)90055-2 [9] Yang Yufeng, Han Anli, Qin Jianhua, et al. Spectral scattering characteristic of non-spherical mars dust particles [J]. Acta Photonica Sinica, 2019, 48(12): 1229001. (in Chinese doi: 10.3788/gzxb20194812.1229001 [10] Yakupu Xiayiding, Tuersun Paerhatijiang, Wu Panpan. Optimization of light absorption and scattering properties of gold nanospheroids [J]. Acta Optica Sinica, 2020, 40(4): 0429001. (in Chinese doi: 10.3788/AOS202040.0429001 [11] Ye Kuntao, Ji'E Musha, Zhai Shengjie. Influence of particle shape on polarization characteristics of backscattering light in turbid media [J]. Chinese Journal of Lasers, 2020, 47(1): 0105004. (in Chinese doi: 10.3788/CJL202047.0105004 -







 下载:
下载: