-
1993年,Taylor等[1] 首次提出基于相位敏感光时域反射计(phase-sensitive optical time domain refle ctometry,Φ-OTDR)的分布式光纤振动传感器。该传感器以其探测灵敏度高、监测距离长以及能够实现多点振动同时定位等优势受到国内外的广泛关注。经过二十多年的发展,Φ-OTDR的性能指标得到了极大的提高,在周界安防、石油管线预警和大型结构监测等多个领域具有广泛的应用前景[1-7]。
不同的应用场合对Φ-OTDR的性能指标提出了不同的要求。为了满足不同领域的应用需求,国内外学者提出了多种不同的技术方案优化Φ-OTDR的监测距离、空间分辨率、频率响应范围和探测灵敏度等各项性能指标。这些方案侧重优化的性能指标不同,光路结构、检测方法以及参数设置也存在显著差异,目前尚无一种方案能够同时满足在各个不同领域的应用需求。
在各种性能优化方法中,有一类是通过调制注入传感光纤的光脉冲的形状、频率、宽度、消光比和重复频率等参数来优化系统的各项性能指标。如果将这类技术方法进行整合,有可能通过脉冲调制实现Φ-OTDR各项性能指标的同步优化。有望使用同一套硬件设备,通过简单的调整探测光脉冲参数来满足不同领域的应用需求以提高系统的通用性。基于该问题,文中对Φ-OTDR脉冲调制方面的研究进展进行了综述,主要内容包括两个方面,一是光脉冲对系统性能的影响机理研究,二是通过调制探测光脉冲优化系统的性能指标。
-
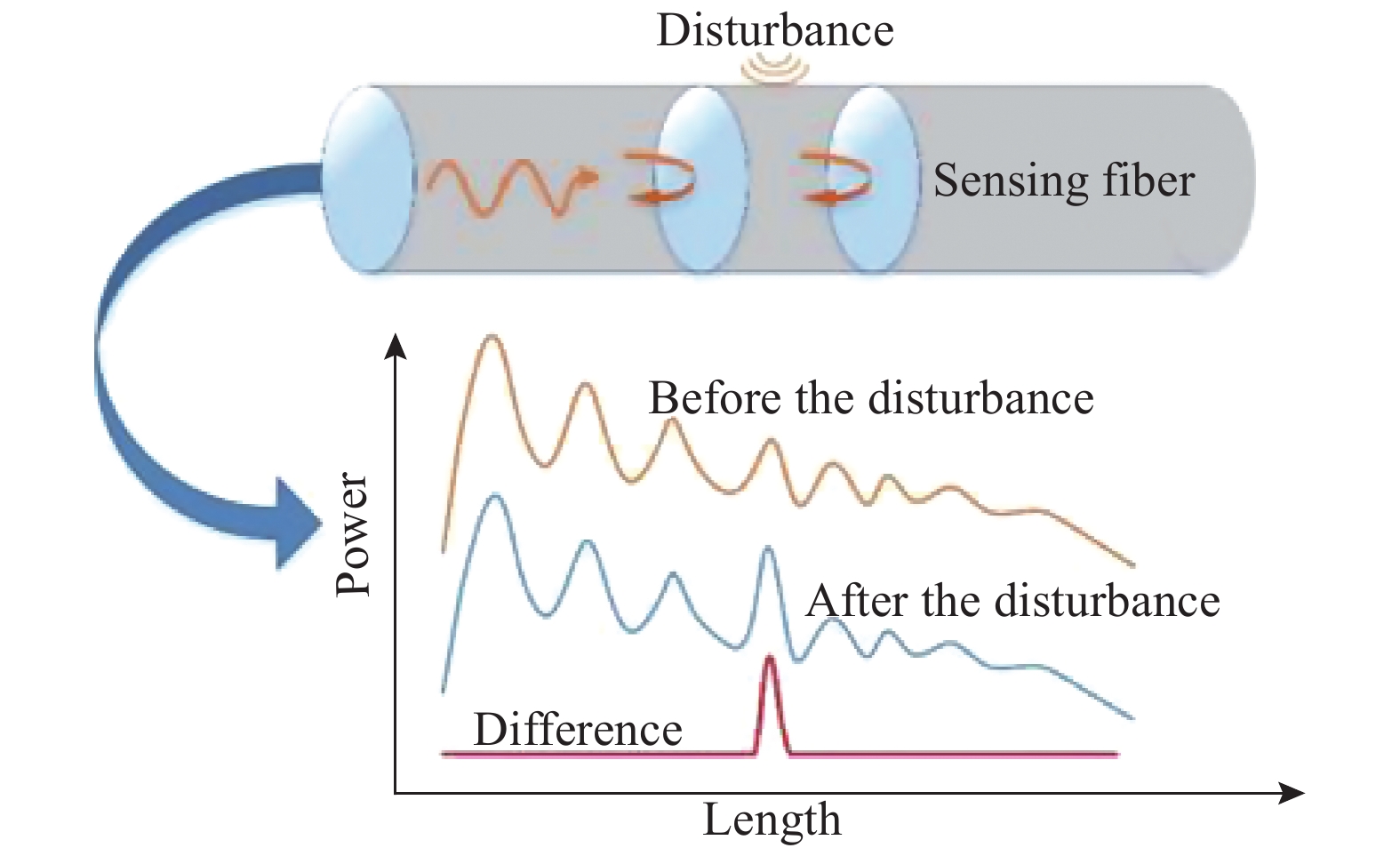
Φ-OTDR的工作原理如图1所示,向传感光纤中注入探测脉冲光,然后测量该脉冲光在传感光纤中传播时产生的背向瑞利散射光。为了提高对振动的敏感性,Φ-OTDR中使用高相干光源来加强背向瑞利散射光之间的干涉,增强其对相位变化的敏感性。理想状态下,传感光纤未受到外界扰动时瑞利散射波形保持不变,当有应变或振动等作用在传感光纤上时,该处的光纤长度和折射率会发生变化,导致瑞利散射光波相位变化,进而引起该位置瑞利散射波形的波动。将扰动前后两条瑞利散射曲线进行差分就能实现对振动的检测和定位。
-
探测光脉冲作为Φ-OTDR实现振动探测的重要部分,其各项参数,如宽度、频率、形状以及消光比等必然对系统系统性能有着重要影响。
-
注入探测光脉冲的宽度
${T_p}$ 决定了系统的空间分辨率[1],即:$$\Delta z = \dfrac{{{T_p}c}}{{2n}}$$ (1) 式中:
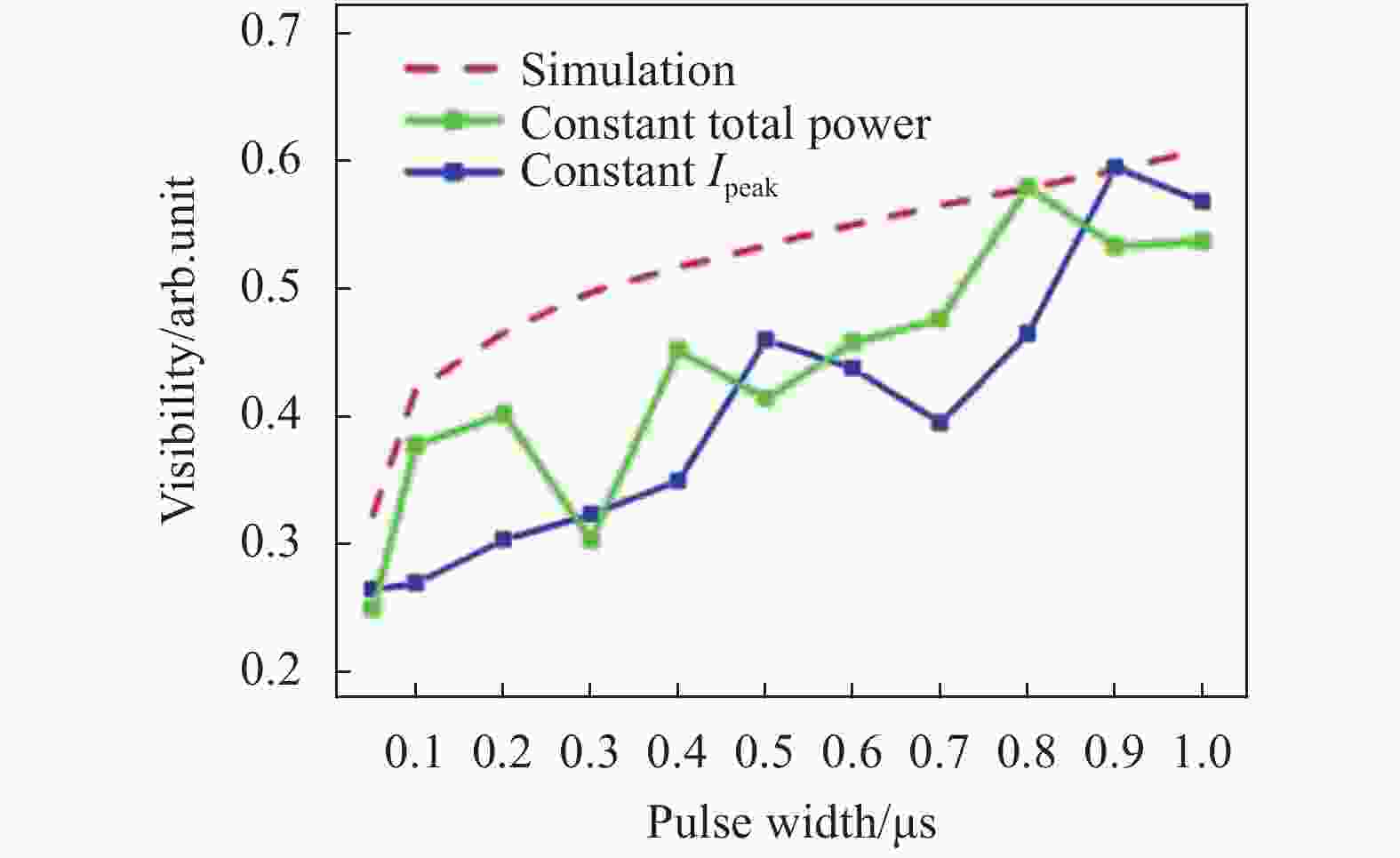
$c$ 为光在真空中速度;$n$ 为光纤折射率。显然,脉冲宽度越小,系统的空间分辨率越高。但同时光脉冲的光功率会降低,随着光脉冲在传感光纤中传播,所能探测的传感距离会降低[8]。因此,脉冲宽度不仅决定了空间分辨率而且限制了传感距离。笔者所在课题组分析了脉冲宽度对Φ-OTDR干涉可见度的影响[9]。干涉可见度是为了评价增大光功率时,时间响应曲线的波动幅度。通过仿真和实验比较了两种情形下脉冲宽度和干涉可见度的关系:(1)保持不同脉冲宽度下脉冲光的总功率恒定;(2)保持不同脉冲宽度下脉冲光的峰值功率恒定,即总功率随着脉宽的增大而线性增加。实验中选取的脉冲宽度区间可避免产生非线性效应。实验结果如图2所示,系统的干涉可见度与光脉冲的功率无关,而随着脉冲宽度的增大而增大。这说明,在传感光缆信号比较微弱的情形下,通过增大脉冲宽度可提高系统的灵敏度。
王坤[10]研究了脉冲宽度对Φ-OTDR系统信噪比的影响。实验中通过调整脉冲宽度测试了信噪比的变化规律,如图3所示,信噪比随脉冲宽度的增加先增加再减小。当脉冲宽度较小时,受光脉冲调制器件特性影响,输出的光脉冲不稳定,脉冲幅值随着脉冲宽度增加,同时系统信噪比也快速增加。当脉冲宽度增大到一定程度,光脉冲幅度保持稳定,系统信噪比最大。当脉冲宽度继续增加会逐渐增加注入传感系统的光功率,此时受到非线性效应影响,信噪比开始下降。选择合适的脉冲宽度可以实现较高信噪比,得到更好的探测性能。
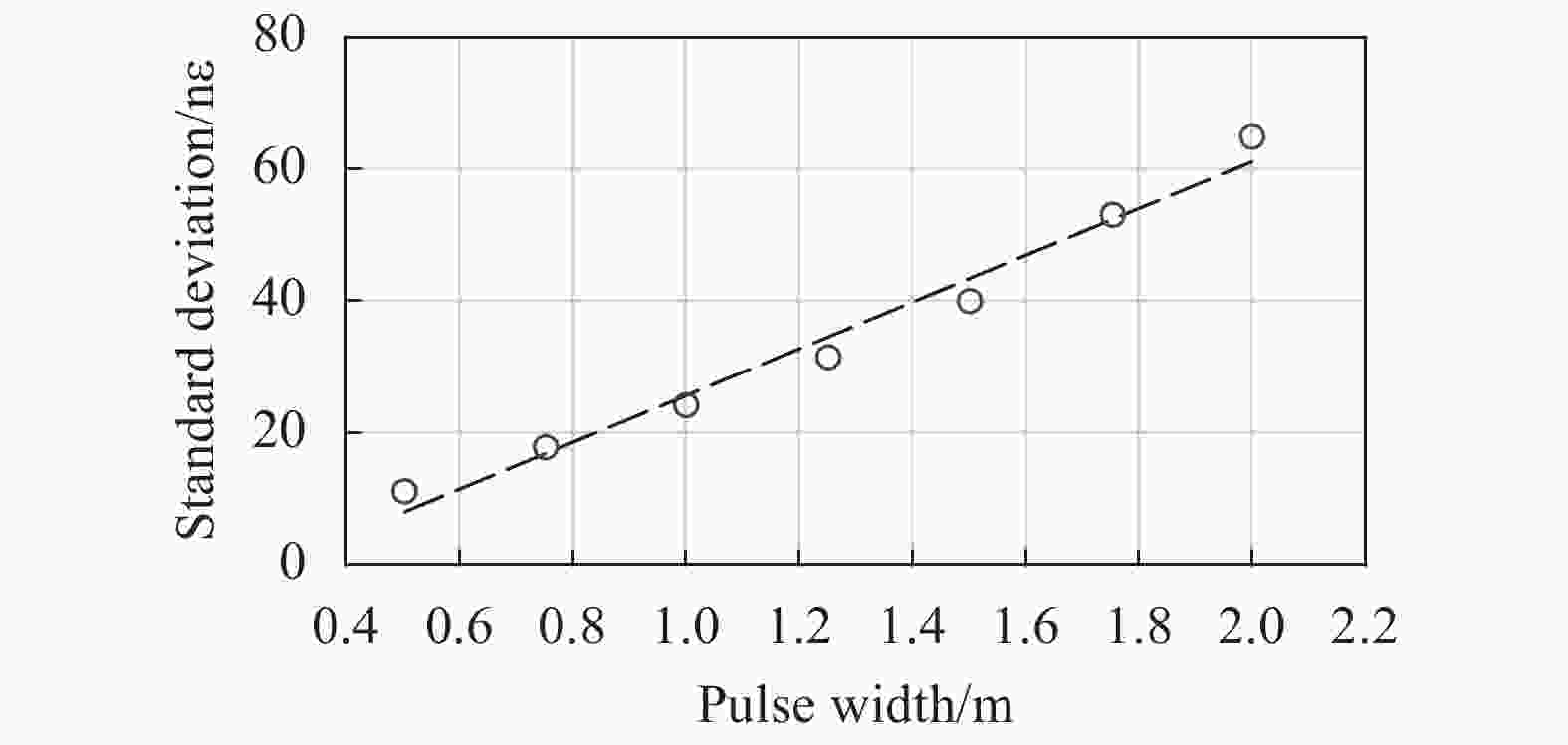
Ali Masoudi等[11]分析了脉冲宽度对应力测量准确度的影响,图4为数值模拟得到的应变水平标准差与脉冲宽度呈现线性关系。对于长的脉冲宽度,散射中心之间的距离很大,即使很小的应变也会导致散射中心显著的重新分布,因此应变前后该位置背向瑞利散射光相位之间的相关性很小。而对于短的脉冲宽度,受到应力时散射中心位移较小,对背向散射光的相位变化影响不明显。因此,通过减小脉冲宽度可以提高Φ-OTDR系统的精度。
脉冲宽度作为影响Φ-OTDR系统性能的重要参数,决定着系统的空间分辨率,影响着传感距离。窄的光脉冲宽度不仅可以提高系统空间分辨率,还能在测量应力时表现出更精高的精度。拓展脉冲宽度在增加传感距离的同时还可以增强时间响应曲线的可见性进而实现探测性能的提升。不同的脉冲宽度可以对应得到不同的信噪比,通过选择合适的脉冲宽度可以有效地提高Φ-OTDR系统的工作性能。
-
理想状况下,Φ-OTDR系统采集的瑞利散射曲线应当在外界没有振动时保持不变。但由于受到激光器频率漂移的影响,曲线会发生畸变,可能导致检测失败。为了更好地反映曲线波动的剧烈程度,文中定义了波动率系数(Fluctuations Ratio Coefficient,FRC):
$$FRC = \dfrac{1}{{{M_k} - 1}}\sum\limits_{i = 2}^{{M_k}} {\left| {{k_i} - {k_{i - 1}}} \right|} /{t_p}$$ (2) 式中:
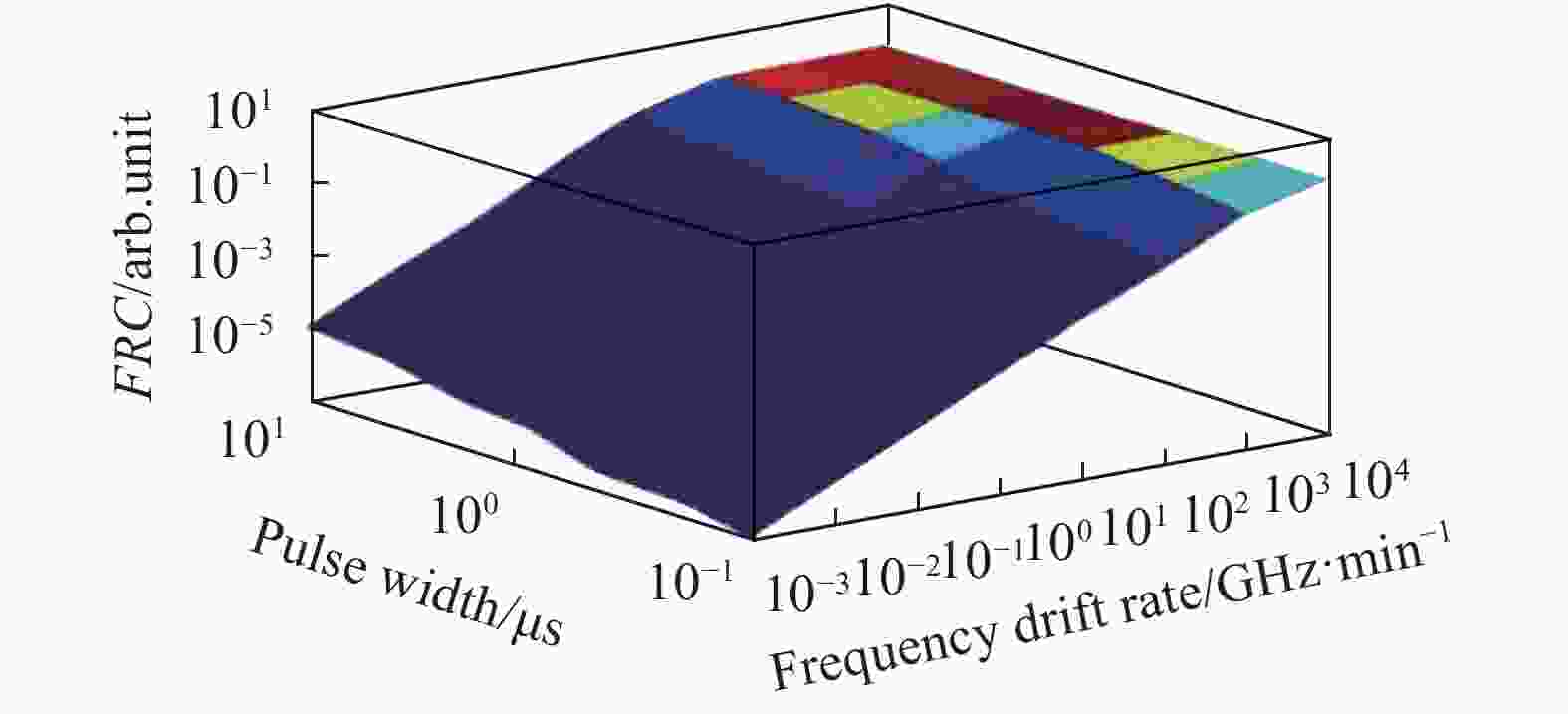
${M_k}$ 是采集的背向瑞利散射曲线总数;${k_i}$ 是第$i$ 条曲线在特定位置处的归一化散射光功率;${t_p}$ 是脉冲间隔。显然波动率系数越大,瑞利散射曲线的波动越剧烈。在此基础上,深入分析了激光器频率漂移引起的曲线波动和脉冲宽度之间的关系。结果表明,FRC随着激光器频率漂移的增大而增大;同时,当激光器的频率漂移保持不变时,FRC随着脉冲宽度的减小而降低,如图5所示[12]。这说明降低脉冲宽度是减小激光器频漂影响的一种简单而有效的办法。针对激光器频漂的问题,张旭苹等[13]提出了主动光频扫描法。该方法基于相同光频的探测脉冲得到的时域曲线形状相同,不同光频探测脉冲得到的时域曲线形状不同的原理。测量时使用互相关计算来衡量扫频曲线与原始曲线的相似程度,并选取互相关值最大的那条曲线作为原始曲线的同频曲线。进而通过曲线相似性的偏移来获取光源频率漂移的大小和方向。通过反复进行上述操作,就可连续对光源频率漂移进行补偿,实现抑制Φ-OTDR曲线畸变的目的。
-
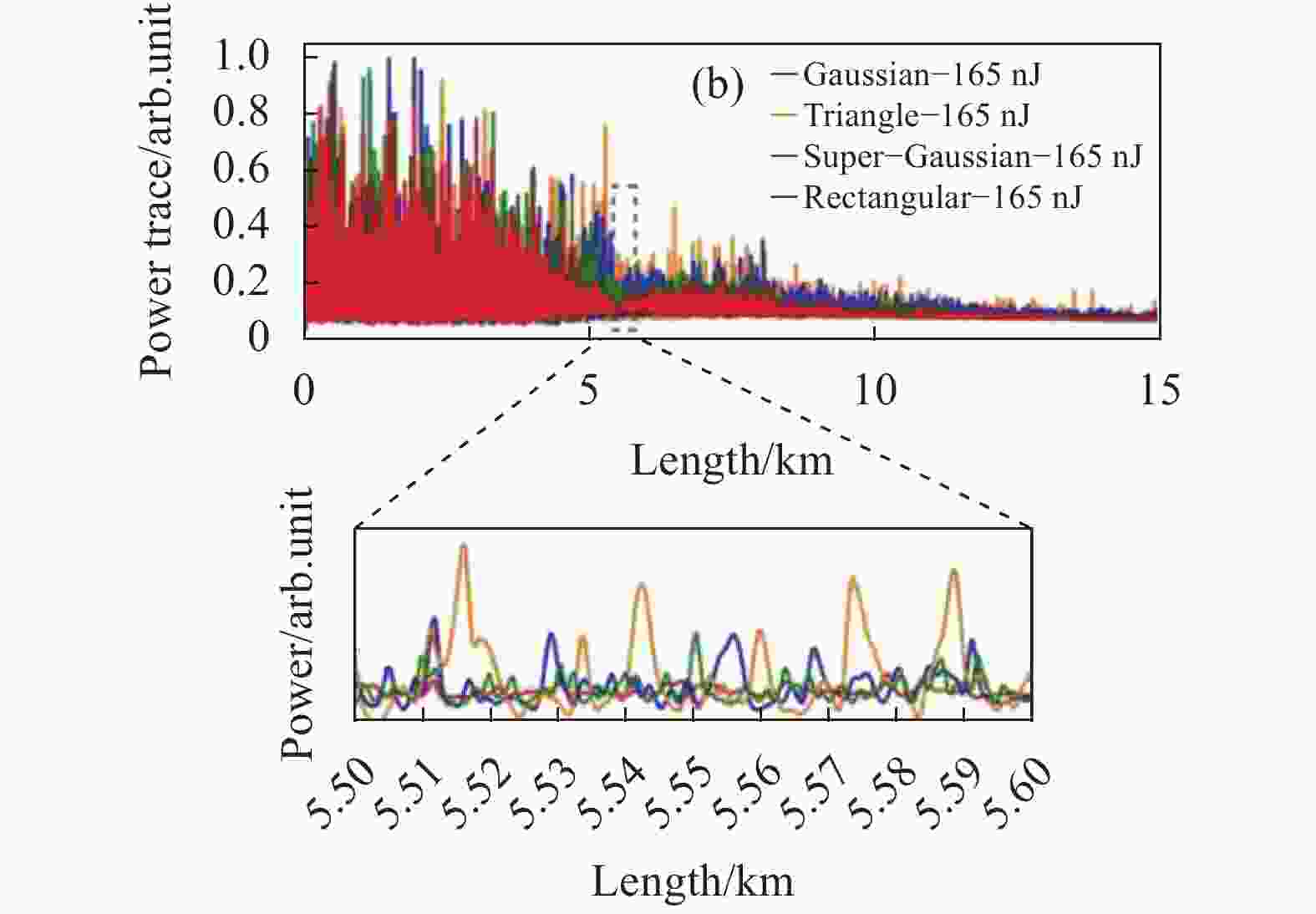
Φ-OTDR系统在进行长距离监测时需要往传感光纤中注入能量较大的光脉冲,以确保传感光纤的远端也能获得较高的光能量。然而,当光脉冲能量较大时,又容易引起调制不稳定效应。Martins等[14]比较了高斯形、三角形、超高斯形和矩形四种不同的脉冲形状下的背向瑞利散射曲线。结果表明,使用矩形脉冲时,曲线的灵敏度和传感距离最差;而高斯形和三角形光脉冲可以限制调制不稳定的影响,使得在相同峰值功率和空间分辨率下,传感距离和灵敏度都得到提高,如图6所示。
-
较低的调制器消光比会导致光脉冲中产生较高的泄露光能量,使得整个传感光纤中分布着较大的瑞利散射噪声,容易导致定位精度降低甚至定位方法失效,同时限制系统的空间分辨率和传感距离。Xiaoyi Bao等[15-16]提出了3种提高消光比的方法:(1) 将非线性光纤环形镜(nonlinear optical loop mirror,NOLM)和电光调制器(electro-optic modulator,EOM)结合,NOLM作为只允许高输入能量通过的光开关;(2) 2个EOM级联,第二个EOM作为附加的光开关;(3) 利用非线性克尔效应使正弦调制光信号进行自相位调制产生侧边带。图7比较了两种不同消光比下1.5 km传感光纤产生的背向瑞利散射曲线,从图中可以看出,高消光比可以显著减小背景噪声水平。
-
光脉冲是影响Φ-OTDR系统性能的重要参量,对光脉冲进行适当的调制能够优化系统的信噪比、报警率、空间分辨率和响应带宽等各项性能参数,并实现对振动信号的相位恢复。
-
信噪比作为反映Φ-OTDR探测性能的重要参数,在实际应用中不仅受到系统器件性能的影响,也受到光纤应用场合环境噪声的影响。国内外学者提出了多种技术方法[17-18]以提高系统相干效果或减小噪声水平,从而提高Φ-OTDR系统的信噪比。
Muanenda等[19]采用了循环编码的光脉冲,探测到的光纤任意位置对应的背向散射光能量是多个脉冲的叠加,随后通过译码过程从编码曲线中得到等效的单脉冲瑞利散射曲线。该方法将信噪比提高了超过8 dB。Martins等[20]提出了一种啁啾相位敏感光时域反射计。该技术采用了2个色散系数大小相等方向相反的线性啁啾光纤布拉格光栅。该方法通过脉冲拉伸,将输入脉冲所携带的能量分布在较长的时域内,降低了其峰值功率,避免了非线性效应,从而在不影响空间分辨率的前提下将信噪比提高了约20 dB。
-
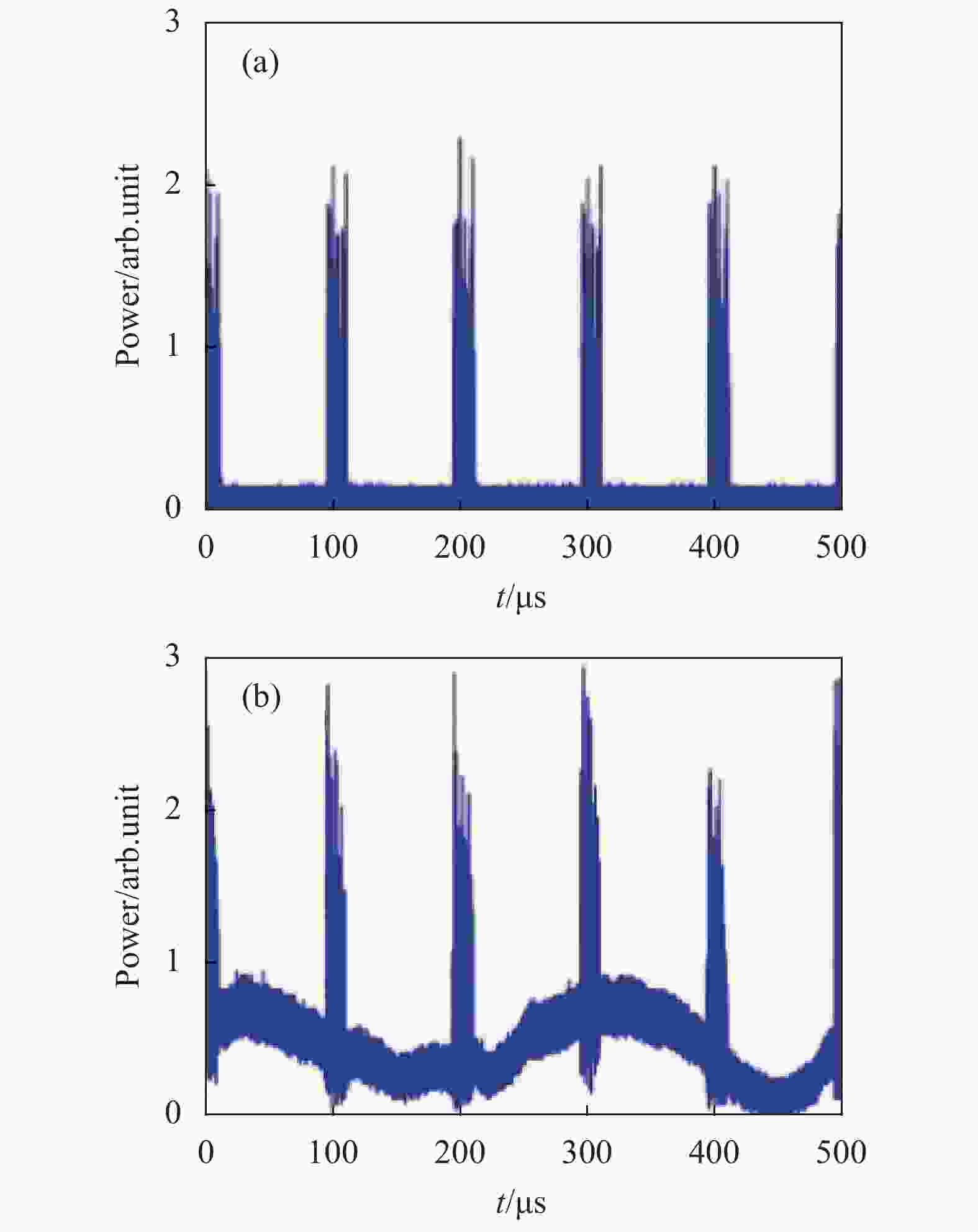
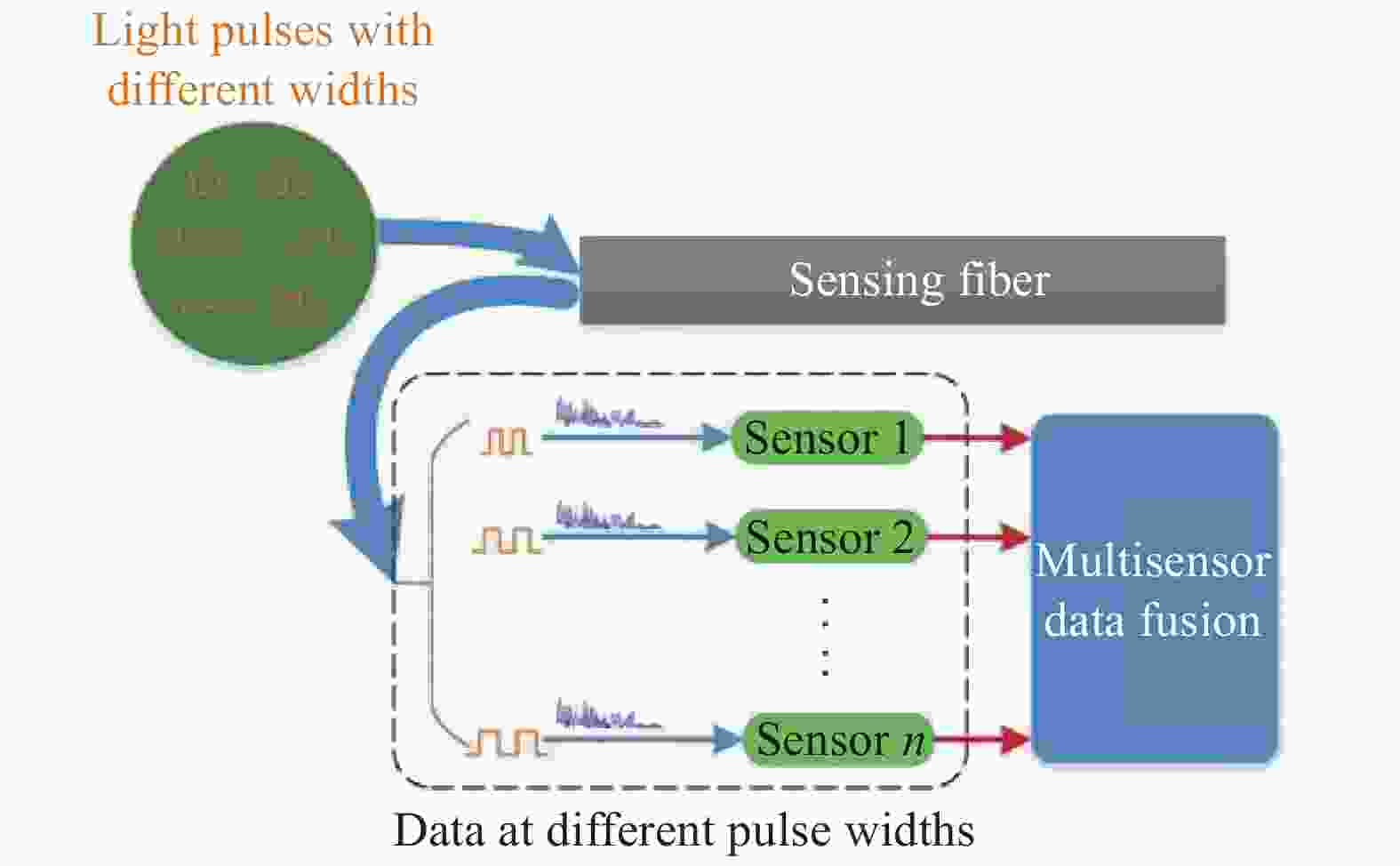
在实际应用中,过高误警率和漏警率严重限制了系统的推广应用。因此,笔者所在课题组提出了一种脉冲宽度复用的方法,即向传感光纤中注入宽度不同的光脉冲,将不同脉宽下的数据视为不同传感器的输出,然后用多传感器信息融合算法对这些数据进行综合处理,其原理如图8所示。该方法充分利用不同脉宽下数据的相关性和差异性来降低系统的误警率和漏警率,实验中使用多个不同宽度光脉冲组成的光脉冲序列,将误警率和漏警率降低了约一个数量级[21- 22]。理论上该方法能够进行无穷多个脉冲宽度的复用,有望进一步降低误警率和漏警率,但它同时降低了系统的高频响应能力,实际应用中需要进行综合考虑。
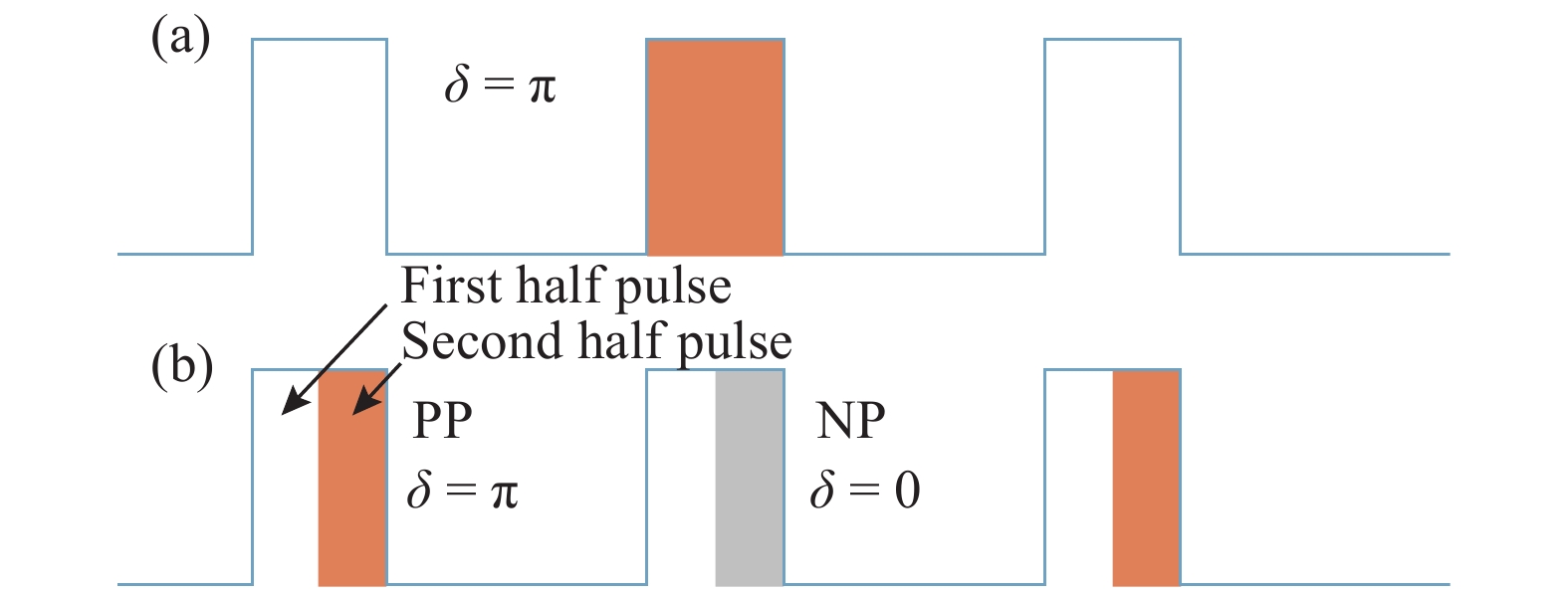
Φ-OTDR存在高误警漏警的一个重要原因是干涉衰弱,系统中使用的高相干光源会使背向瑞利散射曲线在某些位置的幅度接近于零,此时信号淹没在噪声中,容易产生误警。针对衰减问题,蔡海文等提出了一种多频率综合鉴别的方法,向传感光纤中同时注入多个频率的激光,利用不同光频下瑞利散射曲线干涉衰弱点的差异进行综合判别以降低误告警[23]。之后,他们又提出了一种相移双脉冲的方法,在注入传感光纤的两个相邻脉冲之间调制出π的相移,则2个脉冲产生的背向瑞利散射波罕有在同一位置一起出现干涉衰弱点的情况,利用这一特性进行综合判定即可降低误警的发生,如图9(a)所示[24]。但该方法将系统的带宽降低了1倍。因此,蔡海文等进行了改进,对第一个脉冲的后半部分调制出π的相移,而对第二个脉冲不进行调制,此时2个脉冲产生的背向瑞利散射波形同样很少有在同一位置出现干涉衰弱点的情形,而在2个波形都未出现干涉衰弱的位置处,可以将2个脉冲解调出的相位进行拼接,从而避免了带宽的损失,如图9(b)所示[25]。
张旭苹等[26]在相干探测Φ-OTDR系统中利用多频探测结合最优追踪算法持续地实现衰落的抑制。随后该团队[27]提出了超弱光纤布拉格光栅阵列的Φ-OTDR系统结构,采用复合双脉冲进行探测有效地消除了偏振衰减。该复合双脉冲如图10所示,第一个光脉冲是单脉冲,第二个光脉冲由2个正交的宽度相同的脉冲组成,第一个脉冲和第二个复合脉冲宽度相等。朱涛等[28] 对光脉冲进行了多频非线性频率调制来抑制衰减,调制后的非线性多频光脉冲频谱如图11所示。该方式可以抑制非线性效应,在不牺牲空间分辨率的同时增大了光脉冲的能量。
-
如前所述,注入传感光纤中的光脉冲的宽度决定了Φ-OTDR系统的空间分辨率,因此提高系统空间分辨率的通常做法是使用更窄的光脉冲[3, 17]。然而受到脉冲功率、噪声水平等因素的影响,这种难以在较长传感距离中实现。
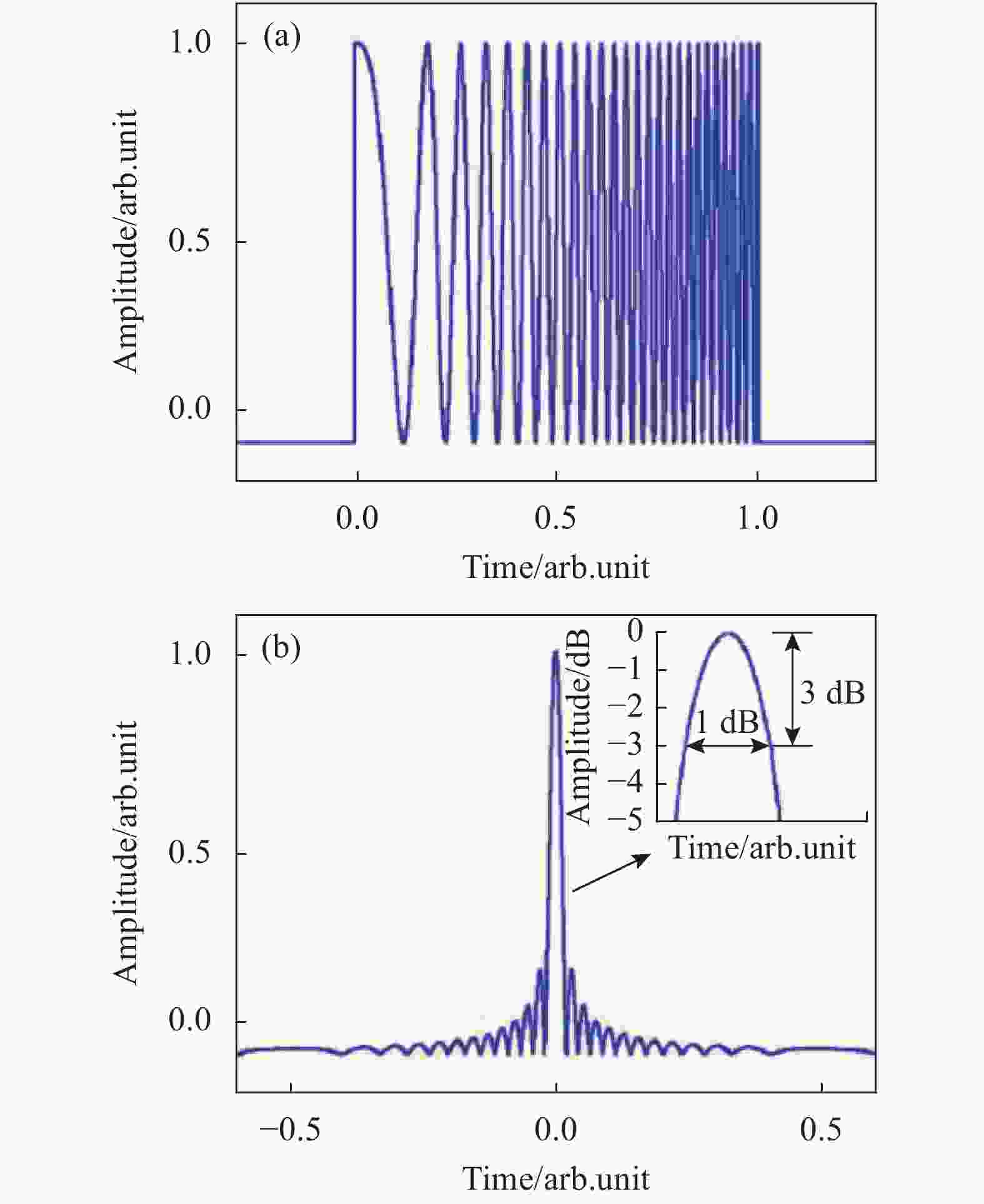
为了克服传感距离与空间分辨率的矛盾,邹卫文等[29]采用扫频脉冲作为探测光,在接收端对信号进行类似于匹配滤波的处理。图12(a)为一种进行线性扫频的探测光脉冲的时域波形,图12(b)为扫频脉冲经过匹配滤波后的波形,其强度分布近似呈很窄的sinc型函数。此时,Φ-OTDR系统的空间分辨率取决于该sinc函数的带宽,即:
$$\Delta z = \dfrac{c}{{2nB}}$$ (3) 式中:
$B$ 为线性频率调制的范围。从式中可以看出,系统的空间分辨率与扫频范围成反比,而与脉冲宽度无关,这就从原理上突破了空间分辨率和传感距离的矛盾。采用该方法,邹卫文等[30]用宽度为1 μs,扫频范围为1 GHz的光脉冲将空间分辨率提升到了10 cm。蔡海文等[31] 使用宽度为2 μs,扫频范围为420 MHz的探测光脉冲在19.8 km的测量范围内实现了30 cm的空间分辨率,首次在较长的传感距离中得到亚米级别的空间分辨率。此后,该团队又进一步优化了实验结构,获得了更加稳定的线性扫频脉冲,使用宽度为1.5 μs,扫频范围为105 MHz的探测光脉冲,在无中继放大的情况下实现了75 km传感距离和0.95 m的空间分辨率[32]。 -
在Φ-OTDR系统中,为了避免不同瑞利散射光波之间的混叠,探测光脉冲之间的间隔应大于光脉冲在传感光纤中一次往返的传输时间。因此,根据香农定理,系统所能探测的最大的频率
$f$ 为:$$f = \dfrac{c}{{4nl}}$$ (4) 式中:
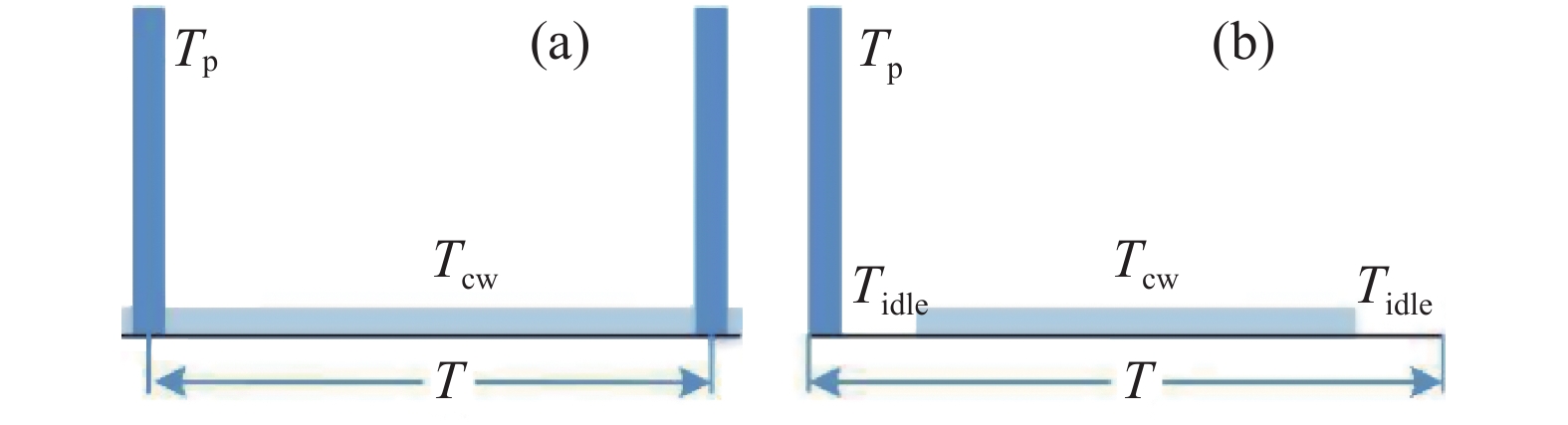
$l$ 是传感光纤长度。从公式(4)中可以看出,Φ-OTDR系统的监测距离越长,其所能探测的最大频率就越低。为了提高系统的频率响应范围,朱涛等[33] 将Φ-OTDR和Mach-Zehnder干涉仪进行复用。采用的探测光脉冲如图13(a)所示,由一个高强度的窄脉冲和低强度的宽脉冲组成,窄脉冲作为Φ-OTDR的探测光实现对振动的定位功能,宽脉冲视为连续光作为Mach-Zehnder干涉仪的探测光恢复出振动的相位。使用该方法在监测距离为1064 m的实验中实现了5 m空间分辨率和高达3 MHz的频率响应。Xiaoyi Bao等[34]将Φ-OTDR和偏振分集检测系统进行时分复用,Φ-OTDR系统用于确定振动的位置,偏振分集检测系统用于解调振动的频率。所采用的探测光脉冲如图13(b)所示,由一个高强度的窄脉冲和低强度的连续波构成,2部分由2个空闲时段隔开,其长度大于光脉冲在传感光纤中往返的时间。实验中在680 m光纤上实现了1 m的空间分辨率和高达0.6 MHz的响应带宽。
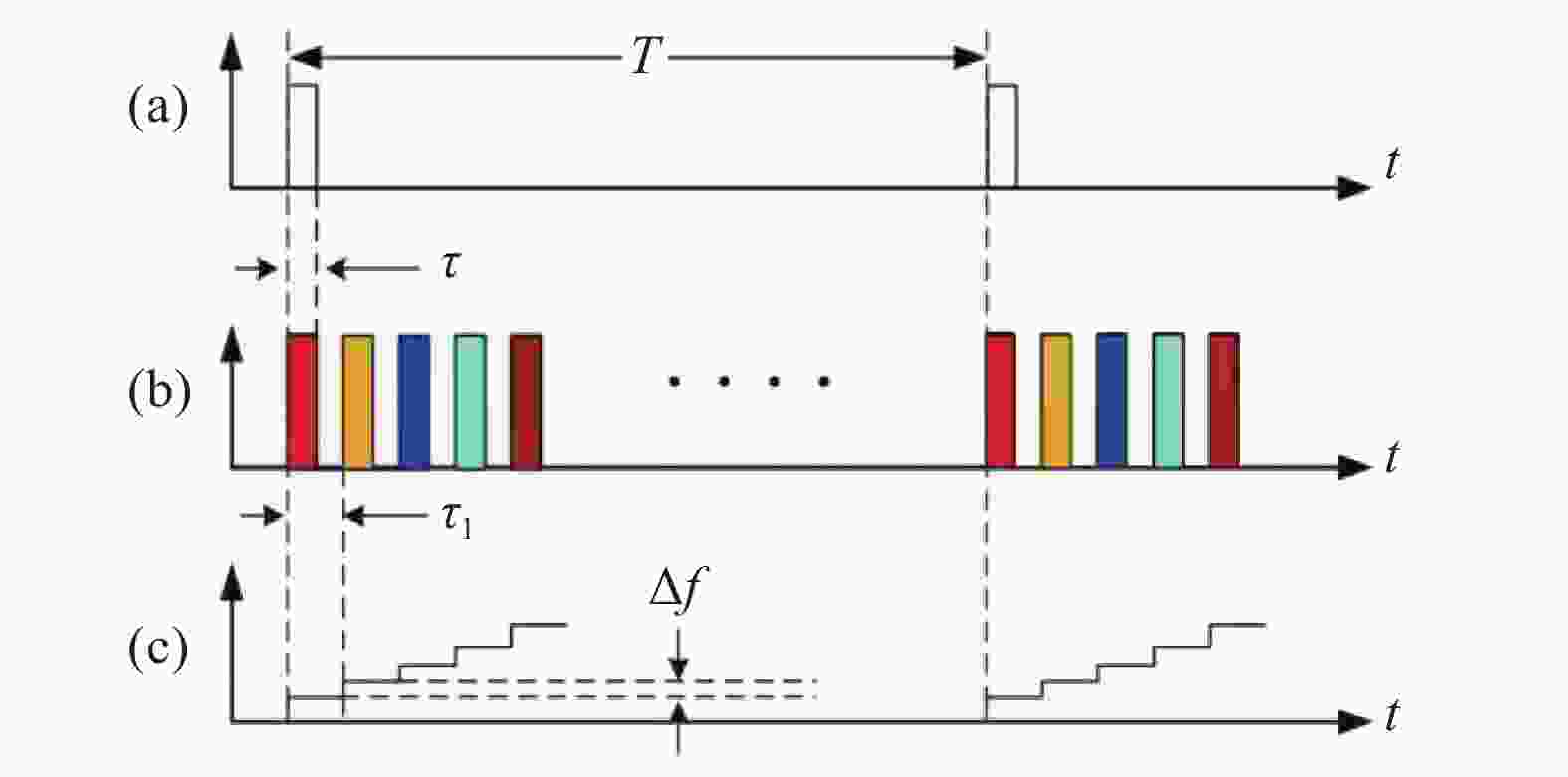
提高系统的频率响应的另一种方法是进行频分复用,如图14所示。其中图14(a)是普通Φ-OTDR的探测光脉冲,图14(b)是频分复用光脉冲序列,图14(c)表示频分复用的各个光脉冲之间的频率差为
$\Delta f$ 。通过将不同频率光脉冲下解调的相位数据按时间顺序连接,重建的相位曲线相比于单脉冲下的曲线响应带宽将提高多倍。使用该方法,潘政清等[35] 采用100个脉冲的频分复用在9.6 km传感长度下实现了0.5 MHz探测带宽。 -
近年来,国内外学者利用振动引起的相位变化与其造成的光纤折射率变化呈线性关系的特点实现了对振动波形的恢复和量化[36-37]。
张旭苹等[38] 利用频率扫描来补偿瑞利散射曲线的波动,向传感光纤中注入M组光脉冲序列,通过比较不同组的信号波形实现了10 nε的应变分辨率,但在高频振动(~1 kHz)的测量中并未恢复振动信号的波形。Martins等[39] 使用线性啁啾脉冲代替单频脉冲,这样脉冲的不同位置对应了不同的频率,当传感光纤某处折射率或长度发生变化时,通过瑞利散射曲线产生的时间位移可推算对应的频移量,进而解调出对应的应力或温度。该技术可以进行kHz速率的测量,同时在几个小时的测量中保持可靠性,实现了1 mK/4 nε的温度/应变分辨率。
Alekseev等[40]使用如图15所示的3个脉冲对结构,每个脉冲对包含两个脉冲,后1个脉冲相对前1个产生一定的相移,3组脉冲对的相移分别为0、–2/3π和2/3π。探测到的干涉信号呈现3种不同的干涉模式,其解调过程与基于
$3 \times 3$ 耦合器的解调方法相似。该方法实现了230 Hz正弦信号和锯齿波信号的相位解调,但每次探测都需要发射3组脉冲对,降低了系统的频率响应范围。为了避免降低系统的频率响应范围,张敏等[41] 使用1组双探测脉冲进行振动波形的恢复。2个光脉冲存在一定的间隔,产生的背向瑞利散射光将发生干涉。2个光脉冲之间调制出一定的频差,这样振动引起的相位变化被调制到外差频率的2个侧带上,通过外差解调即可恢复振动信号波形。使用该方法在470 m的传感距离上实现了20 Hz~25 kHz的频率响应。Muanenda等[42] 则使用了另一种双探测脉冲,对其中1个脉冲施加频率为
${\omega _0}$ 的高频相位载波,然后使用相位载波调制解调算法,在1.5 km的传感距离上实现了2 kHz的频率响应和24.16 dB的信噪比。曾周末等[43]根据不同的振动范围采用不同的探测脉冲。振动范围较小时,采用单探测脉冲,然后从获得的瑞利散射曲线中找出振动区域附近2个点,提取出响应曲线作为解调的2路原始信号,通过对其求和以及作差获得一对正交信号,最后通过IQ解调就能获取振动的相位信息。当振动区域较大时,则采用双探测脉冲,然后从得到的混叠瑞利散射曲线中找出振动区域后方位置的2个点,解调过程与单脉冲探测时一样。这种解调方法能够在直接探测系统中实现,省去了光学混合、干涉仪结构、相干检测等要求,大大简化了系统配置。
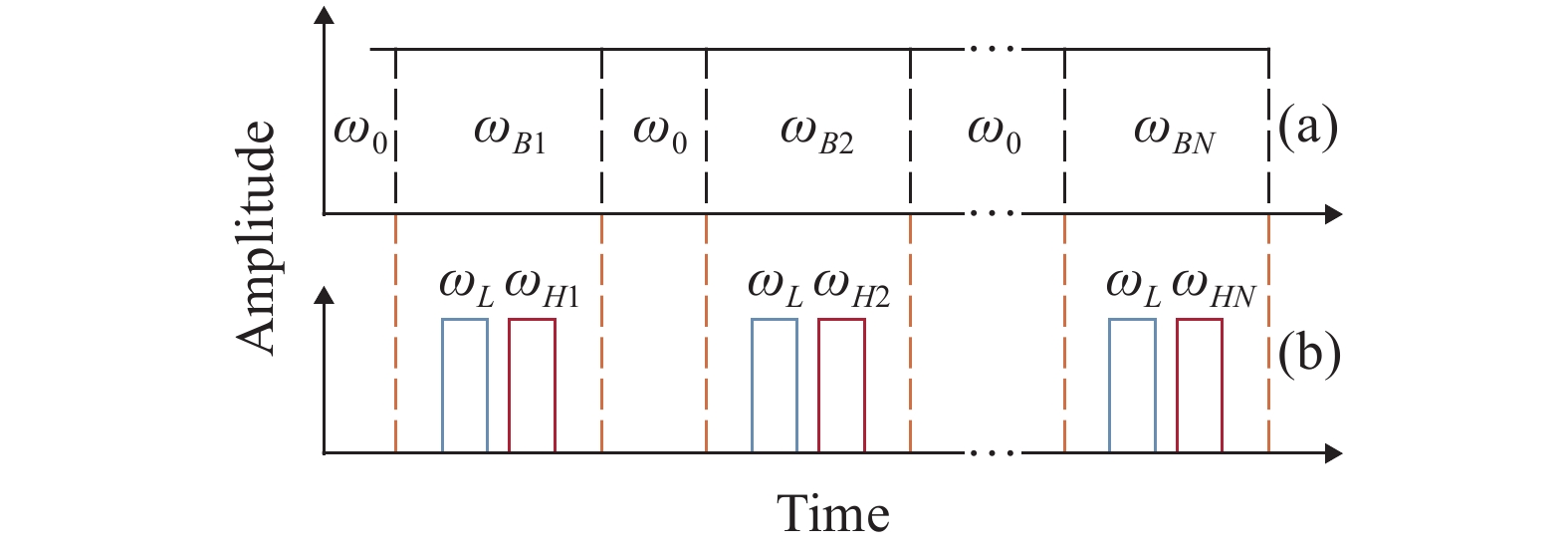
何祖源等[44]通过脉冲调制在直接探测系统中实现相位解调的同时,提升了系统的频率响应范围。采用可调激光光源和声光调制器同时对脉冲的频率进行调制,如图16所示。其中的双探测脉冲用来实现相位恢复,频分复用用来提高系统的频率响应;采用的升余弦型或高斯型脉冲可用来抑制串扰。实验中使用4组升余弦型双探测脉冲,在直接探测中成功解调出了相位,并在10 km的传感距离上实现了20 kHz的频率响应,打破了Φ-OTDR系统传感距离对响应带宽的限制。这一工作说明,通过脉冲调制有可能实现Φ-OTDR系统多项性能指标的共同提升。
-
文中系统回顾了基于Φ-OTDR的分布式光纤振动传感器在脉冲调制方面的研究进展,重点阐述了光脉冲的宽度、频率、形状以及消光比等参数对Φ-OTDR系统影响机理方面,以及通过脉冲调制优化系统信噪比、报警率、空间分辨率和响应带宽等各项性能参数并恢复振动信号波形等方面的研究进展。这些研究进展表明,通过适当的脉冲调制有可能实现系统多项性能指标的同步提升。文中为满足Φ-OTDR系统实际应用需求提供了新思路,为推动Φ-OTDR走向工程化具有重要意义。
Review of research on Φ-OTDR system based on pulse modulation
-
摘要: 基于相位敏感光时域反射计(Φ-OTDR)的分布式光纤振动传感系统向传感光纤中注入探测光脉冲,通过测量光脉冲传输过程中产生的背向瑞利散射光的波动实现对入侵扰动的识别和定位,故探测光脉冲对Φ-OTDR系统性能有重要影响。介绍了Φ-OTDR基于光脉冲调制方面的研究进展,其中包括光脉冲的宽度、频率、形状以及消光比等参数对Φ-OTDR系统性能影响机理,以及通过脉冲调制优化Φ-OTDR系统信噪比、报警率、空间分辨率、响应带宽等参数以及恢复振动信号波形方面的研究进展。旨在通过光脉冲调制实现Φ-OTDR系统多项性能指标同步提升提供新思路,进一步推动Φ-OTDR的工程应用。Abstract: Probe light pulses are injected into the sensing fiber by a distributed optical fiber vibration sensing system based on the phase-sensitive optical time-domain reflectometer (Φ-OTDR), then the vibration can be recognized and located by measuring the Rayleigh-backscattered light generated during the propagation of light pulses, so the probe light pulse has important effect on Φ-OTDR system performance. The research progress of Φ-OTDR in pulse modulation was introduced, including the impact of optical pulse width, frequency, shape, extinction ratio and other parameters on the system mechanism, and the research progress in the optimization of system parameters such as signal-to-noise ratio, alarm rate, spatial resolution, response bandwidth and recovery of vibration signal waveform by pulse modulation. In addition, this paper provides a new idea to ascend multiple performance indicators of the Φ-OTDR system simultaneously by means of optical pulse modulation to promote the engineering applications of Φ-OTDR.
-
-
[1] Taylor H F, Lee C E. Apparatus and method for fiber optic intrusion sensing: US 5194847[P]. 1993-03-16. [2] Juarez J C, Taylor H F. Field test of a distributed fiber-optic intrusion sensor system for long perimeters [J]. Applied Optics, 2007, 46(11): 1968-1971. doi: 10.1364/AO.46.001968 [3] Geng Ming, Liu Chen, Xu Zhijie, et al. Study on the innovative protective technology for the railway tunnel doors based on the micro-structure fiber distributed sensor [J]. Infrared and Laser Engineering, 2019, 48(7): 0722003. (in Chinese) [4] Shang Ying, Wang Chen, Wang Chang, et al. Distributed vibration sensing of perimeter security based on space difference of Rayleigh backscattering [J]. Infrared and Laser Engineering, 2019, 47(5): 0522001. (in Chinese) [5] Sun Qian, Feng Hao, Zeng Zhoumo. Recognition of optical fiber pre-warning system based on image processing [J]. Optics and Precision Engineering, 2015, 23(2): 334-341. (in Chinese) doi: 10.3788/OPE.20152302.0334 [6] Zinsou R, Liu X, Wang Y, et al. Recent progress in the performance enhancement of phase-sensitive OTDR vibration sensing systems [J]. Sensors, 2019, 19(7): 1790. [7] Li Chuan, Liu Jiang, Zhuang Jungang, et al. Strain detection of concrete structures based on Brillouin backscattering [J]. Optics and Precision Engineering, 2014, 22(2): 325-330. (in Chinese) doi: 10.3788/OPE.20142202.0325 [8] Lv Qiying, Li Lijing, Wang Hongbo, et al. Influences of laser on fiber-optic distributed disturbance sensor based on Φ-OTDR [J]. Infrared and Laser Engineering, 2014, 43(12): 3919-3923. (in Chinese) [9] Zhong X, Zhang C X, Li L J, et al. Influences of pulse on phase-sensitivity optical time domain reflectometer based distributed vibration sensor [J]. Optics Communications, 2016, 361: 1-5. doi: 10.1016/j.optcom.2015.10.038 [10] Wang Kun. Research on the practical technique of multifunctional optical fiber security monitoring system based on the phase sensitive OTDR[D]. Shanghai: Donghua University, 2015, 25-26. (in Chinese). [11] Masoudi A, Newson T P. Analysis of distributed optical fibre acoustic sensors through numerical modelling [J]. Optics Express, 2017, 25(25): 32021. doi: 10.1364/OE.25.032021 [12] Zhong X, Zhang C X, Li L J, et al. Influences of laser source on phase-sensitivity optical time-domain reflectometer-based distributed intrusion sensor [J]. Applied Optics, 2014, 53(21): 4645-4650. [13] Zhu F, Zhang X P, Xia L, et al. Active compensation method for light source frequency drifting in Phi-OTDR sensing system [J]. IEEE Photonics Technology Letters, 2015, 27(24): 2523-2526. doi: 10.1109/LPT.2015.2468075 [14] Fenandez-Ruiz M R, Martins H F, Juan P G, et al. Phase-sensitive OTDR probe pulse shapes robust against modulation-instability fading [J]. Optics Letters, 2016, 41(24): 5756-5759. doi: 10.1364/OL.41.005756 [15] Ren M, Zhou D P, Chen L, et al. Influence of finite extinction ratio on performance of phase-sensitive optical time-domain reflectometry [J]. Optics Express, 2016, 24(12): 13325. doi: 10.1364/OE.24.013325 [16] Baker C, Vanus B, Wuilpart M, et al. Enhancement of optical pulse extinction-ratio using the nonlinear Kerr effect for phase-OTDR [J]. Optics Express, 2016, 24(17): 19424. doi: 10.1364/OE.24.019424 [17] Qin Z G, Chen L, Bao X Y. Wavelet denoising method for improving detection performance of distributed vibration sensor [J]. IEEE Photonics Technology Letters, 2012, 24(7): 542-544. doi: 10.1109/LPT.2011.2182643 [18] Zhu T, Xiao X, He Q, et al. Enhancement of SNR and spatial resolution in Φ-OTDR system by using two-dimensional edge detection method [J]. Journal of Lightwave Technology, 2013, 31(17): 2851-2856. doi: 10.1109/JLT.2013.2273553 [19] Muanenda Y, Oyoc C J, Faralli S, et al. A cost-effective distributed acoustic sensor using a commercial off-the-shelf DFB laser and direct detection phase-OTDR [J]. IEEE Photonics Journal, 2015, 8(1): 1-10. [20] Juan P G, Cortes L R, Fernandez-Ruiz M R, et al. SNR enhancement in high-resolution phase-sensitive OTDR systems using chirped pulse amplification concepts [J]. Optics Letters, 2017, 42(9): 1728-1731. doi: 10.1364/OL.42.001728 [21] Zhong X, Gao X C, Deng H X, et al. Pulse-width multiplexing Φ-OTDR for nuisance-alarm rate reduction [J]. Sensors, 2018, 18(10): 3509-3520. doi: 10.3390/s18103509 [22] Zhong X, Zhao S S, Deng H X, et al. Nuisance alarm rate reduction using pulse-width multiplexing Φ-OTDR with optimized positioning accuracy [J]. Optics Communications, 2020, 456(1): 124571. [23] Zhou J, Pan Z Q, Ye Q, et al. Characteristics and explanations of interference fading of a phi-OTDR with a multi-frequency source [J]. Journal of Lightwave Technology, 2013, 31(17): 2947-2954. doi: 10.1109/JLT.2013.2275179 [24] Pan Z, Liang K, Zhou J, et al. Interference-fading-free phase-demodulated OTDR system[C]//OFS2012 22nd International Conference on Optical Fiber Sensors. International Society for Optics and Photonics, 2012. [25] Wang X, Lu B, Wang Z Y, et al. Interference-fading-free Φ-OTDR based on differential phase shift pulsing technology [J]. IEEE Photonics Technology Letters, 2019, 31(1): 39-42. doi: 10.1109/LPT.2018.2881757 [26] Zabihi M, Chen Y S, Zhou T, et al. Continuous fading suppression method for Φ-OTDR systems using optimum tracking over multiple probe frequencies [J]. Journal of Lightwave Technology, 2019, 37(14): 3602. doi: 10.1109/JLT.2019.2918353 [27] Wang F, Liu Y, Wei T, et al. Polarization fading elimination for ultra-weak FBG array-based Φ-OTDR using a composite double probe pulse approach [J]. Optics Express, 2019, 27(15): 20468. doi: 10.1364/OE.27.020468 [28] Zhang J, Zheng H, Zhu T, et al. Long range fading free phase-sensitive reflectometry based on multi-tone NLFM pulse[C]//International Conference on Optical Fiber Sensors, 2018. [29] Zou W, Yang S, Long X, et al. Optical pulse compression reflectometry: proposal and proof-of-concept experiment [J]. Optics Express, 2015, 23(1): 512. doi: 10.1364/OE.23.000512 [30] Zou W, Yang S, Long X, et al. Optical pulse compression reflectometry with 10 cm spatial resolution based on pulsed linear frequency modulation[C]// Optical Fiber Communications Conference & Exhibition. IEEE, 2015. [31] Lu B, Pan Z Q, Wang Z Y, et al. High spatial resolution phase-sensitive optical time domain reflectometer with a frequency-swept pulse [J]. Optics Letters, 2017, 42(3): 391-394. doi: 10.1364/OL.42.000391 [32] 卢斌, 王照勇, 郑汉荣, 等. 高空间分辨率长距离分布式光纤振动传感系统[J]. 中国激光, 2017, 44(10): 1015001. [33] Zhu T, He Q, Xiao X, et al. Modulated pulses based distributed vibration sensing with high frequency response and spatial resolution [J]. Optics Express, 2013, 21(3): 2953. doi: 10.1364/OE.21.002953 [34] Qin Z, Chen L, Zou X. Distributed vibration acoustic sensing with high frequency response and spatial resolution based on time-division multiplexing [J]. Optics Communications, 2014, 331: 287-290. doi: 10.1016/j.optcom.2014.06.030 [35] Wang Z Y, Pan Z Q, Fang Z, et al. Ultra-broadband phase-sensitive optical time-domain reflectometry with a temporally sequenced multi-frequency source [J]. Optics Letters, 2015, 40(22): 5192. doi: 10.1364/OL.40.005192 [36] Wu Jing, Wu Hanping, Huang Junbin, et al. Research Progress in signal demodulation technology of fiber Bragg grating sensors [J]. Chinese Optics, 2014, 7(4): 519-531. (in Chinese) [37] Wang Z N, Zhang L, Wang S, et al. Coherent Φ-OTDR based on I/Q demodulation and homodyne detection [J]. Optics Express, 2016, 24(2): 853-858. doi: 10.1364/OE.24.000853 [38] Zhou L, Wang F, Wang X C, et al. Distributed strain and vibration sensing system based on phase-sensitive OTDR [J]. IEEE Photonics Technology Letters, 2015, 27(17): 1884-1887. doi: 10.1109/LPT.2015.2444419 [39] Pastor-Graells J, Martins H F, Garcia-Ruiz A, et al. Single-shot distributed temperature and strain tracking using direct detection phase-sensitive OTDR with chirped pulses [J]. Optics Express, 2016, 24(12): 13121. doi: 10.1364/OE.24.013121 [40] Alekseev A E, Vdovenko V S, Gorshkov B G, et al. A phase-sensitive optical time-domain reflectometer with dual-pulse phase modulated probe signal [J]. Laser Physics, 2014, 24(24): 115106. [41] He X G, Xie S R, Liu F, et al. Multi-event waveform-retrieved distributed optical fiber acoustic sensor using dual-pulse heterodyne phase-sensitive OTDR [J]. Optics Letters, 2017, 42(3): 442-445. doi: 10.1364/OL.42.000442 [42] Muanenda Y, Faralli S, Oton C J, et al. Dynamic phase extraction in a modulated double-pulse Φ-OTDR sensor using a stable homodyne demodulation in direct detection [J]. Optics Express, 2018, 26(2): 687. doi: 10.1364/OE.26.000687 [43] Sha Z, Feng H, Zeng Z. Phase demodulation method in phase-sensitive OTDR without coherent detection [J]. Optics Express, 2017, 25(5): 4831. doi: 10.1364/OE.25.004831 [44] Yang G, Fan X, Liu Q, et al. Frequency response enhancement of direct-detection phase-sensitive OTDR by using frequency division multiplexing [J]. Journal of Lightwave Technology, 2018, 36(4): 1197-1203. doi: 10.1109/JLT.2017.2767086 -







 下载:
下载: