-
激光以其独特的优势推动了传统非致命武器发生了颠覆性变革[1]。美国早在1978年3月便研制成功了世界上第一枝激光热灼枪[2]，此后美国、俄罗斯、以色列等军事发达国家也相继为其研发投入了大量的资源[3]，20世纪90年代初仅美国的投入就超过90亿美元。该类武器在20世纪80年代中后期的前苏联、英国两国部队就已有了试验性列装[4]，后来美国加州的TRW公司号称研发出了射程在8 km以上的超远程激光热灼枪[4]，此后还有“红宝石”以及俄罗斯的“溪流”等相继登场[5]。相比之下国内研究起步较晚，目前的非致命激光武器类型主要集中在激光炫目方面，代表有ZQ-1、ZM-87、PY141A、WJG-2002、YTX-1以及“闪电”等型激光眩目器[6]，但是对于以光热效应作为攻击手段的非致命激光武器研究却很少。我国现阶段正在研发一款可以精确控制激光生物剂量的非致命激光热灼枪，旨在实现对人体皮肤产生强烈热痛刺激的同时不对其造成永久性损伤。该型武器的出现可以很好地填补国内在该方面研究的空白，但其研发的关键和瓶颈之一是通过光学准直系统整形出满足战术需求的高质量光束。该型武器的战术目的决定了其对光斑边缘效果和能量分布有着极高的要求，但从目前国内装备情况来看，绝大多数激光武器的光学准直镜头不具备此能力，例如国内较新型的WD-GEN3型单兵非致命激光热灼枪，经实际调研后发现其存在能量分布不均、光斑质量不好等诸多问题，且有效射程尚不足50 m。这些问题都极大地限制了激光武器的发展，为此文中提出了一种新的设计和优化方法来满足现代激光武器对光束质量日益增长的需求。首先通过技战术参数分析、光学计算以及非球面优化等步骤得到所需的镜头结构，而后基于ZEMAX验证了镜头的优化效果并做出了加工公差分析，最后依据设计结果加工出镜头实体并装配于枪体中进行了木板烧蚀实验，实验结果验证了镜头性能的优越性，从而证明了所提出设计方法的合理性。
-
在进行镜头设计之前，需要综合考虑实际战术需求，确定技战术指标，并结合枪体机械结构来确定所需的应用参数。
-
激光热灼枪主要用于城市作战，要求武器具有较高的灵活性、便携性和精确性，对武器的高毁伤以及超远距离性能并无过多要求。城市环境中街道、楼房等建筑物较为密集，因此设计枪的有效射程为200 m足以满足城市作战的大部分任务。一方面过长的射程会增加激光器功率、电池数量、枪支重量及价格等，同时会因大气湍流[7]、折射等因素的存在使得光斑在传输过程中发生衰减、抖动，给枪在使用过程中带来很大的不确定性[7-8]；另一方面过短的射程可能会给任务带来局限性。经过综合考虑和比较，200 m的有效射程能够在战术效果和设计工艺上较好地兼容。
-
光斑的尺寸并非越大或者越小越好，在功率密度相同的情况下，过小的光斑产生的热痛刺激以及威慑效果不如大光斑好；但单纯增大光斑会大幅增加能量的损耗，而且不利于精确瞄准。此外，对人造成过大面积的损伤不符合该武器设计的初衷。考虑到两方面限制因素，最终选择5 mm为该型激光热灼枪烧蚀光束的半径。
-
该型武器设计的核心与难点一方面在于要达到功率密度的下限产生足够的热痛刺激来满足战术需求；另一方面不能超过功率密度的上限来确保控制光束的人体效应可逆性，因此对于光斑范围内的能量均匀度需要精确的定量分析。通过查阅文献可知[9]，1064 nm激光作用于人体皮肤造成可逆性损伤的激光剂量阈值为11.51~12.02 W/cm2，由此可以推算出光斑均匀性指标为±(4.2%~4.3%)。
-
热灼枪镜头与普通光学镜头不同，其材质对折射率、透过率及热损伤耐受标准有较高的要求，目前光学玻璃的材料有很多，几种典型光学玻璃的特性见表1。
表 1 常见光学玻璃特性
Table 1. Characteristics of common optical glass
Material Applicable wavelength/μm Refractive index at
1 064 nmAbbe number K5 0.4-1.0 1.523 59.48 K9(BK7) 0.3-2.3 1.516 64.17 MgF2 0.5-0.9 1.360 59.10 ZnS 0.4-14.5 2.250 28.32 CaF2 0.4-11.5 1.430 95.3 ZnSe 0.5-22.0 2.440 24.38 MgO 0.4-9.5 1.690 49.71 由表1可以看出，ZnS、ZnSe等玻璃材料折射率过高且密度大，会导致激光出射后色散严重；CaF2、MgF2等低折射率过低，会导致产生的像差余量较大。从色散、像差余量、性价比和加工性能等因素综合考虑，K5、K9、MgO等玻璃是比较理想的透镜材料。但MgO玻璃在烧蚀光束长时间作用下容易因热应力而受到损伤，因此也不适用。K5玻璃不适合波长在1000 μm以上的激光，而且其色偏移、像散及能量衰减都要大于K9玻璃，因此K9玻璃是该型热灼枪镜头设计的最佳选择。综上所述，将设计所需的主要技战术参数汇总于表2。
表 2 技战术参数
Table 2. Application parameters
Parameter Value Effective range/m 200 Spot diameter/mm 10 Lens diameter/mm 25 Lens material K9 Uniformity of spot energy ±（4.2%-4.3%） -
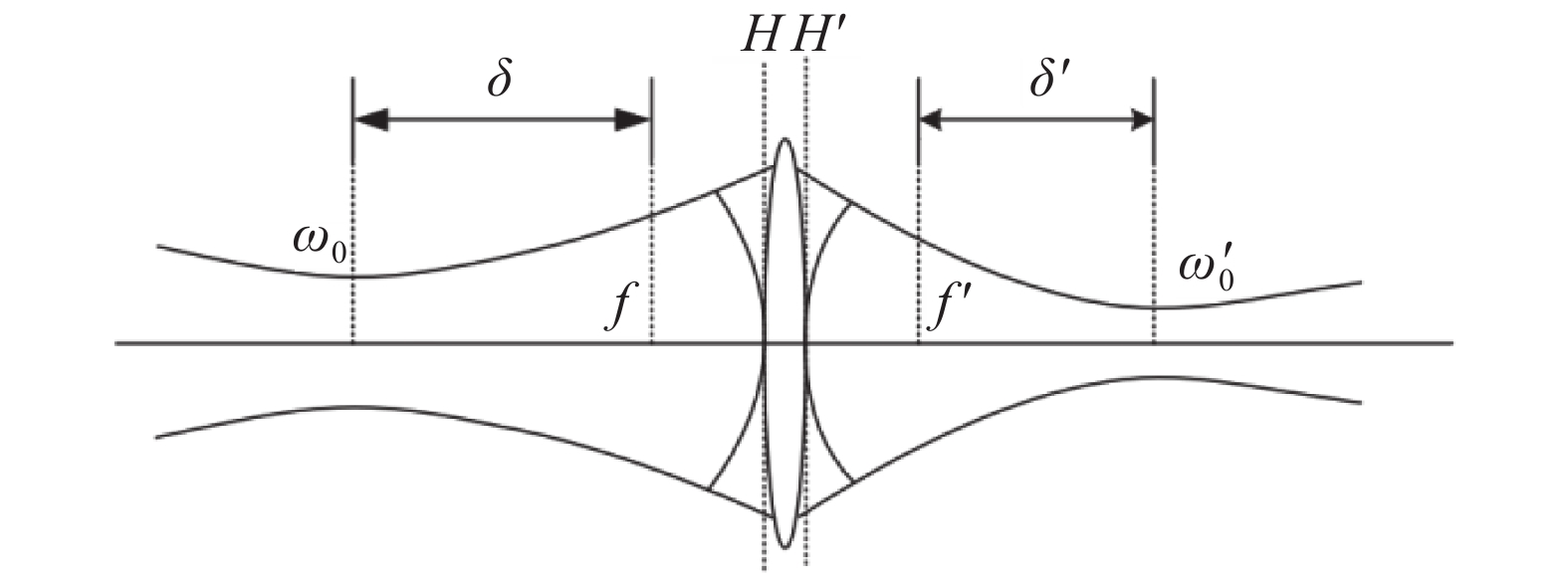
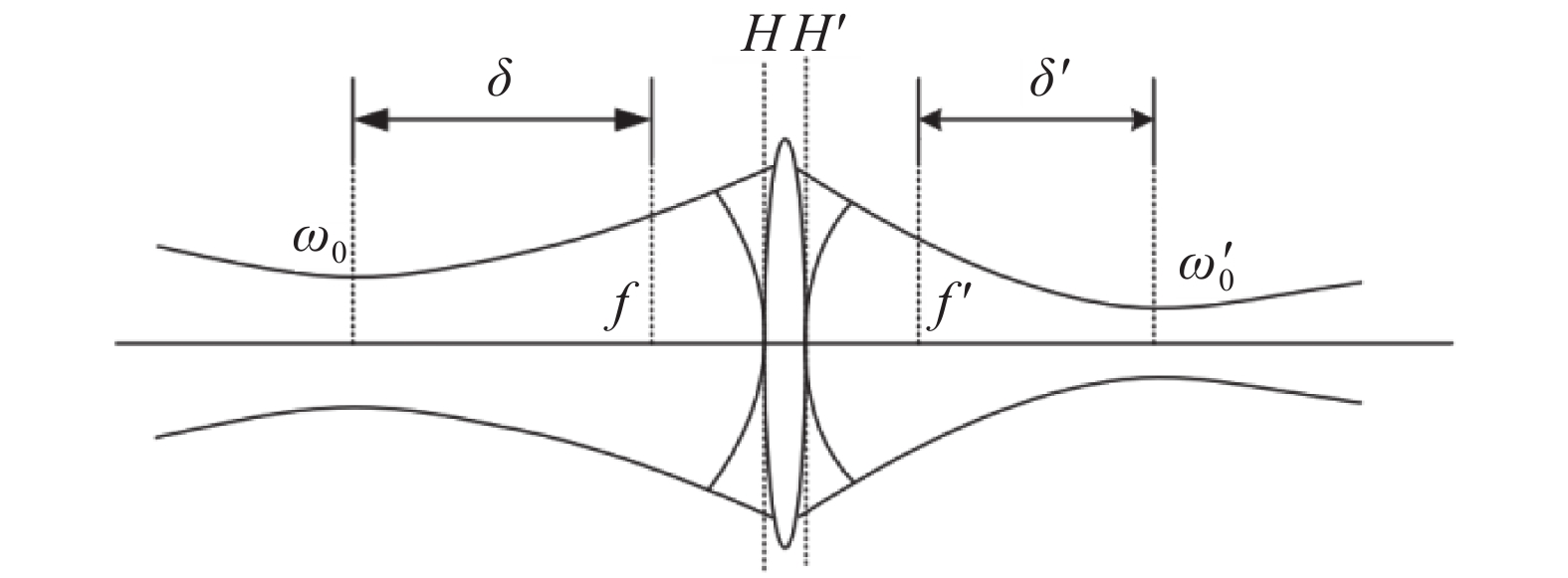
该型激光热灼枪采用光纤激光器作为光源，光纤纤芯直径为10 μm，数值孔径为0.1 NA，纤芯中射出的激光属于高斯型光束，其在单薄透镜中的传播特性及变换规律如图1所示[10]。
图 1 高斯光束经球面单透镜的变换
Figure 1. Transformation of a Gaussian beam through a spherical single lens
定义
${\omega _z}$ 为z点的光斑半径；$\lambda $ 为激光波长；${\omega _0}$ 和${\omega '_0}$ 分别为光束变换前和变换后的束腰半径；$\delta $ 为入射光束的束腰位置到透镜前焦点的距离, 入射光束腰位置在透镜前焦点前方时$\delta $ 为正, 否则为负；$\delta '$ 为出射光束的束腰位置到透镜后焦点的距离, 出射光束腰位置在透镜后焦点后方时$\delta '$ 为正, 否则为负；$\delta {\rm{ + }}f$ 为物距。${\omega _z}$ 为z的函数，其表达式如公式（1）所示[11]：$$ {\omega _z} = {\omega _0}\sqrt {1{\rm{ + }}{{\left( {\frac{{\lambda {{\textit{z}}}}}{{\pi {\omega _0}^2}}} \right)}^2}} $$ (1) 公式（2）、（3）分别表示像方束腰位置和半径[11]：
$$\delta ' = \frac{{\delta {f^2}}}{{{\delta ^2}{\rm{ + }}{{\left( {\dfrac{{\pi {\omega _0}^2}}{\lambda }} \right)}^2}}}$$ (2) $${\omega _0}' = \dfrac{{{\omega _0}f}}{{\sqrt {{\delta ^2} + \left( {\dfrac{{{\pi ^2}\omega _0^6}}{{{\lambda ^2}}}} \right)} }}$$ (3) 式中：
${\omega '_0}$ 的符号由f确定，为负时说明是虚束腰，当光学系统透镜的几何焦距确定后，只能通过改变$\delta $ 和${\omega _0}$ 调节光路确定焦距后的束腰位置和尺寸，激光烧蚀武器属于定向能应用，因此该光路需要增大$\delta '$ 并减小${\omega '_0}$ ，可以有效减小光束在远场的发散角。仅考虑$\delta $ 的影响时, 由公式（2）可知，假设$\delta = \hat \delta $ 时$\delta '$ 存在最大值为$ {\delta }_{{\rm{max}}}^{\rm{'}} $ ，则有：$$\hat \delta = \frac{{\pi {\omega _0}^2}}{\lambda }$$ (4) $$\delta {'_{\max }} = \frac{{\lambda {f^2}}}{{2\pi {\omega _0}^2}}$$ (5) 当
$\delta $ 在区间（0，$\hat \delta $ ）或（$\hat \delta $ ，∞）变化时，可以将$\delta '$ 在区间（0，$ {\delta }_{{\rm{max}}}^{\rm{'}} $ ）上调节，$\delta $ 越大，${\omega '_0}$ 越小。经上述计算可得出准直系统的初始结构参数，其详细参数见表3。表 3 初始系统结构参数
Table 3. Initial system structure parameters
Main lens parameter Value/mm Object numerical aperture NA = 0.1 Effective focal length 181.59 Fiber core diameter 0.01 Paraxial image height 2.5 Pupil diameter 17.64 Radius of curvature 92 Image distance 200000 -
该初始结构及其设计思路代表了现有激光武器镜头的现状，虽然能够满足最基本的距离和直径要求，但仍然存在前文中所述的诸多问题，难以应用于需要精密设计的该型激光热灼枪之中，因此还需做出进一步的优化。在直接对该初始结构进行了多次优化之后发现，基于现有透镜无论怎样优化都难以达到所需的设计要求，因此考虑采用其他镜头，为了尽量消除烧蚀光斑球差的影响可以考虑设计为非球面镜或双分离透镜，但武器设计中应尽量减小光学系统的复杂性以增加武器的可靠性，因此采用单片非球面设计。非球面镜是优化能量分布和处理边缘效果最合适的解决方法，近年来国内外都有其在准直设计方面的应用[12-15]，例如：Rafael等[12]提出了一种非球面准直一般公式来纠正单线态第一面产生球差和像散。此外，非球面设计能减小畸变和光能损失并简化镜头的结构，还能提高该武器的光束质量及耦合效率[16]。
非球面方程中设r为半径孔径，
$Z(r)$ 为镜面凹陷度，二者关系如图2所示[17]。
图 2 镜面凹陷度与半径r的示意图
Figure 2. Schematic diagram of mirror depression degree and radius r
设光轴为z轴，即非球面的对称轴，坐标原点取在顶点，非球面方程可表示为：
$$z(r) = \frac{{c{r^2}}}{{1 + \sqrt {1 - (1 + k){c^2}{r^2}} }} + \sum\limits_{i = 1}^N {{A_i}{r^{2i}}} $$ (6) 式中：
${r^2} = {x^2} + {y^2}$ ；$Z(r)$ 为镜面的凹陷度，r为镜面的半径孔径；1/c为曲率半径；A为r的各阶系数；k为曲面的圆锥系数。当$A = 0$ 时，方程变为二次曲面方程：$$z(r) = \frac{{c{r^2}}}{{1 + \sqrt {1 - (1 + k){c^2}{r^2}} }}$$ (7) 其中，k取不同值时代表不同状态的方程，当
$ k<-1$ 时为双曲线方程，其广泛应用于聚焦成像系统, 可以指导激光和光纤准直透镜的设计。曲率半径和圆锥系数可分别表示为：$$R = {b^2}/a$$ (8) $$k = - ({b^2} + {a^2})/{a^2}$$ (9) 如果切线角度可知, 圆锥系数也可表示为：
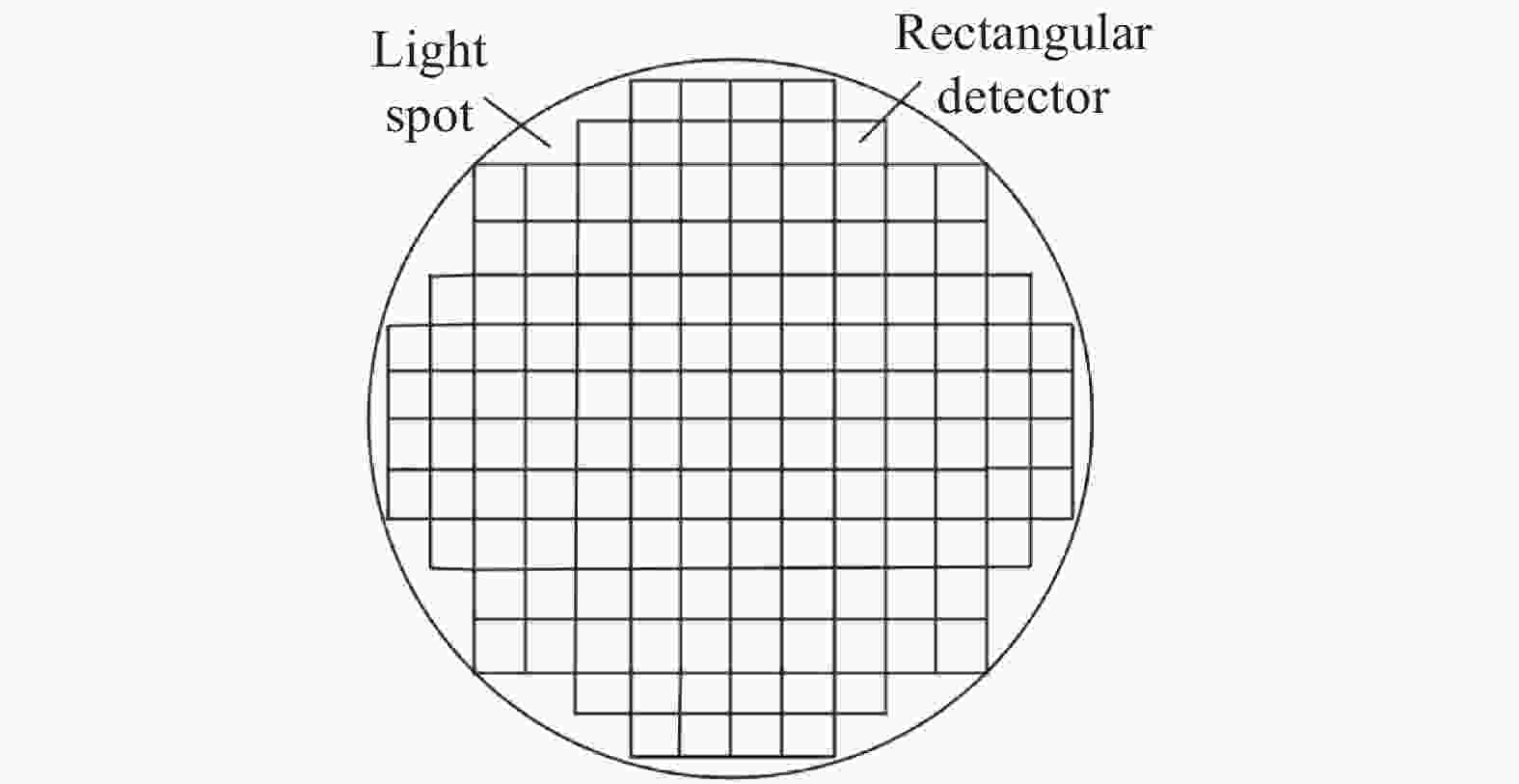
$$ k = - (1 + {\tan ^2}\theta ) $$ (10) 非球面优化过程的核心思想是在非序列模式中对烧蚀光斑进行光斑能量均匀性分析。首先设置波长为1064 nm，根据光学结构依次添加光源（半径为5.0×10−3mm）、偶次非球面透镜和探测器阵列，并将透镜设置为偶次非球面，将曲率半径及偶次方系数设为优化变量，设置半径为5 mm的探测器阵列，评价函数通过NSDD函数来控制返回每个探测器上的能量值，将探测器阵列中每个参测器的能量值均相等作为透镜参数的优化标准，以此来达到光斑范围内的能量均匀分布的目的。取目标光斑的内接正方形，经几何计算后在光斑面内按照坐标依次均匀添加个数为140的矩形探测器阵列，使之尽可能填满代表光斑的圆形区域，每个矩形探测器的X、Y半宽均为0.35 mm，Z位置均设置为2×105 mm，探测器阵列示意图如图3所示。
图 3 矩形探测器阵列示意图
Figure 3. Schematic diagram of a rectangular detector array
经过以上优化过程后，可以得到非球面的非球系数和曲率半径分别为0.584和115.37 mm。
-
通过数值模拟的方法对初始结构和优化结构进行对比分析，以判断优化的效果并确定最终结构，文中所有的仿真均基于ZEMAX OpticStudio 17版本进行。
-
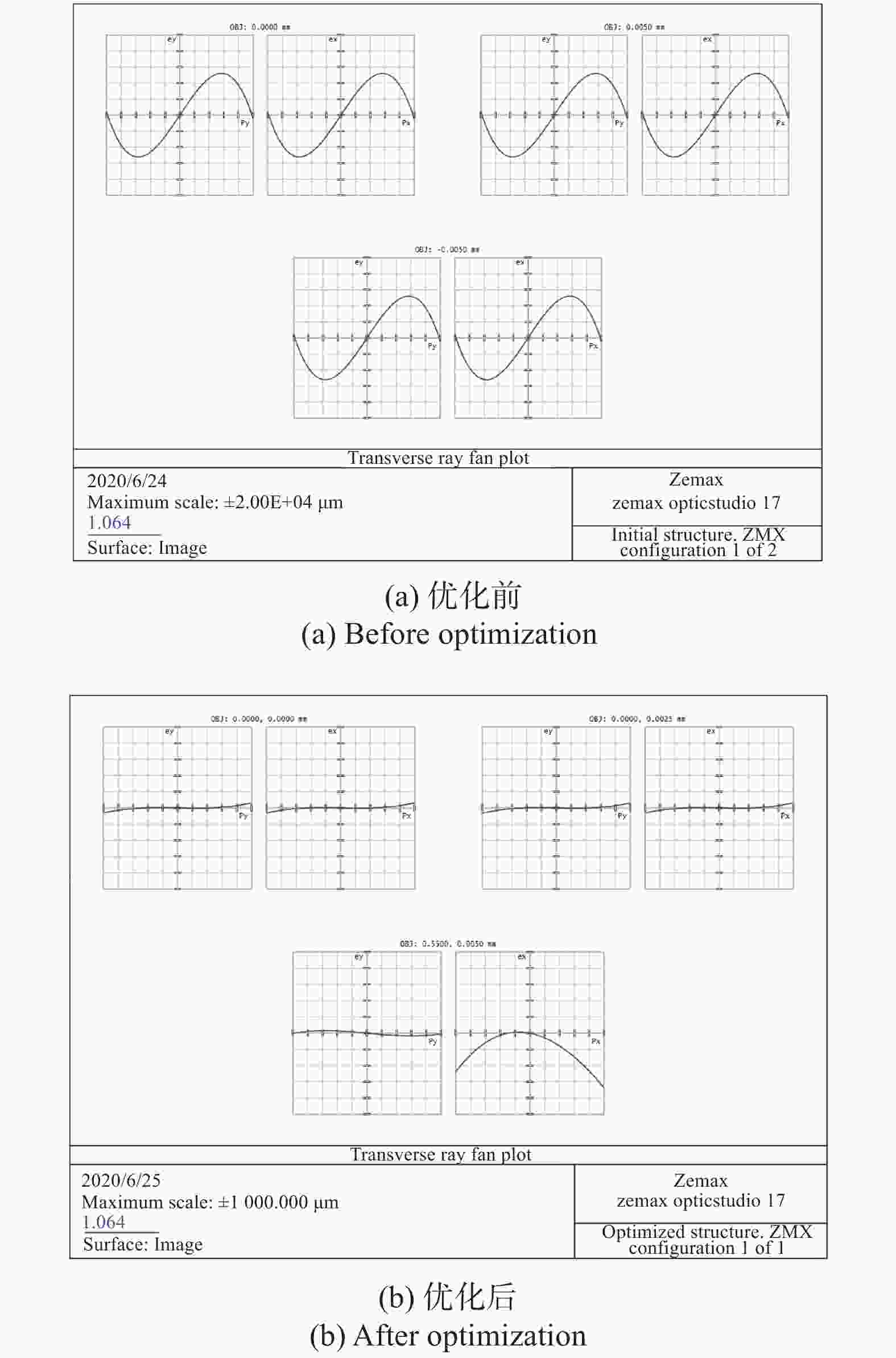
（1）球差分析
图4显示了优化前后的Ray fun对比图，从优化前的结构中可以很明显地观察到坐标原点处的曲线斜率很大，这表示光斑的球差很大，会使得光斑周围出现较强的光晕，不仅会分散光斑的能量密度，而且会使得光斑直径增大，严重影响战术效果，而从优化结构中可以看出球差几乎为零，验证了对于球差的优化取得了非常理想的效果。
图 4 光扇对比图
Figure 4. Comparison diagram of Ray fun
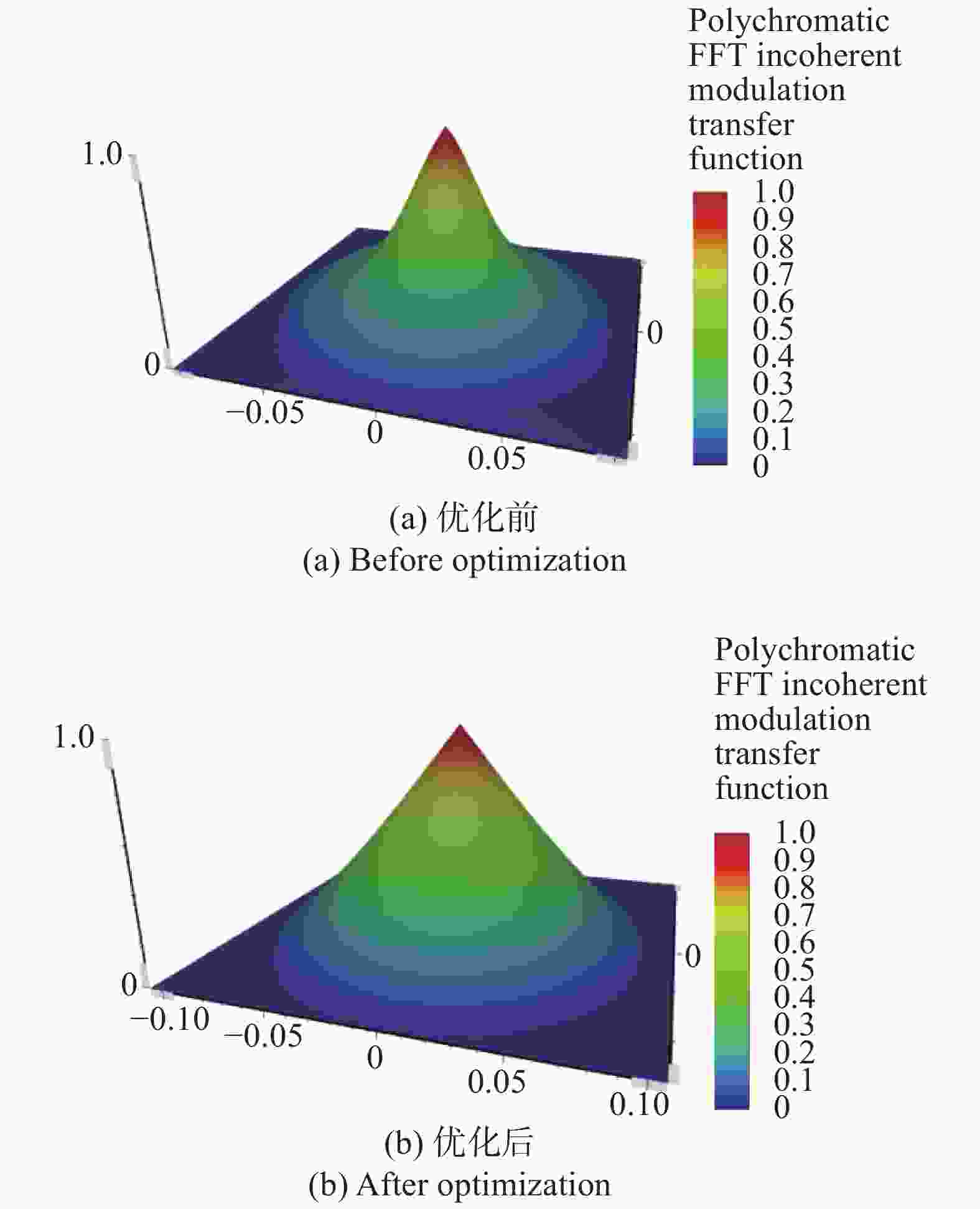
（2） MTF函数分析
MTF函数是最能反映系统实际成像质量的评价指标，但热灼枪的设计目的在于烧蚀而非成像，所以对分辨率、场曲和畸变等像差的分析是次要的，更主要的是观察MTF曲面所围成的体积来判断像点的中心亮度。从图5中可以看出优化结构中曲面所围成的体积明显大于初始结构，这代表优化后的光斑具有更高的中心亮度以及更均匀的能量分布。
图 5 三维MTF函数对比图
Figure 5. Comparison diagram of three-dimensional MTF function
-
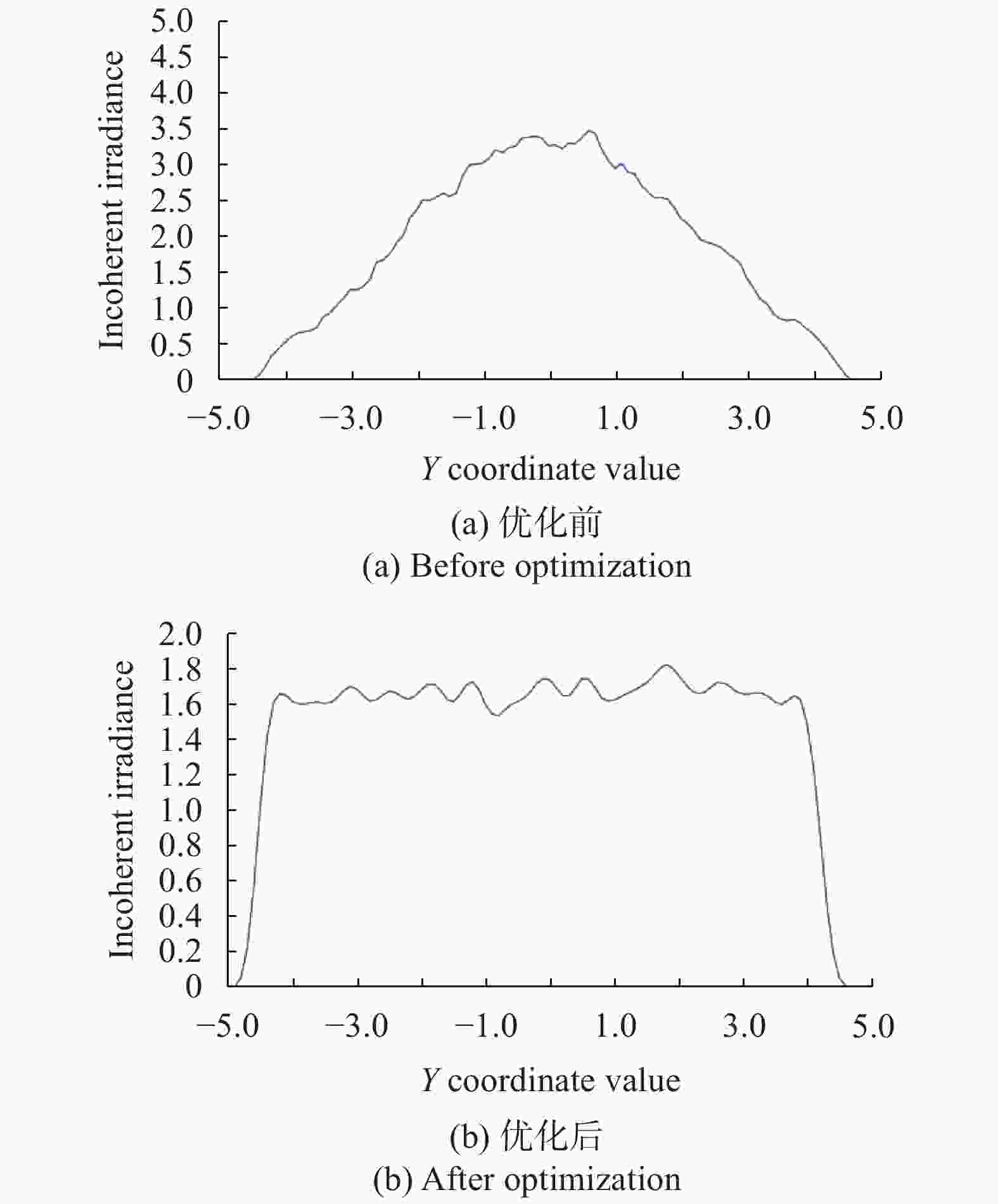
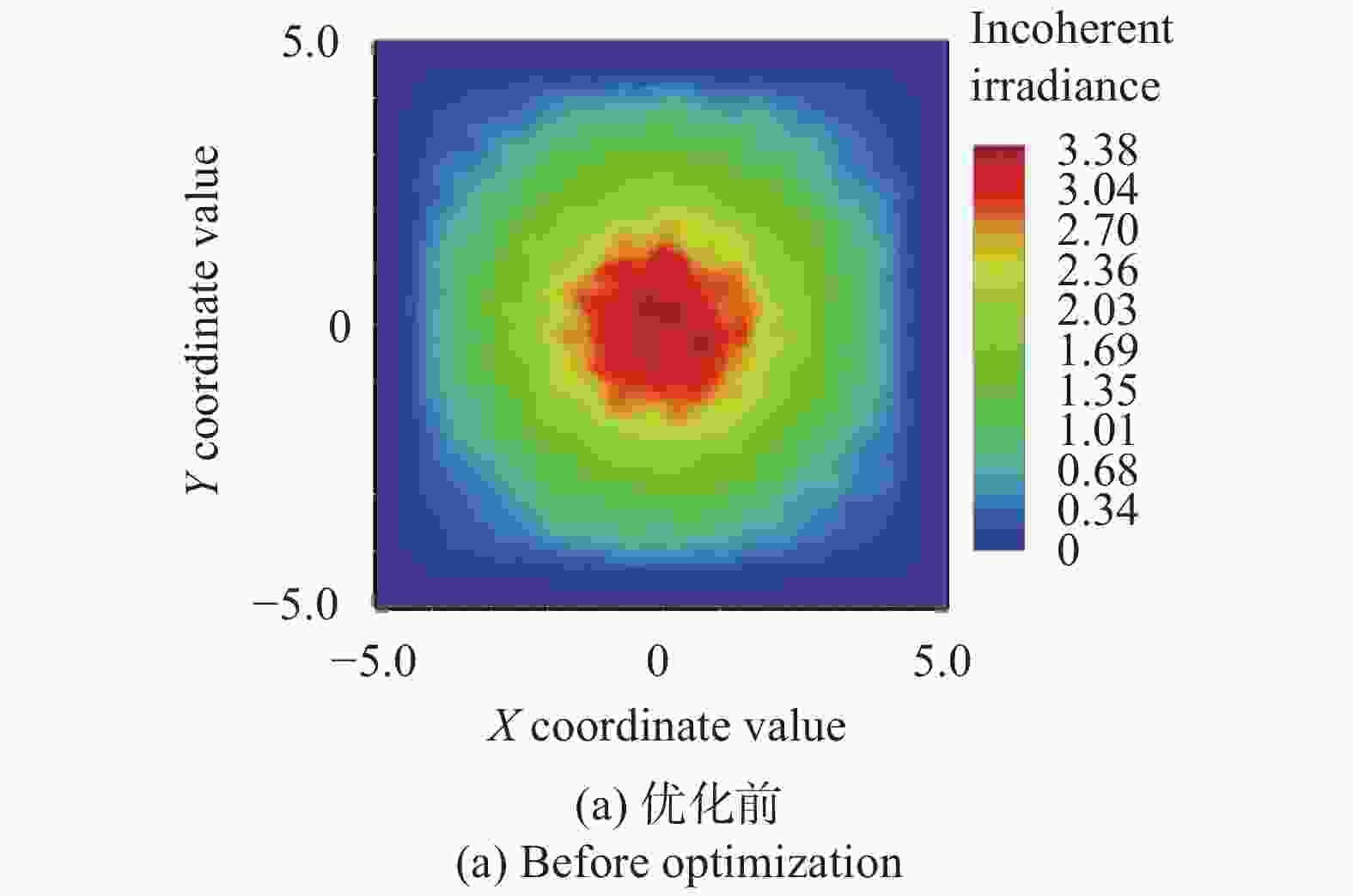
图6和图7分别从一维和二维层面上反映出了光斑辐照度的大小。从图中可以明显看出，优化前光斑范围的烧蚀效果能量分布非常不均匀，中心与边缘差距很大，这会造成额定功率下的激光在光斑中心对人的损伤过大而周边却不足，无法应用于需要精确控制激光生物剂量的热灼枪，也因此带来了战术效果上的极大限制，这也是当前非致命激光武器所凸显的主要技术问题之一。而优化后光斑范围内的能量分布非常均匀，极大地减少了光斑周边光晕的存在，有效减少了光斑边缘的能量损失，且在边缘处不足0.5 mm的范围内迅速达到峰值，体现了边缘处理效果良好且能量分布较为集中，同时还可以看出光斑直径为9.6 mm，满足10 mm的直径设计标准。图7更加直观地显示出光斑范围内的能量分布情况，尤其是从图7（b）可以明显看出光斑范围内能量分布相当均匀，只有最外围边缘处一圈很窄的光晕，由此说明优化结构所获得的光斑质量非常理想。此外，对透镜表面镀以GB 1316-88减反射膜，由图6中数据计算可知，理想情况下光能利用率能达到99.92%。经过以上分析可以看出，ZEMAX的仿真结果证明了光斑的球差及能量分布都得到了很好的优化，优化后的结构可以达到该型武器所需的各项需求，因此将该结构作为最终设计。
图 6 一维辐照度曲线
Figure 6. One-dimensional irradiance curves
图 7 二维辐照度平面
Figure 7. Two-dimensional irradiance plane
-
实际生产前不仅要对光斑进行分析，而且要考虑到加工的可操作性，从而实现光学镜头由设计到应用的转化，所以还需要对最终结构做出公差分析。此处采用蒙特卡洛灵敏度分析法来同时考虑所有公差对系统的影响[18]，以RMS光斑半径作为评价标准，最终设置的所有公差分配总结在表4中。
表 4 公差分配
Table 4. Tolerance distribution
Tolerance type Parameter Value/mm Surface tolerance Radius 0.32 Thickness 0.1 Decenter X, Y 0.1 Tilt X, Y 0.1 S+A irregularity 0.012 Element tolerance Decenter X 0.03 Decenter Y 0.03 Start at surface 1 Stop at surface 4 表5为该公差分配下，运行次数为300次的蒙特卡洛模拟结果。
表 5 公差分析结果
Table 5. Tolerance analysis result
Spot radius Value 90%> 5.01700970 80%> 1.95096272 50%> 0.73902551 20%> 0.33496534 10%> 0.22416649 从以上数据中可以看出，90%以上的光斑在该公差设置下满足设计要求，光学系统具备良好的加工性，可以满足生产要求。
-
首先基于SolidWorks 2018软件对该镜头进行三维建模，并与热灼枪准直系统的三维模型组成如图8（a）所示的装配体，而后按照最终设计结构进行开模制作，加工好的非球面镜可以与激光准直系统很好地吻合，装配体实物图如图8（b）所示。
图 8 激光热灼枪准直系统装配体
Figure 8. Collimation system assembly of laser cauterization gun
-
该型激光武器的烧蚀光束采用人眼不可见的近红外波段且能量很高，因此难以直接测量光斑的直径，故而采用间接测量法。该武器设计的有效射程为200 m，因此采取的实验方法是在距枪口200 m远的位置处架设靶木板，将枪体固定使之稳固，确保不会因人为及风力等因素造成枪口晃动从而导致光斑的弥散程度增大，击发1 s后观察木板的烧蚀情况。
实验中天气晴，温度21.3 ℃，微风2级，光束烧蚀时间为1 s，木板被烧蚀的实际效果如图9所示。
图 9 实验效果图
Figure 9. Experimental effect diagram
-
实验中为了更清楚地观察光斑烧蚀效果，采用了更大的功率和更长的作用时间，实际战术效条件下不会对人体造成如此严重的损伤。从图9中可以看出，经光束烧蚀的木板出现黑色的炭化圆斑，圆斑内部炭化的程度非常均匀，且炭化与非炭化部分的边界非常分明，可知光束经非球面镜整形之后的能量分布均匀且边缘效果处理的较好，这与仿真结果高度一致。而后通过对该炭化黑斑的直径进行测量来得到光束直径，在完全相同的条件下，仅改变烧蚀木板的位置共计进行25组实验，测量出木板上所有的25个炭化黑斑的直径后取平均值，最终可得炭化黑斑的平均直径为10.53 mm。
从图6（a）显示的曲线中可以看出光斑直径的仿真结果为9.6 mm，与实际结果相差0.93 mm，误差主要来源于以下几个因素：
（1）光学部件实际生产、组装与调试过程中的误差；（2）忽略了200 m距离内大气对光束的散射、折射、湍流等因素的影响；（3）热量向周围扩散会造成炭化面积的延展；（4）不同位置的木纤维数量及纹理等特性有所不同，这会导致其炭化的效果不同。
这些误差在实际中难以避免，在今后的设计中需要尽可能减小其影响。在排除掉以上因素的影响后，可以认为该光斑的实际参数与烧蚀效果符合仿真结果及战术评价标准。综合以上分析来看，该实验证明了所设计的该型激光武器准直系统镜头的良好性能。
-
提出了一种将非球面技术应用于激光热灼枪光学准直系统的设计和优化方法，并成功地为一款激光热灼枪制作了光学准直镜头。经ZEMAX软件仿真和木板烧蚀实验验证，通过该方法设计的武器可以在至少200 m以上距离外产生直径为10 mm且能量分布非常均匀的高质量准直光束，烧蚀光束的各项参数都很好地达到了该型激光武器所需的技战术标准。所采用的非球面优化技术效果明显，获得的光斑质量较高，能量分布均匀，且边缘效果处理较好，使得武器性能得到了全方位的提升。通过木板烧蚀实验所获得的结果与仿真结果高度吻合，镜头性能的优越性证明了所提出设计与优化方法的合理性，更为重要的是该方法不仅可以应用于该型武器的设计，对于其他领域的相关问题同样具有参考价值。
Collimating lens design and aspheric optimization method of laser cauterization gun
-
摘要: 为了满足激光武器对光束质量日益增长的需求，提出了一种光学准直系统的设计思路及非球面镜优化方法，并将该方法成功应用于一款激光热灼枪的镜头设计，使该枪可以在更远范围内获得更高质量的准直光束。首先在战技参数分析和光路计算的基础上得到初始结构，而后对其进行非球面优化，并基于ZEMAX对两次仿真结果做出对比分析，数值结果显示优化结构具有显著优势，其非球系数和曲率半径分别为0.584 mm和115.37 mm，光能利用率在使用GB 1316-88减反射膜的情况下可达99.92%。经过公差分析后加工出镜头并与枪体组合进行了木板烧蚀实验，实验与仿真结果吻合度良好，镜头性能的优越性证明了所提出设计及优化方法的可行性与合理性，也为其他领域的类似问题提供了一定的参考价值。Abstract: In order to meet the increasing demand for beam quality of laser weapons, a design and aspheric optimization method of optical collimation system was proposed. This method was successfully applied to the lens design of a laser cauterization gun, so that the gun could obtain a higher quality collimating beam in a farther range. First, the initial structure was obtained based on the analysis of tactical and technical parameters and the calculation of the optical path, then the aspherical optimization was performed, the two simulation results were compared and analyzed based on ZEMAX. Numerical results show that the optimized structure has significant advantages. Its aspheric coefficient and curvature radius are 0.584 mm and 115.37 mm respectively, and the light energy utilization rate can reach 99.92% when the GB 1316-88 anti-reflection film is used. After tolerance analysis, the lens was processed and combined with the gun body for a board ablation experiment. The experimental results are in good agreement with the simulation results. The superiority of lens performance proves the feasibility and rationality of the proposed design and optimization method, and also provides a certain reference value for similar problems in other fields.
-
Key words:
- optical design /
- laser weapon /
- aspheric /
- collimating system /
- tolerance analysis
-
图 1 高斯光束经球面单透镜的变换
Figure 1. Transformation of a Gaussian beam through a spherical single lens
图 2 镜面凹陷度与半径r的示意图
Figure 2. Schematic diagram of mirror depression degree and radius r
表 1 常见光学玻璃特性
Table 1. Characteristics of common optical glass
Material Applicable wavelength/μm Refractive index at
1 064 nmAbbe number K5 0.4-1.0 1.523 59.48 K9(BK7) 0.3-2.3 1.516 64.17 MgF2 0.5-0.9 1.360 59.10 ZnS 0.4-14.5 2.250 28.32 CaF2 0.4-11.5 1.430 95.3 ZnSe 0.5-22.0 2.440 24.38 MgO 0.4-9.5 1.690 49.71 
下载: 导出CSV
表 2 技战术参数
Table 2. Application parameters
Parameter Value Effective range/m 200 Spot diameter/mm 10 Lens diameter/mm 25 Lens material K9 Uniformity of spot energy ±（4.2%-4.3%）
下载: 导出CSV
表 3 初始系统结构参数
Table 3. Initial system structure parameters
Main lens parameter Value/mm Object numerical aperture NA = 0.1 Effective focal length 181.59 Fiber core diameter 0.01 Paraxial image height 2.5 Pupil diameter 17.64 Radius of curvature 92 Image distance 200000
下载: 导出CSV
表 4 公差分配
Table 4. Tolerance distribution
Tolerance type Parameter Value/mm Surface tolerance Radius 0.32 Thickness 0.1 Decenter X, Y 0.1 Tilt X, Y 0.1 S+A irregularity 0.012 Element tolerance Decenter X 0.03 Decenter Y 0.03 Start at surface 1 Stop at surface 4
下载: 导出CSV
表 5 公差分析结果
Table 5. Tolerance analysis result
Spot radius Value 90%> 5.01700970 80%> 1.95096272 50%> 0.73902551 20%> 0.33496534 10%> 0.22416649
下载: 导出CSV
-
[1] Modinger J. Lasers, death rays, and the long, strange quest for the ultimate weapon [J]. Military Review, 2019, 99(4): 133. [2] Affan S, Mohsin M, Zubair A. Survey and technological analysis of laser and its defense applications [J]. Defence Technology, 2020(2): 012. [3] Zohuri B. Laser Beam Energy as Weapon [M]//Zohuri B. Directed-Energy Beam Weapons. Cham: Springer, 2019: 239-268. [4] Hu Haijian. Research on laser light weapons and their application in modern anti-terrorism operations[D]. Changsha: National University of Defense Science and Technology, 2006. (in Chinese) [5] Hecht J. Half a century of laser weapons [J]. Optics and Photonics News, 2009, 20(2): 14-21. [6] Chen Xiaodong, Wang Hongguang. Anti-Terrorist Technical Equipment[M]. Beijing: Science Press, 2010. (in Chinese) [7] Jabczyński J, Gontar P. Impact of atmospheric turbulence on coherent beam combining for laser weapon systems [J]. Defence Technology, 2020(6): 021. [8] Yuan Hui, Hao Minglei, Li Fanxian, et al. Attenuation properties of 1.06 μm laser radiation in water fog [J]. Infrared and Laser Engineering, 2018, 47(10): 1006003. (in Chinese) doi: 10.3788/IRLA201847.1006003 [9] Pu Li, Jiang Xianpei, Liu Xiaohua, et al. Research on the effect of thermal damage on human skin of the low-energy laser weapon [J]. Laser Journal, 2016, 37(8): 13-17. (in Chinese) [10] Zhou Bingkun, Gao Yizhi, Chen Chourong. Principle of Laser[M]. Beijing: National Defence Industry Press, 2009. (in Chinese) [11] Fan Zhigang. Photoelectric Test Technique[M]. Beijing: Electronic Industry Press, 2004. (in Chinese) [12] Acuña R, Vega J. General formula for aspheric collimator lens design free of spherical aberration [C]//Current Developments in Lens Design and Optical Engineering XX, 2019, 11104: 111040P. [13] Wu H, Zhang L, Jiang Q, et al. Design of a fiber coupled diode laser based on a novel beam shaping component which is provided with beam collimating and re-orienting [C]//2019 International Conference on Optical Instruments and Technology: Advanced Laser Technology and Applications, 2020, 11437: 114370W. [14] Zhang Y, Yan G, Li Z, et al. Quality improvement of collimating lens produced by precision glass molding according to performance evaluation [J]. Optics Express, 2019, 27(4): 5033-5047. doi: 10.1364/OE.27.005033 [15] Guo C, Xiong B, Zhang G, et al. LD beam collimation based on aspheric cylindrical lens [C]//9th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies, 2019, 10838: 1083817. [16] Li Meixuan, Wang Li, Dong Lianhe, et al. Application of aspheric technology in immersion lithography lighting system [J]. Infrared and Laser Engineering, 2017, 46(11): 1118003. (in Chinese) doi: 10.3788/IRLA201746.1118003 [17] Chen B, Li S, Deng Z, et al. Grinding marks on ultra-precision grinding spherical and aspheric surfaces [J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2017, 4(4): 419-429. doi: 10.1007/s40684-017-0047-5 [18] Zhang K, Zhong X, Wang W, et al. Ultra-low-distortion optical system design based on tolerance sensitivity optimization [J]. Optics Communications, 2019, 437: 231-236. doi: 10.1016/j.optcom.2018.12.059 -
点击查看大图
图(10) / 表(5)
计量
- 文章访问数: 414
- HTML全文浏览量: 142
- PDF下载量: 62
- 被引次数: 0
