-
实时矿物识别在资源勘探、地质分析、地外星球探测等领域具有重要作用。拉曼光谱检测能够获取被测物分子的振动、转动能级信息，已被应用于天然气探测[1]、火星物质探测[2]等领域的矿物质分析和识别任务。然而，自然界矿物质种类繁多，其拉曼光谱具有一定相似性，因此，对分类算法准确度、实时性都有较高要求。近年来，深度学习技术不断发展，已广泛应用于图像识别[3]、语音识别[4]、生物医学信号处理[5]等领域[6-9]。深度神经网络能够将数据的原始特征从低维空间映射到高维空间，具有优异的特征学习能力，特别在多分类问题中，能够较好地区分差异较小的特征。因此，深度神经网络模型能够快速准确地对光谱数据进行识别，能够较好地识别出相近光谱间的细微差别。目前，已有研究者将深度神经网络模型应用于拉曼光谱分类问题[10-11]。尽管深度神经网络的训练过程能够在GPU （Graphics Processing Unit）上完成，但其推理过程仍需要大量的矩阵运算，因此深度神经网络的应用受到了很大的限制。
随着对神经网络计算速度的需求日益增加，光学神经网络（Optical Neural Network）受到了越来越多的关注，其从实现方式上可分为两类：基于光波导器件的光学神经网络[12-13]和基于空间光器件的光学神经网络[14-16]。光学神经网络利用光束的传播和变换实现计算功能，相比电子平台的计算速度更快，能耗更低。来自UCLA的Lin[14]等给出了一套全光衍射神经网络实现方案，该方案采用太赫兹光源，以及由3D打印技术制作的衍射光栅，验证了全光衍射深度神经网络的可行性。该方案计算部分全部由光学方式实现，充分利用光束的并行特性，极大地提高了深度神经网络的计算速度。该方案已经在图像识别任务（手写数字识别）上取得了一定效果，并完成了原型系统的搭建。全光衍射深度神经网络具有计算速度快、功耗低、抗电磁干扰等有点，将全光衍射深度神经网络分类系统与拉曼光谱探测系统相结合，即可形成一套快速低功耗的拉曼光谱分类系统，为基于拉曼光谱的物质分类提供一种可行的方案，该方案在物质探测领域具有广阔的应用前景。
文中将全光衍射神经网络应用于矿物拉曼光谱智能识别，基于矿物拉曼光谱数据的特征提出了一种矿物拉曼光谱全光衍射深度神经网络模型，并在仿真条件下验证了模型的分类正确率，为今后矿物拉曼光谱智能识别系统的研制提供理论支撑；同时，分析了衍射光栅栅格高度的精度对矿物识别正确率的影响，为衍射光栅的制作提供设计依据。
-
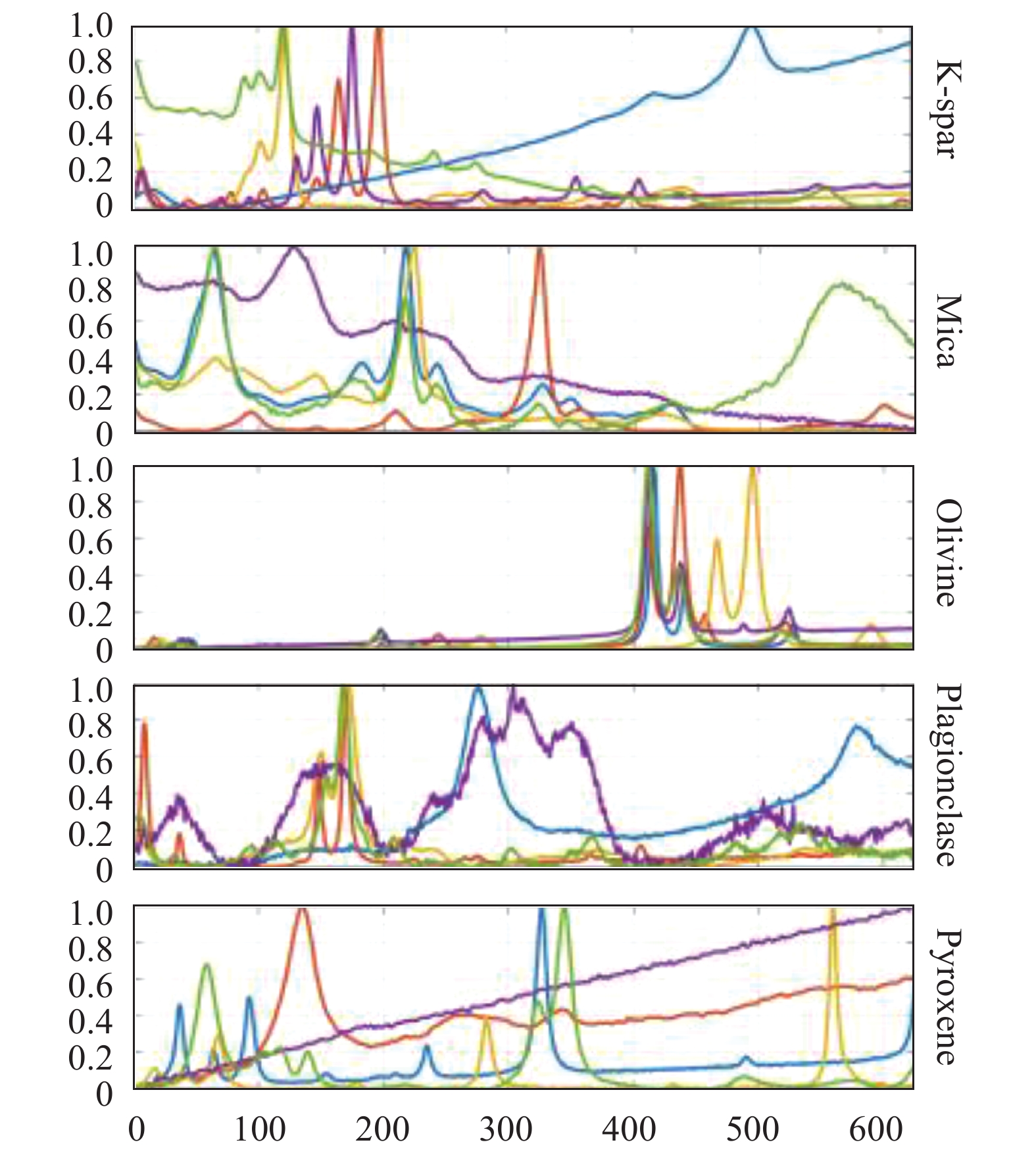
岩石样本中的关键矿物成分往往能够揭示地质结构的成因，不同矿物因其结构不同而在拉曼光谱上体现出不同的特征。RRUFF[17]项目是一个国际开源的光谱数据库，具有较为完整的矿物光谱数据。文中采用RRUFF数据库中的部分拉曼光谱数据作为训练数据集，数据集中包括五大类矿物：K-spar （钾长石）、Mica （云母）、Olivine （橄榄石）、Plagioclase （斜长石）、Pyroxene （辉石），其中，每种矿物类数据又包含多种小类矿物数据，图1为数据集中部分矿物拉曼光谱数据图。
图 1 数据集中的部分光谱数据
Figure 1. Part of the spectrum data in dataset
如图1所示，不同大类矿物的拉曼光谱以及同一大类下矿物的拉曼光谱均存在较大差异；数据集中经过预处理和未经过预处理的数据混杂。以上问题使得光谱数据的识别变得十分困难。
-
图2(a)所示的系统物理模型与图2(b)的光路模型相对应，光线经过每一个栅格后都会被不同厚度的栅格调制，之后被次级光栅上的所有栅格接收到。这种关系可以被等价为图2(c)所示的神经网络模型。
图 2 网络结构示意图
Figure 2. Network structure diagram
这种网络连接模式类似于全连接神经网络，其中第一层光栅接收输入图像，对应神经网络结构中的输入层，中间若干层光栅对应神经网络结构中的隐藏层，探测平面则对应神经网络结构中的输出层。光栅上栅格的高度不同，对输入光的相位调制效果就不同，对应于神经网络结构中的不同权值。与传统全连接神经网络的区别在于，在光学衍射神经网络中由同一栅格发出的连接权值共享。
根据瑞利−索末菲衍射公式，将全光衍射深度神经网络中每层衍射光栅的每一个栅格作为由下式定义的次级波源[14]：
$${w}_{i}^{l}\left(x,y,z\right)=\dfrac{z-{z}_{i}}{{r}^{2}}\left(\dfrac{1}{2\ {\text{π}} r}+\dfrac{1}{j\lambda }\right){\rm{exp}}\left(\dfrac{\rm j2\ {\text{π}} r}{\lambda }\right)$$ (1) 式中：
$l$ 为光栅层数编号；$i$ 为位于坐标（${x}_{i}$ ，${y}_{i}$ ，${z}_{i}$ ）处的栅格编号；$\lambda$ 为入射光波波长；$r$ 为波源到次级光栅某点的距离；$\rm j$ 为虚数单位。衍射光栅上每个栅格在次级光栅上的输出为[14]：
$$ \begin{split} {n}_{i}^{l}\left(x,y,z\right)= &{w}_{i}^{l}\left(x,y,z\right) \cdot {t}_{i}^{l}\left({x}_{i},{y}_{i},{z}_{i}\right) \cdot\\ & {\displaystyle\sum }_{k}^{}{n}_{k}^{l-1}\left({x}_{i},{y}_{i},{z}_{i}\right) =\\ & {w}_{i}^{l}(x,y,z) \cdot \left|A\right| \cdot {\rm e}^{\rm j\Delta \theta } \end{split}$$ (2) 因此，光在衍射光栅间的前向传播过程中有如下关系：
$$\left\{ {\begin{array}{*{20}{c}} {n_{i,p}^l = w_{i,p}^l \cdot t_i^l \cdot m_i^l}\\ {m_i^l = \displaystyle\mathop \sum \nolimits_k n_{k,i}^{l - 1}}\\ {t_i^l = a_i^l{\rm{exp}}\left( {\rm j\phi _i^l} \right)} \end{array}} \right. $$ (3) 式中：
$t$ 为透射系数，表示衍射光栅对输入光场的调制作用；$a$ 表示光栅对振幅的调制，由于系统只利用了衍射光栅的相位调制能力，因此设$a=1$ ，即衍射光栅在不考虑损耗的情况下不影响振幅；$\phi$ 表示衍射光栅对相位的调制；$m$ 表示输入光场，即上级光栅各栅格输出光场的叠加。通过改变每个栅格的高度，即可对出射光的相位进行调制，从而影响次级光栅上的光场分布。针对特定计算任务设计衍射光栅的高度分布，即可在探测平面得到预期的计算结果。
实验所采用的数据集从RRUFF数据库中的拉曼光谱数据中选取制作，共包括2 025条光谱数据。为满足光学衍射神经网络中光栅的实际要求，在制作数据集时对原始数据进行了一定的截取和缩放。如图3所示。
图 3 数据预处理
Figure 3. Data preprocessing
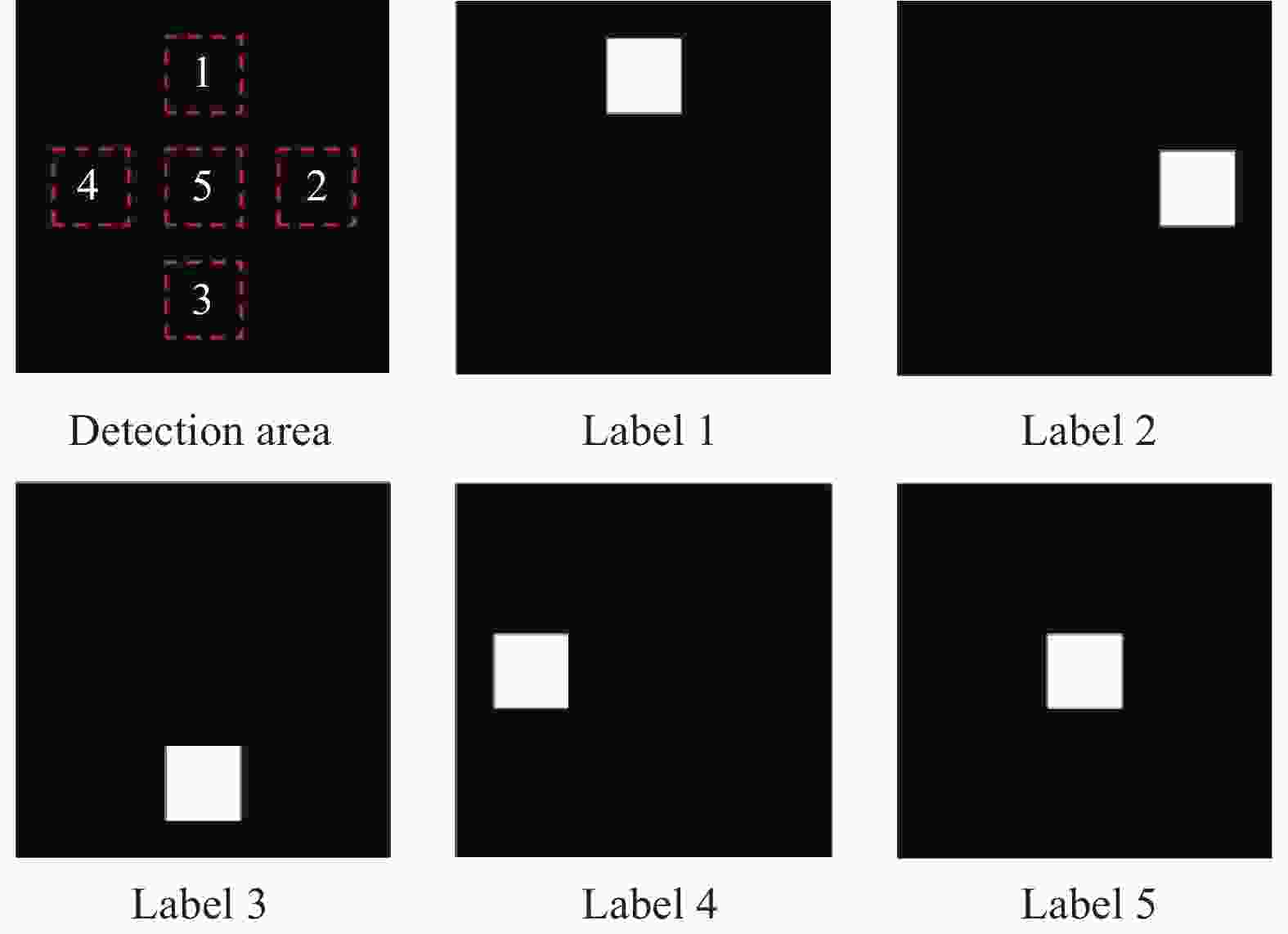
输入光在经过五层光栅的衍射之后会在探测平面输出一副结果图像，探测器对结果图像中的探测区域进行探测以得到网络分类结果。因此需要在参数训练阶段对数据标签进行处理，设计不同标签对应的结果图像中的标志。
如图4所示，通过判断结果图像中探测区域内光强最大的区域即可得到结果图像所表征的标签。为匹配不同长度的输入数据，标签对应的结果图像也要经过缩放处理。
图 4 结果图像中的探测区域以及不同标签对应的标识区域
Figure 4. Detection area in the result image and identification area of different labels
-
网络训练采用batch training的方式，即将训练集分批送入网络进行训练，每个batch中包含20条训练数据，其中包括处理过后的拉曼数据和标签对应的标识区域数据。采用交叉熵作为损失函数：
$$ H\left( {p,q} \right) = - \mathop \sum \nolimits_x p\left( x \right){\rm{{log}}}{q}\left( x \right) $$ (4) 式中：
$p$ 代表期望输出，即标签对应的结果图像；$q$ 代表实际输出，即输出图像。训练共进行1 000个epoch。参数优化方法采用Adam方法，学习率设置为0.001。模型中共五层光栅，每层光栅均由100×100个栅格排列而成，每个栅格均为5 μm×5 μm。各层光栅之间以及光栅与探测平面之间的距离为300 μm。
-
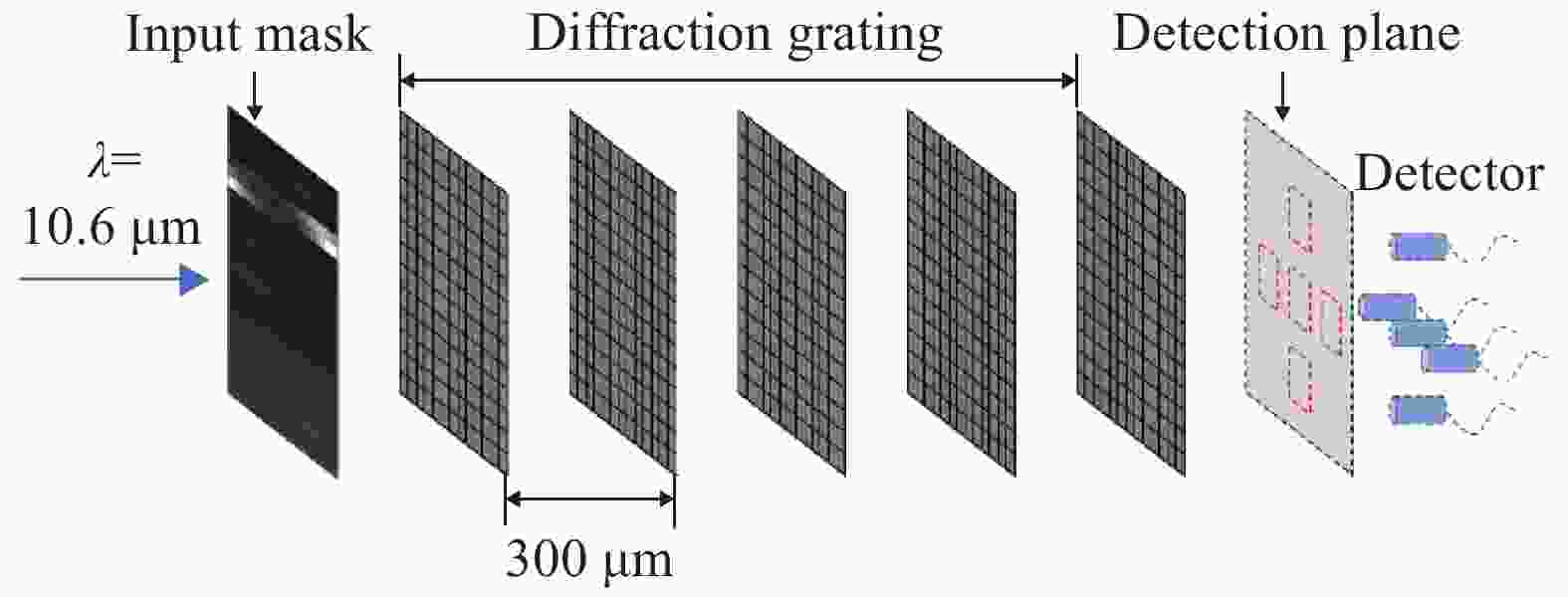
全光衍射深度神经网络分类系统主要由光源、衍射光栅组以及接收器组成。如图5所示。
图 5 全光衍射神经网络分类系统结构示意图
Figure 5. Structure diagram of optical diffractive neural network classification system
系统采用10.6 μm的
$\rm C{\rm O}_{2}$ 激光器作为光源，激光通过根据输入数据制作的模板后照射在衍射光栅上，经过五层衍射光栅的衍射后在探测平面形成结果图像，探测器接收到的结果图像即表征了输入数据的分类结果。如图6所示。
图 6 光栅组示意图
Figure 6. Structure diagram of grating group
采用输入模板的形式实现系统输入时，输入模板本质上也形成了一层衍射光栅，因此在对系统的网络参数进行训练时需要考虑输入模板的衍射对系统输入的影响，具体计算时可将其作为一层参数固定的衍射光栅。
-
栅格高度由计算机针对具体分类任务训练得到，在计算机上完成训练后针对每个光栅将会得到10 000个高度值。然而，光刻工艺每一次刻蚀只能产生一种高度，在同一片材料上每增加一次刻蚀都需要重新对准，工艺难度极大且对准误差无法避免。
为了使光栅的刻制在工艺上可行，对栅格高度进行离散化，使任意一个栅格的高度可由几次不同深度的刻蚀组合近似得到。而在刻蚀的过程中，只需要计算出每次刻蚀需要的掩模版即可通过很少的几次刻蚀完成光栅的制作。
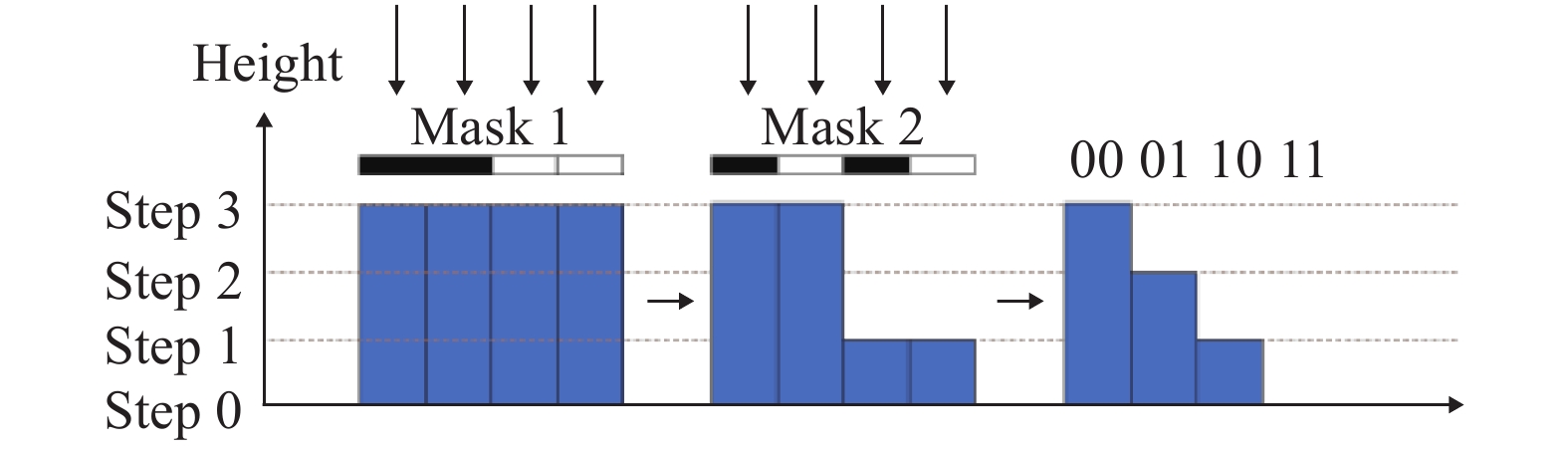
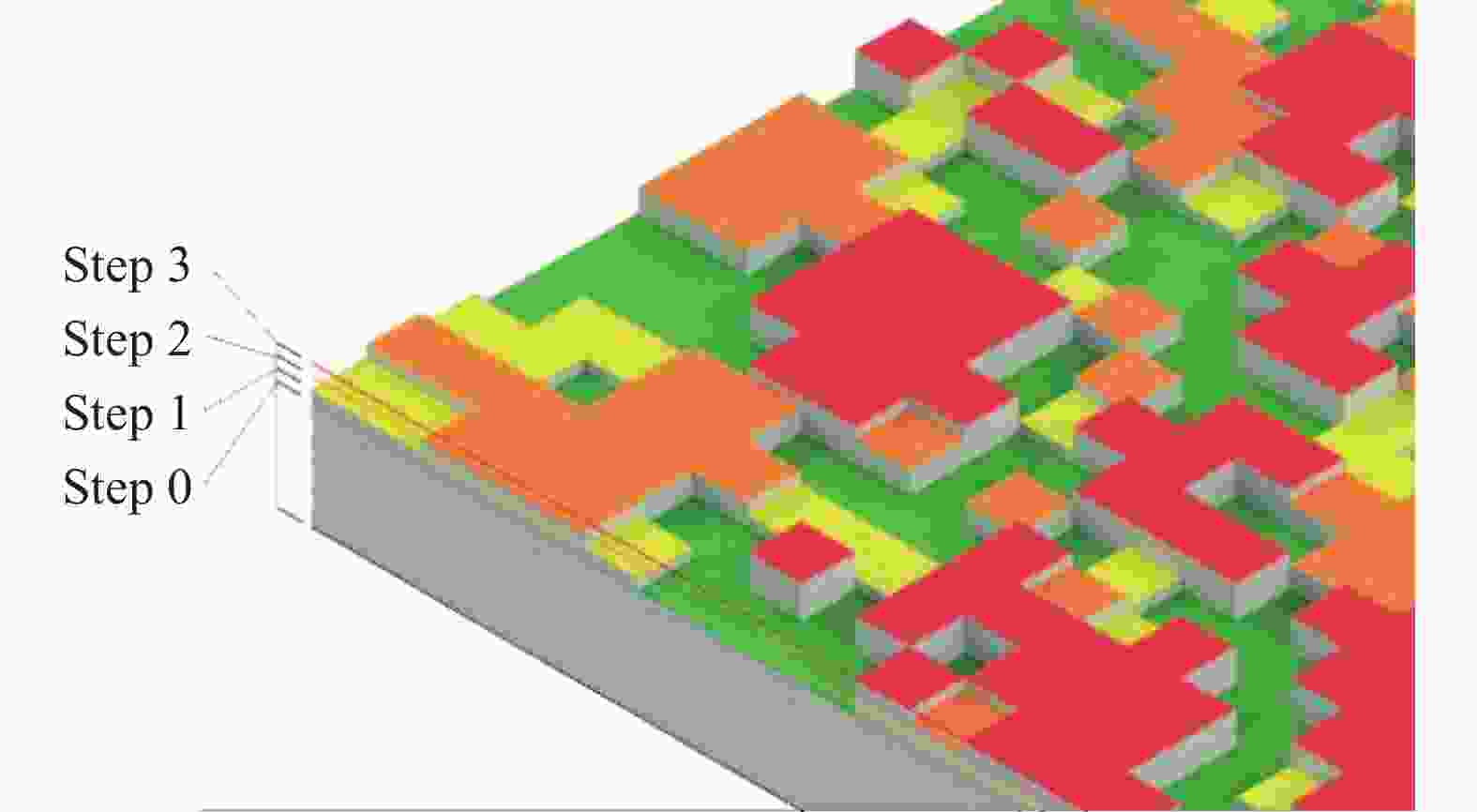
如图7和图8所示，首先确定台阶层数，层数需为2的整数次幂，方便之后的高度离散化。需要注意的是台阶层数越多则高度离散化精度越高，离散化误差越小，但对刻蚀工艺的要求也越高。之后按照台阶层数计算各个台阶的高度值，对原始台阶高度进行离散化。最后对每个栅格的高度按照二进制进行编码，则该层光栅上所有栅格的同一位编码即组成对应的刻蚀掩模版。图9为经过离散化后的衍射光栅模型局部示意图。
图 7 光栅高度离散化
Figure 7. Grating height discretization
图 8 两次刻蚀实现四层台阶
Figure 8. Two etching to achieve four steps
图 9 衍射光栅模型局部示意图
Figure 9. Partial diagram of diffraction grating model
在光栅刻制之前需要对不同的高度离散化精度进行仿真，分析不同精度的高度离散化对扽类正确率的影响，以确定最佳的衍射光栅刻蚀次数。
-
将实验数据集按照80%，20%的比例划分成训练集和测试集，其中训练集用于网络参数的训练，测试集用于网络训练结果的测试。
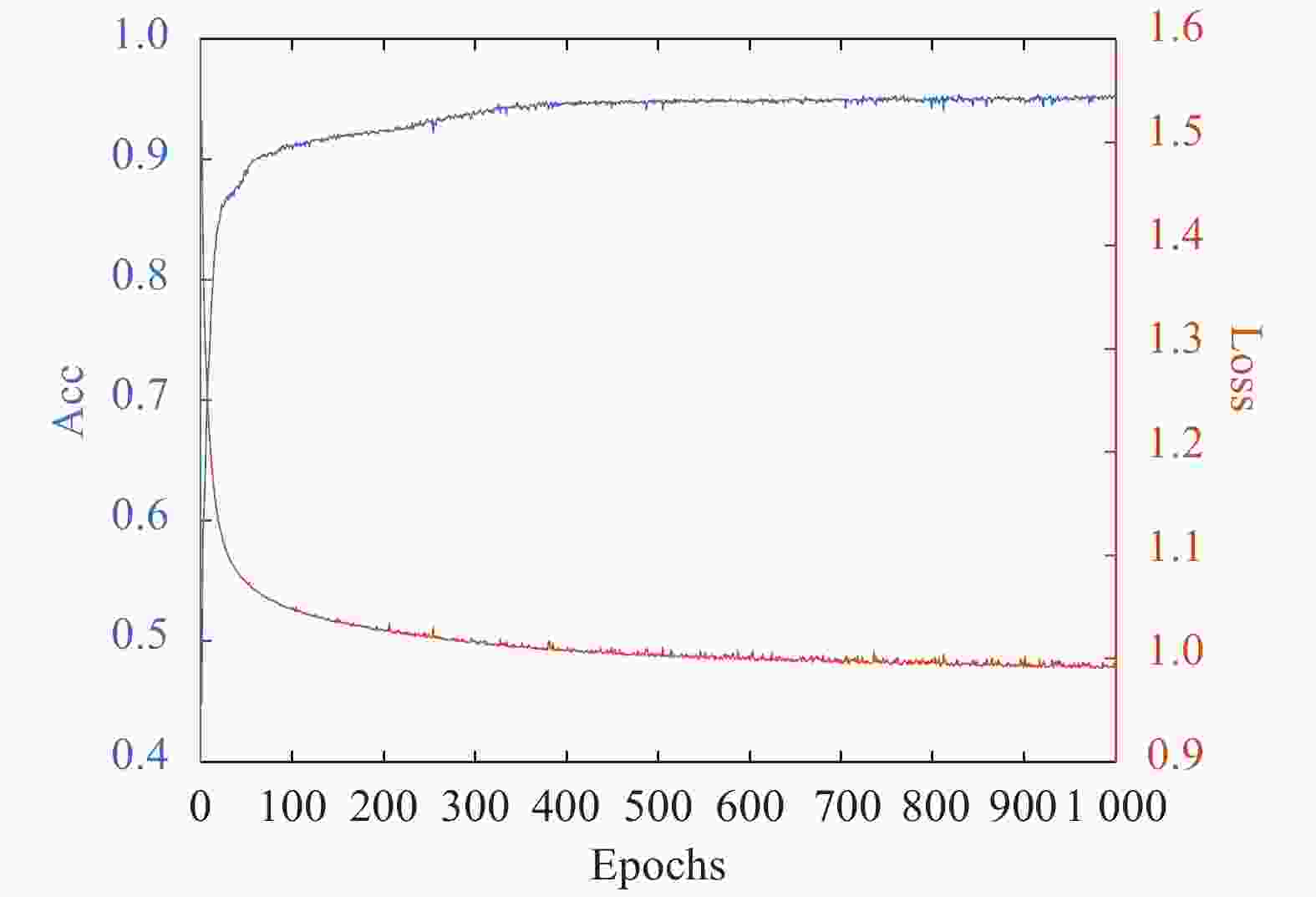
如图10和图11所示，经过1 000个epoch的训练之后，网络基本收敛，网络在测试集上的正确率达到94.2%。
图 10 训练集正确率和误差曲线
Figure 10. Accuracy and error curve of train set
图 11 训练集和测试集正确率曲线
Figure 11. Accuracy curve of train set and test set
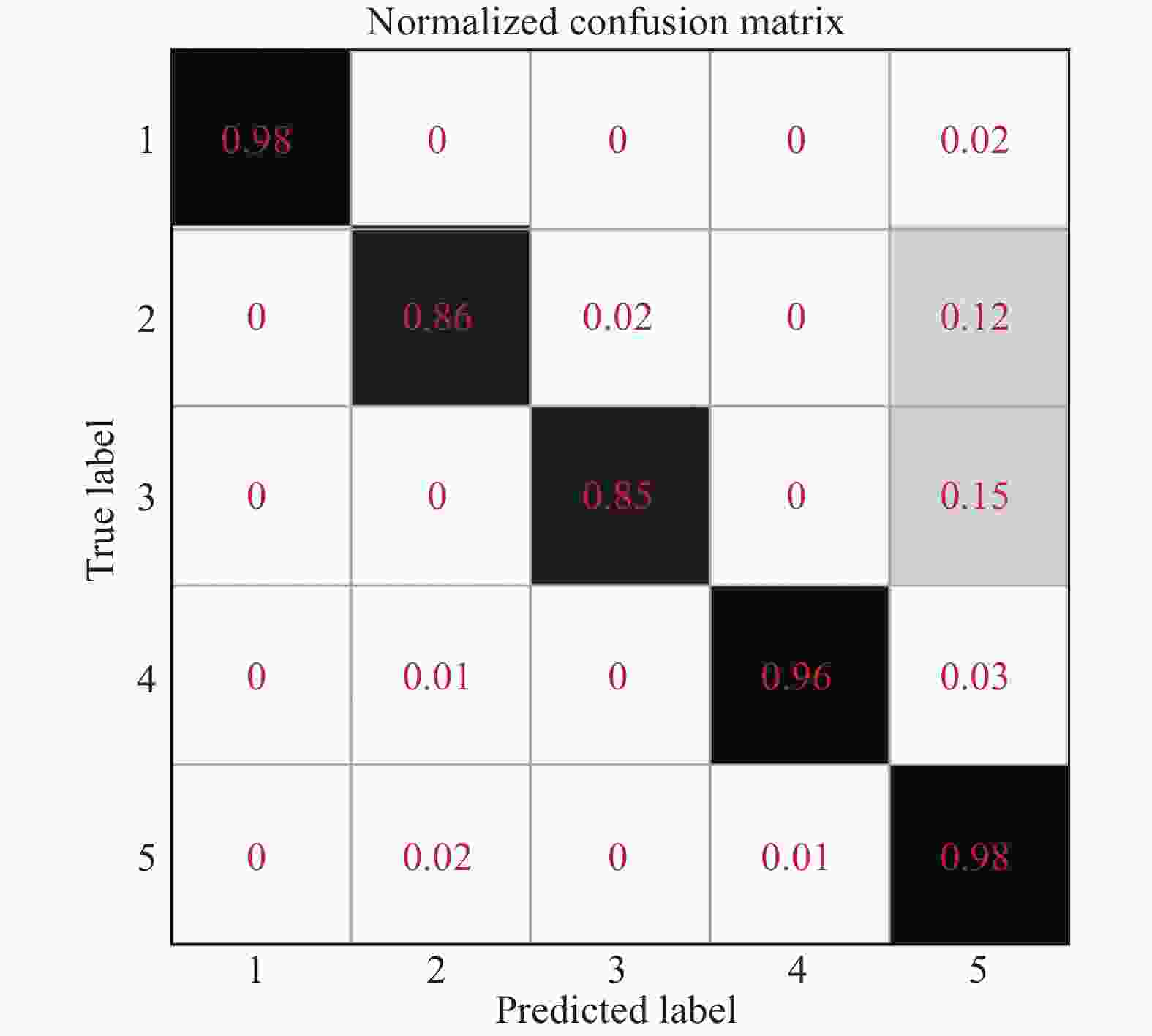
图11为测试结果的混淆矩阵，其中每个数值为真实标签所在行类别的样本被分类为所在列类别的概率。由图12可以看出，分类系统对第二和第三类矿物质识别能力稍差，有12%的第二类矿物和15%的第三类矿物被错分成第五类矿物，而第一类和第五类矿物获得了最高的识别正确率，达到了98%。
图 12 测试结果的混淆矩阵
Figure 12. Confusion matrix of test results
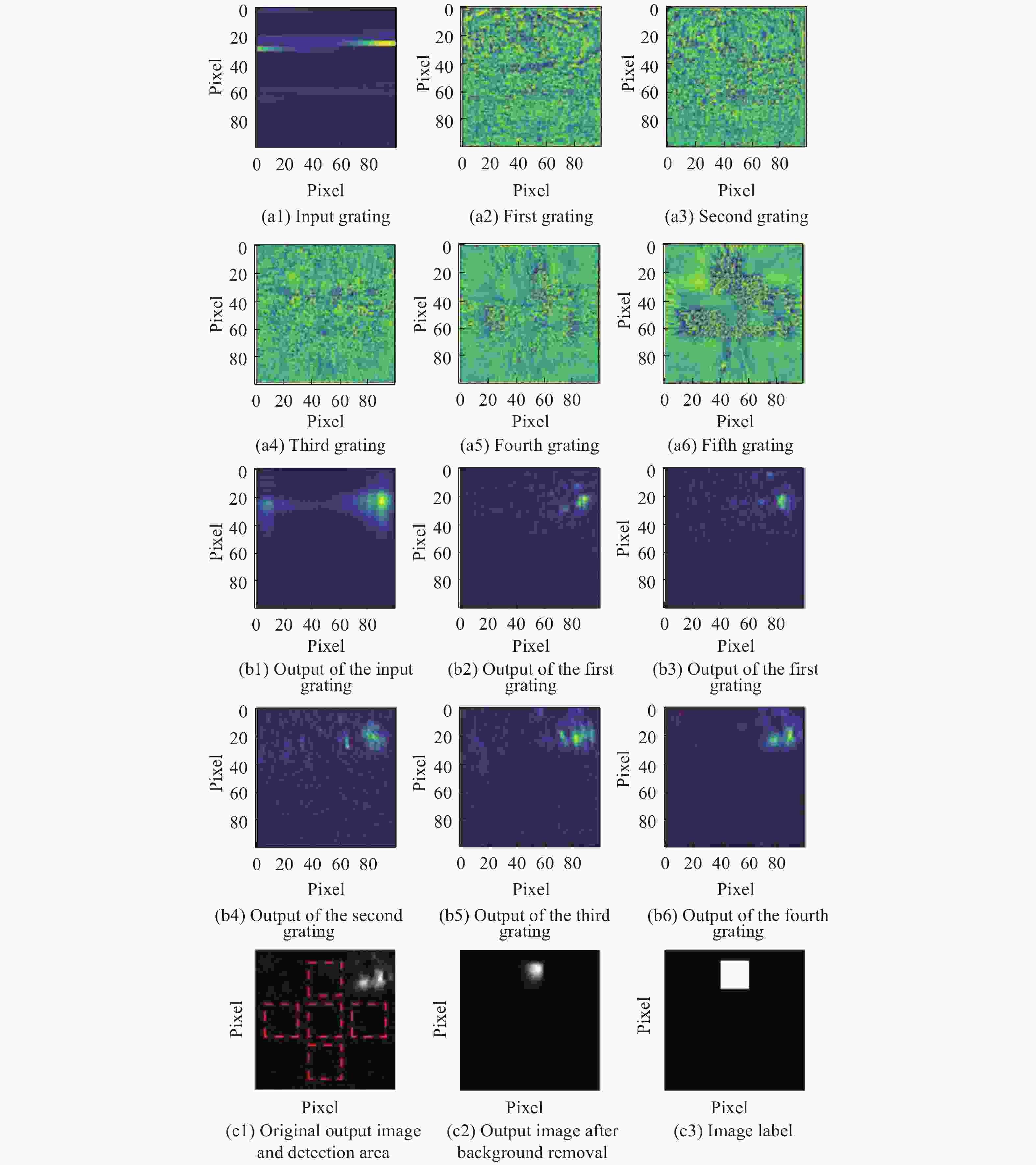
图13为训练完成后各层光栅的高度分布以及各层光栅的输出图像，其中最后一个光栅的输出图像即为最终的结果图像。在判断结果图像所表征的标签时要先去除非探测区域的背景信息影响，使用探测区域模板对结果图像进行提取后即可得到有效的结果信息，得到预测标签。
图 13 训练完成的各层光栅高度分布及各层光栅输出图像。(a1)~(a6) 光栅组；(b1)~(b6) 光栅输出； (c1)~(c3) 识别结果
Figure 13. Height distribution of each layer of grating and the output image of each layer of grating after training. (a1)-(a6) Gratings; (b1)-(b6) Output of gratings; (c1)-(c3) Recognition
-
衍射光栅栅格高度的变化会导致输出光场发生变化，对系统的分类正确率造成一定影响。为了确定衍射光栅高度离散化导致的光栅高度精度降低对最终分类精度的影响，对不同精度的光栅高度分布进行了仿真：
衍射光栅的相位调制范围为0~2
${\text{π}}$ ，将此范围内的数据均匀离散为${2}^{n}$ 个数值，其中n即为离散精度位数，也即为刻制光栅需要的刻蚀次数。需要多次刻蚀的光栅都要在前次刻蚀完成后重新对准才能进行下一次刻蚀，这其中就不可避免地引入了对准误差，并且刻蚀的次数越多，需要重新对准的次数也越多，相应的对准误差就会越大。因此在保证一定精度的前提之下应当尽可能减少刻蚀次数。由表1获悉，6 bit精度下的衍射光栅高度离散化对系统正确率的影响已经小于1%，这说明对衍射光栅进行适当的高度离散化可以在极大降低光栅刻蚀工艺复杂度的情况下较好地保持系统的分类正确率。
表 1 光栅不同高度精度下系统分类正确率
Table 1. System classification accuracy under different height precision of gratings
Height precision Accuracy Loss of accuracy Original data 94.220% 0 6 bit 93.642% 0.613% 5 bit 93.064% 1.227% 4 bit 90.751% 3.682% 3 bit 86.705% 7.976% 2 bit 63.584% 32.513% 1 bit 15.222% 83.844% -
文中提出了一种以10.6 μm的
${\rm CO}_{2}$ 激光器为光源的光学衍射神经网络实现方案，建立了全光衍射深度神经网络的模型，针对矿物拉曼光谱分类任务对衍射光栅的高度分布进行了优化。仿真结果表明基于光学衍射神经网络的拉曼矿物质分类精度达到94.220%。针对衍射光栅高度离散化精度与系统分类正确率的关系进行了研究，在衍射光栅刻蚀工艺可行的范围内给出了衍射光栅高度不同离散化精度下系统的分类正确率，为光学衍射神经网络中的衍射光栅的刻制提供了理论支持。
Raman mineral recognition method based on all-optical diffraction deep neural network
-
摘要: 提出了一种基于全光衍射神经网络的矿物拉曼光谱识别方法。首先，分析矿物拉曼光谱的数据结构特征，对比分析了传统神经网络与光学衍射神经网络的异同，根据预处理后的数据构建光学衍射神经网络；然后，采用交叉熵损失函数和Adam算法对光学衍射神经网络进行训练，得到优化的网络参数；最后，在仿真条件下，验证和分析不同栅格高度精度对矿物识别正确率的影响，给出了不同栅格高度精度对应的网络正确率及正确率损失。该方法在RRUFF矿物拉曼光谱数据库上的测试结果显示：五类矿物识别正确率为94.2%，证明利用光学衍射神经网络进行拉曼光谱分类具有可行性，为光学衍射神经网络的应用提供参考；栅格高度在6 bit精度条件下，五类矿物正确率为93.6%，证明栅格高度离散化能够在保证网络正确率的同时极大降低光栅制作难度，为光栅制备提供理论支撑。Abstract: A recognition method of mineral Raman spectrum based on all-optical diffraction neural network was proposed. Firstly, the data structure characteristics of the Raman spectra of minerals were analyzed, the similarities and differences between traditional neural network and optical diffractive neural network were compared and analyzed, and the optical diffractive neural network was constructed according to the preprocessed data. Secondly, the cross entropy loss function and Adam algorithm were used to train the optical diffractive neural network, and the optimized network parameters were obtained. Finally, under the simulation conditions, the effects of different grid-height accuracy on the accuracy of mineral recognition were verified and analyzed, and the network accuracy and accuracy loss corresponding to the different grid-height accuracy was given. The test results on the RRUFF mineral Raman spectrum database show that the recognition accuracy of five kinds of minerals is 94.2%, which proves the feasibility of Raman spectrum recognition using optical diffractive neural network. It provides a reference for the application of optical diffractive neural network; the accuracy of five kinds of minerals under the condition of 6 bit grid-height resolution is 93.6%, which proves that grid height discretization can not only ensure the accuracy of network, but also greatly reduce the difficulty of grating fabrication. It provides theoretical support for grating fabrication.
-
图 4 结果图像中的探测区域以及不同标签对应的标识区域
Figure 4. Detection area in the result image and identification area of different labels
图 5 全光衍射神经网络分类系统结构示意图
Figure 5. Structure diagram of optical diffractive neural network classification system
图 13 训练完成的各层光栅高度分布及各层光栅输出图像。(a1)~(a6) 光栅组；(b1)~(b6) 光栅输出； (c1)~(c3) 识别结果
Figure 13. Height distribution of each layer of grating and the output image of each layer of grating after training. (a1)-(a6) Gratings; (b1)-(b6) Output of gratings; (c1)-(c3) Recognition
表 1 光栅不同高度精度下系统分类正确率
Table 1. System classification accuracy under different height precision of gratings
Height precision Accuracy Loss of accuracy Original data 94.220% 0 6 bit 93.642% 0.613% 5 bit 93.064% 1.227% 4 bit 90.751% 3.682% 3 bit 86.705% 7.976% 2 bit 63.584% 32.513% 1 bit 15.222% 83.844% 
下载: 导出CSV
-
[1] Liang Weiwei, Chen Qiao, Peng Fang, et al. A novel surface-enhanced Raman scattering (SERS) detection for natural gas exploration using methane-oxidizing bacteria [J]. Talanta, 2018, 184: 156-161. doi: 10.1016/j.talanta.2018.02.099 [2] Veneranda Marco, Antonio Manrique-Martinez Jose, Lopez-Reyes Guillermo, et al. Spectroscopic study of olivine-bearing rocks and its relevance to the ExoMars rover mission [J]. Spectrochimica Acta Part A-Molecular and Biomolecular Spectroscopy, 2019, 223: 117360. doi: 117360 [3] 张腊梅, 陈泽茜, 邹斌. 基于3D卷积神经网络的PolSAR图像精细分类[J]. 红外与激光工程, 2018, 47(7): 0703001. doi: 10.3788/IRLA201847.0703001 Zhang Lamei, Chen Zexi, Zou Bin. Fine classification of polarimetric SAR images based on 3D convolutional neural network [J]. Infrared and Laser Engineering, 2018, 47(7): 0703001. (in Chinese) doi: 10.3788/IRLA201847.0703001 [4] Jia Guimin, Cheng Fangyuan, Yang Jinfeng, et al. Intelligent checking model of Chinese radiotelephony read-backs in civil aviation air traffic control [J]. Chinese Journal of Aeronautics, 2018, 31(12): 2280-2289. doi: 10.1016/j.cja.2018.10.001 [5] Yu Mingxin, Sun Yichen, Zhu Bofei, et al. Diverse frequency band-based convolutional neural networks for tonic cold pain assessment using EEG [J]. Neurocomputing, 2020, 378: 270-282. doi: 10.1016/j.neucom.2019.10.023 [6] 胡善江, 贺岩, 陶邦一, 等. 基于深度学习的机载激光海洋测深海陆波形分类[J]. 红外与激光工程, 2019, 48(11): 1113004. doi: 10.3788/IRLA201948.1113004 Hu Shanjiang, He Yan, Tao Bangyi, et al. Classification of sea and land waveforms based on deep learning for airborne laser bathymetry [J]. Infrared and Laser Engineering, 2019, 48(11): 1113004. (in Chinese) doi: 10.3788/IRLA201948.1113004 [7] Yu Mingxin, Tang Xiaoying, Lin Yingzi, et al. Diesel engine modeling based on recurrent neural networks for a hardware-in-the-loop simulation system of diesel generator sets [J]. Neurocomputing, 2018, 283: 9-19. doi: 10.1016/j.neucom.2017.12.054 [8] Yu Mingxin, Tang Xiaoying, Lin Yingzi, et al. An eye detection method based on convolutional neural networks and support vector machines [J]. Intelligent Data Analaysis, 2018, 22(2): 345-362. doi: 10.3233/IDA-173361 [9] 周宏强, 黄玲玲, 王涌天. 深度学习算法及其在光学的应用[J]. 红外与激光工程, 2019, 48(12): 1226004. doi: 10.3788/IRLA201948.1226004 Zhou Hongqiang, Huang Lingling, Wang Yongtian. Deep learning algorithm and its application in optics [J]. Infrared and Laser Engineering, 2019, 48(12): 1226004. (in Chinese) doi: 10.3788/IRLA201948.1226004 [10] Yu Mingxin, Yan Hao, Xia Jiabin, et al. Deep convolutional neural networks for tongue squamous cell carcinoma classification using raman spectroscopy [J]. Photodiagnosis and Photodynamic Therapy, 2019, 26: 430-435. doi: 10.1016/j.pdpdt.2019.05.008 [11] Yan Hao, Yu Mingxin, Xia Jiabin, et al. Tongue squamous cell carcinoma discrimination with raman spectroscopy and convolutional neural networks [J]. Vibrational Spectroscopy, 2019, 103: 102938. doi: 10.1016/j.vibspec.2019.102938 [12] Shen Yichen, Harris Nicholas C, Skirlo Scott, et al. Deep learning with coherent nanophotonic circuits [J]. Nature Photonics, 2017, 11(7): 441. doi: 10.1038/nphoton.2017.93 [13] Williamson Ian A D, Hughes Tyler W, Minkov Momchil, et al. Reprogrammable electro-optic nonlinear activation functions for optical neural networks [J]. IEEE Journal of Selected Topics In Quantum Electronics, 2020, 26(1): 2930455. doi: :10.1109/JSTQE.2019.2930455 [14] Lin Xing, Rivenson Yair, Yardimei Nezih T, et al. All-optical machine learning using diffractive deep neural networks [J]. Science, 2018, 361(6406): 1004. doi: 10.1126/science.aat8084 [15] Mengu Deniz, Luo Yi, Rivenson Yair, et al. Analysis of diffractive optical neural networks and their integration with electronic neural networks [J]. IEEE Journal of Selected Topics In Quantum Electronics, 2020, 26(1): 2921376. doi: 10.1109/JSTQE.2019.2921376 [16] Chang Julie, Sitzmann Vincent, Dun Xiong, et al. Hybrid optical-electronic convolutional neural networks with optimized diffractive optics for image classification [J]. Scientific Reports, 2018: 8. [17] Lafuente B, Downs R T, Yang H, et al. The Power of Databases: the RRUFF Project[M]//Armbruster T, Danisi R M. Highlights in Mineralogical Crystallography. Berlin: De Gruyter, 2015: 1-30. -
点击查看大图
图(13) / 表(1)
计量
- 文章访问数: 665
- HTML全文浏览量: 157
- PDF下载量: 91
- 被引次数: 0
