-
自适应光学系统是20世纪70年代以来发展起来的光学新技术。传统的自适应光学系统是通过波前传感器测量波前动态误差,再通过快速的电子系统进行计算和控制,用能动器件如变形镜或液晶空间光调制器进行实时的波前校正,使得光学系统具有自动适应外界条件变化、始终保持良好工作状态的能力。典型的自适应光学系统一般是一个由波前测量、波前控制、波前校正组成的负反馈系统[1-2]。
基于光学成像的流场测量技术易受到因各种因素引起的光学畸变而带来的影响。这些光学畸变严重影响了流场速度测量的测量精度。自适应光学系统在光学流场测量中的应用在国内暂无报导。国外研究团队曾将传统闭环自适应光学系统应用于该领域。但这些方法都受到了波前校正器件性能的限制。
近年来,以深度学习为主导的人工智能技术被引入在自适应光学领域,为自适应光学带来了新的研究思路与发展方向。国内外许多研究都已经将人工智能应用于自适应光学的诸多环节中,如波前测量[3],波前整形[4]、波前重建[5],闭环AO的实时控制模型[6]等等。使用人工智能的方法改进自适应光学系统,以期实现更精准的波前探测及校正、更智能的自动化运行以及适应更复杂的应用场景是自适应光学的发展趋势,也是人工智能领域的一个新课题。
在以往的研究中,国内外团队通过神经网络对图像层面的光学像差进行了校正,用以替代或补偿波前校正器件的校正效果。2017年,中国科学院光电技术研究所的Fei Xiao[7]等人通过深度学习方法对人眼视网膜成像自适应光学系统的图像进行了事后重建,并且与传统方法进行了比较,获得了较好的效果。在该方法中,作者运用了一个较为浅层的卷积神经网络结构,建立了退化图像与清晰图像的映射关系,通过训练好的神经网络对退化图像进行重建。同年,Lazareva等人[8]针对同一应用场景,采用机器学习中的随机森林算法,对人眼视网膜成像退化过程中的点扩散函数进行训练预测,再通过预测得到的点扩散函数对退化图像进行解卷积,对退化图像进行重建。
在文中,笔者提出了一种通过特殊卷积神经网络结构,用以重建因光学畸变而退化的流场测速中畸变图像的方法,以降低流体测量中光学像差对测量精度带来的影响。
-
粒子图像测速(PIV)是一种基于图像的光学流场速度测量方法,该技术可以获得流场中的瞬时速度分布以及相关属性信息。通过结合显示测量技术以及单点测量技术的优点,PIV在获得流场整体结构的同时保证了测量的分辨率和精度。是一种高精度实现流场分布瞬态测量的非接触测量方法,可以保证测量时对流场本身不产生任何干扰和影响。通过PIV技术测量流场时,首先通过在流场中投入一定数量的示踪粒子,示踪粒子一般需要和流场中流体密度相当,不会对流场本身产生任何影响且能够很好地跟随流场运动,从而通过示踪粒子的运动来反映流场的运动状态。同时示踪粒子应当具有足够高的光散射率,保证粒子能够在一定光照条件下被相机获得。利用片光源对待测流场区域进行照亮,再通过成像系统对流场中的粒子进行成像,便获得当前时间下流体中粒子分布的图像。一般成像系统都由高速相机和透镜组成。而流场中粒子的速度信息一般是通过相机对测量区域进行连续两次拍照,得到两张粒子图像,通过互相关算法,计算两幅图像间隔时间内粒子的位移,从而计算得到粒子的瞬时速度,最后通过对整个区域的粒子速度进行批量处理,得到整个测量区域内流场的分布矢量图。图1所示为粒子图像测速的工作原理。
PIV技术在一般的流场测量中具有高精度、高分辨率的优势,但是,当测量光路中存在由诸多因素引起的波前畸变时,其测量精度将收到严重影响。而这种波前畸变会严重影响粒子图像中粒子位置的分布,同时也会使得粒子图像的图像质量降低,从而导致粒子位置测量不确定增加,导致整体测量误差。一般情况下,静态波前畸变引起的测量误差可以很轻易地通过标定或者数据处理方法进行校正[9-10],但是随时间变化的动态波前畸变则更加棘手。动态的波前畸变存在于不同的流场测量应用中,例如,流场体积畸变一般由于流体非均匀、动态变化的折射率引起。这些畸变一般时由流体介质的折射率变化引起的,温度、压力或浓度梯度变化都会引起待测介质的折射率变化[11]。此外,流场中不同介质的相面也会因为相面的晃动带来波前畸变,例如在空气−水表面[12]、多相流体(如液体中的气泡)[13]、复杂表面后的流场(如液滴)、薄膜流场等等。所有这些波前畸变都会对PIV的测量精度产生显著影响[14]。
针对流体测量过程中的光学畸变所引起的测量不确定增加,传统及新型自适光学系统被应用与此场景的像差校正当中。2013年,Lars等人[15]首次将自适应光学系统运用于流场测量中,他们通过建立一个闭环的自适应光学系统,用于采用激光多普勒测速方法测量具有气−液介质表面的流场的测量系统中,成功校正了气−液介质表面晃动带来的光学畸变,提高了测量精度。并且这一实践证明,自适应光学是一种适用于复杂环境下流场测量系统的新工具。为了更好的提取介质表面引起的光学畸变信息,2015年Hannes等人[16]建立了一种新型的波前测量手段,即采用两个反射式的菲涅尔激光信标来获取激光多普勒测速技术中两束光路的畸变信息。该方法同样两路闭环自适应光学系统校正了气−液介质表面引起的光学畸变,提高了测量精度。同年,Nektarious[17]等人将液晶空间光调制其运用于流场测量中,也同样运用了该实验室提出的反射式菲涅尔激光信标。通过液晶空间光调制器,该实验成功对液面后的成像进行了校正。次年,Nektarious[18]等人延续了他们的工作,首次将自适应光学系统用于了PIV流场测量技术中,值得一提的是,在该实验中,他们分别采用了传统穿透式的激光信标(Transmission Guide Star)和之前提出的反射式菲涅尔激光信标,解决了不同测量条件下波前测量的问题。同时,在该实验中,他们通过全息相机对波前进行测量,通过液晶空间光调制器对波前进行了校正,显著提升了PIV图像的质量,从而提高了测量精度。此外值得一提的是,Martin等人[19]通过空间光调制器对入射波前进行调整,实现了PTV测量中不同深度图像的信息的提取,实现了PTV的三维测量,虽然这一方面并不属于对光学畸变的校正,但是也成为了自适应光学单元技术在流场测量中的应用。2018年,Martin等[20]成功将无波前自适应光学系统运用于PIV流场测量当中,他们通过计算PIV图像的锐度,以此作为指标,对变形镜进行迭代,从而校正像差,得到清晰的PIV图像。2020年,Hannes等[21]同时采用透射式信标与反射式信标,运用传统闭环自适应光学系统,对晃动水面下的PIV图像进行了实时校正,并且将控制系统实现在了FPGA上。
然而,以上所有的技术路线都是基于波前校正器件的传统闭环自适应光学系统或无波前自适应光学系统,其校正效果严重依赖于波前校正器的性能。而对于基于图像的流场测量中的光学像差,一般具有频率高、动态范围大、空间分辨率高等特点,对于这一应用场景,基于波前校正器件的自适应光学系统受到了器件本身性能的影响。例如,液晶空间光调制器受限于校正带宽限制而无法补偿流体中快速变化的像差,单元数较少的变形镜又受限于其空间分辨率。所以文中将提出一种基于深度学习的无校正器件的新型自适应光学校正技术。
-
通常而言,由波前像差引起的PIV图像退化过程可以描述为理想无畸变的真实PIV图像与带有波前畸变的点扩散函数(PSF)的卷积,再加上独立的噪声。如下式所示:
$$Y = X * k + \varepsilon $$ (1) 式中:
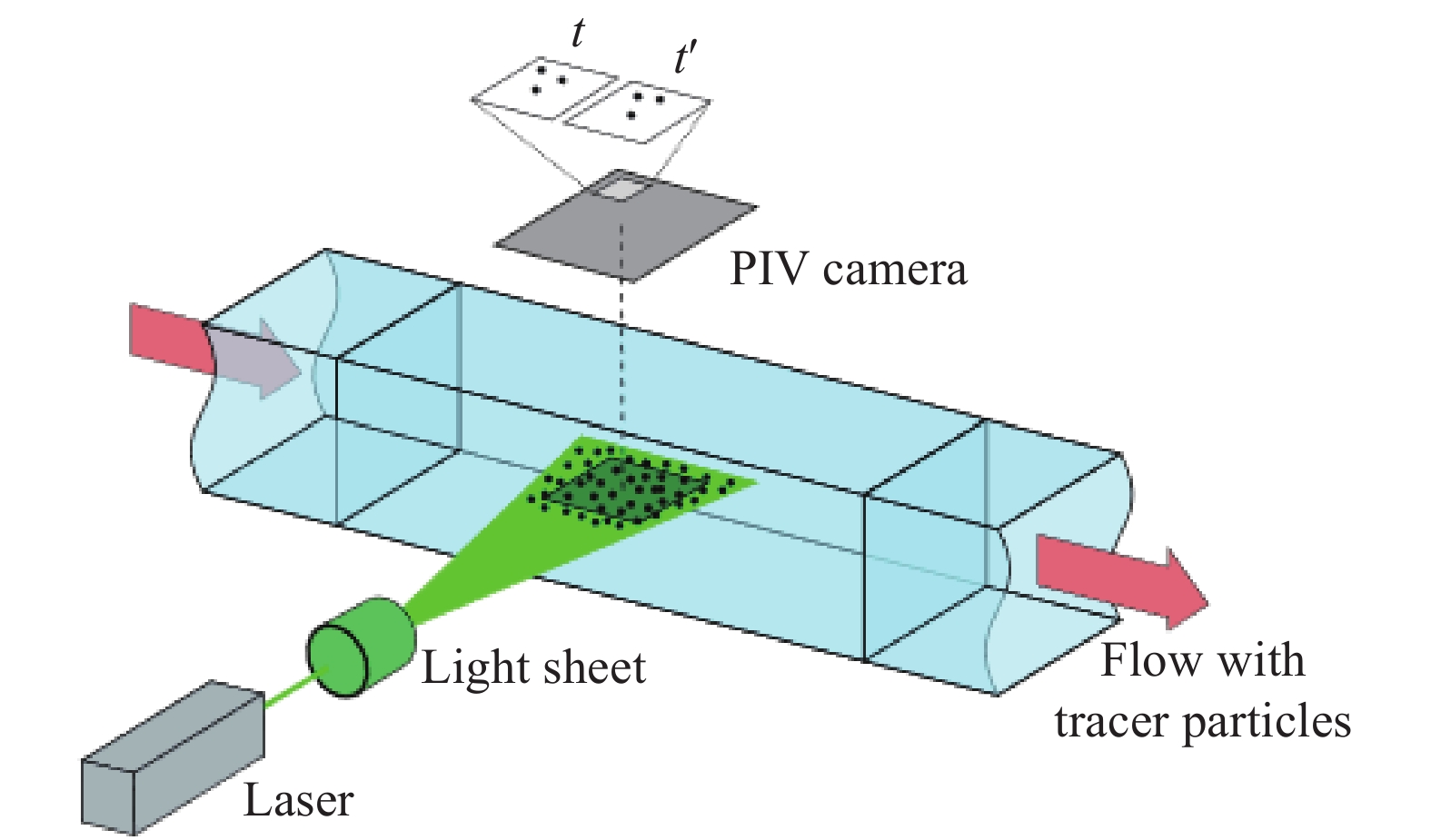
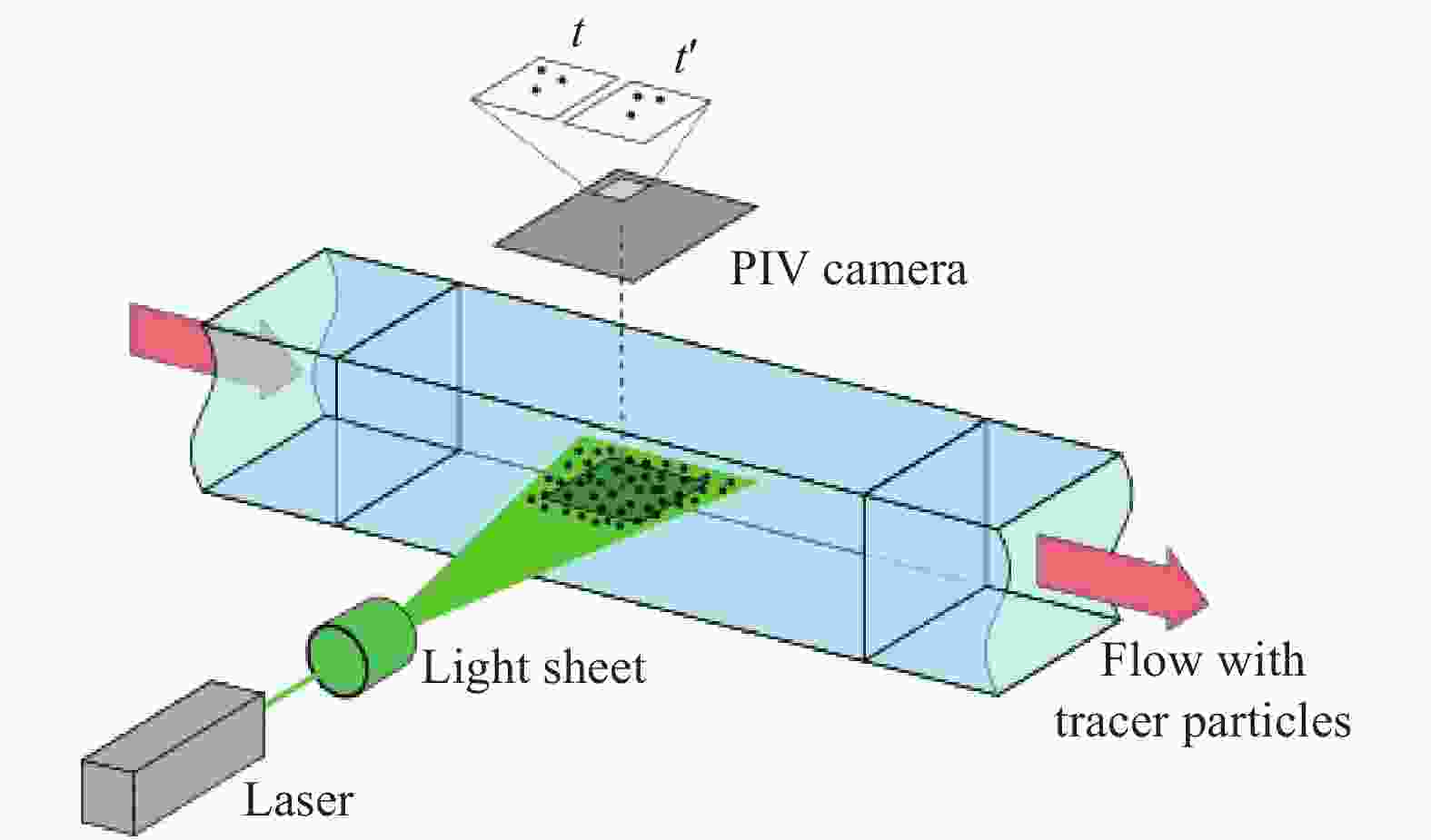
$Y$ 为畸变PIV图像;$X$ 为理想无畸变的真实PIV图像;$k$ 为点扩散函数卷积核;$\varepsilon $ 为独立噪声;$ * $ 为二维卷积运算符。这里笔者的任务是通过畸变PIV图像$Y$ ,建立求解理想真实图像$X$ 的最优解模型。文中,笔者通过一个深度卷积神经网络模型来对这一过程建模为一个通用函数模型:$\hat X = F(Y,\theta )$ ,其中,模型参数$\theta $ 可以通过训练数据集对神经网络训练学习得到。此函数可以建立起在畸变图像和真实图像之间的端到端映射关系。以数据为驱动的神经网络训练过程可以用最小化损失函数来描述,可以得知,神经网络的性能不仅取决于网络的结构,还取决于训练数据集,所以用于训练神经网络的训练集对于反映真实的畸变模型以及畸变校正过程尤为重要。为了生成一个合适的训练数据集,采用了如图2所示的实验平台。该实验平台具有采集PIV图像和波前测量的功能。对于PIV图像采集部分,首先用532 nm激光光源与一个圆柱形透镜相结合,产生一个用于照亮中的示踪粒子片光源,并在液体中加入了Dantec Dynamic公司的银包裹中空玻璃材质的示踪粒子,两者结合通过PIV相机即可采集到反映流场速度分布的PIV图像。其次,通过气泵在容器液体表面产生扰动气流,使得液面受激产生晃动,从而产生畸变波前。为了对畸变波前进行测量,使用660 nm的信标光从容器底部透射经过表面,再由Shack-Hartmann波前传感器进行测量。
对于训练所需的数据集而言,笔者需要同时得到理想无畸变的PIV图像以及所对应的畸变图像,无法直接通过实验平台采集到完全对应的图像对,所以通过上述的图像退化模型来生成训练数据集。首先,在关闭扰动气流并且使得液体表面保持完全稳定的状态下采集PIV图像,同时以这一状态对Shack-Hartmann波前传感器进行标定。采集到的PIV图像认定为理想的无畸变PIV图像,作为神经网络训练时的标签。其次,通过气泵产生气流,使得液体表面产生晃动从而产生波前畸变,通过信标光与Shack-Hartmann波前传感器,对系统中的波前畸变进行测量,得到一组由液体表面晃动产生波前畸变的Zernike系数,计算得到一组波前畸变的点扩散函数,并通过上述图像畸变模型生成与理想PIV图像相对应的畸变PIV图像,合成的畸变PIV图像作为神经网络训练的输入。其中点扩散函数可以近似为:
$$k = PSF = {\left\| {{\rm{FFT}}\left\{ {P(x,y)\exp ( - i\frac{{2\pi }}{\lambda }\varphi (x,y)} \right\}} \right\|^2}$$ (2) 式中:
$P$ 为成像系统孔径函数;$\varphi (x,y)$ 为波前畸变,可以定义为:$$\varphi (x,y) = \sum\limits_m^n {{a_m}{Z_m}(x,y)} $$ (3) 式中:
${a_m}$ 和${Z_m}$ 分别为各阶Zernike系数和Zernike多项式。其中,Zernike系数由Shack-Hartmann波前传感器测量得到。对于波前畸变的测量,笔者采集了10 000帧Shack-Hartmann光斑图像,通过计算光斑质心斜率以及波前复原算法,得到了10 000组Zernike系数值,并对其幅度谱进行了计算分析,结果如图3所示。通过对波前测量结果的分析可知,液体表面晃动所产生的波前畸变主要为低频的低阶像差。此外,对这10 000帧波前测量结果进行统计分析,其中波前畸变RMS平均值为11.1 μm,最大值为39.5 μm,PV值平均值53.8 μm,最大值为171.9 μm。
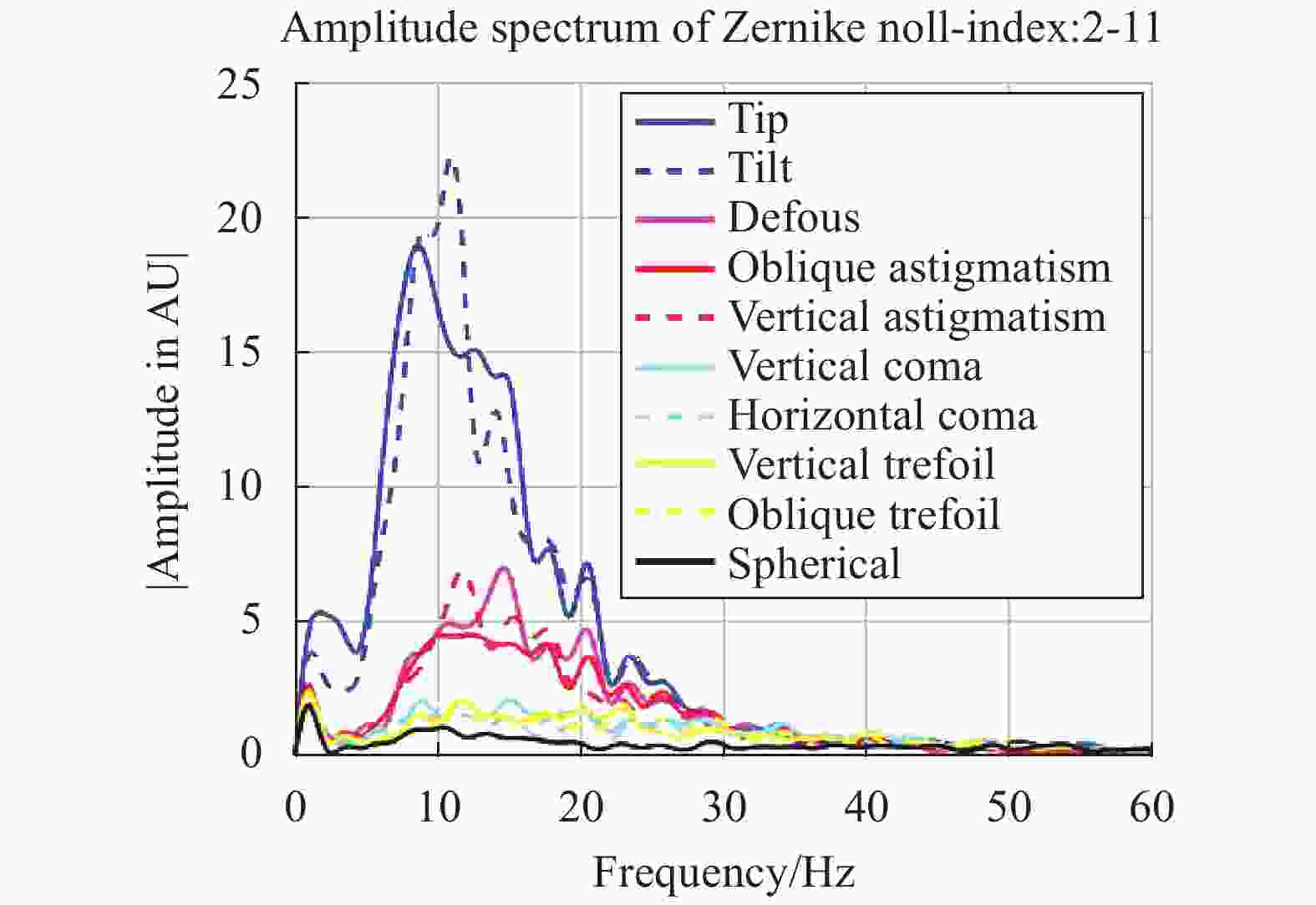
图 3 Zernike系数测量结果(液面晃动引起的波前畸变中前10阶不同Zernike系数幅度谱)
Figure 3. Measurement result of Zernike wavefront (First 10 order Zernike coefficients amplitude spectrum of fluctuating air-water interface induced wavefront aberration)
为了保证神经网络数据集输入与标签的准确性,对于每帧理想PIV图像,根据公式(1)~(3),通过一组PSF卷积核和随机高斯噪声生成了一帧对应的畸变PIV图像。在文中,笔者采集了1 000帧连续的理想PIV图像,由于实验平台中PIV相机与Shack-Hartmann波前传感器相机的帧率比例关系约为1∶10,对10 000组测量Zernike系数按照时间序列1/10比例采样,计算得到了10组1000帧的PSF卷积核,每组卷积核对1 000帧理想PIV图像进行卷积运算,并生成两种不同高斯噪声,从而生成了20 000对畸变/无畸变PIV图像对,用于神经网络的训练。通过不同PSF卷积核,不同噪声与理想PIV图像的合成过程,保证了训练数据集样本分布的覆盖性。
-
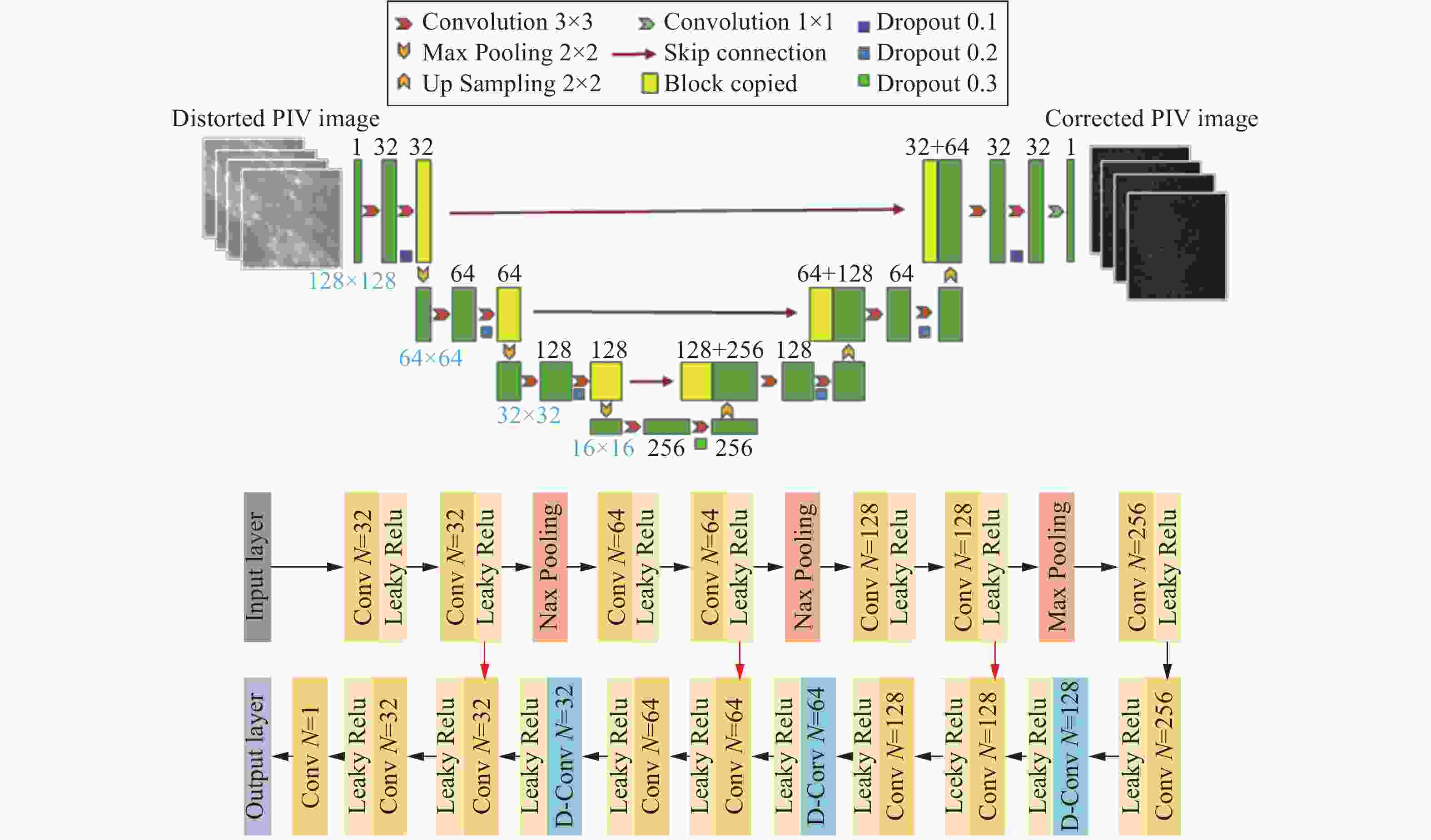
文中,建立了以U-net为框架的深度卷积神经网络。U-net是Olaf.R等人为了解决图像分割这种像素级的图像回归问题而设计的网络结构[22],是计算机视觉领域最先进的网络结构之一。由于U-net在像素级图像回归问题上的优异性能,它及其各种改进的结构被应用于图像重建、图像超分辨率等领域。U-net的独特之处在于它由一个下采样的收缩结构和一个上采样的扩张结构连接,形成了一个U形的体系结构,同时对相同尺寸的卷积层进行桥连接。由于上采样部分的存在,网络可以将二维数据信息传播到更高的尺寸结构上,以获得更高的分辨率。
图4为文中所搭建的深度卷积神经网络结构,它由3个下采样模块和3个上采样模块组成。每个模块中包含了两个3×3大小卷积核的卷积层,每个卷积层后紧跟一个Leaky Relu激活函数层。Leaky Relu是带泄露修正线性单元(Leaky rectified linear unit),是每个模块中两个卷积层后为步长为2×2大小的池化层(Pooling layer)或上采样层(up-convolution layer)。网络的最后是一个卷积核大小为1×1的卷积层,用于建立到校正后图像的映射。为了防止训练过程中出现过拟合的现象,笔者在每个模块中都设置了不同比例的Dropout节点。
根据2.1中的描述,文中所建立的深度神经网络结构可以描述为畸变PIV图像和理想PIV图像最优估计值的映射:
$\hat X = F(Y,\theta )$ ,其中,模型参数$\theta $ 是神经网络中每个隐藏神经元的权重$W$ 和每个隐藏层偏置$B$ 的集合:$\theta = \{ {w_{ik}},{b_i}\} $ 。而训练过程可以表示为最小化损失函数。对于训练中的损失函数(Loss Function)的选取,笔者并未采用U-Net,最初为了图像分割问题所采用的交叉熵损失函数(Corss entropy loss function),因为U-Net的发明最初是为了解决图像分割问题,这一应用可以近似为一个分类问题,而文中的应用是通过神经网络校正光学像差引起的畸变,目的是恢复图像,所以可以归类为图像的回归问题。所以文中笔者采用了更加适合回归问题的均方差损失函数(MSE loss function)。训练过程可以用下式表示:$$\mathop {\arg \min }\limits_{w,b} E(w,b) = \frac{1}{{2N}}\sum\limits_{i = 1}^N {\left\| {F({Y_i}) - {X_i}} \right\|} _2^2$$ (4) 此外,在训练过程中笔者采用Adam优化器作为优化方法,其中,起始学习率(learning rate)和一阶二阶动量参数分别设置为0.001,0.9和0.999。采用pytorch作为工具搭建并训练了网络,并且在一块NVIDIA GeForce RTX 2080Ti的GPU上完成了训练。
-
利用上述生成的数据集和所搭建的网络进行训练后,笔者得到了一个可以直接对畸变PIV图像进行校正的神经网络。为了评价训练后的神经网络校正性能,通过图2所示的实验平台单独采集了200帧连续的无畸变理想PIV图像,然后在实验平台上加扰动气流,通过Shack-Hartmann传感器采集并计算得到的2 000帧波前畸变Zernike系数,通过1/10采样得到200个PSF卷积核,根据2.1中所述的图像退化模型再次生成了一个测试数据集。重新采集PIV图像可以验证神经网络是否产生了过拟合现象。
首先为了对图像的校正效果进行评价,通过计算畸变PIV图像和校正后PIV图像与输入理想PIV图像之间的均方误差(MSE)、峰值信噪比(PSNR)和结构相似性指数(SSIM),来验证了训练后神经网络的性能。这3个评价指标是图像恢复、图像压缩、图像超分辨重建等领域广泛应用的评价指标。其中MSE即两幅
$m \times n$ 大小的图像$Y$ 和$X$ 之间的均方误差值,定义为:$$MSE = \frac{1}{{mn}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{[Y(i,j) - X(i,j)]}^2}} } $$ (5) 而峰值信噪比表示的是信号最大可能功率和影响它表示精度的破坏性噪声功率的比值,单位为分贝,通过MSE定义的,定义如下:
$$PSNR = 10{\log _{10}}\left(\frac{{MAX_Y^2}}{{MSE}}\right) = 20{\log _{20}}\left(\frac{{MA{X_Y}}}{{\sqrt {MSE} }}\right)$$ (6) 式中:
$MA{X_Y}$ 代表图像中像素的最大值。一般像素值由$B$ 位二进制表示的图像数据中,$MA{X_Y} = {2^B} - 1$ 。由于数据集中图像数据格式为uint8型,即每个像素由8位二进制表示,故像素最大值为255。一般来说,MSE值越小,PSNR越大代表图像质量越好,且根据经验,PSNR在30~40 dB之间代表图像质量较好,而低于20 dB说明图像质量非常差。结构相似性指数(Structural Similarity),即SSIM是衡量两幅图片相似性的指标,它基于两幅图片之间亮度
$l$ 、对比度$c$ 和结构$s$ 3个参数的比较,SSIM中的3个参数定义如下:$$SSIM(X,Y) = [l{(X,Y)^\alpha } \cdot c{(X,Y)^\beta } \cdot s{(X,Y)^\gamma }]$$ (6) $$l(X,Y) = \frac{{2{\mu _x}{\mu _y} + {C_1}}}{{{\mu _x}^2 + {\mu _y}^2 + {C_1}}}$$ (7) $$c(X,Y) = \frac{{2{\sigma _x}{\sigma _y} + {C_2}}}{{{\sigma _x}^2 + {\sigma _y}^2 + {C_2}}}$$ (8) $$s(X,Y) = \frac{{{\sigma _{xy}} + {C_3}}}{{{\sigma _x}{\sigma _y} + {C_3}}}$$ (9) 式中:
$\mu $ 为图像均值;$\sigma $ 为图像方差;${\sigma _{xy}}$ 为两幅图像协方差;$C$ 为常数。一般$\alpha = \beta = \gamma = 1$ ,${C_3} = {C_2}/2$ ,从而得到SSIM:$$SSIM(X,Y) = \frac{{(2{\mu _x}{\mu _y} + {C_1})({\sigma _x}{\sigma _y} + {C_2})}}{{({\mu _x}^2 + {\mu _y}^2 + {C_1})({\sigma _x}^2 + {\sigma _y}^2 + {C_2})}}$$ (10) SSIM取值在0~1之间,值越大,即越接近1,则表示图像相似程度越高,对于应用来说,代表畸变造成的失真就越小。
将200帧测试集畸变图片通过训练后的神经网络进行校正,并按照上述评价方法对200帧图像对的图像质量进行计算,结果如表1所示。同时,将结果与Sroubek等人[23]所提出的图像盲反卷积算法进行了比较。该方法是盲反卷积算法中较为快速且鲁棒的一种算法,在这种方法中,盲反卷积问题被近似为了L1正则化优化问题,通过对图像和点扩散函数进行交替迭代优化而找到反卷积的最优解。为了增加迭代的收敛速度,算法通过变量拆分将每步迭代转换为一个约束问题,然后使用增广拉格朗日方法(Augmented Lagrangian method, ALM)进行处理,从而可以在傅立叶域中实现简单快速的实现。算法的实现由作者所公布的开源代码而完成。
表 1 200帧PIV图像对校正前后的图像质量评价结果
Table 1. Quality assessment of PIV images before and after correction by trained neural network for 200 frames image pairs
Distorted PIV image Corrected PIV image Restored PIV image by ALM MSE 0.064 0.00062 0.056 PSNR 12.79 32.16 15.14 SSIM 0.37 0.73 0.39 通过结果可以看出:因为光学畸变严重失真的PIV图像在经过训练得到的神经网络校正后,大部分的失真都被校正。而且单独从PSNR的结果可以看出,校正后的PIV图像质量有了很大的改善。而且可以看出,训练后的神经网络校正效果要远远优于盲反卷积算法。图5是从200帧校正结果中比较典型的一帧,可以看出:在输入波前畸变的作用下,原本清晰的理想PIV图像已经产生了人眼可见的失真与模糊,而且粒子的位置分布也产生了误差,在经过神经网络校正后,图像恢复清晰并且与原本的理想PIV图像结果非常接近,粒子分布清晰,为粒子图像的流速计算提供了更为可靠的数据来源。而盲反卷积算法虽然对图像的锐度有一定的提升,但复原后的图像距离理想PIV图像还是有非常的大的差距。

图 5 单帧PIV图像的光学畸变校正结果。 (a) 输入波前畸变;(b) 理想PIV图像;(c) 畸变PIV图像;(d) 校正后PIV图像;(e) ALM复原后PIV图像
Figure 5. Aberration correction of single frame PIV image. (a) Input wavefront aberration; (b) Original PIV image; (c) Distorted PIV image; (d) Corrected PIV image; (e) Restored PIV image by ALM
此外,为了定量评价神经网络校正对PIV流场测量的改善效果,笔者对上述200帧理想PIV图像,畸变PIV图像以及校正后的PIV图像进行流场速度计算,并以局部和全局的平局测量不确定度作为评价指标,来评价校正效果。在利用图2所示实验装置的采集200帧测试数据集时,PIV相机成像面的流体速度通过水泵喷口控制在6 mm/s左右的范围内进行采集。流场速度的不确定度主要由3部分组成:PIV算法本身引起的测量不确定度
${\sigma _{{\rm{PIV}}}}$ ,流场本身的湍流或不稳定性引起的不确定度${\sigma _{{\rm{flow}}}}$ 以及光学畸变引起的不确定度${\sigma _{{\rm{distortion}}}}$ ,可以定义为:$$\sigma = \sqrt {\sigma _{{\rm{flow}}}^2 + \sigma _{{\rm{distortion}}}^2 + \sigma _{{\rm{PIV}}}^2} $$ (11) 笔者利用Matlab中的PIVlab工具箱对200帧理想无畸变PIV图像,畸变PIV图像以及校正后PIV图像进行了流场速度场计算,并对测量区域的局部不确定度和全局的不确定度的平均值进行计算,结果如图6(其中白色箭头表示局部流场速度大小及方向,背景颜色代表局部测量不确定度大小)和表2所示,可以看出:经过神经网络校正后的PIV图像所计算得到的测量结果相比畸变PIV图像测量精度有了大幅提高,由光学畸变所引起的测量不确定度增加被校正了近97%左右。

图 6 (a)理想PIV图像;(b)畸变PIV图像;(c)校正后PIV图像测量结果
Figure 6. PIV measurement results from (a) Ideal images; (b) Distorted images; (c) Corrected images
表 2 神经网络校正后流场速度标准差及相对标准不确定度分析
Table 2. Velocity standard deviation and relative standard uncertainty reduced by neural network aberration correction
$\sigma $ /mm·s−1 $\sigma {\rm{/}}\bar v$ Reduction Ideal PIV 0.736 12.04 % — Distorted PIV 5.003 88.07 % 0 Corrected PIV 0.846 14.23 % 97 % -
文中,建立了一种基于深度卷积神经网络的无波前校正器的自适应光学新方法,并应用于基于图像的流场测速中,降低了由光学畸变引起的PIV测量不确定度。证明了深卷积神经网络能够直接恢复由波前像差引起的畸变PIV图像,并且这种无波前校正器的校正方法取得了良好的校正效果。并且将该方法与传统图像处理算法进行了对比,效果显著优于传统算法。与传统盲反卷积算法相比,该方法无需对PSF进行预测计算,通过对网络的训练,网络结构可以实现畸变图像到校正图像的端到端映射,这样以样本数据驱动的思路可以对特定场景下的像差进行校正,而且与传统算法相比具有更好的校正效果,同时也大大提升了算法速度。校正速度对于文中的流体测量的场景应用而言具有重要意义,神经网络的应用可以实现对粒子图像的在线校正,从而达到在线测量的目的。除此之外,笔者认为,因为基于图像的流场测量结果来源于图像本身,所以最终目的是提高图像质量,而基于学习的算法由于能够很容易地生成训练数据集,特别是在实验中可以很容易地得到未失真的图像,可以作为训练数据集的标签,所以以数据驱动的基于算法的像差校正方法非常适用于像PIV这样的成像计量技术。通过对校正后图像质量的评定和对PIV测量相对标准不确定度的降低进行评定,验证了该方法的有效性。该方法既是自适应光学技术的一种新的思路,也是自适应光学在新的领域,即流场测量这一领域新的尝试。
-
感谢德国德累斯顿工业大学(TU Dresden)测量与传感器实验室(MST)团队对文中提供的技术支持和实验平台支持,以及德国学术与交流中心(DAAD)对文中提供的资金支持。
Aberration correction for flow velocity measurements using deep convolutional neural networks
-
摘要: 基于光学成像的流场测量技术,如粒子图像测速技术(PIV),易受到因流体中折射率的不均匀性或晃动的介质边界引起的光学畸变而带来的影响。这些畸变会使得示踪粒子在图像上的位置分布产生误差且严重影响图像清晰度,从而增大流场速度测量的误差。为了提高光学流场速度测量的测量精度,自适应光学系统可以应用于其中去校正光学畸变。基于图像流场测量中的光学像差具有频率高,动态范围大,空间分辨率高等特点,对于这一应用场景,基于波前校正器件的自适应光学系统受到了器件本身性能的影响。基于深度学习的自适应光学技术在流场测量中的应用,建立了一种基于深度神经网络的无波前校正器件自适应光学校正技术,以深度神经网络代替传统的波前校正器件,用于粒子图像测速技术中的光学畸变校正。为了生成神经网络所需要的训练和测试数据集,搭建了可以实现波前测量的粒子图像测速实验平台,分析并建立了光学畸变在粒子图像上的图像退化模型。最后,以校正后PIV图像的校正效果和流场速度测量结果作为评价标准,对所建立神经网络的畸变校正性能进行了分析。Abstract: Optical imaging-based flow measurement techniques, like particle image velocimetry, are vulnerable to optical distortions caused by inhomogeneous refractive index or fluctuating phase boundaries. These distortions can lead to blurred particle images and uncertain tracer particle position assignment, resulting in a degradation of velocity measurement accuracy. In order to improve the measurement accuracy, adaptive optics system can be applied to correct distortions. For imaging metrology in fluid mechanics, the optical distortions have features of large frequency range, high spatial frequency and large dynamic range. Actuator-based approaches are limited by its performances. In our work, a novel intelligent adaptive optic system was applied to flow measurement, a learning-based aberration correction method without wavefront corrector was demonstrated, which was used to correct distortions in imaging-based flow measurement. A particle image velocimetry setup which can measure wavefront aberration was built to generate training and test dataset for deep neural network, and also the distortion caused PIV image degradation model. The correction performance of the trained neural network was quantitatively evaluated by corrected PIV image quality and flow measurement result.
-
表 1 200帧PIV图像对校正前后的图像质量评价结果
Table 1. Quality assessment of PIV images before and after correction by trained neural network for 200 frames image pairs
Distorted PIV image Corrected PIV image Restored PIV image by ALM MSE 0.064 0.00062 0.056 PSNR 12.79 32.16 15.14 SSIM 0.37 0.73 0.39 表 2 神经网络校正后流场速度标准差及相对标准不确定度分析
Table 2. Velocity standard deviation and relative standard uncertainty reduced by neural network aberration correction
$\sigma $ /mm·s−1$\sigma {\rm{/}}\bar v$ Reduction Ideal PIV 0.736 12.04 % — Distorted PIV 5.003 88.07 % 0 Corrected PIV 0.846 14.23 % 97 % -
[1] 张雨东, 饶长辉, 李新阳. 自适应光学及激光操控[M].北京: 国防工业出版社, 2016. Zhang Yudong, Rao Changhui, Li Xinyang. Adaptive Optics and Laser Control[M].Beijing: National Defense Industry Press, 2016.(in Chinese) [2] Tyson R K. Principles of Adaptive Optics[M]. Boca Raton: CRC Press, 2015. [3] Hu L, Hu S, Gong W, et al. Learning-based shack-hartmann wavefront sensor for high-order aberration detection [J]. Opt Express, 2019, 27(23): 33504-33517. doi: 10.1364/OE.27.033504 [4] 郑珊珊, 杨婉琴, 司徒国海. 计算光学成像在散射中的应用[J]. 红外与激光工程, 2019, 48(6): 0603005. doi: 10.3788/IRLA201948.0603005 Zheng Shanshan, Yang Wanqin, Situ Guohai. Application of computational optical imaging in scattering [J]. Infrared and Laser Engineering, 2019, 48(6): 0603005. (in Chinese) doi: 10.3788/IRLA201948.0603005 [5] Guo H, Korablinova N, Ren Q, et al. Wavefront reconstruction with artificial neural networks [J]. Opt Express, 2006, 14(14): 6456-6462. doi: 10.1364/OE.14.006456 [6] Ke H, Xu B, Xu Z, et al. Self-learning control for wavefront sensorless adaptive optics system through deep reinforcement learning [J]. Optik, 2019, 178: 785-793. doi: 10.1016/j.ijleo.2018.09.160 [7] Fei X, Zhao J, Zhao H, et al. Deblurring adaptive optics retinal images using deep convolutional neural networks [J]. Biomedical Optics Express, 2017, 8(12): 5675-5687. doi: 10.1364/BOE.8.005675 [8] Lazareva A, Asad M, Slabaugh G. Learning to deblur adaptive optics retinal images[C]//ICIAR,2017:497-506. [9] Reuss D L, Megerle M, Sick V. Particle-image velocimetry measurement errors when imaging through a transparent engine cylinder [J]. Measurement Science and Technology, 2002, 13(7): 1029-1035. doi: 10.1088/0957-0233/13/7/309 [10] Minor G, Oshkai P, Djilali N. Optical distortion correction for liquid droplet visualization using the ray tracing method: Further considerations [J]. Measurement Science and Technology, 2007, 18(11): L23-L28. doi: 10.1088/0957-0233/18/11/L01 [11] Böhm B, Heeger C, Gordon R L, et al. New perspectives on turbulent combustion: Multi-parameter high-speed planar laser diagnostics [J]. Flow, Turbulence and Combustion, 2011, 86(3): 313-341. [12] Gomit G, Chatellier L, Calluaud D, et al. Free surface measurement by stereo-refraction [J]. Experiments in Fluids, 2013, 54(6): 1540. doi: 10.1007/s00348-013-1540-4 [13] Abe Y, Yamamoto Y, Hyuga D, et al. Interfacial stability and internal flow of a levitated droplet [J]. Microgravity Science and Technology, 2007, 19(3): 33-34. [14] Schlüßler R, Czarske J, Fischer A. Uncertainty of flow velocity measurements due to refractive index fluctuations [J]. Optics and Lasers in Engineering, 2014, 54: 93-104. doi: 10.1016/j.optlaseng.2013.10.011 [15] Büttner L, Leithold C, Czarske J. Interferometric velocity measurements through a fluctuating gas-liquid interface employing adaptive optics [J]. Opt Express, 2013, 21(25): 30653-30663. doi: 10.1364/OE.21.030653 [16] Radner H, Büttner L, Czarske J. Interferometric velocity measurements through a fluctuating phase boundary using two fresnel guide stars [J]. Opt Lett, 2015, 40(16): 3766-3769. doi: 10.1364/OL.40.003766 [17] Koukourakis N, König J, Büttner L, et al. Flow-field measurements through phase-boundaries using wavefront shaping[[C]]//Proceedings of the Frontiers in Optics 2015, 2015. [18] Koukourakis N, Fregin B, König J, et al. Wavefront shaping for imaging-based flow velocity measurements through distortions using a fresnel guide star [J]. Opt Express, 2016, 24(19): 22074-22087. doi: 10.1364/OE.24.022074 [19] Teich M, Mattern M, Sturm J, et al. Spiral phase mask shadow-imaging for 3d-measurement of flow fields [J]. Opt Express, 2016, 24(24): 27371-27381. doi: 10.1364/OE.24.027371 [20] Teich M, Grottke J, Radner H, et al. Adaptive particle image velocimetry based on sharpness metrics [J]. Journal of the European Optical Society, 2018, 14: 5. doi: 10.1186/s41476-018-0073-0 [21] Radner H, Stange J, Buttner L, et al. Field programmable system-on-chip based control system for real-time distortion correction in optical imaging[C]//IEEE Transactions on Industrial Electronics, 2020: 10.1109/TIE.2020.2979557. [22] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, 2015: 234-241. [23] Sroubek F, Milanfar P. Robust multichannel blind deconvolution via fast alternating minimization [J]. IEEE Transactions on Image Processing, 2012, 21(4): 1687-1700. doi: 10.1109/TIP.2011.2175740 -






 下载:
下载: