-
近年来，软体机器人作为一项新兴的前沿技术迅速发展，且逐渐在医疗等领域得到应用[1-3]。与传统刚性手术机器人不同，软体机器人采用柔软性材料制作而成，具有多自由度，并在人机交互中本质安全、不易造成损伤，能够柔软连续地变形适应人体各类组织结构，在微创手术等狭小封闭空间操作时具有较高的灵活性、适应性和安全性[4-6]。因此，该技术在空间受限的微创手术等领域表现出巨大的优势，为解决手术机器人临床应用的瓶颈问题提供了新的思路和契机，有望在未来提高微创手术的精度和效率等。
软体机器人的状态测量方法主要分为传统视觉和光纤传感器测量等。基于传统传感器的测量方法主要分为非接触式和接触式测量方法两类，非接触式测量主要包括视觉传感器、电磁传感器和激光传感器测量等，接触式测量主要包括电阻应变传感器、光电传感器和微机电传感器测量等。受微创手术狭小封闭空间和软体机器人材料特性的限制，视觉传感器难以实现微创手术软体机器人的精确测量。光电传感器测量通过集成光传感器与微电子陀螺仪等构建传感系统，利用多传感器融合实现机器人的状态参数测量。但这类传感器尺寸偏大，难以适用于微创手术。微机电传感器测量通过磁力计和陀螺仪等集成实现机器人的状态测量，但这种刚性传感器难以集成到本体柔软和形变较大的软体机器人中，且其测量分辨率较低、易受电磁干扰等。此外，柔性电阻应变微传感器虽然可以集成到可穿戴装备中测量其状态参数，但由于其传感系统存在复杂度高、易受电磁干扰等问题，限制了该技术在微创手术软体机器人中的应用[7-13]。
正是由于传统测量方法存在的若干问题，光纤传感作为一种基于光传感原理和柔性微型器件的测量方法受到广泛研究[12-18]。2010年Clements等提出了基于光纤光栅的柔性机构定位和形状测量系统，通过在软体机构中布置光纤传感器，测量结构的弯曲曲率和挠度，实现软体机构形态的传感检测[15]；2012年Bajo等基于机器人的运动学模型，对机器人的接触位置进行了估计和测量，该方法对模型的准确性过于依赖，不适用于动态手术环境[16]。2015年Searle等提出一种基于光纤曲率传感器的软体机器人姿态传感系统，软体机器人运动时封闭在刚性圆柱体腔体中的光纤发生形变，根据光纤的光强变化计算出机器人的弯曲角度和位置坐标[17]；刘浩与Farvardin等为骨质疏松手术的治疗研制了光纤形状传感器，将与镍钛丝粘贴的两根光纤放置在软体机器人两侧，通过改变形变中心面的位置增大光纤的检测范围，机器人弯曲时其末端跟踪精度为0.4 mm[18]。2017年Wang等将光纤以直线型植入到硅胶机器人中测量曲率，提出了一种机器人运动姿态测量算法，通过实验分析了算法的精度，但该算法基于机器人各段曲率和扭矩均为常数的假设[19]；2018年Ge等将光纤植入柔性硅胶片中，测试了光纤光栅传感在硅胶片中的灵敏度，验证了光纤光栅在软体硅胶片中传感的可行性，并指出光纤传感在柔性物体形态监测及生物医学领域的应用前景[10]。2019年Galloway等人将光纤以直线型植入在单向弯曲的驱动器中，实现了软体驱动器在扭转和弯曲等状态下末端位置和形状的检测[20]。
与以上方法不同，文中提出一种螺旋型光纤光栅传感软体操作臂状态测量方法，并对其传感特性进行了研究。通过将光纤以螺旋型缠绕粘接并封装在带有螺纹导向槽的软体操作臂中，解决直线型光纤可拉伸范围小的问题，满足操作臂伸缩和各向弯曲时的测量需求。通过建立螺旋型光纤光栅软体操作臂的传感模型，得出光纤光栅中心波长偏移量与操作臂弯曲角度之间的关系，实现软体操作臂的运动状态测量。
-
文中所采用的传感器为光纤布拉格光栅（Fiber Bragg grating，FBG），根据模式耦合理论，当宽带光在FBG中传输时，满足布拉格波长条件的光被反射，反射光的中心波长λB满足以下条件[11, 17]：
$${\lambda _{\rm{B}}} = 2{n_{{\rm{eff}}}} \cdot \varLambda $$ (1) 式中：λB为布拉格光纤光栅的中心波长；neff为有效折射率；Λ为光栅周期。考虑到微创手术环境温度的变化较小，所以，文中忽略温度变化对软体操作臂中光纤光栅的影响。则当光纤光栅被拉伸或压缩时，受轴向应变ε的影响，光栅的周期Λ即随之变化，此时光纤光栅的中心波长漂移量ΔλB
为： $$\Delta {\lambda _{\rm{B}}} = {\lambda _{\rm{B}}} \cdot \left( {1 - {P_\varepsilon }} \right) \cdot \varepsilon $$ (2) 式中：Pε为有效弹光系数；ΔλB为光纤光栅的中心波长漂移量。
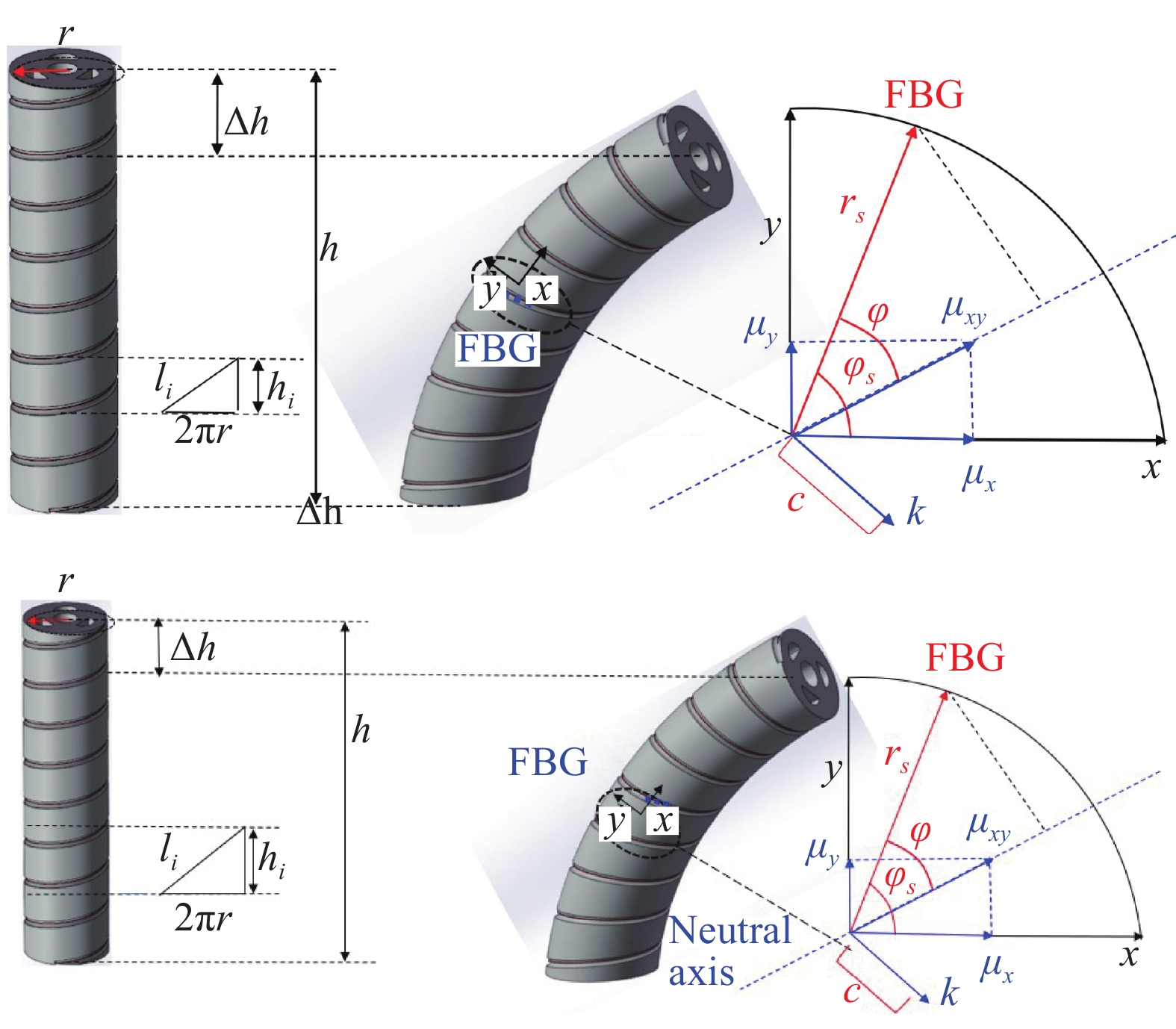
如图1所示，假设操作臂的长度为h，末端截面半径为r，螺旋型光纤缠绕的倾斜角为φs、缠绕圈数为n，光纤的长度为l，则缠绕在操作臂上的螺旋型光纤展开后，构成一个底边为n2πr的直角三角形。
图 1 基于螺旋型光纤光栅的软体操作臂传感模型
Figure 1. Sensing model of a soft mainpulator based on helical FBG
螺旋型光纤传感器的长度l可表示为：
$$ l = \sum\limits_{{{i}} = 1}^n {{l_i} = } \sum\limits_{{{i}} = 1}^n {\sqrt {{{\left( {2\pi r} \right)}^2} + {h_i}^2} } $$ (3) 根据应变与FBG中心波长漂移量的映射关系可以推测，如果所测量的结构当中的变量可以通过FBG空间布设的方式与FBG所受到的应变联系起来，那么FBG的中心波长漂移量将会是对于所测物理量的传感信号。假定软体操作臂的弯曲模型为纯弯曲模型，操作臂弯曲时其高度方向的变化量为Δh，光纤的长度变化量为Δl，则光纤在斜边的伸长量、软体操作臂的弯曲角度φ可表示为：
$$\Delta l = \dfrac{{\Delta h}}{{n \cdot \sin {\varphi _s}}}$$ (4) $$\sin {\varphi _s} = \dfrac{{h - \Delta h}}{{l - \Delta l}}$$ (5) $$h - \Delta h = \dfrac{h}{\varphi }\sin \varphi $$ (6) 联合并整理公式（4）~（7），得出光栅栅区应变与操作臂弯曲角度之间的关系可表示为：
$$\varepsilon = \dfrac{{\Delta l}}{l} = \dfrac{{\Delta h}}{{n \cdot \sin {\varphi _{\rm{s}}} \cdot l}}$$ (7) 即：
$$\varepsilon = \dfrac{{\sin \varphi - \varphi }}{{\sin \varphi - n \cdot \sin \varphi - \varphi }}$$ (8) 由上式可知，当光纤的缠绕圈数一定时，螺旋型光纤光栅受到的应变仅与操作臂的弯曲角度有关，且波长漂移量与轴向应变ε线性相关，光栅的中心波长漂移量与操作臂弯曲角度之间的关系为：
$$\Delta \lambda \infty \dfrac{{\sin \varphi - \varphi }}{{\sin \varphi - n \cdot \sin \varphi - \varphi }}$$ (9) -
软体操作臂由柔性材料制成，在各方向上具有无限自由度，且弹性材料具有非线性特征，所以运动状态呈非线性变化。在此研究中，对软体操作臂进行有限元建模分析其运动状态，并获得输入气压与弯曲角之间的关系。
软体操作臂的气道半径为r1，假设操作臂的气道壁厚为t= r1/4，输入气压为Pin，则可计算出气道内的空气压力相对于软体操作臂末端的弯曲力矩（Tr1）[21]：
$${{{T}}_{{r_1}}} = 0.34{r_1}^3{P_{{\rm{in}}}}$$ (10) 考虑到软体操作臂所用材料的特性，文中构建了输入气压与弯曲角度的分析模型。模型中的变量是软体操作臂的实际尺寸与材料属性，均可通过测量获得。由不可压缩的Neo-Hookean(NH)材料的模型，可计算出软体操作臂的应变能：
$$W{\rm{ = }}\dfrac{\mu }{{\rm{2}}}\left( {{I_1} - 3} \right){\rm{ = }}\dfrac{\mu }{{\rm{2}}}\left( {\gamma _{\rm{1}}^{\rm{2}}{\rm{ + }}\gamma _{\rm{2}}^{\rm{2}}{\rm{ + }}\gamma _{\rm{3}}^{\rm{2}} - {\rm{3}}} \right)$$ (11) 式中：μ为制作软体操作臂材料的初始剪切模量；I1为轴向、圆周与径向3个主拉伸比的第一个常数；γ1为软体操作臂轴向的主要拉伸，圆周方向因凯夫拉线的束缚可忽略不计，因此，γ2=1。另外，考虑到材料的不可压缩性，γ1γ2γ3=1。
由此可以得出：
$${\gamma _{\rm{1}}}{\rm{ = }}\gamma ,\;{\gamma _{\rm{2}}}{\rm{ = 1}},\;{\gamma _{\rm{3}}}{\rm{ = }}\dfrac{{\rm{1}}}{\gamma }$$ (12) 对软体操作臂的一个半圆形气孔通入气压P1（P1> Patm），软体操作臂由于受到凯夫拉线的限制，整体将做弯曲运动，如图2所示。在软体操作臂的模型中，假设无动态加压效应，且操作臂总保持均匀的弯曲曲率。
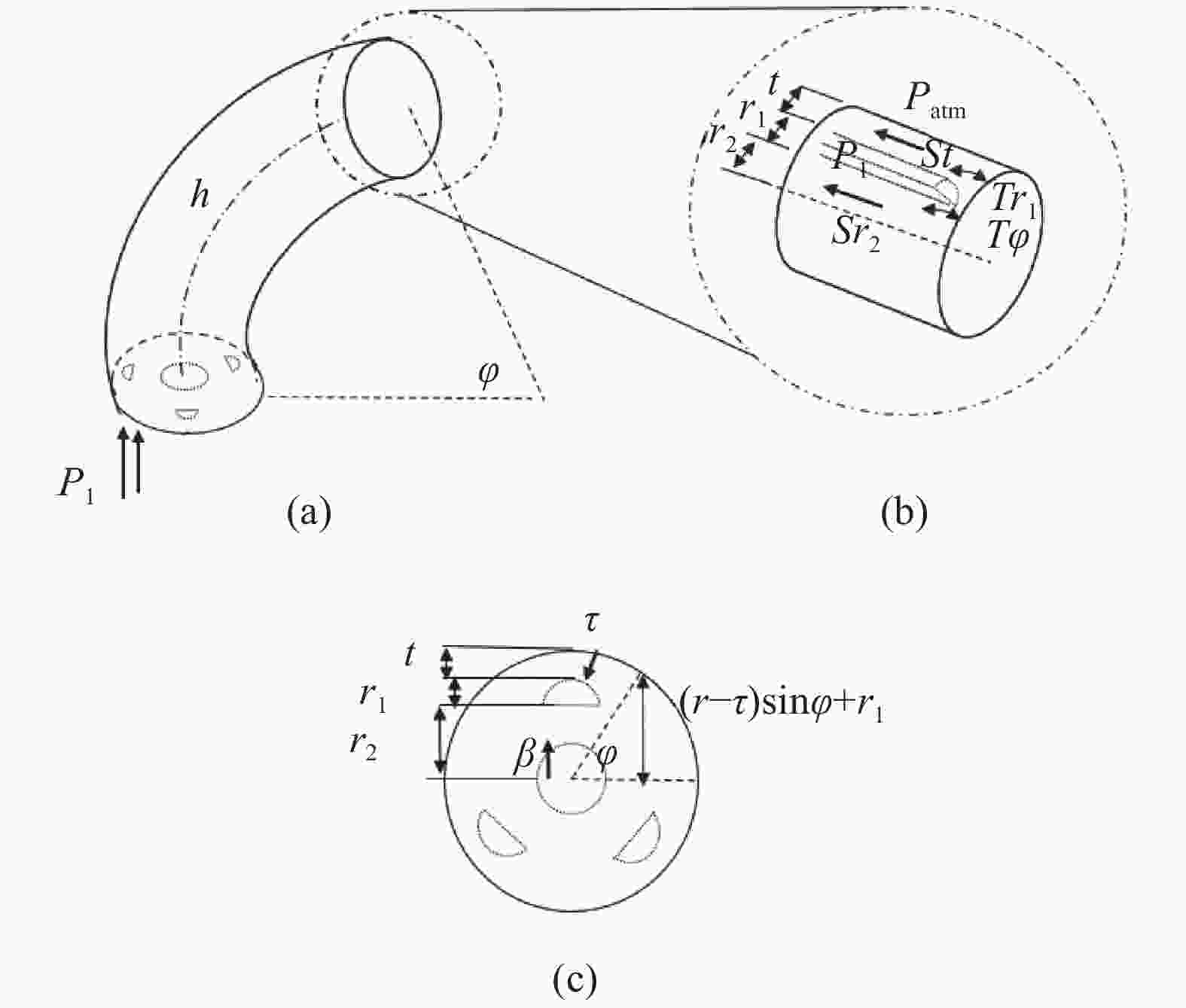
图 2 (a) 侧视图；(b) 末端结构放大图；(c) 横截面视图
Figure 2. (a) Side view; (b) Enlarged view of terminal structure; (c) Cross sectional view
由于软体操作臂在应用伸展范围(1≤γ≤1.5)之内，因此，只考虑轴向拉伸S。
$${{S}} = \frac{{\partial W}}{{\partial {\gamma _1}}} - \dfrac{P}{{{\gamma _1}}} = \overline \mu \left(\gamma - \frac{1}{{{\gamma ^3}}}\right)$$ (13) 弯曲力矩由软体操作臂的内部应变引起，弯曲力矩与每个弯曲状态下的组合力矩可表示为：
$$ \begin{aligned} {T_{{{{r}}_1}}} = &2({P_1} - {P_{{\rm{atm}}}})\int_0^\pi {({r_1}\sin \nu + {r_2})} {r_1}^2{\cos ^2}\nu {\rm{d}}\nu =\\ &{ \dfrac{{4{r_1}^3 + 3\pi {r_1}^2{r_2}}}{3}} ({P_1} - {P_{{\rm{atm}}}}) \\ \end{aligned} $$ (14) $$\begin{aligned} {T_\varphi} =& \displaystyle\int_0^{{{{r}}_2}} {2{s_\beta }({r_1} + t)} {h_\beta }{{\rm{d}}_\beta } +\\ &{ 2\int_0^t {\displaystyle\int_0^\pi {{s_{\tau ,\phi }}} } \left[ {{{({r_1} + \tau )}^2}\sin \phi + {r_2}({r_1} + \tau )h} \right]} {\rm{d}}\phi {\rm{d}}\tau \\ \end{aligned} $$ (15) 式中：Tr1为内部气压相对于软体操作臂远端的弯曲力矩；Tφ为应变的组合力矩，操作臂材料的内布延伸产生相反的弯曲力矩。因此，弯曲力矩Tr1，组合力矩Tφ，输入气压Pin，与操作臂弯曲角度φ之间的关系为：
$${P_{{\rm{in}}}} = {P_1} - {P_{{\rm{atm}}}} = \dfrac{{{\rm{3}}{T_\varphi }(\varphi )}}{{4{r_1}^3 + 3\pi {r_1}^2{r_2}}}$$ (16) -
基于螺旋布设光纤光栅植入的软体操作臂结构如图3所示，如图所示，操作臂一端封闭，一端的4个腔道用于连接驱动气压的输入管道。4个腔道包括一个硬化腔道和3个气动驱动弯曲腔道，通过向3个气动腔道输入气压可以驱动操作臂伸长和弯曲运动，通过向硬化腔道输入气压驱动操作臂实现硬化。气动腔道的半径为4 mm，操作臂的整体长度为100 m，其顶端设置有长度10 mm的连接端口用于连接气动驱动软管。光纤传感器通过操作臂基体表面的螺旋槽粘贴固定在操作臂中，并利用厚度为1 mm的硅胶液封装固定，缠绕在操作臂外部的凯夫拉线，可以限制操作臂气动驱动时产生的径向膨胀。螺旋布设光纤的植入方式可防止操作臂伸缩弯曲等运动时光纤的断裂，解决直线型光纤测量操作臂伸缩弯曲范围小的问题。图3(b)所示为软体操作臂末端连接气道截面的俯视图，图3(c)所示为刻写有传感光栅点的光纤传感器放大详情。
图 3 (a) 螺旋型光纤植入式软体操作臂；(b) 连接件截面俯视图；(c) 光纤光栅传感器放大图
Figure 3. (a) Soft manipulator embedded with FBG-based optical fiber in a helical configuration; (b) Top view of the connecting surface; (c) Enlarged state of the FBG-based optical fiber
文中采用硅胶注模的方式制作植入螺旋型光纤的软体操作臂原型，注模所使用的模具由3D打印而成，主要包括表面带有螺纹槽的模具1 (图4(a))、表面光滑的光纤封装模具2 (图4(c))、气动腔道模具和端口连接件(图4(a))等。软体操作臂的制作及螺旋型光纤植入过程如图4所示，首先将按1∶1混合的Ecoflex-0050A/B硅胶液倒入模具1中，待室温固化后去掉模具，然后将刻有3个光栅传感点的光纤沿螺纹槽缠绕并粘接固定在软体操作臂上，3个光栅传感点的中心波长分别为1549.0250 nm、1552.7563 nm、1556.6750 nm，栅区长度为10 mm，带宽为10 dB，反射率为70 %。然后，将表面缠绕光纤的软体操作臂放置在模具2中，倒入硅胶液进行封装，封装硅胶的厚度为1 mm。接着将凯夫拉线以双螺旋的方式缠绕并粘接在植入光纤的软体操作臂表面，限制操作臂在气动驱动时所产生的径向膨胀。最后，去掉所有注模使用的模具，并将操作臂气道和供气管道的连接件粘接在操作臂末端表面，则完成软体操作臂的制作及螺旋型光纤的植入。
图 4 基于植入式螺旋型光纤的软体操作臂注模过程。 (a) 表面带有螺纹槽的软体操作臂基体制作；(b) 螺旋型光纤缠绕粘接；(c) 硅胶注模封装光纤；(d) 凯夫拉线缠绕；(e) 模具移除及气道入口连接件粘接
Figure 4. Moulding process of the soft manipulator with helically embedded FBGs-based optical fibre sensor. (a) Helical groove moulding step of the manipulator base with helical groove; (b) Optical fibre is wound along the helical groove of the manipulator; (c) The manipulator is encapsulated in a layer of silicone to anchor the optical fibre; (d) Kevlar fiber is wound along the manipulator; (e) All mould are removed and one end of the manipulator is capped
-
为了验证螺旋型光纤光栅的传感特性，首先进行了软体操作臂弯曲及光纤光栅传感的实验测试，实验系统如图5所示，主要包括软体操作臂气动驱动控制系统、光纤传感系统、软体操作臂原型和计算机等。通过气动驱动控制系统中的比例阀等，可以调节输入操作臂气动腔道中的气压大小，驱动操作臂实现不同角度的弯曲。光纤传感系统主要包括宽带光源、解调仪、光谱仪和耦合器等。光源Lightpromotech的光谱范围为1 529~1 605 nm，功率为13 dBm，光平坦度小于2 dB。光谱仪YOKOGAWA AQ6370C的波长范围为600~1700 nm。实验用解调仪采用课题组自主研发的微型多通道解调仪，其解调波长范围为1525~1610 nm，速率为35 kHz，最小分辨率为0.5 pm，可检测光功率范围为−80~20 dBm。
图 5 螺旋型光纤传感操作臂实验系统。 (a) 光纤传感系统；(b) 操作臂及气动控制系统等
Figure 5. Experimental setup of for measuring compression and bending movements. (a) Optical fiber sensing system; (b) Soft manipulator and its pneumatic driving control system, etc
当输入不同的驱动气压时，软体操作臂的弯曲状态如图6 (a)~(g)所示，由图6可以看出，随着输入气压的增大，软体操作臂的弯曲角度也增大。图7所示为软体操作臂弯曲角度和输入气压之间关系的实验结果，为了保证实验测试结果的可靠性，所有实验均进行10次以上，实验结果取平均值。从图中可以对比发现，由于软体材料存在弹性特征，所以存在误差，但实验结果随着输入气压的增大，弯曲角度也增大，
图 6 软体操作臂在不同弯曲角度下的实验图
Figure 6. Snapshots of soft manipulator with different bending angles
图 7 输入气压和软体操作臂弯曲角度的关系
Figure 7. Relationship between input pressure and bending angle of soft manipulator
图8所示为光谱仪采集的操作臂不同弯曲状态下3个光纤光栅点的反射光谱实验结果，由图8可知，3个光纤光栅点的中心波长均随操作臂弯曲角度的增大而增大，光栅点1在不同弯曲状态下的中心波长分别为1 549.025、1 549.227 2、1 549.317、1 549.536 、1 549.769 3、1 549.919 5 nm和1550.341 8 nm，光栅点2在不同弯曲状态下的中心波长分别为155 2.756 2、1 553.086 8、1 553.243 5、1 553.687 8、1 554.130 5、1 554.448 2 nm和1 555.016 2 nm，光栅点3在不同弯曲状态下的中心波长分别为1 556.675、1 556.797、1 556.981 3、1 557.147 3 、1 557.256 8、1 557.332 nm和1557.4253 nm。
图 8 不同弯曲状态下3个光栅点的波长漂移
Figure 8. Wavelength shift of 3 FBGs with different bending states
3个不同光栅点中心波长漂移量和软体操作臂弯曲角度之间的关系如图9所示，由图9可知，由于3个光纤传感器分别对应软体操作臂的底部，中部，顶部，因此，当操作臂的弯曲角度从0°增大至180°时，位于软体操作臂中部的光纤所承受的剪切力最大，3个光栅传感点的中心波长偏移量分别为1.316 83、2.26 nm和0.750 3 nm，与理论结果相近。3个光纤光栅传感点的灵敏度分别为7.32 pm/(°)、12.55 pm/(°)和4.17 pm/(°)，灵敏度满足软体操作臂的测量需求，实验结果表明了螺旋型光纤光栅植入在软体操作臂中传感的可行性。
图 9 光栅中心波长漂移量与操作臂弯曲角度的关系
Figure 9. Relationship of wavelength shift and bending angle
此外，为了验证螺旋型光纤光栅在软体操作臂中传感的稳定性和一致性，文中对操作臂在不同弯曲状态下的传感实验结果进行分析，为了保证实验的准确性，操作臂每个弯曲状态的实验均进行10次并取平均值。文中用偏差指数（DI）来表示螺旋型光纤光栅传感的稳定性：
$${D_I} = \Delta {\lambda _E}/\Delta {\lambda _w} \cdot {\rm{100\% }}$$ (17) 式中：ΔλE为螺旋型光纤光栅反射波长与平均反射波长的差值，ΔλW为操作臂从0°弯曲到180°时的总波长偏移量。
图10所示为螺旋型光纤光栅传感的稳定一致性实验结果，由图10可知，螺旋型光纤光栅在操作臂中传感的波动区间为9.8%，说明螺旋型光纤光栅在软体操作臂中的传感具有较好的稳定性和一致性。
图 10 螺旋型光纤光栅传感稳定性结果
Figure 10. Stability results of the helically embedded FBGs-based optical fiber sensor
表1所示为软体操作臂的理论弯曲角度和光纤传感实验结果及相对误差，如表1所示，由于软体材料的超弹性特征，软体操作臂弯曲角度传感实验测量值与理论值之间的最大误差为9%，平均误差不足4%，表明文中所提出的螺旋型光纤光栅传感方法能够适用于软体操作臂的运动状态传感。
表 1 软体操作臂弯曲角度传感结果及误差比较
Table 1. Sensing results and error comparison of bending angle of soft manipulator
Bending state 1 2 3 4 5 6 7 Theoretical value /(°) 0 10 30 60 120 150 180 Experiment value/ (°) 0 10.2 32.7 59.5 119.5 152 179 Relative error 0 2% 9% 8% 0.4% 5.3% 0.5% -
文中根据生物医疗领域软体手术机器人等柔性结构状态测量的需求，提出了一种基于植入式螺旋型光纤光栅的软体操作臂状态测量方法，建立了螺旋型光纤光栅的软体操作臂传感模型、光纤光栅波长漂移和软体操作臂弯曲角度之间的关系等，并对光纤光栅传感的灵敏度和稳定性进行了实验测试分析。实验测得软体操作臂理论弯曲角度和光纤传感的误差不足9%，螺旋型光纤光栅传感的灵敏度可以达到12.55 pm/(°)。表明螺旋型布设光纤的方法可以满足软体操作臂伸缩和各向弯曲时的测量需求，实现操作臂伸长10%、弯曲角度达到180°时的状态传感，且稳定性较好。文中所提出的螺旋型光纤光栅传感方法在仿生软体机器人操作状态监测和生物医学领域有良好的应用前景。
State measurement and sensing characteristics analysis of soft maniputator based on helical optical fiber
-
摘要: 微创手术软体操作臂是微创外科和机器人领域的科学前沿和研究热点，对提升微创手术水平至关重要。现有视觉、电子和光电等传感方法尚未解决软体操作臂的状态测量问题，以直线型布设在软体操作臂中的光纤传感器，在柔性操作臂伸展和弯曲等运动时存在易断裂和可重复性差等问题，未能实现手术操作臂的闭环控制，限制了其手术应用。为此，提出了一种基于螺旋型光纤传感的软体操作臂状态测量方法，并对其传感特性进行了研究。不同于直线布设光纤的传感方法，螺旋型布设光纤的传感方法可以实现可伸缩软体操作臂的测量，防止光纤在软体操作臂中的错位，满足可伸缩弯曲软体操作臂的测量需求。通过理论分析气动驱动软体操作臂伸缩和弯曲的运动特性，利用光纤上刻写的布拉格光栅传感点，建立软体操作臂中螺旋型光纤光栅的传感模型，推导出光纤光栅中心波长漂移量和软体操作臂弯曲曲率之间的关系。最后，为了验证螺旋型光纤光栅在软体操作臂中的传感性能，对其传感灵敏度和稳定性等进行了实验测试。实验结果表明：提出的螺旋型光纤传感方法可实现操作臂伸长10%、弯曲角度达到180°时的状态测量，且操作臂理论弯曲角度和光纤传感的误差最大为9%，传感灵敏度可达12.55 pm/(°)，满足软体操作臂伸缩和各向弯曲操作时的测量需求。Abstract: The soft surgical manipulator is the scientific frontier and research hotspot in the field of minimally invasive surgery and robotics, which is very important to improve the level of minimally invasive surgery. The existing sensing methods, such as vision, electronics and photoelectricity, have not solved the problem of measuring the state of the arm of soft gymnastics. The optical fiber sensor arranged in a straight line in the soft manipulator is easily broken and repeatable when the flexible manipulator is stretched and bent. Problems such as poor sex, failed to achieve closed-loop control of the surgical manipulator, limiting its surgical application.Therefore, a state measurement method of soft manipulator based on helical optical fiber sensor was proposed, and its sensing characteristics were studied. Different from the linear optical fiber sensor method, the unique helical structure could prevent the sensor from dislocation and support the ductility of the material, which was convenient to meet the measurement requirements of the operating arm when it moved. Based on the theoretical analysis of the movement characteristics of the expansion and bending of the pneumatic soft maniputator, the sensing model of the helical fiber grating in the soft maniputator was established by using the FBG sensing points engraved on the optical fiber, and the relationship between the center wavelength drift of the FBG and the bending curvature of the soft maniputator was deduced. Finally, in order to verify the sensing performance of the helical fiber grating in the soft manipulator, the sensitivity and stability of the sensing were tested. The experimental results show that the helical optical fiber sensing method proposed can realize the state measurement when the manipulator is extended by 10% and the bending angle reaches 180°. The error between the theoretical bending angle of the manipulator and the optical fiber sensing is up to 9%, and the sensing sensitivity is up to 12.55 pm/(°) which can meet the needs of the measurement when the soft maniputator is retracted and bent in all directions.
-
图 1 基于螺旋型光纤光栅的软体操作臂传感模型
Figure 1. Sensing model of a soft mainpulator based on helical FBG
图 2 (a) 侧视图；(b) 末端结构放大图；(c) 横截面视图
Figure 2. (a) Side view; (b) Enlarged view of terminal structure; (c) Cross sectional view
图 3 (a) 螺旋型光纤植入式软体操作臂；(b) 连接件截面俯视图；(c) 光纤光栅传感器放大图
Figure 3. (a) Soft manipulator embedded with FBG-based optical fiber in a helical configuration; (b) Top view of the connecting surface; (c) Enlarged state of the FBG-based optical fiber
图 4 基于植入式螺旋型光纤的软体操作臂注模过程。 (a) 表面带有螺纹槽的软体操作臂基体制作；(b) 螺旋型光纤缠绕粘接；(c) 硅胶注模封装光纤；(d) 凯夫拉线缠绕；(e) 模具移除及气道入口连接件粘接
Figure 4. Moulding process of the soft manipulator with helically embedded FBGs-based optical fibre sensor. (a) Helical groove moulding step of the manipulator base with helical groove; (b) Optical fibre is wound along the helical groove of the manipulator; (c) The manipulator is encapsulated in a layer of silicone to anchor the optical fibre; (d) Kevlar fiber is wound along the manipulator; (e) All mould are removed and one end of the manipulator is capped
图 5 螺旋型光纤传感操作臂实验系统。 (a) 光纤传感系统；(b) 操作臂及气动控制系统等
Figure 5. Experimental setup of for measuring compression and bending movements. (a) Optical fiber sensing system; (b) Soft manipulator and its pneumatic driving control system, etc
图 6 软体操作臂在不同弯曲角度下的实验图
Figure 6. Snapshots of soft manipulator with different bending angles
图 7 输入气压和软体操作臂弯曲角度的关系
Figure 7. Relationship between input pressure and bending angle of soft manipulator
图 8 不同弯曲状态下3个光栅点的波长漂移
Figure 8. Wavelength shift of 3 FBGs with different bending states
图 10 螺旋型光纤光栅传感稳定性结果
Figure 10. Stability results of the helically embedded FBGs-based optical fiber sensor
表 1 软体操作臂弯曲角度传感结果及误差比较
Table 1. Sensing results and error comparison of bending angle of soft manipulator
Bending state 1 2 3 4 5 6 7 Theoretical value /(°) 0 10 30 60 120 150 180 Experiment value/ (°) 0 10.2 32.7 59.5 119.5 152 179 Relative error 0 2% 9% 8% 0.4% 5.3% 0.5% 
下载: 导出CSV
-
[1] Gao Changqing. Robotic Surgery[M]. Beijing: People’s Medical Publishing House, 2015.（in Chinese） [2] Fu Yili, Pan B. Research progress of surgical robot for minimally invasive surgery [J]. Journal of Harbin Institute of Technology, 2019, 51(1): 1-15. [3] Payne J, Wamala I, BautistaSalinas D, et al. Soft robotic ventricular assist device with septal bracing for therapy of heart failure [J]. Science Robotics, 2017, 2(12): eaan6736. doi: 10.1126/scirobotics.aan6736 [4] Ranzani T, Gerboni G, Cianchetti M, et al. A bioinspired soft manipulator for minimally invasive surgery [J]. Bioinspiration & Biomimetics, 2015, 10(3): 35-38. [5] Laschi C, Mazzolai B, Cianchetti M, et al. Soft robotics: Technologies and systems pushing the boundaries of robot abilities [J]. Science Robotics, 2016, 1(1): eaah3690. doi: 10.1126/scirobotics.aah3690 [6] Hu Wenqi, Lum G Z, Mastrangeli M, et al. Small-scale soft-bodied robot with multimodal locomotion [J]. Nature, 2018, 554: 81-85. doi: 10.1038/nature25443 [7] Wang H, Totaro M, Beccai L. Toward perceptive soft robots: progress and challenges [J]. Advanced Science, 2018, 5(9): 1800541. doi: 10.1002/advs.201800541 [8] Shen T, Sun Binchao, Feng Y. Mach-Zehneder interference all-fiber sensor measurement of magnetic field and temperature [J]. Optics and Precision Engineering, 2018, 26(6): 1338-1345. doi: 10.3788/OPE.20182606.1338 [9] Wang Huaping, Xiang P. Optimization design of optical fiber sensors based on strain transfer theory [J]. Optics and Precision Engineering, 2016, 24(6): 1233-1241. doi: 10.3788/OPE.20162406.1233 [10] Ge J, James A E, Li X, et al. Bidirectional soft silicone curvature sensor based on off-centered embedded fiber bragg grating [J]. IEEE Photonics Technolonics Letters, 2016, 28(20): 2237-2240. doi: 10.1109/LPT.2016.2590984 [11] Westbrook P S, Kremp T K, Feder K S, et al. Continuous multicore optical fiber grating arrays for distributed sensing applications [J]. Journal of Lightwave Technology, 2017, 35(6): 1248-1252. doi: 10.1109/JLT.2017.2661680 [12] Zhao Y, Wang C, Yin G, et al. Simultaneous directional curvature and temperature sensor based on a tilted few-mode fiber Bragg grating [J]. Applied Optics, 2018, 57(7): 1671-1678. doi: 10.1364/AO.57.001671 [13] Zhang Kaiyu, Yan G, Meng Fanyong, et al. Temperature decoupling and high strain sensitivity fiber Bragg grating sensor [J]. Optics and Precision Engineering, 2018, 26(6): 1330-1337. doi: 10.3788/OPE.20182606.1330 [14] Guo Yongxing, Xiong L, Kong Jianyi, et al. Sliding type fiber Bragg grating displacement sensor [J]. Optics and Precision Engineering, 2017, 25(1): 50-58. doi: 10.3788/OPE.20172501.0050 [15] Clements G M. Fiber optic sensor for precision 3-D position measurement: US, 10/376184[P]. 2004-08-26. [16] Bajo A, Simaan N. Kinematics-based detection and localization of contacts along multisegment continuum robots [J]. IEEE Transactions on Robotics, 2012, 28(2): 291-302. doi: 10.1109/TRO.2011.2175761 [17] Sareh S, Noh Y, Li M, et al. Macrobend optical sensing for pose measurement in soft robot arms [J]. Smart Materials & Structures, 2015, 24(12): 125024. [18] Liu H, Farvardin A, Grupp R, et al. Shape tracking of a dexterous continuum manipulator utilizing two large deflection shape sensors [J]. IEEE Sensors Journal, 2015, 15(10): 5494-5503. doi: 10.1109/JSEN.2015.2442266 [19] Wang H, Zhang R, Chen W, et al. Shape detection algorithm for soft manipulator based on fiber Bragg gratings [J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(6): 2977-2982. doi: 10.1109/TMECH.2016.2606491 [20] Galloway K C, Chen Yue, Templeton Emily, et al. Fiber optic shape sensing for soft robotics [J]. Soft Robotics, 2019, 6(5): 671-684. doi: 10.1089/soro.2018.0131 [21] Xu R, Asadian A, Atashzar S F, et al. Real-time trajectory tracking for externally loaded concentric-tube robots[C]//IEEE International Conference on Robotics and Automation, 2014: 4374-4379. -
点击查看大图
计量
- 文章访问数: 596
- HTML全文浏览量: 161
- PDF下载量: 37
- 被引次数: 0
