因其具有能量密度高、寿命长、稳定性强和对环境影响小等优点，锂离子电池（Lithium-ion Batteries, LIBs）已经被广泛应用于电动交通工具、动力电源、二次充电及储能设备和移动穿戴设备之中。但是，容量低于其初始容量的80%的电池可能会导致容量快速降低，无法使用，甚至对设备造成永久性损坏。

因此，准确的锂离子电池健康状态（State of Charge，SOH）估计^[1-2]可以使用户更合理地进行电池维护，以提高电池的安全使用率。但是，锂离子电池的内部化学结构复杂，工作环境不同，导致电池的老化过程相当复杂，难以准确直接地获取锂离子电池的SOH。目前，为了获取锂离子电池SOH，研究人员提出了很多SOH估计方法，这些方法通常可分为三类^[3]：（1）直接测量方法；（2）基于模型的方法；（3）数据驱动方法。直接测量方法拟用实验测试的方法直接测量表征电池老化程度的量化指标，例如电池容量与电池内阻等。这类方法计算度小而且非常简单，但是受限于实验室环境，无法在线实现。基于模型的方法则是主要根据电路或电化学机理先验知识建立等效电路模型或者电化学模型。这类方法往往是基于其他参数（如开路电压和SOC）结合观测器或者滤波器^[4]等估计电池的SOH，预测结果的准确性高度依赖于电池模型的精度，而且电池模型由于型号和工作状态的不同而对模型进行不断修正，较难扩展实现。

与基于模型的方法相比，数据驱动方法无需考虑锂离子电池老化机理和内部电化学反应，把电池作为一个黑箱模型，利用机器学习算法如支持向量机^[5]、高斯过程回归^[6]、神经网络^[7]等提取老化特征与外部测量参数之间的映射关系。参考文献[6]采用数据集的前49%被选作训练集，训练高斯过程回归（Gaussian Preocess Regression, GPR）模型来预测SOH，该方法能够将估计结果的不确定性纳入输出结果中，并以一定的概率对SOH估计值可能的结果进行描述，但是在预测中性能存在一定退化。参考文献[8]采用概率神经网络（Probabilistic Neural Network，PNN）实现锂离子电池SOH的估计，然而瞬态电压尖峰可能会误导PNN的预测性能。为了避免采用较多的训练数据，参考文献[9]提出采用一种数据处理的分组方法建立微分几何特性和SOH之间的关系以预测当前状态。尽管这些基于数据驱动的锂离子电池SOH估计方法取得了一定的效果，但是仍存在一些问题。锂离子电池是一个具有长时依赖性影响的动态系统，其充放电时的电压、电流、温度随时间连续变化的时序数据，如何挖掘考虑输入数据的时序依赖与输出SOH之间的关系设计SOH估计方法是一大难题。

近年来，随着深度学习技术^[10-13]的飞速发展，研究人员将门控循环神经网络（Recurrent Neural Networks with Gated Recurrent Unit, GRU-RNN）用于锂离子电池状态估计任务，该方法能够利用网络内部结构从时序数据中学习数据特征和时间依赖关系，从而将锂离子电池状态随时间连续变化的特性保留。实际上，具有门控循环神经网络是循环神经网络（Recurrent Neural Networks，RNN）^[14]的改进形式，通过在RNN隐藏层节点中引入不同的“门控”机制，从而能够处理间隔更长的时序信号并获取更多的数据特征和时间依赖关系。参考文献[15]提出采用一小时段（500 s）放电时的电压、电流、温度来预测SOC，并且在三个数据集上取得了估计误差低于2%的优异效果。类似地，参考文献[16]提出采用放电时电压和电流以估计SOC，并引入一种动量梯度算法来优化网络的权值。近年来，参考文献[17]提出了一种基于GRU-RNN的锂电池寿命预测方法，考虑采用过去时间的电池寿命变化来对将来的电池寿命进行预测。

基于此，文中将GRU-RNN方法引入到SOH估计问题中，提出一种新的数据驱动框架下的SOH估计方法。根据对公开的锂离子电池老化数据分析可知，锂离子电池恒流−恒压充电过程具有固定形式且该过程中的电压与SOH之间存在较强的联系，适合作为估计SOH的输入量。当电池使用时间短，老化程度小，SOH较大，充电电压上升至截止电压较缓慢，这符合电池越新则内部化学反应时间较长、容量较大的实质；而当电池使用过一段时间，老化程度较为明显，SOH减小后，则呈现出完全相反的现象，充电电压迅速上升至截止电压。一次恒流-恒压充电过程中的电压曲线均是随时间变化的一维时序数据且均对应一个共同的SOH估算值，而GRU-RNN能够挖掘这种长时依赖特性，适合于处理锂离子电池老化数据所展现出的这种特征。在两个公开数据集上进行实验结果表明，文中提出的方法泛化能力强，估计效果超过两种经典数据驱动框架下的SOH估计方法，且只需要获取充电过程的低频电压数据，更容易在线实现。

锂离子电池老化实验周期较长，目前公开的老化实验数据集比较少，主要为NASA随机老化数据集（NASA-Randomized Battery Usage Data Set）和牛津大学电池老化数据集（Oxford Battery Degradation Dataset）。表1给出了两个数据集的参数对比。

NASA锂离子电池随机数据集^[18]所使用的电池为LG Chem 18650锂离子电池，其额定容量为2.1 Ah，常规工作电压范围为3.2~4.2 V。测试平台则包括可编程直流电源、恒温箱、传感器、数据记录仪、电化学阻抗谱测试仪等。该数据集均是在随机测试工况下获取，共对28块相同的锂离子电池进行测试，并根据不同实验工况将测试电池分为7组。按照测试工况进行测试后的锂离子电池会进行定容测试，所采集的数据包括锂离子电池充放电过程中的电压、电流、温度等。而牛津大学电池老化数据集^[19]测试所采用的锂离子电池为Kokam公司所生产的钴酸锂离子电池，其额定容量为740 mAh，在40 ℃恒定环境温度下，通过使用ARTEMIS市区行驶工况对8块测试锂离子电池重复进行2C （1.48 A）恒定电流放电并重新充电，反复循环以达到加速老化的目的，记录数据主要为充放电过程中的电压、电流、温度等。

通过对两个数据集进行分析，可以发现，电池的容量随着电池的使用逐渐衰减。而每次电池循环充电过程电压曲线因充电方式为固定的恒流-恒压方式而相对稳定，且随着锂离子电池的老化存在规律性的变化。如图1所示，给出了两个电池老化数据集中充电电压随SOH变化曲线图，其中电池寿命衰减由黄色→绿色→蓝色的渐变色表示，左边每条曲线代表不同老化程度时电池的恒压恒流充电电压变化，右边图代表了电池在使用过程中老化程度随着时间或者循环次数变化的曲线。由图1中可以发现，当电池使用时间短，SOH较大（曲线黄色部分），充电电压上升至截止电压较缓慢，电池温度较高，这符合电池越新则内部化学反应时间较长、容量较大的实质。而当电池使用过一段时间，SOH减小后（曲线蓝色部分），则呈现出完全相反的现象，充电电压迅速上升至截止电压。因此，电池充电过程中的电压变化曲线（简称为充电电压数据）和SOH有较强的规律，可以作为用于估计SOH的输入量。

图  1  锂离子电池老化数据集中充电电压随SOH变化曲线

Figure 1.  Voltage curves of Li-ion battery degradation dataset with SOH

由于充电电压数据是随时间变化的一维时序数据，为了挖掘出一维电压数据中的时序特征和SOH之间的映射规律，文中提出了一种基于门控循环神经网络的锂电池SOH估计方法。

GRU-RNN是RNN的一种改进形式。简单来说，RNN的神经元的某些输出可以作为其输入再次传输至神经元中，可以保留并利用历史信息，这对于处理时序问题非常有效。

如图2所示，它由输入层${\bf{X}}$、隐藏层${\bf{H}}$和输出层${\bf{Y}}$组成，和常规神经网络相比，多了一个保留历史信息的延时器。$W,U,V$分别是是输入层、输出层和上一时刻隐藏层到本时刻隐藏层权值矩阵。那么，在$t$时刻，隐藏层状态${h_t}$由当前输入${{{x}}_t}$和之前隐藏层状态${{{h}}_{t - 1}}$同时决定。

图  2  循环神经网络原理图

Figure 2.  Architecture of RNN unfolded in time

式中：${\bf{\varphi}} \left( \bullet \right)$为激励函数；$b$为偏置。

尽管RNN在解决许多时序预测问题上取得了较好的效果，但是在误差反向传播过程中，长时间序列和复杂的隐藏层可能会引发梯度爆炸或梯度消失。为了在解决RNN的长期依赖性的问题，同时降低对计算开销和存储空间的需求并提高收敛速度，GRU-RNN被提出。其主要是引入络引入门机制来控制信息传递的路径。其中，更新门决定了前一时刻状态对当前时刻状态的影响程度，重置门决定了当前输入与前一时刻状态的结合程度。

由图3可以得出GRU-RNN获得隐藏层输出${h_t}$的计算公式为：

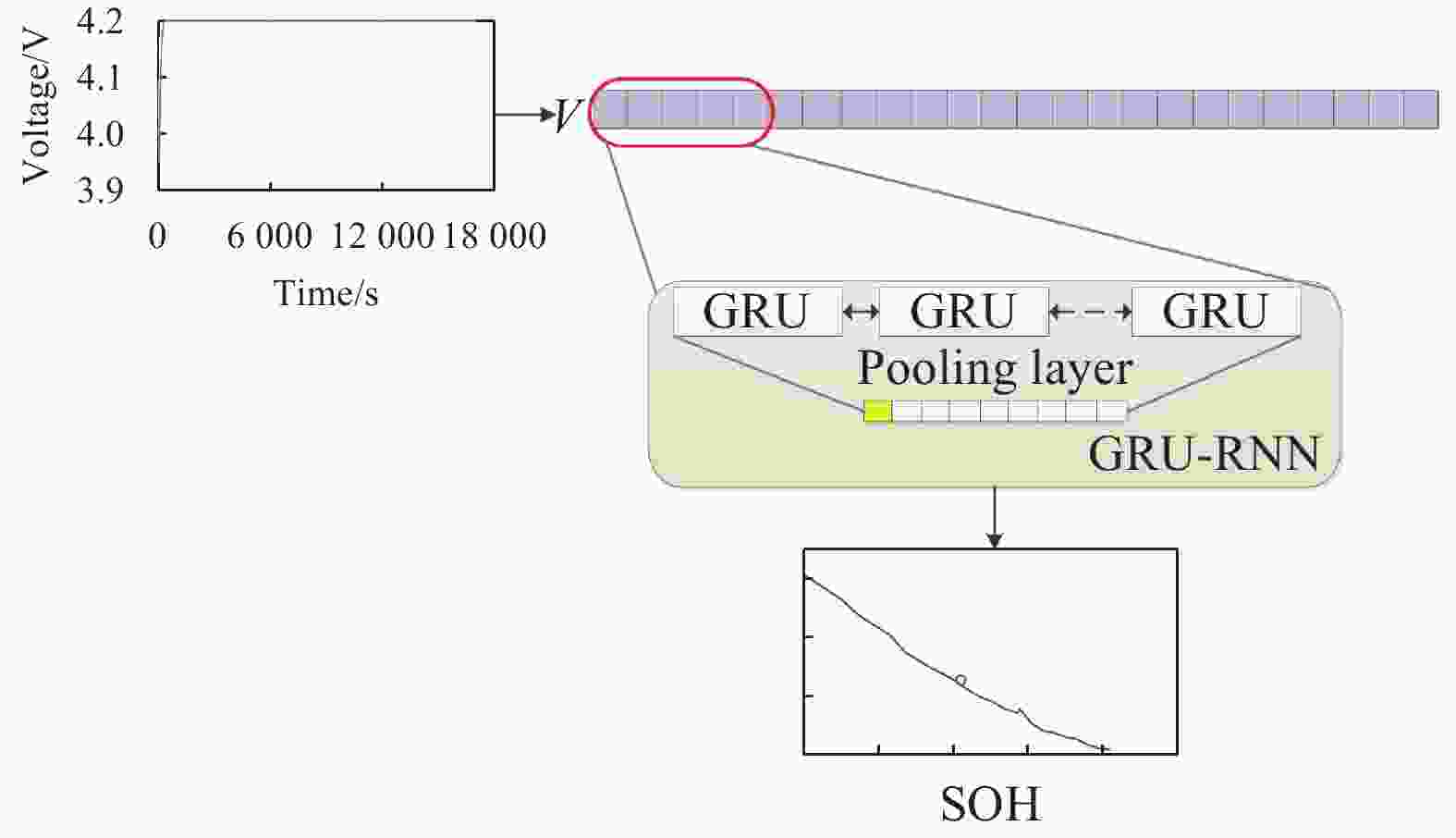
式中：${x_t}$、${h_{t - 1}}$、${{\textit{z}}_t}$、${f_t}$分别为GRU-RNN隐藏层节点的输入、输出、更新门输出以及重置门输出，输入${x_t}$和前一时刻隐藏层输出${h_{t - 1}}$共同决定过程量${\tilde h_t}$；$w$和$b$分别为训练所获得的权重参数和偏置参数；$ \odot $表示矩阵对应位置元素相乘；$\sigma $和tanh分别代表sigmoid函数和双曲正切函数。然后，通过公式（2）即可获得输出${y_t}$。

图  3  GRU-RNN隐藏层节点结构

Figure 3.  Architecture of GRU-RNN cell

基于GRU-RNN的锂离子电池SOH估计流程如图4所示。其主要步骤包括：

步骤1：获取训练数据。将锂离子电池充满，然后进行恒流放电，直至电压下降至截止电压，利用安时积分法记录该放电过程中的电量，即为容量作为训练GRU-RNN的输出；将电池静置一段时间后对电池进行恒流-恒压满充操作，记录该充电过程中的电压测量量作为训练GRU-RNN的输入；

步骤2：搭建GRU-RNN网络并设置网络参数。构建网络结构并选择合适的激活函数、目标函数、优化算法和评价函数；设置卷积神经网络采样间隔、训练迭代次数、学习率等超参数，并初始化网络权值和偏置量；

步骤3：训练GRU-RNN网络。通过优化算法实现网络权值和偏置量等参数的学习，直至目标函数满足要求。

步骤4：实现锂离子电池SOH估计。将锂离子电池恒流−恒压满充过程中所采集的电压到输入训练好的网络并输出容量估计值，将该估计值与恒流满放过程中记录的容量通过评价函数进行分析，从而评价方法的性能。

图  4  基于门控循环网络的锂离子电池SOH估计流程图

Figure 4.  Flow chart of Lithium-ion battery SOH estimation based on GRU-RNN

为了验证文中所提出的锂离子电池SOH估计方法的有效性，此节在NASA锂离子电池随机老化数据集和牛津大学电池老化数据集上进行了实验，并将实验结果与常见的SOH估计方法进行了对比。

此实验基于CPU （Intel Core i7-6700 HQ 2.6 GHz）、GPU （NVIDIA GeForce GTX 1050Ti 4 GB）、RAM内存（16 GB）、Linux操作系统和Keras环境（以Tensorflow为后端）等软硬件实施。实验所采用的GRU-RNN由一个输入层、一个隐藏层、一个全连接层和一个输出层组成。原始的充电电压数据都被转换到固定的维度256维，GRU隐藏层节点设置为256，然后连接了一个64节点的全连接层。以预测值和实测值的平均绝对误差（Mean Absolute Error，MAE）为目标函数，并采用Adam方法进行优化网络权值，其学习率设置为0.0001，一阶动量衰减系数为0.9，二阶动量衰减系数为0.999，最小批量为128，迭代次数设置为10000。样本数据都被归一化到[−1, 1]的范围内。为了对锂离子电池SOH估计方法的性能进行定量描述，采用平均绝对值误差（Mean Absolute Error，MAE）和最大误差（Max Error，MAX）作为性能评价函数。

式中：$n$代表充电曲线，总共有$N$个充电电压—SOH数据对；${\kappa _n}$和${\kappa '_n}$分别表示估算值和实际值。

NASA锂离子电池随机老化数据集包含了7个不同的测试组共28块锂离子电池的测试数据。文中实验选取了16号（25 ℃、低倍率）、20号（25 ℃、高倍率）、24号（40 ℃、低倍率）、28号（40 ℃、高倍率）电池作为测试样本，并将剩下的24块锂离子电池测试数据作为训练样本。对比方法包括常见的机器学习算法支持矢量回归（Support Vector Regression, SVR）^[5]和高斯过程回归（Gaussian Process Regression, GPR）^[6]，采用一维充电电压直接作为特征量进行训练SVR和GPR，SVR和GPR所使用的核函数分别为poly核函数和Matern核函数。实验结果如图5所示，定量结果如表2所示。

图  5  NASA随机老化数据集SOH估计结果示例

Figure 5.  Examples of Li-ion battery SOH estimation for NASA-Randomized Battery Usage Data Set

图5给出了电池RW 16#，20#，24#和28#的SOH估计结果和误差。对于所有四个测试电池，这三种方法的SOH估计曲线与实测SOH曲线比较接近。其中，玫红色曲线（GRU-RNN）在三种方法中实现了最小的估计误差。表2列出了MAE和MAX形式的定量结果。通过对表2中的结果进行简单计算，SVR （绿色曲线）、GPR （黑色曲线）以及GRU-RNN的SOH估计结果MAE和MAX的全局量分别为2.76%，2.17%，1.40%和16.64%，9.13%，5.12%。显然，GRU-RNN的估计性能超过对比的两种方法。另外，所提出的方法的另一个优点是对电池放电条件没有特殊要求，仅仅采用恒流恒压充电数据就取得获得了较好的结果。

接下来，在牛津大学老化数据集上进行了实验验证。与NASA随机老化数据集相比，牛津大学老化数据集的放电工况要简单得多，在40 ℃以1C的电流恒流放电。把Cell 4#和Cell8#作为测试集，其余6个电池数据作为训练集。类似于NASA随机老化数据集，该数据集的估计结果如图6和表3所示。

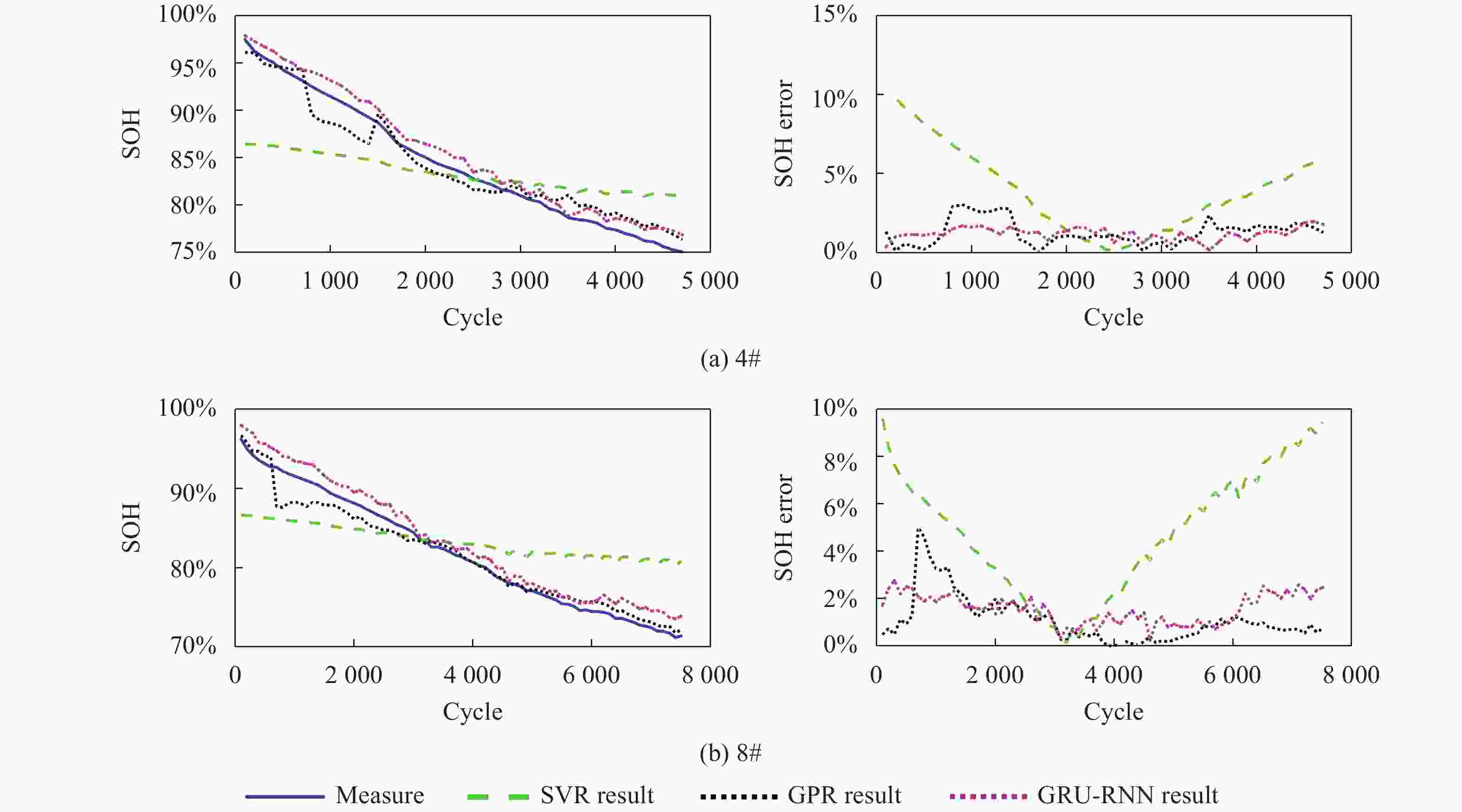
图  6  牛津大学电池老化数据集SOH估计结果示例

Figure 6.  Examples of Li-ion battery SOH estimation for Oxford Battery Degradation Database

可以观察到，对于三种方法，MAE均小于5%时，可以准确估计SOH。详细来说，GPR方法对4#电池实现了4.02%的MAE和11.35%的MAX，对于单元8#实现了4.83%的MAE和9.73%的MAX。GPR方法的估计结果显示出与真实SOH曲线相似的趋势，但最大振荡超过5%的MAX。与NASA随机老化数据集的实验结果相似，文中提出GRU-RNN的性能优于其他两种方法。具体来说，GRU-RNN对于4#实现了1.10%的MAE和1.87%的MAX，对于单元8#实现了1.32%的MAE和2.34%的MAX。很明显地，与NASA随机老化数据集相比，提出的方法在牛津大学老化数据集上通常具有更高的估计准确性。这主要是因为牛津大学数据集在恒定电流下重复进行充电和放电，老化状态比较稳定。

文中基于数据驱动的框架，提出了一种基于门控循环神经网络的锂离子电池SOH估计方法。方法以恒流-恒压充电阶段内的电压作为输入，以容量作为输出训练门控循环神经网络模型。测试时直接提供恒压恒流充电时的电压曲线即可获得SOH。文中所选取的可测量具有数量合适、相关性高、易于直接获取的优势。同两种常见的基于机器学习的SOH方法对比实验证明了方法的有效性，文中提出的方法取得了较高的估计精度。下一步将对算法的计算代价进行优化，将算法在面向嵌入式的电池管理系统上进行实现。