下载:
-
光子晶体概念由Yablonovitch E和John S在1987年分别提出，它是由不同的介电常数薄膜介质周期性排列形成的人工微结构光学材料。自从光子晶体概念问世后，学者们对其进行了广泛而深入的研究，大量的研究成果表明光子晶体可以很好地控制光运动（传播）的行为，因为光子晶体存在阻碍某些特定频率光子通过的特性，即存在光子禁带，处于禁带频率范围的光是无法通过光子晶体的，而处于通带频率范围的光则可以通过光子晶体，这种奇异的光学特性给人为控制和利用光的行为提供了新的理论依据，特别是对利用光作为信息传输的载体具有巨大的应用前景[1-12]。当在光子晶体的适当位置合理置入缺陷时，入射到光子晶体的光子被局域限制在缺陷处使该处光子态密度增大，被局域在缺陷处的大量光子可增强该处的受激辐射，从而使光子能够透过光子晶体形成带宽很窄的缺陷模（透射峰），这种特性对研究和设计高品质的光学滤波器件具有积极的意义[2-3, 10-11]。近年研究还发现，当在组成光子晶体的介质中掺入激活性杂质（如铒等）形成复介质时，还可进一步增强光子晶体中局域态的光子态密度及其自发辐射的强度，甚至出现光学的增益放大效果等[8-11]。已有的文献报道，缺陷介质层大多是嵌入周期性排列的基元介质之间，以及激活性杂质也普遍是掺入基元介质或单层缺陷中，而缺陷置于光子晶体模型两端且掺入激活性杂质的报道很少见。对于光子晶体尤其是对称结构光子晶体，两端的介质相当于光子晶体的外层介质，而且缺陷介质层又不同于基元介质，则两端缺陷对光子晶体传输特性的影响一定也不同于普通的嵌入式缺陷，即两端复缺陷光子晶体的光子晶体的透射特性也会有别于普通缺陷模式的光子晶体。
基于这种思考，文中构造了两端含复缺陷的对称结构的光子晶体C(AB)n(BAB)(BA)nC模型，利用传输矩阵法理论，并通过MATLAB软件编程计算，模拟出光子晶体的光传输特性及其调制规律，力图为光子晶体设计新型光学器件提供理论参考。
-
计算和研究的光子晶体模型为C(AB)n(BAB)(BA)nC，其中A、B是结构模型的基元介质薄膜，C是置入模型两端的对称缺陷介质薄膜，A、B、C对应的介质及参数分别为：A为TiO2薄膜，B为MgF2薄膜，C为聚苯乙烯薄膜，折射率和厚度nA=2.96，dA=50.68 nm，nB=1.39，dB=108.00 nm，nC=4.6，dC=32.61 nm。当缺陷层C介质中掺入激活性杂质时，它的折射率为复数亦称复折射率，表示成nC=4.6±ki，其中k是复折射率的虚部，可理解为激活系数或杂质含量，+ k 时表示掺入具有衰减效应的激活性杂质，- k时则表示掺入具有增益放大效应的激活性杂质，i为虚数单位。普通材料的折射率是实数称为实介质，掺入激活性杂质介质的折射为复数称为复介质或增益性介质[8-11]。当C掺入激活性杂质后即为复介质，则计算和研究的结构模型C(AB)n(BAB)(BA)nC即为两端含复缺陷的光子晶体模型。N组成光子晶体薄膜的排列周期数，取正整数。
计算方法采用传输矩阵法，根据薄膜光学理论，电磁波在单层介质薄膜中的传输行为可用一个分传输矩阵来表示，而在周期性排列的多层介质薄膜整体中的传输行为，则等于单层介质薄膜中的分传输矩阵之乘积，根据乘积结果的总传输矩阵即可求出电磁波通过光子晶体的透射率、反射率和电场分布等[2-3, 5, 8-12]。
-
当缺陷C中未掺入激活性杂质时为实介质，此时激活系数k=0，折射率为实数nC=4.6，取排列周期数n=5，可计算模拟出两端缺陷C为实介质时光子晶体C(AB)5(BAB)(BA)5C的透射谱，如图1所示。
图 1 nC=4.6时光子晶体的透射谱
Figure 1. Transmission spectrum of photonic crystals when nC=4.6
从图1可见，当光子晶体C(AB)5(BAB)(BA)5C的两端缺陷C介质中未掺入激活性杂质时，其透射谱出现了多条带宽不同但透射率均为100%的透射峰，尤其值得关注的是，在552.7 nm和656.5 nm波长位置处出现了两条精细的窄带透射峰，以及在1052.0~1201.0 nm波长范围也开始分裂出两条透射率为100%透射峰。说明当光入射到两端含实介质缺陷的光子晶体C(AB)n(BAB)(BA)nC时，光在光子晶体的内部被局域限制得到增强并产生受激辐射，而且被局域的光产生频率量子化效应并通过隧穿方式通过光子晶体，在宏观上表现为两条透射率很高且带宽很窄的透射峰。两端置入实介质缺陷C后光子晶体的这种光传输特性，对设计新型双通道光学滤波器件具有一定的参考价值。
-
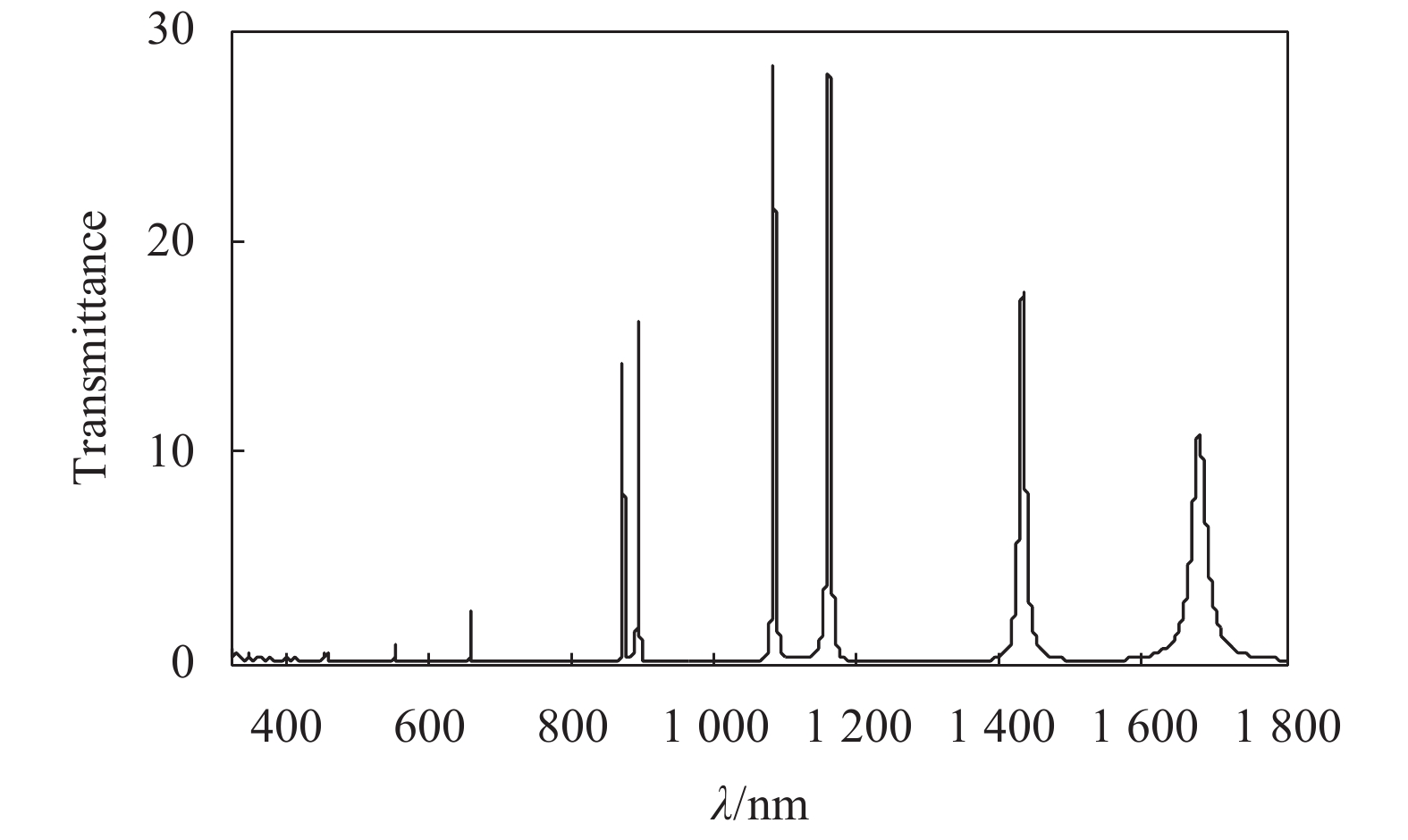
当两端缺陷C介质中掺入具有增益放大效应的激活性杂质时，C介质的折射率由实数变成含负虚部的复数，即激活系数k不等于零，假设激活系数k=3.76，则nC=4.6-3.76i，其他参数不变的情况下，可计算模拟出两端含缺陷光子晶体C(AB)5(BAB)(BA)5C的透射谱，如图2所示。
图 2 nC=4.6-3.76i时光子晶体的透射谱
Figure 2. Transmission spectrum of photonic crystals when nC=4.6-3.76i
对比图2和图1可得，当光子晶体两端缺陷C介质中掺入具有增益放大效应的激活性杂质后，其透射谱中仍然出现分立的透射峰，而且各透射峰中心所处位置与图1相同，但是各透射峰的透射率均大于100%，出现了明显的增益放大现象。如，从左至右透射谱中的552.5、656.7、871.4、892.9、1083.0、1160.0、1431.0和1678.0 nm等波长位置处透射峰透射率分别为：1.03、2.51、14.30、16.20、28.29、27.96、17.58和10.90。可见，当光子晶体两端缺陷C介质中掺入具有增益放大效应的激活性杂质后，激活性杂质明显激发并增强了光子晶体内部局域电场的自发辐射，从而使透射谱中分立透射峰的透射率得到不同程度的增益放大，其中透射率增益放大最明显为1083.0 nm和1160.0 nm波长处的分立透射峰，增益放大倍数最高可达28.29倍。
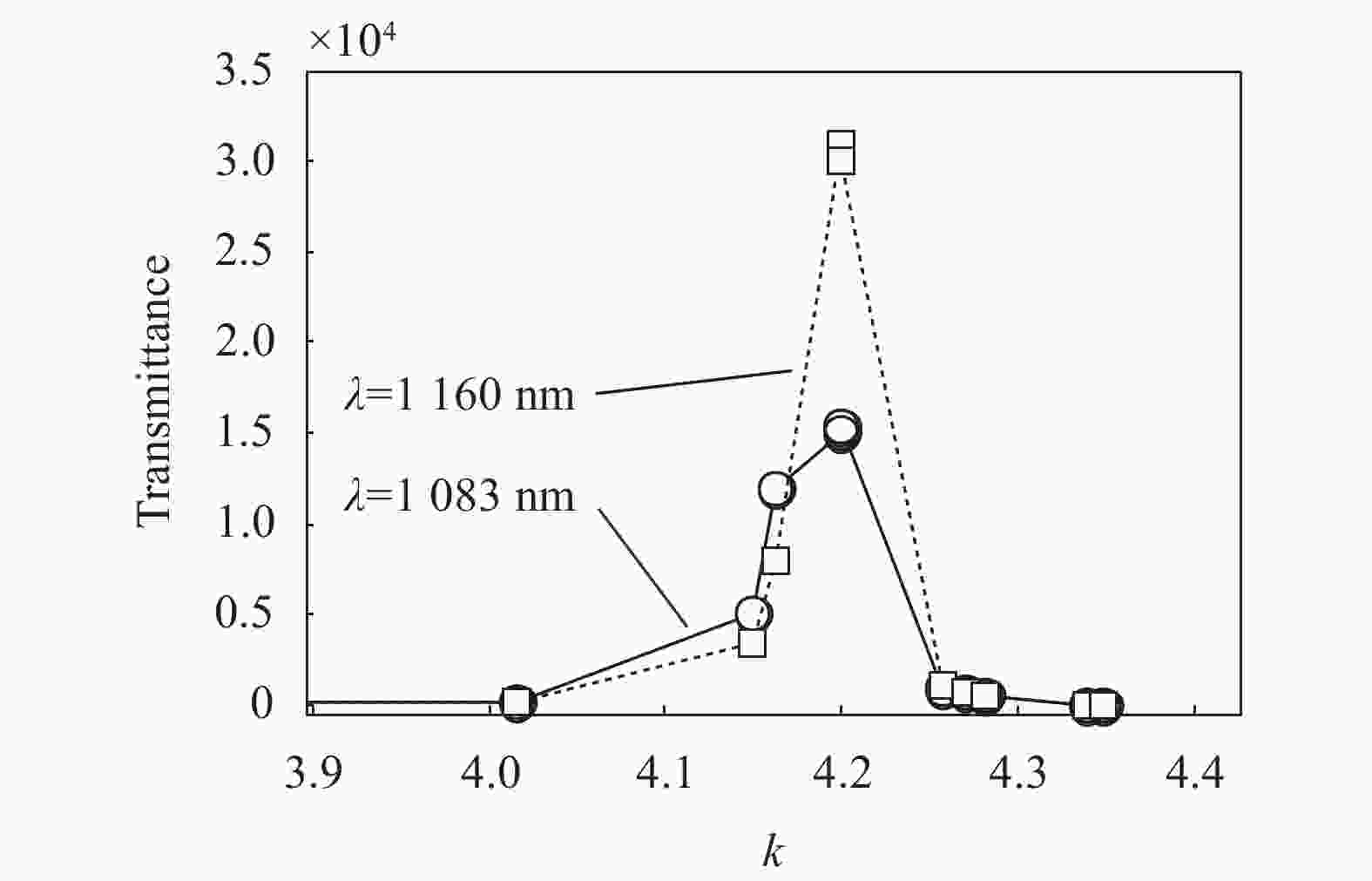
进一步的，可计算出光子晶体C(AB)5(BAB)(BA)5C的透射增益放大倍数对缺陷C折射率负虚部的响应规律。为简洁而直观，以λ=1083.0 nm和1160.0 nm波长位置处的透射峰为研究对象，并以负虚部k值的大小为横坐标，以两透射峰的透射率为纵坐标，可绘制出两条透射峰透射率随负虚部k值大小变化的曲线T～k，如图3所示。
图 3 nC=4.6-ki时k对光子晶体透射率的影响
Figure 3. Transmissivity of photonic crystals versus k when nC=4.6-ki
在计算模拟中k从0.3606~4.3474之间取了15个不同的值，且发现k从0.3606~4.0162之间增大时，透射峰的透射率增益放大倍数从1.1倍增大到58.5倍，而当k值从4.0162开始透射峰的透射率出现增益放大倍数明显剧增现象，达到178.0倍，为凸显k对透射峰透射率增益倍数放大的明显效果，所以图3选择呈现4.0162~4.3474范围内10个k值对应的变化曲线。从图3可见，λ=1083.0 nm和1160.0 nm两处的透射峰透射率对负虚部k值大小的响应趋势基本相同，首先都是随k值增大透射峰的透射率增益放大，而当k增大到一定数值时透射峰的透射率达到最大值，随后开始出现透射率下降现象，但透射峰的透射率还是大于100%。如，对于λ=1083.0 nm处的透射峰，当k从0.361增大到4.199时，透射峰透射率保持增益放大倍增状态，当k=4.199时透射峰透射率达到最大值Tmax=15300；k再进一步增大时，透射峰透射率则呈现快速下降趋势，但透射率仍然大于100%，即仍然处于增益放大激活状态，当k=4.350时透射峰的透射率增益放大幅度趋于最小，Tmin=1.001。同样地，对于λ=1160.0 nm处的透射峰，当复介质k从0.361增大到4.199时，透射峰透射率保持增益放大倍激活状态，k=4.199时透射率达到最大值， Tmax=3×104；k进一步增大时，透射峰的透射率也呈现下降趋势，但透射率仍然大于100%，当k=4.347时透射峰的透射率增益放大幅度达到最小。经计算还发现，光子晶体C(AB)5(BAB)(BA)5C的透射率增益放大倍数对缺陷C的实部与负虚部的响应规律基本相同，透射率增益放大倍数也是随着实部增大快速上升到极大值后再快速下降。
可见，当光子晶体C(AB)5(BAB)(BA)5C的两端缺陷C中掺入具有增益放大效应的激活性杂质时，可有效地实现光增益放大功能，而且增益放大的倍数对杂质含量（激活系数k）响应非常灵敏，这特性对光学放大器的研究具有积极意义。
-
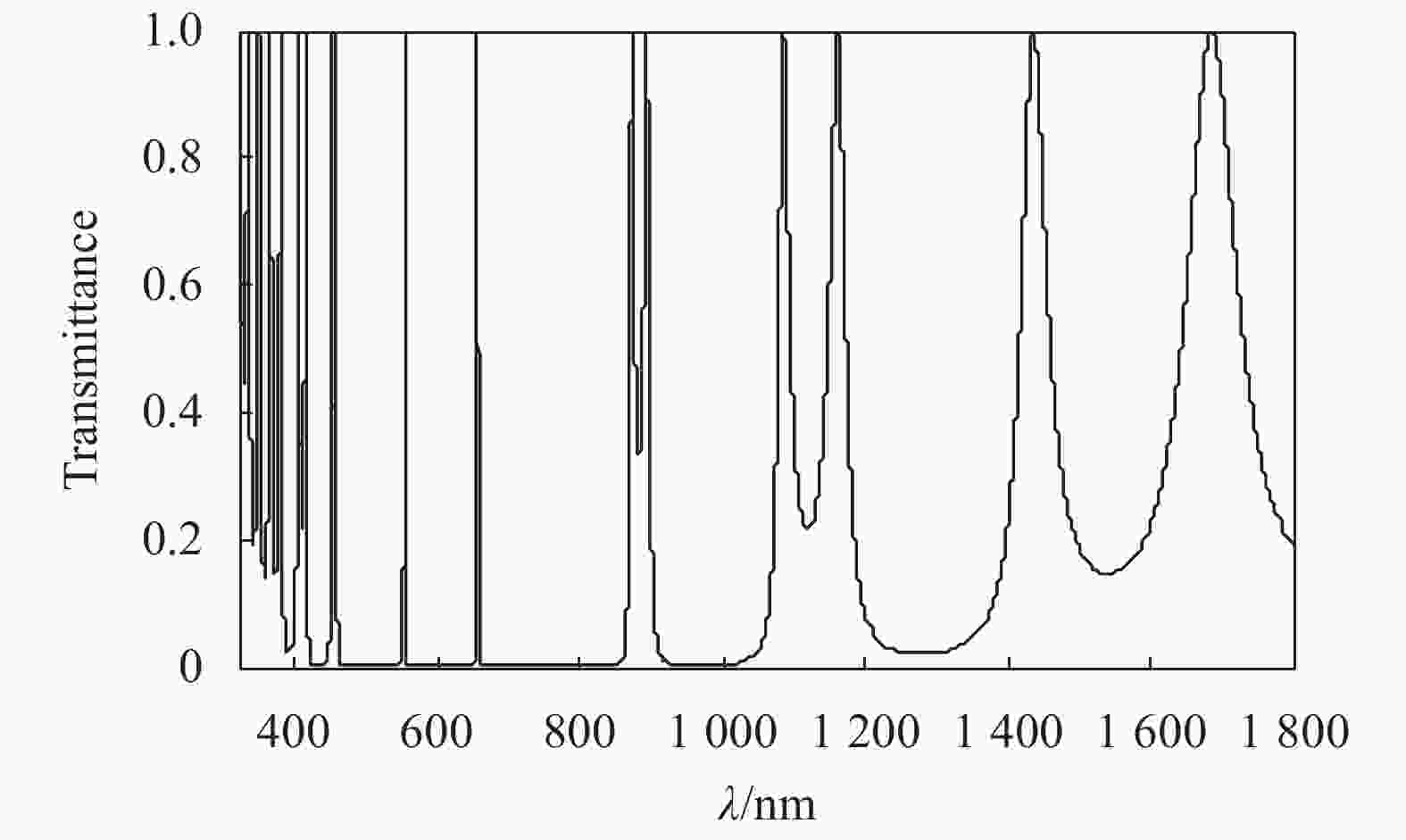
同样，其他参数不变的情况下，在缺陷介质C中掺入具有衰减效应的激活性杂质，则缺陷C的折射率为含正虚部的复数。取nC=4.6+1.1i，则可计算模拟出光子晶体C(AB)5(BAB)(BA)5C的透射谱，如图4所示。
图 4 nC=4.6+1.1i时光子晶体的透射谱
Figure 4. Transmission spectrum of photonic crystals when nC=4.6+1.1i
由图4可知，当两端缺陷介质C中掺入具有衰减效应的杂质后，光子晶体透射谱中的分立透射峰出现了明显的透射率衰减现象，即透射峰的透射率均小于100%，最高透射率甚至达不到50%。如，透射谱中从左至右的561.6、658.9、722.5、768.3、787.6、835.6、871.2、915.6、974.5、1015.0、1084.0、1249.0 nm等波长位置处的透射峰透射率分别为：0.223、0.267、0.318、0.345、0.352、0.363、0.369、0.372、0.378、0.383、0.398、0.456。从图中还可以看到，自1249.0 nm波长位置往长波方向，光子晶体的透射率还更加低，不再出现明显的透射峰。
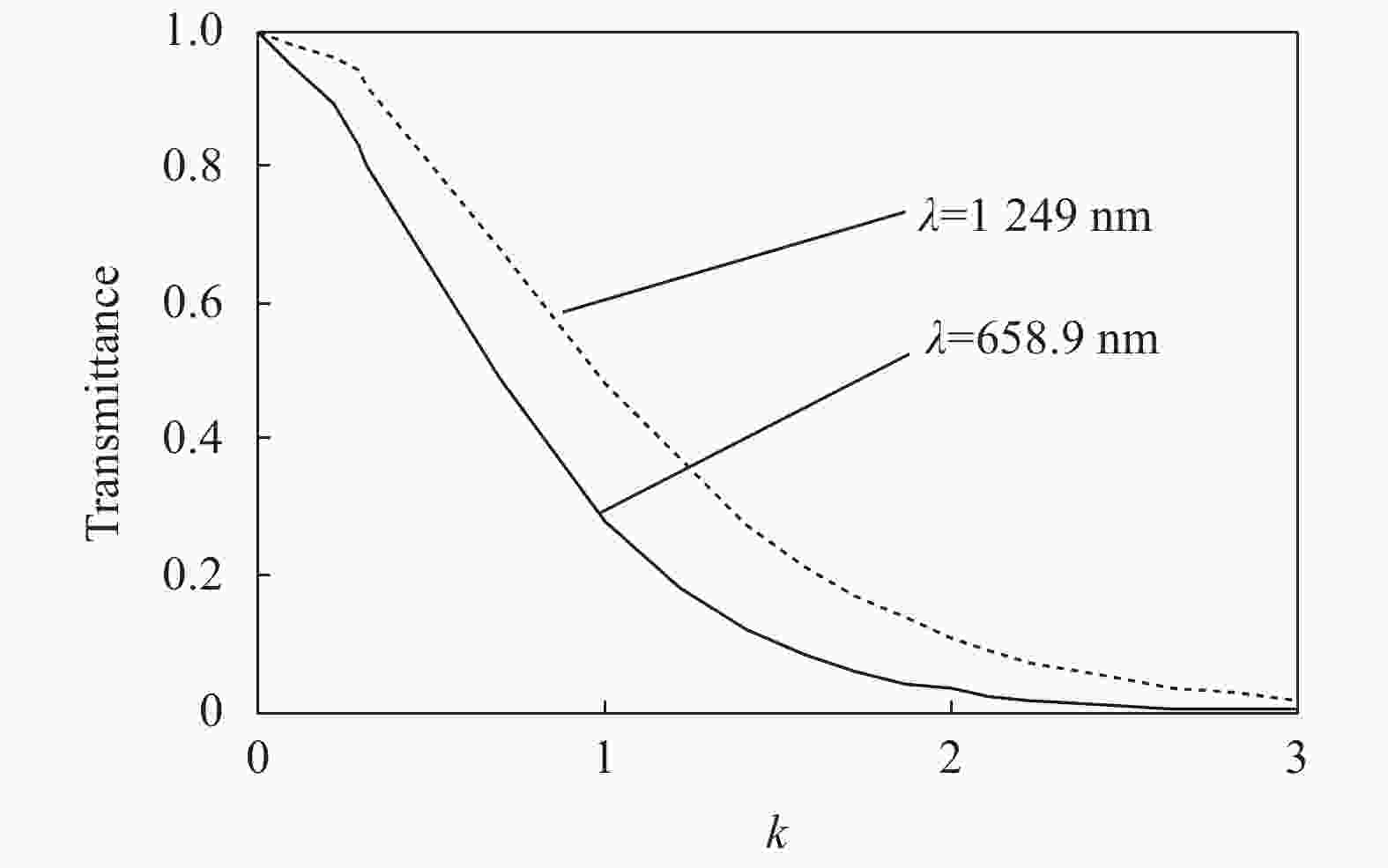
为直观地呈现光子晶体C(AB)5(BAB)(BA)5C的透射衰减效应对复缺陷C折射率正虚部的响应规律，以λ=658.9 nm和λ=1249.0 nm波长位置处的两透射峰为研究对象，并以正虚部k值的大小为横坐标，以两透射峰的透射率为纵坐标，可绘制出两透射峰透射率随正虚部k值大小变化的曲线T～k，如图5所示。
图 5 nC=4.6+ki时k对光子晶体透射率的影响
Figure 5. Transmissivity of photonic crystals versus k when nC=4.6+ki
从图5可见，λ=658.9 nm和λ=1249.0 nm两处的透射峰透射率对正虚部k值大小的响应规律基本相同，都是随k值增大透射率不断下降。当正虚部k值无限接近0，即缺陷C介质中杂质含量很小缺陷无限接近实介质时，λ=658.9 nm和λ=1249.0 nm两波长位置处透射峰透射率均无限接近100%；随着正虚部k值不断增加，透射峰的透射率快速下降，当k=3.00时，λ=658.9 nm波长位置处透射峰的透射率衰减至0，而λ=1249.0 nm波长位置处透射峰的透射率衰减至0.00001，即两透射峰已经趋于消失状态。进一步计算还发现，复缺陷C介质折射率的实部对光子晶体C(AB)5(BAB)(BA)5C的透射衰减效应同样也具有调制作用，但灵敏度低于正虚部k的调制作用，而且随着复折射率实部增大光子晶体透射峰的透射率均低于0.5，鉴于规律相似及文中的篇幅，在略去计算模拟结果的图形。另外，对比已经报道的文献[9-11]可知，当在普通结构光子晶体模型的基元介质中掺入激活性杂质时，光子晶体透射谱也会出现光增益放大或衰减现象，但不出现从实介质到复介质的新精细透射峰现象，如图1和图2、图4中1200 nm波长附近的透射峰所示。
可见，当光子晶体C(AB)5(BAB)(BA)5C的两端缺陷C中掺入具有衰减效应的激活性杂质时，可有效实现光学衰减功能，而且衰减的倍数对杂质含量（激活系数k）响应非常灵敏，这特性对光学衰减器、反射镜或吸收器等的研究具有一定参考意义。
-
利用传输矩阵法理论，通过计算机计算模拟仿真，研究两端对称复缺陷对一维光子晶体C(AB)n(BAB)(BA)nC光传输特性的激活效应，得出如下结论：
（1）当两端对称缺陷的激活杂质为零时，光子晶体透射谱分布多条带宽不等透射率均为100%的分立透射峰。
（2）当两端对称缺陷中掺入具有增益放大效应的激活性杂质时，光子晶体透射谱中透射峰的透射率出现增益放大现象，增益放大倍数最可高达104数量级，而且复介质的负虚部和实部对增益放大的倍数具有灵敏的调制作用。
（3）当两端对称缺陷中掺入具有衰减效应的激活性杂质时，光子晶体透射谱中透射峰的透射率出现衰减下降现象，而且复介质的正虚部和实部对透射率衰减效果具有灵敏的调制作用。
两端对称复缺陷对光子晶体光传输的增益放大和衰减特性的调制作用规律，可为新型光学滤波器件、光学放大器、衰减器或全反射镜等器件的研究和设计提供理论参考。
Activation effect of complex defects with two ends symmetry on transmission properties of photonic crystals
-
摘要: 为研究和设计高品质、高性能的光学滤波、光学放大、光学衰减和全反射镜等器件，通过计算模拟的方式，研究两端对称复缺陷对光子晶体C(AB)n(BAB)(BA)nC光传输特性的激活效应，研究表明：在对称结构光子晶体的两端置入缺陷C，当缺陷C为实介质时，光子晶体透射谱中出现多条透射率为100%的分立透射峰。当C中掺入具有增益放大效应的杂质形成含负虚部的复折射率缺陷时，透射谱中各分立透射峰的透射率均出现增益放大现象，而且缺陷层复折射率的虚部或实部对透射峰的增益放大倍数均具有调制作用，随着缺陷层复折射率的负虚部或实部增大，透射增益放大倍数先增大，达到极大值后再减小，增益放大倍数最高达可达104数量级。当C中掺入具有衰减效应的杂质形成含正虚部的复折射率缺陷时，透射谱中各分立透射峰均出现透射率衰减现象，而且缺陷层复折射率的虚部或实部对透射峰的衰减倍数也具有调制作用，随着缺陷层复折射率的正虚部增大，各分立透射峰的透射率不断衰减，直至透射率趋于零，出现全反射或全吸收现象。两端对称复缺陷对光子晶体光传输特性的调制规律，可为新型光学器件的研究与设计提供理论参考。Abstract: In order to research and design high performance optical filters, optical amplifiers, optical attenuators and total reflection mirrors, activation effect of complex defects with two ends symmetry on the optical propagation properties of photonic crystal C(AB)n(BAB)(BA)nC has been studied by computer simulation. The results show that, when C is real medium defect, there are several discrete transmission peaks with 100% transmittance in the transmission spectrum of photonic crystal with symmetrical structure. When the impurity with gain amplification effect is doped into C to form complex refractive index defect with negative imaginary part, transmittance of each discrete transmission peak in the transmission spectrum will have an amplified gain. Both the imaginary part and the real part of the complex refractive index of the defect layer can modulate the gain amplification of the transmission peak. With the increase of the negative imaginary part or real part of the complex refractive index of the defect layer, the transmission gain magnification increases first, reaches the maximum value and then decreases, and the gain magnification can reach up to 104 orders of magnitude. When the impurity with gain amplification effect is doped into C to form complex refractive index defect with positive imaginary part, transmittance of each discrete transmission peak in the transmission spectrum will have attenuation phenomenon. Both the imaginary part and the real part of the complex refractive index of the defect layer can modulate the attenuation multiple of the transmission peak. With the increase of the positive imaginary part of the complex refractive index of the defect layer, the transmittance of the discrete transmission peaks decreases until the transmittance tends to zero, and total reflection or total absorption occurs. The modulation law of symmetrical complex defects at both ends on the transmission characteristics of photonic crystals can provide theoretical reference for the research and design of new optical amplifiers, filters, attenuators and total reflection mirrors.
-
Key words:
- photonic crystal /
- complex defects with two ends /
- filtering /
- gain amplification /
- modulation
-
图 2 nC=4.6-3.76i时光子晶体的透射谱
Figure 2. Transmission spectrum of photonic crystals when nC=4.6-3.76i
图 3 nC=4.6-ki时k对光子晶体透射率的影响
Figure 3. Transmissivity of photonic crystals versus k when nC=4.6-ki
图 4 nC=4.6+1.1i时光子晶体的透射谱
Figure 4. Transmission spectrum of photonic crystals when nC=4.6+1.1i
-
[1] Hou Shanglin, Lei Jingli, Wu Qiling, et al. Enhanced femtosecond optical pulses compression in highly nonlinear photonic crystal fibers(invited) [J]. Infrared and Laser Engineering, 2019, 48(1): 0103004. (in Chinese) doi: 10.3788/IRLA201948.0103004 [2] Su An, Wang Gaofeng, Meng Chengju, et al. Light propagation characteristic of dual defect microcavity of photonic crystal [J]. Infrared and Laser Engineering, 2017, 46(6): 0620004. (in Chinese) doi: 10.3788/IRLA201746.0620004 [3] Su An, Gao Yingjun. Light propagation characteristics of one-dimensional photonic crystal with double-barrier quantum well [J]. Acta Physica Sinica, 2012, 61(23): 234208. (in Chinese) doi: 10.7498/aps.61.234208 [4] Li Tianqi, Mao Xiaojie, Lei Jian, et al. Analysis and comparison of solid-state lasers and fiber lasers on the coupling of rod-type photonic crystal fiber [J]. Chinese Optics, 2018, 11(6): 958-973. (in Chinese) doi: 10.3788/co.20181106.0958 [5] Su An, Meng Chengju, Tang Xiufu, et al. Optical Tamm state on the surface of photonic crystal of symmetric structure [J]. Infrared and Laser Engineering, 2019, 48(8): 0817001. (in Chinese) doi: 10.3788/IRLA201948.0817001 [6] Liu Jie, Tie Shengnian, Lu Huidong. Multi-channel drop filter based on two-dimensional photonic crystal [J]. Optics and Precision Engineering, 2016, 24(5): 1021-1027. (in Chinese) doi: 10.3788/OPE.20162405.1021 [7] Jiang Qiang, Chen Jiabi, Zhang Lei, et al. Phase evolution of inverse Doppler effect in two-dimensional photonic crystal [J]. Optics and Precision Engineering, 2017, 25(1): 34-41. (in Chinese) doi: 10.3788/OPE.20172501.0034 [8] Chen Ying, Cao Huiying, Han Shuaitao, et al. Sensing property of photonic crystal Fabry-Pérot heterogeneous structure with absorption medium [J]. Acta Optica Sinica, 2017, 37(2): 0223003. (in Chinese) doi: 10.3788/AOS201737.0223003 [9] Su An, Meng Chengju, Jiang Siting, et al. Activation effect of complex medium on the optical propagation properties of optical quantum well [J]. Chinese Optics, 2020, 13(2): 396-410. (in Chinese) doi: 10.3788/co.20201302.0396 [10] Su An, Meng Chengju, Gao Yingjun, et al. Modulation of activated impurity on filter property of photonic crystal quantum well [J]. Chinese Journal of Lasers, 2014, 41(3): 0306001. (in Chinese) doi: 10.3788/CJL201441.0306001 [11] Meng Chengju, Su An, Gao Yingjun. Photonic crystal quantum well with active impurity possessing high-efficient optical filtering and amplifying functions [J]. Infrared and Laser Engineering, 2013, 42(12): 3207-3212. (in Chinese) [12] Wang Hui, Li Yongping. An eigen matrix method for obtaining the band structure of photonic crystals [J]. Acta Physica Sinica, 2001, 50(11): 2172-2178. (in Chinese) doi: 10.3321/j.issn:1000-3290.2001.11.025 -
点击查看大图
图(5)
计量
- 文章访问数: 180
- HTML全文浏览量: 63
- PDF下载量: 12
- 被引次数: 0
