-
近年来，衍射光学系统得到了快速发展[1]，其轻量化大口径的特点使高分辨率成像易于实现，但其光谱范围较窄，一般认为适于激光雷达使用[2-4]，当其用于红外相机时，需采用色差校正技术[5]。然而，即便经过色差校正，红外相机所能利用的信号能量也将大幅降低，导致红外探测信噪比大幅降低。假定衍射光学系统的光谱范围仅为传统光学系统光谱范围的1/20，探测信噪比在原理上将减少至原来的1/20，这使其红外应用受到影响。衍射光学系统轻量的特点使其大口径容易实现，增加其直径4.5倍，其红外探测信噪比也可以保证。
上述红外探测通常用于对地成像场合，当红外相机用于目标探测时，考虑到地物背景和目标光谱特性不同，衍射光学系统窄的光谱范围，实际上有助于地物背景和目标分离，并将有利于目标探测。
近年来单光子探测技术得到快速发展，红外相机是否能借鉴相关技术进一步提高其探测性能是值得思考的。时宽（积分时间）一定的红外信号是宽带噪声信号的特点使其等效噪声功率较高，从原理上讲，细分光谱会降低红外等效噪声功率，有助于提高红外相机的探测性能。
在衍射光学系统和细分红外光谱的基础上，分析对地观测红外相机的目标探测性能，研究新的降低红外等效噪声功率方法，对非制冷红外相机技术的发展和应用具有重要意义。
文中第1节对基于衍射光学系统的红外系统进行了介绍，并对其参数进行了分析，包括信噪比、灵敏度、比探测率和光学系统角分辨率；第2节基于信噪比研究了衍射光学系统红外相机的探测性能；第3节对电子学系统、激光系统和红外系统的等效噪声功率进行了对比分析；第4节对文中工作进行了总结，给出了研究结论。
-
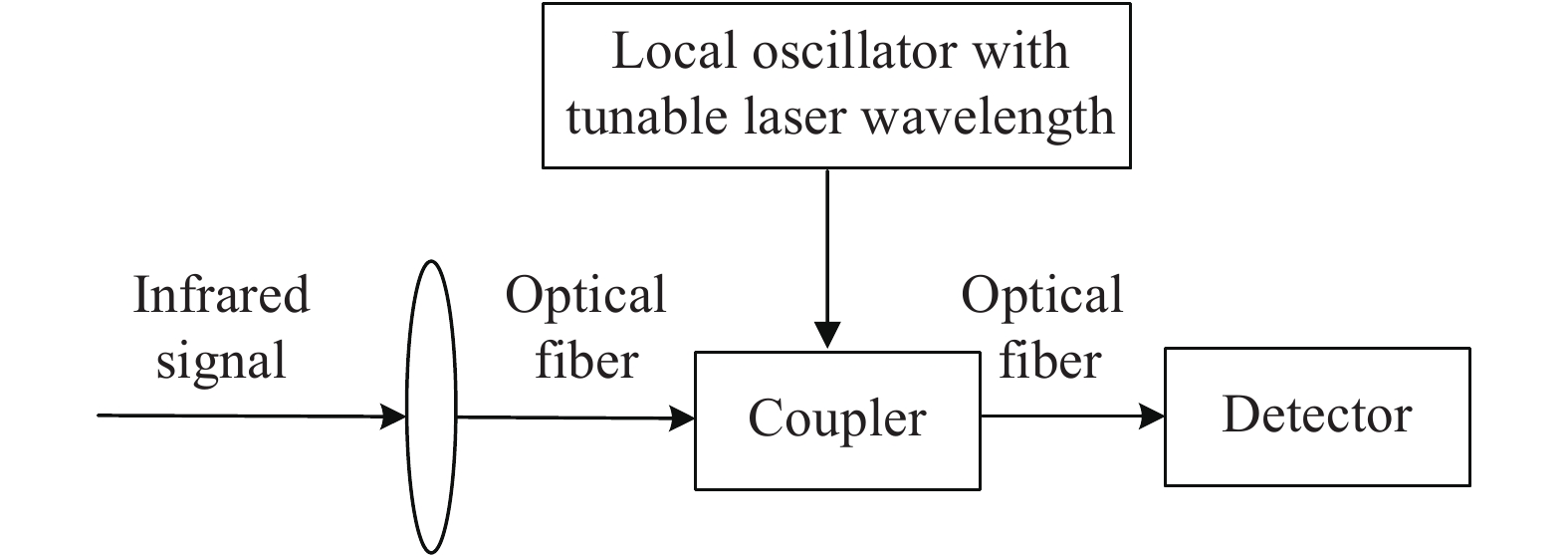
图1为衍射光学系统红外相机系统光路示意图，红外信号经衍射主镜接收后，利用与衍射主镜具有相同色散、相反光焦度的衍射透镜进行色差校正，该方法也称为Schupmann消色差方法，最后由光电探测器探测后成像。
图 1 衍射光学系统红外相机系统光路示意图
Figure 1. Optical path diagram of infrared camera system based on diffractive optical system
此节对红外系统中的信噪比、灵敏度及比探测率等重要参数进行了介绍；由于红外系统的比探测率计算较为复杂，将给出一个计算示例，并重点分析了使用如图1所示的衍射光学系统后比探测率不变的本质原因；最后推导了比探测率与光学系统角分辨率关系。
-
假设单个目标像元在受到红外辐射时产生的目标信号电压峰值为
${V_{ts}}$ ，其可描述为[6]：$${V_{ts}} = {P_t}R' = {P_t}{D^*}{V_N}{\left( {{A_d}/\left( {2{t_{{\rm{int}} 2}}} \right)} \right)^{ - 1/2}}$$ (1) 式中：
${P_t}$ 为单个目标像元接收到的辐射功率；$R'$ 表示探测器光谱范围内的波段响应度；${D^*}$ 为探测器的比探测率，是归一化的波段探测度，其表示在某一波段内，面积为$1\;{\rm{c}}{{\rm{m}}^2}$ 的焦平面上有1 W的入射功率，并用1 Hz带宽的电路测量时的信噪比；${A_d}$ 表示探测器单个像元面积；${t_{{\rm{int}} 2}}$ 为实际工作中探测器的积分时间；${V_N}$ 为探测器噪声电压峰值。类似的，单个背景像元对应的信号电压峰值${V_{bs}}$ 为：$${V_{bs}} = {P_{bg}}R' = {P_{bg}}{D^*}\left( \lambda \right){V_N}{\left( {{A_d}/\left( {2{t_{{\rm{int}} 2}}} \right)} \right)^{ - 1/2}}$$ (2) 式中：
${P_{bg}}$ 为单个背景像元接收到的辐射功率。联立可知红外探测器输出的、可检测的最小信噪比SNR为：$$SNR = \left( {{V_{ts}} - {V_{bs}}} \right)/{V_N} = \Delta P{D^*}\left( \lambda \right){\left( {{A_d}/\left( {2{t_{{\rm{int}} 2}}} \right)} \right)^{ - 1/2}}$$ (3) 式中：
$\Delta P$ 是单个目标像元和背景像元上的辐射功率差。 -
作为可检测的最小接收功率，红外探测器的接收灵敏度
$\Delta P$ 与探测距离$R$ 的关系可表示为[6]：$$\Delta P = |\left( {{L_t} - {L_{bg}}} \right)/{N_t}|{A_t}{A_0}{\tau _a}{\eta _0}/{R^2}$$ (4) 式中：
${N_t}$ 表示目标在焦平面上所占的像元个数；${A_t}$ 和${A_0}$ 分别表示目标的有效辐射面积和光学系统入瞳面积，而${A_0}$ 与光学系统口径${D_0}$ 的关系可表示为${A_0} = $ $ \pi {\left( {\dfrac{{{D_0}}}{2}} \right)^2}$ ；${\tau _a}$ 和${\eta _0}$ 分别表示大气透过率和光学系统透过率；${L_t}$ 和${L_{bg}}$ 分别表示目标和背景的辐射亮度，其可通过下式计算得到[7]：$$L = \frac{{\varepsilon M\left( T \right)}}{\pi }$$ (5) 式中：
$M\left( T \right) =\displaystyle\int_{{\lambda _1}}^{{\lambda _2}} {\dfrac{{{c_1}}}{{{\lambda ^5}}}\dfrac{1}{{\exp \left( {{c_2}/\lambda T} \right) - 1}}\rm{d}\lambda }$ 表示黑体红外辐出度，${c_1}$ 和${c_2}$ 分别为第一、第二辐射常数；$T$ 为目标或者背景的温度；$\varepsilon $ 为目标或背景的发射率。为便于计算，一般通过下式并结合查找黑体相对辐出度表来计算此积分[8]。$$M\left( T \right) = \left[ {F\left( {{\lambda _2}T} \right) - F\left( {{\lambda _1}T} \right)} \right]\sigma {T^4}$$ (6) 式中：
$\sigma $ 为斯蒂芬常数；$F\left( {\lambda T} \right)$ 为黑体相对辐出度函数。 -
从公式(3)中可以看出，在除
${D^*}$ 外其余参数不变的情况下，${D^*}$ 越大，探测信噪比越高，所以进一步研究${D^*}$ 是值得的。对于光电探测器，${D^*}$ 可描述为下式[6]：$${D^*} = \frac{{4K \cdot {F^2} \cdot {T_B}^2 \cdot {\lambda _P}}}{{{c_2} \cdot {\eta _{0t}} \cdot NETD \cdot {{\left( {2{t_{{\rm{int}} 1}} \cdot {A_d}} \right)}^{1/2}}M\left( {{T_B}} \right)}}$$ (7) 式中：
$K$ 为峰值探测率到有效探测率的转换系数；$F$ 为光学系统F数；${\lambda _P}$ 为峰值波长；$NETD$ 表示噪声等效温差，对于制冷型探测器，其值较低，从而可得到较大的比探测率值；${\eta _{0t}}$ 和${t_{{\rm{int}} 1}}$ 分别为测试$NETD$ 时的光学系统透过率和积分时间；$M\left( {{T_B}} \right)$ 为背景辐出度。表1给出了一个利用公式(7)计算非制冷探测器${D^*}$ 的具体示例，得到其计算值为$5.{\rm{4}} \times {10^{10}}\;{\rm{cm}} \cdot {\rm{H}}{{\rm{z}}^{1/2}} \cdot {{\rm{W}}^{ - 1}}$ 。表 1
${D^*}$ 计算相关参数Table 1. Relevant parameters for calculating
${D^*}$ Parameters Value Parameters Value Conversion factor $K$ 0.7 F number of optical systems 1 Grass background temperature in Summer ${T_B}$ 303 K Detector peak wavelength ${\lambda _p}$ $10.8\;{\text{μm}}$ First radiation constant ${c_1}$ $3.741\;5 \times {10^8}\;{\rm{W}} \cdot \;{{\text{μm}}^4} \cdot \;{{\rm{m}}^2}$ Second radiation constant ${c_2}$ $1.438\;8 \times {10^4}{\text{μm}} \cdot \;{\rm{K}}$ Optical system transmittance during testing ${\eta _{0t}}$ 0.6 Background emissivity 0.93 Noise equivalent temperature difference $NETD$ $40 \times {10^{ - 3}}\;{\rm{K}}$ Integration time during testing ${t_{{\rm{int}} 1}}$ $34.56 \times {10^{ - 6}}\;{\rm{s}}$ Detector pixel area ${A_d}$ ${\left( {14 \times {{10}^{ - 6}}} \right)^2} \times {10^4}\;{\rm{c}}{{\rm{m}}^2}$ Detector specific detectivity ${D^*}$ $5.{\rm{4}} \times {10^{10}}\;{\rm{cm}} \cdot \;{\rm{H}}{{\rm{z}}^{1/2}} \cdot \;{{\rm{W}}^{ - 1}}$ 由于背景辐出度
$M\left( {{T_B}} \right)$ 是波长的函数，当输入主镜使用衍射光学系统后，由于光谱范围变窄，将直接导致$M\left( {{T_B}} \right)$ 变化，下面给出具体分析。图2为黑体相对辐出度函数$F\left( {\lambda T} \right)$ 随着$\lambda T$ 的变化曲线，假设$\lambda $ 的变化范围为$0\sim 15\;{{\text{μm}}}$ ，$T = 1\;000\;$ K，即$\lambda T$ 的变化范围为$0\sim 15 \times {10^3}\;{{\text{μm}}} \cdot {\rm{K}}$ 。图2(a)、(b)和(c)分别给出$\lambda T$ 取不同范围时黑体相对辐出度函数曲线。
图 2
$\lambda T$ 取不同范围时黑体相对辐出度函数图。(a)$\lambda T$ 取全部范围；(b)$\lambda T$ 取2.4×103~3.6×103 μm·K；(c)$\lambda T$ 取$0\sim 1.5 \times {10^3}\;{\text{μm}} \cdot {\rm{K}}$ Figure 2. Graph of relative radiant exitance function of black-body when
$\lambda T$ takes different ranges. (a)$\lambda T$ takes entire range; (b)$\lambda T$ takes 2.4×103-3.6×103 μm·K ; (c)$\lambda T$ takes 0-1.5×103 μm·K假定输入主镜使用衍射光学系统，中心波长为
$10.8\;{\text{μm}}$ ，其可用的光谱宽度为$0.2\;{\text{μm}}$ ，相比于探测器$8\sim 12\;{\text{μm}}$ 的光谱范围，相应的的积分区间会减少为原来的1/20。虽然从图2(a)中$\lambda T$ 的全部范围看，$F\left( {\lambda T} \right)$ 并非$\lambda T$ 的线性函数，但是在特定温度下（如$T = 300\;$ K），小光谱范围内（如$8\sim 12\;{\text{μm}}$ ）时，从图2(b)中可以看出$F\left( {\lambda T} \right)$ 近似为$\lambda T$ 的线性函数。此时，由公式(6)可知，目标/背景辐出度会由于使用衍射光学系统后波段积分区间缩小为原来的1/20而同比缩小。另外从图2(c)中也可以看出，当
$\lambda T$ 减小到一定程度后，黑体相对辐出度已趋近于零，正如背景辐出度非常小的深空背景，其光学系统部件所产生的红外杂散辐射就成为影响背景辐射的主要因素[9]。而对地观测时，背景辐出度较强不可忽略，且由公式(5)知当目标和背景的光谱特性相同时，目标和背景的辐亮度都会随着光谱范围的缩小会同比减小。此外，受到光谱范围缩减影响的参数还有
$NETD$ ，在$NETD$ 数值的实验室测量中，其可由下式计算[10]：$$NETD = \frac{{\Delta T}}{{\left( {{V_{ts}} - {V_{bs}}} \right)/{V_N}}}$$ (8) 式中：
$\Delta T$ 为目标/背景温差。从该式可知，随着光谱范围的缩小，目标/背景峰值电压差同比缩小，而$NETD$ 则同比增大。所以，最终从公式(7)中可以看出，随着光谱范围的缩小，背景辐出度
$M\left( {{T_B}} \right)$ 同比缩小，而$NETD$ 又同比增大，在此基础上${D^*}$ 一般不会变化。参考文献[9]研究了深空背景条件下的红外探测器比探测率与光学系统工作温度的关系，明确了制冷条件下可获得较高比探测率的结论。根据参考文献[9]，当深空背景条件下口径300 mm，光学系统F=2，系统工作温度300 K （非制冷）时，8~14 μm长波红外的
${D^*}$ 可达到$3.82 \times {10^{11}}\;{\rm{cm} } \cdot \;{\rm{H} }{ {\rm{z} }^{1/2} } \cdot \;{ {\rm{W} }^{ - 1} }$ 。根据参考文献[7]，对于大气背景条件下口径44 mm，光学系统F=2，峰值波长${\lambda _P} = 4.167$ μm，等效噪声温差NETD<16 mK时，制冷型探测器的${D^*}$ 估算结果为$1.159 \times {10^{10}} \;{\rm{cm} } \cdot $ $ \;{\rm{H} }{ {\rm{z} }^{1/2} } \cdot \;{ {\rm{W} }^{ - 1} }$ 。上述两例均为对空观测，当探测器选为非制冷且用于对地观测时，
${D^*}$ 将有所减少。考虑到影响${D^*}$ 估算的因素较多，为保证文中分析结果的可靠性，后文中${D^*}$ 取值为文献[7]中的1/8，即为$1.4 \times {10^9}\;{\rm{cm} } \cdot \;{\rm{H} }{ {\rm{z} }^{1/2} } \cdot \;{ {\rm{W} }^{ - 1} }$ 。 -
将红外相机用于对地观测时，光学系统俯仰向和方位向的角分辨率可分别描述为：
$$\left\{ \begin{array}{l} {\rho _a} = \arctan \left( {a/f} \right) \approx a/f \\ {\rho _r} = \arctan \left( {b/f} \right) \approx b/f \end{array} \right.,\left( {a,b \ll f} \right)$$ (9) 式中：
$a$ 和$b$ 分别为两个方向上的像元尺寸；$f$ 为光学系统的焦距，其可表示为光学系统口径${D_0}$ 和F数的乘积$f = {D_0}F$ 。当两个方向的像元尺寸均为14 μm，焦距
$f = $ $ 100\;{\rm{mm}}$ 时，两维的角分辨率均为0.14 mrad，对应15 km处空间分辨率约为2 m。以焦距与口径的比值替换光学系统F数，并将公式(9)代入公式(7)可得
${D^*}$ 与光学系统角分辨率的关系如下：$${D^*} = \frac{{K \cdot {T_B}^2 \cdot {\lambda _P} \cdot \pi \cdot {A_d}^{1/2}}}{{{c_2} \cdot {\eta _{0t}} \cdot NETD \cdot {A_0} \cdot {{\left( {2{t_{{\rm{int}} 1}}} \right)}^{1/2}} \cdot {\rho _a} \cdot {\rho _r} \cdot M\left( {{T_B}} \right)}}$$ (10) 从该式可以看出，相机角分辨率越高，每个像元接收的来自单位立体角内的背景辐出度越小，
${D^*}$ 越大。 -
在上节对红外系统参数分析的基础上，此节以探测信噪比作为红外相机探测性能的表征，具体分析使用衍射光学系统前后红外探测性能的变化。
联立公式(3)和公式(4)，红外探测信噪比可描述如下：
$$SNR = \frac{{\delta |\left( {{L_t} - {L_{bg}}} \right)/{N_t}|{A_t}{A_0}{\tau _a}{\eta _0}{D^*}}}{{{R^2} \cdot {{\left( {{A_d}/\left( {2{t_{{\rm{int}} 2}}} \right)} \right)}^{1/2}}}}$$ (11) 当红外相机用于对地观测时，假设背景为夏季草地，在距离15 km处，相应地设置大气透过率
${\tau _a} = 0.75$ 。对不同温度的车辆目标，下面对一个衍射光学系统非制冷红外相机的探测信噪比进行分析，表2为系统参数。表 2 系统参数
Table 2. System parameters
Parameters Value Parameters Value Signal extraction factor $\delta $ 0.707 Number of pixels occupied by the vehicle target on the focal plane ${N_t}$ 1 Atmospheric transmittance ${\tau _a}$ 0.75 Optical system aperture ${D_0}$ 100 mm Optical system transmittance ${\eta _0}$ 0.6 Optical system entrance pupil area ${A_0}$ $79 \times {10^{ - 4}}\;{{\rm{m}}^2}$ Integration time in actual work ${t_{{\rm{int}} 2}}$ $10 \times {10^{ - 3}}\;{\rm{s}}$ Target effective radiation area ${A_t}$ $4 \times {10^4}\;{\rm{c}}{{\rm{m}}^2}$ Background surface temperature 303 K Target surface temperature 304/306/308 K Detection range R 15 km Detector specific detectivity ${D^*}$ $1.4 \times {10^9}\;{\rm{cm} } \cdot \;{\rm{H} }{ {\rm{z} }^{1/2} } \cdot \;{ {\rm{W} }^{ - 1} }$ 假定探测器光谱范围为
$8\sim 12\;{\text{μm}}$ ，且目标和背景的辐出度光谱特性相同，如图3所示（不同仅由温差引起），当输入主镜使用衍射光学系统后，其可用的光谱宽度缩小为$0.2\;{\text{μm}}$ （如10.7~10.9 μm），由公式(5)和1.3节分析可知，当积分区间减少为原来的1/20时，目标和背景亮度均会缩减为原来的1/20，而${D^*}$ 保持不变，由公式(11)可得，给定探测距离下的信噪比会同比降低。
图 3 目标/背景温差1 K时相同的辐出度光谱曲线
Figure 3. Same spectral curve of radiance at target/background temperature difference of 1 K
表3给出了目标/背景光谱特性相同时在不同光学系统下的红外探测信噪比，可以看出，对于温差1 K的目标/背景，在传统光学系统下的信噪比为3.9，而在衍射光学系统下仅为0.19，信噪比下降为原来的1/20，此时需增大衍射光学系统口径直径4.5倍才能保证原有的探测信噪比。
表 3 目标/背景光谱特性相同时不同光学系统下红外探测信噪比
Table 3. Infrared detection SNR under different optical systems when the spectral characteristics of target/ background are same
Parameters Value Target/background emissivity 0.93/0.93 Target/background spectral range 8-12 μm Target radiance $\left( {3.82/3.94/4.06} \right) \times {\rm{1}}{{\rm{0}}^{{\rm{ - 3}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ Background radiance $3.75 \times {\rm{1}}{{\rm{0}}^{{\rm{ - 3}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ SNR of infrared detection with traditional optical system 3.9/11.9/20 SNR of infrared detection with diffractive optical system 0.19/0.55/0.92 当目标和背景的光谱特性不同，典型的如目标光谱范围本身就较小在
$0.6\;{\text{μm}}$ 量级，如图4所示，目标辐出度对波长的响应强点主要集中在$10.4\sim 11\;{\text{μm}}$ 光谱范围内，其余幅值较小，为简化问题，设其为零。输入主镜使用衍射光学系统后窄谱段的目标亮度减小为原来的1/3，而背景亮度减小为原来的1/20，此时两者差的绝对值并不会同比下降而导致信噪比也同比大幅降低。这表明，在一定条件下红外相机的探测性能不会因为衍射光学系统的使用而大幅下降，而通常目标和背景光谱特性不同的特点，也为衍射光学系统的使用提供了机会。在此基础上，增大衍射光学系统口径，将弥补能量损失甚至进一步提升红外探测性能。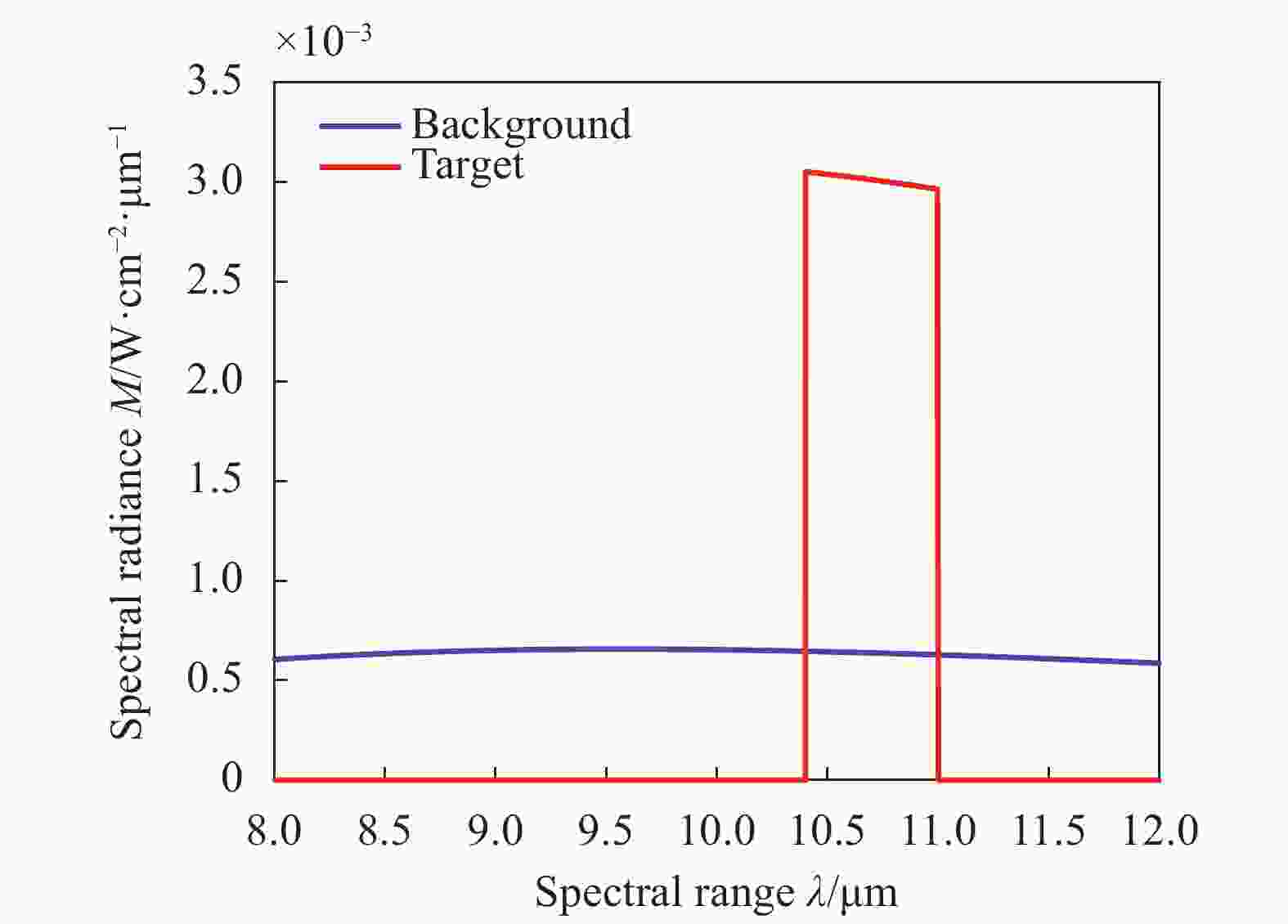
图 4 目标/背景温差1 K时不同的辐出度光谱曲线
Figure 4. Differrent spectral curve of radiance at target background temperature difference of 1 K
表4为目标/背景光谱特性不同时在不同光学系统下的红外探测信噪比，可以看出，对于温差1 K的目标/背景，在传统光学系统下的信噪比为15.2，而在衍射光学系统下为9.7，信噪比仅下降为原来的1/1.5。因此，基于衍射光学系统，采用非制冷探测器，对地面温差目标仍具有良好的探测性能。
表 4 目标/背景光谱特性不同时不同光学系统下红外探测信噪比
Table 4. Infrared detection SNR under different optical systems when the spectral characteristics of target/background are different
Parameters Value Target/background emissivity 0.93/0.2 Target/background spectral range 10.4-11 μm/8-12 μm Target radiance $\left( {5.75/5.92/6.1} \right) \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ Background radiance $8.08 \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ SNR of infrared detection with traditional optical system 15.2/14/12.9 SNR of infrared detection with diffractive optical system 9.7/10.1/10.5 -
探测系统的等效噪声功率，与探测灵敏度对应，是衡量探测系统性能的主要指标，并适用于微波雷达、毫米波辐射计、射电望远镜、激光雷达、激光通信和红外相机等系统。此节将对比分析电子学系统、激光系统和红外系统的等效噪声功率。
-
在以微波雷达[11]和射电望远镜[12-13]为典型代表的电子学系统中，均采用了本振接收机，主要考虑了热噪声影响。在温度
$T = 300\;{\rm{K}}$ ，热噪声能量$kT = $ $ 4.1 \times {10^{ - 21}}\;{\rm{J}}$ ，其中玻耳兹曼常数$k = 1.38 \times {10^{ - 23}}\;{\rm{J/K}}$ 。微波雷达通常使用窄带信号，信号带宽为其时宽的倒数。为获得最大的探测信噪比，其匹配滤波器的系统接收带宽一般设置为其信号带宽。射电望远镜接收带宽通常较宽，其热噪声信号带宽即为系统接收带宽，为降低热噪声影响，通常也会采用制冷接收机。
设电子学系统接收带宽为
${B_n}$ ，等效噪声功率表达式为${P_{tn}} = kT{B_n}$ ，当射电望远镜${B_n}$ 为4 GHz时，其等效噪声功率为$1.6 \times {10^{ - 11}}\;{\rm{W}}$ 。射电望远镜接收信号时宽为10 ms时，对应的信号带宽为100 Hz，基于此可根据需要对4 GHz带宽射电信号进行窄带滤波处理，降低等效噪声功率。增加信号时宽，可增加输入信号能量，利用更窄的滤波带宽降低等效噪声功率，有助于目标和背景信号分离并提高探测性能。
-
在激光雷达和激光SAR[14]中，主要需考虑散弹噪声的影响。以波长
$10.8\;{\text{μm}}$ 的激光雷达为例，散弹噪声$h\nu = 1.8 \times {10^{ - 20}}\;{\rm{J}}$ （单光子能量），其中普朗克常量$h = $ $ 6.63 \times {10^{ - 34}}\;{\rm{J}} \cdot {\rm{s}}$ ，$\nu $ 为激光频率。传统的直接探测激光雷达，其探测灵敏度在100个光子水平，近年来也出现了基于单光子计数的直接探测高灵敏度激光雷达。激光也属于窄带信号，其信号带宽通常为其时宽的倒数，为获得最大的探测信噪比，匹配滤波时的系统接收带宽通常也设置为其信号带宽。设激光系统接收带宽为
${B_n}$ ，等效噪声功率表达式为${P_{sn}} = h\nu {B_n}$ ，当信号时宽为0.25 ns，对应的${B_n}$ 为4 GHz时，其等效噪声功率为$7.3 \times {10^{ - 11}}\;{\rm{W}}$ ；当信号时宽为10 ms，对应带宽为100 Hz时，其等效噪声功率为$1.8 \times {10^{ - 18}}\;{\rm{W}}$ 。通常条件下，激光信号的线宽在10 kHz量级，${B_n}$ 也在10 kHz量级，此时其等效噪声功率为$1.8 \times {10^{ - 16}}\;{\rm{W}}$ 。相比直接探测激光雷达，基于激光本振的相干探测激光雷达技术近年得到快速发展，其探测灵敏度已远优于1个光子。2014年，美国Montana州立大学进行了微弱回波合成孔径激光雷达SAL成像实验，证明SAL可在分辨单元回波能量接近单光子的情况下进行相干成像[15]，其图像信噪比在0 dB水平，假定其相干成像用了100个脉冲，目标的单脉冲信噪比在–20 dB量级。该实验从一个方面表明了相干探测具有良好的微弱信号探测能力，其探测灵敏度已远优于单光子探测器。此外，近年发展起来的相干探测激光通信技术[16]，已明确了其探测灵敏度可大幅提高的结论。
通常激光本振功率可设置得足够高（在mW量级），这使得接收端仅受限于量子噪声且容易实现窄带滤波[17]，由此可获得较高的探测灵敏度。由于工作波段接近，基于激光本振的探测技术很值得红外相机系统借鉴。
-
对于红外相机系统，其等效噪声功率可由探测器噪声电压和响应度表示如下：
$${P_N} = \frac{{{V_N}}}{{R'}}$$ (12) 将公式(1)中的响应度公式代入可得：
$${P_N} = \frac{{{{\left( {{A_d}/\left( {2{t_{{\rm{int}} 2}}} \right)} \right)}^{1/2}}}}{{{D^*}}}$$ (13) 对于中心波长为
$10.8\;{\text{μm}}$ ，光谱宽度为$4\;{\text{μm}}$ 的红外信号，其所对应的带宽约为10300 GHz；当光谱宽度为$0.2\;{\text{μm}}$ ，其所对应的带宽约为500 GHz。红外信号是宽带噪声信号，不同的光谱宽度对应的红外信号能量不同。光谱宽度相差20倍，对应的信号能量也相差20倍，但由于${D^*}$ 不随光谱范围变化，红外相机的等效噪声功率也不随光谱范围变化。当积分时间（信号时宽）为10 ms，由上式知此时的等效噪声功率为
$6.8 \times {10^{ - 12}}\;{\rm{W}}$ ，适当增大积分时间，可增加信号能量进一步减少其等效噪声功率。表5给出了不同系统中不同时宽对应的等效噪声功率，可以看出，与信号时宽为10 ms激光窄带系统相比，信号时宽为10 ms的红外系统的等效噪声功率要高出4个数量级。表 5 不同系统中的等效噪声功率
Table 5. Equivalent noise power in different systems
Signal time width Equivalent noise power Electronics system 0.25 ns $1.6 \times {10^{ - 11}}\;{\rm{W}}$ Laser system 0.25 ns $7.3 \times {10^{ - 11}}\;{\rm{W}}$ 10 ms $1.8 \times {10^{ - 16}}\;{\rm{W}}$ Infrared system 10 ms $6.8 \times {10^{ - 12}}\;{\rm{W}}$ 红外系统的等效噪声功率较高的原因，是由于红外探测器是一个光电转换器件，其性能最终还是在电子学表征，目前有限的电子学带宽，会对宽带红外信号探测产生影响。从具体分析看，在光谱宽度
$0.2\;{\text{μm}}$ 条件下，其所对应的信号带宽约为500 GHz，远大于积分时间10 ms对应的100 Hz信号带宽，光电转换后当电子学带宽有限如4 GHz时，频谱严重混叠大幅提高了噪声信号的功率谱密度，并大幅降低了100 Hz窄带滤波的效果。显然，有限的电子学带宽和严重的红外信号频谱混叠，是红外相机等效噪声功率高的主要原因。假定以时宽为10 ms的激光窄带系统等效噪声功率作为红外相机探测灵敏度参考，目前红外相机探测性能的改善，还有很大空间。除了采用制冷型探测器，目前提升其探测灵敏度的另一个方法就是引入激光本振信号，去除宽带红外信号的频谱混叠。
借鉴相干激光雷达和射电望远镜探测方式，在红外相机接收系统中引入激光本振，基于光纤耦合的单元探测器原理框图如图5所示：
图 5 激光本振单元探测器原理框图
Figure 5. Principle block diagram of the laser local oscillator unit detector
该激光本振为中心波长可调谐的激光种子源，其可调谐的光谱宽度为
$0.2\;{\text{μm}}$ ，通过对激光本振的波长步进调整，可对宽谱段红外信号在电子学频域实现无混叠的范围选通，同时等效细分红外光谱。假定电子学带宽在4 GHz量级（对应的光谱范围是1.5 nm），当波长步进为1.5 nm时，通过本振波长步进调谐完成$0.2\;{\text{μm}}$ 光谱范围覆盖约需125次，再通过非相干积累提升宽谱段红外信号能量对应的信噪比。对于阵列探测器，目前有空间光路混频和基于光纤阵列网络混频两种方式可供选择。空间光路混频结构简单但容易引入较大的空间相差使得混频效率低，为此，一种考虑是采用带有激光本振耦合器的光纤阵列结构，使用多个红外波段的激光单元探测器拼接形成阵列探测器，此处的探测器为平衡探测器；另一种考虑是将激光相控阵[18-19]中的光波导馈电网络与阵列探测器耦合，引入激光本振信号后对每个探测单元都实施光电探测，显然这是一个新型的红外阵列探测器。
当红外信号光谱宽度为
$0.2\;{\text{μm}}$ ，假定引入激光本振实施光电探测后在电子学频域无混叠条件下可将红外信号的带宽控制在4 GHz （对应的光谱范围为1.6 nm），原理上可降低红外等效噪声功率125倍，达到$2.7 \times {10^{ - 15}}\;{\rm{W}}$ ，进一步利用数字信号处理实施窄带滤波，即可使红外等效噪声功率与激光窄带系统接近。红外等效噪声功率的降低可增大
${D^*}$ ，假定实际工作中可将红外等效噪声功率降低20倍，${D^*}$ 即可增大20倍，由此可弥补目标/背景辐出度光谱特性相同时引入衍射光学系统所带来的信号能量损失，提高探测信噪比SNR。上述方法的本质是细分红外信号光谱，将光学不便实现的纳米分辨率光谱分光，转到电子学频域实现。该方法可大幅降低红外等效噪声功率，其高的光谱分辨率也为目标和背景信号分离提供了有利条件，同时为提高非制冷红外相机探测性能提供了新的技术途径。
值得说明的是，对地观测时地物背景辐射对等效噪声功率的影响较大，通过细分光谱可大幅减少其影响，但同时也可能会降低目标信号能量，实际应用中应考虑联合处理目标不同的光谱信息，避免探测性能损失，如通过对不同光谱获取的图像进行非相干累积，提高图像中目标检测所需的信噪比。
-
基于衍射光学系统，文中分析了对地观测红外相机的目标探测性能，给出了一个非制冷红外相机信噪比计算示例。研究表明当地物背景和目标光谱特性不同时，红外相机的目标探测性能不会因为衍射光学系统的使用而大幅下降，基于衍射光学系统的红外相机仍可能具有良好的目标探测性能。
文中将红外相机等效噪声功率与激光和电子学系统进行对比，其在红外系统引入激光本振结合电子学滤波细分红外光谱降低等效噪声功率的方法，为提高非制冷红外相机探测性能提供了新的技术途径。目前光电探测器的电子学带宽在不断扩大（已超过40 GHz），有利于文中激光本振红外探测器的技术实现，持续开展相关研究工作具有重要意义。
Target detection performance of infrared spectrum with diffractive optical system
-
摘要: 衍射光学系统具有大口径轻量化的优点，但其光谱范围较窄，能利用的红外信号能量较小，通常认为采用后会使红外相机的探测信噪比降低。基于衍射光学系统，分析了对地观测红外相机的目标探测性能，结合一个非制冷红外相机信噪比计算示例，明确了在地物背景和目标光谱特性不同的条件下，基于衍射光学系统的红外相机仍可能具有良好的目标探测性能。同时将红外相机等效噪声功率与激光和电子学系统进行对比，提出了红外探测系统的性能还可能进一步提高的观点，给出了一种引入激光本振结合电子学滤波细分红外光谱降低等效噪声功率的方法。Abstract: The diffractive optical system has the advantages of large diameter and light weight, but its spectral range is narrow and the infrared signal energy that can be used is small. Therefore, it is generally believed that the detection signal to noise ratio (SNR) of the infrared camera will be reduced when it is adopted. Based on the diffractive optical system, the target detection performance of the ground observation infrared camera was analyzed, combined with an example of the calculation of the SNR of the uncooled infrared camera, the viewpoint that infrared cameras based on diffractive optical systems may still have good target detection performance was clarified when the spectral characteristics of ground object background and target were different. Meanwhile, the equivalent noise power of the infrared camera was compared with the laser and the electronic system. As a conclusion, the viewpoint that the performance of the infrared detection system may be further improved was proposed, and a method of introducing the laser local oscillator combined with the electronic filter which can subdivide infrared spectrum to reduce equivalent noise power was given.
-
图 1 衍射光学系统红外相机系统光路示意图
Figure 1. Optical path diagram of infrared camera system based on diffractive optical system
图 2
$\lambda T$ 取不同范围时黑体相对辐出度函数图。(a)$\lambda T$ 取全部范围；(b)$\lambda T$ 取2.4×103~3.6×103 μm·K；(c)$\lambda T$ 取$0\sim 1.5 \times {10^3}\;{\text{μm}} \cdot {\rm{K}}$ Figure 2. Graph of relative radiant exitance function of black-body when
$\lambda T$ takes different ranges. (a)$\lambda T$ takes entire range; (b)$\lambda T$ takes 2.4×103-3.6×103 μm·K ; (c)$\lambda T$ takes 0-1.5×103 μm·K
图 3 目标/背景温差1 K时相同的辐出度光谱曲线
Figure 3. Same spectral curve of radiance at target/background temperature difference of 1 K
图 4 目标/背景温差1 K时不同的辐出度光谱曲线
Figure 4. Differrent spectral curve of radiance at target background temperature difference of 1 K
图 5 激光本振单元探测器原理框图
Figure 5. Principle block diagram of the laser local oscillator unit detector
表 1
${D^*}$ 计算相关参数Table 1. Relevant parameters for calculating
${D^*}$ Parameters Value Parameters Value Conversion factor $K$ 0.7 F number of optical systems 1 Grass background temperature in Summer ${T_B}$ 303 K Detector peak wavelength ${\lambda _p}$ $10.8\;{\text{μm}}$ First radiation constant ${c_1}$ $3.741\;5 \times {10^8}\;{\rm{W}} \cdot \;{{\text{μm}}^4} \cdot \;{{\rm{m}}^2}$ Second radiation constant ${c_2}$ $1.438\;8 \times {10^4}{\text{μm}} \cdot \;{\rm{K}}$ Optical system transmittance during testing ${\eta _{0t}}$ 0.6 Background emissivity 0.93 Noise equivalent temperature difference $NETD$ $40 \times {10^{ - 3}}\;{\rm{K}}$ Integration time during testing ${t_{{\rm{int}} 1}}$ $34.56 \times {10^{ - 6}}\;{\rm{s}}$ Detector pixel area ${A_d}$ ${\left( {14 \times {{10}^{ - 6}}} \right)^2} \times {10^4}\;{\rm{c}}{{\rm{m}}^2}$ Detector specific detectivity ${D^*}$ $5.{\rm{4}} \times {10^{10}}\;{\rm{cm}} \cdot \;{\rm{H}}{{\rm{z}}^{1/2}} \cdot \;{{\rm{W}}^{ - 1}}$ 
下载: 导出CSV
表 2 系统参数
Table 2. System parameters
Parameters Value Parameters Value Signal extraction factor $\delta $ 0.707 Number of pixels occupied by the vehicle target on the focal plane ${N_t}$ 1 Atmospheric transmittance ${\tau _a}$ 0.75 Optical system aperture ${D_0}$ 100 mm Optical system transmittance ${\eta _0}$ 0.6 Optical system entrance pupil area ${A_0}$ $79 \times {10^{ - 4}}\;{{\rm{m}}^2}$ Integration time in actual work ${t_{{\rm{int}} 2}}$ $10 \times {10^{ - 3}}\;{\rm{s}}$ Target effective radiation area ${A_t}$ $4 \times {10^4}\;{\rm{c}}{{\rm{m}}^2}$ Background surface temperature 303 K Target surface temperature 304/306/308 K Detection range R 15 km Detector specific detectivity ${D^*}$ $1.4 \times {10^9}\;{\rm{cm} } \cdot \;{\rm{H} }{ {\rm{z} }^{1/2} } \cdot \;{ {\rm{W} }^{ - 1} }$
下载: 导出CSV
表 3 目标/背景光谱特性相同时不同光学系统下红外探测信噪比
Table 3. Infrared detection SNR under different optical systems when the spectral characteristics of target/ background are same
Parameters Value Target/background emissivity 0.93/0.93 Target/background spectral range 8-12 μm Target radiance $\left( {3.82/3.94/4.06} \right) \times {\rm{1}}{{\rm{0}}^{{\rm{ - 3}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ Background radiance $3.75 \times {\rm{1}}{{\rm{0}}^{{\rm{ - 3}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ SNR of infrared detection with traditional optical system 3.9/11.9/20 SNR of infrared detection with diffractive optical system 0.19/0.55/0.92
下载: 导出CSV
表 4 目标/背景光谱特性不同时不同光学系统下红外探测信噪比
Table 4. Infrared detection SNR under different optical systems when the spectral characteristics of target/background are different
Parameters Value Target/background emissivity 0.93/0.2 Target/background spectral range 10.4-11 μm/8-12 μm Target radiance $\left( {5.75/5.92/6.1} \right) \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ Background radiance $8.08 \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\;{\rm{W}} \cdot {\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{s}}{{\rm{r}}^{ - 1}}$ SNR of infrared detection with traditional optical system 15.2/14/12.9 SNR of infrared detection with diffractive optical system 9.7/10.1/10.5
下载: 导出CSV
表 5 不同系统中的等效噪声功率
Table 5. Equivalent noise power in different systems
Signal time width Equivalent noise power Electronics system 0.25 ns $1.6 \times {10^{ - 11}}\;{\rm{W}}$ Laser system 0.25 ns $7.3 \times {10^{ - 11}}\;{\rm{W}}$ 10 ms $1.8 \times {10^{ - 16}}\;{\rm{W}}$ Infrared system 10 ms $6.8 \times {10^{ - 12}}\;{\rm{W}}$
下载: 导出CSV
-
[1] Jiao Jianchao, Su Yun, Wang Baohua, et al. Development and application of GEO membrane based diffraction optical imaging system [J]. Space International, 2016, 6: 49-55. (in Chinese) [2] Zhu Jinyi, Xie Yongjun. Large aperture lidar receiver optical system based on diffractive primary lens [J]. Infrared and Laser Engineering, 2017, 46(5): 0518001. (in Chinese) doi: 10.3788/IRLA201746.0518001 [3] Hu Xuan, Li Daojing. Space-based synthetic aperture LiDAR system with 10 m diffractive aperture [J]. Chinese Journal of Lasers, 2018, 45(12): 0510010. (in Chinese) [4] Li Daojing, Hu Xuan, Zhou Kai, et al. Synthetic aperture Lidar imaging detection based on conformal diffractive optical system [J]. Acta Optical Sinica, 2020, 40(4): 0428001. (in Chinese) [5] Ren Zhibin, Hu Jiasheng, Tang Honglang, et al. Study on chromatic aberration correction of 10 meter large aperture membrane diffractive primary lens [J]. Acta Optica Sinica, 2017, 46(4): 422004. (in Chinese) [6] Wang Bingxue, Zhang Qiheng, Chen Changbin, et al. A mathematical model for operating range of a staring IR search and track system [J]. Opto-Electronic Engineering, 2004, 031(7): 8-11. (in Chinese) [7] 况耀武. 红外/激光双模导引头光学系统设计研究[D]. 哈尔滨工业大学, 2009. Kuang Yaowu. Study on the optical system of dual-mode infrared/laser seeker[D]. Harbin: Harbin Institute of Technology, 2009. (in Chinese) [8] Luo Zhenying, Bai Lu, Ning Hui, et al. Analysis of operating range of infrared detection system based on NETD [J]. Infrared, 2017, 38(5): 27-30. (in Chinese) doi: 10.3969/j.issn.1672-8785.2017.05.005 [9] Wu Limin, Zhou Feng, Wang Huaiyi. Study on the relationship between the infrared detectors background limit detectivity and the optical systems work temperature [J]. Spacecraft Recovery & Remote Sensing, 2010, 31(1): 36-41. (in Chinese) doi: 10.3969/j.issn.1009-8518.2010.01.006 [10] Wang Xiaojian, Liu Yang, Chen Lei, et al. Discussion on the operation range of the infrared imaging system for point target expressed by NETD and ΔT [J]. Infrared and Laser Engineering, 2008, 37(S2): 2. (in Chinese) [11] Skolnik M I. Radar Handbook[M]. New York: The McGraw-Hill Companies Inc, 2010. [12] Nan Rendong, Jiang Peng. 500 m aperture spherical radio telescope (FAST) [J]. Journal of Mechanical Engineering, 2017, 53(17): 1-3. (in Chinese) [13] EVN and Global VLBI results and images[EB/OL]. [2019-12-13]. http://old.evlbi.org/gallery/images.html. [14] Li Daojing, Du Jianbo, Ma Meng, et al. System analysis of spaceborne aperture ladar [J]. Infrared and Laser Engineering, 2016, 45(11): 262-269. (in Chinese) [15] Barber Z W, Dahl J R. Synthetic aperture ladar imaging demonstrations and information at very low return levels [J]. Applied Optics, 2014, 53(24): 5531-5537. doi: 10.1364/AO.53.005531 [16] Ke X, Chen J. Experimental investigation on non-optical heterodyne detection technology of 1 km atmospheric laser communication system [J]. Journal of Applied Sciences, 2014(4): 7. [17] 王海. 相干光通信零差BPSK系统的设计[D]. 电子科技大学. Wang Hai. Design of a homodyne BPSK system for coherent optical communication[D]. Chengdu: University of Electronic Science and Technology of China, 2009. [18] Yaacobi A, Sun J, Moresco M, et al. Intergrated phased array for wide-angle beam steering[J]. Optics Letters, 2014, 39(15): 4575-4578. [19] Jie Sun, Erman Timurdogan, Ami Yaacobi, et al. Large-scale nanophotonic phased array [J]. Nature, 2013, 493.7431: 195-199. -
点击查看大图
计量
- 文章访问数: 331
- HTML全文浏览量: 165
- PDF下载量: 50
- 被引次数: 0
