-
以目标识别为代表的合成孔径雷达（SAR）图像解译在军事领域广泛运用[1-3]。高频区目标后向散射特性可等效为若干局部现象的叠加效应，即散射中心[4]。散射中心对于SAR图像的分析具有重要意义[5-6]。早期，研究人员主要利用峰值特征描述SAR图像中目标的局部散射特性。但峰值特征参数有限（仅包括位置和相对强度），不能有效反映目标的局部结构等信息。随着电磁散射建模理论的发展，研究人员提出更为精细化的参数模型，如GTD模型[7]、属性散射中心模型[8]等。然而，这类模型的形式复杂，给正确参数估计带来了挑战。参考文献[8-11]针对属性散射中心参数估计进行研究，主要通过图像域解耦这种“分治”策略实现单个散射中心由强到弱的序惯估计，避免了复杂度极高的全局优化问题。随着压缩感知技术的发展[12-13]，基于稀疏表示的算法也在散射中心参数估计中得以运用[14-15]。相比传统图像域估计算法，稀疏表示算法避免了图像域的处理过程、总体效率更高。然而，稀疏表示算法本身没有在图像域考察散射中心的分布规律，使得参数估计过程失去了一定的物理意义。稳健估计散射中心参数对于SAR图像的分析及解译具有重要意义[16-18]。参考文献[17-18]就是基于属性散射中心设计匹配策略，其研究结果也验证了属性散射中心对于实现稳健SAR目标识别的重要作用。
参考文献[9]验证了粒子群优化算法[19]对于属性散射中心参数估计的积极作用。为进一步提高属性散射中心参数估计精度，文中引入狼群优化算法。按照传统图像域“分治”的序惯估计算法，在单个属性散射中心参数估计时运用狼群优化算法获得最佳估计参数。狼群优化算法是由吴虎胜等在2013年设计提出[20]，通过分析自然界中狼群的协作捕猎集猎物分配等行为，抽象出3种人工狼，探狼游走、头狼召唤、猛狼围攻3种智能行为以及“胜者为王”的头狼角逐规则、“优胜劣汰”的狼群2种更新规则，并基于马尔可夫链理论证明了算法收敛性。狼群算法是一种新的智能群优化算法，在全局搜索和局部开发能力上具有良好的表现。近年来，狼群算法在智能决策、图像处理等领域得到广泛运用并验证了其有效性[21-23]。因此，通过在单个散射中心估计过程中运用狼群算法可提高估计精度。为了验证所提方法的有效性，基于MSTAR数据集开展实验，分别在原始SAR图像以及噪声干扰条件下进行测试。实验结果表明了所提方法的有效性以及对于噪声干扰的稳健性。
-
属性散射中心模型是描述高频区目标局部后向散射特性的一种代表性参数模型[4-5]。因其类别丰富、物理意义清晰的属性参数而在SAR目标识别中得到广泛运用。属性散射中心模型参数化形式如下：
$$ \begin{split} {E_i}(f,\phi ;{\theta _i}) = &{A_i} \cdot {\left( {j\frac{f}{{{f_c}}}} \right)^{{\alpha _i}}} \cdot \exp \left( {\frac{{ - j4\pi f}}{c}({x_i}\cos \phi + {y_i}\sin \phi )} \right)\cdot \\ & {\text{sinc}}\left( {\frac{{2\pi f}}{c}{L_i}{\text{sin}}(\phi - \overline {{\phi _i}} )} \right) \cdot {\rm{exp( - 2}}\pi f{\gamma _i}{\rm{sin}}\phi {\rm{)}} \\ \end{split} $$ (1) 式中：
$f$ 代表电磁波频率；$\phi $ 为入射波与目标的相对方位角；$\theta = \{ {\theta _i}\} = [{A_i},{\alpha _i},{x_i},{y_i},{L_i},\overline {{\phi _i}} ,{\gamma _i}](i = 1,2, \cdots ,P)$ 为目标上P个散射中心的属性参数集；${A_i}$ 代表相对幅度；${x_i},{y_i}$ 位散射中心的位置；${\alpha _i}$ 表示频率依赖因子；${L_i}$ 和$\overline {{\phi _i}} $ 分别对应分布式散射中心的长度和方向角；${\gamma _i}$ 表示局部式散射中心的方位依赖性参数。目标整体的后向散射场可等效于P个散射中心的叠加效应，如公式（2）所示：
$$E(f,\phi ;\theta ) = \sum\limits_{i = 1}^P {{E_i}(f,\phi ;{\theta _i})} $$ (2) 属性散射中心参数描述了与目标局部相关联的若干特性，对于SAR图像中目标特性的分析具有重要意义。
-
SAR图像的属性散射参数估计问题即求解目标的属性散射中心集，获得各个散射中心的参数。对于观测得到的SAR数据
$D(f,\phi )$ ，可在属性散射中心模型的基础上对其进行建模如下：$$D(f,\phi ){\rm{ = }}E(f,\phi ;\theta ){\rm{ + }}N(f,\phi )$$ (3) 式中：
$N(f,\phi )$ 表示噪声分量，可采用高斯分布进行建模分析。在此基础上，散射中心参数集的极大似然估计可表达为：$${\hat \theta _{ML}} = \arg \mathop {\min }\limits_\theta ||D - E(\theta )|{|^2}$$ (4) 公式（4）给出了所有散射中心联合参数估计的整体形式。然而，从公式（1）中也可以看出，属性散射中心模型的形式十分复杂。此外，一个目标往往涉及多个位置、强弱、结构不同的散射中心。这种条件下，公式（4）中的目标函数往往是非凸的，难以获得可靠解。并且，这种涉及大量参数的优化过程极其复杂，效率十分低下。为此，研究人员根据散射中心在图像域的分布特点提出图像域解耦算法，实现“分治”估计。在SAR图像上，散射中心呈现局部亮斑特点，可采用图像分割算法实现单个散射中心数据的分离。在此基础上，即可按照由强至弱的顺序实现各个散射中心的参数估计。
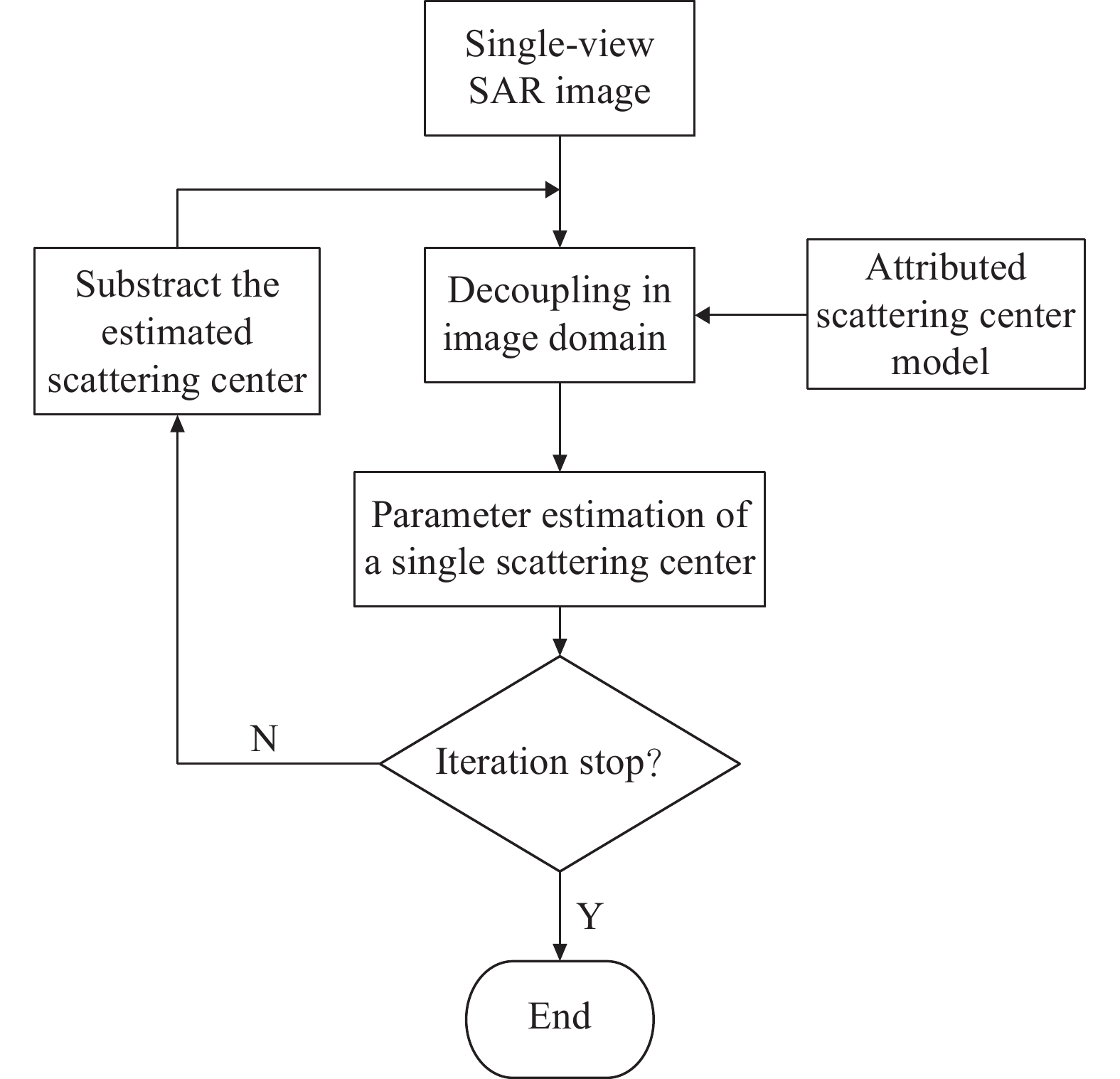
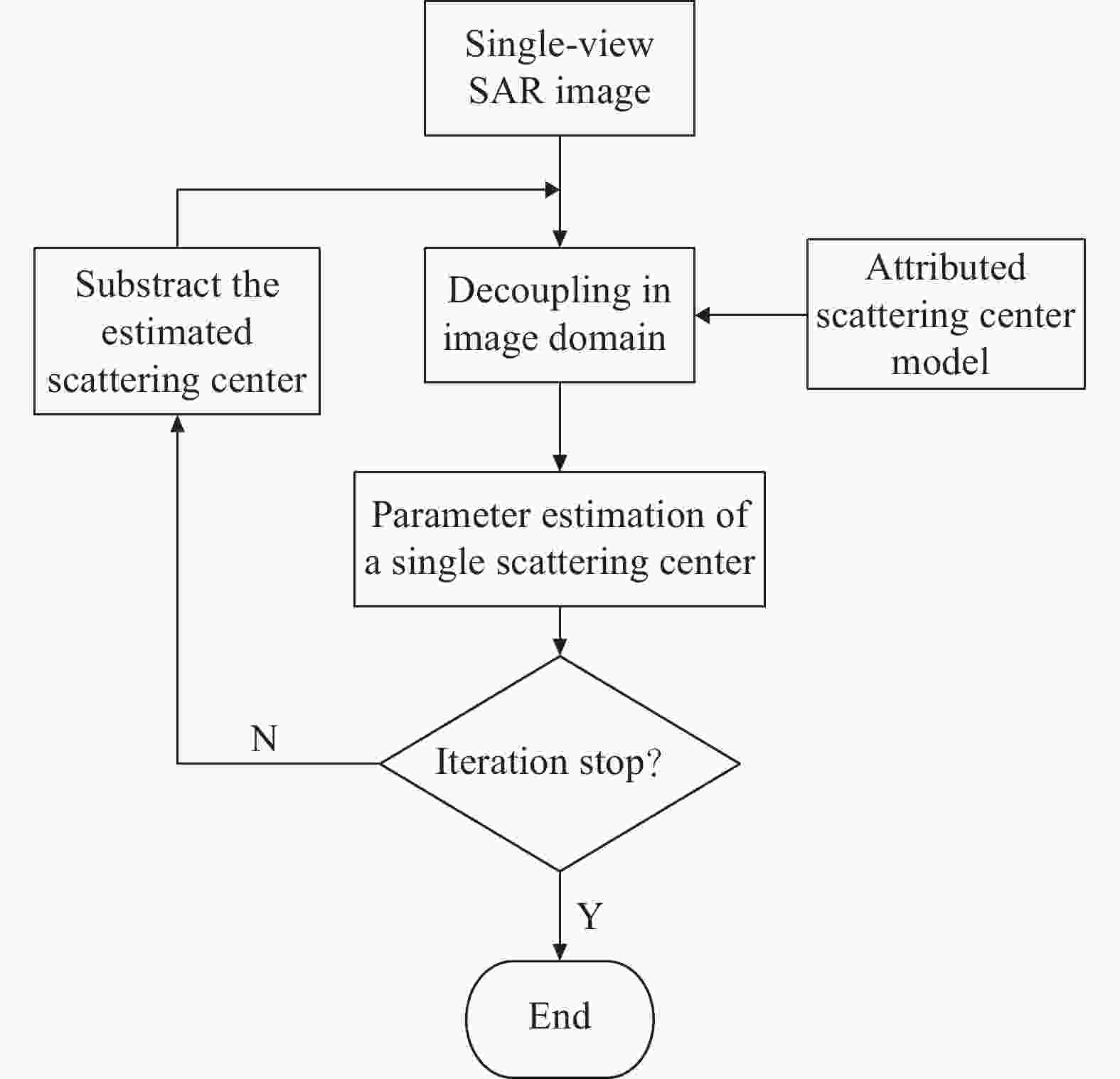
根据上述思想，图像域解耦的属性散射中心参数估计算法可描述为图1所示的基本流程，其中涉及5个关键步骤[8-9]：（1）局部图像分割，获得图像中的局部高能量区域，代表性方法是分水岭算法；（2）模型定阶：明确图像中散射中心的上限，作为迭代优化的一个终止条件；（3） 结构选择，明确当前散射中心为分布式或局部式；（4）参数初值求解，为单个散射中心提供参数初值；（5） 参数优化：通过优化算法对参数初值进行迭代，获得最佳参数。
图 1 图像域解耦的属性散射中心估计基本流程
Figure 1. Basic procedure of attributed scattering center estimation via image decoupling
-
狼群算法主要包括探狼游走、头狼召唤、猛狼围攻3种智能行为；“胜者为王”的头狼角逐规则以及“优胜劣汰”的狼群更新规则[20-23]。由于属性散射中心参数估计可等效为一个最小值优化过程，故以最小值优化描述狼群算法的主要步骤如下：
步骤1：初始化狼群的空间坐标，根据目标函数值角逐出人工头狼；
步骤2：探狼开始随机游走搜索猎物，若某个位置的目标函数值小于头狼的目标函数值，则更新头狼位置并发出召唤行为；若没有发现，探狼继续游走直至最大游走次数，头狼在原本位置发出召唤行为；
步骤3：听到召唤的猛狼以较大步长向头狼奔袭，若途中猛狼的目标函数值小于头狼的目标函数值，则更新头狼位置；否则，猛狼继续奔袭直至进入围攻范围；
步骤4：靠近头狼的猛狼与探狼仪器对猎物（头狼位置视）进行围捕。过程中若其他人工狼的目标函数值小于头狼的目标函数值，则更新头狼位置，直到捕获猎物；
步骤5：淘汰狼群中目标函数值较大的人工狼，并通过随机生成新的人工狼实现狼群更新；
步骤6：判断头狼的目标函数值是否达到精度要求或是否达到最大迭代次数，倘未达到，则从探狼游走开始继续迭代；若达到，则输出头狼的空间坐标及相应目标函数值，获得优化结果。
狼群算法中主要涉及游走步长
${\rm{ste}}{{\rm{p}}_a}$ ，奔袭步长${\rm{ste}}{{\rm{p}}_b}$ 以及攻击步长${\rm{ste}}{{\rm{p}}_c}$ 参数，计算方式如下：$${\rm{step}}_a^d = {\rm{step}}_b^d/2 = 2 \times {\rm{step}}_c^d = \left| {\mathop {\max }\limits_d - \mathop {\min }\limits_d } \right|/S$$ (5) 式中：
$\mathop {\max }\limits_d $ 、$\mathop {\min }\limits_d $ 分别对应狼群在第d维坐标的最大和最小值；S表示步长因子。在狼群算法中，探狼的游走行为主要反映了算法的全局搜索能力，猛狼的围攻行为则体现了算法的局部开发能力。“优胜劣汰”的狼群更新机制确保了人工狼的多样性，从而避免算法陷入局部最优解。“胜者为王”的头狼产生机制引导整个狼群算法在求解过程朝着有利的方向进行。因此，狼群算法能够较好地兼顾对解空间的全局搜索和局部开发，具备良好的优化求解能力。
文中将狼群优化算法引入属性散射中心参数估计中。在图1流程中的“单个散射中心参数估计”阶段采用狼群算法对单个散射中心的属性参数进行迭代优化，获得最佳的参数结果。按照图像由强到弱的解耦过程中，实现单个散射中心的序惯参数估计，获得整个SAR图像的属性散射中心集。
-
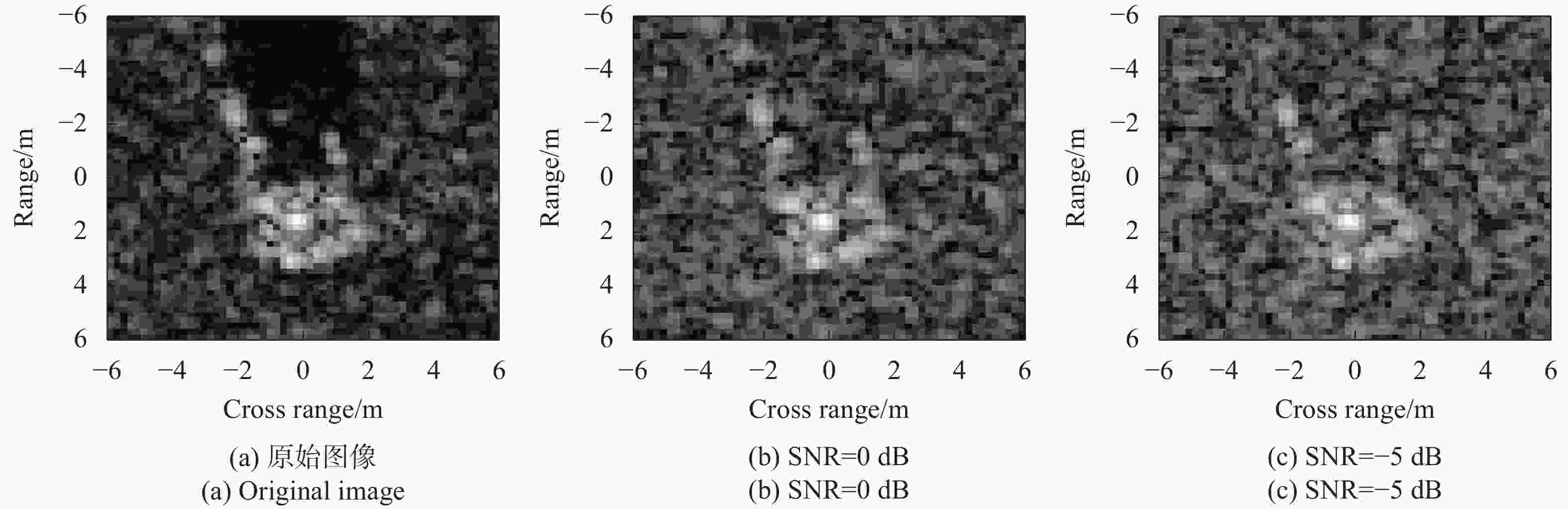
采用MSTAR数据集对所提参数估计算法进行验证及分析。该数据集包含10类地面车辆目标X波段HH极化下的机载SAR图像，距离和方位分辨率均达到0.3 m。MSTAR数据集中的原始SAR图像多采集自高信噪比（SNR）条件，为测试所提方法在噪声干扰条件下的识别性能，按照参考文献[17]中方法对原始图像进行不同程度的噪声条件，获得不同信噪比下的可用测试样本。具体地，以原始SAR图像能量为参照，根据预设的信噪比构造加性高斯白噪声，然后添加到原始图像中获得相应的噪声样本。图2显示了原始SAR图像及其两个不同信噪比下的结果，可以看出噪声干扰下目标区域及散射中心特征受到了一定影响，给正确参数估计造成障碍。
图 2 原始MSTAR图像及构造的噪声样本
Figure 2. Original MSTAR image and generated noisy samples
-
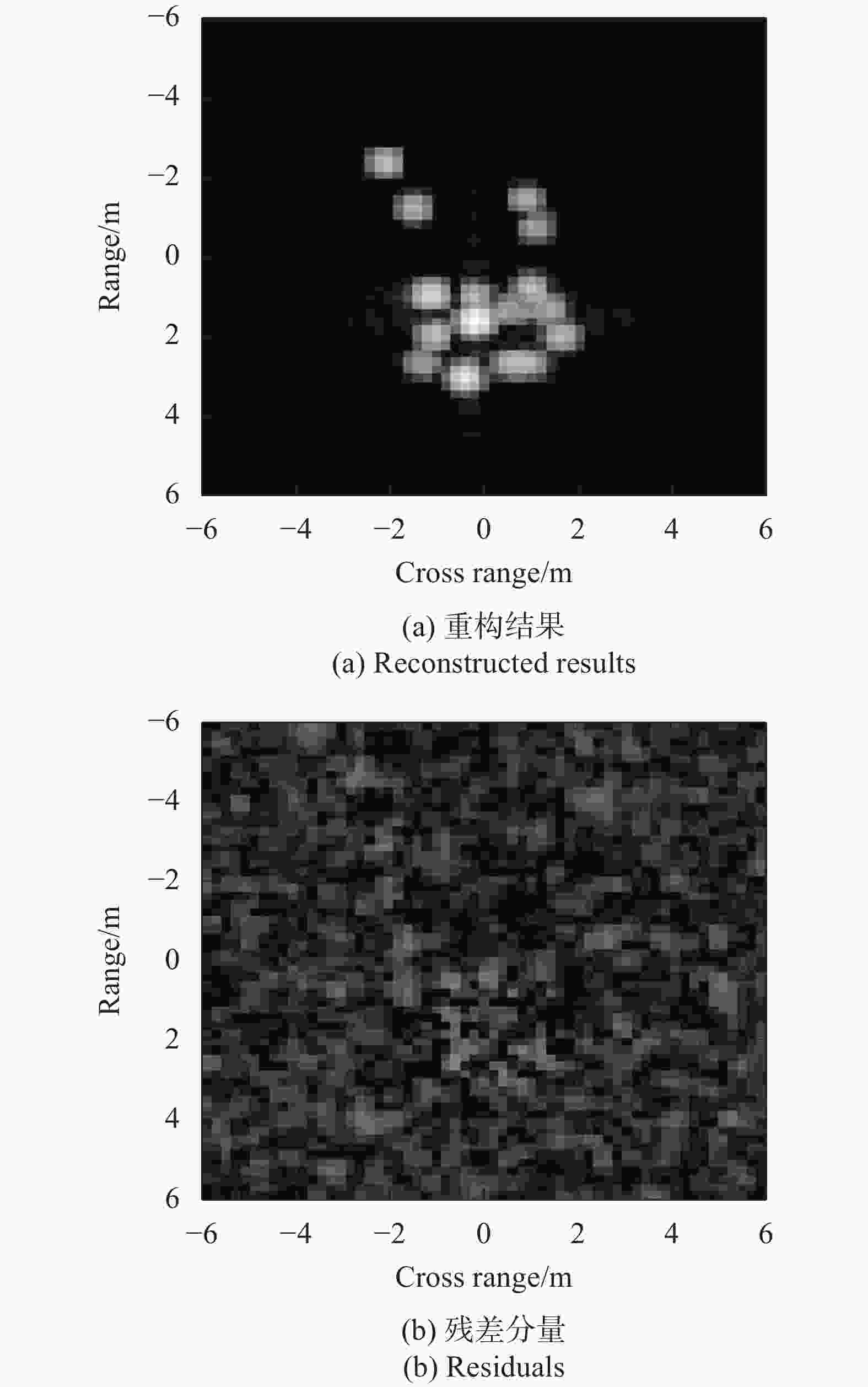
首先基于MSTAR原始图像进行参数估计。以图2（a）中的SAR图像为输入，采用所提方法估计得到的参数集如表1所示，其中相对幅度参数仅列出绝对值。在具体实施中，设置散射中心的数目上限为15，故相应获得由强到弱的15个散射中心的属性参数。从表中可以看出，该图像中目标既包含了分布式散射中心又包含了局部式散射中心。图3将估计得到的位置参数投影到原始SAR图像上，直观可见估计结果与图像上的局部强散射点具有良好的一致性。这一结果表明位置参数的估计精度较高。图4显示了基于估计散射中心集的重构结果以及最终的分解残差。从图4（a）可以看出，基于所提方法的重构结果有效保留了原始SAR图像中的目标成分，如散射中心分布规律、外形尺寸等。从图4（b）可以看出，分解残差多为背景杂波及噪声成分，反映了所提方法能够通过稳健的狼群算法剔除杂波、噪声带来的不良影响。
表 1 原始SAR图像的参数估计结果
Table 1. Parameter estimation results of the original SAR image
Index $A$ ${x_p}/{\rm{m} }$ ${y_p}/{\rm{m} }$ ${L_p}/{\rm{m} }$ $\alpha $ ${\gamma _p}$ ${\phi _p}$ 1 474.68 −0.95 7.78 0.00 1.00 0.00 0.00 2 342.72 −1.73 14.85 0.00 1.00 −0.16 0.00 3 921.02 −3.86 4.81 5.05 1.00 0.00 0.41 4 207.27 4.65 4.30 0.00 0.00 0.00 0.00 5 202.58 −0.29 13.10 4.27 1.00 0.00 0.85 6 173.25 7.74 10.01 0.00 0.00 0.00 0.00 7 168.74 −7.53 −5.93 0.00 1.00 0.00 0.00 8 168.17 −10.20 −11.21 0.00 0.00 0.00 0.00 9 151.65 −5.00 9.77 0.00 1.00 0.00 0.00 10 130.78 4.47 11.42 0.00 1.00 −0.18 0.00 11 115.22 5.60 13.17 0.00 1.00 −0.19 0.00 12 110.69 −6.28 13.03 0.00 0.00 0.00 0.00 13 106.40 5.06 −3.78 0.00 1.00 −0.19 0.00 14 94.21 0.62 2.14 0.00 0.00 1.02 0.00 15 89.32 −10.94 −14.31 0.00 1.00 −0.19 0.00 
图 3 散射中心位置在原始SAR图像上的投影
Figure 3. Projection of positions of scattering centers onto the original image
图 4 基于估计散射中心的重构结果及残差分量
Figure 4. Reconstructed results and residuals based on the estimated scattering center set
-
真实场景中获得的SAR图像往往伴随着较为严重的噪声干扰。噪声的引入给属性散射中心参数估计带来了挑战。为了测试所提方法在噪声干扰下的性能，采用图2（c）所示的SNR=−5 dB的噪声样本进行测试。表2列出了噪声样本的散射中心集参数估计结果。对比表2与表1的参数估计结果，由于噪声的影响，部分参数，如相对强度以及位置参数均出现了不同程度的变化，但总体上保持稳定性。图5显示了位置参数在噪声图像上的投影结果，仍然能够有效反映目标实际散射中心的分布规律。图6给出了噪声图像的重构结果及残差分量，与原始图像的相应结果保持良好的一致性。因此，在噪声干扰条件下的实验结果表明，文中引入的狼群算法可较为有效地克服噪声影响。
表 2 SNR=−5 dB图像的参数估计结果
Table 2. Parameter estimation results of the noisy SAR image with SNR=−5 dB
Index $A$ ${x_p}/{\rm{m} }$ ${y_p}/{\rm{m} }$ ${L_p}/{\rm{m} }$ $\alpha $ ${\gamma _p}$ ${\phi _p}$ 1 378.70 −1.00 7.93 0.00 0.00 0.00 0.00 2 240.09 −1.87 14.76 0.00 0.00 0.00 0.00 3 161.99 −5.64 4.76 0.00 0.00 2.85 0.00 4 164.57 4.64 4.04 0.00 1.00 0.00 0.00 5 122.81 7.87 9.71 0.00 0.00 2.22 0.00 6 147.56 2.57 13.48 0.00 0.00 0.00 0.00 7 126.69 −0.97 4.78 0.00 1.00 −0.17 0.00 8 123.77 −10.33 −11.67 0.00 0.00 1.64 0.00 9 119.77 −7.43 −5.92 0.00 0.00 0.00 0.00 10 105.84 5.08 12.16 0.00 1.00 0.00 0.00 11 105.50 −5.19 9.74 0.00 1.00 0.00 0.00 12 89.34 0.66 1.98 0.00 0.00 0.00 0.00 13 82.88 −6.69 12.75 0.00 0.00 0.00 0.00 14 76.74 5.60 6.55 4.40 0.00 0.00 0.17 15 67.00 5.02 −4.01 0.00 0.00 2.05 0.00 
图 6 基于估计散射中心的重构结果及残差分量
Figure 6. Reconstructed results and residuals based on the estimated scattering center set
图 5 散射中心位置在SNR=−5 dB噪声图像上的投影
Figure 5. Projection of positions of scattering centers onto the noisy image with SNR=−5 dB
-
文中提出基于狼群算法的SAR图像属性散射中心参数估计方法。对于图像域解耦的单个散射中心，基于狼群算法进行最优属性参数的搜索求解，获得稳健的结果。最终，按照“分治”策略序惯获得所有散射中心的属性参数集。基于MSTAR原始SAR图像及其构造的噪声样本进行所提方法的性能测试。实验结果验证了提出方法的有效性及噪声稳健性。
Parameter estimation of attributed scattering centers in SAR images based on wolf pack algorithm
-
摘要: 针对合成孔径雷达（SAR）图像属性散射中心估计问题，提出基于狼群算法的新思路。方法首先在图像域上对SAR图像进行“分治”解耦。对每一个属性散射中心进行序贯估计时，采用狼群算法作为基础优化算法，获得散射中心最佳的参数集。狼群算法通过分析狼群的协作捕猎活动及猎物分配等特点，具备良好的全局搜索能力和局部开发能力。算法通过结合传统图像域解耦的思想和狼群算法的稳健优化性能，提高SAR图像整体的属性散射中心估计精度。实验中，采用所提方法对MSTAR数据集中的原始SAR图像及加噪样本进行参数估计，实验结果验证了其有效性和噪声稳健性。Abstract: For the attributed scattering center estimation problem of synthetic aperture radar (SAR) images, a new idea based on wolf pack algorithm was proposed. The method first decoupled the SAR image using the “divide and conquer” strategy. Afterwards, the wolf pack algorithm was adopted as the basic optimization method to sequentially estimate individual scattering centers with the optimal parameter sets. By analyzing the characteristics of cooperative hunting activities and prey distribution, the wolf pack algorithm has good global search ability and local development ability. The algorithm combines the traditional image decoupling with the robust estimation capability of wolf pack algorithm. Hence, the estimation precision of the overall SAR image can be improved. In the experiments, the proposed method was tested on the original SAR images and noisy samples based on the MSTAR dataset. The results validate the effectiveness and noise-robustness of the proposed method.
-
图 1 图像域解耦的属性散射中心估计基本流程
Figure 1. Basic procedure of attributed scattering center estimation via image decoupling
图 3 散射中心位置在原始SAR图像上的投影
Figure 3. Projection of positions of scattering centers onto the original image
图 4 基于估计散射中心的重构结果及残差分量
Figure 4. Reconstructed results and residuals based on the estimated scattering center set
图 6 基于估计散射中心的重构结果及残差分量
Figure 6. Reconstructed results and residuals based on the estimated scattering center set
图 5 散射中心位置在SNR=−5 dB噪声图像上的投影
Figure 5. Projection of positions of scattering centers onto the noisy image with SNR=−5 dB
表 1 原始SAR图像的参数估计结果
Table 1. Parameter estimation results of the original SAR image
Index $A$ ${x_p}/{\rm{m} }$ ${y_p}/{\rm{m} }$ ${L_p}/{\rm{m} }$ $\alpha $ ${\gamma _p}$ ${\phi _p}$ 1 474.68 −0.95 7.78 0.00 1.00 0.00 0.00 2 342.72 −1.73 14.85 0.00 1.00 −0.16 0.00 3 921.02 −3.86 4.81 5.05 1.00 0.00 0.41 4 207.27 4.65 4.30 0.00 0.00 0.00 0.00 5 202.58 −0.29 13.10 4.27 1.00 0.00 0.85 6 173.25 7.74 10.01 0.00 0.00 0.00 0.00 7 168.74 −7.53 −5.93 0.00 1.00 0.00 0.00 8 168.17 −10.20 −11.21 0.00 0.00 0.00 0.00 9 151.65 −5.00 9.77 0.00 1.00 0.00 0.00 10 130.78 4.47 11.42 0.00 1.00 −0.18 0.00 11 115.22 5.60 13.17 0.00 1.00 −0.19 0.00 12 110.69 −6.28 13.03 0.00 0.00 0.00 0.00 13 106.40 5.06 −3.78 0.00 1.00 −0.19 0.00 14 94.21 0.62 2.14 0.00 0.00 1.02 0.00 15 89.32 −10.94 −14.31 0.00 1.00 −0.19 0.00 
下载: 导出CSV
表 2 SNR=−5 dB图像的参数估计结果
Table 2. Parameter estimation results of the noisy SAR image with SNR=−5 dB
Index $A$ ${x_p}/{\rm{m} }$ ${y_p}/{\rm{m} }$ ${L_p}/{\rm{m} }$ $\alpha $ ${\gamma _p}$ ${\phi _p}$ 1 378.70 −1.00 7.93 0.00 0.00 0.00 0.00 2 240.09 −1.87 14.76 0.00 0.00 0.00 0.00 3 161.99 −5.64 4.76 0.00 0.00 2.85 0.00 4 164.57 4.64 4.04 0.00 1.00 0.00 0.00 5 122.81 7.87 9.71 0.00 0.00 2.22 0.00 6 147.56 2.57 13.48 0.00 0.00 0.00 0.00 7 126.69 −0.97 4.78 0.00 1.00 −0.17 0.00 8 123.77 −10.33 −11.67 0.00 0.00 1.64 0.00 9 119.77 −7.43 −5.92 0.00 0.00 0.00 0.00 10 105.84 5.08 12.16 0.00 1.00 0.00 0.00 11 105.50 −5.19 9.74 0.00 1.00 0.00 0.00 12 89.34 0.66 1.98 0.00 0.00 0.00 0.00 13 82.88 −6.69 12.75 0.00 0.00 0.00 0.00 14 76.74 5.60 6.55 4.40 0.00 0.00 0.17 15 67.00 5.02 −4.01 0.00 0.00 2.05 0.00
下载: 导出CSV
-
[1] Wu W D, Zhang B, Hong Y F, et al. Design of co-aperture antenna for airborne infrared and synthetic aperture radar [J]. Chinese Optics, 2020, 13(3): 595-604. (in Chinese) [2] Zhang P P, Luo H B, Ju M R, et al. An improved capsule and its application in target recognition of SAR images [J]. Infrared and Laser Engineering, 2020, 49(5): 20201010. (in Chinese) doi: 10.3788/irla.26_invited-zhangpanpan [3] Xu Y, Gu Y, Peng D L, et al. SAR ATR based on disentangled representation learning generative adversarial networks and support vector machine [J]. Optics and Precision Engineering, 2020, 28(3): 727-735. (in Chinese) doi: 10.3788/OPE.20202803.0727 [4] Guo K Y, Yin H C, Sheng X Q. Research on scattering center modeling for radar target [J]. Chinese Journal of Radio Science, 2020, 35(1): 106-115. (in Chinese) [5] Wen G J, Zhu G Q, Yin H C, et al. SAR ATR based on 3D parametric electromagnetic scattering model [J]. Journal of Radar, 2017, 6(2): 115-135. (in Chinese) [6] Ding B Y, Zhong J R, Ma C H, et al. SAR target reconstruction visualization enhancement based on attributed scattering center model [J]. Journal of Radar, 2013, 2(4): 499-506. (in Chinese) [7] Zhan R H, Hu J M, Zhang J. A novel method for parametric estimation of 2D geometrical theory of diffraction model based on compressed sensing [J]. Journal of Electronics & Information Technology, 2013, 35(2): 419-425. (in Chinese) [8] Zhang J K, Ji K F, Xing X W, et al. Feature extraction and analysis of attributed scattering centers on SAR targets [J]. Radar Science and Technology, 2011, 9(3): 207-213. (in Chinese) doi: 10.3969/j.issn.1672-2337.2011.03.003 [9] Zhang H, Zhang S L, He S J. Parameter estimation of attributed scattering centers in SAR images based on amplitude-phase separation and DPSO [J]. Journal of China Academy of Electronics and Information Technology, 2019, 14(9): 993-1000. (in Chinese) doi: 10.3969/j.issn.1673-5692.2019.09.017 [10] Jiang W, Li W Z. A new method for parameter estimation of attributed scattering centers based on amplitude-phase separation [J]. Journal of Radar, 2019, 8(5): 606-615. (in Chinese) doi: 10.12000/JR18097 [11] Duan J, Zhang L, Sheng J L, et al. Parameter decouple and estimation of independent attributed scattering centers [J]. Journal of Electronics & Information Technology, 2012, 34(8): 1853-1859. (in Chinese) [12] Tan C M, Xu T F, Ma X, et al. Graph-spectral hyperspectral video restoration based on compressive sensing [J]. Chinese Optics, 2018, 11(6): 949-957. (in Chinese) doi: 10.3788/co.20181106.0949 [13] Zhu F Z, Liu Y, Huang X, et al. Remote sensing image super-resolution based on improved sparse representation [J]. Optics and Precision Engineering, 2019, 27(3): 718-725. (in Chinese) doi: 10.3788/OPE.20192703.0718 [14] Li F, Jiu B, Liu H W, et al. Sparse representation based algorithm for estimation of attributed scattering center parameter on SAR imagery [J]. Journal of Electronics & Information Technology, 2014, 36(4): 931-937. (in Chinese) [15] Zhang X, Yan H Z, Zhou J J, et al. Extraction of 2D full polarization scattering centers based on group sparse representation [J]. Electronics Optics & Control, 2016, 23(2): 26-30. (in Chinese) [16] Liu Y. Target recognition of SAR images based on multi-level matching of attributed scattering centers [J]. Journal of Electronic Measurement and Instrumentation, 2019, 33(11): 192-198. (in Chinese) [17] Ding B Y, Wen G J, Yu L S, et al. Matching of attributed scattering center and its application to synthetic aperture radar Automatic Target Recognition [J]. Journal of Radar, 2017, 6(2): 157-166. (in Chinese) [18] Ding B Y, Wen G J, Zhong J R, et al. A robust similarity measure for attributed scattering center sets with application to SAR ATR [J]. Neurocomputing, 2017, 219: 130-143. doi: 10.1016/j.neucom.2016.09.007 [19] Ye H, Tan G Z, Li G et al. De-noising nonstationary signal based on sparse representation and particle swarm optimization [J]. Infrared and Laser Engineering, 2018, 47(7): 0726005. (in Chinese) doi: 10.3788/IRLA201847.0726005 [20] Wu H S, Zhang F M, Wu L S. New swarm intelligence algorithm—wolf pack algorithm [J]. Systems Engineering and Electronics, 2013, 35(11): 2430-2438. (in Chinese) [21] Hui X B, Guo Q, Wu P P, et al. A improved wolf pack algorithm [J]. Control and Decision, 2017, 32(7): 1163-1172. (in Chinese) [22] Hui X B, Guo Q, Wu P P, et al. Adaptive grouping difference variation wolf pack algorithm [J]. Journal of East China Normal University (Natural Science), 2017, 3(5): 79-87. (in Chinese) [23] Cao S, An J C. A fast two-dimensional Otsu image segmentation algorithm based on wolf pack algorithm optimization [J]. Computer Engineering & Science, 2018, 40(7): 1221-1226. (in Chinese) doi: 10.3969/j.issn.1007-130X.2018.07.011 -
点击查看大图
图(6) / 表(2)
计量
- 文章访问数: 344
- HTML全文浏览量: 116
- PDF下载量: 38
- 被引次数: 0
