-
成像光谱仪可以获取目标物的空间信息和光谱信息,是光学探测在对地、大气、海洋等观测领域的强有力的手段[1]。光谱仪常用的分光元件是光栅和棱镜:光栅是通过光的衍射进行分光,有色散线性好、光谱分辨率高等优点;棱镜通过光的色散进行分光,有光通量高、工作光谱范围宽、长期稳定性高等优点[2]。然而,光栅型和棱镜型光谱仪系统都存在着谱线弯曲(Smile)和系统不共轴的问题[3],难以满足光谱仪小型化、紧凑型的发展要求[4]。
PGP型光谱仪系统具有衍射效率高、易装调和体积小等优点,PGP元件由棱镜、光栅、棱镜组成,其中体全息光栅的Bragg衍射可提升系统衍射效率,棱镜的作用是使中心波长的0视场主光线在分光前后都与光栅法线平行,实现光谱仪系统共轴[4-6],可以满足光谱仪小型化的发展要求。PGP分光元件于1991年由AIKIO在专利中提出,1995年应用于农用光谱仪系统中,2001年,AIKIO在其博士论文中详细介绍了该元件的光学原理[6]。在近20年间,该类型光谱仪也在艺术和科学等很多领域都有着应用与发展[7-9]。
但PGP型光谱仪仍存在明显的谱线弯曲,弯曲方向为短波方向,目前,对于谱线弯曲校正的研究主要是在定标和光学设计两个方向[10-11]。在光学设计方向,2011年,袁立银在PGP型光谱仪设计中,以倾斜会聚镜的方式有效降低了系统的谱线弯曲[12];2014年,张晓龙提出会聚镜部分透镜离轴所产生的彗差可以降低光谱仪系统的谱线弯曲[13];2014年,陈洪福利用棱镜和光栅型光谱仪谱线弯曲方向相反的特性,提出棱镜-光栅型光谱仪系统[14]。这些方法都可以明显地降低光谱仪系统中的谱线弯曲,但却都是在失去系统共轴特性的条件下实现的。
为了兼顾PGP型光谱仪系统共轴和谱线弯曲校正,文中提出了一种校正PGP型光谱仪谱线弯曲的方法,通过减少PGP分光元件中第一个棱镜的顶角来校正中心波长谱线弯曲、狭缝离轴以保持光栅的Bragg波长和系统共轴、用会聚镜的畸变校正其它波长的谱线弯曲。并设计了一套光学系统验证方法的可行性,设计结果分析表明,该方法在满足技术指标和成像质量要求的同时,可有效地校正谱线弯曲。
-
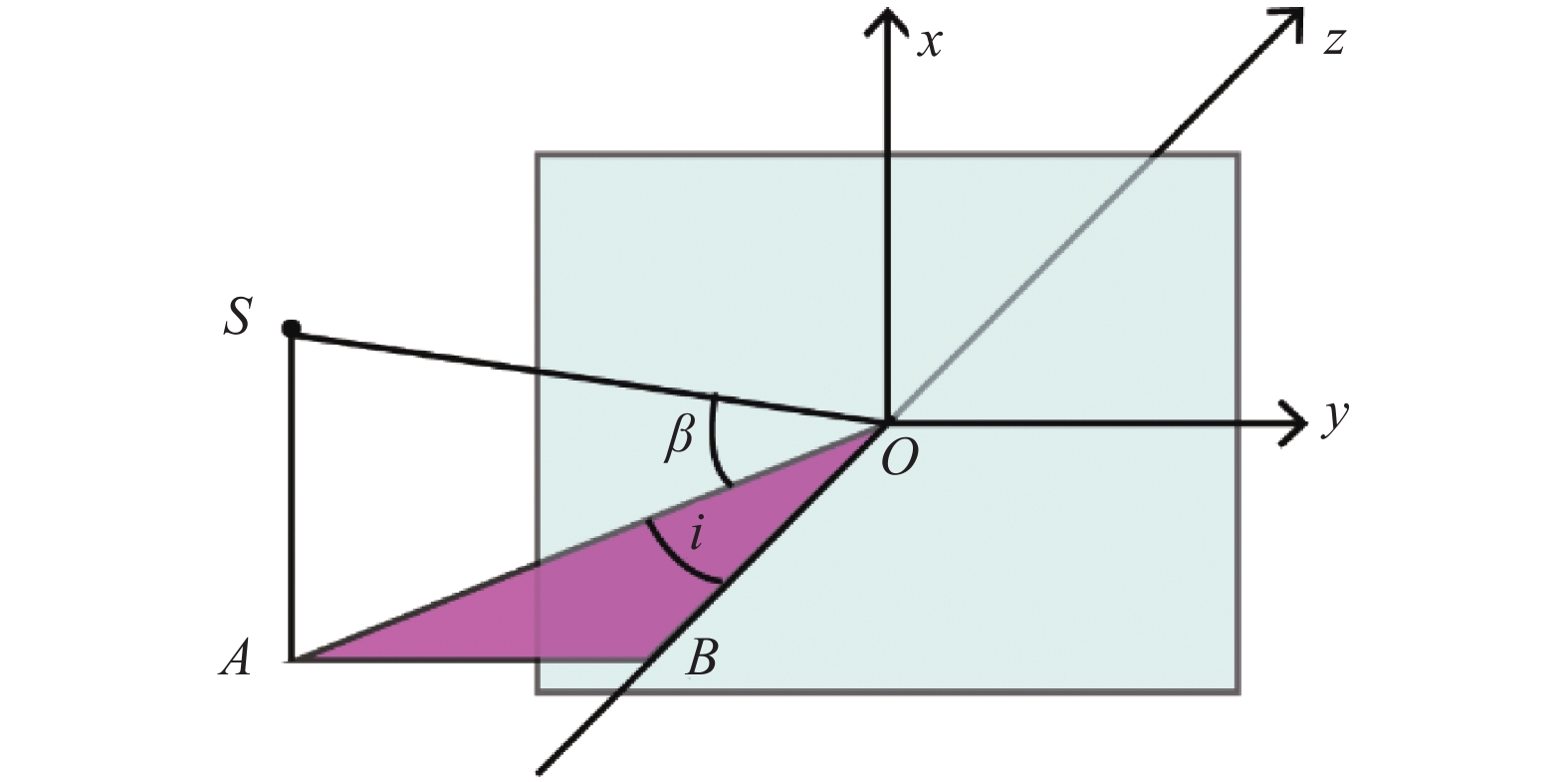
光谱仪系统的谱线弯曲被称为“微笑畸变”,是由非主截面色散之间的差异造成的。狭缝上点光源的主光线与分光元件主截面所成夹角为
$\;\beta $ ,其大小与物点在狭缝长度方向的位置x和准直镜焦距${f_1}$ 有关:$$\beta = \arctan \left( {\frac{x}{{{f_1}}}} \right)$$ (1) 由于棱镜和光栅在空间方向都不参与分光,
$\beta $ 在分光前后不发生变化。将入射光线到主截面做投影,如图1所示,得到其在主截面内的入射角投影为$i$ ,入射面为xoy平面。此时,棱镜的折射率为“假折射率”${N_{\lambda - \beta }}$ ,光栅方程为“完整光栅方程”[3]。$${N_{\lambda - \beta }} = \sqrt {n_\lambda ^2 + \left( {n_\lambda ^2 - 1} \right) \cdot {{\tan }^2}\left( \beta \right)} $$ (2) $$\cos \beta \cdot \left( {\sin \left( i \right) + \sin \left( \theta \right)} \right) = k \cdot \lambda \cdot \nu $$ (3) 式中:
${n_\lambda }$ 为波长$\lambda $ 在棱镜中的折射率;$\theta $ 为衍射角在光栅主界面的投影;$k$ 为光栅衍射级次;$\nu $ 为光栅刻线密度。光线在棱镜中的出射角${\varphi _{\lambda - \beta }}$ 和光栅中的出射角${\theta _{\lambda - \beta }}$ 分别表示为:$$\begin{array}{l} \sin \left( {{\varphi _{\lambda - \beta }}} \right) = \sin \left( \alpha \right) \cdot \sqrt {N_{\lambda - \beta }^2 - {{\sin }^2}\left( {{i_{\rm{P}}}} \right)} - \cos \left( \alpha \right) \cdot \sin \left( {{i_{\rm{P}}}} \right) \end{array} $$ (4) $$\sin \left( {{\theta _{\lambda - \beta }}} \right) = \frac{{k \cdot \lambda \cdot \nu }}{{\cos \left( \beta \right)}} - \sin \left( {{i_{\rm{G}}}} \right)$$ (5) 式中:
$\alpha $ 为棱镜顶角;${i_{\rm{P}}}$ 和${i_{\rm{G}}}$ 分别为棱镜和光栅的入射角,分别对公式(4)和(5)做微分:$$\frac{{{\rm{d}}{\varphi _{\lambda - \beta }}}}{{{\rm{d}}\beta }} = \frac{{\sin \left( \alpha \right) \cdot \left( {n_\lambda ^2 - 1} \right) \cdot \tan \left( \beta \right) \cdot {{\sec }^2}\left( \beta \right)}}{{\cos \left( {{\varphi _{\lambda - \beta }}} \right) \cdot \sqrt {N_{\lambda - \beta }^2 - {{\sin }^2}\left( {{i_{\rm{P}}}} \right)} }} \geqslant 0$$ (6) $$\frac{{{\rm{d}}{\theta _{\lambda - \beta }}}}{{{\rm{d}}\beta }} = \frac{{k \cdot \lambda \cdot \nu \cdot \tan \left( \beta \right)}}{{\cos \left( {{\theta _{\lambda - \beta }}} \right) \cdot \cos \left( \beta \right)}} \geqslant 0$$ (7) 由公式(6)和(7)可知,棱镜和光栅的色散角都随
$\;\beta $ 值的增加而增加。棱镜的出射角为逆时针方向,色散角向短波方向增大,光栅的出射角为顺时针方向,色散角向长波方向增大。即棱镜型光谱仪谱线向短波方向弯曲,光栅型光谱仪谱线向长波方向弯曲。 -
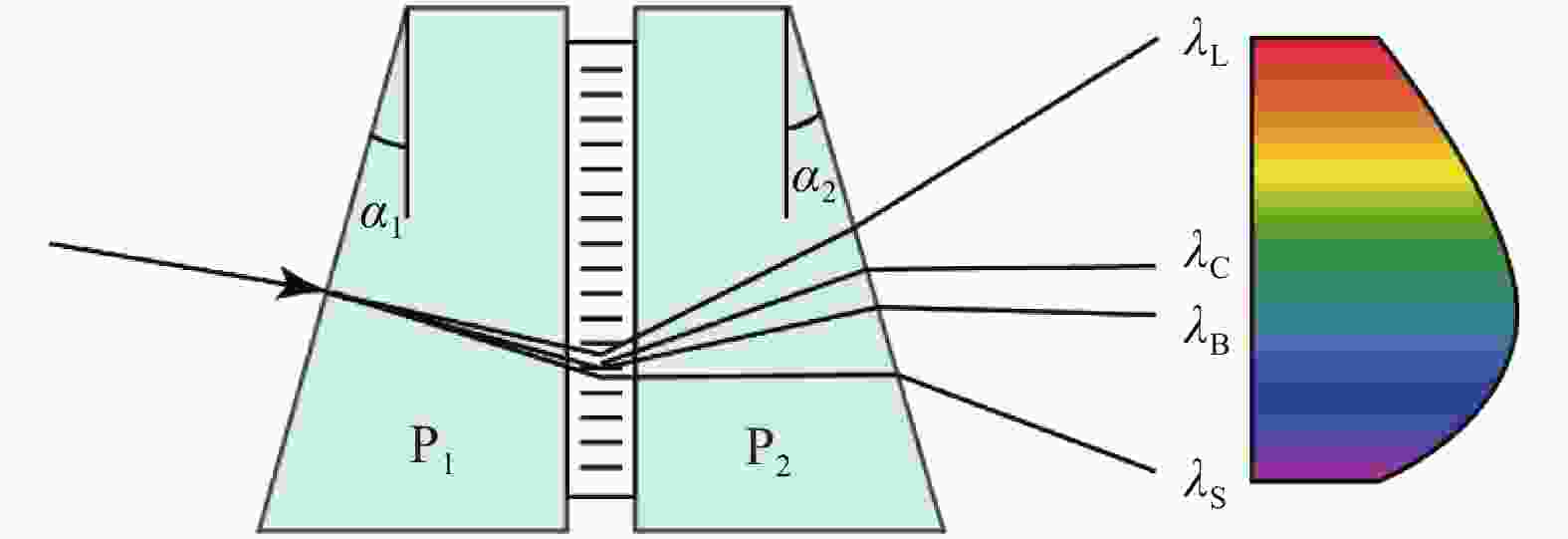
PGP元件由棱镜和光栅组成,可实现光谱仪系统谱线弯曲的校正,但传统型PGP型光谱仪系统中心波长的入射和出射方向相同,实现了系统共轴,却未校正系统的谱线弯曲。为了同时校正PGP型光谱仪系统的谱线弯曲,在传统型基础上做出改进,改进型PGP元件原理图如图2所示,其由棱镜
${{\rm{P}}_1}$ 、体全息光栅G和棱镜${{\rm{P}}_2}$ 组成,0视场主光线与光栅法线存在一定夹角。${{\rm{P}}_1}$ 顶角为${\alpha _1}$ ,光栅G竖直放置,衍射级次$k = 1$ ,${{\rm{P}}_2}$ 顶角为${\alpha _2}$ 。光谱范围的最小波长为${\lambda _{\rm{S}}}$ ,最大波长为${\lambda _{\rm{L}}}$ ,中心波长为${\lambda _{\rm{C}}}$ ,Bragg波长为${\lambda _{\rm{B}}}$ ,即${\lambda _{\rm{B}}}$ 关于光栅G的入射角和衍射角相等,满足Bragg衍射条件:$$2 \cdot \sin \left( {{\theta _{\rm{B}}}} \right) = {\lambda _{\rm{B}}} \cdot \nu $$ (8) 式中:
${\theta _{\rm{B}}}$ 是光栅G在空气介质中的光线入射角,可由折射定律换算得到。参考公式(4),棱镜${{\rm{P}}_1}$ 的顶角${\alpha _1}$ 和光线入射角的关系为:$$ \begin{array}{l} \sin \left( {{\alpha _1}} \right) \cdot \sqrt {n_{1 - {\rm{B}}}^2 - {{\sin }^2}\left( i \right)} - \cos \left( {{\alpha _1}} \right) \cdot \sin \left( i \right) = \sin \left( {{\theta _{\rm{B}}}} \right) \\ \end{array} $$ (9) 式中:
${n_{1 - {\rm{B}}}}$ 为棱镜${{\rm{P}}_1}$ 对于${\lambda _{\rm{B}}}$ 的折射率;$i$ 为棱镜${{\rm{P}}_1}$ 的入射角;在传统型PGP元件中$i = {\alpha _1}$ 。中心波长0视场主光线与光栅法线平行,即中心波长在棱镜${{\rm{P}}_2}$ 的出射角等于其顶角${\alpha _2}$ :$${\alpha _2} = \arctan \left( {\frac{{\sin \left( {{\theta _{\rm{C}}}} \right)}}{{\sqrt {{n_{2 - {\rm{C}}}}^2 - {{\sin }^2}\left( {{\theta _{\rm{C}}}} \right)} - 1}}} \right)$$ (10) 式中:
${n_{2 - {\rm{C}}}}$ 为棱镜${{\rm{P}}_2}$ 对于${\lambda _{\rm{C}}}$ 的折射率;${\theta _{\rm{C}}}$ 为${\lambda _{\rm{C}}}$ 关于光栅G在空气中的衍射角。棱镜和光栅所产生的谱线弯曲方向相反,PGP型光谱仪系统的谱线弯曲是三个分光元件共同作用的结果,由公式(4)和(5)可以得出中心波长的不同视场主光线在各元件中的出射角:$$ \begin{split} \sin \left( {{\varphi _{1 - {\rm{C}} - \beta }}} \right) =& \sin \left( {{\alpha _1}} \right) \cdot \sqrt {N_{1 - {\rm{C}} - \beta }^2 - {{\sin }^2}\left( i \right)} - \cos \left( {{\alpha _1}} \right) \cdot\\ & \sin \left( i \right) \sin \left( {{\varphi _{{\rm{G}} - {\rm{C}} - \beta }}} \right) = \dfrac{{\lambda \cdot \nu }}{{\cos \left( \beta \right)}} - \sin \left( {{\varphi _{1 -{ \rm{C}} - \beta }}} \right) \cdot\\ & \sin \left( {{\varphi _{2 \!-\!{\rm{ C}} \!-\! \beta }}} \right) \!=\! \sin \left( {{\alpha _2}} \right) \! \cdot \!\sqrt {N_{2 \!-\! {\rm{C}} \!-\! \beta }^2 \!-\! {{\sin }^2}\left( {{\varphi _{{\rm{G}} \!-\! {\rm{C}} \!-\! \beta }}} \right)} \!-\!\\ & \cos \left( {{\alpha _2}} \right) \cdot \sin \left( {{\varphi _{{\rm{G}} - {\rm{C}} - \beta }}} \right) \end{split} $$ (11) 式中:
$i$ 为主光线通过棱镜${{\rm{P}}_1}$ 的入射角;${\varphi _{1 - {\rm{C}} - \beta }}$ 为主光线通过棱镜${{\rm{P}}_1}$ 的出射角,同时也是光栅的入射角,${N_{1 -{\rm{ C}} - \beta }}$ 为中心波长在棱镜${{\rm{P}}_1}$ 中的假折射率;${\varphi _{{\rm{G}} - {\rm{C}} - \beta }}$ 为中心波长的光栅衍射角,同时也是棱镜${{\rm{P}}_2}$ 的入射角;${\varphi _{2 -{\rm{ C}} - \beta }}$ 为棱镜${{\rm{P}}_2}$ 的出射角;${N_{2 - {\rm{C}} - \beta }}$ 为中心波长在棱镜${{\rm{P}}_2}$ 中的假折射率。由公式(4)和(5)可知,棱镜和光栅的出射角公式形式不同,所以光谱仪系统的谱线弯曲很难完全校正,只能使得$\beta $ 对应位置的谱线弯曲为0,系统的谱线弯曲趋近于零。因此中心波长在PGP元件中的出射角为:$${\varphi _{{\rm{PGP}} - {\rm{C}} - \beta }} = {\varphi _{2 - {\rm{C }}- \beta }} - {\alpha _2} \approx 0$$ (12) 光栅方程结合公式(9)和公式(12),可以得出改进型PGP元件中棱镜
${{\rm{P}}_1}$ 的顶角${\alpha _1}$ 和入射角$i$ ,进而求得PGP元件的其他参数。PGP元件中棱镜${{\rm{P}}_1}$ 的入射角$i$ 由狭缝离轴实现,准直镜、PGP元件和会聚镜三者共轴,光谱仪系统中心波长的谱线弯曲近似为零。 -
结合应用需求,设计了一台光谱范围为400~1000 nm的PGP型光谱仪,光学设计指标如表1所示。根据光栅刻线密度,Bragg波长定为650 nm,光栅基底材料选用B270,棱镜材料选用H-K9L,狭缝长度定为9.2 mm。计算得到传统型PGP光谱仪的技术指标,准直镜焦距约为25.58 mm,棱镜
${{\rm{P}}_1}$ 顶角约为12.92°,棱镜${{\rm{P}}_2}$ 顶角约为14.95°,谱线弯曲如图3(a)所示,系统存在严重的谱线弯曲,谱线弯曲最大值约120 μm,谱线向短波方向弯曲,说明在传统型PGP型光谱仪系统中棱镜对谱线弯曲的影响比光栅大。表 1 PGP成像光谱仪设计指标
Table 1. Design parameters of PGP imaging spectrometer
Parameter Value Spectral range/nm 400-1000 Spectral resolution/nm 2.8 Object space NA 0.18 Slit length/mm ≥9 Image width (spectral)/mm ≤6.2 Grating frequency/lp·mm−1 360 因此,若要减小PGP型光谱仪系统的谱线弯曲,需要减小PGP组件中棱镜的顶角。若改变棱镜
${{\rm{P}}_2}$ 的顶角,会聚镜光轴与光栅法线将不再平行,会破坏系统共轴。因此PGP型光谱仪的改进方法是减小棱镜${{\rm{P}}_1}$ 的顶角,以校正中心波长的谱线弯曲,入射狭缝做光谱维离轴处理,即入射光线0视场主光线与光栅法线成一个夹角,以保持系统共轴特性和Bragg波长。改进型PGP型光谱仪的模型谱线弯曲如图3(b)所示,中心波长的谱线弯曲得到了很好的校正,其他波长的谱线向中心波长谱线两侧弯曲,最大值约为50 μm。改进型PGP元件参数计算结果如表2所示。表 2 改进型PGP组件参数
Table 2. Parameters of the improved PGP component
Parameter Value Bragg wavelength/nm 650 Central wavelength/nm 700 Vertex angle of the first prism/(°) 1.91 Vertex angle of the second prism/(°) 14.95 Prism material H-K9L Grating material B270 Collimating lens focal length/mm 26 Off-axis slit position/mm 2.6 由视场角和数值孔径,选用双高斯系统作为准直镜结构[15],利用Zemax光学设计软件进行光学结构的设计,将原肖特库的玻璃材料改成对应的成都光明库的玻璃材料。其中正透镜选用材料为H-ZK9B和H-ZK50,材料5 mm厚度在波段范围的透过率分别为:[0.996, 0.998]和[0.993, 0.999];负透镜选用材料为H-F1, 5 mm厚度在波段范围内的透过率为[0.963, 0.998],均具有良好的透过率。改进型PGP元件校正了中心波长的谱线弯曲,狭缝在空间维方向离轴,所以准直镜的畸变需要被校正,减小其对光谱仪系统中心波长谱线的影响。其他波长的谱线向两侧弯曲,需要会聚镜的负畸变进行补偿校正。
-
经过光学系统设计,Bragg波长约为650 nm,光谱维宽小于6.2 mm,与表1中的设计指标和表2中的组件参数一致。在像面上,2.8 nm对应最小线色散在1000 nm处的值约为28 μm,光谱采样为3,光谱维像素宽度为9 μm,空间维以三个像元作为一个像素,像素宽度为27 μm。
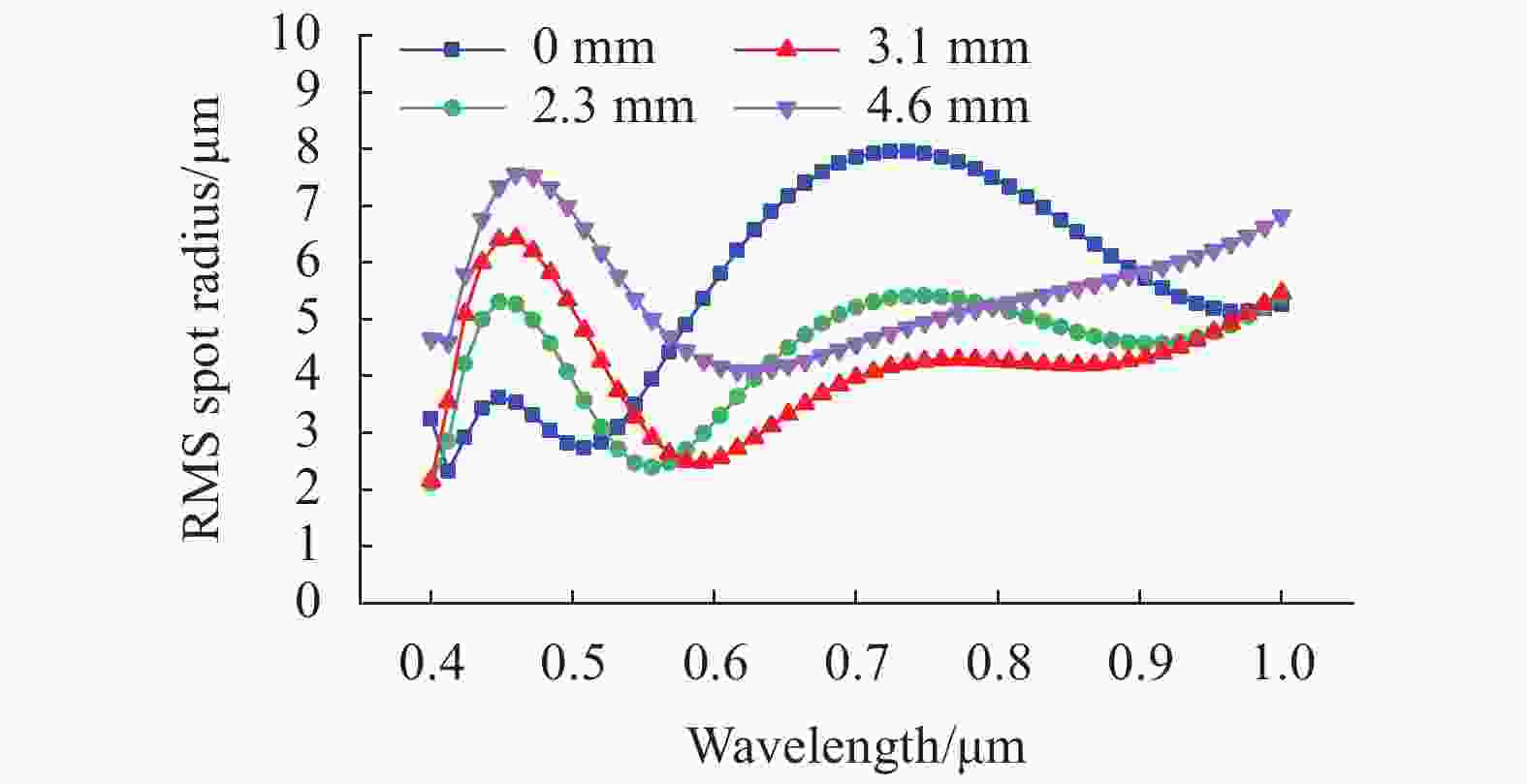
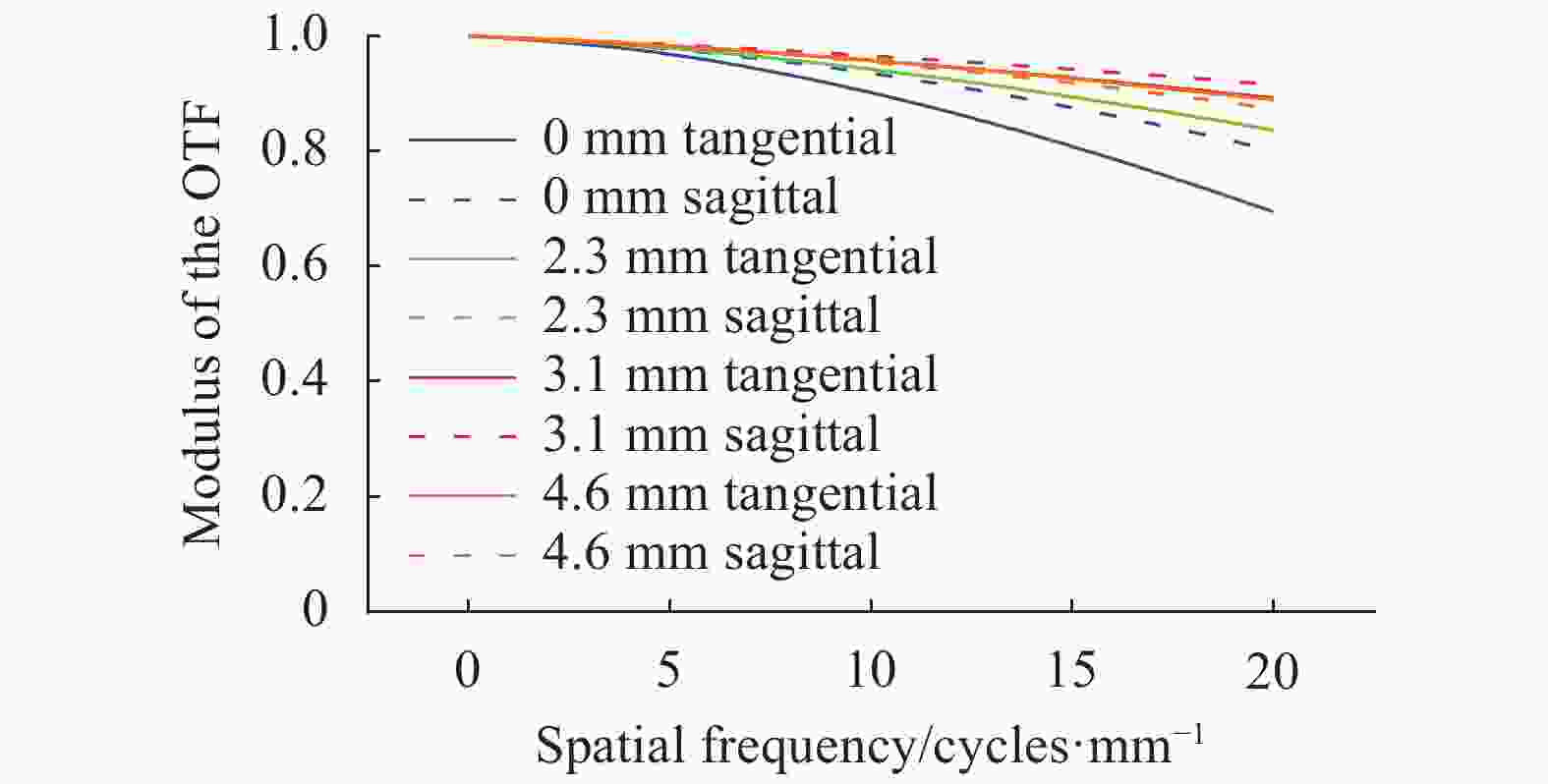
具体设计结果如图4所示,图4为系统光路图,系统双方远心且共轴,为了补偿位置色差,系统像面关于x轴旋转的角度约为6.86°;图5为光谱仪系统狭缝上0 mm、2.3 mm、3.1 mm和4.6 mm视场高度对应的RMS半径随波长的变化,所有视场的
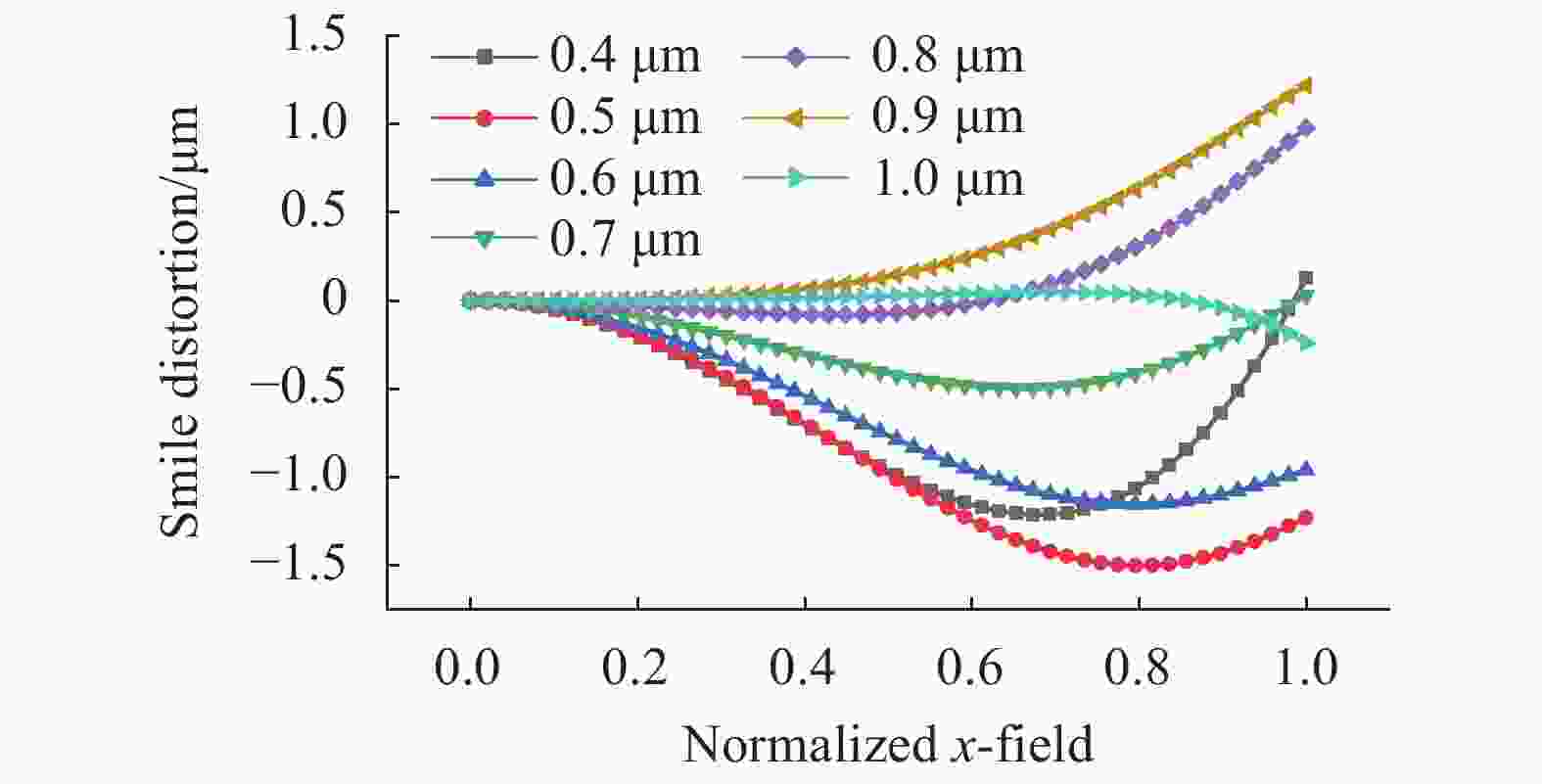
${\rm{RMS}} \leqslant $ 8 μm,中心波长的弥散斑RMS最大;图6为中心波长在探测器特征频率下的光学调制传递函数(MTF)曲线,在0~20 lp/mm范围内$MTF \geqslant 0.7$ ,满足成像质量要求;图7为光谱仪系统不同波长对应的谱线弯曲(Smile),波长为0.5 μm对应的谱线弯曲最大,${{Smile}} \leqslant$ 1.50 μm;图8为光谱仪系统狭缝上2.3 mm、3.1 mm和4.6 mm视场高度对应的色畸变(Keystone),视场物高3.1 mm时对应的色畸变最大,小于3.52 μm。光谱维
${{{{RMS} } < 8 \; }}$ μm,小于狭缝宽度的三分之一;空间维${{RMS < 5 \; }}$ μm,满足成像质量要求。最大谱线弯曲小于光谱维0.2个像素,最大的色畸变小于空间维0.2个像素,满足计算光谱仪对谱线弯曲的要求。相比于传统型PGP成像光谱仪,谱线弯曲量从120 μm校正到1.50 μm,降低到了原来的1.25%;传统型PGP成像光谱仪中心波长有谱线弯曲,会聚镜畸变难以校正,改进型PGP型成像光谱仪很好地弥补了其这方面的不足。考虑到加工和装调,需要对设计结果进行公差分析。玻璃材料的公差由成都光明数据文件可知,折射率公差为±3e-4,阿贝数公差为±0.5%。以现在工艺可以达到的一组公差数作为模型的公差限定,如表3所示,以评价函数作为评估。
表 3 光学系统允许的公差
Table 3. Allowable tolerance of optical system
Parameter Value Index 0.0003 Abbe 0.5% Radius/fr 2 Thickness/mm 0.02 Decenter (surface and element)/mm 0.01 Tilt (surface and element)/(') 0.5 Irregularity 0.25 经过200组蒙特卡洛模拟,获得最优和最差的模拟结果。在公差的最差结果中,光谱维
${{RMS < 9 \;}}$ μm,空间维${{RMS < 9 \;}}$ μm,依然满足成像质量要求,Smile小于4.5 μm,Keystone小于4.5 μm,均小于0.5个像素,满足对系统谱线弯曲的设计要求。 -
提出了一种改进型PGP型成像光谱仪,该方法采用狭缝离轴、减小系统中棱镜的角度和会聚镜畸变相结合校正传统型PGP型成像光谱仪系统的谱线弯曲。减小棱镜顶角可以校正光谱仪系统中心波长的谱线弯曲,狭缝离轴用来保持系统的Bragg波长和共轴特性,会聚镜的负畸变校正其他波长谱线弯曲和色畸变。设计结果表明:狭缝的离轴距离小于像面谱维半宽,不会增加准直镜的设计难度;弥散斑半径满足成像质量要求,达到了光谱分辨率2.8 nm的技术指标;谱线弯曲小于0.2个像元尺寸,满足计算光谱对谱线弯曲的要求。改进型PGP型光谱仪在不改动传统型光谱仪的衍射效率高和系统共轴等特性、不增加系统体积的同时,弥补了传统型PGP型光谱仪谱线弯曲大、难以校正的不足,对PGP型光谱仪向高分辨率、宽视场发展具有重要的意义。
Design of PGP imaging spectrometer with eliminating spectral line bending
-
摘要: 针对棱镜-光栅-棱镜(PGP)型成像光谱仪谱线弯曲(Smile)难校正的问题,提出了一种利用狭缝离轴和减小第一块棱镜顶角,再结合会聚镜畸变校正PGP型光谱仪谱线弯曲的方法。该方法在保留了PGP型光谱仪的布拉格(Bragg)衍射和系统共轴等优点的基础上,校正了光谱仪的谱线弯曲和色畸变(Keystone)。在相同的技术指标下,对传统型和改进型PGP模型做了谱线弯曲对比。为了验证该方法的可行性,设计了一款光谱分辨率为2.8 nm的光谱仪,点列图均方根(RMS)半径小于8 μm,满足成像质量要求,Smile为1.50 μm、Keystone为3.52 μm,均小于0.2倍像素。设计结果表明,通过减小棱镜顶角校正中心波长的Smile,利用狭缝离轴实现光谱仪系统共轴,利用会聚镜畸变校正剩余波长的Smile可以有效校正PGP型光谱仪的谱线弯曲。Abstract: A method was put forward to eliminate spectral line bending (Smile) of Prism-Grating-Prism(PGP) spectrometer by reducing the vertex angle of the first prism and combining with off-axis slit and the distortion of convergent lens. The method could be used to retain the Bragg diffraction and coaxial characteristic of the PGP spectrometer and eliminate spectral line bending and spectral Keystone of the spectrometer. The Smile of the traditional PGP model and the improved PGP model with the same technical indexes were compared. In order to verify the feasibility of the method, a spectrometer with a spectral resolution of 2.8 nm was designed. The root mean square (RMS) of the spot radius was less than 8 μm, both imaging quality and design index requirements could be satisfied. The Smile and Keystone of the system were 1.50 μm and 3.52 μm respectively, which were both less than 0.2 pixel. The design result indicates that the Smile and Keystone of the PGP spectrometer can be effectively eliminated by reducing the vertex Angle of the prism to eliminate the Smile of the center wavelength, using the slit off axis to retain coaxial characteristic of the PGP spectrometer, using the distortion of convergent lens to eliminate the Smile and Keystone of the remaining wavelength.
-
Key words:
- optical design /
- imaging spectrometer /
- prism-grating-prism /
- Bragg diffraction /
- Smile
-
表 1 PGP成像光谱仪设计指标
Table 1. Design parameters of PGP imaging spectrometer
Parameter Value Spectral range/nm 400-1000 Spectral resolution/nm 2.8 Object space NA 0.18 Slit length/mm ≥9 Image width (spectral)/mm ≤6.2 Grating frequency/lp·mm−1 360 表 2 改进型PGP组件参数
Table 2. Parameters of the improved PGP component
Parameter Value Bragg wavelength/nm 650 Central wavelength/nm 700 Vertex angle of the first prism/(°) 1.91 Vertex angle of the second prism/(°) 14.95 Prism material H-K9L Grating material B270 Collimating lens focal length/mm 26 Off-axis slit position/mm 2.6 表 3 光学系统允许的公差
Table 3. Allowable tolerance of optical system
Parameter Value Index 0.0003 Abbe 0.5% Radius/fr 2 Thickness/mm 0.02 Decenter (surface and element)/mm 0.01 Tilt (surface and element)/(') 0.5 Irregularity 0.25 -
[1] Lucke R L, Corson M, McGlothlin N R, et al. Hyperspectral imager for the coastal ocean: instrument description and first images [J]. Appl Opt, 2011, 50(11): 1501-1516. doi: 10.1364/AO.50.001501 [2] James J F. Spectrograph Design Fundamentals[M]. New York: Cambridge University Press, 2007: 57-88. [3] Wu Guoan. Design of Spectrograph[M]. Beijing: Science Press, 1987: 84-87, 104-105. (in Chinese) [4] Yuan Liyin, Xie Jianan, Hou Jia, et al. Optical design of compact infrared imaging spectrometer [J]. Infrared and Laser Engineering, 2018, 47(4): 0418001. (in Chinese) doi: 10.3788/IRLA201847.0418001 [5] Braam B M, Okkonen J T, Aikio M, et al. Design and first test results of the Finnish airborne imaging spectrometer for different applications (AISA)[C]//SPIE, 1993, 1937: 142-151. [6] Aikio M. Hyperspectral prism-grating-prism imaging spectrograph [J]. VTT Publications, 2001(435): 15-114. [7] Dirk C W, Delgado M F, Olguin M, et al. A prism-grating-prism spectral imaging approach [J]. Studies in Conservation, 2009, 54(2): 77-89. doi: 10.1179/sic.2009.54.2.77 [8] Xue Qingsheng, Tian Zhongtian, Yang Bai, et al. Underwater hyperspectral imaging system using a prism-grating-prism structure [J]. Appl Opt, 2021, 60(4): 894-900. doi: 10.1364/AO.415351 [9] He Tianbo, Bayanheshig, Li Wenhao, et al. Integration design and diffraction characteristics analysis of prism-grating-prism [J]. Spectroscopy and Spectral Analysis, 2014, 34(1): 279. (in Chinese) [10] Fisher J, Baumback M M, Bowles J H, et al. Comparison of low-cost hyperspectral sensors[C]//SPIE, 1998, 3438: 23-30. [11] Jorgensen R N. The VTTVIS line imaging spectrometer: principles, error sources, and calibration[D]. Denmark: Forskningscenter Risoe, 2002. [12] Yuan Linyin, He Zhiping, Shu Rong, et al. Optical design of a SWIR PGP imaging spectrometer [J]. Acta Photonica Sinica, 2011, 40(6): 831-834. (in Chinese) doi: 10.3788/gzxb20114006.0831 [13] Zhang Xiaolong, Liu Ying, Sun Qiang, et al. Design of long-wave infrared imaging spectrometer with eliminating spectral curvature [J]. Optics and Precision Engineering, 2014, 22(2): 266-273. (in Chinese) doi: 10.3788/OPE.20142202.0266 [14] Chen Hongfu, Gong Yan, Luo Cong, et al. Design of prism-grating imaging spectrometer with eliminating spectral line curvature [J]. Acta Optica Sinica, 2014, 34(9): 0922004. (in Chinese) doi: 10.3788/AOS201434.0922004 [15] Geary J M. Introduction to Lens Design : with Practical ZEMAX Examples[M]. Richmond: Willmann-Bell, Inc., 2002: 5-6. -







 下载:
下载: