-
三维主被动测距成像技术具有探测距离远、精度高等优点[1-2],被广泛地应用于工业测量、人工智能、航天遥感和军事目标物体追踪等领域。雪崩光电二极管(Avalanche Photodiode, APD)[3]具有高内增益、高灵敏度和高信噪比等特点,作为高性能光电探测器在检测微弱信号方面具有良好的应用前景。它具有两种工作模式:盖革模式(Geiger-mode, GM)和线性模式(Linear-mode, LM),其性能对比如表1所示。
表 1 盖革和线性模式APD性能对比
Table 1. Geiger and linear mode APD performance comparsion
Type GM-APD LM-APD Gain 105-106 10-103 Dynamic range Low High Quenching circuit Yes No Intensity information No Yes Continuous detection capability No Yes 盖革模式具有灵敏度高、能实现单光子探测等优点,在早期被广泛应用在硅基APD和InGaAs APD。美国国家航天局戈达德航天飞行中心应用于火星全球探勘任务的火星轨道高度激光计(Mars Orbiter Laser Altimeter, MOLA)基于盖革模式Si APD能够实现25 cm的精度[4],美国宇航局兰利研究中心研发的应用于自主着陆和危险规避技术项目的激光雷达,运用的是盖革模式下InGaAs APD,能实现20 cm的精度[5]。
盖革模式因死区时间长导致不能连续探测和不能获得强度信息等原因,使得在近些年线性模式APD被大量研究,它能够克服盖革模式下的缺点,能够实现连续探测目标物体的强度和时间信息,实现三维主被动探测。
目前在国外的相关报道中,线性模式APD有法国Sofradir公司研制的一种320×256面阵的HgCdTe APD焦平面,能实现30 m的测试量程以及300 ps的时间分辨率[6-8],Raytheon公司报道的线性APD读出电路测试能够分辨400 ps的时间精度[9-10];国内的大多数报道主要集中在盖革模式下APD,其中东南大学InGaAs材料的APD时间分辨率可以达到0.8 ns [11]和长春理工大学的APD时间分辨率可以实现1.33 ns的精度[12-13],而对于线性模式APD的主被动探测的测试研究报道甚少。
文中对一种线性模式HgCdTe APD的读出电路结构进行了分析,对飞行渡越时间(Time of flight, TOF)的计算方法进行了研究,在此基础上搭建了一套测试平台,该系统噪声为253 μV,即系统带来的时间抖动为179 ps,对影响TOF相关的参数(斜率α、输入电压Vref、电容值C及V2d和V3d)进行了理论分析,同时对测试仪器带来的固定时延等参数进行了校准修正,在77 K下对该款线性模式HgCdTe APD读出电路进行了测试分析。为探索线性模式下APD的主被动探测的测试方法提供了新的思路。
-
线性HgCdTe APD读出电路作为三维成像系统中的核心单元,它能实现对光子的飞行时间进行高精度和高速的实时量化和传输处理。目前量化时间精度的方法有模拟电压去量化时间(TVC)和数字去量化时间(TDC)。
-
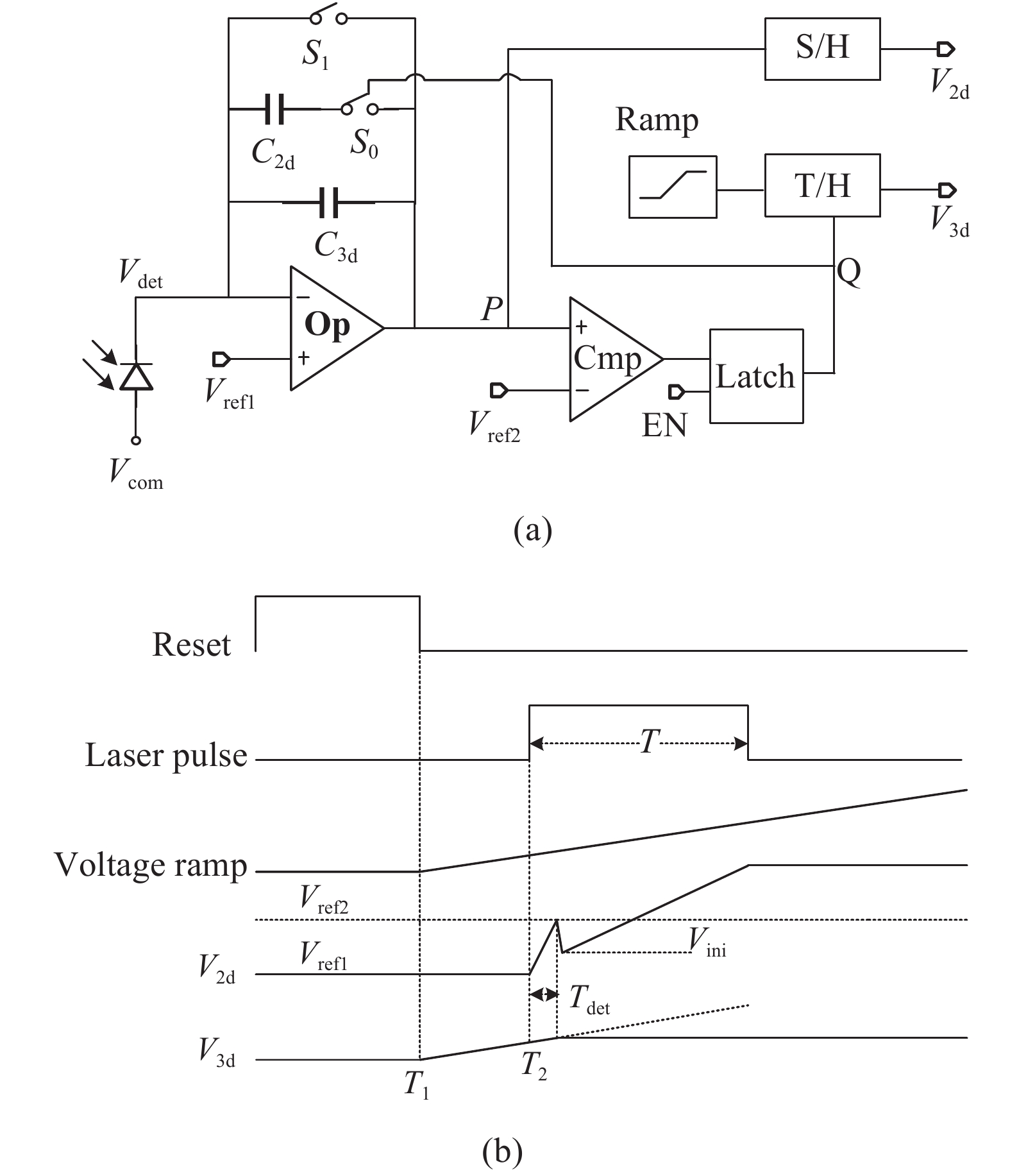
文中基于模拟电压量化时间的方式,提出了一种128×128线性HgCdTe APD读出电路,针对TOF的精度测量对其单元电路进行了分析,其结构和工作时序如图1所示。
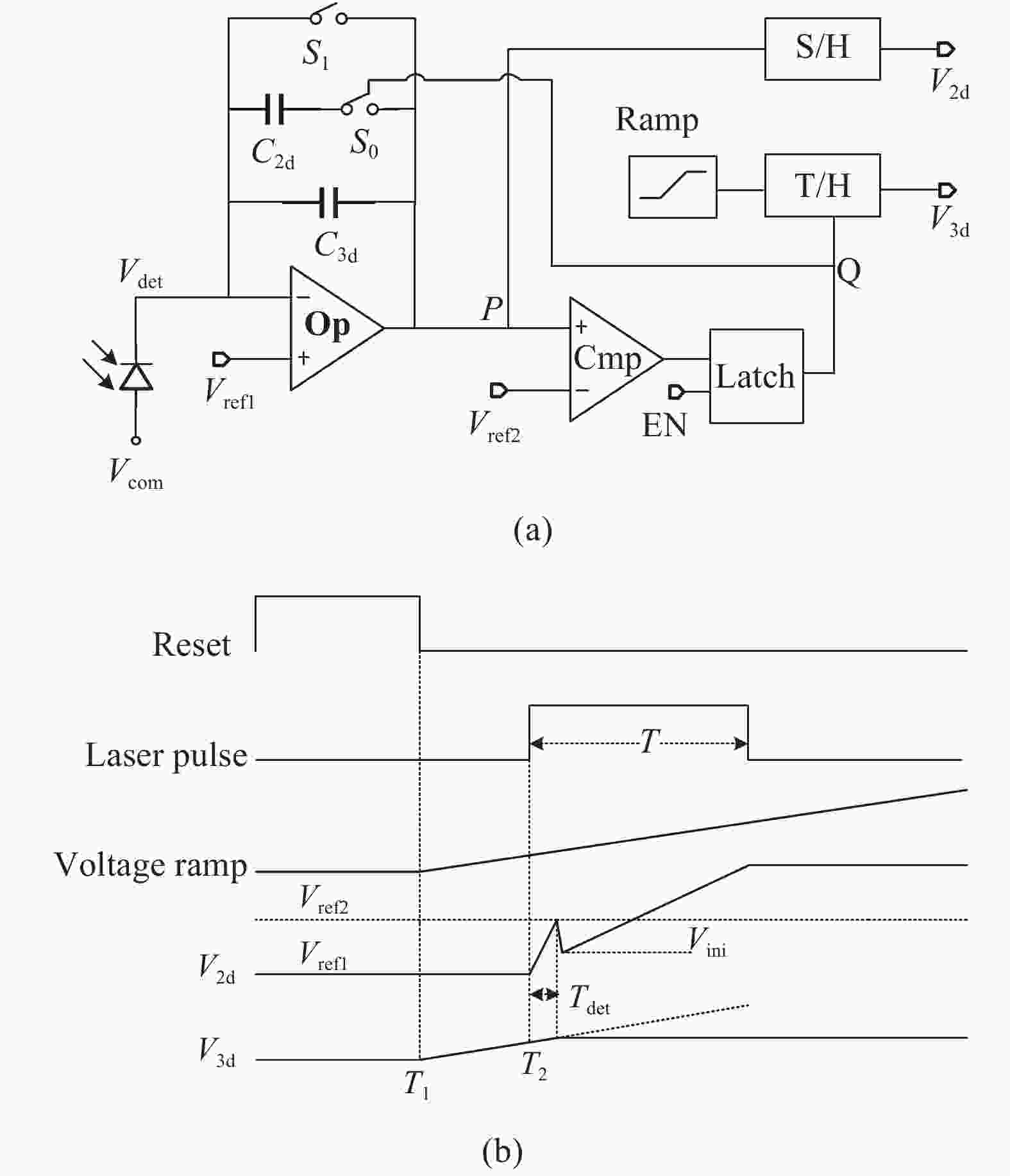
图 1 (a) APD读出电路单元结构;(b) APD读出电路工作时序
Figure 1. (a) APD readout circuit Unit structure; (b) APD readout circuit working sequence
单元电路包括了CTIA输入级结构、比较器、锁存器、采样保持电路等模块。如图1(a)所示,其中CTIA运放增益高达62 dB,以保证高的注入效率和稳定的偏压。比较器用于检测CTIA输出端P点电压,及时触发锁存器翻转,因此需要比较器提供较高的精度;当比较器无需翻转时应具有较低的静态电流来降低系统功耗。因此设计的比较器增益为70 dB,阈值电压Vref2为3 V,静态电流为10 μA,响应时间为1 ns。电路有两个积分电容C3d和C2d,分别为50 fF和400 fF。
电路有两种工作模式:被动探测和主动探测。为了准确直观地了解电路工作状态,通过对采样保持模块(S/H)保持常开对节点P进行实时监控,得到V2d的完整积分过程,如图1(b)所示。
首先,线性HgCdTe APD接收到光信号时,在一定反偏下,PN结中载流子获得动能,与晶格中原子碰撞使价带电子激发至导带,形成新的电子空穴对,耗尽层内运动的载流子因碰撞电离效应而获得雪崩倍增。从而形成光电流流入CTIA结构中。
当工作在被动探测下,使能信号EN 为低电平,通过锁存结构控制S0开关闭合,同时比较器处于静态工作点下以降低功耗。当CTIA复位信号下降沿到来时,电容C3d和C2d共同参与积分获得目标物体的强度信息。此时激光脉宽T不能使得电容积分达到饱和,否则无法分辨强度信息。
主动模式下的使能信号EN为高电平,首先CTIA结构完成复位操作,复位信号Reset的下降沿触发斜坡发生器Ramp开始发射斜坡电压,并同步触发激光脉冲发射激光。当激光脉冲到达APD探测器时,小电容C3d会开始积分,节点P电压迅速达到比较器阈值Vref2使其翻转,触发Latch模块控制开关S0闭合和采样保持开关断开,对当下斜坡电压值进行锁定,得到与时间信息相关的电压V3d值,其所对应的时间为(TOF+Tdet),此时电路将进入大电容积分模式,直至激光脉冲结束读出V2d电压值,得到对应的强度信息。
电路流片采用TSMC 0.18 μm 1P6M CMOS工艺,其中数字电压1.8 V,模拟电压5 V。基本性能参数如表2所示。
表 2 读出电路性能参数
Table 2. Readout circuit performance parameters
Parameter Description Technology TSMC 0.18 μm 1P6M CMOS Temperature/K 77 Pixel/μm2 50×50 Output swing/V 1.5-4 Power/mW 17.5 -
测试过程中,APD探测器开始处于待测状态,通过时序控制激光发射脉冲,同时控制斜坡发生器产生斜坡,当激光碰到被测目标返回到探测器上产生光电流,使得电路翻转存储此时斜坡的电压值,根据标准斜坡电压可以计算出飞行时间TOF值,即发射激光脉冲到接收激光脉冲的时间。因电路积分存在一定延时,因此可以得到以下公式:
$$ {V_{{\rm{3}}{\rm{d}}}} = \alpha (2TOF + {T_{\det }}) $$ (1) $$ I \times {T_{{\rm{det}}}} = {C_{{\rm{3d}}}}({V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}) $$ (2) $$ I\left( {T - {T_{{\rm{det}}}}} \right) = \left( {{C_{3{\rm{d}}}} + {C_{2{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ini}}}}} \right) $$ (3) $$ {C_{{\rm{3d}}}}\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right) = \left( {{C_{{\rm{3d}}}} + {C_{2{\rm{d}}}}} \right)\left( {{V_{{\rm{ini}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right) $$ (4) 式中:α为斜坡发生器的斜率;
${T_{\det }}$ 为小电容的延迟时间;T为激光脉宽;${V_{{\rm{ini}}}}$ 为电容切换后${V_{2{\rm{d}}}}$ 下掉最低点的电压值。通过上述公式(1)~(4)计算得出TOF值:$$ {\rm{2}}TOF = \frac{{{V_{3{\rm{d}}}}}}{\alpha } - \frac{{{C_{3{\rm{d}}}}\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right)}}{{\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times T $$ (5) 由公式(5)可知,V2d、V3d的测量精度会影响最终TOF的探测精度,Vref1和Vref2的精度也会对TOF产生影响,所以需采用高精度电压源提供该电压或者由设计片上基准电压源提供。高精度的线性斜坡电压非常关键,它的每个LSB直接影响能分辨的V3d的电压值,斜坡斜率α的抖动对测试结果也影响很大。在相同的读出噪声情况下,斜率α值越大,则TOF的精度会越高,但相应的探测范围变小。
通过对同一激光脉宽下进行多次采样,计算每次采样的V2d、V3d和斜率α值,即可计算TOF的均方根值,其公式为:
$$ {V_{RMS}} = \sqrt {\frac{1}{N}\sum\limits_{{{i}} = 1}^N {V_{{i}}^{\rm{2}}} } $$ (6) -
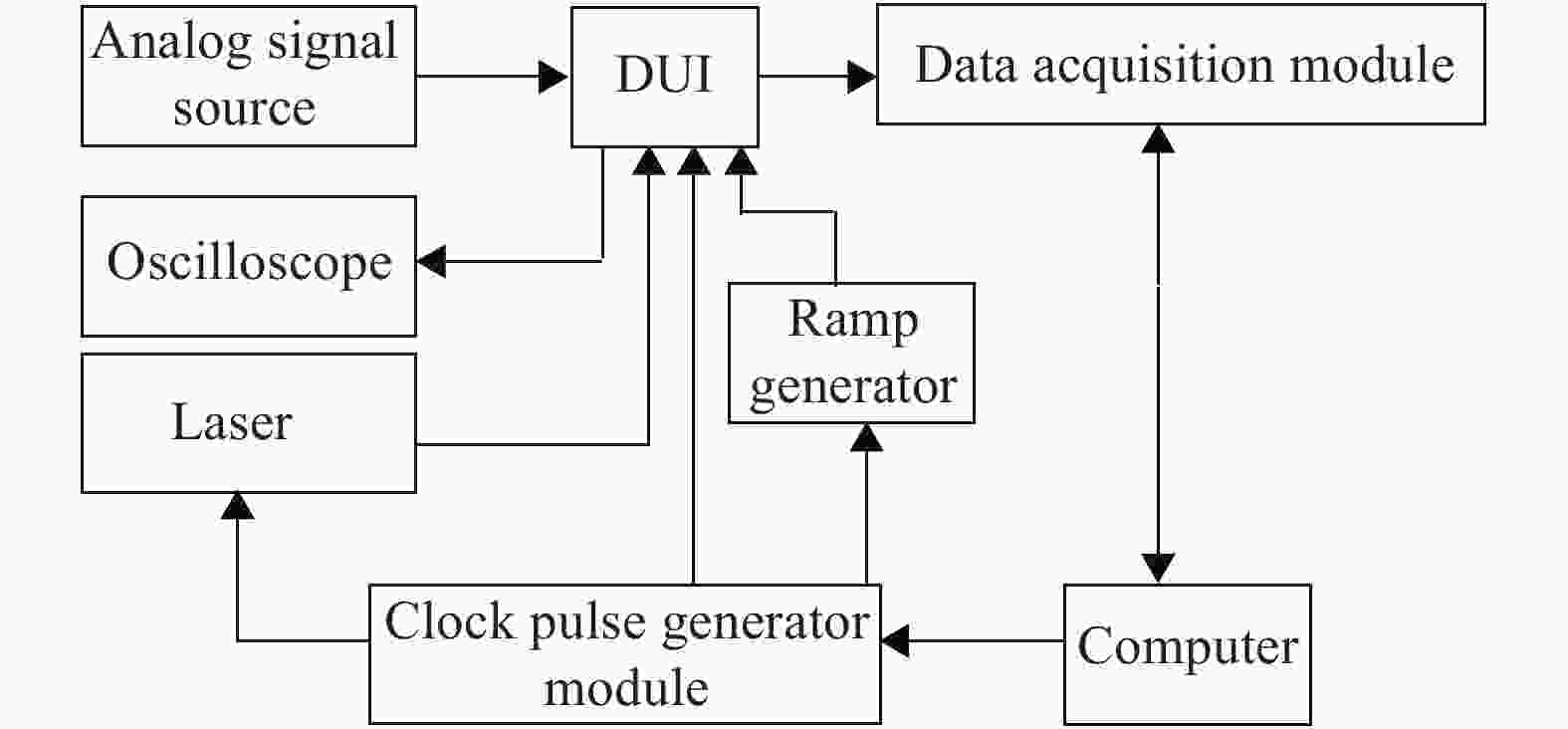
高精度时间分辨的性能测试对测试平台的精度要求很高,基于上述的单元电路结构和工作原理,文中利用Labview软件和模拟采集卡等硬件自主搭建了一套高精度时间标定的测试平台,如图2所示。测试平台主要包括激光脉冲源、高精度模拟信号源、斜坡发生器、时钟脉冲发生器模块、数据采集模块、示波器和计算机。
时钟脉冲发生器模块发射数字时序提供给探测器和芯片(DUT),以及提供同步信号给斜坡发生器和激光发生器。激光脉冲为探测器提供一个宽幅可控的光脉冲,激光发生器的重频大小跟随时序发生器的帧频变化,且最小激光脉宽为重频倒数的千分之一。因项目需实现10 ns以下的精度,所以斜坡发生器采用keysight 81150A能实现最高频率为5 MHz的频率,其精度为1 μHz,对斜坡进行测试得到精度为118.2 ps。高精度模拟信号源采用Agilent N6700B,其内置分辨率高达24 bits的DAC,能提供精准的输入模拟电压和数字电源电压,抖动小于1 mV,满足指标需求。数据采集模块用于对输出电压的采集,考虑到采集速度和精度的问题,采取NI 5122板卡,2 V电压下能实现0.122 mV的电压分辨率。仪器精度如表3所示。
表 3 仪器参数
Table 3. Instrument parameters
Instrument Resolution Highest frequency 5122 14 bits 100 MHz 81150A 118.2 ps 5 MHz Agilent N6700B <1 mV - 在硬件的基础上,建立一套实时、操作简便的软件系统是必不可少的。文中基于美国NI公司开发的Labview搭建了软件系统。主要包括两个部分:数字时序模块、模拟采集模块。其软件前面板如图3所示。在数字时序模块上可以设置所需加载的时序、通道数和数字电压范围,时钟频率最高可设置为100 MHz,模拟采集模块实现四路采集,可以自行设置采样点数、采样频率、采样电压挡位以及采样起始点,最高采集频率为100 MHz。
在搭建好软硬件测试平台下,根据电路工作原理对DUT进行测试,其测试过程如图4所示。通过模拟信号源和时钟脉冲发生器模块给探测器施加所需偏置和时序,控制斜坡发生器给电路提供所需波形,安装波长为1550 nm的激光源用于发射激光脉冲;启动Labview软件,设置好时序发生器和模拟采集部分的参数。运行软件,使封装于测试杜瓦的被测单元器件(液氮冷却)正常工作;被测器件输出数据,然后通过测试软件采集若干次并保存数据至计算机。
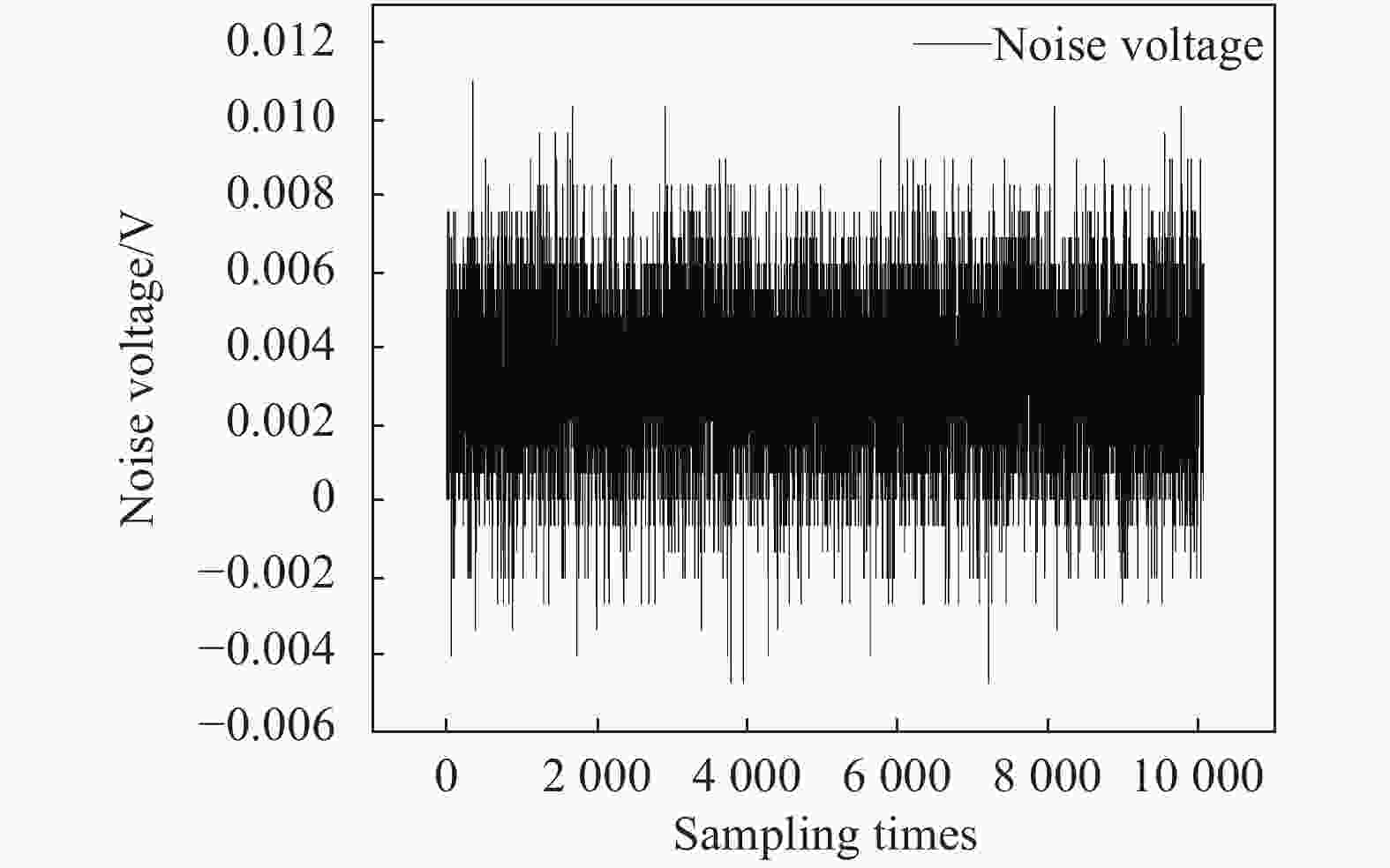
基于该测试平台,文中对平台的测试误差进行了分析。首先,在空载下(即采集端不接入任何信号)对系统以及环境噪声进行测试,如图5所示,给出了多次测量的噪声电压值,此噪声电压使公式(5)中的V2d、V3d产生一定的偏移量,从而影响TOF的精度。通过公式(6)计算得到系统均方根噪声为253.8 μV,代入公式(5)中得到能分辨的时间精度为179 ps。
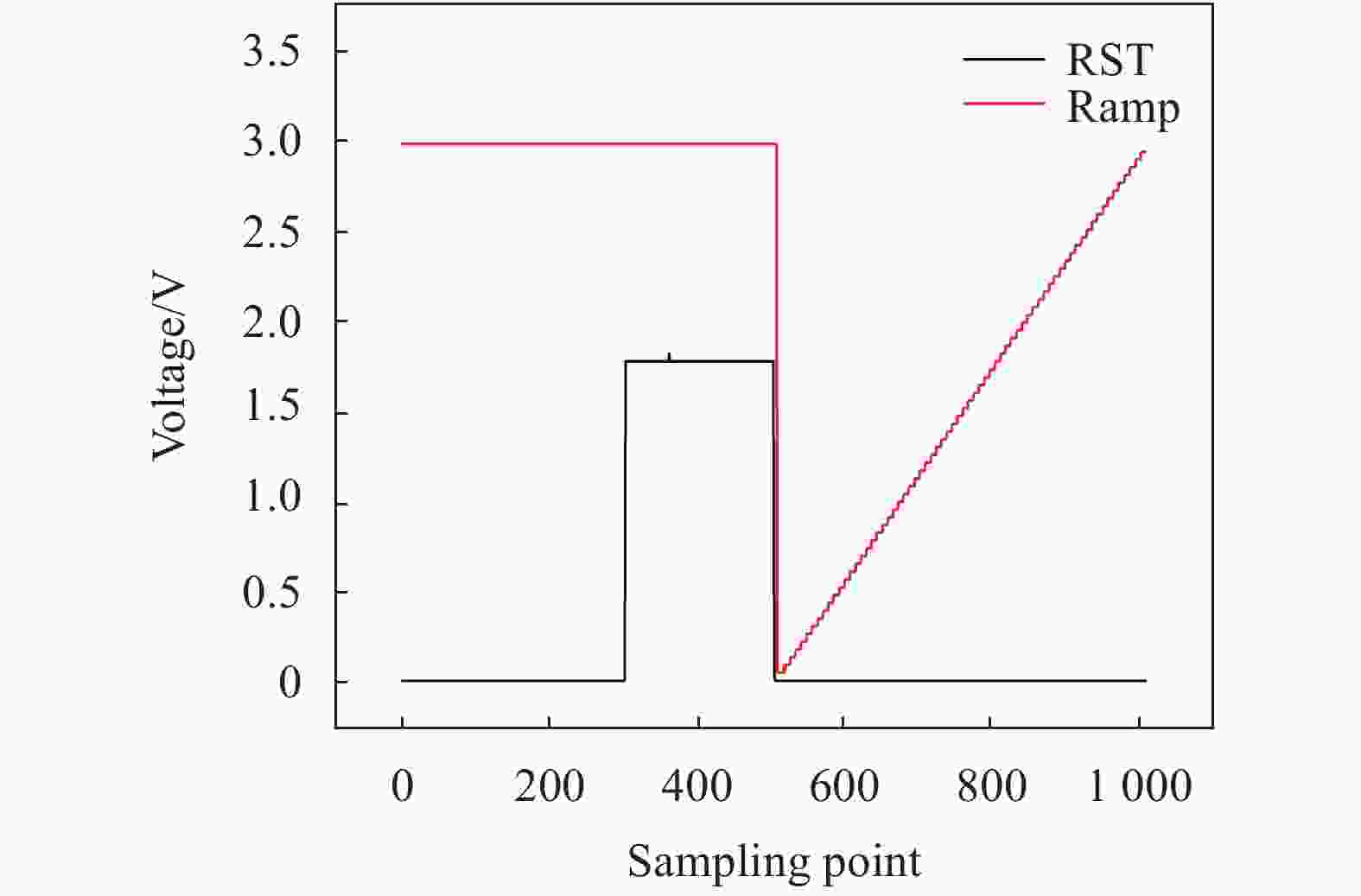
同时文中也分析了测试平台中斜坡发生器带来的固定时延对时间精度的影响。如图6所示,用5122板卡的最高频率对斜坡发生器信号进行重复采样,得到斜坡发生器的一个固定时延为370 ns,可以通过校准来消除,最终可以通过公式(5)中的增加修正项消除,即:
$$ \begin{array}{l} TOF = \dfrac{1}{2}\left[\dfrac{{{V_{3{\rm{d}}}}}}{\alpha } - \dfrac{{{C_{3{\rm{d}}}}\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right)}}{{\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times T\right] + {T_0} \end{array} $$ (7) 式中:T0为修正项,为370 ns。
-
基于上述理论计算和搭建的测试平台对该款线性HgCdTe APD探测器和读出电路进行耦合互联测试,探测器前端未加1.55 μm窄带滤光片和冷屏下,对探测器进行I/V测试,如图7所示。从图中可以得到当反偏电压为2.5 V以及激光光功率为0时,背景光电流大约为15.89 nA.
APD电路采用QFP64封装,与探测器互联置于杜瓦内,在77 K环境下测试。实验测试中把激光器直接对准杜瓦里面的探测器,探测器前端不加1.55 μm窄带滤光片和冷屏,即在没有激光脉冲的情况下也有15.89 nA的背景光电流进行积分,电路测试加载的条件如表4所示。
表 4 电路测试条件
Table 4. Circuit test conditions
Parameter Value Temperature/K 77 Preamp CTIA bias voltage/V 1.5 Comparator voltage/V 3 Ramp frequency/K 200 Ramp delay/μs 1 Laser pulse width/μs 4.5 APD reverse bias voltage/V 2.5 (p=110 μW) Sampling frequency/MHz 100 -
将图1(a)中的使能信号EN置低电平,处于被动模式下测试。测试在不同的激光光功率和探测器在不同反偏电压下的强度信息变化情况。如图8所示。横坐标代表一帧下的采样点数,采样频率在100 MHz下每个点的时间为10 ns,纵坐标为V2d值。当固定激光光功率P为78 μW时,随着探测器的反偏电压Vdet不断增加,产生的电流变大,积分到达饱和值的时间更短。同样当探测器反偏电压为3 V时,不断增大光功率积分也更快达到饱和。从测试结果来看,低温下电路的线性度高达99.9%,电路的输出范围为1.5 V到4 V,即电路的饱和电荷容量为7 Me−,符合电路的仿真结果。
-
当使能信号EN置高电平时,进入主动探测模式,激光器直接贴敷在杜瓦窗口上,电路测试采取改变斜坡起始时间来模拟目标物体的距离,通过改变斜坡信号相对复位信号下降沿延迟时间t得到对应该时间下的电压值V3d,如图9(a)所示。当斜坡信号相对复位信号下降沿延迟时间分别为t1和t2时,对应的电压值V3d也相应地变化,即得到不同的TOF值。其测试结果如图9(b)所示。
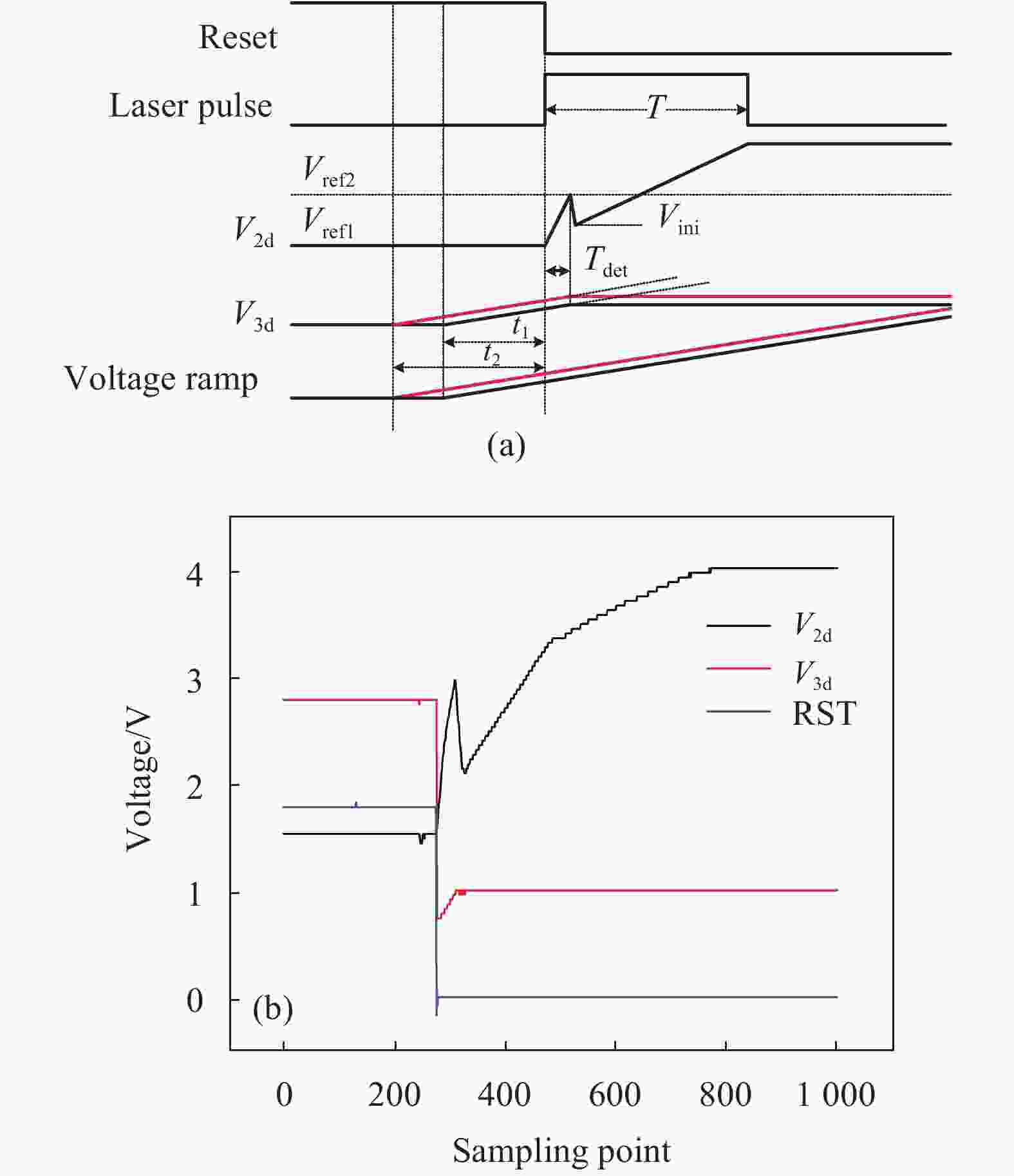
图 9 (a) 电路测试时序;(b) 碲镉汞APD探测器和电路耦合测试结果
Figure 9. (a) Circuit test sequence; (b) HgCdTe APD detector and circuit coupling test results
V2d和V3d分别为目标物体强度信息和时间信息,RST为电路的复位信号。CTIA积分电压V2d分为三段:小电容C3d的快速积分使得电压值达到比较器的翻转电压;大电容C2d与C3d并联积分到激光脉宽结束;背景光电流的积分直到电容饱和。当比较器翻转后,控制锁存模块记录当下斜坡发生器值并输出,即V3d。
根据公式(7),文中分析了斜坡斜率α、电容值C、高精度电压源输出电压V、采样电压V2d和V3d值对TOF的精度带来的影响。
-
斜坡发生器发射的斜坡轻微抖动会使得TOF也存在一定的偏差,且是不可逆的。其表述为公式(8):
$$ TOF = \frac{1}{2}\left[\frac{{{V_{3{\rm{d}}}}}}{{\alpha + \Delta \alpha }} - \frac{{{C_{3{\rm{d}}}}\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right)}}{{\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times T\right] + {T_0} $$ (8) 根据公式(8)可以计算斜坡变化对TOF的抖动,表述为公式(9):
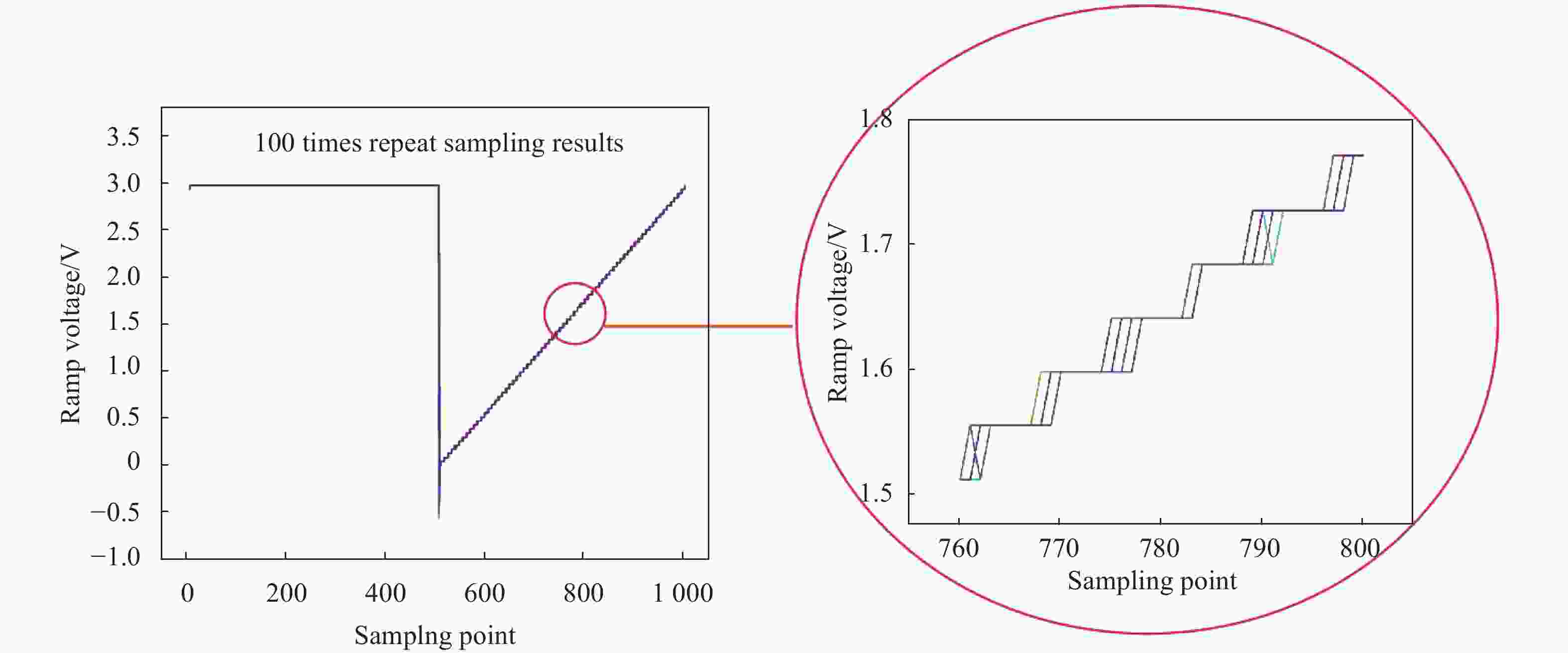
$$ \Delta TOF = \frac{{{V_{3{\rm{d}}}}}}{2}\left[ {\frac{{\Delta \alpha }}{{\alpha \left( {\alpha + \Delta \alpha } \right)}}} \right] $$ (9) 图10是对斜坡发生器发射的斜坡进行多次重复采样输出图。通过采集100组数据计算得到斜坡抖动RMS值为0.00846 mV/ns。即在上面测试的V3d下带来TOF的抖动为118.20 ps。
-
针对电路不管采用何种工艺流片,电路的寄生效应和工艺偏差都会对电容值产生一定的偏差。对公式(7)修正得到公式(10),即:
$$ \begin{split} TOF =& \dfrac{1}{2}\Bigg[\dfrac{{{V_{3{\rm{d}}}}}}{\alpha } - \\ &\dfrac{{\left( {\Delta {C_{3{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right)}}{{\left( {{C_{2{\rm{d}}}} + \Delta {C_{2{\rm{d}}}} + {C_{3{\rm{d}}}} + \Delta {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \end{split}\times T\Bigg] + {T_0} $$ (10) 分别讨论公式(10)中C2d和C3d对TOF的影响,得到公式(11)~(12):
$$ \begin{array}{l} \Delta TOF\! = \!\dfrac{{T\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right)}}{{2\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times \dfrac{{{C_{3{\rm{d}}}} \times \Delta {C_{2{\rm{d}}}}}}{{\left( {{C_{2{\rm{d}}}} \!+ \!{C_{3{\rm{d}}}}} \right)\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}} \!+\! \Delta {C_{2{\rm{d}}}}} \right)}} \end{array} $$ (11) $$ \begin{array}{l} \Delta TOF \!=\! \dfrac{{T\left( {{V_{{\rm{ref}}2}} \!-\! {V_{{\rm{ref}}1}}} \right)}}{{2\left( {{V_{2{\rm{d}}}} \!-\! {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times \dfrac{{\Delta {C_{3{\rm{d}}}} \times {C_{2{\rm{d}}}}}}{{\left( {{C_{2{\rm{d}}}} \!+\! {C_{3{\rm{d}}}}} \right)\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}} \!+\! \Delta {C_{2{\rm{d}}}}} \right)}} \end{array} $$ (12) 在激光脉宽为4.5 μs下V2d值为3.347 V,代入公式(11)可以计算得到电容存在0.222 fF的偏差,使得TOF有100 ps的抖动。为电路流片工艺选择提供了参考。
-
测试中电路激励和偏置电压都是采用高精度模拟信号发生器产生,它内置24 bits DAC,但其输出结果存在一定的抖动。对公式(7)修正得到公式(13),即:
$$ TOF \!=\! \frac{1}{2}\left[\frac{{{V_{3{\rm{d}}}}}}{\alpha } \!-\! \frac{{{C_{3{\rm{d}}}}\left( {{V_{{\rm{ref}}2}} \!+\! \Delta {V_{{\rm{ref}}2}} \!-\! {V_{{\rm{ref}}1}} -\! \Delta {V_{{\rm{ref}}{\rm{1}}}}} \right)}}{{\left( {{C_{2{\rm{d}}}}\! +\! {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} \!-\! {V_{{\rm{ref}}{\rm{1}}}} \!-\! \Delta {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times T\right] + {T_0} $$ (13) 同样分开讨论给TOF带来的影响,得到公式(14)和(15):
$$ \Delta TOF = \frac{{T \times {C_{3{\rm{d}}}} \times \Delta {V_{{\rm{ref}}2}}}}{{2\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right)}} $$ (14) $$ \Delta TOF = \frac{{T \times {C_{3{\rm{d}}}}\left( {{V_{{\rm{ref}}2}} - {V_{2{\rm{d}}}}} \right)\Delta {V_{{\rm{ref}}{\rm{1}}}}}}{{2\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}{\rm{1}}}}} \right)}} $$ (15) 从电压源上采集的结果显示电压的抖动在1 mV以内,代入公式(10)可以得到其对时间TOF的偏差为135.36 ps。
-
采集系统的精度直接影响V2d和V3d的精度,这决定了TOF的抖动范围。因此对公式(7)修正得到公式(16)和(17),即:
$$ \begin{split} &\\ TOF \!= \!\dfrac{1}{2}\left[\dfrac{{{V_{3{\rm{d}}}}}}{\alpha } \!- \! \dfrac{{{C_{3{\rm{d}}}}\left( {{V_{{\rm{ref}}2}} \!-\! {V_{{\rm{ref}}1}}} \right)}}{{\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} \!+\! \Delta {V_{2{\rm{d}}}} \!-\! {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times T\right] \!+\! {T_0} \end{split} $$ (16) $$ \begin{array}{l} TOF\! =\! \dfrac{1}{2}\left[\dfrac{{{V_{3{\rm{d}}}}\! +\! \Delta {V_{3{\rm{d}}}}}}{\alpha } \!- \! \dfrac{{{C_{3{\rm{d}}}}\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right)}}{{\left( {{C_{2{\rm{d}}}}\!+\! {C_{3{\rm{d}}}}} \right)\left( {{V_{2{\rm{d}}}} \!-\! {V_{{\rm{ref}}{\rm{1}}}}} \right)}} \times T\right] \!+\! {T_0} \end{array} $$ (17) 由公式(16)、(17)可以分别得到V2d和V3d的抖动对TOF的影响,即:
$$ \begin{array}{l} \Delta TOF = \dfrac{{T \times {C_{3{\rm{d}}}}}}{{2\left( {{C_{2{\rm{d}}}} + {C_{3{\rm{d}}}}} \right)}} \times \dfrac{\Delta {V_{2{\rm{d}}}\left( {{V_{{\rm{ref}}2}} - {V_{{\rm{ref}}1}}} \right)}}{{\left( {{V_{2{\rm{d}}}} - {V_{{\rm{ref}}1}}} \right)\left( {{V_{2{\rm{d}}}} + \Delta {V_{2{\rm{d}}}} - {V_{{\rm{ref}}1}}} \right)}} \end{array} $$ (18) $$ \Delta TOF = \frac{{\Delta {V_{3{\rm{d}}}}}}{{2\alpha }} $$ (19) 即在V3d抖动为1 mV的情况下,TOF的偏移量为0.833 ns;在V2d抖动为1 mV的情况下,TOF的偏移量为24.335 ps。因此V3d的稳定性对TOF的精度起到决定性的影响,而V2d是对TOF值偏差的修正项。
因此测试系统和电路对TOF精度影响的具体参数如表5所示。从中可以得到为了预留一定量,V3d的抖动需控制在10 ns范围内,采集系统在2 V范围下能实现5 mV的精度。
表 5 影响TOF精度的性能参数
Table 5. Performance parameters that affect TOF resolution
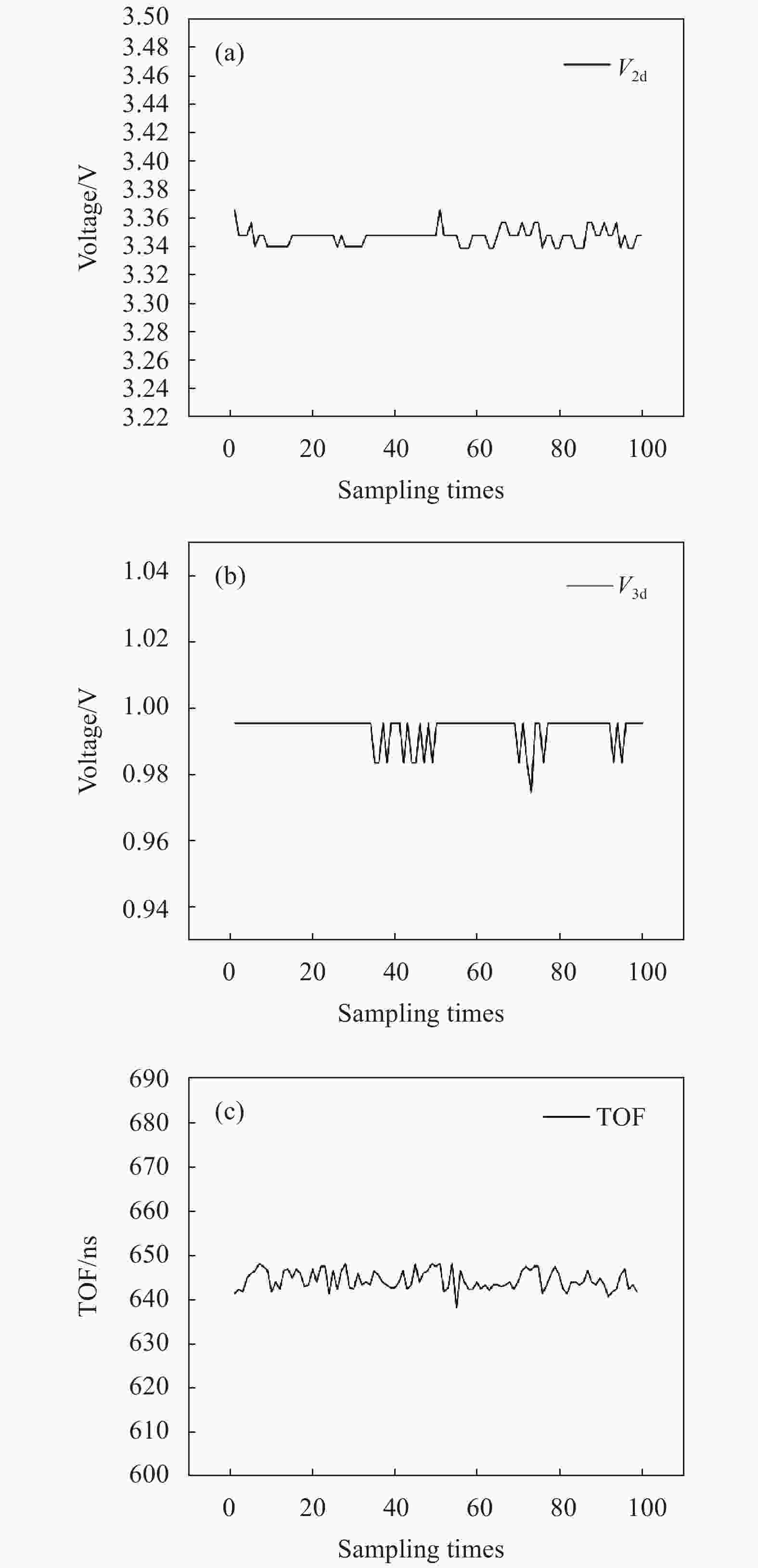
Type Sub-type Resolution System System noise 179 ps Ramp jitter 118.20 ps Voltage source error 135.36 ps@1 mV Circuit Capacitance deviation 100 ps@0.222 fF Output jitter(V2d) 24.335 ps@1 mV Output jitter(V3d) 833 ps@1 mV 在表4的工作条件下进行100次重复采样,得到100组V2d和V3d值,如图11(a)、(b)所示,从测试结果看出,V2d和V3d的测量值存在一定的抖动,对100组数据进行计算得到V3d的RMS值为0.00753 V,V2d的RMS值为0.02076 V。
根据电路测试条件计算TOF的理论值为斜坡的时延(1 μs)减去固定延时(370 ns),即为630 ns。图11(c)展示了通过Matlab对数据进行处理后每帧下的TOF的值。从实验数据得到TOF的最大值为647.961 ns,最小值为638.014 ns,TOF抖动是由采样的斜坡斜率、V2d和V3d不相同导致,代入公式(6)计算得到TOF的RMS为2.107 ns。
在不改变工作条件下重复上述测试,采集10次100组样本计算RMS得到的结果如图12所示。可以得到TOF的RMS值为2.017~2.073 ns,证明了测试平台在验证ns级别的可行性。
最后,对文中工作和法国Sofradir公司测试平台参数和测试结果进行了比较,如表6所示。斜坡发生模块中最高频率都是一样,但文中每格可分辨的电压值范围大,有利于采集的区分,在A/D部分,文中的采集频率最高可达100 MHz,最终TOF测试结果略低于Sofradir的精度。
表 6 文中工作与Sofradir的测试平台和测试结果的比较
Table 6. Comparison of the proposed work with the Sofradir test platform and test results
Proposed work Sofradir[14] Temperature/K 77 80 Laser:min step/ns 10 12.5 Ramp 200 ns max; slope
15 mV/ns200 ns; slope
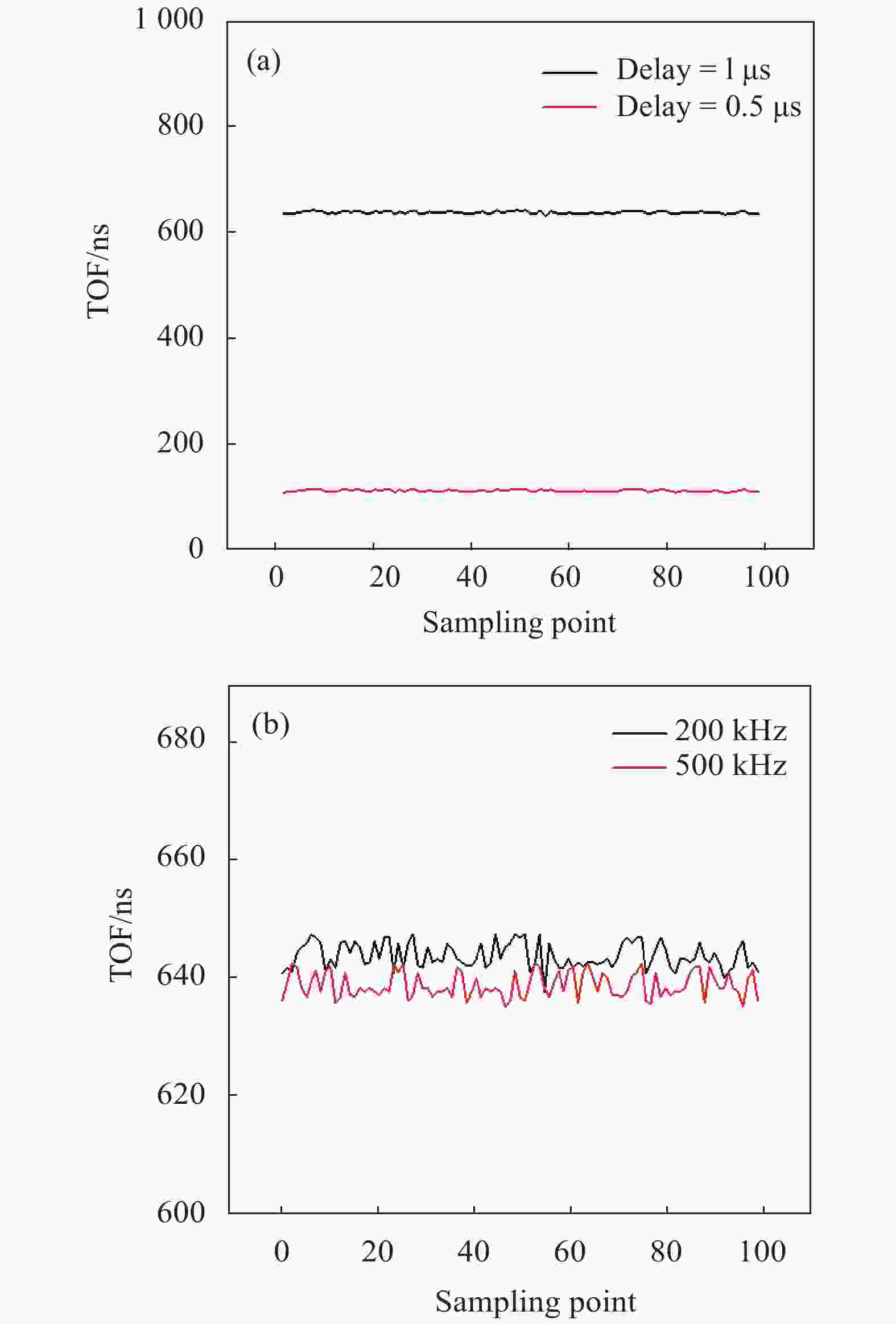
10 mV/nsA/D 14 bits; 2 V; 100 MHz 14 bits; 4 V; 100 kHz Resolution/cm 63.21 60 同时分析了改变斜坡延迟时间(即改变被测目标物体的距离)和斜率对TOF的影响,如图13所示。在0.5 μs的时延下TOF的最大值为119.960 ns,最小值为112.508 ns,其RMS值为2.109 ns。验证了不同景深情况下的RMS基本不变。从图13(b)中可以看出,相对于200 kHz,在500 kHz下测试的结果值与理论值(630 ns)更接近,因为斜坡频率提高了,使得分辨每个台阶的时间缩短,即增加了测试结果的精度。相对应地测量距离的范围变小。相应的也可以从电路设计中减小模拟电源电压,牺牲输出摆幅来减小TOF的抖动。
基于上述测试结果得到,在被动模式下,电路实现了随激光光强增大和反偏电压的变大,积分的速度变大,和电路仿真结果吻合。在主动模式下,分析了TOF相关的参数(斜率α、输入电压Vref、电容值C及V2d和V3d)对其带来的精度影响。测试得到电路能很好地展现不同状态下的积分情况,测得TOF的RMS为2.107 ns,能实现对线性APD读出电路的性能进行有效的评估,为探索线性模式下APD的主被动探测的测试方法提供了新的思路。
-
文中首先提出了一种适用线性模式碲镉汞APD探测器的主被动读出电路结构,并对电路进行了分析和TOF时间计算方法的研究。搭建了一套适合线性碲镉汞APD探测器和电路互联的软硬件测试平台,测量系统噪声得到RMS值为253.8 μV,通过对测试平台固定时延等参数进行校准来提高测试准确性,在77 K下完成了该款线性模式HgCdTe APD读出电路的主、被动信息的测试。测试结果表明,被动模式下电路功能正常,与电路的仿真结果基本符合,主动模式下分析了斜率α、输入电压Vref、电容值C及V2d和V3d等对TOF精度带来的影响。最终计算得到电路TOF的RMS值为2.107 ns。测试结果证明该测试方法和测试平台能有效地对线性APD读出电路进行评估,在红外精准探测领域具有实际工程应用的价值。
Research on testing of active and passive HgCdTe APD detector in linear mode
-
摘要: 碲镉汞雪崩光电二极管(Avalanche Photodiode, APD)探测器在主被动模式下能同时获取目标物体的强度信息和时间信息,实现实时的三维探测。高精度时间标定的测试方法是验证三维测距的基础。文中分析了盖革模式和线性模式的优缺点,针对一种线性模式主被动HgCdTe APD探测器的读出电路结构进行了分析,并对TOF计算方法进行了研究,在此基础上搭建了一套高精度时间标定的测试平台,对系统和环境噪声进行了测试,得到噪声带来的时间抖动为179 ps。对测试仪器带来的固定时延进行了校准,对影响TOF精度的电压、电容、斜坡发生器的精度以及高精度电压源的精度等参数进行了理论分析,在77 K下完成了线性模式HgCdTe APD探测器的主、被动信息的测试。测试结果得到低温下电路线性度高达99.9%,饱和电荷容量为7 Me−,时间精度抖动的均方根为2.107 ns,证明该测试平台和方法能有效地评估探测器的性能,为红外精准探测提供了参考。Abstract: The mercury cadmium telluride avalanche photodiode (HgCdTe APD) detector can simultaneously obtain the intensity information and time information of the target object in the active and passive mode, to realize real-time three-dimensional detection. The testing method of high-resolution time calibration is the basis for verifying three-dimensional ranging. The advantages and disadvantages of Geiger mode and linear mode were analyzed. Besides, the readout circuit structure of a linear mode active and passive HgCdTe APD detector was analyzed, and the time-to-flight (TOF) calculation method was studied. On this basis, a set of high-precision time calibration test platform was built, the system and environmental noise were tested, and the time jitter caused by the noise was 179 ps. The fixed time delay caused by the test instrument was calibrated, and theoretical analysis was conducted on the voltage, capacitance, the accuracy of the ramp generator and the high-precision voltage source and other parameters that affected the TOF resolution. The active and passive information test of the linear mode HgCdTe APD detector was completed at 77 K. The test results show that the circuit linearity is as high as 99.9% at low temperature, the saturation charge capacity is 7 Me−, the root mean square (RMS) value of the time resolution jitters is 2.107 ns. It proves that the test platform and method can effectively evaluate the performance of the detector, and provide reference for precise infrared detection.
-
Key words:
- linear mode APD /
- active and passive detection /
- time of flight (TOF) /
- time resolution
-
表 1 盖革和线性模式APD性能对比
Table 1. Geiger and linear mode APD performance comparsion
Type GM-APD LM-APD Gain 105-106 10-103 Dynamic range Low High Quenching circuit Yes No Intensity information No Yes Continuous detection capability No Yes 表 2 读出电路性能参数
Table 2. Readout circuit performance parameters
Parameter Description Technology TSMC 0.18 μm 1P6M CMOS Temperature/K 77 Pixel/μm2 50×50 Output swing/V 1.5-4 Power/mW 17.5 表 3 仪器参数
Table 3. Instrument parameters
Instrument Resolution Highest frequency 5122 14 bits 100 MHz 81150A 118.2 ps 5 MHz Agilent N6700B <1 mV - 表 4 电路测试条件
Table 4. Circuit test conditions
Parameter Value Temperature/K 77 Preamp CTIA bias voltage/V 1.5 Comparator voltage/V 3 Ramp frequency/K 200 Ramp delay/μs 1 Laser pulse width/μs 4.5 APD reverse bias voltage/V 2.5 (p=110 μW) Sampling frequency/MHz 100 表 5 影响TOF精度的性能参数
Table 5. Performance parameters that affect TOF resolution
Type Sub-type Resolution System System noise 179 ps Ramp jitter 118.20 ps Voltage source error 135.36 ps@1 mV Circuit Capacitance deviation 100 ps@0.222 fF Output jitter(V2d) 24.335 ps@1 mV Output jitter(V3d) 833 ps@1 mV 表 6 文中工作与Sofradir的测试平台和测试结果的比较
Table 6. Comparison of the proposed work with the Sofradir test platform and test results
Proposed work Sofradir[14] Temperature/K 77 80 Laser:min step/ns 10 12.5 Ramp 200 ns max; slope
15 mV/ns200 ns; slope
10 mV/nsA/D 14 bits; 2 V; 100 MHz 14 bits; 4 V; 100 kHz Resolution/cm 63.21 60 -
[1] Rogalski. Next decade in infrared detectors[C]//Electro-Optical and Infrared Systems: Technology and Applications XIV, 2017, 10433: 0L-1-0L-25. [2] Bu Yuming, Zeng Chaoyang, Du Xiaoping. Research progress of photoelectric mixing technology in laser three-dimensional imaging [J]. Laser & Optoelectronics Progress, 2019, 56(8): 1-8. (in Chinese) doi: 10.3788 [3] Antoni Rogalski, Antoszewski J, Faraone L. Third-generation infrared photodetector arrays[J]. Journal of Applied Physics, 2009, 105(9): 091101. [4] Zuber M T, Smith D E, Solomon S C, et al. Mars observer laser altimeter investigation[C]//SPIE, 1993, 1943(97): 14-18. [5] Amzajerdian F, Bulyshev A E, Pierrottet D F, et al. Imaging flash LIDAR for safe landing on solar system bodies and spacecraft rendezvous and docking[C]//SPIE Defense, Security and Sensing, 2015: 355-358. [6] Eric de Borniol, Fabrice Guellec, Johan Rothman, et. al. HgCdTe-based APD focal plane array for 2D and 3D active imaging: first results on a 320×256 with 30 µm pitch demonstrator[C]//Infrared Technology and Applications XXXVI, 2010, 7660 (3D): 1-9. [7] Eric de Borniol, Johan Rothman, Fabrice Guellec, et al. Active three-dimensional and thermal imaging with a 30-µm pitch 320×256 HgCdTe avalanche photodiode focal plane array [J]. Optical Engineering, 2012, 51(6): 061305. doi: 10.1117/1.OE.51.6.061305 [8] Rothman J, Borniol Eric de, Gravrand O, et al. MCT APD focal plane arrays for astronomy at CEA-LETI[C]//SPIE Astronomical Telescopes, 2016, 99150B: 1-12. [9] William McKeag, Tricia Veeder. New developments in HgCdTe APDs and LADAR receivers[C]//Infrared Technology and Applications XXXVII, 2011, 8012 (30): 1-14. [10] Parahyba Victor E, Eric de Borniol, Regis Perrier, et al. Time-of-flight calibration of an MCT-APD sensor for a flash imaging LiDAR system[C]//International Conference on Space Optics, 2018, 11180(2K): 1-7. [11] 郑丽霞. 盖革模式雪崩光电二极管阵列读出电路的研究与实现[D]. 南京: 东南大学, 2017. Zheng Lixia. Research and implementation of GM-avalanche photodiode array readout circuit[D]. Nanjing: Southeast University, 2017. (in Chinese) [12] Wang Dan, Zou Yonggang, Zhao Xin, et al. Semiconductor laser range system and precision analysis[C]//International Conference on Optoelectronics and Microelectronics, 2015: 128-131. [13] Shen Guangyue, Zheng Tianxiang, Du Bingcheng, et al. Near-range large field-of-view three-dimensional photon-counting imaging with a single-pixel Si-avalanche photodiode [J]. Chinese Physical Letters, 2018, 114204: 42-45. [14] Fabrice Guellec, Andresen B F, Eric de Borniol, et al. Advanced pixel design for infrared 3D LADAR imaging[C]//SPIE, 2008, 6940: 69402M. -






 下载:
下载: