-
偏振探测是测量目标场景中电磁波偏振态的过程[1],与传统的光强、光谱探测技术相比,不仅更容易识别目标,而且还可以获得更多目标信息,例如偏振度、偏振角等信息[2]。因此,偏振探测在遥感成像[3]、医学诊断[4-5]、大气环境检测[6]等领域具有重要的应用价值。
传统的偏振探测系统一般通过集成诸多偏振元件或相位延迟器来实现对景物入射光的调制,按探测方式可分为分时型和同时型[7]。分时型探测系统通过旋转玻片以探测各偏振光强并估算部分或者完整的斯托克斯矢量,比较耗时。该过程中必须保证场景和系统处于静止状态,难以应用于高动态目标的探测,限制了其应用范围。为了弥补这一缺点,研究人员提出了同时型偏振测量系统[8-11],实现对多个偏振态实时探测。然而,无论是分时型还是同时型都存在测量系统体积庞大,复杂且昂贵的问题,不符合未来光学器件的微型化和轻量化发展趋势。
超表面作为一种新型的人工表面结构,可以在极薄的二维平面上实现对电磁波相位,振幅和偏振的精确调控[12-14],它具有紧凑且轻量化等优点,这为解决上述问题带来新的契机。研究显示超表面在偏振控制、波前调控方面具有明显的优势,在聚焦透镜[15]、光的自旋轨道相互作用[16-18]和全息显示[19]中扮演着重要角色。此外,超表面也适用于偏振测量及成像[20-22]。起初,基于几何相位原理设计的超表面实现了对入射光波圆偏振度的探测[23-24]。为了获得光的完全偏振信息,Anders Pors等人利用Au-SiO2-Au结构构建的等离子体光栅,可以将不同偏振态的光衍射到不同区域,并计算衍射对比度来表征入射光偏振态[25]。随后他们进一步增加了光谱探测的功能,获得了750~950 nm波段的全Stokes参数[26],但是入射光方向仅限于垂直入射。并且由于金属结构具有吸收损耗,导致效率降低,而介质结构避免了这一问题,因此受到了广泛关注。Miyata Masashi等人提出了一种介质型复眼超表面,实现了对线偏振光的高灵敏度成像[27]。合肥工业大学郭忠义团队采用双相位调制的方式,分别实现了对左右旋圆偏振光以及正交线偏振光的灵活调控[28-29],提高了能量的利用率。Ehsan Arbabi等人利用介质型超表面实现了完整的Stokes参数测量并实现了偏振成像[1]。杨振宇等人首次把超透镜阵列引入到系统设计中,实现了对入射光偏振态和相位信息的检测[30]。随后,郭凯等人设计了一种介质紧凑型超表面,通过测量4个偏振态的聚焦光强重构出全Stokes参数[31]。然而,这些研究中入射光的方向通常局限在固定角度,不能满足实际的应用需求。基于超表面的大角度波前调控已有相关研究,笔者所在团队研究人员利用二次相位将入射光的旋转对称性转化为焦点光斑的平移对称性,实现了大视场聚焦[32]。刘文玮等人利用此原理设计了宽带的超表面透镜可以用于广角傅里叶分析[33]。随后,笔者所在研究团队又设计了双层几何相位超表面,利用二次相位波前和结构的局部悬链线场分布实现了高效率的大视场光束调控[34]。虽然这些研究只是针对圆偏振光的波前调控,但是为大角度的偏振探测工作奠定了理论基础。最近的研究结果也进一步证明了二次相位在大角度入射光偏振探测的可行性[35],然而研究还存在设计不紧凑的缺点。
文中提出了一种基于二次相位超表面的紧凑型大视场偏振探测器件。该器件由2×2个子阵列构成,每个阵列利用二次相位设计波前,可实现对预设大角度偏振光的聚焦。这里预设的4个偏振态为水平线偏振(X)、垂直线偏振(Y)、+45°线偏振态(A)和左旋圆偏振态(L)。同时还分别介绍了入射角的测量原理和Stokes公式修正过程,并通过入射不同角度的具有不同偏振态的入射光证明了设计器件的可靠性。与传统偏振探测系统相比,所设计的超表面不仅可以探测大角度入射光的入射角及偏振态,并且更加紧凑。
-
偏振态的表征方法中,Stokes矢量法不仅可以表述任意偏振态、而且容易探测,因此,在偏振探测中得到了广泛的应用。Stokes矢量由4个光强参数S0、S1、S2、S3描述,表示如下[31]:
$$ S = \left[ {\begin{array}{*{20}{c}} {{S_0}}\\ {{S_1}}\\ {{S_2}}\\ {{S_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{I_x} + {I_y}}\\ {{I_x} - {I_y}}\\ {{I_a} - {I_b}}\\ {{I_l} - {I_r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{I_x} + {I_y}}\\ {{I_x} - {I_y}}\\ {2 \times {I_a} - {S_0}}\\ {2 \times {I_l} - {S_0}} \end{array}} \right] $$ (1) 式中:S0为总光强;S1、 S2、 S3分别为入射光在正交基矢
$ \left( {\overrightarrow x ,\overrightarrow y } \right) $ 、$ \left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {1/\sqrt 2 } \right)\left( {\overrightarrow x + \overrightarrow y ,\overrightarrow x - \overrightarrow y } \right) $ 和$ \left( {\overrightarrow r ,\overrightarrow l } \right) = \left( {1/\sqrt 2 } \right)\left( {\overrightarrow x + i\overrightarrow y ,\overrightarrow x - i\overrightarrow y } \right)$ 下测量的光强差。为了数据更加直观,通常对Stokes参数用S0进行归一化。由公式(1)可知任意一束偏振光的Stokes矢量可通过测量垂直于传播方向平面内的光强$ I_x $ 、$I_y $ 、$ I_a$ 、$ I_l $ 得到。一般而言,探测器平行于设计器件,当入射光倾斜入射时,只有部分光被分解聚焦在焦平面上,这会导致得到的Stokes参数不准确。因此,需要明确Stokes参数与入射角和获得的4个光强之间的关系。在推导过程中,建立了两个笛卡尔坐标系x′y′z′和x″y″z″,其中z′轴和z″轴分别对应实际入射光的方向和超表面的法线,探测器平行于x″y″。假设一束单色平面波沿x′z′平面以θ角入射,其电场的振幅可以由琼斯矩阵表示为下式:$$ \left[ {E_0^{'}} \right] = {\left[ {A_x^{'}\;\;\;\;A_y^{'}{e^{i\delta }}} \right]^{\rm{T}}} $$ (2) 式中:
$ A_x^{'} $ 、$ A_y^{'}$ 、δ分别为水平与垂直电场分量的振幅与相位差。分别在两个坐标系下表示预设偏振分量的光强,将两个结果进行比较,得到矫正的Stokes参数公式,通过公式揭示Stokes矢量与入射角和焦平面聚焦光强的关系。为了得到在不同偏振态下的光强值,将入射光分解为所设计的偏振分量。在x′y′z′坐标系下,得到4个偏振分量的光强为:$$ \left[ {\begin{array}{*{20}{c}} {I_x^\prime }\\ {I_y^\prime }\\ {I_a^\prime }\\ {I_l^\prime } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {A_x^{\prime 2} + A_y^{\prime 2}}\\ {A_x^{\prime 2} - A_y^{\prime 2}}\\ {\left( {A_x^{\prime 2} + A_y^{\prime 2}} \right)/2 + A_x^\prime \times A_y^\prime \times {\rm{cos}} \delta }\\ {\left( {A_x^{\prime 2} + A_y^{\prime 2}} \right)/2 + A_x^\prime \times A_y^\prime \times {\rm{sin}} \delta } \end{array}} \right] $$ (3) 因此,x′y′z′坐标系下入射光的Stokes参数可以表示为:
$$ {S^\prime } = \left[ {\begin{array}{*{20}{c}} {S_0^\prime }\\ {S_1^\prime }\\ {S_2^\prime }\\ {S_3^\prime } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {I_x^\prime + I_y^\prime }\\ {I_x^\prime - I_y^\prime }\\ {2 \times I_a^\prime - S_0^\prime }\\ {2 \times I_l^\prime - {S_0^\prime }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {I_x^\prime + I_y^\prime }\\ {I_x^\prime - I_y^\prime }\\ {2 \times A_x^\prime \times A_y^\prime \times {\rm{cos}} \delta }\\ {2 \times A_x^\prime \times A_y^\prime \times {\rm{sin}} \delta } \end{array}} \right] $$ (4) 同样地,在探测坐标系x″y″z″下,分解可得到各个偏振态的光强为:
$$ \left[ {\begin{array}{*{20}{c}} {I_x^{\prime \prime }}\\ {I_y^{\prime \prime }}\\ {I_a^{\prime \prime }}\\ {I_l^{\prime \prime }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {A_x^{\prime 2} \times {{\rm{{cos }}}^2}\theta + A_y^{\prime 2}}\\ {A_x^{\prime 2} \times {{\rm{{cos }}}^2}\theta - A_y^{\prime 2}}\\ {\left( {A_x^{\prime 2} \times {{\rm{{cos }}}^2}\theta + A_y^{\prime 2}} \right)/2 + A_x^\prime \times A_y^\prime \times {\rm{cos}} \delta \times {\rm{cos}} \theta }\\ {\left( {A_x^{\prime 2} \times {{\rm{{cos }}}^2}\theta + A_y^{\prime 2}} \right)/2 + A_x^\prime \times A_y^\prime \times {\rm{sin}} \delta \times {\rm{cos}} \theta } \end{array}} \right] $$ (5) 得到x″y″z″坐标系下的计算结果,表示如下:
$$ \left[ {\begin{array}{*{20}{c}} {I_x^{\prime \prime } + I_y^{\prime \prime }}\\ {I_x^{\prime \prime } - I_y^{\prime \prime }}\\ {2*I_a^{\prime \prime } - \left( {I_x^{\prime \prime } + I_y^{\prime \prime }} \right)}\\ {2*I_l^{\prime \prime } - \left( {I_x^{\prime \prime } + I_y^{\prime \prime }} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {I_x^\prime \times {{\rm{{cos }}}^2}\theta + I_y^\prime }\\ {I_x^\prime \times {{\rm{{cos }}}^2}\theta - I_y^\prime }\\ {2 \times A_x^\prime \times A_y^\prime \times {\rm{cos}} \delta \times {\rm{cos}} \theta }\\ {2 \times A_x^\prime \times A_y^\prime \times {\rm{sin}} \delta \times {\rm{cos}} \theta } \end{array}} \right] $$ (6) 对比公式(4)和(6),可以发现通过测量的4个光强值可以重构Stokes参数,校正的Stokes参数公式如下:
$$ {S^\prime } = \left[ {\begin{array}{*{20}{c}} {S_0^\prime }\\ {S_1^\prime }\\ {S_2^\prime }\\ {S_3^\prime } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {I_x^{\prime \prime }/{{\rm{{cos }}}^2}\theta + I_y^{\prime \prime }}\\ {I_x^{\prime \prime }/{{\rm{{cos }}}^2}\theta - I_y^{\prime \prime }}\\ {\left( {2 \times I_a^{\prime \prime } - I_x^{\prime \prime } - I_y^{\prime \prime }} \right)/{\rm{cos}} \theta }\\ {\left( {2 \times I_l^{\prime \prime } - I_x^{\prime \prime } - I_y^{\prime \prime }} \right)/{\rm{cos}} \theta } \end{array}} \right] $$ (7) 式中:
$I_x^{''} $ 、$I_y^{''} $ 、$ I_a^{''} $ 、$ I_l^{''} $ 分别为x″y″z″坐标系下的光强,可以通过仿真进行测量;θ角为入射角。通过公式(7)可知要实现对大角度入射光的偏振态探测,需要准确地确定入射光的角度。二次相位具有将倾斜入射光的旋转效应转换为聚焦光束的平移对称性的性质,并且平移量与入射光角度密切相关,因此这里采用二次相位设计聚焦相位波前[32, 34]:$$ \varPhi \left( r \right) = {k_0}\dfrac{{{r^2}}}{{2f}} $$ (8) 式中:k0为自由空间中的波数,k 0=2π/ λ ,λ为10.6 μm;f为预设焦距;
$ r = \sqrt {{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}} $ 为任意像素的中心点(x,y)与焦点中心(x0,y0)的距离。前面提到的以θ角入射的入射光通过二次透镜时,出射光所携带的相位为[32]:$$ \begin{split} \varPhi (r) =& {k_0}\dfrac{{{r^2}}}{{2f}} + {k_0}x{\rm{sin}} \theta =\\ &\dfrac{{{k_0}}}{{2f}}\left( {{{(x + f{\rm{sin}} \theta )}^2} + {y^2}} \right) - \dfrac{{f{k_0}{{\rm{{\sin }}}^2}\theta }}{2} \end{split} $$ (9) 式中:
$ {k_0}x sin \theta $ 为由斜入射引入的梯度相位;等式右边最后一项与r无关,可以忽略。与正入射相比,仅在x方向上存在fsinθ的横向偏移[32]。二次相位的波前调控原理如图1(a)所示,根据焦点位置的偏移量可以得到光束的入射角。
图 1 紧凑型大视场偏振探测超表面示意图。(a) 利用二次相位超表面的旋转−平移对称性变换原理图;(b) 设计的超表面。上图为超表面俯视图,下图为单元结构示意图;(c) 设计的紧凑型大角度偏振探测3D原理图
Figure 1. Schematic illustration of metasurface of the compact polarimetry for large field of view. (a) Schematic diagram of rotational-translational symmetry conversion with quadratic phase metasurface; (b) Designed metasurface. The upper one is the top view of the designed metasurface, and the lower picture is illustration of a unit cell; (c) 3D schematic of the compact polarimetry for large field of view
为了实现紧凑型大视场偏振探测,设计了如图1(b)所示的超表面。设计的超表面由4个子透镜组成,以2×2阵列形式排布,这些子阵列由硅衬底上周期排布的不同尺寸的椭圆硅柱组成,分别使一个特定的偏振态聚焦。这里预设的4个偏振态为水平线偏振(X)、垂直线偏振(Y)、+45°线偏振态(A)和左旋圆偏振态(L),如图1(b)中红色箭头所示。调控Y和A偏振的子阵列可以通过简单地旋转调控X偏振的子阵列来获得。其中单元结构如图1(b)中下图所示,硅柱位于单元结构的中心。设计的紧凑型大视场偏振探测器工作原理如图1(c)所示,入射光正入射时,光沿
$ Z^{''} $ 传播,设计的超表面将出射的不同偏振光集中在图像传感器像素的中心,由黑色虚线圆圈表示。当光以θ角斜入射时,光沿$ z^{'} $ 传播,焦点由实心红点表示,与垂直入射相比,焦点横向偏移了fsinθ。 -
利用商用仿真软件CST对设计的紧凑型大视场偏振探测器进行分析。仿真频率为28.3 THz,设计采用的硅折射率为3.42。实现对光偏振态的检测需要单元结构在大视场情况下仍具有0~
$2{\pi} $ 的相位覆盖。这里笔者采用传输相位调控线偏振光,即改变椭圆硅柱的长轴和短轴(L,W)来调节透射相位。对于圆偏振光的调控,采用几何相位的方法,即旋转角度以调节透射相位。对于结构的选择,采用八阶相位调控方法。首先在CST中建模,对单元结构进行参数扫描,得到不同入射角度下的多组透射场的相位和振幅,随后从中筛选出对角度不敏感的结构,最后在这些结构中找到所需的八阶相位。通过优化,单元结构周期和高度确定为4.3 μm和5.5 μm。优化出的单元结构短轴和长轴参数参考文献[35],分别如图2(a)、(b)所示。前8个结构用来调控线偏振光,这些结构分别产生从0~$ 7{\pi}/4$ 的八阶离散相移。第9个结构用于调控圆偏振光。由于调控Y、A线偏振光的阵列可以通过旋转调控X偏振光的阵列获得,因此,这里只呈现了调控X偏振光的结构参数。调控X偏振光的8个单元结构的相位响应如图2(c)所示。当入射角为50°时,单元结构6和7的透射相位几乎相同,不能覆盖0~2${\pi}$ 。但是,在40°入射角内,8个单元结构的相对相位响应分布均匀,这表明在40°范围内单元结构的相对相位响应与入射角无关,因此,视场角为40°。由于调控圆偏振光的结构只有一个,不需要考虑斜入射对结构相位响应的影响,并且理论上限为90°,且已经实验验证圆偏振光的入射角可达80°[32]。因此,设计中视场角的大小主要由调控线性偏振光的结构的角度响应限制。图2(d)为不同入射角下的单元结构的透射振幅。不同的是,第九个结构是针对圆偏振的调控,采用了几何相位的方法,因此,这里的透射振幅主要关注交叉偏振部分。优化设计的单元结构在宽入射角下具有相对较高的透射率,为偏振探测具有更好的性能提供保障。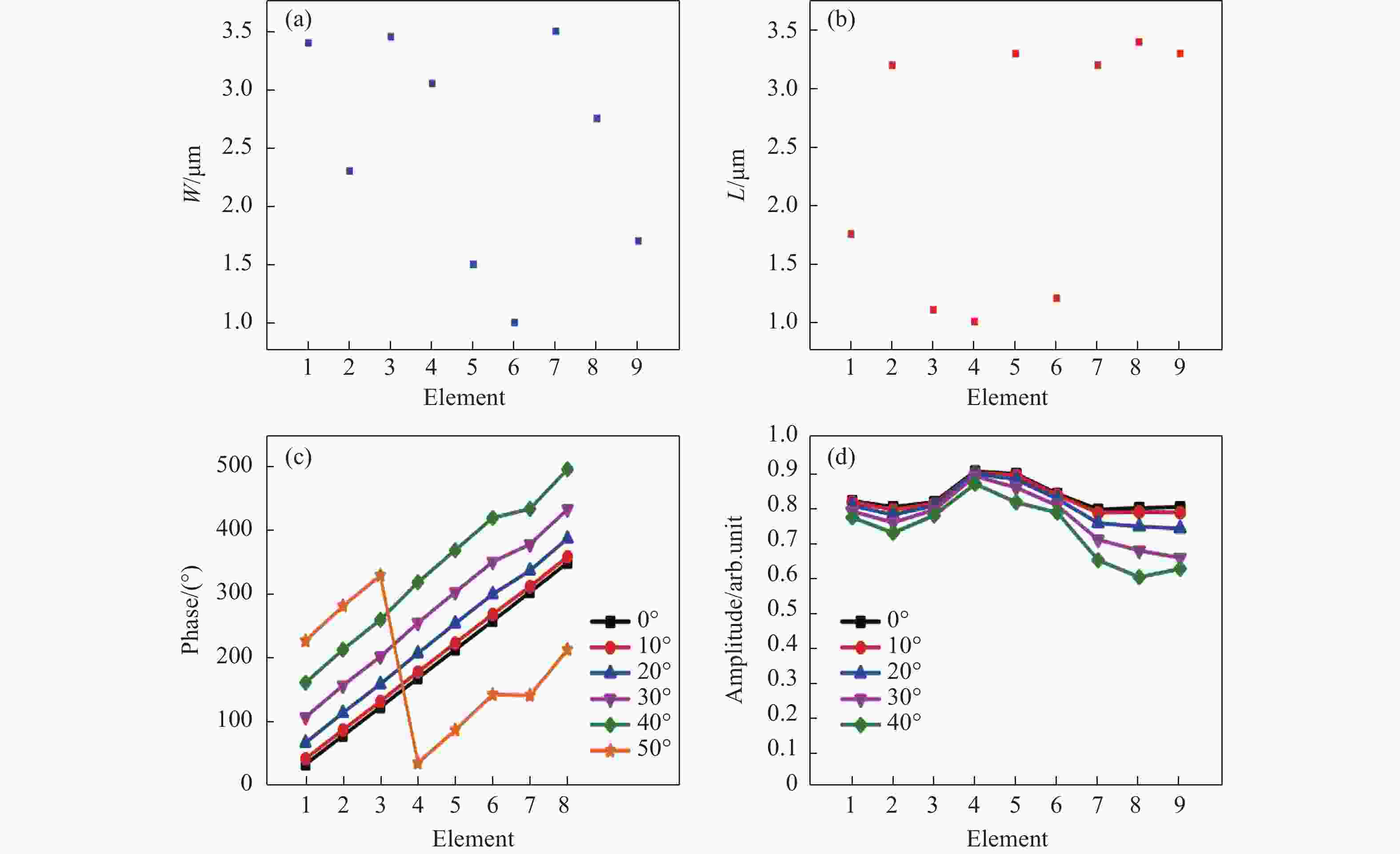
图 2 设计的单元结构。(a), (b) 优化的单元结构的短轴(W)和长轴(L)尺寸;(c) 0°、10°、20°、30°、40°和50°入射时前8个结构对应的相位响应;(d)单元结构在0°,10°,20°,30°和40°入射时的透射振幅
Figure 2. Designed unit cells. (a), (b) Short axis (W) and long axis (L) dimensions of the optimized unit cells; (c) Corresponding phases response of the first eight elements for incident angles of 0°, 10°, 20°, 30°, 40°, and 50°, respectively; (d) Corresponding transmitted amplitudes of all elements for incident angles of 0°, 10°, 20°, 30°, and 40°, respectively
为了证明器件具有对入射光角度探测的能力,利用CST对调控X偏振光的子透镜进行仿真。透镜由45×45个单元结构组成,子透镜口径193.5 μm×193.5 μm,预设的焦距为90 μm。由于二次透镜比普通透镜具有更大的焦深,因此在入射角为0°、10°、20°、30°和40°时,最大强度偏移至z=64 µm,这与数值仿真结果一致。不同角度入射的仿真结果如图3所示,图3(a)为z=64 µm处的焦斑光强分布图,从左到右对应的入射角分别为0°、10°、20°、30°和40°,可以看到不同的入射角度对应于不同的焦点位置。通过图3(a)中焦点的偏移量(fsinθ)计算出入射角,如图3(b)所示。黑色圆点为计算的入射角,黑线为拟合曲线。计算的入射角与实际入射角之间的绝对误差由红色三角形表示,均小于0.29°,这表明超表面可以准确地检测入射光的角度。入射角的精确检测是准确测量斯托克斯参数的先决条件。
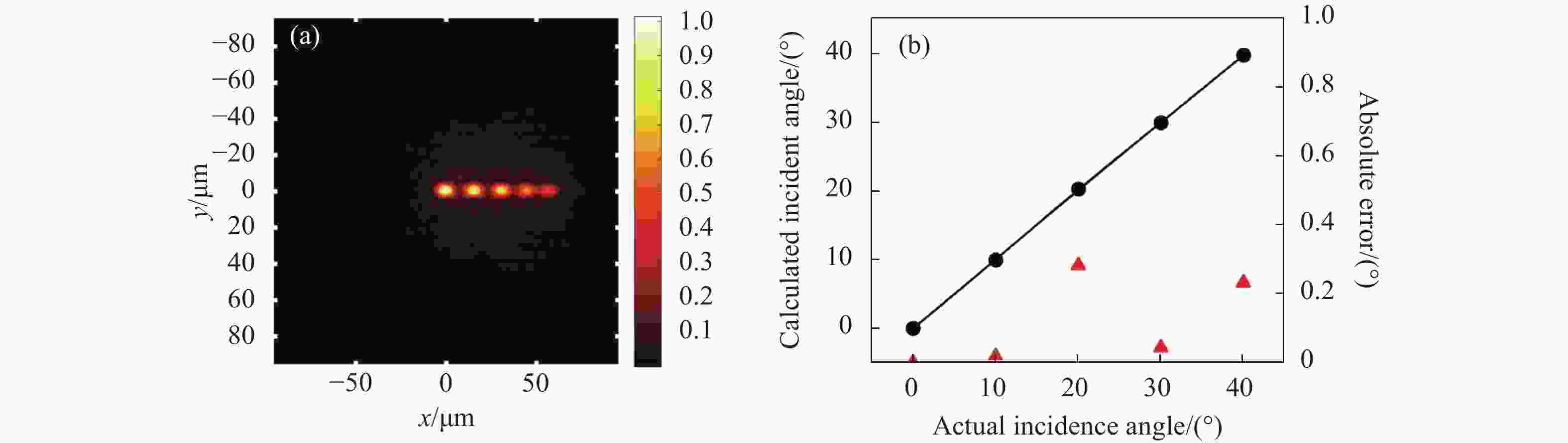
图 3 利用子阵列实现对入射角的检测。(a) z=64 µm处不同入射角下的焦斑强度分布图;(b) 通过图3(a)计算的入射角以及绝对误差
Figure 3. Simulations verification of incident angle detection by the sub-array. (a) Focal focula intensity distribution at z=64 µm; (b) Calculated incident angles from Fig.3(a) and absolute errors
在入射角可以被精确测量的基础上,为了获得斜入射光的偏振信息,将设计的4个超表面进行集成,如图1所示。将具有不同偏振态的斜入射光通过超表面,并计算对应的Stokes参数,结果如图4所示。图4(a),(b)和(c)分别对应0°,20°和40°入射光的仿真结果。上排图为相同角度不同入射偏振态(X、Y、A、B、L、R偏振光)的焦平面光斑分布图,每个偏振态产生独特的强度分布,根据公式(7)可计算出入射光的Stokes参数,如下排条形图所示。值得指出的是,由于结构选取时尽可能使其透过率均衡,使得焦平面上的总光强值接近理论上的
$ I_x^{\prime \prime } + I_y^{\prime \prime } = I_a^{\prime \prime } + I_b^{\prime \prime } = I_b^{\prime \prime } + I_r^{\prime \prime } $ ,因此透过率对测量的影响可以忽略,这也是可以进行紧凑型设计的基础。理论上,入射的六个偏振态的归一化Stokes参数分别为[1,1,0,0]T、[1,–1,0,0]T、[1,0,1,0]T、[1,0,–1,0]T、[1,0,0,1]T和[1,0,0,–1]T。仿真结果与理论结果基本吻合,证明设计的紧凑型超表面具有大的视场。
图 4 超表面的表征结果。(a)、(b)、(c) 分别代表入射角为0°、20°和40°时的仿真结果,从左到右入射光偏振态为X、Y、A、B、L、R偏振光,每个插图的上排是不同偏振态入射的焦平面光斑分布图,下排为对应的归一化Stokes参数
Figure 4. Characterization results of the metasurface. (a), (b), and (c) Simulation results at incident angles of 0°, 20°, and 40°, respectively. The incident light from left to right corresponds to X, Y, A, B, L, and R polarization states. The upper rows of every illustration are facula distributions at the focal plane. The lower rows are calculated normalized Stokes parameters corresponding with the upper one
最后,为了证明器件的可靠性,测量了一个给定的椭圆偏振光。入射的椭圆偏振光位于x′z′平面,与超表面法线夹角为25°,短轴与长轴的比值为0.6,因此,入射光的琼斯矩阵为:
$E_0^{'} = {\left[ {a\;\;\;0.6 * a * {{\rm{e}}^{i \frac{\pi }{2}}}} \right]^{\rm{T}}} $ 。理论计算的Stokes参数为$ S = {\left[ {1.36a\;\;\;0.64{a^2}\;\;\;0\;\;\;1.2{a^2}} \right]^{\rm{T}}} $ ,归一化得到$ S = {\left[ {1\;\;\;0.4706\;\;\;0\;\;\;0.8824} \right]^{\rm{T}}} $ 。仿真结果如图5所示,图5(a)为焦平面光斑分布图,通过焦斑偏移量计算得到入射角为25.195°,归一化的Stokes参数为$S' = {\left[ {1\;\;\;0.4387\;\;\;0.0347\;\;\;0.9561} \right]^{\rm{T}}}$ ,如图5(b)所示。这里笔者定义平均误差$\Delta = \dfrac{{\left| {S_1^{'} - {S_1}} \right| + \left| {S_2^{'} - {S_2}} \right| + \left| {S_3^{'} - {S_3}} \right|}}{3}$ ,计算的到平均误差为0.047。 -
文中提出了一种紧凑型超表面,利用二次相位和修正的Stokes公式实现了对大角度入射光的偏振探测。仿真结果证明,设计的全介质结构的超表面可以在−40°~40°范围内准确探测到入射角并实现对入射光全Stokes参数的表征,与现有的偏振探测器件相比,不仅可探测大角度入射光的偏振态,并且更加紧凑。同时,设计的超表面可作为一个紧凑型大视场偏振成像系统,通过增加像素实现更高的分辨率。这项工作为当前的红外偏振和成像技术提供了功能扩展,可促进工程光学2.0的发展[36]。
Large field-of-view and compact full-Stokes polarimetry based on quadratic phase metasurface
-
摘要: 偏振是光的固有属性之一,然而传统的光强、光谱探测技术会造成电磁波的偏振信息的丢失。同时,基于偏振测量的器件及技术不仅存在视场局限的问题,而且系统复杂。基于介质型超表面设计了一种紧凑型大视场偏振探测器件,实现了对入射光的角度及偏振态的探测。该器件由2×2的二次相位超表面组成,每个超表面可实现对特定偏振的对称性变换,即将入射角旋转对称性转变为焦平面内焦点平移对称性。二次相位的对称性变换理论使得此文可以在宽角度范围内(-40°~+40°)通过测量焦点的偏移量实现对入射角的表征。在此基础上,分析了斜入射对测量Stokes参数的影响,得到矫正的Stokes公式。利用4个焦点的强度和矫正的Stokes公式可计算出入射光的Stokes参数。在视场角为0°、20°、40°时,测量的Stokes参数与理论值吻合良好。Abstract: Polarization is one of the inherent characteristics of light, but the polarization information of electromagnetic waves is lost by traditional intensity and spectral detection technology. At the same time, not only the devices and technologies based on polarimetry have the problem of limited field of view, but also the measuring systems are complicated. In this paper, a compact large field-of-view polarimeter was designed based on dielectric metasurface, which realized the detection of the angle and polarization state of the incident light. The device was composed of 2×2 quadratic phase metasurfaces, each of which realized the symmetry transformation for a specific polarization, that is, the rotational symmetry of the incident angle was converted into the translational symmetry of focus in the focal plane. The theory of the symmetry transformation of the quadratic phase made it possible to characterize the angle of incidence by measuring the offset of the focus over a wide angle range (−40°—+40°). On this basis, the influence of oblique incidence on the measurement of Stokes parameters was elaborated, and the modified Stokes formula was obtained. The Stokes parameters of the incident light can be calculated by utilizing the intensities of the four focal points and the modified Stokes formula. The measured Stokes parameters agree well with the theoretical values, when the field-of-view is 0°, 20°, and 40°.
-
Key words:
- metasurface /
- quadratic phase /
- wavefront modulation /
- polarimetry /
- compact /
- large field-of-view
-
图 1 紧凑型大视场偏振探测超表面示意图。(a) 利用二次相位超表面的旋转−平移对称性变换原理图;(b) 设计的超表面。上图为超表面俯视图,下图为单元结构示意图;(c) 设计的紧凑型大角度偏振探测3D原理图
Figure 1. Schematic illustration of metasurface of the compact polarimetry for large field of view. (a) Schematic diagram of rotational-translational symmetry conversion with quadratic phase metasurface; (b) Designed metasurface. The upper one is the top view of the designed metasurface, and the lower picture is illustration of a unit cell; (c) 3D schematic of the compact polarimetry for large field of view
图 2 设计的单元结构。(a), (b) 优化的单元结构的短轴(W)和长轴(L)尺寸;(c) 0°、10°、20°、30°、40°和50°入射时前8个结构对应的相位响应;(d)单元结构在0°,10°,20°,30°和40°入射时的透射振幅
Figure 2. Designed unit cells. (a), (b) Short axis (W) and long axis (L) dimensions of the optimized unit cells; (c) Corresponding phases response of the first eight elements for incident angles of 0°, 10°, 20°, 30°, 40°, and 50°, respectively; (d) Corresponding transmitted amplitudes of all elements for incident angles of 0°, 10°, 20°, 30°, and 40°, respectively
图 4 超表面的表征结果。(a)、(b)、(c) 分别代表入射角为0°、20°和40°时的仿真结果,从左到右入射光偏振态为X、Y、A、B、L、R偏振光,每个插图的上排是不同偏振态入射的焦平面光斑分布图,下排为对应的归一化Stokes参数
Figure 4. Characterization results of the metasurface. (a), (b), and (c) Simulation results at incident angles of 0°, 20°, and 40°, respectively. The incident light from left to right corresponds to X, Y, A, B, L, and R polarization states. The upper rows of every illustration are facula distributions at the focal plane. The lower rows are calculated normalized Stokes parameters corresponding with the upper one
-
[1] Arbabi Ehsan, Kamali Seyedeh Mahsa, Arbabi Amir, et al. Full-Stokes imaging polarimetry using dielectric metasurfaces [J]. ACS Photonics, 2018, 5: 3132-3140. doi: 10.1021/acsphotonics.8b00362 [2] Liu Jing, Xia Runqiu, Jin Weiqi, et al. Review of imaging polarimetry based on Stokes Vector [J]. Optical Technique, 2013, 39(1): 56-62. (in Chinese) [3] Scott Tyo J, Goldstein Dennis L, Chenault David B, et al. Review of passive imaging polarimetry for remote sensing applications [J]. Applied Optics, 2006, 45: 5453-5469. doi: 10.1364/AO.45.005453 [4] Liu Gang L, Li Yanfang, Cameron Brent D. Polarization-based optical imaging and processing techniques with application to the cancer diagnostics[C]//Laser Tissue Interaction XIII: Photochemical, Photothermal, and Photomechanical, 2002, 4617: 208–220. [5] Garcia Missael, Edmiston Christopher, Marinov Radoslav, et al. Bio-inspired color-polarization imager for real-time in situ imaging [J]. Optica, 2017, 4: 1263-1271. doi: 10.1364/OPTICA.4.001263 [6] Dou Chenhao, Wang Shurong, Zhang Zihui, et al. The design of atmosphere polarimetry sensing with multi-bands [J]. Optics Communications, 2018, 410: 863-866. doi: 10.1016/j.optcom.2017.11.031 [7] Xia Runqiu, Wang Xia, Jin Weiqi, et al. Progress in development of imaging polarimeter for Stokes parameter measurement[C]//Photoelectronic Technology Committee of the Chinese Society of Astronautics: Optical Imaging, Remote Sensing, and Laser-Matter Interaction, 2014, 9142: 914211. [8] Krishnan Shankar, Hampton Scott, Rix James, et al. Spectral polarization measurements by use of the grating division-of-amplitude photopolarimeter [J]. Applied Optics, 2003, 42: 1216-1227. doi: 10.1364/AO.42.001216 [9] Pernechele Claudio, Giro Enrico, Fantinel D. Device for optical linear polarization measurements with a single exposure [J]. Polarimetry in Astronomy, 2013, 4843: 156-163. [10] Myhre Graham, Hsu Wei-Liang, Peinado Alba, et al. Liquid crystal polymer full-stokes division of focal plane polarimeter [J]. Optics Express, 2012, 20: 27393-27409. doi: 10.1364/OE.20.027393 [11] Zhang Junchao, Luo Haibo, Hui Bin, et al. Image interpolation for division of focal plane polarimeters with intensity correlation [J]. Optics Express, 2016, 24: 20799-20807. doi: 10.1364/OE.24.020799 [12] Yu Nanfang, Capasso Federico. Flat optics with designer metasurfaces [J]. Nature Materials, 2014, 13: 139-150. doi: 10.1038/nmat3839 [13] Wei Shibiao, Wang Dapeng, Lin Jiao, et al. Demonstration of orbital angular momentum channel healing using a Fabry-Pérot cavity [J]. Opto-Electronic Advances, 2018, 1: 180006. [14] Pu Mingbo, Li Xiong, Ma Xiaoliang, et al. Catenary optics for achromatic generation of perfect optical angular momentum [J]. Science Advances, 2015, 1: e1500396. doi: 10.1126/sciadv.1500396 [15] Nemati Arash, Wang Qian, Hong Minghui, et al. Tunable and reconfigurable metasurfaces and metadevices [J]. Opto-Electronic Advances, 2018, 1: 180009. [16] Luo Xiangang, Pu Mingbo, Li Xiong, et al. Broadband spin Hall effect of light in single nanoapertures [J]. Light: Science & Applications, 2017, 6(6): e16276. [17] Guo Yinghui, Pu Mingbo, Zhao Zeyu, et al. Merging geometric phase and plasmon retardation phase in continuously shaped metasurfaces for arbitrary orbital angular momentum generation [J]. Acs Photonics, 2016, 3(11): 2022-2029. doi: 10.1021/acsphotonics.6b00564 [18] Zhang Fei, Pu Mingbo, Li Xiong, et al. All dielectric metasurfaces for simultaneous giant circular asymmetric transmission and wavefront shaping based on asymmetric photonic spin–orbit interactions [J]. Advanced Functional Materials, 2017, 27(47): 1704295. doi: 10.1002/adfm.201704295 [19] Patrice Genevet, Federico Capasso. Holographic optical metasurfaces: a review of current progress Patrice [J]. Reports on Progress in Physics, 2015, 78(2): 024401. doi: 10.1088/0034-4885/78/2/024401 [20] Ding Fei, Yang Yuanqing, Deshpande Rucha A, et al. A review of gap-surface plasmon metasurfaces: fundamentals and applications [J]. Nanophotonics, 2018, 7: 1129-1156. doi: 10.1515/nanoph-2017-0125 [21] Faraon Andrei, Arbabi Amir, Kamali Seyedeh Mahsa, et al. Applications of wavefront control using nano-post based dielectric metasurfaces[C]//Dielectric Metamaterials, Cambridge: Woodhead Publishing, 2020: 175-194. [22] Intaravanne Yuttana, Chen Xiaozhong. Recent advances in optical metasurfaces for polarization detection and engineered polarization profiles [J]. Nanophotonics, 2020, 9(5): 1003-1014. [23] Shaltout Amr, Liu Jingjing, Kildishev Alexander, et al. Photonic spin Hall effect in gap–plasmon metasurfaces for on-chip chiroptical spectroscopy [J]. Optica, 2015, 2(10): 860. doi: 10.1364/OPTICA.2.000860 [24] Wen Dandan, Yue Fuyong, Kumar Santosh, et al. Metasurface for characterization of the polarization state of light [J]. Optics Express, 2015, 23(8): 10272-10281. doi: 10.1364/OE.23.010272 [25] Pors Anders, Nielsen Michael G, Bozhevolnyi Sergey I. Plasmonic metagratings for simultaneous determination of Stokes parameters [J]. Optica, 2015, 2: 716-723. doi: 10.1364/OPTICA.2.000716 [26] Ding Fei, Anders Pors, Chen Yiting, et al. Beam-size-invariant pectropolarimeters using gap-plasmon metasurfaces [J]. ACS Photonics, 2017, 4: 943-949. doi: 10.1021/acsphotonics.6b01046 [27] Miyata Masashi, Nakajima Mitsumasa, Hashimoto Toshikazu. Compound-eye metasurface optics enabling a high-sensitivity, ultra-thin polarization camera [J]. Optics Express, 2020, 28(7): 9996-10014. doi: 10.1364/OE.389591 [28] Guo Zhongyi, Tian Lihua, Shen Fei, et al. Mid-Infrared polarization devices based on the double-phase modulating dielectric metasurface [J]. Journal of Physics D: Applied Physics, 2017, 50: 254001. doi: 10.1088/1361-6463/aa6f9b [29] Guo Zhongyi, Xu Haisheng, Guo Kai, et al. High-efficiency visible transmitting polarizations devices based on the GaN metasurface [J]. Nanomaterials, 2018, 8: 333. doi: 10.3390/nano8050333 [30] Yang Zhenyu, Wang Zhaokun, Wang Yuxi, et al. Generalized Hartmann-Shack array of dielectric metalens sub-arrays for polarimetric beam profiling [J]. Nature communications, 2018, 9(1): 1-7. doi: 10.1038/s41467-017-02088-w [31] Guo Kai, Xu Haisheng, Peng Zhiyong, et al. High-efficiency full-vector polarization analyzer based on GaN metasurface [J]. IEEE Sensors Journal, 2019, 19(10): 3654-3659. doi: 10.1109/JSEN.2019.2894436 [32] Pu Mingbo, Li Xiong, Guo Yinghui, et al. Nanoapertures with ordered rotations: symmetry transformation and wide-angle flat lensing [J]. Optics Express, 2017, 25: 31471-31477. doi: 10.1364/OE.25.031471 [33] Liu Wenwei, Li Zhancheng, Cheng Hua, et al. Metasurface enabled wide-angle Fourier lens [J]. Advanced Materials, 2018, 30(23): 1706368. doi: 10.1002/adma.201706368 [34] Guo Yinghui, Ma Xiaoliang, Pu Mingbo, et al. High-efficiency and wide-angle beam steering based on catenary optical fields in ultrathin metalens [J]. Advanced Optical Materials, 2018, 6: 1800592. doi: 10.1002/adom.201800592 [35] Zhang Yaxin, Jin Jinjin, Pu Mingbo, et al. Full Stokes polarimetry for wide-angle incident light [J]. Physica Status Solidi (RRL)-Rapid Research Letters, 2020, 14(5): 2000044. doi: 10.1002/pssr.202000044 [36] Luo Xiangang. Subwavelength artificial structures: opening a new era for engineering optics [J]. Advanced Materials, 2019, 31(4): 1804680. doi: 10.1002/adma.201804680 -






 下载:
下载:







































