-
当前,光学成像技术日益成熟,已经在高清晰、高分辨、大视角等成像性能上取得了长足的进步。高品质的光学成像也逐渐从科学研究、工业生产走向消费级民用市场。因此,人们对成像系统的便携性、稳定性的要求越来越高,相关的器件和系统也正朝着小型化、集成化的趋势发展。不过,迄今为止大多数的成像系统都还是采用传统折射型光学透镜,通过光程积累来调制光的波前,并且由于材料的色散效应,通常需要多种材料的镜头组合来实现透镜的消色差成像,这些原理局限决定了传统的成像系统很难进一步缩小尺寸。具有平面结构的衍射光学元件(DOE)为高集成的成像系统提供了可能的方案[1],不过传统的工艺技术所加工的衍射器件(如菲涅尔透镜)往往存在衍射色差严重、多焦点、效率偏低等缺点,很难在高品质成像系统中获得应用。近十余年来,基于亚波长结构单元的超构表面(metasurface)作为一种新的光学设计被提出[2],为小型化高集成的光学成像系统提供了新方案,超构透镜(metalens)也应运而生[3]。
由于超构表面及超构透镜都是基于亚波长的结构单元设计,它们可以有效地消除高阶衍射,从而一定程度上提高光场的调控效率。然而,由于衍射色散的存在,这类超构透镜的色差往往也非常严重,如何实现宽波段的消色差,一直是近年来超构透镜领域最为关注的热点问题[4-6]。虽然,人们已经发展出在一定的波长范围获得消色差超构透镜的设计方案,不过其透镜的尺寸非常有限,工作效率也不够理想,还达不到高品质成像的需求。而且,以亚波长的结构单元构建厘米以上级的宏观光学透镜在加工制造上也面临着巨大挑战。另一方面,随着灰度曝光和光刻等微纳加工工艺的进步,传统衍射光学元件的设计也得到进一步优化,人们结合算法优化已经能够设计并制造出多阶衍射透镜(Multilevel Diffractive Lens,MDL),也可以获得宽带的消色差成像性能,同时它的结构单元尺寸可以远大于超构透镜的单元结构,大大减少了设计数据量,并降低了工艺难度[7-10]。然而,目前所报道的这些消色差MDL往往都是基于很小的数值孔径或较小的透镜尺寸,而且其工作效率和成像性能也非常依赖结构的台阶数以及整体透镜膜层的高度。
通过分析超构透镜以及MDL消色差的原理及目前表现出的性能,不难发现它们的工作带宽、数值孔径、透镜大小、透镜厚度等参量之间存在一定的制约关系。理解这种制约关系对于消色差平面透镜的设计和进一步发展十分重要。文中将以拓扑优化的消色差超构透镜和多阶衍射透镜为例,从理论分析和模拟计算两方面来分析这些参量之间的制约关系,并对其作一定的讨论。
-
消色差平面透镜较为重要的参量有:透镜的数值孔径(Numerical aperture,NA)、透镜尺寸大小、透镜聚焦效率、消色差频率范围(或消色差工作带宽)。这一节将定量分析这些参量之间的关系。首先,作如下假设:对经过透镜且频率处于消色差频率范围内的光场,其波前相位分布满足[11]:
$$\phi (r,\omega ) = - \dfrac{\omega }{c}(\sqrt {{f^2} + {r^2}} - f) + C(\omega )$$ (1) 式中:r为径向坐标;ω为光角频率;f为焦距;c为真空中光速;C(ω)是只与ω有关的一个常数项。依照参考文献[12],可以构造一个新的函数ψ:
$$\begin{split} \psi (\omega ) =& \phi (0,\omega ) - \phi (R,\omega )= \\ & \dfrac{\omega }{c}\left.(\sqrt {{R^2} + {f^2}} - f) \right.=\\ & \dfrac{\omega }{c}R\left( {\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} } \; \right)\\ \end{split} $$ (2) 式中:R为透镜半径;NA为透镜数值孔径(
$NA = {R/ {\sqrt {{R^2} + {f^2}} }}$ )。假设消色差频率上下界分别为ω2和ω1,并用Δψ表示这两个频率下的ψ函数差值,利用分部积分可以得到:$$\begin{split} \Delta \psi (\omega ) = & \displaystyle\int_{{\omega _1}}^{{\omega _2}} {\dfrac{{{\rm{d}}\psi (\omega )}}{{{\rm{d}}\omega }}} {\rm{d}}\omega =\\ & \left. {\omega \dfrac{{{\rm{d}}\psi (\omega )}}{{{\rm{d}}\omega }}} \right|_{{\omega _1}}^{{\omega _2}} - \displaystyle\int_{{\omega _1}}^{{\omega _2}} \omega \dfrac{{{{\rm{d}}^2}\psi (\omega )}}{{{\rm{d}}{\omega ^2}}}{\rm{d}}\omega \\ \end{split} $$ (3) 在只考虑传播相位的情况下(不考虑发生共振),根据以往研究结果,无论是超构透镜还是MDL,其相位对于频率都是近线性分布[6,12],所以相位对于频率的二阶微分项可以作为一个小量消去,最后可以得到Δψ的近似表达式为:
$$\Delta \psi \approx {\omega _2}{\psi ^\prime }\left( {{\omega _2}} \right) - {\omega _1}{\psi ^\prime }\left( {{\omega _1}} \right)$$ (4) 将公式(1)、(2)代入公式(4)的左边,并对公式(4)右边做如下代换:
$$\begin{array}{l} \Delta \omega = {\omega _2} - {\omega _1} \\ {\omega _c} = \left( {{\omega _1} + {\omega _2}} \right)/2 \\ {\kappa _1} = {\psi ^\prime }\left( {{\omega _2}} \right) - {\psi ^\prime }\left( {{\omega _1}} \right) \\ {\kappa _2} = \left( {{\psi ^\prime }\left( {{\omega _2}} \right) + {\psi ^\prime }\left( {{\omega _1}} \right)} \right)/2 \\ \end{array} $$ (5) 可得:
$$R \approx \dfrac{{c{\omega _c}{\kappa _1}}}{{\Delta \omega \left( {\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} } \right)}} + \dfrac{{c{\kappa _2}}}{{\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} }}$$ (6) 注意到,该公式成立的前提为相位分布满足公式(1),这实际上要求透镜对于光场能够完美聚焦[11],也即要求透镜拥有较高的聚焦效率,所以,该式是高效率聚焦的透镜各参量所需要满足的关系。接下来将分别分析消色差超构透镜和消色差多阶衍射透镜的参量满足的制约关系,并通过设计不同参量下的透镜,对所得出的制约关系进行验证和讨论。
-
该节将根据近年来消色差超构透镜设计的研究进展,考察拓扑优化的设计方案。
-
通常用于设计超构透镜、实现波前调控的方法有多种,如共振相位、几何相位、传播相位等。目前在透射性的消色差超构透镜的设计中,利用传播相位补偿色差是效果最好的方法。人们也通常都是通过调节纳米柱的形状和尺寸来调控柱内导波的传播相位作补偿来获得消色差功能的[5-6, 12]。考虑采用传播相位作为调控相位的方式,则出射波前的相位可以表示为[12]:
$$\phi (r,\omega ) = \beta (r,\omega )H = \frac{\omega }{c}{n_{{\rm{eff}}}}(r,\omega )H$$ (7) 式中:β为传播常数;neff为有效折射率;H为透镜的厚度。将公式(7)代入公式(6)中,注意到neff小于介质折射率n,作适当近似可得:
$$R \leqslant \dfrac{{c{\omega _c}{\alpha _1}H}}{{\Delta \omega \left( {\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} } \right)}} + \dfrac{{c{\alpha _2}H}}{{\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} }}$$ (8) 式中:α1, α2为只与n相关的系数。上式可以简化为几个半定量关系式:
$${R_{\max }} \simeq {v_1}H$$ (9) $${R_{\max }} \simeq \dfrac{{{v_2}}}{{\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} }}$$ (10) $${R_{\max }} \simeq \dfrac{{{v_3}}}{{\Delta \omega }} + {v_4}$$ (11) 式中:Rmax为透镜最大半径,v1~v4为四个参数,指代除考察参量外,其他参量固定时的系数。如之前分析,公式(9)~(11)表示在较高聚焦效率下超构透镜各个参量之间的制约关系。其中,公式(9)反映了Rmax跟透镜厚度成正比,当数值孔径NA较小时,公式(10)反映Rmax与NA成反比关系,同样公式(11)也反映了Rmax与工作频宽成反相关。
-
通常超构透镜设计方法为定域周期近似法[13],这种方法有一种内禀的周期性,并未用上平面内的所有调控自由度,从而无法达到更高的效率。近年来拓扑优化方法在光学领域兴起[14],采用拓扑优化设计的超透镜,不存在内禀的周期性,能够最大化调控平面内的自由度,对于光场的调控一定程度上也可以类比为传播相位。因此,笔者等采用拓扑优化的方式来设计超构透镜。
简单介绍一下拓扑优化设计流程。首先将对应的电磁学问题化为一个优化问题:
$$\begin{array}{*{20}{c}} {{{\min }_\varepsilon }}&{F(\varepsilon )} \\ {{\rm{ }}s.{\rm{ }}t:}&{\nabla \cdot D = \rho } \\ {}&{\nabla \times E = - \dfrac{{\partial B}}{{\partial t}}} \\ {}&{\nabla \cdot B = 0} \\ {}&{\nabla \times H = J + \dfrac{{\partial D}}{{\partial t}}} \end{array}$$ (12) 式中:F为目标函数;ε为相对介电常数分布,也可以看作是结构的分布。这里取
${{F}}= \displaystyle\sum _{\omega }\left|I\right(\omega )-{I}_{0}|$ ,其中I为焦面实际场分布,通过全波仿真得到,I0为理想场分布。之后,通过伴随场方法,求解$ {\nabla }_\in F $ ,再利用梯度下降等优化方法,便可以对原问题进行求解,得到结构分布ε。由于拓扑优化设计需要进行全波仿真,所需时间较长,因此这里仅考虑二维超构透镜[14]。此时,透镜尺寸由透镜宽度W来描述,与三维透镜对比,宽度W相当于透镜直径,也就是2R。由于二维消色差超构透镜的相位分布也近似符合之前的假设公式(1),所以W与其余参量的制约关系理论上与公式(9) ~ (11)一致。首先作为对拓扑优化设计方案的验证,设计了一个宽度为30 μm,数值孔径为0.15,消色差波段为450~650 nm,厚度为600 nm,材料为SiNx(折射率n = 2)的透镜,结果如图1所示。之后,为考察参量间的制约关系,采用上述方法设计了一系列消色差超构透镜,设计的具体参数如表1所示。
图 1 (a) 基于拓扑优化设计的消色差超构透镜,工作波段为450~650 nm,右图为结构局部放大图;(b) 六个波长对应的轴向光场强度分布,白色虚线对应的位置为所设计的焦平面;(c) 焦平面光场的归一化强度分布;(d) 光场聚焦效率分布,定义为焦面上聚焦斑三倍半高宽区域内的能量与入射总能量之比
Figure 1. (a) Achromatic metalens designed by topological optimization. Working wavelength of this lens ranges from 450 nm to 650 nm. The figure on the right is the partial enlarged view. (b) Light field on six wavelength along the propagation axis, the white dotted lines are the designed focus plane. (c) Normalized intensity profile in focus plane. (d) Focus efficiency, which is defined as the power within a spot of diameter equal to 3 times the Full Width Half Maximum of the focus spot divided by the total incident power
表 1 消色差超构透镜设计参数
Table 1. Parameters of achromatic metalens
Parameters Value Width of lens/μm 6-30 Wavelength/nm 450-650 Height of lens/nm 400-1 000 NA 0.05-0.3 Material SiNx (n = 2) 在考察每一对参量(R-H、R-NA、R-Δω)的制约关系时,保持其他参量不变,近连续地改变这一对参量进行透镜设计,并求出对应效率。最终得到的仿真结果如图2所示。

图 2 消色差超构透镜。 (a) W-H关系图(保持NA = 0.15,Δω =6.28×1014 s−1, 即波长范围500~600 nm); (b) W-NA关系图(保持H = 0.6 μm, Δω = 6.28×1014 s−1);(c) W-Δω关系图(保持H = 0.6 μm,NA = 0.15)。图中暗红色实线为理论预测的参量所满足的关系式公式(9) ~ (11)
Figure 2. Achromatic metalens. (a) Relation between W-H with fixed NA = 0.15 and Δω = 6.28×1014 s−1 (wavelength range of 500-600 nm); (b) Relation between W-NA with fixed H = 0.6 μm and Δω = 6.28×1014 s−1; (c) Relation between W-Δω with fixed H = 0.6 μm and NA = 0.15. The dark-red lines are the predicted relation based on Eq. (9) - (11)
图中深红线表示由公式(9) ~ (11)所预测的关系,色度图表示实际计算的效率随参量对的变化。可以看到,对于超构透镜,在保持较高效率的前提下(即图中色度由红向黄转变的分界线,大约80%),透镜的最大尺寸与数值孔径和消色差频宽保持反相关的关系,与理论预测基本一致。然而,透镜尺寸与厚度的对应关系较之理论公式(9)预测曲线相差较大。这个主要原因是,对于超构透镜设计来说,考虑的加工深宽比不能太大,它通常厚度设计比较小,通常接近甚至小于自由空间光的波长。因此,超构透镜结构柱状结构单元中能容纳的导波模式非常有限,其传播相位调制的影响在较小厚度透镜中还不能完全体现。也就是说该理论的前提条件公式(7)对低厚度超构表面性能考量时并不完全适用。不过从图2(a)也能看出,当透镜厚度增加后(如H >0.8 μm),其效率变化曲线已经逐渐符合理论值(深红线)。总体而言,超构透镜的尺寸与厚度还是正相关的。
-
上述结果反映出拓扑优化的超构透镜参量间的关系式基本符合第一节理论结果。不过由于在厚度较小时,超构单元内有限的波导模式限制了传播相位的贡献,使得其效率随厚度变化的规律不是很明显。而对于局域高度足够大的衍射透镜来说,传播相位将完全起主导。因此,接下来重点考察多阶衍射透镜(MDL)的消色差设计以及相关参量之间的制约关系。
-
对于MDL,出射波前的相位可以表示为[7]:
$$\phi (r,\omega ) = \dfrac{\omega }{c}(n(\omega ) - 1)h(r)$$ (13) 式中:h为r处结构高度。将公式(12)代入公式(5)中,考虑到h不大于总高度H,适当近似可得:
$$R \leqslant \dfrac{{c{\omega _c}{\gamma _1}H}}{{\Delta \omega \left( {\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} } \right)}} + \dfrac{{c{\gamma _2}}}{{\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} }}$$ (14) γ1为只与折射率n有关的系数,γ2为与n和原点处的高度h(0)有关的系数。上式同样可以简化为几个半定量关系式:
$${R_{{\rm{max}}}} \simeq {\upsilon _1}H + {\upsilon _0}$$ (15) $${R_{{\rm{max}}}} \simeq \dfrac{{{\upsilon _2}}}{{\dfrac{1}{{NA}} - \sqrt {\dfrac{1}{{N{A^2}}} - 1} }}$$ (16) $${R_{{\rm{max}}}} \simeq \dfrac{{{\upsilon _3}}}{{\Delta \omega }} + {\upsilon _4}$$ (17) v0 ~ v4为五个参数。对比公式(9) ~ (11)和公式(15) ~(17),形式上几乎完全一致,体现了超构透镜和多层衍射透镜的一致性。
-
根据公式(13),MDL的相位分布完全由高度分布决定,因此可以直接通过衍射计算的方式来进行设计,而不必进行全波仿真。此时设计透镜所需时间大大降低,因此可以对更大的参量空间进行设计和分析。设计具体流程如下:
用Pf表示衍射距离为f的菲涅尔衍射算子,则离透镜距离为f的面上光强分布为:
$$I(\omega ) = |{P_f}{e^{i\phi }}{|^2}$$ (17) 其中
$\phi $ 为公式(13)。考虑目标场分布为I0,则可以将原设计问题转换为一个优化问题:$$\begin{array}{l} \mathop {min}\limits_{h(r)} \displaystyle\sum_\omega | I(\omega ) - {I_0}| \\ s.t:0 \leqslant h(r) \leqslant H \\ \end{array} $$ (18) 之后,便可采用最优化方法对该问题进行求解,从而得到高度分布h(r)。文中采用的最优化方法为直接二值搜索法(Direct Binary Search,DBS),具体细节参见参考文献[7]。
首先将对计算结果进行一个仿真验证。综合考虑仿真耗时与透镜尺寸等问题,仿真采用的的消色差MDL参量如表2所示。
表 2 单个消色差MDL设计参数
Table 2. Parameters of a single achromatic MDL
Parameters Value Radius of lens/μm 75 Wavelength/nm 1 204-1 624 Height of lens/μm 1.5 Width of one ring/μm 3 NA 0.15 Height levels 64 Material Si (n = 3.49-3.42) 最终设计结构的二维俯视图与沿径向一维结构分布图如图3所示。通过标量衍射理论和FDTD,可以分别得到该结构在所设计焦面上的理论衍射结果和仿真结果,如图4所示。同时可以计算出衍射效率和焦斑的半高宽(Full Width at Half Maximum,FWHM),如图5所示,其中Sim表示仿真结果,Cal表示计算结果,The表示理论预测结果。

图 3 MDL结构分布。(a)二维俯视图 ;(b)径向高度分布
Figure 3. Schematic of a single achromatic MDL. (a) 2D top view; (b) Height distribution along radius
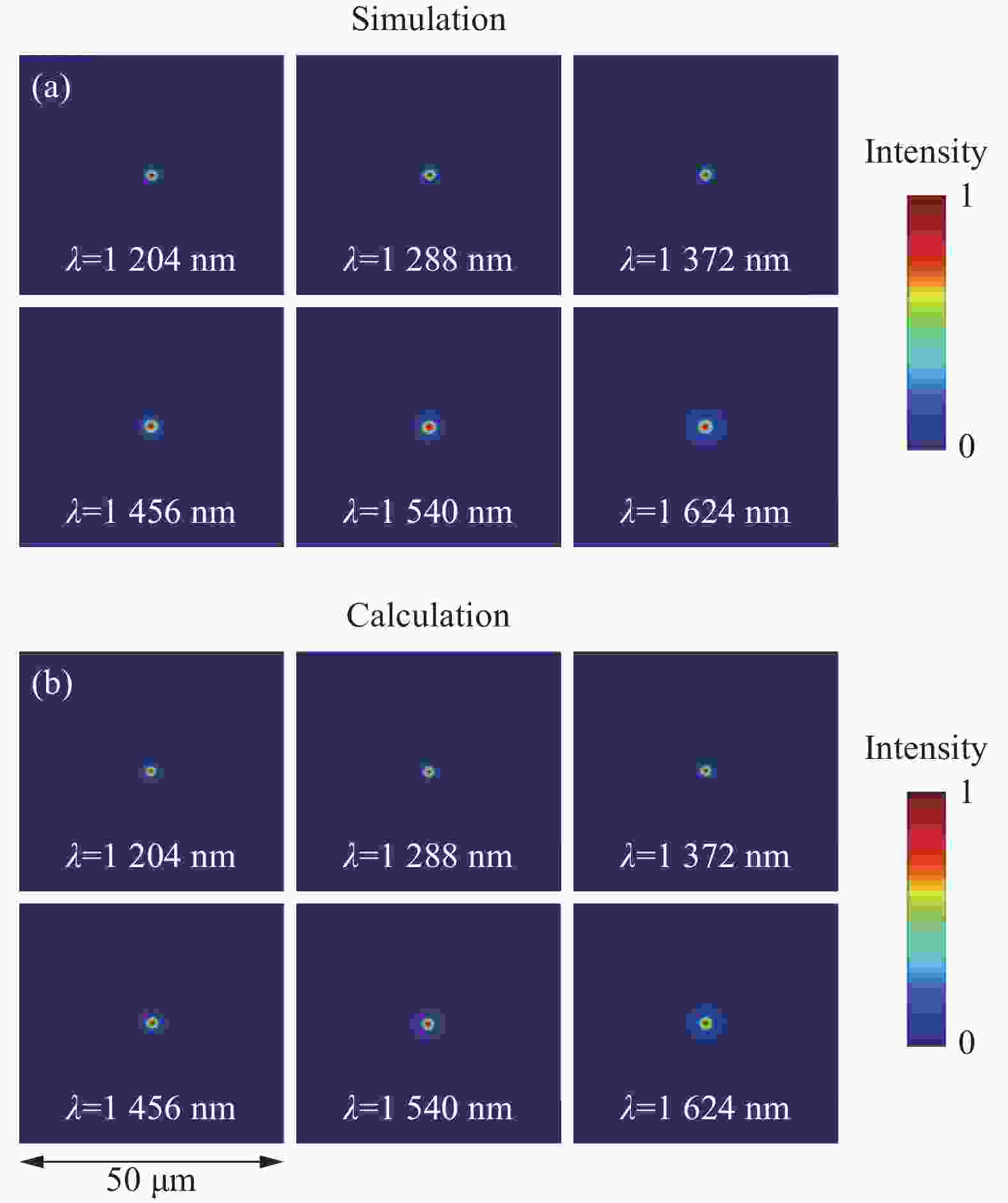
图 4 焦面光场强度分布。(a)仿真结果; (b)计算结果
Figure 4. Intensity distribution of the light field in the focal plane. (a) Simulation result; (b) Calculation result
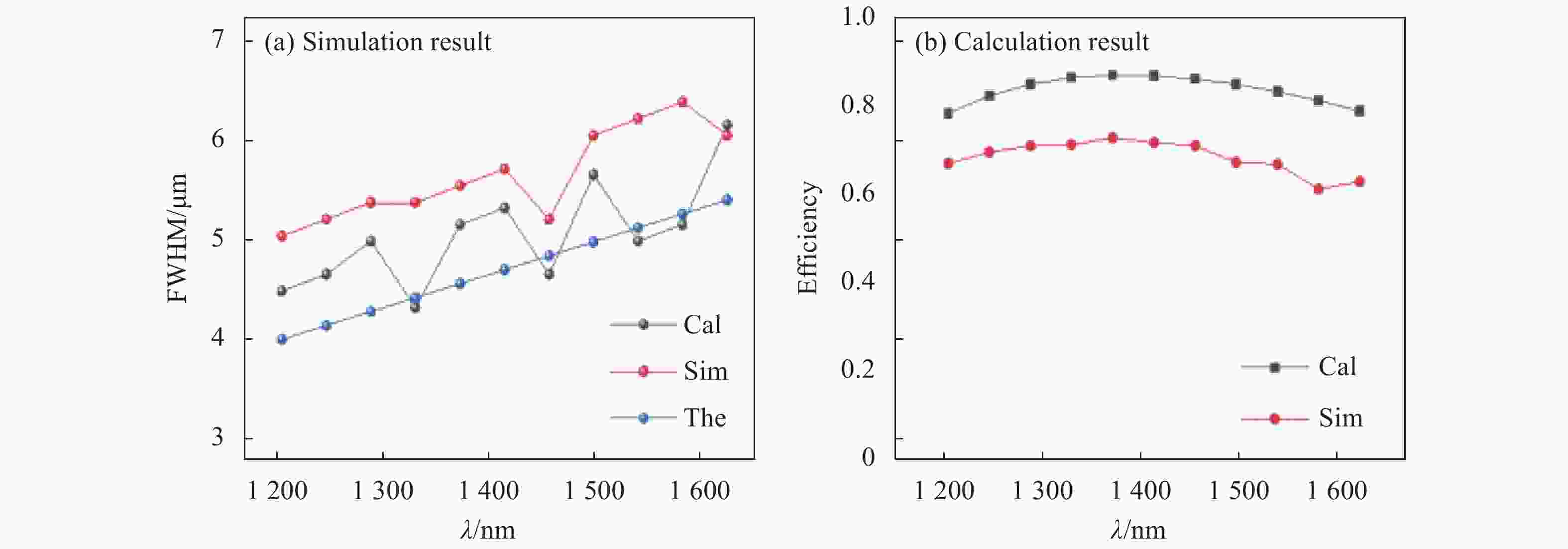
图 5 (a) 理论(蓝)、仿真(红)、计算(黑)半高宽;(b)仿真(红)、计算(黑)聚焦效率
Figure 5. (a) Full Width at Half Maximum of theory (blue), simulation (red) and calculation (black); (b) Focus efficiency of simulation (red) and calculation (black)
从聚焦焦斑和半高宽的角度,理论计算与仿真基本一致,不过在聚焦效率上仿真结果要略低于理论结果,原因主要有两点:理论计算未考虑光场在界面上的反射损耗,以及未考虑由于高阶衍射而带来的能量损失。
综上,通过FDTD仿真验证,可以证实通过衍射计算设计的MDL的确能实现消色差功能。接下来将设计不同参量的MDL,并将设计结果与之前理论作分析对比。
这里考察两个波段——可见光波段(400 ~ 700 nm)和近红外波段(1200 ~1600 nm)进行消色差设计时透镜参量的制约关系。基本方法为控制变量法:每次考察两个参量之间的制约关系(称为一个参量对),设计时保持其他参量不变,近连续地改变这两个参量的取值,并计算出对应透镜在该波段内的效率均值。两个波段透镜设计参量范围如表3所示。
表 3 消色差MDL设计参数
Table 3. Parameters of achromatic MDLs
Visible Infrared Radius of lens/μm 64-512 192-1 536 Wavelength/nm 400-700 1 200-1 600 Height of lens/μm 1-6 0.5-3 Width of one ring/μm 1 3 NA 0.025-0.2 0.025-0.2 Height levels 32 32 Material Polymer (n = 1.55) Si (n = 3.49-3.42) 与考察超构透镜时采用的方法相同,考察每一对参量时(R-H,R-NA,R-Δω),保持其他参量不变,在预设的参量范围内连续改变尺寸和频率范围并设计出对应的MDL,最终得到的结果如图6所示。

图 6 消色差MDL可见光波段。(a) R-H关系图,保持NA = 0.1, Δω = 6.28×1014 s−1 (500~600 nm);(b) R-NA关系图,保持H=3 μm,Δω = 6.28×1014 s−1;(c) R-Δω关系图,保持H = 3 μm,NA = 0.1;红外波段:(d) R-H关系图,保持NA = 0.15, Δω = 1.54×1014 s−1(1330~1492 nm);(e) R-NA关系图,保持H = 1.5 μm,Δω = 1.54×1014 s−1;(f) R-Δω关系图,保持H = 1.5 μm,NA = 0.15。图中暗红色实线为理论预测的参量所满足的关系式公式(15) ~ (17)
Figure 6. Achromatic MDL in visible. (a) Relation between R-H with fixed NA = 0.1 and Δω
= 6.28×1014 s−1 (500 - 600 nm); (b) Relation between R-NA with fixed H = 3 μm and Δω =6.28×1014 s−1 ; (c) Relation between R-Δω with fixed H = 3 μm and NA = 0.1; In infrared: (d) Relation between R-H with fixed NA = 0.15 and Δω = 1.54×1014 s−1 (1330-1492 nm); (e) Relation between R-NA with fixed H = 1.5 μm and Δω = 1.54×1014 s−1 ; (f) Relation between R-Δω with fixed H = 1.5 μm and NA = 0.15. The red lines are the predicted relation based on Eq. (15) - (17) 与超构透镜设计结果图示含义一致,图中深红线表示由公式(14)~(16)所预测的关系,色度图表示实际计算的效率随参量对的变化。可以看到,对于MDL,在保持较高效率的前提下(即图中色度由红向黄转变的分界线,大约80%),每对参量之间满足的制约关系与理论结果基本一致,即透镜尺寸与透镜厚度呈线性递增关系,透镜尺寸与数值孔径呈近反比例关系,透镜尺寸与消色差频谱宽度呈反相关。跟预测相符,MDL的理论和设计结果符合程度较超构更高。除了之前提到的衍射透镜厚度较大传播相位作用更明显之外,还有个原因是MDL采用衍射计算进行设计,耗时较短,可以获得大量样本,减小随机误差,而超构透镜的参数优化基于仿真,耗时较长,所设计得到的样本较少,误差较大。不过,MDL的模拟结果与理论预测曲线之间仍然存在一定偏差,应该是由于优化过程不可避免引入的随机性导致。
-
综上,通过对消色差平面透镜进行理论分析、仿真与计算设计,半定量地给出了消色差超构透镜和消色差MDL各个参量之间满足的制约关系。从结果来看,这两种平面透镜虽然采用不同的设计方式,但符合几乎相同的规律,即透镜尺寸与透镜厚度正相关,与数值孔径和消色差频谱宽度反相关。因此,在保持高效率的前提下,为了设计更大尺寸的消色差平面透镜,要么增加透镜厚度,要么降低数值孔径,或者减小消色差工作带宽。
该研究所得出的结果验证并阐释了过去几年中超构透镜和MDL领域各种结构和算法优化下总是很难突破透镜的工作效率、消色差带宽、数值孔径可透镜尺寸之间制约局限,而获得综合性能特别优异的平面透镜。从文中的分析可以看出,在遵守基本的衍射光学规律下,如果要打破参量间的这种制约关系,方法之一就是要改变透镜对相位的调制方式,即打破公式(7)和(13)的限制规律。而这是由单层超构单元或衍射结构决定的,往往很难突破。幸运的是,最近有理论研究表明采用多层超构表面结构、利用层间耦合有希望能够打破这种相互制约从而使得平面透镜的综合性能再次获得提升[15]。相信随着研究的不断深入,人们一方面有可能进一步拓展结构设计的参数空间去进一步提升平面透镜的综合性能;另一方面,根据文中得出的结论可以选择性地根据具体的应用场景去优化平面透镜的成像性能[16],使其最优秀的一面发挥最大的功效,推动新型光学器件和技术的发展。
Design and parametric analysis of the broadband achromatic flat lens
-
摘要: 大尺寸、大数值孔径、宽波段的消色差平面透镜设计是成像技术的一个瓶颈性问题,也是近年来超构透镜研究领域的一个重要挑战,主要原因是透镜的各个参量之间存在内禀的制约关系。文中结合消色差透镜的群时延理论及透镜的相位分布,通过理论分析给出各参量之间的半定量制约关系。同时,分别通过拓扑优化和直接二值搜索的方法,设计了不同参量下的消色差超构透镜和多阶衍射透镜,发现在保持效率80%左右的前提下,透镜尺寸增加了一倍,数值孔径或波段宽度减少了一半,而透镜厚度则随尺寸成线性增长。该结果表明,这两类平面透镜具有相同的內禀参数依赖关系,即透镜尺寸与数值孔径和波段宽度呈现反相关、与透镜厚度呈现正相关的关系,这与理论预测基本一致。Abstract: The design of large scale, high numerical aperture, and broadband achromatic flat lens is a bottleneck of imaging technology and also a big challenge in metalens researches in recent years. The major reason is that there are some internal constraints between these parameters. In this paper, considering both the group dispersion theory and the phase distribution of the flat lens, the semi-quantitative relationship between these parameters was derived. Then, the achromatic flat lenses (including metalenses and multi-level diffractive lenses) with different parameters were designed by using directly binary search and topology optimization. It was found that under the condition of maintaining an efficiency of 80%, when doubling the size of flat lens (i.e., the diameter), the numerical or achromatic bandwidth was cut in half, and the thickness of lens increased linearly with lens scale. The results definitely show that these two types of flat lenses have the same internal constraint relations in parameters, that is, as that the lens size has negative correlation with the numerical aperture and achromatic bandwidth, while positive correlation with the thickness of the lenses. This result is in coincidence with the theoretical prediction.
-
Key words:
- flat lens /
- achromatism /
- parameter optimization
-
图 1 (a) 基于拓扑优化设计的消色差超构透镜,工作波段为450~650 nm,右图为结构局部放大图;(b) 六个波长对应的轴向光场强度分布,白色虚线对应的位置为所设计的焦平面;(c) 焦平面光场的归一化强度分布;(d) 光场聚焦效率分布,定义为焦面上聚焦斑三倍半高宽区域内的能量与入射总能量之比
Figure 1. (a) Achromatic metalens designed by topological optimization. Working wavelength of this lens ranges from 450 nm to 650 nm. The figure on the right is the partial enlarged view. (b) Light field on six wavelength along the propagation axis, the white dotted lines are the designed focus plane. (c) Normalized intensity profile in focus plane. (d) Focus efficiency, which is defined as the power within a spot of diameter equal to 3 times the Full Width Half Maximum of the focus spot divided by the total incident power
图 2 消色差超构透镜。 (a) W-H关系图(保持NA = 0.15,Δω =6.28×1014 s−1, 即波长范围500~600 nm); (b) W-NA关系图(保持H = 0.6 μm, Δω = 6.28×1014 s−1);(c) W-Δω关系图(保持H = 0.6 μm,NA = 0.15)。图中暗红色实线为理论预测的参量所满足的关系式公式(9) ~ (11)
Figure 2. Achromatic metalens. (a) Relation between W-H with fixed NA = 0.15 and Δω = 6.28×1014 s−1 (wavelength range of 500-600 nm); (b) Relation between W-NA with fixed H = 0.6 μm and Δω = 6.28×1014 s−1; (c) Relation between W-Δω with fixed H = 0.6 μm and NA = 0.15. The dark-red lines are the predicted relation based on Eq. (9) - (11)
图 6 消色差MDL可见光波段。(a) R-H关系图,保持NA = 0.1, Δω = 6.28×1014 s−1 (500~600 nm);(b) R-NA关系图,保持H=3 μm,Δω = 6.28×1014 s−1;(c) R-Δω关系图,保持H = 3 μm,NA = 0.1;红外波段:(d) R-H关系图,保持NA = 0.15, Δω = 1.54×1014 s−1(1330~1492 nm);(e) R-NA关系图,保持H = 1.5 μm,Δω = 1.54×1014 s−1;(f) R-Δω关系图,保持H = 1.5 μm,NA = 0.15。图中暗红色实线为理论预测的参量所满足的关系式公式(15) ~ (17)
Figure 6. Achromatic MDL in visible. (a) Relation between R-H with fixed NA = 0.1 and Δω
= 6.28×1014 s−1 (500 - 600 nm); (b) Relation between R-NA with fixed H = 3 μm and Δω =6.28×1014 s−1 ; (c) Relation between R-Δω with fixed H = 3 μm and NA = 0.1; In infrared: (d) Relation between R-H with fixed NA = 0.15 and Δω = 1.54×1014 s−1 (1330-1492 nm); (e) Relation between R-NA with fixed H = 1.5 μm and Δω = 1.54×1014 s−1 ; (f) Relation between R-Δω with fixed H = 1.5 μm and NA = 0.15. The red lines are the predicted relation based on Eq. (15) - (17) 表 1 消色差超构透镜设计参数
Table 1. Parameters of achromatic metalens
Parameters Value Width of lens/μm 6-30 Wavelength/nm 450-650 Height of lens/nm 400-1 000 NA 0.05-0.3 Material SiNx (n = 2) 表 2 单个消色差MDL设计参数
Table 2. Parameters of a single achromatic MDL
Parameters Value Radius of lens/μm 75 Wavelength/nm 1 204-1 624 Height of lens/μm 1.5 Width of one ring/μm 3 NA 0.15 Height levels 64 Material Si (n = 3.49-3.42) 表 3 消色差MDL设计参数
Table 3. Parameters of achromatic MDLs
Visible Infrared Radius of lens/μm 64-512 192-1 536 Wavelength/nm 400-700 1 200-1 600 Height of lens/μm 1-6 0.5-3 Width of one ring/μm 1 3 NA 0.025-0.2 0.025-0.2 Height levels 32 32 Material Polymer (n = 1.55) Si (n = 3.49-3.42) -
[1] O' Shea D C, Suleski T J, Kathman A D, et al. Diffractive Optics: Design, Fabrication, and Test[M]. Washington: SPIE Press, 2004: 57-82. [2] Yu N, Gnevet P, Mikhail A K, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction [J]. Science, 2011, 334(6054): 333. doi: 10.1126/science.1210713 [3] Khorasaninejad M, Chen W T, Devlin R C, et al. Metalenses at visible wavelengths: diffraction limited focusing and subwavelength resolution imaging [J]. Science, 2016, 352(6290): 1190-1194. doi: 10.1126/science.aaf6644 [4] Khorasaninejad M, Shi Z, Zhu A Y, et al. Achromatic metalens over 60 nm bandwidth in the visible and metalens with reverse chromatic dispersion [J]. Nano Lett, 2017, 17(3): 1819-1824. doi: 10.1021/acs.nanolett.6b05137 [5] Chen W T, Zhu A Y, Sanjeev V, et al. A broadband achromatic metalens for focusing and imaging in the visible [J]. Nat Nanotechnology, 2018, 13(3): 220-226. doi: 10.1038/s41565-017-0034-6 [6] Wang S, Wu P, Su V, et al. A broadband achromatic metalens in the visible [J]. Nat Nanotechnology, 2018, 13(3): 227-232. doi: 10.1038/s41565-017-0052-4 [7] Wang P, Mohammad N, Menon R, et al. Chromatic-aberration-corrected diffractive lenses for ultra-broadband focusing [J]. Scientific Reports, 2016, 6: 21545. doi: 10.1038/srep21545 [8] Wang P, Mohammad N, Shen B, et al. Broadband imaging with one planar diffractive lens [J]. Scientific Reports, 2018, 8: 2799. doi: 10.1038/s41598-018-21169-4 [9] Meem M, Majumder A, Menon R, et al. Full-color video and still imaging using two flat lenses [J]. Opt Express, 2018, 26(21): 26866-26871. doi: 10.1364/OE.26.026866 [10] Meem M, Soueangsu B, Majumder A, et al. Broadband lightweight flat lenses for long-wave infrared imaging [J]. PNAS, 2019, 116(43): 21375-21378. doi: 10.1073/pnas.1908447116 [11] Francisco A, Patrice G, Mikhail A, et al. Aberration--free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces [J]. Nano Lett, 2012, 12(9): 4932-4936. doi: 10.1021/nl302516v [12] Shrestha S, Overvig A C, Lu Ming, et al. Broadband achromatic dielectric metalenses [J]. Light: Science & Applications, 2018, 7(6): 85. [13] Pestourie R, Pérez-Arancibia C, Lin Z, et al. Inverse design of large-area metasurfaces [J]. Opt Express, 2018, 26(26): 33732-33747. doi: 10.1364/OE.26.033732 [14] Chung H J, Owen M. High-NA achromatic metalenses by inverse design [J]. Opt Express, 2020, 29(5): 6945-6965. [15] Lin Z, Johnson S G. Overlapping domains for topology optimization of large-area metasurfaces [J]. Opt Express, 2019, 27(22): 32445-32453. doi: 10.1364/OE.27.032445 [16] Chen C, Song W, Chen J W, et al. Spectral tomographic imaging with aplanatic metalens [J]. Light: Science & Applications, 2019, 8(6): 99. -






 下载:
下载:


























