非线性光学研究的是强激光与物质之间发生的非线性相互作用^[1-2]。相位失配是影响传统非线性光学晶体转换效率的主要问题之一。为了获得高效的非线性光学器件，传统的相位匹配方法包括双折射相位匹配技术和准相位匹配技术^[3-6]。这两种方法都可以使非线性介质中基频光与谐波光的群速度匹配，实现非线性信号的相长干涉，提高转换效率，已经被广泛应用于各种非线性效应中。然而它们分别存在着一定的局限：双折射相位匹配方法的调节范围有限，对泵浦激光线宽有较大的限制，对角度调节精度要求较高；准相位匹配方法要求对非线性晶体晶向进行周期性反转，加工难度较大。

近年来，人们开始思考是否存在一种无需考虑相位匹配的、集成化的非线性光学器件。一种新颖的微纳光学器件，非线性超构表面（metasurface）应运而生。超构表面是指由亚波长结构构成的纳米光学天线阵列^[7-9]。由于其亚波长的光与物质相互作用距离，超构表面将相位失配的影响尽可能地降低。与传统体晶体相比，超构表面的光学性能不再仅仅取决于组成超构表面的非线性材料，还与光学天线的谐振响应有关。通过对材料的选择和光学天线结构的设计，可以获得基于不同材料的多种谐振效应，增强局域光场，在很小的体积中实现较大的非线性响应，有利于实现小型化的高效非线性光学器件。

金属超构表面支持表面等离子体谐振，光场大都局域在金属表面，可以在界面处获得较大的非线性响应，被广泛用于具有非中心对称形状的金属超构表面的二次谐波产生的研究中。然而，金属的损伤阈值通常较低，并且光场与材料的重叠体积较小，限制了非线性转换效率的进一步提升。低损耗的介质超构表面具有更高的损伤阈值，并且其支持的米氏谐振可以与光场有更大的重叠体积，有望实现更高效率的非线性频率转换过程。除了谐振增强，超构表面还可以在亚波长的空间分辨率上灵活控制光的相位、偏振和振幅，进而实现对基频光和谐波光的波前调控。

在该综述中，讨论了包括二次谐波产生、三次谐波产生、高次谐波产生和差频太赫兹波产生等频率转换过程，以及非线性波前调制、超快全光调制等非线性光学应用，对非线性超构表面在每个具体应用中的研究进展和具有的独特优势进行了概述，同时也会指出当前超构表面面临的不足和挑战，并针对某些问题给出可能的解决方案和发展方向。

光学频率转换是扩宽相干光源种类的重要手段，利用二次谐波产生、三次谐波产生、高次谐波产生等频率上转换以及差频产生等频率下转换过程，人们已经把激光信号的波长从极紫外扩展到太赫兹波段。超构表面不仅可以利用光学谐振增强，在亚波长的厚度中实现较大的非线性光学响应，还具有无需考虑相位匹配条件、尽可能小的材料吸收损耗等优点，对于实现增强的谐波产生、宽带的非线性光源、特征吸收带内谐波的高效辐射等具有重要意义。除此之外，超构表面还可以对产生的谐波信号的波前进行灵活调控。

二阶非线性过程是微扰理论体系下最强的非线性光学效应。由于受到晶体对称性的限制，二次谐波产生很难发生在具有中心对称性的晶体中。但在晶体的界面和表面处，这种对称性被打破，可以产生二阶非线性效应。利用金属天线在界面处支持的表面等离子体谐振所导致的场增强效应，仍然可以在金属中观测到二次谐波的产生。非中心对称的金属天线会产生非对称的的局域电场分布，可能具有较大的二阶非线性响应。例如，对于开口环结构，当泵浦光偏振方向沿着底臂时，会在天线中产生环形电流，两个侧臂中的电场相位相反，得到非零的磁偶极矩。因此可以激发出天线的磁偶极谐振，增强非线性信号的辐射。2006年，Klein等人利用开口环超构表面，在磁偶极谐振的作用下，获得了增强的二次谐波产生^[10]。基于类似的想法，具有电偶极谐振，电四极谐振或者更高阶谐振效应的不同结构的金属天线被广泛用于二次谐波产生的研究。2009年，Valev等人在G型金属结构中，观测到了等离激元模式增强的、手性相关的二次谐波信号^[11]。2012年，Husu等人通过研究不同排列的L型金属天线，发现天线取向和排列方式可以控制二次谐波产生的非线性响应，这主要是天线间的长程衍射耦合引起的^[12]。2015年，Celebrano等人通过对带有间隙的V型天线和单纳米棒的复合结构的设计，使其在基频光和二次谐波波长处均支持谐振效应，并且模式重叠，实现了高效的二次谐波辐射^[13]。这几种不同的金属超构表面如图1（a）所示。但是由于在光频和近红外波段具有较高的损耗，金属超构表面的损伤阈值较低，使其难以应用于高功率的激光辐照下，限制了二次谐波产生的效率。氮化钛(TiN)作为一种非线性耐火材料，可以承受更高强度的激光照射，并且具有较大的非线性响应，是一种良好的等离子体材料。2016年，Gui等人加工了如图1（b）所示的TiN超构表面，通过设计使其在1 μm左右具有等离激元谐振^[14]。通过将泵浦功率不断提高，达到最大值后再逐渐降低，重复测量，可以发现，在每个泵浦强度下的两个数据点基本重合，进而说明结构并未受到损伤。TiN超构表面可以承受的激光峰值功率密度可以达到15 GW•cm⁻²，远高于金属材料的损伤阈值。具有体非线性效应的非中心对称的材料更有利于获得高效的二次谐波产生。因此，近年来人们将目光投向了具有更低损耗且支持体谐振的介质超构表面。硅、锗等具有高折射率的良好的非线性材料由于晶体的中心对称性，不具有二阶非线性响应。因此基于介质超构表面的二次谐波产生的研究多集中于III-V族半导体材料，尤其是二阶非线性极化率较大的砷化镓(GaAs)和铝镓砷(AlGaAs)材料。2016年，Liu等人利用砷化镓超构表面观测到了增强的二次谐波产生^[15]。如图1（c）所示，超构表面由砷化镓纳米柱阵列组成，并且支持电偶极和磁偶极谐振。在磁偶极谐振波长处以3.4 GW• cm⁻²的峰值功率密度泵浦，可以获得2$ \times$10⁻⁵的转换效率。与无结构的砷化镓薄膜相比，二次谐波产生增强了四个数量级。二次谐波产生的效率可以通过使用具有更高品质因子（Q值）的谐振腔进一步提升。如图1（d）所示，利用对称性破坏的砷化镓超构表面演示了增强的二次谐波产生^[16]。该结构支持法诺谐振，可以在结构内实现更强的场局域。与砷化镓纳米柱阵列相比，法诺超构表面具有更高的场增强作用，因此可以实现更高效率的二次谐波产生。最近，一种被称为连续辐射中的束缚态（bound-state-in-the-continuum, BIC）的概念开始被应用于实现高Q值的介质超构表面。如图1（e）所示，Koshelev等人通过单个AlGaAs天线，利用BIC模式抑制辐射损耗，在约70 MW• cm⁻²的激光泵浦下，实现了转换效率为9.36$ \times$10⁻⁶二次谐波产生^[17]。

图  1  非线性超构表面的二次谐波产生。 （a） 几种不同结构的金属超构表面 ；（b） 具有高损伤阈值的TiN等离子体超构表面； （c） 支持米氏谐振的砷化镓超构表面； （d）支持法诺谐振的砷化镓超构表面；（e） 支持BIC模式的铝镓砷超构表面；（f） 等离子体与子带间跃迁耦合的多量子阱超构表面 ；（g） 电场诱导二次谐波产生的硅基超构表面

Figure 1.  Nonlinear metasurfaces for second-harmonic generation. (a) Several metallic metasurfaces based on different structures; (b) TiN plasmonic metasurface with high damage threshold; (c) GaAs metasurface supporting Mie resonance; (d) GaAs metasurface supporting Fano resonance; (e) AlGaAs metasurface supporting BIC mode; (f) Multi-quantum-well metasurface with plasmon coupled to intersubband transitions; (g) Silicon metasurface with electric-field-induced-second-harmonic-generation

除了自身具有的较大的非线性响应，III-V族半导体还可以被人为构造成多量子阱异质结构，通过设计获得比天然材料更高的非线性极化率。2014年，通过构造一个400 nm厚的多量子阱超构表面，Lee等人获得了5$ \times$10⁴ pm/V的非线性极化率^[18]。这种巨大的非线性增强作用主要来源于等离激元超构表面的电磁模式与半导体异质结构中电子子带间跃迁的耦合。如图1（f）所示，超构表面由不对称纳米十字阵列构成的金属层和多量子阱层构成。在15 kW cm⁻²的低泵浦峰值功率密度下，就可以实现2$ \times$10⁻⁶的转换效率。2016年，Lee等人进一步通过对金属和半导体层的刻蚀，定义了T型的纳米腔多量子阱超构表面^[19]。该结构通过优化使得基频光和二次谐波在纳米谐振腔中的模式体积尽可能地重叠，进而提高非线性的响应，实验获得了0.075%的二次谐波产生效率，为当前已报道的最高纪录。

针对具有中心对称性的晶体，为了获得二阶的非线性效应，可以利用直流电场诱导产生二次谐波。通过施加电压，引入直流电场，利用材料的三阶非线性极化率，产生等效的二阶非线性效应，其产生的二次谐波信号强度与施加的电压大小正相关。2014年，Kang等人利用金属孔阵列超构表面，通过施加10 V的电压，实现了9%调制深度的电场诱导的二次谐波产生^[20]。2019年，Lee等人基于该方法在硅基超构表面中实现了二次谐波的产生^[21]。如图1（g）所示，超构表面为支持磁偶极谐振的光栅结构，利用光刻、金属沉积以及剥离工艺形成金属电极。在10 V的电压下，可以获得对二次谐波信号大于12%的调制深度。该方法不仅实现了硅基超构表面的二次谐波产生，还提供了一种在亚波长像素分辨率下，对非线性信号进行主动调控的可能。基于不同材料体系的多种谐振效应，二次谐波产生已经得到广泛的研究。然而，由于亚波长的光与物质作用距离，与传统的体晶体相比，超构表面的二次谐波产生效率仍需进一步的提高。

与二阶非线性效应相比，三阶非线性不受晶体对称性的限制。三次谐波产生可以发生在任何非线性材料中。最早利用超构表面观测到三次谐波产生是基于金属纳米结构。2007年，利用中心波长为1 500 nm的飞秒激光泵浦开口环谐振器，激发其磁偶极谐振，Klein等人得到了增强的三次谐波信号^[22]。2012年，Hentschel等人利用二聚体金属天线增强光场，实现了较大的非线性响应，天线的形状、尺寸和间隙大小都会影响三次谐波的发射光谱^[23]。2014年，Metzger等人在支持法诺谐振的金属超构表面中实现了三次谐波信号的高效辐射^[24]。这几种典型的金属超构表面如图2（a）所示。

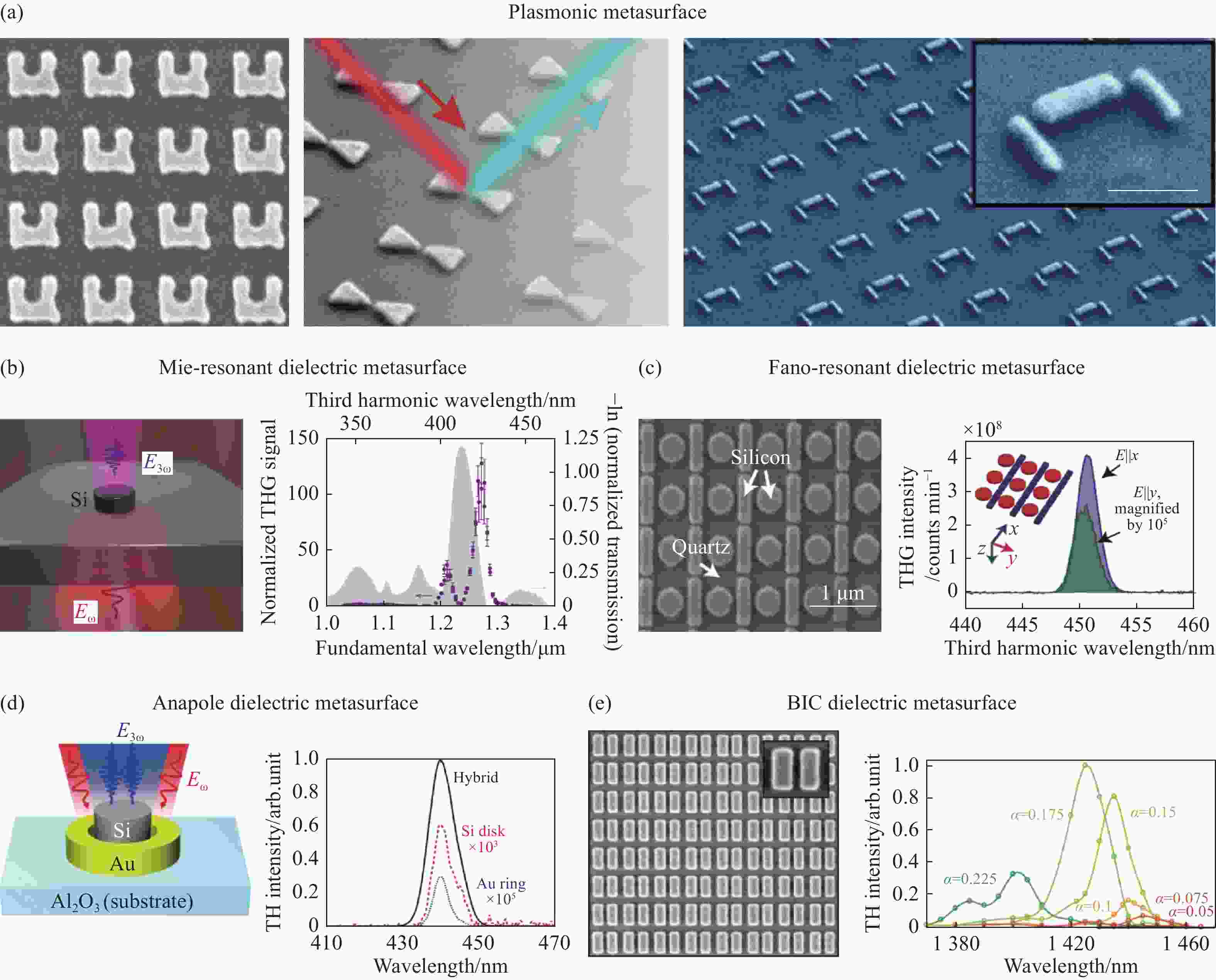
图  2  非线性超构表面的三次谐波产生。（a） 几种不同结构的金属超构表面；（b） 支持米氏谐振的硅基超构表面；（c） 支持法诺谐振的硅基超构表面；（d） 支持anapole模式的硅基超构表面；（e）支持BIC模式的硅基超构表面

Figure 2.  Nonlinear metasurfaces for third-harmonic generation. (a) Several metallic metasurfaces based on different structures; (b) Silicon metasurface supporting Mie resonance；(c) Silicon metasurface supporting Fano resonance; (d) Silicon metasurface supporting anapole mode; (e) Silicon metasurface supporting BIC mode

随后，由高折射率材料构成的介质超构表面开始广泛被应用于三次谐波产生的研究。2014年，利用如图2（b）所示的硅纳米柱，Shcherbakov等人观测到了米氏谐振增强的三次谐波产生^[25]。利用中心波长在磁偶极谐振1240 nm处的飞秒激光泵浦，可以得到约为10⁻⁷的转换效率。与无结构的硅薄膜相比，三次谐波产生的强度提高了两个数量级。后来，介质天线中更多的谐振模式受到广泛研究，并应用于增强的三次谐波产生。2015年，Yang等人利用法诺谐振的超构表面，进一步提高了非线性转换效率^[26]。如图2（c）所示，超构表面由耦合的矩形棒和圆盘谐振器周期排列而成。当激光偏振沿棒长轴时，矩形棒激发出的电偶极谐振为圆盘提供了纵向的磁场分量，进而激发出圆盘的磁偶极谐振，使得光场被很好地局域在硅谐振器内部，从而实现了较大的光场增强。通过线性光谱的表征，法诺谐振出现在1 346 nm处，Q值为466。在此波长处对结构进行泵浦，在3.2 GW• cm⁻²的激光峰值功率密度下，获得了1.2$ \times$10⁻⁶的转换效率，比无结构的硅膜提高了5个数量级。2017年，在硅和金组成的纳米谐振腔中，利用具有非辐射特性的无极子(anapole)模式，Shibanuma等人进行了三次谐波产生的演示^[27]。这种复合超构表面如图2（d）所示，硅纳米柱位于金纳米环的中心，金属的等离子体谐振可以增强硅的无极子模式，进一步提高硅内部的局域电场。通过非线性光谱的测量，在三次谐波440 nm处的非线性转换效率达到了0.007%。与单独的硅纳米柱和金纳米环相比，产生的三次谐波强度分别高了三个数量级和五个数量级。随后，2018年，Xu等人利用类似的方法将支持anapole模式的硅纳米柱谐振器放在金属镜上，获得了接近0.01%的三次谐波产生效率^[28]。2019年，Koshelev等人基于BIC模式，设计加工了一种对称性破坏的硅纳米结构，实验演示了增强的三次谐波产生^[29]。硅基超构表面的结构如图2（e）所示，由一组不对称的硅矩形棒周期性排列而成。通过对具有不同不对称度的结构进行线性和非线性的表征，可以发现，这种BIC模式来源于结构平面内对称性的破坏，并且不对称度会影响三次谐波产生的效率。随后，同样利用BIC模式，Liu等人在2019年设计加工了具有超高Q值的硅基超构表面^[30]。在正入射的激光泵浦下，BIC谐振的Q值高达18 511。归一化的三次谐波产生转换效率为1.4$ \times$10⁻⁸/W²，比当前硅基超构表面获得的最大值高了至少五个数量级。与二次谐波产生相同，较低的效率也是超构表面在三次谐波产生中面临的主要问题。

高次谐波是产生相干软X射线和深紫外脉冲的基础，已被广泛用于时间分辨光电子能谱和孤立阿秒脉冲的生成^[31-34]。与低阶的谐波产生过程不同，高次谐波产生是一种在激光光场强度和原子束缚能强度相当时发生的非微扰过程。对于传统的气态高次谐波源，原子密度较低，因此往往需要很高的泵浦功率。而固态的高次谐波源，虽然原子密度较大，但谐波转换效率受限于材料对光子能量大于带隙宽度的高阶信号的强吸收^[35-37]，实际起作用的只有纳米级的趋肤深度以下部分的晶体。

近年来，超构表面开始广泛应用于高次谐波产生的研究。其中，超构表面主要起到两方面的作用。一种思路为超构表面本身不作为非线性介质，利用其谐振效应增强泵浦光场，降低泵浦功率。2008年，Kim等人基于气态非线性媒质，实现了超构表面增强的高次谐波的产生^[38]。如图3（a）所示，超构表面由蓝宝石衬底上的蝴蝶结阵列构成。利用等离子体的谐振效应增强氩气周围的泵浦光场，在0.1 TW• cm⁻²的激光强度下，产生了高达17阶的谐波信号。其相比传统的气态高次谐波源，所需的激光强度低了两个数量级。此后，应用类似的结构，Sivis等人研究了这种蝴蝶结纳米结构引起的场增强效果。在获得相同的非线性信号条件下，通过有无超构表面所需的泵浦强度，可以估算出纳米结构所提供的局域场增强达到了380倍，与理论计算相符^[39]。但是这种气态的高次谐波源往往需要复杂的实验装置。

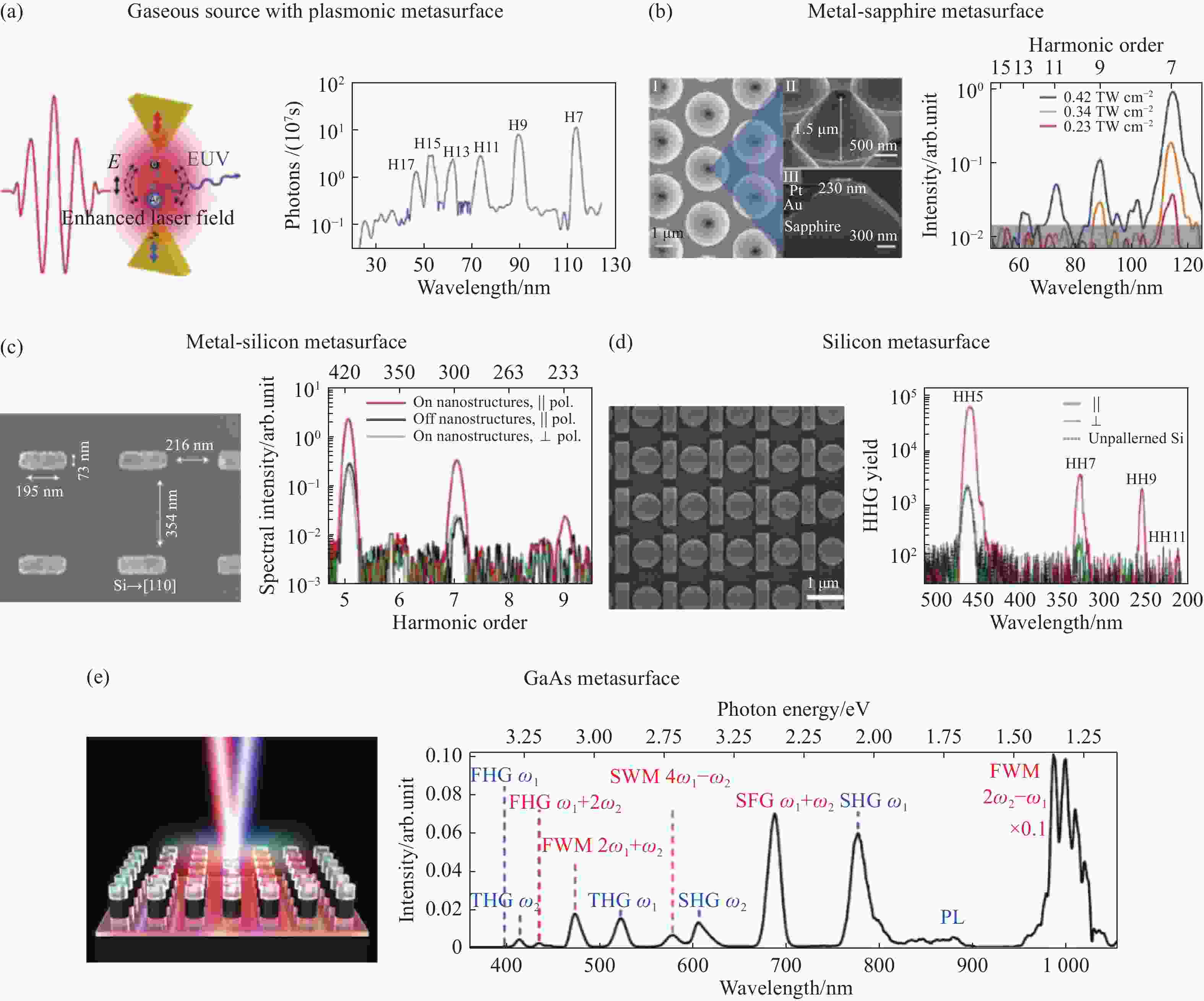
图  3  非线性超构表面的高次谐波产生。（a）利用金属超构表面实现近场增强的气态高次谐波源；（b） 等离子体增强的金属-蓝宝石超构表面；（c）等离子体增强的金属-硅复合超构表面；（d） 支持法诺谐振的硅基超构表面；（e）支持磁偶极谐振的砷化镓超构表面

Figure 3.  Nonlinear metasurfaces for high-harmonic generation. (a) Gaseous high harmonic sources with near-field enhancement based on a metallic metasurface; (b) Plasmon-enhanced metal-sapphire metasurface; (c) Plasmon-enhanced hybrid metal-silicon metasurface; (d) Silicon metasurface supporting Fano resonance; (e) GaAs metasurface supporting magnetic-dipole resonance

近年来利用超构表面本身作为非线性介质，获得全固态高次谐波源成为了研究热点。除了谐振增强，超构表面还具有较低的谐波传输损耗。2016年，利用表面等离激元的场局域作用，Han等人通过如图3（b）所示的金属−蓝宝石锥型纳米结构观测到了13阶的高次谐波产生^[40]。所用的泵浦激光峰值功率密度为0.1 TW cm⁻²。2017年，利用等离子体增强硅的高次谐波产生的工作也被报道^[41]。如图3（c）所示，结构由沉积在500 nm厚的多晶硅上的金天线阵列构成，在0.03 TW• cm⁻²的激光泵浦下，观测到了九次谐波的信号，更高阶的信号收集受限于探测器的光谱范围。与无谐振增强时相比，高次谐波信号增强了五到十倍。正如前面提到的金属超构表面存在的限制，人们开始将目光转向介质超构表面。如图3（d）所示，Liu等人利用具有高Q值的法诺谐振硅基超构表面实现了增强的高次谐波产生^[42]。与相同厚度的硅薄膜相比，高阶信号得到了两个数量级的增强。在0.071 TW• cm⁻²的激发强度下，探测到了五到11阶的高次谐波信号。其中五次谐波信号强度与无结构的薄膜相比增强30多倍。以上工作均基于金属和硅基超构表面，由于中心对称性的限制，只有奇数阶高次谐波的辐射。砷化镓超构表面提供了实现偶数阶谐波产生的可能。如图3（e）所示，基于砷化镓纳米柱阵列，同时实现了包括二次谐波产生等七种不同的非线性光学混频过程，获得了从紫外到近红外的光谱范围^[43]。该结构有希望实现同时具有奇偶阶信号的高次谐波源。支持谐振效应的超构表面是实现低泵浦阈值以及高转换效率的高次谐波源的重要媒介。当前，材料的多光子吸收仍会导致超构表面较低的损伤阈值，是当前亟待解决的主要问题。

太赫兹波（Terahertz，THz波），通常被定义为频率在0.1~10 THz之间的远红外电磁辐射。随着太赫兹源和探测器的发展，太赫兹技术已经逐渐被应用于通信、雷达、遥感、安检等领域^[44]。宽带太赫兹光源可以利用非线性差频（光整流）的方式来实现^[45-46]。

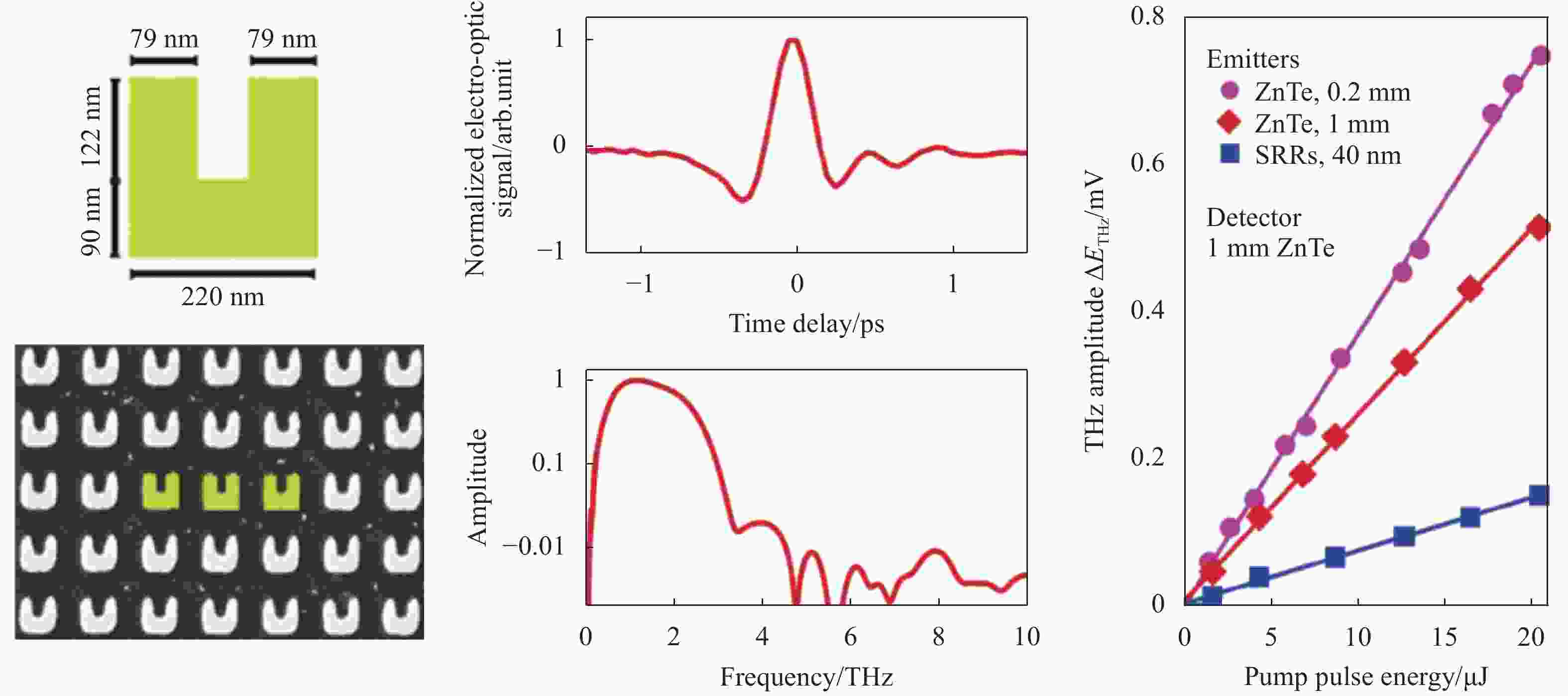
当前基于非线性效应的太赫兹源多采用的是满足相位匹配条件的体晶体，如锑化锌等^[45-47]。然而由于材料的色散，相位匹配条件通常会限制利用差频方法产生的太赫兹波的带宽^[48]，分子振动和转动能级引起的强吸收也会使得太赫兹光谱出现带隙^[49]。为了解决这些问题，人们开始将目光转向无相位匹配限制的亚波长传播距离的非线性超构表面。2014年，Luo等人利用金属超构表面演示了0.1~4 THz的宽带太赫兹辐射^[50]。如图4所示，超构表面由开口环谐振器阵列构成，结构在1 500 nm处支持磁偶极谐振。利用中心波长为1500 nm，脉冲时间为140 fs的激光进行泵浦，40 nm厚的超构表面产生了较为宽带的太赫兹波辐射。在磁偶极谐振的近场增强作用下，超构表面产生的太赫兹波强度与在相同泵浦条件下1 mm厚的锑化锌体晶体相当。此外，文中指出，太赫兹波带宽最有可能是受到了激光脉宽的限制。2018年，Fang等人利用类似的结构，通过理论计算与数值仿真验证了这一想法，差频产生的太赫兹带宽可以由更短脉宽的激光泵浦获得^[51]。

图  4  基于非线性金属超构表面的宽带太赫兹波产生

Figure 4.  Broadband terahertz wave generation based on a nonlinear metallic metasurface

与传统的光学元件不同，超构表面可以实现相位突变，而不再依赖于在介质中的传播效应。通过对光学天线形状尺寸的设计以及空间排列，可以获得具有亚波长空间分辨率的光学响应。超构表面可以对谐波信号进行波前调控，实现非线性涡旋光产生、光束偏折、平面透镜、全息等应用。

特定的空间相位分布是实现波前调控的基础。一种常用的方法为几何相位^{[52- 53]}。这一方法已被延伸并应用于非线性光学。在圆偏振光的激发下，可以等效为电偶极子的纳米天线会发生极化，与入射光手性相同和相反的圆偏振谐波光会产生与阶次和方位角相关的相位，进而可以通过对光学天线的排列构造所需的相位分布。值得注意的是，非线性几何相位对波长不敏感，具有无色散的宽带特性，但受到天线旋转对称性的限制。如图5（a）所示，Li等人利用具有双重（C2）和四重旋转对称性（C4）的纳米天线对此理论进行了实验验证^[54]。用右旋的圆偏振光激发两个超构表面，在C2超构表面中，相反旋性的两种圆偏振光由于不同的相位梯度，具有不同的偏折角度。而C4超表面由于对称性选择定则的限制，只有相反旋性的偏振光出射。另一种引入相位变化的方法是传播相位，这与单个天线的光学响应有关。通过设计天线的形状尺寸，可以得到每个天线对应的谐波相位，进而按照需要的相位分布排列不同的天线来实现特定的波前。基于该理论，Wang等人利用介质超构表面演示了对三次谐波的波前调控^[55]。如图5（b）所示，超构表面由十个具有不同椭圆度的纳米柱阵列构成。利用在泵浦光和三次谐波处激发的米氏谐振间的相互作用，挑选出具有相近的三次谐波的振幅，并且覆盖了0~2$\pi $相位范围的圆柱。通过对圆柱的排列构造不同的相位分布，分别实现了对于三次谐波的偏折和涡旋光束的产生。其中在特定角度出射的谐波衍射效率高达92%。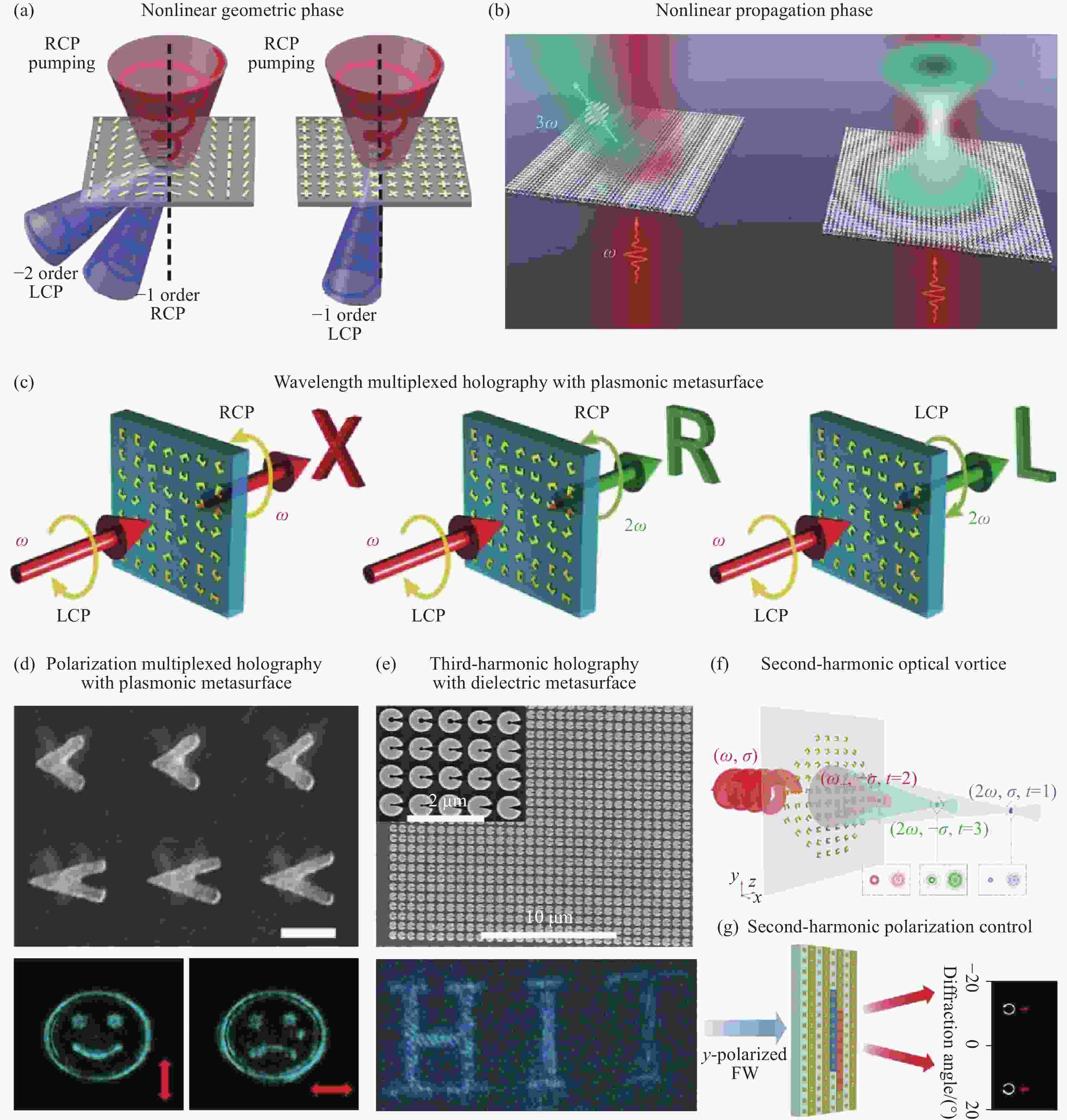

图  5  非线性超构表面的波前调控。（a） 利用非线性几何相位实现不同阶次谐波的偏折；（b）利用非线性传播相位实现三次谐波的偏折和涡旋光产生；（c）利用金属超构表面实现的基频与不同手性二次谐波的全息图；（d）利用金属超构表面实现的正交偏振的全息图；（e） 利用硅基超构表面实现的三次谐波全息图；（f） 利用金属超构表面实现的二次谐波光学涡旋；（g）利用金属超构表面实现的二次谐波偏振调控

Figure 5.  Nonlinear metasurfaces for wavefront control. (a) Using nonlinear geometric phase to achieve deflection of different orders of harmonics; (b) Using nonlinear propagation phase to achieve deflection and vortex light generation of third-harmonic signal; (c) Holograms of the fundamental frequency and the different chirality-dependent second-harmonics based on a metallic metasurface; (d) Holograms of orthogonal polarization based on a metallic metasurface; (e) Third-harmonic holograms based on a silicon metasurface; (f) Optical vortices of second-harmonics based on a metallic metasurface; (g) Polarization manipulation of second-harmonics based on a metallic metasurface

基于几何相位和传播相位，超构表面已经被广泛应用于非线性光学全息的研究。2016年，Ye等人利用非线性几何相位超构表面，实现了自旋和波长复用的光学全息^[56]。如图5（c）所示，超构表面由无旋转对称性的开口环谐振器阵列组成，在相同的排列分布下，基频光和两种相反旋性的二次谐波具有完全不同的全息图案。这种独立的无串扰的非线性全息为多维的光信息存储提供了可能的方案。随后，利用多层的金属超构表面，Almeida等人实现了偏振敏感的非线性全息图^[57]。通过改变V形金属天线的臂长和夹角，可以调谐天线的等离子体谐振，进而改变产生的三次谐波的相位。不同偏振的全息图像由超构表面不同层经过编码排列生成，如图5（d）所示的笑脸和哭脸图案即在竖直偏振和水平偏振的泵浦光照射下得到的。此外通过对于全息图的设计，可以使得不同的图像成像在不同的位置，从而为三维的光学全息奠定了基础。以上的非线性全息演示都是基于金属超构表面，高损耗和低损伤阈值一直是金属走向实际应用的最大限制，而低损耗的介质材料可以很好地解决这一问题。2018年，Gao等人利用硅基超构表面进行了三次谐波全息图的演示^[58]。如图5（e）所示，超构表面由蓝宝石衬底上的C型单晶硅纳米柱阵列而成。结构在1400 nm处具有米氏谐振，可以增强硅柱内泵浦光的强度，而三次谐波部分被局域在空气间隙中，可以降低材料对其的吸收，进而有效地辐射到远场。在用磁偶极谐振波长的激光泵浦时，三次谐波信号达到最强，增强了230倍，远高于之前的研究。通过调整纳米柱的外层半径、内层半径以及开口角度，可以控制谐振的性质，引入相位变化。利用十个不同的纳米天线，可以实现三次谐波信号从0到2$\pi $的相位改变。并通过算法编码排列超构表面，实验演示了三次谐波全息图案。2019年，同样利用硅基超构表面，Reineke等人基于三次谐波的非线性几何相位操控，进行了非线性全息的演示^[59]。相比于传播相位，该方法设计更加简单，对于加工过程具有更高的容忍度。

除了光学全息，基于非线性的相位控制，超构表面在其他方面也有许多重要的应用。例如Li等人利用二次谐波的几何相位，实现了在不同焦点处具有不同拓扑荷数的光学涡旋产生^[60]。如图5（f）所示，超构表面由在1550 nm处支持磁偶极谐振的开口环谐振器阵列构成。通过引入非线性几何相位，将不同拓扑荷数的基频光与两种圆偏振的二次谐波同时聚焦到不同位置，获得了三倍信息容量的光学涡旋。另外，非线性超构表面也可以实现对偏振的控制。Zang等人基于开口环超构表面实现了对二次谐波的偏振控制与分离^[61]。如图5（g）所示，开口环和旋转了90°的开口环互补结构可以产生正交偏振的二次谐波信号，通过改变臂长，调整谐波的相位与振幅，可以实现对偏振的调制。文中通过对超构表面的设计，将线偏振的基频光转换成了空间分离的相反旋性的圆偏振光。由于对光操纵的亚波长分辨率，非线性超构表面可以实现灵活的波前调控，加上非线性过程引入的新的频率和结构的偏振选择，超构表面在多通道高容量的全息显示，数据存储等方面有望实现应用。

基于三阶非线性效应的四波混频、自相位调制等过程，不仅可以产生新的谐波，还可以在基频处引起强度相关的折射率变化，从而对信号光的相位、偏振以及强度进行调控。利用材料的克尔效应或者自由载流子的非线性折射率响应，结合超构表面的场增强作用，往往可以实现超快且高效的全光调控。

介质材料的调控速度通常取决于自由载流子的寿命和双光子吸收效应。对于传统的波导结构，双光子吸收引起的额外的自由载流子效应通常会导致几百皮秒到几纳秒的电子空穴对复合速率^[62-63]，严重限制了调控速度。而介质超构表面支持的磁偶极谐振可以很好地抑制这种载流子效应。如图6（a）所示，Shcherbakov等人利用硅基超构表面，实现了65 fs的透过率调控^[64]。在磁偶极谐振的作用下，与无结构的硅薄膜相比，调控获得了80倍的增强效果。相对于介质材料，限制金属全光调控速度的主要是电子和声子之间的能量交换速率，往往具有更短的调控时间，通常可以达到几个皮秒甚至几十飞秒^[65-66]。2011年，Baida等人在单个金纳米棒的表面等离子体谐振处观测到了皮秒量级的非线性响应^[67]。基于超快的非线性折射率变化，金纳米棒阵列构成的超构表面实现了80%的透过率变化，调控时间在几个皮秒^[68]。这种大的调制深度以及超快响应来源于等离子体模式的非局域特性，可以通过对结构的合理设计获得。随后，利用如图6（b）所示的非对称开口环谐振器，Ren等人在金超构表面中实现了更快更强的全光控制^[69]。在270 μJ•cm⁻²的激光能流泵浦下，获得了100 fs以内的40%的相对透射调制，比上述的纳米棒超构表面所需的能流低了至少一个数量级。近年来，透明金属氧化物(TCOs)由于良好的非线性性能被广泛用于超快全光调控。一方面，TCOs具有比金属更小的电子比热容，可以实现更快的电子和声子间的能量交换，利用金属和TCOs的复合结构，通常可以获得更快的调控速度。如图6（c）所示，金属天线阵列沉积在ITO上，利用金属谐振器的等离子体增强和ITO衬底提供的热电子能量弛豫通道，得到了190 fs的全光调控^[70]。另一方面，TCOs本身在介电常数近零(ENZ)波长附近具有很大的非线性折射率^[71-72]，已经在AZO^[73-74]、CdO^[75]等薄膜中实现了较大调制深度的超快全光调控。通过将TCOs的ENZ模式和超构表面的谐振效应结合，可以得到更大的非线性响应。如图6（d）所示，谐振波长均为1420 nm的ITO薄膜和金天线阵列构成了强耦合体系，结构在超过200 nm的波长范围内都具有2.5的折射率变化，同时响应时间在飞秒量级，有利于实现宽带的超快调控^[76]。

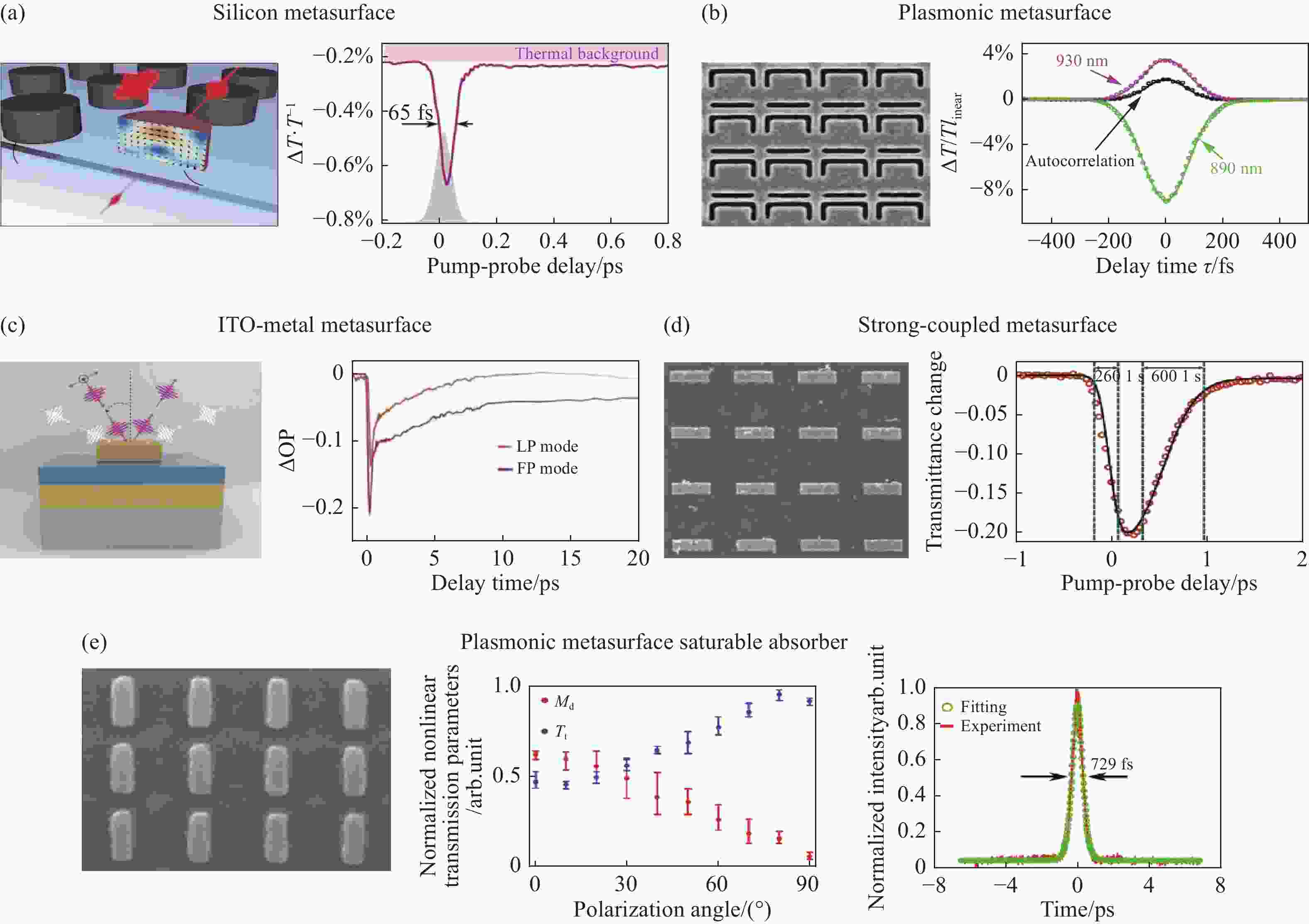
图  6  非线性超构表面的超快调控。 （a）硅基超构表面实现全光调控；（b） 金属超构表面实现全光调控；（c） ITO作为弛豫通道的金属超构表面；（d）金属与ITO复合的强耦合超构表面；（e）金属超构表面作为可饱和吸收体实现的激光调Q与锁模

Figure 6.  Nonlinear metasurfaces for ultrafast control. (a) All-optical control based on a silicon metasurface ; (b) All-optical control based on a metallic metasurface; (c) Metallic metasurface with the relaxation channel of ITO; (d) Strong-coupled metasurface combined with metal and ITO; (e) Laser Q-switching and mode-locking with metallic metasurface as a saturable absorber

支持谐振效应的超构表面不仅可以提供较大的调制深度，还具有超快的调控速度，对于实现低功耗、超快的全光纳米器件具有重要价值。例如2020年，Wang等人利用金属超构表面，实现了激光调Q与锁模^[77]。如图6（e）所示，超构表面由金纳米棒阵列构成，通过对其饱和吸收性质的表征，获得了60%的调制深度，这一数值比当前的其他可饱和吸收体要高得多。进一步将超构表面放入激光腔中，实现了光孤子锁模，得到了脉宽为729 fs的激光脉冲。

超构表面具有亚波长的光与物质作用距离，是解决非线性光学中相位失配问题的新兴媒介。构成超构表面的光学天线支持各种谐振模式，例如等离子体谐振、米氏谐振、法诺谐振、无极子模式以及BIC模式等，可以在很小的体积中获得较大的场增强，进而提高非线性响应。谐振增强的光学频率转换过程是当前非线性超构表面的重要研究方向之一，尤其是在二次谐波产生和三次谐波产生中。然而，目前为止，超构表面的非线性转换效率相对仍然较低。除了应用具有更大非线性极化率的材料，利用反向设计实现在泵浦光和谐波信号处具有更高Q值以及更大模式重叠体积的谐振的谐振腔是进一步提高超构表面非线性转换效率的可能的有效手段。主要的方法包括邻近算法^[78]、拓扑优化^[79]以及深度学习^[80]等。超构表面的谐振增强以及对高频谐波的弱吸收等特点使得其可以在低泵浦能量下获得高转换效率的高次谐波产生。但是对于进一步的实际应用，往往需要更高的谐波截止频率，这就要求材料具有更高的损伤阈值以承受更大强度的激光泵浦，因此需要更宽带隙的晶体材料。无相位匹配限制的超构表面是实现宽带非线性光源的重要介质。除了文中提到的太赫兹源，利用超构表面获得宽带的纠缠光子对也是量子光学域的热点问题^[81]。基于亚波长空间分辨率的波前调控能力，超构表面除了在非线性光学全息成像中具有重要应用，也可用于获得具有特定波前的太赫兹源^[82]和高次谐波源^[83]。此外，结合不同材料的超快调控能力，超构表面已经被广泛应用于全光开关、激光调Q与锁模技术中，有望实现高密度的多功能纳米器件。

如上所述，非线性超构表面具有许多独特的优势，也存在许多需要进一步解决的问题。随着技术的进一步发展，笔者等期待，非线性超构表面会在更多的应用中发挥重要的价值。