-
当今世界,信息正以惊人的速度增长,海量数据的传输、处理和存储是世界性的难题。蓬勃发展的新技术,如增强现实、自动驾驶和智能手机等,要求实时处理图像、语音等多媒体信息,因此快速的数字计算是亟需的,但颇具挑战性[1-2]。目前的图像处理方法多采用集成电子电路和程序算法来进行,但标准电子元件的速度和功耗等性能很难再大幅提升,因为其特征尺寸已经接近量子极限。因此,研究全新的非电子类器件成为解决这些问题的关键,其中,基于光子的计算处理为克服这些限制提供了一条潜在的途径。近几年,光学模拟计算受到了特别的关注,其天然的并行操作特性,为某些计算任务提供了高速度、低功耗的解决思路。光学计算以光速对整个图像进行大规模并行处理,这与基于电子计算机的图像数字处理相比,具有显著的速度优势。光学计算的想法可追溯到20世纪60年代早期,是借助于傅里叶光学的开创性工作而发展起来的[3-5]。在傅里叶光学中[6],传统的图像处理方法涉及到多个光学元件,且通常体积庞大,不适用于紧凑型图像传感器。作为一种重要的图像处理类型,图像边缘检测近期取得了诸多进展,尤其是通过纳米结构来实现。
近几年,光学超表面的发展使光在亚波长厚度范围内得到精准调控,通过改变微纳结构的横向尺寸和形状来有效地操纵光的波前和振幅[7-15],其能实现传统光学元件的各种功能,可取代笨重、体积大的传统光学元件,为研发紧凑、轻量化、多功能平板光学系统开辟一条全新的道路[16-19]。用于光学计算的超表面受益于高速度、低功耗和可单片集成等特点,其使在单个芯片上处理光和电子数据成为可能。在光学计算中,边缘检测是目标检测、特征分类和数据压缩的首要步骤,其能提取并保留物体的重要特征信息,显著减少待处理的数据量。因此,边缘检测或增强[20-21]对数据压缩[22]、物体识别[23]、显微镜成像和计算机视觉等领域具有重要应用前景[20-21, 23-33]。然而,在实时图像处理的应用中,如医疗手术、智能汽车等,传统的高通量边缘检测极其耗时。针对这一问题,利用微纳结构进行图像边缘检测成为一个重要的替代手段,其实现途径主要包括:调节超表面的相对介电常数和磁导率[16]、调控传播模式耦合[17-19, 34-41]、螺旋相位滤波法[42]、偏振和空间复用的双超表面[43]、几何相位正反梯度[44]和利用自旋霍尔效应的结构[45-46]等。与传统的傅里叶光学装置相比,基于微纳结构的图像边缘检测器件的体积更紧凑,调控精度更高,更有潜力集成到图像传感系统。文中介绍了上述全光学边缘检测方法的工作原理和实现途径,讨论了各种边缘检测的优缺点,为未来的全光学边缘检测系统设计提供参考。
-
2014年Silva等人首次提出并实现基于超材料的模拟光学计算,其基于特殊设计的超材料结构来控制入射波,对其波的横截面进行数学运算(如空间微分、积分或卷积)[16]。当入射波经过超材料时,通过改变每层超材料的电磁响应,使输出波与输入波之间满足预期的数学运算操作。为了实现这一功能,他们提出了两种方法:(1)具有亚波长尺寸的梯度折射率波导;(2)多层平板来实现所需的格林函数功能。这两种技术均可提供小型化、可积的电磁计算系统,比基于傅里叶光学的传统信号和数据处理器薄几个数量级。
梯度折射率波导法是在傅里叶频谱域中利用平面薄材料执行数学运算。一个线性卷积
$g\left(y\right)= \displaystyle \int f\left(u\right)G(y-u){\rm{d}}u$ ,其中,$f\left(u\right)$ 为任意入射场,$ G\left(y\right) $ 为该系统的格林函数。在傅里叶频谱域,该卷积可表示为$ \tilde{g}\left({k}_{y}\right)=\tilde{G}\left({k}_{y}\right)\tilde{f}\left({k}_{y}\right) $ ,$ \tilde{g} $ ,$ \tilde{G} $ 和$ \tilde{f} $ 分别为g, G和f的傅里叶变换。在该方法中,超材料体系包括三个级联模块:傅里叶变换单元,一个空间滤波器$ \tilde{G}\left({k}_{y}\right) $ 和逆傅里叶变换单元。对于第一个单元,用一个二维渐变折射率(GRIN)介质板,具有磁导率$ \mu ={\mu }_{0} $ 和具有抛物线变化的介电常数:$$ \varepsilon \left(y\right)={\varepsilon }_{c}\left[1-{\left(\dfrac{\pi }{2{L}_{g}}\right)}^{2}{y}^{2}\right] $$ (1) 式中:
$ {\varepsilon }_{c} $ 为GRIN平面中心的介电常数;$ {L}_{g} $ 为特征长度。在图1中,GRIN+表示介电常数和磁导率为正。在傍轴近似下,沿传播方向在“焦距”$ {L}_{g} $ 处可实现傅里叶变换,其功能相当于傅里叶透镜。GRIN-表示介电常数和磁导率为负,$ \mu ={-\mu }_{0} $ ,$ \varepsilon =-\varepsilon \left(y\right) $ ,沿传播方向在“焦距”$ {L}_{g} $ 处作逆傅里叶变换。用于空间滤波的超结构可采用两种不同的方法设计:(1)概念上薄的超表面(metasurfaces),具有体积参数$ {\varepsilon }_{ms}\left(y\right)/{\varepsilon }_{0}= {\mu }_{ms}\left(y\right)/{u}_{0} $ (如图1所示)。(2)一种真实的三层薄超材料,基于有不同程度损失的两种材料适当交替,比如,铝掺杂氧化锌(AZO)和硅(Si)。基于这些概念,可实现一些基本的数学运算操作。
图 1 基于波的超材料计算。一种设计适当的超材料块的概念草图,该超材料块可在任意波信号传播时对其进行所需的数学运算,在GRIN+和GRIN-的结构之间,设计合理的薄结构可以在傅里叶域进行数学运算
Figure 1. Wave-based metamaterial computing. A conceptual sketch of a suitably designed metamaterial block that may perform a desired mathematical operation on arbitrary wave signals as they propagate through it. A thin, properly designed metasurfaces sandwiched between two GRIN structures with positive and negative parameters, can perform mathematical operations in the Fourier domain
对于一阶微分:
$g\left(y\right)\propto {\rm{d}}f\left(y\right)/{\rm{d}}y$ 。这种情况下,其相应的格林函数为$ \tilde{G}\left({k}_{y}\right)\propto \left(i{k}_{y}\right) $ 。在具有厚度Δ<λ0(λ0是自由空间中的光波长)的横向非均匀超表面中,其横坐标y上位相和振幅代表的是$ {k}_{y} $ 的调制,用于实现空间滤波的功能。该超要求实现与$ 2iy/w $ 成正比的归一化传递函数,此相对介电常数和磁导率(在范围$ \left|y\right|\le W/2 $ ):$$\frac{{{\varepsilon _{ms}}\left( y \right)}}{{{\varepsilon _0}}} = \dfrac{{{\mu _{ms}}}}{{{\mu _0}}} = {{i}}\left( {\dfrac{{{\lambda _0}}}{{2\pi \Delta }}} \right)\ln \left( {\dfrac{{ - iW}}{{2y}}} \right) $$ (2) 由于超表面被夹在GRIN+和GRIN-之间,该超材料系统获得了具有一阶微分的数学运算操作。原理上,该光学计算系统适用于任何波长,因此不限于光学频段,也能应用于微波、毫米波等短波长领域。在图像处理领域,该一阶差分运算可用于检测图像的一维边缘。
二阶微分:
$g\left(y\right)\propto {{\rm{d}}}^{2}f\left(y\right)/{\rm{d}}{y}^{2}$ 。尽管两个一阶微分单元的级联可执行该二阶空间微分操作,但由于超表面功能强大,单个超表面也可执行二阶微分操作。由于采用了模块化方案,只需简单地用传递函数$ {[iy/(W/2\left)\right]}^{2} $ 替换超表面单元,该传递函数需要体积介电常数和磁导率函数:$$\frac{{{\varepsilon _{ms}}\left( y \right)}}{{{\varepsilon _0}}} = \dfrac{{{\mu _{ms}}}}{{{\mu _0}}} = {{i}}2\left( {\dfrac{{{\lambda _0}}}{{2\pi \Delta }}} \right)\ln \left( {\dfrac{{ - iW}}{{2y}}} \right)$$ (3) 式中:
$ \left|y\right|\le W/2 $ 。该方案是除了一阶和二阶微分等基础操作外,还能执行积分、卷积等复杂操作。其在理论上验证了超材料进行数学运算的可能性,但材料介电常数根据需求变化和实验上的制造复杂度较大,故基于该方案的实验结果尚未报道。物理上,该工作开辟了利用微纳结构执行光学模拟计算的新方向。
-
借助傅里叶变换和数学运算的具体操作可通过频率域或动量域的幅值调制来实现,即光在不同入射角下的透射或反射满足特定的数学运算需求。以y方向的一阶微分为例,其频率域的振幅调制为
$ {ik}_{y} $ ,这要求微纳结构的透射或反射率随着入射角增大而呈线性增加的趋势。因此,只要合理选择结构形状和参数,其在入射角改变的情况下激发不同的谐振模式,实现透射率或反射率的调控,以实现具体的数学运算。近几年,开环谐振器[17]、表面等离激元[19, 35]、光子晶体平板[18, 37, 34]和介质柱超表面[42-43]等微纳结构都被用来实现光学微分运算。Alu课题组发现,超表面的非定域性可被悉心设计,以实现在超薄空间下动量域的光信号操纵,从而执行基本数学运算。在实际设计中,把慢周期空间调制引入超表面,来提高其非局域响应幅度,再通过适当地调制参数,可实现不同类型的数学运算,如一维一阶微分、一维二阶微分和二维拉普拉斯运算[17]等。如图2(a)所示,对于一维二阶操作,用一个基本的正弦调制,在开环谐振器(split-ring resonators,SRRs) 间隙中引入介质调制,其介电常数
$ {\varepsilon }_{n}= {\varepsilon }_{c}[1+mcos(2\pi na/p\left)\right] $ ,$ {\varepsilon }_{n} $ 为第n个SRR隙中的介电常数,$ {\varepsilon }_{c} $ 为平均介电常数,m为调制幅值,p为调制周期,a为相邻SRRs之间的距离。这种结构支持由入射波沿超表面与表面模式耦合而产生的漏波共振[47],这入射波与共振辐射的干涉导致了Fano谐振。对于给定的入射角θ,共振频率由带有波数${k}_{0}{\rm{sin}}\theta +{k}_{m}$ 的表面波频率决定,其中$ {k}_{m}=2\pi /p $ 。这导致了随着表面模的色散,共振频率随入射角而强烈变化。如果工作频率与正入射时法诺谐振频率的零点一致,由于其相应的漏模具有强色散特性,当增加入射角时,超表面的透射系数将迅速增加。满足这种性质的超表面可用于实现二阶微分,即在频谱域实现幅度调制$ T\left({k}_{x}\right)=-\alpha {{k}_{x}}^{2} $ ,α是一个常数。图2(d)比较超表面的实际响应与理想的二阶导数响应,当入射角小于39°时两者非常一致。对于一维一阶操作,它在频谱域有一个传递函数${{T}}\left({k}_{x}\right)={{i}}{\text{α}}{k}_{x}$ ,α是一个常数。因为其需要一个横波数$ {k}_{x} $ 具有奇相位响应的传递函数,一维一阶操作较难实现。通过在SRR阵列的一侧添加平行于x轴的水平错位金属线阵列来修改开环超表面,以打破水平和垂直对称,如图2(b)所示。通过控制单元的几何形状,可以得到一个近似于一阶导数运算的响应,在kx=0处有一个相位跃变,如图2(e)所示,对于较大的$ {k}_{x} $ ,与理想响应的偏差是由于$ T\left({k}_{x}\right) $ 对$ {k}_{x} $ 展开中高阶项($ {k}_{x}^{2} $ ,$ {k}_{x}^{3} $ ,…)的存在。它不能用简单的正弦调制来抵消,因为随着$ {k}_{x} $ 的增加高阶项变得更加重要,但可以使用更复杂的调制这些高阶项可以被消除。为扩展到二维,他们设计了具有旋转对称响应的超表面。最简单的情况是将两个相同的超表面旋转90°再组合(如图2(c)所示),组合后的超表面具有90°旋转对称,有望在x和y轴上对TM极化波提供相同的二阶导数响应。理想的拉普拉斯操作对TE和TM偏振的作用方式相同,若使用非偏振光对图2(f)进行照明,可以很好地检测图像所有方向的边缘(见图2(g))。
图 2 非局域超表面。(a) 平行于x-z平面的裂环谐振器阵列示意图。超表面被TM偏振光激发,在x-z平面传播;(b) 设计的超表面对于正和负的
$ {k}_{x} $ 打破x和z对称性获取不对称响应,实现一个一阶导数的要求操作;(c) 超表面具有90°旋转对称实现二维的二阶导数;(d) 二阶导数运算的超表面传输与入射角关系;(e) 一阶导数运算的超表面传输与入射角关系;(f) 该图像用于测试在$ f=0.98{f}_{0} $ ,其中$ {f}_{0} $ 为未调制的超表面的共振频率;(g)法线方向的非偏振光照明图(f)的输出。图(a)~(f)的改动经过参考文献[17]的许可Figure 2. Nonlocal metasurface. (a) Schematic of an array of split-ring resonators parallel to the x-z plane. The measurface is excited by TM-polarized waves propagating on the x-z plane; (b) Metasurface with broken x and z symmetry to obtain an asymmetric response with respect to positive and negative
$ {k}_{x} $ , as required in order to implement a first-derivative operation; (c) Metasurface with a 90° rotational symmetry to implement the second derivative in 2D; (d) Transmission versus incident angle for the metasurface for an second-derivative operation; (e)Transmission versus incidence angle for the metasurface and for an first-derivative operation; (f) Image used to test the response of the metasurface at$ f=0.98{f}_{0} $ , where$ { f}_{0} $ is the resonance frequency of the unmodulated metasurface; (g) Output for illumination (f) with unpolarized light from the normal direction. Panel (a)-(f) adapted with permission from reference [17]金属−介质界面处表面激元的干涉效应也可进行空间微分[19]。一个p偏振波以入射角
${{\rm{\theta }}_0}$ 从玻璃侧面照明金属表面,通过傅里叶变换,入射场和反射场可写成平面波的叠加:${S}_{{\rm{in}}\left({\rm{out}}\right)}=\displaystyle\int {s}_{{\rm{in}}\left({\rm{out}}\right)}\left({k}_{x}\right)\exp\left(i{k}_{x}x\right){\rm{d}}{k}_{x}$ ,其中$ {k}_{x} $ 是沿着x方向的波矢分量,${s}_{{\rm{in}}\left({\rm{out}}\right)}\left({k}_{x}\right)$ 是对应的振幅。因此,从入射光到反射光的场变换,可用空间谱的传递函数$H\left({k}_{x}\right)={s}_{{\rm{out}}}\left({k}_{x}\right)/{s}_{{\rm{in}}}{(k}_{x})$ 来描述。当入射角$ {{\rm{\theta }}_0}$ 满足相位匹配情况,即平面波有一个平行于界面的波矢分量,其与金属−空气界面上传播的表面等离子激元(SPP)波矢相匹配,从而激发SPP[48]的强烈震荡。由于材料损耗,SPP的衰减导致传递函数$ H\left({k}_{x}\right) $ 在$ {k}_{x}=0 $ 处下降;此外,当激发的SPP沿着金属表面传播时,它会泄漏并辐射。这样,反射光的振幅是由介质-金属界面的直接反射和SPP泄漏模辐射之间的干涉来确定。采用空间耦合模理论[49-50],该空间谱传递函数在$ {k}_{x}=0 $ 附近可以表示为,$H\left({k}_{x}\right)= {{\rm{e}}}^{i\varphi }\dfrac{i{k}_{x}+A}{i{k}_{x}+B}$ ,$\varphi$ 是介质-金属界面直接反射时的相位变化量,$A=({\alpha }_{spp}-{\alpha }_{1})/{\rm{cos}}{\theta }_{0}$ ,$B=({\alpha }_{spp}+{\alpha }_{1})/{\rm{cos}}{\theta }_{0}$ ,$ {\alpha }_{1} $ 是光波辐射泄漏率,$ {\alpha }_{spp} $ 是金属材料内在损耗。当$ {\alpha }_{spp} $ =$ {\alpha }_{1} $ ,A=0,满足临界耦合条件。$ {k}_{x}=0 $ 附近$ H\left({k}_{x}\right) $ 近似表达为:$H\left({k}_{x}\right)\approx \dfrac{{{\rm{e}}}^{i\varphi }}{B}i{k}_{x}$ ,为一阶空间微分器的传递函数;相应地,在空间域中的反射场为:$$ {S}_{{\rm{out}}}\left(x\right)=\frac{{{\rm{e}}}^{i\varphi }}{B}\frac{{\rm{d}}{S}_{{\rm{in}}}}{{\rm{d}}x}。$$ (4) 为实现空间微分,在图3(a)所示的Kretschmann装置中,需控制金属膜的厚度以满足临界耦合条件,他们确定波长为532 nm的入射光在50 nm处的银膜厚度满足临界耦合条件。将银沉积在BK7玻璃基板上,用Kretschmann装置测量反射率,得到空间传递函数谱,图3(b)~(d) 为三种不同厚度样品的实验空间传递函数谱图。这三种薄膜在金属−空气界面上的相匹配耦合到SPP的传输光谱中都显示出明显的下降。将实验数据与数值计算结果进行拟合,得到银层厚度分别为46.0 nm、50.0 nm和55.5 nm,这里银的介电常数是
${\varepsilon }_{{\rm{Ag}}}=-11.51+0.51i$ 。对于厚度为50.0 nm的薄膜,传递函数的值最低为0.017 0,这表明该结构已接近临界耦合条件,空间谱传递函数确实与$ {k}_{x} $ 呈线性关系。在该装置中,微分运算作用于光场,故其可用来检测强度或位相物体的轮廓。为显示该效果,用空间光调制器分别产生振幅型和相位型物体。图3为一个振幅型物体,其中“字母”与“鹰”内外的强度不同;图3(e)显示该等离激元微分器的反射强度,其清楚地显示 了“字母”与“鹰”的轮廓。图3(f)是相位型物体,其中字母的内外具有不同的相位,但强度相同;其反射光清晰显示字母和标识轮廓。上述实验结果证明,单个亚波长金属薄膜可计算光场的空间微分,其边缘检测的分辨率约为7 μm,这表征可分辨两条边的最小间距。该微分运算的特点是:(1)结构简单,可用标准的薄膜沉积技术制备,适用于大规模生产;(2)强烈依赖表面等离激元共振,只能在与谐振的反射零点附近工作,故仅适用于窄空间谱的斜入射波;(3)只能做一维的空间微分,归因于等离激元的激发特性;(4)需要棱镜,系统体积较大。但该方案证明无傅里叶滤波系统,也能进行图像的边缘检测,为纳米级等离子体结构的光学模拟计算提供了一种简洁优美的物理机制。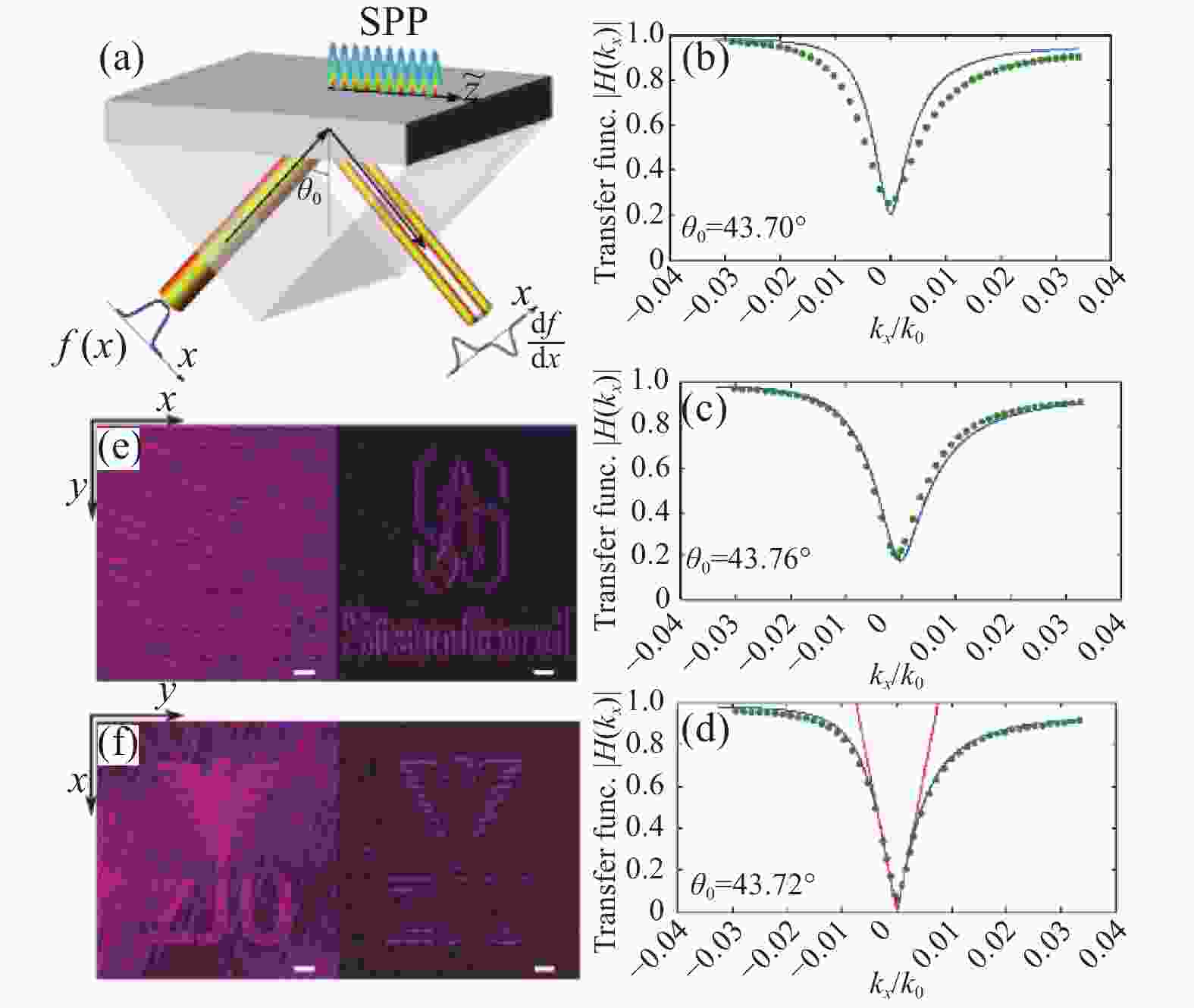
图 3 基于表面等离子体的空间微分器设计。(a) 利用Kretschmann 装置激发表面等离子体极化子(SPP)的等离子体空间微分器的原理图。深灰色层和浅灰色区域分别对应于银膜和玻璃;(b)~(d) 通过实验测量(虚线)和数值拟合(实线)得到三个样本的空间传递函数谱。在数值计算中,银层厚度分别为46.0 nm、50.0 nm和55.5 nm。
${{\rm{\theta }}_0}$ 对应相位匹配的入射角;(e) 左边:相位调制产生的斯坦福标志字母组成入射图像相对应的反射强度图像,其中字母和标志的内外具有不同的相位,但强度相同;右边:反射强度图像。(f) 左边:由字母“ZJU”和“鹰”标志组成的入射图像,其中“字母”标志的内外与“鹰”标志的强度不同;右边:反射强度图像。比例尺:100 μm。图(a)~(f)的改动经过参考文献[19]的许可Figure 3. Design of surface-plasmon-based spatial differentiator. (a) Schematic of the plasmonic spatial differentiator with the Kretschmann configuration to excite the surface plasmon polariton(SPP). The dark grey layer and the light grey area correspond to the silver film and the glass, respectively; (b)-(d) Spatial transfer function spectra of the three samples by the experimental measurement (dotted lines) and the numerical fitting (solid lines). In the numerical calculation, the thicknesses of the silver layer were 46.0 nm, 50.0 nm and 55.5 nm, respectively.
${{\rm{\theta }}_0}$ corresponds to the incident angle for the phase matching; (e) Left: incident image consisting of the Stanford tree logo and letters generated with phase modulation, where the inside and the outside of the letters and the logo have different phases but the same intensity. Right: reflected intensity image. (f) Left: incident image consisting of the ZJU eagle logo and letters with amplitude modulation where the inside and the outside of the letters and the eagle have different intensities. Right: reflected intensity image. Scale bar:100 μm. Panel (a)-(f) adapted with permission from reference [19]光子晶体谐振模式间的耦合也可用来调制空间频率分量的幅值[18],以实现光学计算。对于沿z轴传播的正入射光束
${S}_{{\rm{in}}}(x,y)$ ,若设计一种光学装置,使其透射光为${S}_{{\rm{out}}}(x,y)\propto {\nabla }^{2}{S}_{{\rm{in}}}(x,y)$ ,其中$ {\nabla }^{2}={\partial }_{x}^{2}+{\partial }_{y}^{2} $ 是Laplacian算符。如果要实现拉普拉斯运算,则需实现其响应函数为:$$ \begin{split} {{t}}\left({k}_{x},{k}_{y}\right)=&\left(\begin{array}{c}{t}_{ss}\left({k}_{x},{k}_{y}\right){t}_{sp}\left({k}_{x},{k}_{y}\right)\\ {t}_{ps}\left({k}_{x},{k}_{y}\right){t}_{pp}\left({k}_{x},{k}_{y}\right)\end{array}\right)=\\ &\left(\begin{array}{cc}{\alpha }_{ss}\left({k}_{x},{k}_{y}\right)& 0\\ 0& {\alpha }_{pp}\left({k}_{x},{k}_{y}\right)\end{array}\right) \end{split} $$ (5) 其中
$ {{\rm{\alpha }}_{ss}} \ne {{\rm{\alpha }}_{pp}} $ ,公式(5)需要在$\left|{{k}}\right|=0$ 时$t\left({{k}}\right)=0$ 。由于在无损耗光子晶体板中,正入射光在引导模式谐振(guided resonance)附近处的透射消失[51]。对于一个引导模式谐振的光子带,k决定共振频率w(k),辐射线宽γ(k),面内波矢${{k}}=\left({k}_{x},{k}_{y}\right)$ 。在共振频率附近,透射振幅t表示为:$$ t\left({w}_{0},{{k}}\right)=-\dfrac{i}{{\gamma }_{0}}\delta w\left({{k}}\right) $$ (6) 在k=0附近t(k)仅与色散δw(k)成正比。若
$\delta w\left({{k}}\right)\propto |{{{k}}|}^{2}$ ,则$t\left({{k}}\right)\propto |{{{k}}|}^{2}$ ,从而实现公式(5)。光子晶体平板作为二维拉普拉斯算子,其需满足三个充分条件:(1) td=1(td是直接透射系数);(2)只耦合一个引导谐振频带;(3)该频带满足色散$(w\left({{k}}\right)-{w}_{0})\propto |{{{k}}|}^{2}$ 。为实现第一个条件,在光子晶体板附近放置均匀的电介质板(如图4所示),且通过调节与平板之间的距离可实现$ {t}_{d}=1 $ 。第二、三个条件,需设计光子晶体板的频带结构。由于Laplacian在k空间中是各向同性的,故考虑具有旋转对称的光子晶体平板结构,如圆形孔。要实现这样的各向同性频带结构,需对参数进行详细调整,在Γ导共振(guided resonances)附近频率${\omega }_{0}= 0.476\;56\times 2\pi c/a$ ,其中复系数$ a=0.68-0.14i $ ,$ b= 1.11-0.12i $ ,$ c=2.24+0.15i $ ,$ c/2b=0.99+0.17i\approx 1 $ 。
图 4 光子晶体平板微分器。(a) 光子晶体平板微分器的几何结构,该微分器由一个通过气隙将光子晶体平板与均匀介电平板分开的光子晶体平板组成。
$ {\rm{\epsilon}} =12 $ , 几何参数:$d=0.55{\rm{a} }$ ,$r=0.111{\rm{a }}$ ,${d}_{s}=0.07{\rm{a} }$ ,${d}_{g}=0.21{\rm{a} }$ ,其中a是晶格常数;(b)坐标系;(c) 系统的布里渊区;在频率${\omega }_{0}=0. 476\;56\times 2\pi c/{\rm{a} }$ 时$ \left|t\right| $ 和$ {k}_{x} $ 和$ {k}_{y} $ 函数关系,对于(d) S光$ \left|{t}_{ss}\right| $ ,(e)P光$ \left|{t}_{pp}\right| $ , 和(f)无偏振光$ \left|{t}_{u}\right| $ ,这些都是各向同性Γ附近;(g) 沿着φ=14°方向$ \left|{t}_{u}\right| $ 作为$\left|{{k}}\right|$ 函数,二次拟合${t}_{u}={{\rm{a}}}_{u}{\left|{{k}}\right|}^{2}$ ,${{\rm{a}}}_{u}$ 是仅有的拟合参数;(h) 小为2 610a ×1 729a的Stanford徽章;(i) 计算传输的无偏振光图像,清晰显示不同方向的边缘。图(a)~(h)的改动经过参考文献[18]的许可Figure 4. Photonic crystal slab differentiator. (a) Geometry of the photonic crystal slab differentiator, which consists of a photonic crystal slab separated from a uniform dielectric slab by an air gap. For
$ {\rm{\epsilon}}=12 $ , the geometry parameters are:$d=0.55{\rm{a} }$ ,$r=0.111{\rm{a} }$ ,${d}_{s}=0.07{\rm{a }}$ ,${d}_{g}=0.21{\rm{a}}$ , where a is the lattice constant; (b) Coordinate system; (c) Brillouin zone of the system; Contour plots of transmittance$ \left|t\right| $ as a function of$ {k}_{x} $ and$ {k}_{y} $ at frequency${\omega }_{0}=0. 476\;56\times 2\pi c/{\rm{a}}$ for (d) S light$ \left|{t}_{ss}\right| $ , (e) P light$ \left|{t}_{pp}\right| $ , and (f) unpolarized light$ \left|{t}_{u}\right| $ , which are all isotropic near Γ; (g)$ \left|{t}_{u}\right| $ as a function of$\left|{{k}}\right|$ along the φ=14° direction, and the quadratic fitting${t}_{u}={{\rm{a}}}_{u}{\left|{{k}}\right|}^{2}$ where$ {a}_{u} $ is the only fitting parameter; (h) Incident Stanford emblem with a size of 2 610 a × 1 729a; (i) Calculated transmitted image with unpolarized light, which clearly shows the edges with different orientations. Panel (a)-(h) adapted with permission from reference [18] 图4(d)和4(e)是在
$\omega =0.47656\times 2\pi c/{\rm{a}}$ 时,面内波矢k和透射系数$ \left|{t}_{ss}\right| $ 和$ \left|{t}_{pp}\right| $ 关系图,$ \left|{t}_{ss}\right| $ 和$ \left|{t}_{pp}\right| $ 都正比于${\left|{{k}}\right|}^{2}$ 。图4(f)绘制了同频率下非偏振光$ \left|{t}_{u}\right| $ 的透射系数:$$ \left|{t}_{u}\right|=\sqrt{\dfrac{{\left|{t}_{ss}\right|}^{2}+{\left|{t}_{pp}\right|}^{2}}{2}} $$ (7) $ | {t}_{u}| $ 显示各向同性响应。沿着$ {\rm{\varphi}}=14° $ 方向,$ \left|{t}_{u}\right| $ 和$ \left|k\right| $ 展示出二次相关性(见图4(g)),其曲线拟合函数为$\left|{t}_{u}\right|={\rm{\alpha}} _{u}{\left|{{k}}\right|}^{2}$ ,${\rm{\alpha}}_{u} $ 是拟合参数。在$ \left|k\right| $ 小于$6\times {10}^{-3}\times 2\pi /{\rm a}$ 范围内,拟合接近完美。$6\times {10}^{-3}\times 2\pi /{\rm{a}}$ 对应于接收角$ {\rm{\theta }}_{a}=0.72 $ ,数值孔径NA=0.013,这为图像微分提供了足够的波矢范围。图4(h)和4(i)展示原始图像和模拟仿真的图像二阶差分结果,清晰地显示出强度均匀的边缘。该微分器的理论空间分辨率约20 μm,足以满足大多数图像处理应用。基于光子晶体的信号处理,其局限于二维二阶微分运算,对透射效率和角孔径有一定限制,这意味着其空间分辨率无法大幅提高或任意调节。作为孔型光子晶体平板的互补结构,高折射率的介质纳米柱超表面也可用来做光学微分计算[37]。为得到所需的传递函数,采用支持准引导模(quasi-guided modes)的超表面结构。其与引导模不同,准引导模是泄露模式,在光锥内的高折射率介质板中传播[51-52]。当频率、动量和对称性与准导模匹配时,透射模和准引导模之间会发生Fano干涉,导致接近1的背反射或透射[53-54]。实验中,在二氧化硅(SiO2)衬底上硅纳米棒嵌入聚甲基丙烯酸甲酯(PMMA)组成的超表面器件(如图5所示),其中纳米棒的高度为440 nm,直径为280 nm,周期为600 nm。这种一维硅介质纳米柱阵列超表面,在透射模式下也能执行一阶或二阶空间微分[36]。

图 5 使用纳米光子材料的二维图像微分。光子晶体板作为拉普拉斯操作变换图像
${E}_{{\rm{in}}}$ 生成其二阶微分${E}_{{\rm{out}}} \propto {\nabla }^{2}{E}_{{\rm{in}}}$ 的示意图,微分器的单元由硅纳米棒组成Figure 5. Two-dimensional image differentiation using nanophotonic materials. Schematic of a photonic crystal slab acting as a Laplacian operator that transforms an image,
${E}_{{\rm{in}}}$ , into its second-order derivative,${E}_{{\rm{out}}} \propto {\nabla }^{2}{E}_{{\rm{in}}}$ . The unit cell of the differentiator is composed of Si nanorods -
由于某些生物样本通常缺乏大量的天然色素,为了增强光学成像过程,可通过在入射光路径中放置适当的光学元件并改变其相位、振幅和采样平面上的空间频率来调节输入光场[6]。很多年前,人 们就提出利用螺旋位相进行边缘检测[55-62]。在此操作的基础上,许多提高相位对比度的方法被广泛研究,如泽尼克相位对比度成像和差分干涉对比度成像[63-64]。螺旋相位滤波器的传输函数是一个螺旋相位,
$T(x,y)= {\rm{exp}}\left(i{\rm{\varphi }}\right)$ ,$ {\rm{\varphi }} $ 是角坐标。如果将该滤波器引入到傅里叶面,其输出平面内的场振幅可由其傅里叶变换与复透射函数$ O(x,y) $ 的卷积得到:$$ \begin{split} E\left(x,y\right)=&O\left(x,y\right)\otimes {\cal{F}}\left\{{{{{{{\rm{e}}}}}}}^{i\varphi }\right\}=O\left(x,y\right)\otimes i\dfrac{{{\rm{e}}}^{i\varphi }}{2\pi {r}^{2}} \\ & \displaystyle\iint {\rm{d}}\bar{x}{\rm{d}}\bar{y}O\left(x-\bar{x},y-\bar{y}\right)i\dfrac{{{\rm{e}}}^{i\bar{\varphi }}}{2\pi {\bar{r}}^{2}} \end{split} $$ (8) 式中:
$ {\cal{F}} $ 是傅里叶变换;$ r=\sqrt{{x}^{2}+{y}^{2}} $ ;$\varphi ={\rm{arctan}}(y/x)$ ;$ r,\varphi $ 和$\bar{r},\bar{\varphi }$ 在与光轴垂直的两个平面上。螺旋相位核的卷积揭示,光场沿增强后样品边缘的相位与几何形状成正比。考虑到螺旋相位板具有无限孔径,卷积的泰勒展开有[65]:$$ {E}_{{\rm{out}}}\propto {{\rm{e}}}^{i{\psi }_{{\rm{in}}}}{g}_{{\rm{am}}}{{\rm{e}}}^{i{\delta }_{{\rm{am}}}}+i{E}_{{\rm{in}}}{g}_{{\rm{ph}}}{{\rm{e}}}^{i{\delta }_{{\rm{ph}}}} $$ (9) 式中:
${E}_{{\rm{in}}}$ 和${E}_{{\rm{out}}}$ 分别是输入场和输出场的复振幅;${\psi }_{{\rm{in}}}$ 是输入场相位;${g}_{{\rm{am}}}$ 和${g}_{{\rm{ph}}}$ (${\delta }_{{\rm{am}}}$ 和${\delta }_{{\rm{ph}}}$ )是输入 幅值和相位梯度大小(位相),其值为:$$ \begin{array}{l} {{g}}_{{\rm{am}}}=\overrightarrow{\nabla }\left|{E}_{{\rm{in}}}\right|={g}_{{\rm{am}}}{{\rm{{\rm{e}}}}}^{i{\delta }_{{\rm{am}}}}{{{\rm{e}}}}_{{\rm{am}}}\\ {{g}}_{{\rm{ph}}}=\overrightarrow{\nabla }\left|{\psi }_{{\rm{in}}}\right|={g}_{{\rm{ph}}}{{\rm{{\rm{e}}}}}^{i{\delta }_{{\rm{ph}}}}{{{\rm{e}}}}_{{\rm{ph}}} \end{array} $$ (10) 则输出场由描述输入场在螺旋相位滤波中的幅值和相位变化影响的两项组成。假设他们有一个相位样本,振幅变化可忽略,若
${g}_{{\rm{am}}}\approx 0$ ,输出场的相位仅由${\delta }_{{\rm{ph}}}$ 的方向决定[65]。因此,该原理揭示,在傅里叶平面加载一个涡旋位相可实现相位物体的边缘提取。早期的研究多采用空间光调制器来实现该涡旋相位[55, 57, 60-62],近年来,具有微纳结构的超表面也被用来实现基于涡旋相位的边缘提取[42]。若超表面滤波器沿两垂直对称性轴相移
$ \left({\varphi }_{x}{,\varphi }_{y}\right) $ ,相对快轴的取向角$ \theta $ ,$ {\varphi }_{x}=\left({c}_{0}+\phi \right)/2 $ ,$ {\varphi }_{y}=\left({c}_{0}+\phi \right)/2-\pi $ ,$ \theta =({c}_{0}-\phi )/4 $ 。$ {\varphi }_{x} $ 和$ {\varphi }_{y} $ 相差$ \pi $ 要求超表面为一个半波片,图6(a)~6(c)为所提出的超表面滤波器原理图,在二氧化硅衬底上生长二氧化钛纳米颗粒形成超表面,所有的纳米柱高度都固定为600 nm,周期450 nm。TiO2被选作超表面的材料,是因为其折射率大,在可见光频率下损耗低。相移$ \left({\varphi }_{x}{,\varphi }_{y}\right) $ 是通过改变二氧化钛纳米柱平面尺寸$ {D}_{x} $ 和$ {D}_{y} $ 来实现,而几何相位利用相对于快轴的旋转角度$ \theta $ 来控制[42]。
图 6 螺旋相位微分器。(a)为设计的全介电元表面空间滤波器示意图。插图:位于二氧化硅衬底上的无定形二氧化钛纳米颗粒形成的元表面单元的透视图和俯视图;(b) 制作的超表面的光学照片。比例尺:500 μm;(c) TiO2纳米阵列SEM图像的俯视图和斜视图。比例尺:1 μm;(d) 自旋相关的螺旋相位对比成像实验装置示意图。LP和QWP可以使入射光形成圆偏振。CP可以用来消除光路中的背景光;(e)~(h)用LCP入射光分别在480、530、580、630 nm波长处捕获的传统亮场图像;(i)~(l) 用对应波长的RCP入射光捕获的螺旋相位对比度图像。比例尺:100 μm。图6(a)~6(l)的改动经过参考文献[42]的许可
Figure 6. Spiral phase differentiator. (a) Schematic of the designed all-dielectric metasurface spatial filter. Inset: perspective and top view of the metasurface unit-cell formed by amorphous TiO2 nanopillar sitting on a silica substrate; (b) Optical photograph of the fabricated metasurface device. Scale bar: 500 μm; (c) Top view and oblique view of the SEM images of TiO2 nanopillar array. Scale bars: 1 μm; (d) Sketch of the experimental setup for spin-dependent spiral phase contrast imaging. LP and QWP can make the incident light with circular polarization. CP can be used to eliminate background light in the optical path. (e)-(h) Traditional bright-field images captured with LCP incident light at the wavelength of 480, 530, 580, 630 nm, respectively; (i)-(l) Spiral phase contrast images captured with RCP incident light at the corresponding wavelengths. Scale bar:100 μm. Panel 6(a)-6(l) adapted with permission from reference [42]
成像装置如图6(d)所示,20倍显微物镜用于图像放大,利用由两个透镜组成的4f系统进行空间频率操控,超表面滤波器位于其频谱面(共焦面)上。图6(e)~6(h)显示了分别在480 nm、530 nm、580 nm和630 nm波长的左旋圆偏振(LCP)光照射下捕获的洋葱表皮细胞的亮场图像,细胞壁与细胞质之间的微小振幅和相位差异使单细胞边界难以分辨。然而,在右旋圆偏振(RCP)入射光照射下的螺旋相位对比度成像中,图像对比度完全改变(图6(i)~6(l))。边缘增强图像可显示更多的细胞表皮细节,使单细胞轮廓更易识别,便于观察细胞形态。
尽管利用涡旋相位当作滤波器可实现边缘检测的目的,但其功能单一,无法实现一阶微分等其他基础操作。另外,基于涡旋相位的滤波器无法控制边缘的分辨率,导致其检测精度受限,且不可调控。系统采用了多透镜元件,不利于整体装置的微型化和集成化。
-
根据差分干涉对比(DIC)显微镜的原理,利用超表面的偏振和空间复用等功能,将两个垂直级联的超表面器件集成为一个小型定量相位梯度显微镜(QPGM)[43](见图7)。实验证明,该尺寸毫米级光学器件能从相位分辨目标和生物样本中获取定量的相位梯度图像(PGIs)。第一层的超表面捕获横向电场(TE)和横向磁场(TM)偏振的两个图像,它们的焦点沿y轴分开,并将捕获到的光均匀地分成三个独立的方向,分别照明第二层的三个超表面透镜。在第一层超表面使用偏振[66]和空间复用技术[67-68];第二层超表面由三个双折射离轴透镜组成,在TE和TM偏振之间形成三个不同相位偏移的DIC图像,第二层的每个超表面分别与第一层超表面组成各自的DIC显微镜系统。输入和输出的两个线性偏振器沿45°和-45°方向,捕获的三个独立DIC图像具有不同的相位偏移。对一个具有单位振幅光场的二元相位物体
$U\left(x,y\right)= {{\rm{e}}}^{i\phi (x,y)}$ ,QPGM同时捕获三个DIC图像($ {I}_{1} $ ,$ {I}_{2} $ 和$ {I}_{3} $ ),其中$ {I}_{1} $ ,$ {I}_{2} $ 和$ {I}_{3} $ 可以写成:
图 7 基于QGPM微分器的原理。采用两个超表面层的QPGM原理图,第二层由三个独立的超表面透镜组成。第一超表面与第二超表面层中的每一个透镜一起,超表面一对TE和TM偏振产生两个剪切聚焦,并将场向三个不同的方向向着第二层的三个透镜。在偏振片下,第二层的三个超表面透镜形成三个DIC图像(
$ {I}_{1} $ ,$ {I}_{2} $ 和$ {I}_{3} $ ),在TE和TM偏振之间有不同的相位偏移Figure 7. Principle of QPGM-based differentiator. Schematic of the QPGM employing two metasurface layers, where the second layer is composed of three separate metasurface lenses. The first metasurface, together with each of the lenses in the second metasurface layer. Metasurface 1 makes two sheared focuses for TE and TM polarizations and splits the field in three different directions towards the three lenses in the second layer. With the polarizer, the three metasurface lenses in layer 2 form three DIC images (
$ {I}_{1} $ ,$ {I}_{2} $ and$ {I}_{3} $ ) having different phase offsets between the TE and TM polarizations$$ {I}_{j}=\left|U\left(x,y\right)-{{{\rm{e}}}}^{i{\phi }_{j}}U\left(x,y-\Delta y\right)\right| $$ (11) 式中:
${\phi }_{j}={\phi }_{0}+\dfrac{2\pi }{3}(j-1)$ ;$ \Delta y $ 是在物平面TE和TM偏振剪切(sheared)距离,即表征在物体平面上沿y轴相距$ \Delta y $ 的两个点,对于两种不同的偏振光,在像平面上具有相同的像点。利用I1、I2和I3,可计算相位样本相对于y的单向梯度$ {\nabla }_{y}\phi (x,y) $ ,通过三步相移法:$$ {\nabla }_{y}\phi =\dfrac{1}{\Delta y}\arctan\left(\sqrt{3}\dfrac{{I}_{2}-{I}_{3}}{2{I}_{1}-{I}_{2}-{I}_{3}}\right)-{\nabla }_{y}{\phi }_{{\rm{cali}}} $$ (12) 式中:
${\nabla }_{y}{\rm{\phi }}_{{\rm{cali}}}$ 是为了消除实验条件不完善而产生的背景,是一个校正项,即在不需要任何样本的情况下测量的背景信号,然后从三张DIC图像计算出PGI。在理想情况下,y方向单向相位梯度成像仅在上下边缘的对比度强,左右边缘的对比度较弱。该方案利用垂直集成的多功能超表面,实验捕获了多个透明样本的相位梯度图像,验证了系统定量相位成像的能力。但是该系统需要计算PGI才能得到较好的边缘,且只在一维方向进行,成像质量还有待提高;同时,三个超表面离轴操作会使成像产生像差,对原始图像产生扭曲,不利于细节的提取和操作。但该方案显示介质超表面平台在集成方面的巨大潜力,在定量相位成像系统中,制造微型成像设备,如微型显微镜或内窥镜,超表面器件将在这类技术的研发中发挥重要作用。
-
高效率介质超表面也能进行宽带边缘检测,设计Pancharatnam–Berry (PB)相位超表面之间插入两个垂直对齐的线性偏振器[44]。与其它空间微分方法不同,该方案是基于自旋与轨道的相互作用。当一个线偏振平面波以入射到PB相位超表面产生相位梯度,
$\varphi \left(x,y\right)=\dfrac{\pi x}\varLambda$ ,$\varLambda$ 表示沿着x方向周期,对应右旋偏振(RCP)和左旋偏振(LCP)分量的相位分别增加$ +2\varphi $ 和$ -2\varphi $ 。如果在一个图像的傅里叶频谱面插入一个PB位相元件,则输出电场${E}_{{\rm{out}}}(x,y)$ 可表示为:$$ \begin{split} {E}_{{\rm{out}}}\left(x,y\right)=&{E}_{{\rm{in}}}\left[\left(x-\Delta \right),y\right]\left[\begin{array}{c}1\\ -i\end{array}\right]+\\ &{E}_{{\rm{in}}}\left[\left(x+\Delta \right),y\right]\left[\begin{array}{c}1\\ i\end{array}\right] \end{split} $$ (13) 若另一偏振片在样品之后放置,且其透振方向与输入端的线偏振片正交,则其输出电场为:
$$ \begin{split} {E}_{{\rm{out}}\_{\rm{edge}}}\left(x,y\right)=&({E}_{{\rm{in}}}\left[\left(x+\Delta \right),y\right] -\\ &{E}_{{\rm{in}}}\left[\left(x-\Delta \right),y\right])\left[\begin{array}{c}0\\ i\end{array}\right] \end{split} $$ (14) 式中:
$ \Delta =\dfrac{\lambda f}\varLambda $ ,如果$ \Delta $ 足够小,则输出电场振幅与输入电场的一阶空间微分近似成正比:$$ \left|\begin{array}{c}{E}_{{{\rm{out}}}_{{\rm{edge}}}}\left({x,y}\right)\end{array}\right|\simeq2\Delta \dfrac{d{E}_{{\rm{in}}}(x,y)}{d\left(x\right)}$$ 实验上,利用飞秒激光器在玻璃内部加工带状纳米结构。玻璃基板的直径为2.5 cm,厚度为3 mm,样品的面积为8 mm×8 mm,如8(a)和8(b)所示。超表面放在4f系统中傅里叶频谱面(见图8(c)),波长分别为430 、500 、670 nm,其不仅验证边缘检测的概念,也证明其宽带性能(见图8(d)~8(f))。超表面的宽带特性来源于纳米结构取向的几何相位,它在本质上独立于波长。此外,图像边缘的检测分辨率对应于不同的PB相位梯度周期
$ \Delta $ ,该系统最高分辨率约2 μm,接近光学系统的衍射极限。通过改变一维相位梯度,该超表面被扩展到二维边缘检测,只需将$ \varphi \left(x,y\right)=\pi x/\varLambda $ 变为$\varphi \left(x,y\right)=\pi \sqrt{{x}^{2}+{y}^{2}}/\varLambda$ 。得益于透明的玻璃基元结构和高透射率,在透射模式时,其比金属超表面展现明显优势。由于该超表面的高效率,该方法在一些非常微弱信号中的图像边缘检测具有重要作用。但该4f系统需一系列光学元件,其集成度还需改进。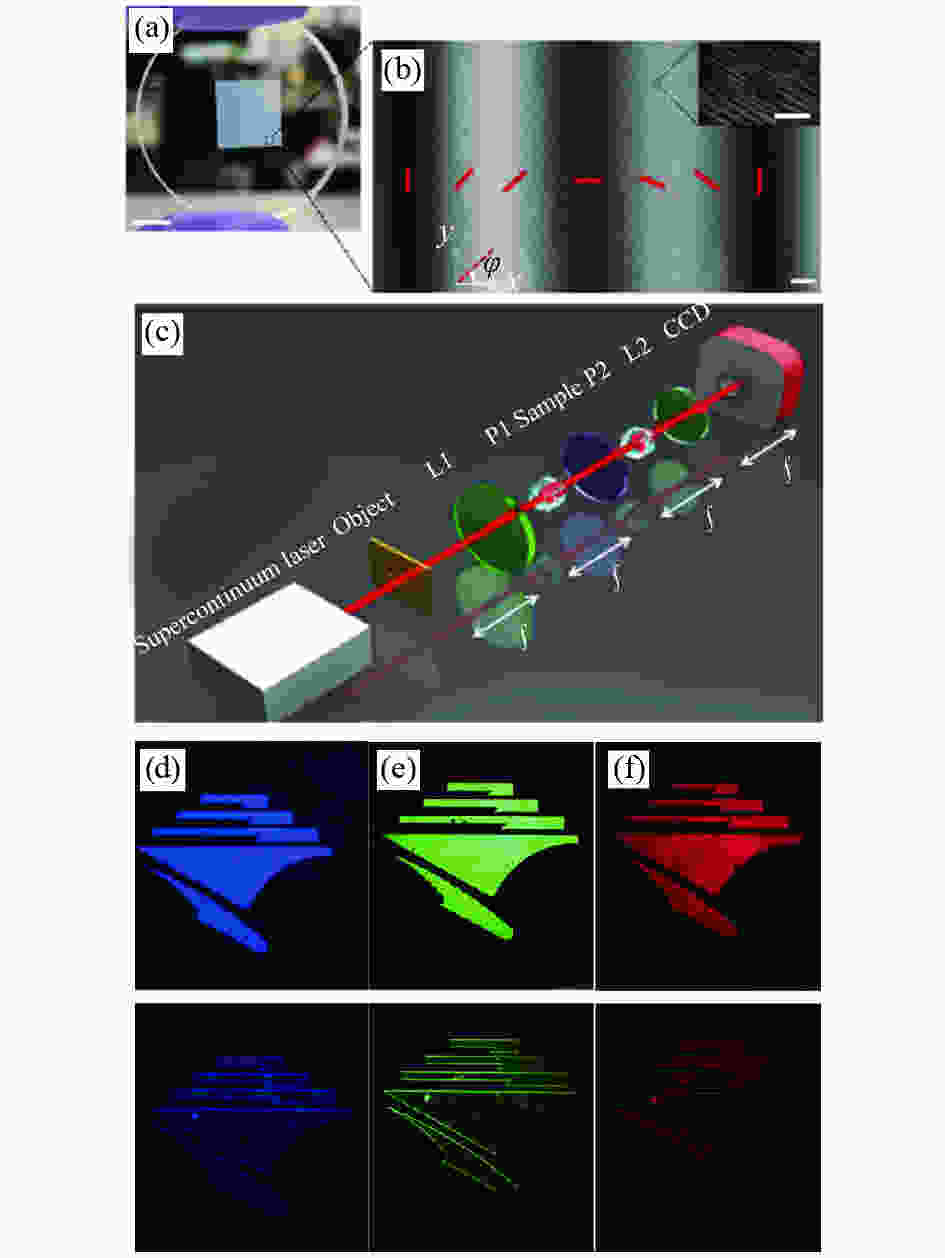
图 8 基于PB相位的微分器。(a) 直径1 in (1 in=2.54 cm)的样品照片。超表面图案区域8 mm×8 mm (比例尺:5 mm);(b) 在(a)区域标记样本的光学图像。红色的条表示结构在一个周期内的方向。(插图)纳米结构的SEM图像(比例尺:500 nm);(c)实验装置:入射光穿过物体,物体后面是一个4f系统。样本(超表面)被放置在P1和P2之间。L:镜头,P:偏振片;(d)~(f) 第一行显示是样本后没有偏振片的图像;照明波长分为430 nm、500 nm和670 nm。图像是用周期Λ为8000 μm。第二行显示样本后有偏振片的结果图像。图8(a)~8(f)的改动经过参考文献[44]的许可
Figure 8. Differentiator based PB phase. (a) Photograph of a 1 in (1 in=2.54 cm) diameter sample. Metasurface patterned area, 8 mm × 8 mm (scale bar:5 mm); (b) Polariscope optical image of the sample pattern area marked in (a). The red bars indicate structures orientation in one period. (Inset) SEM image of the induced nanostructure(Scale bar: 500 nm); (c) Experimental setup: The incident light then passes through the object, which is followed by a 4f system. The sample (metasurface) is placed in between of the P1 and P2. L: lens, P: polarizer; (d)-(f) The first row shows images without the analyzer; the illumination wavelengths are 430 nm, 500 nm, and 670 nm, respectively. The images are taken with metasurface period Λ of 8,000 μm. The second row shows resultant images after adding an analyzer. Panel 8(a)-8(f) adapted with permission from reference [44]
-
基于自旋霍尔效应的光学微分是通过分析光的特定正交偏振态,实现在单一界面上的反射或折射过程中引起的计算方法[46]。若初始自旋态为
$\left| u \right\rangle = \left( {\dfrac{1}{{\sqrt 2 }}} \right)\left( {\left| + \right\rangle + \left| - \right\rangle } \right)$ ,后选择正交自旋态$\left| v \right\rangle = \left( {\dfrac{1}{{\sqrt 2 i}}} \right)\left( {\left| + \right\rangle - \left| - \right\rangle } \right)$ ,最终测量波函数为:$$ \begin{split} \left| {{\varphi _{{\rm{out}}}}} \right\rangle =& \left\langle v \right|\hat U\left| {{\varphi _{{\rm{in}}}}} \right\rangle \left. u \right\rangle = \dfrac{i}{2} \int {\rm{d}}{k_y}{{\tilde \varphi }_{{\rm{in}}}}\left( {{k_y}} \right) \times\\ &\left[ {{\rm{exp}}\left( {i{k_y}\delta } \right) - {\rm{exp}} \left( { - i{k_y}\delta } \right)} \right]\left| {{k_y}} \right\rangle =\\ &\dfrac{i}{2}\int {\rm{d}}y\left[ {{\varphi _{{\rm{in}}}}\left( {y + \delta } \right) - {\varphi _{{\rm{in}}}}\left( {y - \delta } \right)} \right]\left| y \right\rangle \end{split} $$ (16) 如果初始波函数信息远远大于
$ \delta $ 的变化,最终输出波函数$\left| {{\varphi _{{\rm{out}}}}} \right\rangle$ 正比于输入波函数的一阶空间微分。$\left| {{\varphi _{{\rm{out}}}}} \right\rangle\simeq i\delta \int {\rm{d}}y\xi \left(y\right)\left| y \right\rangle$ ,$\xi \left(y\right)={\rm{d}}{\varphi }_{{\rm{in}}}\left(y\right)/{\rm{d}}y$ ,空间微分是由平行自旋态和反平行自旋态的相反位移引起的,后置的自旋态与初始自旋态正交,而产生相消干涉。假设近轴光束斜入射在界面上,入射和反射光束的矢量电场在横向上分别为${{E}}_{{\rm{in}}}$ 和${{E}}_{{\rm{out}}}$ 。对应沿x和y方向的入射电场和反射电场如图9(a)所示,${{E}}_{{\rm{in}}}={{u}}_{x}{E}_{x}^{{\rm{in}}}(x,y)$ ,${{E}}_{{\rm{out}}}={{u}}_{y}{E}_{y}^{{\rm{out}}}(x,y)$ ,其中${{u}}_{x}$ 和${{u}}_{y}$ 分别代表沿着x和y方向偏振,通过矢量空间傅里叶变换,将入射(反射)光束写成平面波的叠加,${E}_{x}^{{\rm{in}}}(x,y)$ 和$ {E}_{y}^{{\rm{out}}}(x,y) $ 可以表示为:
图 9 基于自旋霍尔效应的微分器。(a) 两种各向同性材料(如空气-玻璃界面)由于光的SHE在光学平面界面上的空间微分示意图。(b)~(c)分别测量的入射和反射光束的强度分布图;(d) 入射图像由汉字“光”振幅图像
${E}_{x}^{{\rm{in}}}$ ;(e) 测量${E}_{y}^{{\rm{out}}}$ 对应于(d)的反射强度图像。比例尺:50 μm。图9(a)~(e)的改动经过参考文献[46]的许可Figure 9. Differentiator based SHE. (a) Schematic of spatial differentiation from the SHE of light on an optical planar interface between two isotropic materials, e.g., an air-glass interface; (b)-(c) Measured intensity profiles of the incident and reflected beams, respectively; (d) Incident image consisting of the Chinese character for “light” with amplitude modulation on
${E}_{x}^{{\rm{in}}}$ ; (e) Reflected intensity image corresponding to (d) by measuring${E}_{y}^{{\rm{out}}}$ . Scale bar: 50 μm. Panel 9(a)-(e) adapted with permission from reference [46]$$ \begin{split} E_{x\left( y \right)}^{{\rm{in}}\left( {{\rm{out}}} \right)} =& \displaystyle\iint \tilde E_{x\left( y \right)}^{{\rm{in}}\left( {{\rm{out}}} \right)}\left( {{k_x},{k_y}} \right){\rm{exp}}\left( {i{k_x}x} \right)\times\\ &{\rm{exp}}\left( {i{k_y}y} \right){\rm{d}}{k_x}{\rm{d}}{k_y} \end{split} $$ (17) 由于沿界面切向波矢量的连续条件,产生与入射平面波
$ ({k}_{x},{k}_{y}) $ 相同的反射平面波。因此,入射电场与反射电场之间的空间变换是由空间谱传递函数$ H({k}_{x},{k}_{y}) $ 决定的,$H\left(kx,ky\right)={\tilde{E}}_{y}^{{\rm{out}}}({k}_{x},{k}_{y})/{\tilde{E}}_{x}^{{\rm{in}}}({k}_{x},{k}_{y})$ ,在傍轴近似下,空间谱传递函数可以简化为:$$ H=\dfrac{i\left({r}_{s}+{r}_{p}\right)}{4}({{\rm{e}}}^{i{k}_{y}\delta }+{{\rm{e}}}^{-i{k}_{y}\delta }) $$ (18) 公式(18)中两个指数项的正负号表明,通过分析与初始项的正交偏振分量,反射场是两电场分量之间的相消干涉。若
$ \delta \left|{k}_{y}\right|\ll 1 $ ,则:$$ H\simeq -\dfrac{\delta \left({r}_{s}+{r}_{p}\right)}{2}{k}_{y} $$ (19) 这是一阶y向空间微分器的传递函数。相应地,在空间域内,反射出的
$ {E}_{y}^{{\rm{out}}}\left(x,y\right) $ 场具有${E}_{y}^{{\rm{out}}}\left(x,y\right)= \dfrac{i\delta ({r}_{s}+{r}_{p})}{2}\dfrac{\partial {E}_{x}^{{\rm{in}}}}{\partial y}$ ,由此可知,通过光在界面处的自旋霍尔效应能实现空间微分。为验证该空间微分效应,他们测量了高斯光束照明下的反射场分布。准直的532 nm激光束通过聚焦透镜L1照亮玻璃界面。反射光束投射到具有L2和L3共轭成像系统的光束分析仪上, 利用两个偏振器P1和P2,通过制备和分析正交方向上的偏振态,实现空间微分。图9(b)和图9(c)分别展示了入射光和反射光的测量强度分布。确实,反射光束在y = 0处呈现出一阶振幅最小的Hermite-Gaussian剖面,对应于入射高斯场的y方向空间微分。该微分器还可用于检测带有相位或幅值分布的入射场的边缘。图9(d)为
${E}_{x}^{{\rm{in}}}$ 的场分量光的中文字符组成的入射图像场,其中字符的内外有不同的振幅强度。图9(e)为$ {E}_{y}^{{\rm{out}}} $ 的实测反射强度,清晰地展示了空间微分的特征。由于微分是沿y方向的,垂直于y方向的边缘是最明显的。实验验证的空间分辨率3.2 μm,其主要受限于成像系统的数值孔径。与基于表面等离激元共振的微分器[19]不同,光的SHE是一种非共振效应。因此,该系统不受频率带宽限制,而且材料简单,但其仅适用于单方向的空间微分。当入射角和材料不同时,图像边缘清晰展现,故该空间微分是广义的。该自旋光学方法是一种简单、通用的途径来实现矢量场计算和边缘检测,实现对超快图像的处理。 -
文中总结了全光图像边缘检测方法,从机制上梳理每种检测方法的物理原理,并简述其具体实现途径,根据实际检测结果,客观地分析其优缺点,清晰地展示该领域的发展脉络,为其未来的研究提供简洁的技术路线图。尽管全光图像边缘检测已经取得一系列成果,但目前的全光图像处理器件在功能、集成度、应用场景等方面,还远不能满足实际需求。因此,基于现有技术的分析,预测该技术的未来发展趋势有:
(1)新机制:目前的全光图像处理技术基本来源于光学差分运算,通过光的空间频率调制或偏振态控制来实现最终目的。由于差分运算在功能上的单一性,基于此开发的技术也无法处理更复杂的操作。而实际图像处理的种类繁多,比如,边缘提取、图像增强、降噪、滤波和特征提取等,为完成这些操作,需开发一个全局性的新机制和新方法,以实现全光图像的通用处理器。另外,研究的新机制应与电子图像处理保持兼容,从而使全光图像处理器能顺利应用到现有光电产品或智能系统中。因此,新机制的研发可借鉴现有数字图像处理的工作原理。
(2)功能多样化:尽管差分是图像处理技术中的重要操作,但图像信息的精确提取和有效识别需多个操作共同使用才会有效。目前的全光图像技术仅能处理基于差分的边缘检测,且多数是针对单个方向的检测,因此,其在功能上完全无法满足图像处理的实际需求。功能多样化的图像处理技术是亟需研究的,也是决定该全光图像处理技术实用化过程中最重要的一步。根本上讲,这取决于底层物理机制的创新,从而允许构建一个能实现各种操作和功能的通用平台。
(3)集成度:器件小型化和集成化已成为光学系统发展的重要趋势,这是消费类光电子产品的轻便化、多功能化等特点所决定的。因此,未来研发的全光图像处理技术应兼顾体积、质量、功能复用、性能等参数,实现单片或少量光学元件集成到现有光电系统中,以达到良好的兼容性。目前,具有亚波长厚度和横向尺寸的超表面光子器件在实现该功能的方法中颇具潜力,因其能满足上述参数的所有要求,而且还能实现光的任意操控,其优势已在超表面差分干涉显微镜的研究中得以展现。
(4)多应用场景:随着智能系统的快速发展,通过光学图像来识别变化的环境将是各种智能系统面临的核心问题,而图像处理是信息识别的最重要途径,也是基于卷积神经网络的人工智能技术的基础。大数据时代,快速的图像处理会是人工智能发展的关键。光学手段实现图像处理的速度在纳秒量级,这对智能系统的发展极具诱惑。因此,全光图像处理技术会顺应人工智能的发展而迅速发展,在科研投入、产业布局、人力投放、资源调配等方面得到更多支持,极大地扩展全光图像处理技术的应用场景。
All-optical image processing technology and applications based on micro-/nano-devices
-
摘要: 纳米技术的飞速发展促进了微纳结构的加工制造、科学研究及工业应用。而微纳结构的光学特性是近年来光学领域的研究热点之一,其带动了纳米光子学、表面等离激元光学、超表面/超材料光学、拓扑光子学、非厄米光学等新兴学科的发展,为实现光的高精度、全方位操控奠定了重要技术基础。文中主要针对全光图像处理中的边缘检测技术,系统地梳理了微纳光学结构和器件在实现光计算(如微分、卷积等)时涉及的基础、原理、技术和应用,并展望了其在超快图像处理、高对比度显微成像、卷积神经网络和智能光学系统等领域的应用研究。Abstract: The rapid development of nanotechnology has promoted the processing and manufacturing of micro-nano structures, scientific research and industrial applications. The investigation on optical properties of micro-nano structures has recently been one of the hotspots in the field of optics, which has driven emerging disciplines such as nanophotonics, surface plasmonic optics, metasurface/metamaterial optics, topological photonics, and non-Hermitian optics. It provides the important technical fundamentals for full control of light with high precision. This article focused on the edge detection in all-optical image processing. The fundamentals, principles, technologies and applications of micro-/nano-scale structures and devices were discussed to realize optical mathematical computing (such as differential, convolution), followed by a detailed prospect about its future applications in ultrafast image processing, high-contrast microscopic imaging, convolutional neural networks and intelligent optics.
-
图 1 基于波的超材料计算。一种设计适当的超材料块的概念草图,该超材料块可在任意波信号传播时对其进行所需的数学运算,在GRIN+和GRIN-的结构之间,设计合理的薄结构可以在傅里叶域进行数学运算
Figure 1. Wave-based metamaterial computing. A conceptual sketch of a suitably designed metamaterial block that may perform a desired mathematical operation on arbitrary wave signals as they propagate through it. A thin, properly designed metasurfaces sandwiched between two GRIN structures with positive and negative parameters, can perform mathematical operations in the Fourier domain
图 2 非局域超表面。(a) 平行于x-z平面的裂环谐振器阵列示意图。超表面被TM偏振光激发,在x-z平面传播;(b) 设计的超表面对于正和负的
$ {k}_{x} $ 打破x和z对称性获取不对称响应,实现一个一阶导数的要求操作;(c) 超表面具有90°旋转对称实现二维的二阶导数;(d) 二阶导数运算的超表面传输与入射角关系;(e) 一阶导数运算的超表面传输与入射角关系;(f) 该图像用于测试在$ f=0.98{f}_{0} $ ,其中$ {f}_{0} $ 为未调制的超表面的共振频率;(g)法线方向的非偏振光照明图(f)的输出。图(a)~(f)的改动经过参考文献[17]的许可Figure 2. Nonlocal metasurface. (a) Schematic of an array of split-ring resonators parallel to the x-z plane. The measurface is excited by TM-polarized waves propagating on the x-z plane; (b) Metasurface with broken x and z symmetry to obtain an asymmetric response with respect to positive and negative
$ {k}_{x} $ , as required in order to implement a first-derivative operation; (c) Metasurface with a 90° rotational symmetry to implement the second derivative in 2D; (d) Transmission versus incident angle for the metasurface for an second-derivative operation; (e)Transmission versus incidence angle for the metasurface and for an first-derivative operation; (f) Image used to test the response of the metasurface at$ f=0.98{f}_{0} $ , where$ { f}_{0} $ is the resonance frequency of the unmodulated metasurface; (g) Output for illumination (f) with unpolarized light from the normal direction. Panel (a)-(f) adapted with permission from reference [17]图 3 基于表面等离子体的空间微分器设计。(a) 利用Kretschmann 装置激发表面等离子体极化子(SPP)的等离子体空间微分器的原理图。深灰色层和浅灰色区域分别对应于银膜和玻璃;(b)~(d) 通过实验测量(虚线)和数值拟合(实线)得到三个样本的空间传递函数谱。在数值计算中,银层厚度分别为46.0 nm、50.0 nm和55.5 nm。
${{\rm{\theta }}_0}$ 对应相位匹配的入射角;(e) 左边:相位调制产生的斯坦福标志字母组成入射图像相对应的反射强度图像,其中字母和标志的内外具有不同的相位,但强度相同;右边:反射强度图像。(f) 左边:由字母“ZJU”和“鹰”标志组成的入射图像,其中“字母”标志的内外与“鹰”标志的强度不同;右边:反射强度图像。比例尺:100 μm。图(a)~(f)的改动经过参考文献[19]的许可Figure 3. Design of surface-plasmon-based spatial differentiator. (a) Schematic of the plasmonic spatial differentiator with the Kretschmann configuration to excite the surface plasmon polariton(SPP). The dark grey layer and the light grey area correspond to the silver film and the glass, respectively; (b)-(d) Spatial transfer function spectra of the three samples by the experimental measurement (dotted lines) and the numerical fitting (solid lines). In the numerical calculation, the thicknesses of the silver layer were 46.0 nm, 50.0 nm and 55.5 nm, respectively.
${{\rm{\theta }}_0}$ corresponds to the incident angle for the phase matching; (e) Left: incident image consisting of the Stanford tree logo and letters generated with phase modulation, where the inside and the outside of the letters and the logo have different phases but the same intensity. Right: reflected intensity image. (f) Left: incident image consisting of the ZJU eagle logo and letters with amplitude modulation where the inside and the outside of the letters and the eagle have different intensities. Right: reflected intensity image. Scale bar:100 μm. Panel (a)-(f) adapted with permission from reference [19]图 4 光子晶体平板微分器。(a) 光子晶体平板微分器的几何结构,该微分器由一个通过气隙将光子晶体平板与均匀介电平板分开的光子晶体平板组成。
$ {\rm{\epsilon}} =12 $ , 几何参数:$d=0.55{\rm{a} }$ ,$r=0.111{\rm{a }}$ ,${d}_{s}=0.07{\rm{a} }$ ,${d}_{g}=0.21{\rm{a} }$ ,其中a是晶格常数;(b)坐标系;(c) 系统的布里渊区;在频率${\omega }_{0}=0. 476\;56\times 2\pi c/{\rm{a} }$ 时$ \left|t\right| $ 和$ {k}_{x} $ 和$ {k}_{y} $ 函数关系,对于(d) S光$ \left|{t}_{ss}\right| $ ,(e)P光$ \left|{t}_{pp}\right| $ , 和(f)无偏振光$ \left|{t}_{u}\right| $ ,这些都是各向同性Γ附近;(g) 沿着φ=14°方向$ \left|{t}_{u}\right| $ 作为$\left|{{k}}\right|$ 函数,二次拟合${t}_{u}={{\rm{a}}}_{u}{\left|{{k}}\right|}^{2}$ ,${{\rm{a}}}_{u}$ 是仅有的拟合参数;(h) 小为2 610a ×1 729a的Stanford徽章;(i) 计算传输的无偏振光图像,清晰显示不同方向的边缘。图(a)~(h)的改动经过参考文献[18]的许可Figure 4. Photonic crystal slab differentiator. (a) Geometry of the photonic crystal slab differentiator, which consists of a photonic crystal slab separated from a uniform dielectric slab by an air gap. For
$ {\rm{\epsilon}}=12 $ , the geometry parameters are:$d=0.55{\rm{a} }$ ,$r=0.111{\rm{a} }$ ,${d}_{s}=0.07{\rm{a }}$ ,${d}_{g}=0.21{\rm{a}}$ , where a is the lattice constant; (b) Coordinate system; (c) Brillouin zone of the system; Contour plots of transmittance$ \left|t\right| $ as a function of$ {k}_{x} $ and$ {k}_{y} $ at frequency${\omega }_{0}=0. 476\;56\times 2\pi c/{\rm{a}}$ for (d) S light$ \left|{t}_{ss}\right| $ , (e) P light$ \left|{t}_{pp}\right| $ , and (f) unpolarized light$ \left|{t}_{u}\right| $ , which are all isotropic near Γ; (g)$ \left|{t}_{u}\right| $ as a function of$\left|{{k}}\right|$ along the φ=14° direction, and the quadratic fitting${t}_{u}={{\rm{a}}}_{u}{\left|{{k}}\right|}^{2}$ where$ {a}_{u} $ is the only fitting parameter; (h) Incident Stanford emblem with a size of 2 610 a × 1 729a; (i) Calculated transmitted image with unpolarized light, which clearly shows the edges with different orientations. Panel (a)-(h) adapted with permission from reference [18] 图 5 使用纳米光子材料的二维图像微分。光子晶体板作为拉普拉斯操作变换图像
${E}_{{\rm{in}}}$ 生成其二阶微分${E}_{{\rm{out}}} \propto {\nabla }^{2}{E}_{{\rm{in}}}$ 的示意图,微分器的单元由硅纳米棒组成Figure 5. Two-dimensional image differentiation using nanophotonic materials. Schematic of a photonic crystal slab acting as a Laplacian operator that transforms an image,
${E}_{{\rm{in}}}$ , into its second-order derivative,${E}_{{\rm{out}}} \propto {\nabla }^{2}{E}_{{\rm{in}}}$ . The unit cell of the differentiator is composed of Si nanorods图 6 螺旋相位微分器。(a)为设计的全介电元表面空间滤波器示意图。插图:位于二氧化硅衬底上的无定形二氧化钛纳米颗粒形成的元表面单元的透视图和俯视图;(b) 制作的超表面的光学照片。比例尺:500 μm;(c) TiO2纳米阵列SEM图像的俯视图和斜视图。比例尺:1 μm;(d) 自旋相关的螺旋相位对比成像实验装置示意图。LP和QWP可以使入射光形成圆偏振。CP可以用来消除光路中的背景光;(e)~(h)用LCP入射光分别在480、530、580、630 nm波长处捕获的传统亮场图像;(i)~(l) 用对应波长的RCP入射光捕获的螺旋相位对比度图像。比例尺:100 μm。图6(a)~6(l)的改动经过参考文献[42]的许可
Figure 6. Spiral phase differentiator. (a) Schematic of the designed all-dielectric metasurface spatial filter. Inset: perspective and top view of the metasurface unit-cell formed by amorphous TiO2 nanopillar sitting on a silica substrate; (b) Optical photograph of the fabricated metasurface device. Scale bar: 500 μm; (c) Top view and oblique view of the SEM images of TiO2 nanopillar array. Scale bars: 1 μm; (d) Sketch of the experimental setup for spin-dependent spiral phase contrast imaging. LP and QWP can make the incident light with circular polarization. CP can be used to eliminate background light in the optical path. (e)-(h) Traditional bright-field images captured with LCP incident light at the wavelength of 480, 530, 580, 630 nm, respectively; (i)-(l) Spiral phase contrast images captured with RCP incident light at the corresponding wavelengths. Scale bar:100 μm. Panel 6(a)-6(l) adapted with permission from reference [42]
图 7 基于QGPM微分器的原理。采用两个超表面层的QPGM原理图,第二层由三个独立的超表面透镜组成。第一超表面与第二超表面层中的每一个透镜一起,超表面一对TE和TM偏振产生两个剪切聚焦,并将场向三个不同的方向向着第二层的三个透镜。在偏振片下,第二层的三个超表面透镜形成三个DIC图像(
$ {I}_{1} $ ,$ {I}_{2} $ 和$ {I}_{3} $ ),在TE和TM偏振之间有不同的相位偏移Figure 7. Principle of QPGM-based differentiator. Schematic of the QPGM employing two metasurface layers, where the second layer is composed of three separate metasurface lenses. The first metasurface, together with each of the lenses in the second metasurface layer. Metasurface 1 makes two sheared focuses for TE and TM polarizations and splits the field in three different directions towards the three lenses in the second layer. With the polarizer, the three metasurface lenses in layer 2 form three DIC images (
$ {I}_{1} $ ,$ {I}_{2} $ and$ {I}_{3} $ ) having different phase offsets between the TE and TM polarizations图 8 基于PB相位的微分器。(a) 直径1 in (1 in=2.54 cm)的样品照片。超表面图案区域8 mm×8 mm (比例尺:5 mm);(b) 在(a)区域标记样本的光学图像。红色的条表示结构在一个周期内的方向。(插图)纳米结构的SEM图像(比例尺:500 nm);(c)实验装置:入射光穿过物体,物体后面是一个4f系统。样本(超表面)被放置在P1和P2之间。L:镜头,P:偏振片;(d)~(f) 第一行显示是样本后没有偏振片的图像;照明波长分为430 nm、500 nm和670 nm。图像是用周期Λ为8000 μm。第二行显示样本后有偏振片的结果图像。图8(a)~8(f)的改动经过参考文献[44]的许可
Figure 8. Differentiator based PB phase. (a) Photograph of a 1 in (1 in=2.54 cm) diameter sample. Metasurface patterned area, 8 mm × 8 mm (scale bar:5 mm); (b) Polariscope optical image of the sample pattern area marked in (a). The red bars indicate structures orientation in one period. (Inset) SEM image of the induced nanostructure(Scale bar: 500 nm); (c) Experimental setup: The incident light then passes through the object, which is followed by a 4f system. The sample (metasurface) is placed in between of the P1 and P2. L: lens, P: polarizer; (d)-(f) The first row shows images without the analyzer; the illumination wavelengths are 430 nm, 500 nm, and 670 nm, respectively. The images are taken with metasurface period Λ of 8,000 μm. The second row shows resultant images after adding an analyzer. Panel 8(a)-8(f) adapted with permission from reference [44]
图 9 基于自旋霍尔效应的微分器。(a) 两种各向同性材料(如空气-玻璃界面)由于光的SHE在光学平面界面上的空间微分示意图。(b)~(c)分别测量的入射和反射光束的强度分布图;(d) 入射图像由汉字“光”振幅图像
${E}_{x}^{{\rm{in}}}$ ;(e) 测量${E}_{y}^{{\rm{out}}}$ 对应于(d)的反射强度图像。比例尺:50 μm。图9(a)~(e)的改动经过参考文献[46]的许可Figure 9. Differentiator based SHE. (a) Schematic of spatial differentiation from the SHE of light on an optical planar interface between two isotropic materials, e.g., an air-glass interface; (b)-(c) Measured intensity profiles of the incident and reflected beams, respectively; (d) Incident image consisting of the Chinese character for “light” with amplitude modulation on
${E}_{x}^{{\rm{in}}}$ ; (e) Reflected intensity image corresponding to (d) by measuring${E}_{y}^{{\rm{out}}}$ . Scale bar: 50 μm. Panel 9(a)-(e) adapted with permission from reference [46] -
[1] Holyer R J, Peckinpaugh S H. Edge detection applied to satellite imagery of the oceans [J]. IEEE Transactions on Geoscience and Remote Sensing, 1989, 27(1): 46-56. doi: 10.1109/36.20274 [2] Pham D L, Xu C, Prince J L. Current methods in medical image segmentation [J]. Annual Review of Biomedical Engineering, 2000, 2(1): 315-337. doi: 10.1146/annurev.bioeng.2.1.315 [3] Athale R, Psaltis D. Optical computing: past and future [J]. Optics and Photonics News, 2016, 27(6): 32-39. doi: 10.1364/OPN.27.6.000032 [4] Cutrona L, Leith E N, Porcello L, et al. On the application of coherent optical processing techniques to synthetic-aperture radar [J]. Proceedings of the IEEE, 1966, 54(8): 1026-1032. doi: 10.1109/PROC.1966.4987 [5] Abu-mostafa Y S, Psaltis D. Optical neural computers [J]. Scientific American, 1987, 256(3): 88-95. doi: 10.1038/scientificamerican0387-88 [6] Goodman J W. Introduction to Fourier Optics[M]. Colorado: Roberts and Company Publishers, 2005. [7] Yu N, Capasso F. Flat optics with designer metasurfaces [J]. Nature Materials, 2014, 13(2): 139-150. doi: 10.1038/nmat3839 [8] Yu N, Genevet P, Kats M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction [J]. Science, 2011, 334(6054): 333-337. doi: 10.1126/science.1210713 [9] Kildishev A V, Boltasseva A, Shalaev V M. Planar photonics with metasurfaces [J]. Science, 2013, 339(6125): 1232009. doi: 10.1126/science.1232009 [10] Sun S, Yang K-Y, Wang C-M, et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces [J]. Nano Letters, 2012, 12(12): 6223-6229. doi: 10.1021/nl3032668 [11] Monticone F, Estakhri N M, Alu A. Full control of nanoscale optical transmission with a composite metascreen [J]. Physical Review Letters, 2013, 110(20): 203903. doi: 10.1103/PhysRevLett.110.203903 [12] Esfandyarpour M, Garnett E C, Cui Y, et al. Metamaterial mirrors in optoelectronic devices [J]. Nature Nanotechnology, 2014, 9(7): 542. doi: 10.1038/nnano.2014.117 [13] Kim M, Wong A M H, Eleftheriades G V. Optical Huygens' metasurfaces with independent control of the magnitude and phase of the local reflection coefficients [J]. Physical Review X, 2014, 4(4): 041042. doi: 10.1103/PhysRevX.4.041042 [14] Asadchy V, Daz-rubio A, Tcvetkova S, et al. Flat engineered multichannel reflectors [J]. Physical Review X, 2017, 7(3): 031046. doi: 10.1103/PhysRevX.7.031046 [15] Ra’di Y, Sounas D L, Alu A. Metagratings: beyond the limits of graded metasurfaces for wave front control [J]. Physical Review Letters, 2017, 119(6): 067404. doi: 10.1103/PhysRevLett.119.067404 [16] Silva A, Monticone F, CastaldI G, et al. Performing mathematical operations with metamaterials [J]. Science, 2014, 343(6167): 160-163. doi: 10.1126/science.1242818 [17] Kwon H, Sounas D, Cordaro A, et al. Nonlocal metasurfaces for optical signal processing [J]. Phys Rev Lett, 2018, 121(17): 173004. doi: 10.1103/PhysRevLett.121.173004 [18] Guo C, Xiao M, Minkov M, et al. Photonic crystal slab Laplace operator for image differentiation [J]. Optica, 2018, 5(3): 251-256. doi: 10.1364/OPTICA.5.000251 [19] Zhu T, Zhou Y, Lou Y, et al. Plasmonic computing of spatial differentiation [J]. Nat Commun, 2017, 8: 15391. doi: 10.1038/ncomms15391 [20] Canny J. A computational approach to edge detection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, PAMI-8(6): 679-698. doi: 10.1109/TPAMI.1986.4767851 [21] Marr D, Hildreth E. Theory of edge detection [J]. Proceedings of the Royal Society of London. Series B. Biological Sciences, 1980, 207(1167): 187-217. doi: 10.1098/rspb.1980.0020 [22] Hsu H-S, Tsai W-H. Moment-preserving edge detection and its application to image data compression [J]. Optical Engineering, 1993, 32(7): 1596-1609. doi: 10.1117/12.139804 [23] Brosnan T, Sun D-W. Improving quality inspection of food products by computer vision—a review [J]. Journal of Food Engineering, 2004, 61(1): 3-16. doi: 10.1016/S0260-8774(03)00183-3 [24] Liu Y, Cheng M-M, Hu X, et al. Richer convolutional features for edge detection.[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017:3000-3009. [25] Martin D R, Fowlkes C C, Malik J. Learning to detect natural image boundaries using local brightness, color, and texture cues [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 5: 530-549. [26] Shrivakshan G, Chandrasekar C. A comparison of various edge detection techniques used in image processing [J]. International Journal of Computer Science Issues (IJCSI), 2012, 9(5): 269. [27] Roddier F. Curvature sensing and compensation: a new concept in adaptive optics [J]. Applied Optics, 1988, 27(7): 1223-1225. doi: 10.1364/AO.27.001223 [28] Marmanis D, Schindler K, Wegner J D, et al. Classification with an edge: Improving semantic image segmentation with boundary detection [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 135: 158-172. doi: 10.1016/j.isprsjprs.2017.11.009 [29] Chen L-C, Barron J T, Papandreou G, et al. Semantic image segmentation with task-specific edge detection using cnns and a discriminatively trained domain transform.[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 4545-4554. [30] Choudhry P. High-throughput method for automated colony and cell counting by digital image analysis based on edge detection [J]. PloS one, 2016, 11(2): 0148469. [31] Xie S, Tu Z. Holistically-nested edge detection[C]// Proceedings of the IEEE International Conference on Computer Vision, 2015: 1395-1403. [32] Geb C K T, Koumoutsakos P. Edge detection in microscopy images using curvelets [J]. BMC Bioinformatics, 2009, 10(1): 75. doi: 10.1186/1471-2105-10-75 [33] Haralick R M, Shapiro L G. Computer and Robot Vision[M]. Massachusetts: Addison-wesley Reading, 1992. [34] Wang H, Guo C, Zhao Z, et al. Compact incoherent image differentiation with nanophotonic structures [J]. ACS Photonics, 2020, 7(2): 338-343. doi: 10.1021/acsphotonics.9b01465 [35] Pors A, Nielsen M G, Bozhevolnyi S I. Analog computing using reflective plasmonic metasurfaces [J]. Nano Lett, 2015, 15(1): 791-797. doi: 10.1021/nl5047297 [36] Cordaro A, Kwon H, Sounas D, et al. High-index dielectric metasurfaces performing mathematical operations [J]. Nano Letters, 2019, 19(12): 8418-8423. doi: 10.1021/acs.nanolett.9b02477 [37] Zhou Y, Zheng H, Kravchenko I I, et al. Flat optics for image differentiation [J]. Nature Photonics, 2020, 14(5): 316-323. [38] Bykov D A, Doskolovich L L, Morozov A A, et al. First-order optical spatial differentiator based on a guided-mode resonant grating [J]. Optics Express, 2018, 26(8): 10997-11006. doi: 10.1364/OE.26.010997 [39] Doskolovich L L, Bykov D A, Bezus E A, et al. Spatial differentiation of optical beams using phase-shifted Bragg grating [J]. Optics Letters, 2014, 39(5): 1278-1281. doi: 10.1364/OL.39.001278 [40] Fang Y, Ruan Z. Optical spatial differentiator for a synthetic three-dimensional optical field [J]. Optics Letters, 2018, 43(23): 5893-5896. doi: 10.1364/OL.43.005893 [41] Ruan Z. Spatial mode control of surface plasmon polariton excitation with gain medium: from spatial differentiator to integrator [J]. Optics Letters, 2015, 40(4): 601-604. doi: 10.1364/OL.40.000601 [42] Huo P, Zhang C, Zhu W, et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging [J]. Nano Letters, 2020, 20(4): 2791-2798. [43] Kwon H, Arbabi E, Kamali S M, et al. Single-shot quantitative phase gradient microscopy using a system of multifunctional metasurfaces [J]. Nature Photonics, 2019, 14(2): 109-114. [44] Zhou J, Qian H, Chen C-F, et al. Optical edge detection based on high-efficiency dielectric metasurface[J]// Proceedings of the National Academy of Sciences, 2019: 201820636. [45] He S, Zhou J, Chen S, et al. Spatial differential operation and edge detection based on the geometric spin Hall effect of light [J]. Optics Letters, 2020, 45(4): 877-880. doi: 10.1364/OL.386224 [46] Zhu T, Lou Y, Zhou Y, et al. Generalized spatial differentiation from the spin hall effect of light and its application in image processing of edge detection [J]. Physical Review Applied, 2019, 11(3): 034043. doi: 10.1103/PhysRevApplied.11.034043 [47] Hadad Y, Sounas D, Alu A. Space-time gradient metasurfaces [J]. Physical Review B, 2015, 92(10): 100304. doi: 10.1103/PhysRevB.92.100304 [48] Kou E F, Tamir T. Excitation of surface plasmons by finite width beams [J]. Applied Optics, 1989, 28(6): 1169-1177. doi: 10.1364/AO.28.001169 [49] Lou Y, Pan H, Zhu T, et al. Spatial coupled-mode theory for surface plasmon polariton excitation at metallic gratings [J]. JOSA B, 2016, 33(5): 819-824. doi: 10.1364/JOSAB.33.000819 [50] Ruan Z, Wu H, Qiu M, et al. Spatial control of surface plasmon polariton excitation at planar metal surface [J]. Optics Letters, 2014, 39(12): 3587-3590. doi: 10.1364/OL.39.003587 [51] Fan S, Joannopoulos J D. Analysis of guided resonances in photonic crystal slabs [J]. Physical Review B, 2002, 65(23): 235112. doi: 10.1103/PhysRevB.65.235112 [52] Zhou W, Zhao D, Shuai Y-C, et al. Progress in 2D photonic crystal Fano resonance photonics [J]. Progress in Quantum Electronics, 2014, 38(1): 1-74. doi: 10.1016/j.pquantelec.2014.01.001 [53] Suh W, Yanik M, Solgaard O, et al. Displacement-sensitive photonic crystal structures based on guided resonance in photonic crystal slabs [J]. Applied Physics Letters, 2003, 82(13): 1999-2001. doi: 10.1063/1.1563739 [54] Winn J N, Fink Y, Fan S, et al. Omnidirectional reflection from a one-dimensional photonic crystal [J]. Optics Letters, 1998, 23(20): 1573-1575. doi: 10.1364/OL.23.001573 [55] Davis J A, Mcnamara D E, Cottrell D M, et al. Image processing with the radial Hilbert transform: theory and experiments [J]. Optics Letters, 2000, 25(2): 99-101. doi: 10.1364/OL.25.000099 [56] Crabtree K, Davis J A, Moreno I. Optical processing with vortex-producing lenses [J]. Applied Optics, 2004, 43(6): 1360-1367. doi: 10.1364/AO.43.001360 [57] Rhapter S, Jesacher A, Bernet S, et al. Spiral phase contrast imaging in microscopy [J]. Optics Express, 2005, 13(3): 689-694. doi: 10.1364/OPEX.13.000689 [58] Jesacher A, Rhapter S, Bernet S, et al. Shadow effects in spiral phase contrast microscopy [J]. Physical Review Letters, 2005, 94(23): 233902. doi: 10.1103/PhysRevLett.94.233902 [59] Bernet S, Jesacher A, Rhapter S, et al. Quantitative imaging of complex samples by spiral phase contrast microscopy [J]. Optics Express, 2006, 14(9): 3792-3805. doi: 10.1364/OE.14.003792 [60] Maurer C, Jesacher A, Bernet S, et al. What spatial light modulators can do for optical microscopy [J]. Laser & Photonics Reviews, 2011, 5(1): 81-101. [61] Ritsch-marte M. Orbital angular momentum light in microscopy [J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2017, 375(2087): 20150437. doi: 10.1098/rsta.2015.0437 [62] Wang J, Zhang W, Qi Q, et al. Gradual edge enhancement in spiral phase contrast imaging with fractional vortex filters [J]. Scientific Reports, 2015, 5: 15826. doi: 10.1038/srep15826 [63] Zernike F. Diffraction theory of the knife-edge test and its improved form, the phase-contrast method [J]. Monthly Notices of the Royal Astronomical Society, 1934, 94: 377-384. doi: 10.1093/mnras/94.5.377 [64] Dodd J G. Interferometry with Schlieren microscopy [J]. Applied Optics, 1977, 16(2): 470-472. doi: 10.1364/AO.16.000470 [65] Jesacher A F, Rhapter S, Bernet S, et al. Spiral interferogram analysis [J]. JOSA A, 2006, 23(6): 1400-1409. doi: 10.1364/JOSAA.23.001400 [66] Arbabi A, Horie Y, Bagheri M, et al. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission [J]. Nature Nanotechnology, 2015, 10(11): 937. doi: 10.1038/nnano.2015.186 [67] Maguid E, Yulevich I, Veksler D, et al. Photonic spin-controlled multifunctional shared-aperture antenna array [J]. Science, 2016, 352(6290): 1202-1206. doi: 10.1126/science.aaf3417 [68] Arbabi E, Arbabi A, Kamali S M, et al. Multiwavelength polarization-insensitive lenses based on dielectric metasurfaces with meta-molecules [J]. Optica, 2016, 3(6): 628-633. doi: 10.1364/OPTICA.3.000628 -






 下载:
下载:



















































































































































































































































