下载:
-
自由空间激光通信是以激光作为信息载体，以自由空间作为信息传输通道，在不同平台之间开展的信息传递和交换的一种新一代信息技术[1]。自由空间激光通信以通信容量大、速率高，且易搭载于不同平台等优势，得到了研究人员的广泛关注。自由空间激光通信需要空间光-光纤耦合技术的配合进行信号的传递与交换。然而，在进行空间光-光纤耦合之前，激光需传输经过大气湍流，大气中的微粒、气溶胶及温度梯度引起的气体折射率起伏（大气湍流）会造成激光束波前随机起伏变化，光斑形变、光束随机漂移，光强闪烁等负面效应，从而使光接收带来困惑，严重制约光通信系统性能的提升[2]。因此，研究如何降低或克服大气湍流对激光束带来的负面影响，从而提高大气湍流中光束质量和光纤耦合效率显得尤为重要。
众所周知，部分相干光束作为信息载体进行传输的方法是一种重要的大气湍流负面效应抑制方法[3-4]。部分相干光束相比于其对应的相干光束具有更强的抗湍流能力，其抗湍流的物理机制可以从部分相干光束的相干模式展开角度进行解释[5]。自从2007年，Gori提出了一种构建具有特殊相干结构（非高斯形式）部分相干光束的方法之后[6]，大量具有特殊相干结构的部分相干光束被构建且对其在自由空间和湍流大气中的传输特性进行了研究[7-11]。值得注意的是，大量研究成果表明：具有特殊相干结构的部分相干光束不仅具有奇特的传输性质，而且可以进一步降低大气湍流引起的负面效应[4, 12-16]，这为提高空间光-光纤耦合效率提供了一种有效途径。
然而，目前关于提高光纤耦合效率的研究工作主要集中于如何设计光纤耦合系统。关于调控光源本身特性实现提高光纤耦合效率的相关工作报道较少，研究光场相干结构调控对空间光-光纤耦合效率的影响更为少之又少。因此，文中基于光场相干结构调控技术，研究提高光束经过大气湍流后的光纤耦合效率的方法。
-
图1为大气湍流中空间光-光纤耦合示意图，激光束在大气湍流中传输一段距离z后，入射到耦合透镜的表面，透镜将由于大气湍流影响而畸变的光束汇聚，并耦合进光纤内部。
图 1 大气湍流中空间光-光纤耦合示意图
Figure 1. Schematic diagram of spatial light-fiber coupling in turbulent atmosphere
设定一部分相干光束经过大气湍流之后，通过一焦距为f的透镜耦合进单模光纤。标定光源面坐标为
$r \equiv (x,y)$ ，透镜端（接收端）坐标为$\rho \equiv \left( {{\rho _x},{\rho _y}} \right)$ 。在文中，将耦合效率ηc定义为耦合进光纤的平均光功率和入射在光学系统接收平面内的平均光功率的比值[17-18]，即$$\left\langle {{\eta _{\rm c}}} \right\rangle = \left\langle {{P_{\rm c}}} \right\rangle /\left\langle {{P_{\rm a}}} \right\rangle ,$$ (1) 其中
$\left\langle {{P_{\rm c}}} \right\rangle$ 和$\left\langle {{P_{\rm a}}} \right\rangle$ 具体表达式分别为：$$ \begin{split} {P_{\rm c}} = & \displaystyle\int {\int_A {W\left( {{\rho _1},{\rho _2},{\textit{z}}} \right)F_A^*\left( {{\rho _1}} \right){F_A}\left( {{\rho _2}} \right)} } \times\\ & \exp \left[ { - \dfrac{1}{{{w^2}}}\left( {\rho _1^2 + \rho _2^2} \right)} \right]{\rm {d^2}}{\rho _1}{{\rm {d^2}}}{\rho _2}, \\ \end{split} $$ (2) $${P_{\rm a}} = \int_A {W\left( {\rho ,\rho ,{\textit{z}}} \right)} \exp \left( { - \frac{{2{\rho ^2}}}{{{w^2}}}} \right){d^2}\rho ,$$ (3) 式中：
$W\left( {{\rho _1},{\rho _2},{\textit{z}}} \right)$ 为光束经过大气湍流传输至z处（接收端）的交叉谱密度函数；${w^2} = {{{D^2}}/ 8}$ ，D为接收孔径直径；${F_A}\left( \rho \right)$ 为接收孔径平面处的模场分布，其表达式为$${F_A}\left( \rho \right) = \frac{1}{{{w_{\rm a}}}}\sqrt {\frac{2}{\pi }} \exp \left( { - \frac{{{\rho ^2}}}{{{w_{\rm a}}^2}}} \right),$$ (4) 式中：
${w_{\rm a}} = \lambda f/\left( {\pi {w_j}} \right)$ ，为孔径平面上的有效模宽，λ为波长，wj为光纤模场半径，f为耦合透镜的焦距。若需求得光束经过大气湍流之后的耦合效率，则首先需要得到光束在接收端z处的交叉谱密度函数表达式。因此，下面将介绍研究对象-非均匀关联光束在接收端的交叉谱密度函数。
在空间-频率域中，标量部分相干光束可以用交叉谱密度函数来描述。近年来，交叉谱密度函数作为一种常用的方法用来研究准单色部分相干场，源平面处场的交叉谱密度函数定义为两点间的相关函数[19]：
$$W\left( {{{{r}}_1},{{{r}}_2}} \right) = \left\langle {{E^*}\left( {{{{r}}_1}} \right)E\left( {{{{r}}_2}} \right)} \right\rangle ,$$ (5) 式中：E(r)表示垂直于传输方向的电场涨落，角括号表示系综平均。
2007年，Gori指出：交叉谱密度函数必须满足以下非负正定条件，才能成为数学上可实现的真实函数[6]，
$$W\left( {{{{r}}_1},{{{r}}_2}} \right) = \int {p\left( v \right)} {H^*}\left( {{{{r}}_1},v} \right)H\left( {{{{r}}_2},v} \right)dv,$$ (6) 式中：H(r,v)为任意函数；p(v)为非负函数。从上式可以看出，通过选择合适的H(r,v)和p(v)函数，可以构建物理上可实现的交叉光谱密度函数及具有特殊相干结构的部分相干光束模型。
为得到非均匀关联光束，在公式(6)中，笔者设[7]
$$p\left( v \right) = {\left( {4\pi } \right)^{ - 1/2}}\left( {\frac{2}{a}} \right)\exp \left( { - \frac{{{v^2}}}{{{a^2}}}} \right),$$ (7) $$H\left( {{{r}},v} \right) = \exp \left( { - \frac{{{{{r}}^2}}}{{w_0^2}}} \right)\exp \left( { - ikv{{{r}}^2}} \right),$$ (8) 将公式(7)、(8)代入公式(6)，经过积分运算得到非均匀关联光束在光源处的交叉谱密度函数，即，
$$W\left( {{{{r}}_1},{{{r}}_2}} \right) = \exp \left( { - \frac{{{{r}}_1^2 + {{r}}_2^2}}{{w_0^2}}} \right)\exp \left[ { - \frac{{{{\left( {{{r}}_1^2 - {{r}}_2^2} \right)}^2}}}{{r_{ \rm c}^4}}} \right],$$ (9) 式中：w0为光束束腰；rc=(2/ka)(1/2)为光束相干长度，k=2π/λ为波数，a为正实常数。
下面，笔者将推导非均匀关联光束经过大气湍流后的交叉光谱密度函数。基于广义惠更斯-菲涅尔衍射积分公式[2]，部分相干光束经过弱湍流大气传输，其交叉光谱密度函数可以表示为：
$$ \begin{split} W\left( {{{{\rho }}_1},{{{\rho }}_2}} \right) =& \dfrac{1}{{{\lambda ^2}{{\textit{z}}^2}}} \displaystyle\int {\int {\int {\int_{ - \infty }^\infty {W\left( {{{{r}}_1},{{{r}}_2}} \right)} } } } \times\\ &\exp \left[ { - \dfrac{{ik}}{{2{\textit{z}}}}{{\left( {{{{r}}_1} - {{{\rho }}_1}} \right)}^2} + \dfrac{{ik}}{{2{\textit{z}}}}{{\left( {{{{r}}_2} - {{{\rho }}_2}} \right)}^2}} \right] \times\\ & \left\langle {\exp \left[ {\varPsi \left( {{{{r}}_1},{{{\rho }}_1}} \right) + {\varPsi ^*}\left( {{{{r}}_2},{{{\rho }}_2}} \right)} \right]} \right\rangle {\rm d^2}{{{r}}_1}{\rm d^2}{{{r}}_2}, \end{split} $$ (10) 式中：Ψ为随机介质的折射率波动引起的复杂相位扰动。上式中的统计平均表达式为[2]：
$$\begin{array}{l} \left\langle {\exp \left[ {\varPsi \left( {{{{r}}_1},{{{\rho }}_1}} \right) + {\varPsi ^ * }\left( {{{{r}}_2},{{{\rho }}_2}} \right)} \right]} \right\rangle {\rm{ = }} \exp \bigg\{ - 4{\pi ^2}{k^2}{\textit{z}} \displaystyle\int_0^1 \displaystyle\int_0^\infty {{\kappa }}{\varPhi _n}\left( {{\kappa }} \right) \cdot \\ \left\{ {1 - {J_0}\left[ {\left| {\left( {1 - \xi } \right){{P}} + \xi {{Q}}} \right|{{\kappa }}} \right]} \right\} {\rm {d^2}}{{\kappa }}{\rm d}\xi \bigg\}, \end{array} $$ (11) 其中，P=ρ1−ρ2, Q=r1−r2, J0为零阶贝塞尔函数，可以近似表示为：
$${J_0}\left[ {\left| {\left( {1 - \xi } \right){{P}} + \xi {{Q}}} \right|{{\kappa }}} \right] \sim {\rm{1}} - \frac{1}{4}{\left[ {\left( {1 - \xi } \right){{P}} + \xi {{Q}}} \right]^2}{{{\kappa }}^2}.$$ (12) 将公式(12)代入到公式(11)，得到：
$$ \begin{array}{l} \left\langle {\exp \left[ {\varPsi \left( {{ r_1},{ \rho _1}} \right) + {\varPsi ^*}\left( {{ r_2},{ \rho _2}} \right)} \right]} \right\rangle = \exp \Biggr\{ { - \dfrac{{{\pi ^2}{k^2}{\textit{z}}T}}{3}\left[ {{{\left( {{ \rho _1} - { \rho _2}} \right)}^2} + } \right.} \\ {\left. {\left( {{ \rho _1} - { \rho _2}} \right) \cdot \left( {{ r_1} - { r_2}} \right) + {{\left( {{ r_1} - { r_2}} \right)}^2}} \right]} \Biggr\} ,\\ \end{array} $$ (13) 式中：
$T = \displaystyle\int_0^\infty {{\kappa ^3}\varPhi \left( \kappa \right)\rm d\kappa }$ ，$\varPhi \left( \kappa \right)$ 表示湍流大气的折射率起伏强度谱。笔者选择van Karman湍流谱[20-21]进行接下来的研究，即$$\varPhi \left( \kappa \right) = A\left( \alpha \right)C_n^2{\left( {{\kappa ^2} + \kappa _0^2} \right)^{ - \alpha /2}}\exp \left( { - {{{\kappa ^2}} / {\kappa _m^2}}} \right),$$ (14) 基于van Karman谱，公式(13)中的T可以表示如下：
$$\begin{array}{l} T = \dfrac{{A(\alpha )}}{{2(\alpha - 2)}}C_n^2 \times \left[ {\beta \kappa _m^{2 - \alpha }\exp \left( {\dfrac{{\kappa _0^2}}{{\kappa _m^2}}} \right){\varGamma _1}\left( {2 - \dfrac{\alpha }{2},\dfrac{{\kappa _0^2}}{{\kappa _m^2}}} \right) - 2\kappa _0^{4 - \alpha }} \right], \\ \;\;\left( {3 < \alpha < 4} \right), \\ \end{array} $$ (15) 式中：
$C_n^2$ 为折射率起伏结构常数；Γ1为伽马函数；$\;\beta = 2\kappa _0^2 - 2\kappa _m^2 + \alpha \kappa _m^2$ ；κ0=2π/L0，L0为湍流的外尺度； κm=5.92/ l0，l0为湍流的内尺度。将公式(6)~(8)代入到公式(10)，为了使积分运算简化，交换积分次序后公式(10)等效为：
$$W\left( {{{{\rho}} _1},{{{\rho}} _2},{\textit{z}}} \right) = \int {p\left( v \right)P\left( {{{{\rho}} _1},{{{\rho}} _2},v,{\textit{z}}} \right)} {\rm d}v,$$ (16) 其中，
$$ \begin{split} P\left( {{ \rho _1},{ \rho _2},v,{\textit{z}}} \right) = &{\left( {\dfrac{k}{{2\pi {\textit{z}}}}} \right)^2}\int {\int\limits_{ - \infty }^\infty {H_0^*\left( {{ r_1},v} \right){H_0}\left( {{ r_2},v} \right)} } \times \hfill \\ & \exp \Biggr\{ { - \frac{{{\pi ^2}{k^2}{\textit{z}}T}}{3}} \left[ {{{\left( {{ \rho _1} - { \rho _2}} \right)}^2} + \left( {{ \rho _1} - { \rho _2}} \right) \cdot } \right. \\ & {\left. {\left( {{ r_1} - { r_2}} \right) + {{\left( {{ r_1} - { r_2}} \right)}^2}} \right]} \Biggr\} \times \exp \Biggr[ { - \frac{{ik}}{{2{\textit{z}}}}} \\ & {\left[ {{{\left( {{ r_1} - { \rho _1}} \right)}^2} - {{\left( {{ r_2} - { \rho _2}} \right)}^2}} \right]} \Biggr]{\rm d^2}{r_1}{\rm d^2}{r_2} .\\ \end{split} $$ (17) 将公式(8)代入上式，经过繁琐积分之后，得到：
$$ \begin{split} P\left( {{{{\rho }}_1},{{{\rho }}_2},v,{\textit{z}}} \right) =& \dfrac{{w_0^2}}{{2w_{\textit{z}}^2}}\exp \left[ { - \dfrac{{ik}}{{2{\textit{z}}}}\left( {{{\rho }}_1^2 - {{\rho }}_2^2} \right)} \right] \times \exp \Biggl[ - \Biggl( \dfrac{{w_0^2{k^2}}}{{8{{\textit{z}}^2}}} +\\ & \dfrac{1}{3}{\pi ^2}{k^2}{\textit{z}}T \Biggl){{( {{{{\rho }}_1} - {{{\rho }}_2}} )}^2} \Biggl] \times {\rm{exp}} \Biggl\{ - \dfrac{1}{{w_{\textit{z}}^2}}\Biggl| - i\Biggl[ \dfrac{{kw_0^2}}{{4{\textit{z}}}}( {1- }\\ & {2v{\textit{z}}} ) - \dfrac{1}{3}{\pi ^2}k{{\textit{z}}^2}T \Biggl]( {{{{\rho }}_1} - {{{\rho }}_2}} ) +\Biggl ( {\dfrac{{{{{\rho }}_1} + {{{\rho }}_2}}}{2}} \Biggl) \Biggl|^2 \Biggl\} \end{split} $$ (18) 其中，
$$w_{\textit{z}}^2 = \dfrac{{w_0^2}}{2}{\left( {1 - 2v{\textit{z}}} \right)^2} + {\left( {\dfrac{{\sqrt 2 {\textit{z}}}}{{k{w_0}}}} \right)^2} + \dfrac{{4{\pi ^2}{{\textit{z}}^3}}}{3}T.$$ (19) 至此，笔者根据公式(16)和公式(18)可以计算非均匀关联光束传输经过大气湍流后在接收面上的交叉光谱密度函数。
基于公式(16)和公式(18)，并结合公式(1)~(4)，经过积分运算之后得到非均匀关联光束经过大气湍流之后的耦合效率：
$$\left\langle {{\eta _{\rm c}}} \right\rangle = \dfrac{{ \displaystyle\int {p\left( v \right)} \pi {w_0}^2/\left( {{w_{\textit{z}}}^2{w_{\rm a}}^{\rm{2}}{C_{\textit{z}}}} \right){\rm d}v}}{{ \displaystyle\int {p\left( v \right)} \pi {w_0}^2{w^2}/\left( {2{w^2} + 4{w_{\textit{z}}}^2} \right){\rm d}v}},$$ (20) 其中
$$ \begin{split} {C_{\textit{z}}} =& {\left( {{A_{\textit{z}}} + \dfrac{{{B_{\textit{z}}}^2}}{{{w_{\textit{z}}}^2}} + \dfrac{1}{{4{w_{\textit{z}}}^2}} + \dfrac{1}{{{w_a}^{\rm{2}}}} + \dfrac{1}{{{w^2}}}} \right)^2} +\\ & {\left( {\dfrac{k}{{2{\textit{z}}}}} \right)^2} - {\left( {{A_{\textit{z}}} + \dfrac{{{B_{\textit{z}}}^2}}{{{w_{\textit{z}}}^2}} - \dfrac{1}{{4{w_{\textit{z}}}^2}}} \right)^2}, \end{split} $$ (21) $$\begin{array}{l} {A_{\textit{z}}} = \dfrac{{w_0^2{k^2}}}{{8{{\textit{z}}^2}}} + \dfrac{1}{3}{\pi ^2}{k^2}{\textit{z}}T; \\ {B_{\textit{z}}} = \dfrac{{kw_0^2}}{{4{\textit{z}}}}\left( {1 - 2v{\textit{z}}} \right) - \dfrac{1}{3}{\pi ^2}k{{\textit{z}}^2}T. \\ \end{array} $$ (22) 根据公式(7)和(20)可以计算非均匀关联光束经过大气湍流传输后在接收面上的光纤耦合效率。
-
笔者利用上文推导得到的相关公式研究非均匀关联光束经过大气湍流之后在接收平面上的光纤耦合效率。在下面的数值模拟中，初始光束参数，大气湍流参数和耦合透镜参数设定为：w0=0.05 m，λ=632.8 nm，rc=3 cm, D=0.15 m，f=0.1 m，
$C_n^2$ =5×10−15 m−2/3，wj=5.15 μm，l0=1 mm，L0=1 m。下文讨论中，若无特别指出，参数则选取为以上初始值。图2为不同相干长度的非均匀关联光束经过大气湍流传输之后的光纤耦合效率演化图，其中黑实线表示相干长度为3 cm的高斯谢尔模光束经过相同条件下的大气湍流之后在接收面上的光纤耦合效率。图2中，对比高斯谢尔模光束和非均匀关联光束（即，黑线和其他虚线）可以发现，高斯谢尔模光束经过大气湍流后的光纤耦合效率随着传输距离的增加而减小，这个结论与人们普遍认为的结论是一致的；而非均匀关联光束经过大气湍流传输之后的耦合效率随着传输距离z的增加先急剧增加，待耦合效率增加至最大值后随着传输距离的增加又逐渐降低。出现这种情况的原因是非均匀关联光束在传输过程中展现出自聚焦传输特性（详细传输行为见参考文献[7, 12]），自聚焦传输特性引起的光斑尺寸减小以及能量汇聚，提高光束远距离传输之后耦合进光纤的能量，从而促使耦合效率的提高。然而，短距离传输范围内，笔者发现，非均匀关联光束的耦合效率很低，且小于高斯谢尔模光束的耦合效率。出现这种情况是因为短距离传输时，由于非均匀关联光束自身的自聚焦传输特性和透镜的聚焦作用，使光斑的实际焦点出现了焦移，即，实际焦点位于透镜几何焦点之前，导致光纤切面处的光强发散，降低耦合效率。因此在短距离传输时，高斯谢尔模光束的耦合效率要稍微优于非均匀关联光束。
图 2 不同相干长度的非均匀关联光束在大气湍流中的光纤耦合效率随传输距离z的变化曲线
Figure 2. Curves of fiber coupling efficiency of non-uniformly correlated beams propagation in atmosphere turbulence for different values of coherence length
对比不同相干长度的非均匀关联光束的耦合效率，笔者发现耦合效率的最大值随着光束相干长度的变化而变化，这是由于具有不同相干长度的非均匀关联光束具有不同的自聚焦特性引起的。从图2中大致可以发现，非均匀关联光束经过大气湍流之后的最大耦合效率随着相干长度的增大先增大后减小。接下来详细分析非均匀关联光束的光纤耦合效率随相干长度变化的演化过程。
图3为非均匀关联光束在大气湍流中传输至不同距离处的最大光纤耦合效率随相干长度的变化曲线。笔者发现，非均匀关联光束的最大光纤耦合效率随着光束相干长度的增大先增大后减小，这与图2中得到的结果相一致。从图3还可以发现，不同传输距离处的最大耦合效率对应不同的光束相干长度，这是由于不同相干长度的非均匀关联光束在大气湍流中的自聚焦“焦点”位置不同引起的，即，非均匀关联光束的相干长度越小，出现光束自聚焦“焦点”所需传输距离越短；相干长度越大，出现光束自聚焦“焦点”所需传输距离越长，在文中，为了避免过多地重复描述，笔者不再做具体展开，因为在之前的工作中已经进行了详细的讨论，读者可参阅参考文献[7,12]。
图 3 非均匀关联光束在大气湍流中不同传输距离处的最大光纤耦合效率随相干长度的变化曲线
Figure 3. Curves of maximum fiber coupling efficiency of non-uniformly correlated beams versus the coherence length for different propagation distances
图4为不同束腰和不同波长的非均匀关联光束在大气湍流中的光纤耦合效率随传输距离的变化曲线。从图4(a)中发现，非均匀关联光束的光纤耦合效率随着光束束腰的增加而减小；从图4(b)中发现，光纤耦合效率随光束波长的增加而增加。这个研究结果表明，具有小束腰和长波长的非均匀关联光束经过大气湍流传输后的光纤耦合效率要优于大束腰和短波长的非均匀关联光束，即表明，具有小束腰和长波长的非均匀关联光束更适合于空间光-光纤耦合中的应用。
图 4 (a)不同束腰, (b)不同波长的非均匀关联光束在大气湍流中的光纤耦合效率随传输距离的变化曲线
Figure 4. Curves of fiber coupling efficiency of non-uniformly correlated beams propagation in atmospherer turbulence for (a) different beam widths, (b) different beam wavelengths
下面分析不同聚焦透镜参数和不同湍流强度对非均匀关联光束经过大气湍流后的光纤耦合效率的影响。
图5为耦合透镜的焦距与接收孔径对非均匀关联光束经过大气湍流之后在z=2 km处的光纤耦合效率的变化曲线图。研究结果表明：光纤耦合效率曲线随着接收孔径D的增加而减小，这是由于当耦合透镜焦距一定时，接收孔径越大，在焦平面上的聚焦光斑尺寸越大，导致耦合进光纤的光强越小，耦合效率越低。当接收孔径一定时，光纤耦合效率随着焦距 f增加先增大后减小。出现该现象是因为非均匀关联光束自身的自聚焦性质和透镜聚焦性质共同作用的结果。因此，根据图5，当所选光束参数确定时，还可以通过调控耦合透镜接收孔径和透镜焦距来优化光纤耦合效率。
图 5 不同接收口径情况下，非均匀关联光束在大气湍流中的光纤耦合效率随耦合透镜焦距的变化曲线
Figure 5. Curves of fiber coupling efficiency of non-uniformly correlated beams propagation in atmospherer turbulence versus focal length of coupling lens for different apertures
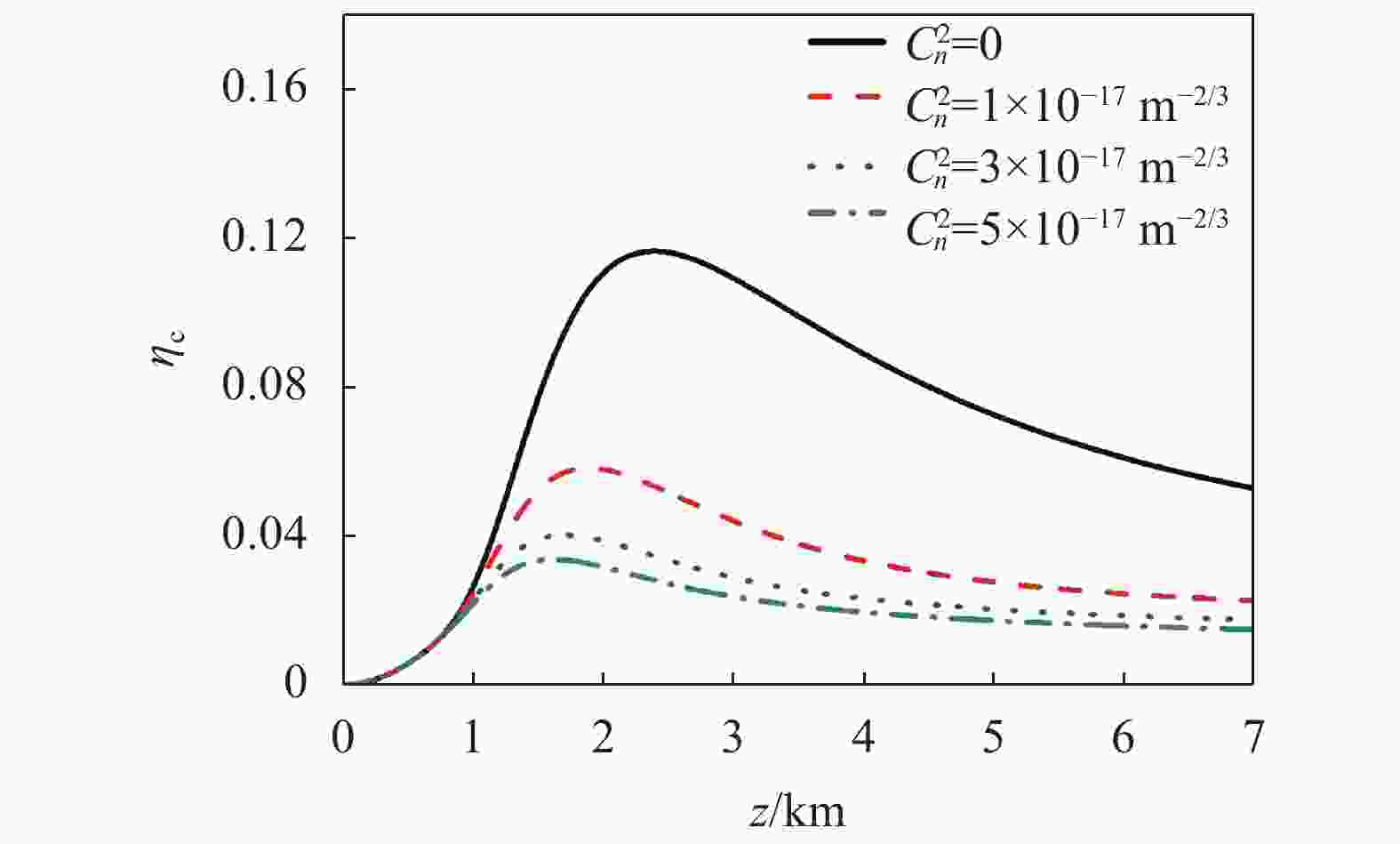
图6为不同湍流强度下非均匀关联光束在大气湍流中的光纤耦合效率随传输距离的变化曲线。笔者发现，在自由空间中，非均匀关联光束的耦合效率优于其在大气湍流中的光纤耦合效率，这是由于大气湍流导致光束光强散射的负面影响，从而降低了光束在接收端的能量，降低光束光纤耦合效率。从图6还可以发现，大气湍流强度对光束光纤耦合效率存在影响，光束在大气湍流中的光纤耦合效率随着大气湍流强度的增加而降低。
图 6 不同湍流强度下，非均匀关联光束在大气湍流中的光纤耦合效率随传输距离的变化曲线
Figure 6. Curves of fiber coupling efficiency of non-uniformly correlated beams propagation in turbulence for different turbulence intensities
-
文中研究了光场相干结构调控技术对光束经过大气湍流之后的光纤耦合效率的影响。首先，通过广义惠更斯-菲涅尔积分公式，得到非均匀关联光束经过大气湍流之后的交叉谱密度函数；其次，根据接收端的交叉谱密度函数得到非均匀关联光束经过大气湍流后的光纤耦合效率。研究发现，非均匀关联光束经过大气湍流后的光纤耦合效率要优于同等情况下的传统高斯谢尔模光束；调控非均匀关联光束的相干长度可以提升光纤耦合效率，且针对不同传输距离的情况，可以通过光束相干长度的调控实现耦合效率的最优化。笔者还发现，非均匀关联光束的束腰和波长大小对耦合效率也存在影响，即，小束腰和长波长的非均关联光束具有更好的光纤耦合效率。耦合透镜参数和大气湍流强度大小对耦合效率的影响在文中也进行了讨论，相关研究结果可供读者们根据他们的实际需求选取适当的参数。
Coupling efficiency of non-uniformly correlated beams into a single-mode fiber in turbulence (Invited)
-
摘要: 研究了非均匀关联光束经过大气湍流后的光纤耦合效率。研究结果表明，大气湍流中非均匀关联光束的光纤耦合效率优于传统高斯谢尔模光束；且调控光束相干长度可以提高光纤耦合效率；针对不同传输距离的情况，可以通过调控光束相干长度实现耦合效率的最优化。同时，文中还讨论了光源参数：束腰和波长；耦合透镜参数：接收孔径和焦距；湍流强度对光纤耦合效率的影响。该研究成果证明光场相干结构调控技术在提升光纤耦合效率中的应用，在自由空间激光通信研究领域存在重要价值。Abstract: The coupling efficiency of non-uniformly correlated beams through atmospheric turbulence was studied. The results show that the fiber coupling efficiency of such beams is higher than that of the traditional Gaussian Schell-model beam; and the regulation of the coherence length of such beams can improve the fiber coupling efficiency; for different transmission distances, the optimization of the coupling efficiency can be achieved by adjusting the coherence length of such beams. Moreover, the effect of the light source parameters: beam waist and wavelength; coupling lens parameters: received aperture and focal length; turbulence intensity on the coupling efficiency of optical fiber was also discussed. The results show that the application of optical field correlation structure manipulation technology in improving the coupling efficiency of optical fiber has important value in the field of free space optical communication.
-
Key words:
- atmosphere turbulent /
- correlation structure /
- coupling efficiency
-
图 1 大气湍流中空间光-光纤耦合示意图
Figure 1. Schematic diagram of spatial light-fiber coupling in turbulent atmosphere
图 2 不同相干长度的非均匀关联光束在大气湍流中的光纤耦合效率随传输距离z的变化曲线
Figure 2. Curves of fiber coupling efficiency of non-uniformly correlated beams propagation in atmosphere turbulence for different values of coherence length
图 3 非均匀关联光束在大气湍流中不同传输距离处的最大光纤耦合效率随相干长度的变化曲线
Figure 3. Curves of maximum fiber coupling efficiency of non-uniformly correlated beams versus the coherence length for different propagation distances
图 4 (a)不同束腰, (b)不同波长的非均匀关联光束在大气湍流中的光纤耦合效率随传输距离的变化曲线
Figure 4. Curves of fiber coupling efficiency of non-uniformly correlated beams propagation in atmospherer turbulence for (a) different beam widths, (b) different beam wavelengths
图 5 不同接收口径情况下，非均匀关联光束在大气湍流中的光纤耦合效率随耦合透镜焦距的变化曲线
Figure 5. Curves of fiber coupling efficiency of non-uniformly correlated beams propagation in atmospherer turbulence versus focal length of coupling lens for different apertures
-
[1] 王飞, 余佳益, 刘显龙, 等. 部分相干光束经过湍流大气传输研究进展[J]. 物理学报, 2018, 67(18): 184203. doi: 10.7498/aps.67.20180877 Wang Fei, Yu Jiayi, Liu Xianlong, et al. Research progress of partially coherent beams propagation in turbulent atmosphere [J]. Acta Physica Sinica, 2018, 67(18): 184203. (in Chinese) doi: 10.7498/aps.67.20180877 [2] Andrews L C, Phillips R L. Laser beam propagation through random media[M]. Bellingham, WA: SPIE, 2005: 9-15. [3] Gbur G. Partially coherent beam propagation in atmospheric turbulence [Invited] [J]. Journal of the Optical Society of America A, 2018, 31(9): 2038-2045. [4] Wang F, Liu X, Cai Y. Propagation of partially coherent beam in turbulent atmosphere: a review (invited review) [J]. Progress In Electromagnetics Research, 2015, 150: 123-143. doi: 10.2528/PIER15010802 [5] Gbur G, Wolf E. Spreading of partially coherent beams in rando. media [J]. Journal of the Optical Society of America A, 2002, 19(8): 1592-1598. doi: 10.1364/JOSAA.19.001592 [6] Gori F, Santarsiero M. Devising genuine spatial correlation functions [J]. Optics Letters, 2007, 32(24): 3531-3533. doi: 10.1364/OL.32.003531 [7] Lajunen H, Saastamoinen T. Propagation characteristics of partially coherent beams with spatially varying correlations [J]. Optics Letters, 2011, 36(20): 4104-4106. doi: 10.1364/OL.36.004104 [8] Sahin S, Korotkova O. Light sources generating far fields with tunable flat profiles [J]. Optics Letters, 2012, 37(14): 2970-2972. doi: 10.1364/OL.37.002970 [9] Korotkova O, Sahin S, Shchepakina E. Multi-Gaussian Schell-model beams [J]. Journal of the Optical Society of America A, 2012, 29(10): 2159-2164. doi: 10.1364/JOSAA.29.002159 [10] Mei Z, Korotkova O. Random sources generating ring-shaped beams [J]. Optics Letters, 2013, 38(2): 91-93. doi: 10.1364/OL.38.000091 [11] Chen Y, Wang F, Liu L, et al. Generation and propagation of a partially coherent vector beam with special correlation functions [J]. Physical Review A, 2014, 89: 013801. doi: 10.1103/PhysRevA.89.013801 [12] Yu J, Wang F, Liu L, et al. Propagation properties of Hermite non-uniformly correlated beams in turbulence [J]. Optics Express, 2018, 26(13): 16333-16343. doi: 10.1364/OE.26.016333 [13] Yu J, Chen Y, Liu L, et al. Splitting and combining properties of an elegant Hermite-Gaussian correlated Schell-model beam in Kolmogorov and non-Kolmogorov turbulence [J]. Optics Express, 2015, 23(10): 13467-13481. doi: 10.1364/OE.23.013467 [14] Dan Y, Zhang B. Beam propagation factor of partially coherent flat-topped beams in a turbulent atmosphere [J]. Optics Express, 2008, 16(20): 15563-15575. doi: 10.1364/OE.16.015563 [15] Yu J, Zhu X, Wang F, et al. Experimental study of reducing beam wander by modulating the coherence structure of structured light beams [J]. Optics Letters, 2019, 44(17): 4371-4374. doi: 10.1364/OL.44.004371 [16] Korotkova O, Avramovzamurovic S, Nelson C, et al. Scintillation reduction in multi-Gaussian Schell-model beams propagating in atmospheric turbulence[C]// Proc SPIE, 2014, 9224: 92240M. [17] Salem M, Agrawal G P. Coupling of stochastic electromagnetic beams into optical fibers [J]. Optics Letters, 2009, 34(18): 2829-2831. doi: 10.1364/OL.34.002829 [18] Salem M, Agrawal G P. Effects of coherence and polarization on the coupling of stochastic electromagnetic beams into optical fibers [J]. Journal of the Optical Society of America A, 2009, 26(11): 2452-2458. doi: 10.1364/JOSAA.26.002452 [19] Wolf E. Introduction to the Theory of Coherence and Polarization of Light[M]. Cambridge: Cambridge University, 2007, 1-30. [20] Toselli I, Andrews L C, Phillips R L, et al. Angle of arrival fluctuations for free space laser beam propagation through non Kolmogorov turbulence[C]//Atmospheric Propagation IV. International Society for Optics and Photonics, 2007, 6551: 65510E. [21] Toselli I, Andrews L C, Phillips R L, et al. Free-space optical system performance for laser beam propagation through non-Kolmogorov turbulence [J]. Optical Engineering, 2008, 47(2): 026003. doi: 10.1117/1.2870113 -
点击查看大图
计量
- 文章访问数: 501
- HTML全文浏览量: 145
- PDF下载量: 30
- 被引次数: 0
