-
人类所处的物理世界空间是三维的,对三维信息的获取和处理技术体现了人类对客观世界的把握能力,因而从某种程度上来说它是体现人类智慧的一个重要标志。传统光探测器仅对被测场景的二维强度敏感而无法感知其三维形貌与深度信息。人类虽可通过自己的双眼来感知三维的世界,但无法对客观事物的三维形貌进行准确定量的描述。三维成像与传感技术作为感知真实三维世界的重要信息获取手段,为重构物体真实几何形貌及后续的三维建模、检测、识别等方面提供数据基础。2016年,国内实施的制造强国战略《中国制造2025》中明确指出“用信息化和工业化两化深度融合来引领和带动整个制造业的发展”。而三维传感作为智能制造中一项关键性信息输入环节,使机器“感知世界”,是一切制造的自动化、智能化、再创造化的新起点。近年来,随着计算机技术、光学和光电技术的发展,以光信号为载体的光学三维传感技术融合光电子学、图像处理、计算机视觉与现代信号处理等多学科为一体,已发展成为光学计量和信息光学的最重要的研究领域和研究方向之一。
三维信息获取与处理技术以各种不同的风貌与特色渗透到我们身边的众多领域之中。在工业设计中,基于三维数字化模型的逆向设计方法可快速获得现有成熟产品的准确和完整的计算机模型,大大缩短产品或模具的研发周期。在虚拟现实领域,大量景物的三维彩色模型化数据已被用于国防、模拟训练、科学试验、3D动画的建构。在医学整形领域,三维数字化技术已广泛用于面部软组织形态修复,外科检测,假牙假肢的量身定做。在文物保护领域中,三维彩色数字化技术能以不损伤物体的手段,获得文物的三维信息和表面色彩、纹理,便于长期保存与再现。但在某些领域,如三维测量加工、机器人导航、快速逆向成型、自动化生产线控制、产品质量监控等,仅仅捕获待测物体的三维信息是不够的,三维数据获取的速度与效率直接关系到制造系统的响应能力、产品研制生产能力、以及产品质量保证能力。此外在诸如压模件尺寸监测、冲压板几何形状和形变检测、机车冲撞试验等应用中以及压力波传播、不连续边界的应力集中、汽车制导中障碍检测、流体力学、流程可视化、运动力学、高速旋转等实验记录中,高速瞬态过程的三维数据快速记录与准确定量再现将有助于描绘和分析动态过程中物体表面三维形态的变化,并为进一步提取与被测物体相关的结构、形变、应力等物理参量提供数据基础。
近年来,消费电子与个人身份验证对3D技术日益增长的需求促进了三维成像与传感技术的蓬勃式发展。站在当前时点,笔者认为摄像头从2D向3D的转变将成为继黑白到彩色、低分辨率到高分辨率、静态图像到动态影像后的“第四次影像革命”。触摸屏实现了交互方式从一维到平面的转变,而3D摄像头将让交互方式从平面变成立体。这为许多“痛点型应用场景”打开了新局面,如当前科技界炙手可热的领域如体感交互、AR/VR等。另一方面,近年来“身份认证”也成了三维传感技术的一大重要应用领域。小到与个人相关的考勤系统,门禁系统,支付系统等,大到关乎国家安全层面的机场、信息安全、金融、军事等领域,归根结底都需要验证“你是谁”。随着近几十年来计算机技术和生物工程技术的飞速发展,利用人体生物特征的唯一性来鉴别每一个人的身份的方法得到了国际社会的普遍认同。相较于其他生物特征,人脸识别方法具有非接触性、信息完备、采集便捷、人机友好等优点,已经成为身份验证和身份识别应用中最为理想的技术途径之一。但二维人脸图像对光照,姿态,表情变化的敏感性严重制约了其识别结果的准确性、稳定性和可靠性,这些因素也因此成为了二维人脸识别技术进一步向前发展的最大障碍。在2017年的央视315晚会上,主持人现场展示了使用视频模拟的方式来破解二维人脸识别[1]。在FIT互联网安全创新大会[2]上安全研究员甚至展示了5种人脸识别技术的破解手法。可见二维人脸识别技术由于其数据本身的局限性,还是存在着很大安全隐患。三维人脸识别技术由于采用了三维数据,有望从根本上解决二维人脸识别所面临的“光照、姿态和表情”难题。当然,从工业应用逐渐向消费电子的迁移也为3D传感技术的小型化、低成本、可靠性等提出了更高的要求。
以光信号为载体的光学三维成像与传感技术融合光电子学、信息光学、图像处理、计算机视觉等多学科为一体,具有非接触、高精度、点云重建效率高等优点,已发展成为光学计量和光信息学的最重要的研究领域和研究方向之一。近年来,数字光投影器、空间光调制器、光探测器等光电成像器件,高性能计算机、嵌入式处理器等运算处理单元,数字信号处理、计算机视觉、机器学习等研究领域得到了跨越式发展,为光学三维成像与传感技术的进一步发展开启了更广阔的空间和机遇,相关的新机理、新体制、新技术、新应用不断涌现。为了促进相关研究人员在光学三维成像与传感技术及其应用领域交流最新的研究成果,《红外与激光工程》于2020年第3期精心策划组织了“光学三维成像与传感”专题,并得到了来自相关领域专家和学者的积极响应。此次专栏共包含高水平论文20篇,其中综述论文15篇,研究论文5篇。这些论文系统介绍了光学三维成像传感领域热点专题的研究进展或动态,主题全面涵盖了当前三维光学成像领域的前沿热点研究方向:结构光三维成像、条纹投影轮廓术、干涉测量技术、相位测量偏折术、三维立体显示技术(全息显示、集成光场显示等)、三维成像传感技术与计算成像相关交叉领域(如三维鬼成像等)等。而该文作为本期专栏的引子,概括性地综述了典型的三维传感技术(见图1),并着重介绍了三维结构光传感器技术的发展现状、关键技术、典型应用;讨论了其现存问题、并展望其未来发展方向,以求抛砖引玉。
-
三维传感技术从感知方式上分类可以分为接触式测量和非接触式测量。接触式测量主要依靠标定的被动机械臂直接接触物体表面,逐点对物体轮廓数据进行釆集,对其形态信息进行三维测量。这种方法的优点是测量精度高,可达到微米级别。但是其缺点也包括了测量效率低,不适合形态复杂物体测量,对测量环境要求较高等。非接触式测量主要指依靠光、声、电磁学等方式接触物体表面以获取物体三维信息的方法。而其中基于光学的三维测量技术是目前最典型也是应用最广泛的三维传感技术。如图1所示,典型的光学三维传感技术主要包括光度立体视觉、双(多)目立体视觉、飞行时间法、激光线扫法、散焦恢复形状法、结构光投影法等,而结构光投影又包括条纹投影与散斑投影法等。该节对这些常见的光学传感方法进行了简要介绍。
-
光度立体视觉技术最早由Woodham[3]提出,其假设了一个已知的重构函数,即理想的朗伯体反射模型。采用一个相机和几个发光强度相同的光源,保持相机和拍摄物体静止,通过改变光源方向,同时拍摄物体在不同光源照射条件下的一组图像,然后根据这些图像计算出物体的表面法向,再由法向求解出物体表面三维形状,图2给出了光度立体法对斯坦福兔的三维测量结果。随后一系列方法被提出[4–9]以解决光度立体法模型、对高光物体测量及标定等问题。光度立体法的设备较简单,但对环境要求严格,并需要待测物表面为严格平滑的漫反射朗伯体,对于具有陡变或者反射特性较为复杂的物体难以适用。
-
立体视觉是一种模拟人类视觉原理的被动深度感知方法[10–20]。测量系统基于三角测距原理,用两个或多个相机从不同角度获取同一场景的多幅图像,通过对同一物点在各幅图像上检测和匹配,根据立体视差进行测距,得到物体该点的深度信息。其原理如图3所示。立体视觉测量系统硬件结构简单,易实现。其主要难点在于立体匹配,实际应用中由于遮挡或阴影的影响,可能会产生视觉信息不足的问题,导致误匹配。另外,对于无明显表面特征的物体,也难以从多个视角中找到对应点,因而无法进行准确的三维重建。但值得提及的是,立体视觉法的基本三维重建原理和后面所介绍的结构光投影法是一致的。
-
ToF技术通过记录光束传播时间来计算被测物体表面的深度距离[21–23]。其原理如图4所示,系统发射装置发射脉冲信号,经被测物体反射后被探测器接收,通过光信号从发出到接收的时间与光速便可以计算出深度值。该方法可避免阴影和遮挡带来的问题,但由于设备装置的限制,测量精度一般在毫米级。若想达到更高的精度,就需要更加复杂、昂贵的设备。虽然许多学者尝试将飞行时间法与多视几何相结合来提高测量空间分辨率与测量精度[25–27],但与高精度测量方法相比,飞行时间法还存在一定的差距。
-
激光线扫法的原理如图5所示,它是一种最简单的结构光三维测量技术。该技术利用线激光器投射一维线激光到物体表面,图像采集装置采集到物体表面变形的线激光,然后根据三角测量原理得到物体表面相应位置的三维信息。线激光扫描方法的优点是其数据采集不依赖外部光照环境,对目标场景要求低,操作简单直观,自动化程度高[28–30]。但由于激光扫描仪本身技术的限制,它也存在以下不足:扫描速度较慢,激光扫描仪造价高[31];其最高精度和最大扫描距离是固定的,无法像摄影测量那样通过方案设计来得到提高;无法获取高质量纹理数据[32]等。宽泛意义上来说,激光线扫法其实是结构光投影法的一种极端特例。但由于投影图案就是一条直线,所以测量效率要比全场结构光技术低得多。
-
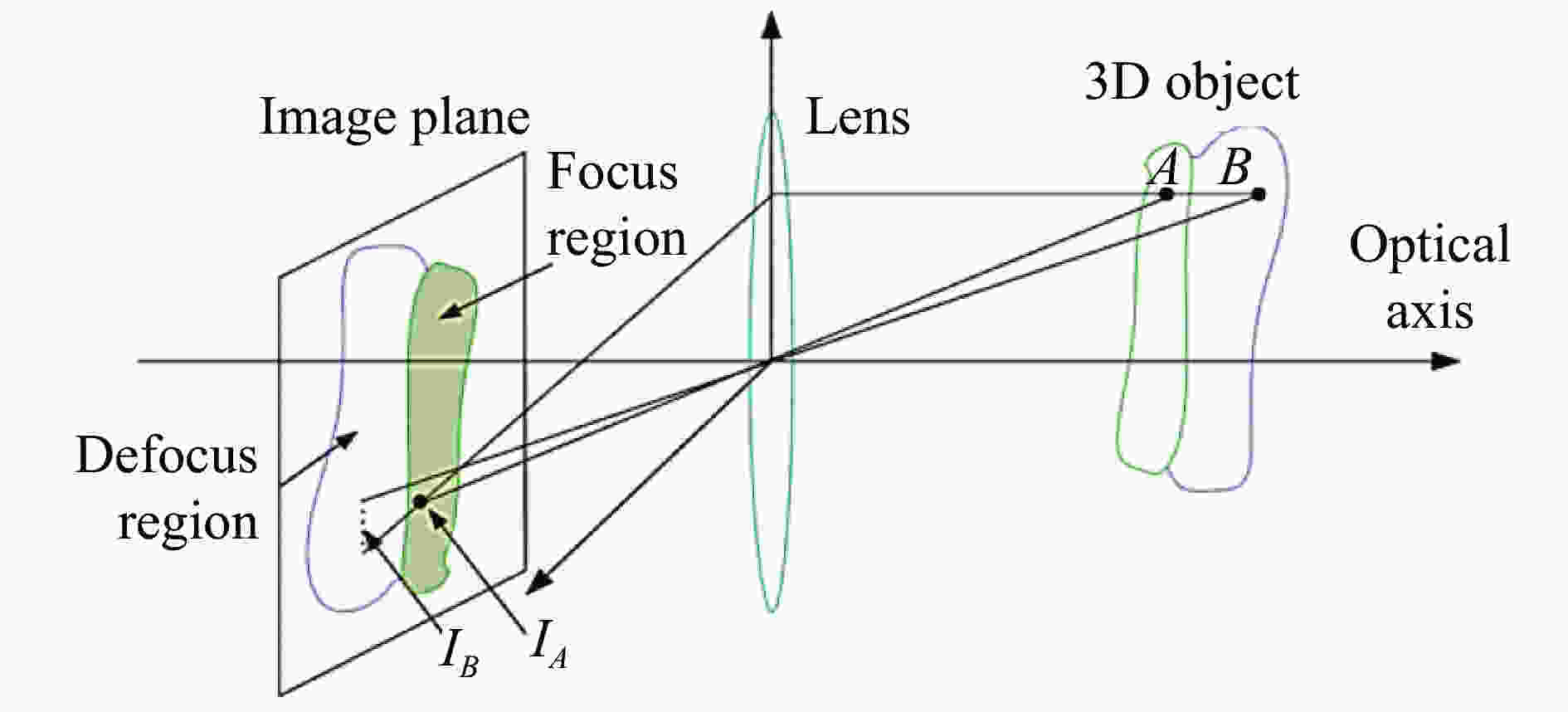
散焦恢复形状法(Shape-from-defocus, SfD)的原理如图6所示,散焦恢复形状是通过处于不同深度方向物体在图像中离焦的程度来恢复物体的深度值,测量过程中需要移动被测物或是相机,拍摄至少两张不同聚焦程度的图像。1995年,哥伦比亚大学的Nayer[33]首次实现基于离焦投影恢复的三维面型测量法,其向被测物体投射设计好的图案,经被测物体反射后,通过分束棱镜将光线分离,由两个相机在同一个方向分别采集,由于两幅图像具有不同的离焦信息,因此可以计算出相机图像中每个像素的深度值,如图7所示。测量过程中,投影与采集方向几乎一致,因此测量时很少会受到遮挡与阴影的影响,并且计算过程较为简单,在不依赖于高性能硬件条件下便可以实现实时动态三维面形测量。1998年,Nayer等人[34]在不使用主动光源的情况下,实现了具有纹理表面物体的三维测量。然而,该方法的深度测量精度还有待进一步提升。
-
结构光投影法是一种非常流行的非接触式三维形貌测量技术,其具有硬件配置简单、测量精度高、点密度高、速度快、成本低等优点,已在工业和科学研究中得到广泛应用。从本质上讲,结构光投影法可以看作是立体视觉法的一种改进形式,其通过将立体视觉中一个摄像机替换成光源发生器(如投影仪)而实现,原理如图8所示。光源向被测物体投影按一定规则和模式编码的图像,编码图案受到物体表面形状的调制而产生形变。带有形变的结构光被另外位置的相机拍摄到,通过相机与投影光源之间的位置关系和结构光形变的程度可以确定出物体的三维形貌。相比于立体视觉法,其最大优点在于投影仪将结构光图像投射到物体上,由于物体表面被编码图案所覆盖,可以很容易地克服立体视觉中的立体匹配问题。此外求解物体初相位时是点对点的运算,即在原理上某点的相位值不受相邻点光强值的影响,从而避免了物面反光率不均匀或观察视角的偏差引起的误差,测量精度可以达到几十分之一到几百分之一个等效波长。有关结构光投影法的基本原理可见Geng等[37]的结构光教学论文。
在过去的几十年中,基于结构光投影法的三维形状测量技术在计算机视觉和光学测量领域得到了迅速发展。在计算机视觉领域中,结构光投影技术通常被称为3D扫描,且所使用的结构光投影图案主要集中于基于离散强度方案。它们可进一步分为空间编码(单次拍摄)和时间编码(多次拍摄)的方案。空间编码方法有De Bruijn编码[39–41],非正规码[42, 43]和M-array码[44]。这些方法的关键思想是保证局部编码在全局图像中的唯一性。时间编码方法是将有一定编码的图案连续投影到物体表面上,方法包括时间二进制码[45]、时间n元码[46]和格雷码[47]。此外,还有学者提出使用红、绿、蓝三通道的彩色图案或彩色多路复用结构光投影法来提高编码效率并减少三维重建所需的结构光图案[46, 48–50]。关于这些编码方案的基本原理和实际性能的更多细节,可见Salvi等人[51]的综述文章。由于数字光学投影仪的快速发展,使得所投影的面结构光可以通过计算机编程更为灵活地进行选择,并最大限度地提高测量精度和速度,这些优点使结构光投影技术成为最具潜力的三维面形测量技术之一。
-
在光学测量领域,最具代表性的结构光投影技术被称为条纹投影轮廓术(Fringe Projection Profilometry,FPP)。FPP具有结构简单、精度高、速度快、成本低、易实现等优点,其在工业和科学研究领域都有较广泛的应用。当代条纹投影轮廓术主要采用数字光栅投影技术,该技术通过利用数字设备取代机械装置生成与投影面结构光光栅,使得编码过程更加灵活准确[48, 52–60]。此外由于现代电子设备的高速发展,数字投影设备和采集设备的速度越来越快,结构光条纹投影技术的应用可完全满足三维面形的高速实时测量要求。基于条纹投影轮廓术的三维测量系统和结构光投影法的硬件系统相一致,一般由一个投影仪和一个或多个相机组成,如图8所示。在测量过程中,投影仪将光栅条纹投向物体,条纹图案经物体调制后变形,再由相机采集。从采集到的条纹图中可获取物体相位信息,相位图中可以找出相机在投影仪中的对应点,然后根据三角关系可求出物体的深度信息。在此过程中存在三个重要步骤:相位测量,相位展开,相位-深度映射。
FPP中两种主要的相位测量技术是(时域)相移轮廓术(Phase Shifting Profilometry,PSP)[38, 61]和(空域)傅里叶变换轮廓术(Fourier Transform Profilometry, FTP)[62–64]。FTP是一种基于空间滤波的单帧光栅投影法,其最初于1982年被Takeda等[62]首先提出,之后Su,Zhang等针对此方法开展了系统深入的研究工作[63, 64]。此外,加窗傅里叶变换(Windowed Fourier Transform, WFT)[65-66]和小波变换(Wavelet Transform, WT)[67]也可用于单帧条纹图的相位解调。有关傅里叶变换轮廓术的更多详细的技术细节及其在动态三维测量方面的应用,可见参考文献[65-66]。不同于FTP,PSP需要至少三幅相移条纹图案以实现逐像素的高精度相位测量。PSP源于激光干涉技术,Srinivasan等[68-69]首先将相移干涉技术引入三维形貌测量领域。相比于FTP,PSP具有更高的空间分辨率和相位测量精度,并对环境光和物体表面反射率的变化更加鲁棒[70-71]。由于其多帧测量特性,当测量动态场景时,尤其当帧间间隔内的物体运动不可忽略时将导致相位误差。严格来说,运动引起的相位误差是PSP固有且不可避免的问题。但近年来,随着高帧率图像传感器、高性能处理器和高速数字投影技术的发展,PSP已逐渐应用于动态场景的高速实时三维测量[72, 73]。笔者所在课题组自2011年起针对相移轮廓术及其快速三维测量应用方面也开展了系统性的研究工作,有关更多PSP的技术细节及其相位误差分析的内容可见参考文献[38]。
无论是PSP和FTP,与目标高度所对应的相位分布都由反正切函数得出,其范围限制在-π和π之间,这样的相位称为截断相位或包裹相位。为了建立相机和投影仪之间一对一的像素对应关系,并正确重建三维形貌,需对相位进行展开/相位去包裹。常见的相位展开法分为空间相位展开和时间相位展开两大类。空间相位展开通常只需一幅单独的相位图,依据像素邻域内的相位值实现相位展开。代表性的空间相位展开法主要包括可靠度引导的相位展开法[74]、剪枝法[75]、多网格法[76]、最小
${L_p}$ 范数法[77]、掩膜切割法[78]、最小二乘相位展开法[79]等。但对于孤立物体和不连续表面的相位分布,利用空间相位展开法理论上是无法无歧义地实现可靠的相位展开的,如图9所示。时间相位展开方法通过采用多个包裹相位分布或添加额外的黑白编码图案来提供关于条纹级次的额外信息,以解决相位歧义问题[80–90]。与空间相位展开相比,时间相位展开中的每个像素的条纹级次都是独立计算,无需参考邻近像素,因此可以展开任意复杂形状表面的包裹相位分布。其中常用的算法包括格雷编码法[47, 82]与多频时间相位展开法[80, 81, 91–96]。有关于时域相位展开的基本原理和各类算法的技术对比可见参考文献[97]。
通过解算出的物体的绝对相位信息,就可以找出相机所拍摄图像在投影仪图像中的对应点,然后根据三角关系可求出物体的深度信息。这种三角测量与立体视觉的三维重建原理是立体视觉与所有结构光三维测量技术的基础,在第三章进行了详细讨论。
-
与条纹投影轮廓术类似,散斑结构光投影法也属于结构光投影技术。其三维重建的基本流程为:首先,对物体投射随机散斑图案,利用提前标定好的双目相机同时拍摄物体获取左右原始散斑图;其次,对原始散斑图像进行极线校正和散斑区域提取,在此基础上利用数字散斑相关方法搜索整像素对应点并根据视差约束剔除误匹配;然后通过合适的亚像素搜索方法得到准确的亚像素对应点;最后,利用三角测量原理重建出物体的三维形貌。数字散斑相关测量技术具有系统简单,单帧重建,测量范围大等诸多优点。散斑结构光投影法是文中所要讨论的主要内容。文章的后续章节将对其基本原理、关键技术、典型应用等进行了详细分析与讨论,因此这里只做简单介绍。
-
让人意想不到的是:三维光学传感技术是伴随着体感游戏的诞生而进入消费电子行业的!自2006年日本任天堂(Nintendo)发布了新时代游戏主机Wii起便拉开了体感技术的序幕[98]。其将惯性传感器作为主要的外部设备,如重力传感器、陀螺仪等,通过一系列的传感器设备来实现对使用者的肢体动作加以感测,获得包括肢体加速度、运动方向、角速度等空间物理参数完成人体姿态估计和动作识别(见图10)。虽然创造式的交互游戏操作方式使Wii取得了巨大成功,然而传感测量设备需要人体手持或者穿戴,并不符合当下“无接触”式体感交互设备的发展趋势。
2010年,微软(Microsoft)发布了跨时代全新体感感应套件—Kinect[100],如图11所示。其使用了PrimeSense公司专利技术的深度摄像头。Kinect标志着三维光学传感器正式登台亮相。该产品一经推出,便掀起了新一轮的体感游戏热潮,上市60天内销售超过800万台,当时取代了iPhone成为“60天内最畅销的消费电子产品”[101-102]。
Kinect能让用户脱离任何控制器,只通过用语音和手势去操控Xbox360游戏机[104],是因为机器里内置的红外摄像头、红外结构光投影器、多种传感器的通力合作。红外结构光投影器将30万个红外线光点投射在待测场景上,如图12所示。红外摄像头拍摄到这些光电图像用来重建三维深度信息。Kinect能够捕捉12帧每秒1 280 pixel×960 pixel的彩色图像或者以30帧每秒捕捉640 pixel×480 pixel的彩色图像,也能够同时以30帧每秒的速度捕捉640 pixel×480 pixel的深度图像。不同于同时代的Wii,用户并不需要任何手持设备去配合它,只要站在摄像头前,Kinect就能识别人的动作,并精准地投射在电视屏幕上。跳舞、运动、绘画、冒险,一切都是那么的轻松与真实,真正把人从控制器里解放了出来。而这样一部充满黑科技的体感设备,当时的售价只有149美元。
2011年6月,微软官方发布Kinect for Windows SDK Beta并对代码进行了开源,国内外研究机构和科研人员纷纷以此为平台进行研究和开发,使Kinect的应用更加广泛,例如人机交互、机器视觉等。随后,国外的许多厂家也投身于三维光学传感器的研发行列,例如英特尔的RealSense、苹果收购的PrimeSense、以及谷歌的Project Tango等。2013年起,国内一些3D结构光传感器公司也如雨后春笋般出现,并均效仿微软Kinect推出了自己的结构光传感器模组。
Kinect在初期的表现可谓是现象级的,然而,这样的繁华只是表象,有太多隐藏在阳光下的阴影没有被当时的消费者所发现。而这也为Kinect的迅速溃败埋下了隐患。然而微软却一意孤行地认为,Kinect就是游戏的未来,甚至在次世代主机Xbox One发售时,强行把基于ToF的Kinect 2.0和它捆绑在一起发售,售价比性能强劲、第三方游戏阵营强大的PS4贵了100美元。其结果可想而知,硬件赚不到钱、没有足够有杀伤力的游戏软件、开发者们不买账、核心玩家不感兴趣、非核心玩家的大量出走、还有对游戏未来形势的错误估计,使得Kinect刚开始大获成功之后便从神坛上跌落。和Xbox One强行捆绑销售的Kinect 2.0就像是压倒骆驼的最后一根稻草。2017年,微软不得不宣布其针对游戏主机Xbox360推出的体感设备Kinect停产[105],正式宣告体感时代的终结。
-
尽管微软的体感游戏时代伴随着Kinect的失败而终结,但3D传感技术却并没有因此凋零。实际上其原理“利用红外摄像头来接收景深距离信息”也在被许多人使用的iPhone X所利用,其“刘海儿”里藏着的正是一台迷你版的Kinect。几乎在微软宣布Kinect停产的同时,2017年9月,苹果推出带有3D结构光传感器技术的iPhone X,如图13所示。iPhone X独特的“刘海”上集成了大量元器件以实现异型屏幕的边缘显示与容纳Face-ID组件,Face-ID的组件中包括了红外摄像头、泛光灯、距离传感器、环境光传感器、听筒、麦克风、正面摄像头和红外点投射器。苹果通过收购PrimeSense公司把 Kinect硬件缩小到手机上,而PrimeSense曾经就是Kinect传感器制造商,其运作的基本原理与Kinect也是类似的,都是使用点阵投影器将数万个肉眼不可见的红外线光点投射在用户面部,从而绘制出三维面谱。
iPhone X的巨大成功标志着三维光学传感器全面走入了大众的视野,成为目前科技节最火爆的话题之一,2017也被普遍认为是开启了“三维传感元年”。只不过这次三维光学传感技术不再是用来识别人的人体和手势,而被苹果用来识别人的面部信息,使Face-ID(如图14所示)替代Touch-ID成为iPhone独特的安全系统。悄然谢幕的Kinect与华丽登场的iPhone似乎形成了一种微妙的映照,苹果公司前CEO Steve Jobs曾经调侃Kinect道:“The problem with Microsoft, is they just have no taste.”(微软最大的问题就是他们真的没有品位)。
人脸识别技术的发展历史可以追溯到20世纪初,当时的人脸识别技术特指二维人脸识别技术。同为人脸识别技术,二维人脸识别只需要一个普通的RGB摄像头就能实现,其基本原理是通过提取二维图片中的人脸特征,比如五官的大小、相对比例间距等,进而与数据库中的标准照片进行比对验证,确认照片中人的身份信息。二维人脸识别技术的最大优势就是简单直接、识别迅速。但是由于其还是基于图片信息识别的,因此无法从根本上防止照片欺骗等手段,难以承担移动支付的需求。此外还存在对环境光照过于依赖的弊端,以至于弱光、强光、不均匀照明环境下识别精度下降甚至无法识别,存在着很大的安全隐患。而iPhone X主打的Face ID人脸识别基于3D结构光传感器的三维数据,是二维人脸识别向三维人脸识别的转变。使用Face ID作为手机“密码”,不用担心“拿照片就能解锁”等安全问题。
iPhone X推出之后,其主打的Face ID人脸识别功能更是成为了安卓手机制造商跟进的目标。有很多国内厂家及时的跟上了这一波浪潮。以华为和小米为例,这两家企业在此前的新品上,分别搭载了不同的三维传感方案。其中,华为MATE和P系列使用的是ToF方案,而小米8则使用的是结构光方案。一直以来,小米8都被认为是首款配备三维人脸解锁国产手机,不过其三维结构光技术来自以色列Mantis Vision公司。而后发布的OPPO Find X采用了国内奥比中光的三维传感硬件及旷视科技的算法;华为Mate 20 Pro上的三维结构光采用华为自研的算法。到2018年底,三维人脸解锁几乎成了中高端智能手机的标配。
-
当上中下游的三维传感公司纷纷找到自己的伙伴,并达成一定默契,三维传感技术的落地推进开始不断切入到更多垂直领域和场景。如果说手机人脸解锁是众厂家的练兵试水领域,那么人脸支付则是互联网巨头主导下的矩阵式流量收割战场。苹果的Face ID像一颗火种,将三维传感技术浓缩化、精细化,进而在手机人脸解锁、人脸支付、三维传感创作等领域释放出燎原之势。
2018年4月,在OPPO和奥比中光合作Find X的人脸解锁之际,奥比中光与支付宝合作,成立了蚂里奥公司投入“人脸支付”的开发,支付宝也计划三年内在人脸支付领域投资30亿[108]。蚂里奥在2018年12月发布了第一代“蜻蜓”刷脸支付终端,打响了刷脸支付落地的第一枪。2019年4月,第二代“蜻蜓”发布,整机重量比第一代减轻了55%。在发布会现场,1 000台机器在10 s内被抢光,仅仅两天之后,订单量就突破了1万台[109]。实际上,支付宝一开始计划合作的并非奥比中光,而是成立于2014年底的华捷艾米。而华捷艾米最终和微信站在了一起,并于2019年3月发布了“青蛙”刷脸支付终端。就技术而言,两大刷脸支付终端“青蛙”与“蜻蜓”并没有特别大的区别。2019年5月,云从科技宣布正式发布一款刷脸支付终端产品“CF-FP-E1”[109]。同年8月,云从科技的如意支付Pad作为全国首家,通过了国家标准检测。这些逐渐发展出来的人脸支付产品代表着人脸支付产业在朝着更加标准化的方向发展,如图15所示。
之后众多玩家纷纷各显神通,深度相机硬件商与算法商联合,将方案打包卖给互联网巨头、运营商,这成为上中下游三维传感玩家典型的分工合作玩法。三维硬件和算法厂商们纷纷转而关注人脸支付,和腾讯、阿里等互联网巨头在刷脸支付、刷脸进站、刷脸挂号等场景中浅唱共舞,让三维传感又火了一把。未来,安防、工业应用、智能零售等领域有望带来三维传感技术新的风口。前瞻产业研究院报告显示,到2022年全球人脸识别市场规模将达75.95亿美元,增速达每年20%[111, 112]。此外,阿里和腾讯等企业争夺的不仅是广为人知的餐厅、商场、超市等场景,还有各种公共服务端口及垂直领域。在一些城市,地铁刷脸受到了政府的支持,2019年4月济南已经开始实施三维刷脸进站;医院也成为刷脸终端的栖息地,余杭区医疗已试点“蜻蜓”用于看诊挂号。如果说人脸解锁的兴起,是人与手机设备的一种进一步融合,那么刷脸支付时代的到来,可算是用户和商家关系的再一次重构。顾客从繁杂的支付步骤中获得“豁免”,但同时也把主动权交到了商家手上。在人进入商店被摄像头识别的那刻起,其消费爱好、购物习惯数据就已经被机器调用,至于如何运用这些数据,聪明的营销家永远不会让人失望。而三维传感技术默默在底层技术层面推动了这一切。
如果说依托三维传感技术的刷脸支付正站在风口,那么新的风口在哪里呢?在智能货柜、安防及工业应用领域,“精细化”的三维传感展现出独特的问题解决潜力。虽然在这些方面落地仍有一定的技术难度,但前景却十分宽广。目前已经在商场、高校宿舍、地铁进站口随处可见人脸支付自动柜的身影,如图16所示。然而,目前依然有很多人认为三维传感现在还处于发展的初级阶段,未来还会不断地迭代和提升,将被应用于AIoT等多个领域,有非常大的发展空间。三维传感技术不仅孕育着一个被低估的市场,它也将是未来基建的重要组成部分,为人们带来更加智慧的人工智能,精确安全的人脸支付,身临其境的游戏体验,安全高效的社会运转,更加有温度的虚拟社交等。它还有望颠覆性地改变人与机器、人与人的交互形式,成为无处不在的一种生活方式。
-
散斑结构光三维传感技术的基本原理非常简单,即基于人类的双眼立体视觉原理。在自然界中,同样的景物在不同动物的眼里是有所差异的。大多数食草类哺乳动物,如牛、马、羊等,它们的双眼长在头的两侧,因此具有更广阔的视野(为了更全面地搜索附近是否有危险物种)[113]。但它们的双眼视野完全不重叠,左眼和右眼各自感受不同侧面的光刺激,因此这些动物仅有单目视觉而不具有立体视觉。而人和灵长类动物不同,他们的双眼都在头部的前方,双眼的鼻侧视野相互重叠,因此落在此范围内的任何物体都能同时被双眼所见形成立体视觉(为了更精准地捕获猎物)。当两只眼睛分别形成的物体被转化成神经信号传输到大脑以后,大脑就会对它们进行综合加工处理,主观上可产生被视物体的厚度以及空间的深度或距离等感觉。
有些读者也许会问:为什么必须用两只眼睛才能得到深度?闭上一只眼只用一只眼来观察,也能知道哪个物体离我们近哪个离我们远啊!是不是说明单目相机也可以获得深度?的确,人通过一只眼也可以获得一定的深度信息,不过这背后其实有一些容易忽略的因素在起作用:首先,人本身对自己所处的世界是非常了解的(先验),对日常物品的大小尺寸也有基本预判,因此根据近大远小的常识确实可以推断出图像中物体离我们的远近;其次,人在单眼观察物体的时候其实人眼往往是在不停扫视的,这相当于一个移动的单目相机,这类似于运动恢复结构(Structure from Motion, SfM)的原理[114–116],移动的单目相机通过比较多帧差异确实可以得到深度信息。但相机不是人眼,它只会拍照,不会学习和思考。
图17从原理上展示了单目相机不能感知深度而双目可以的原因。如图所示,红色线条上三个不同远近的绿色的点P、Q、R在下方相机C1上的投影在图像的同一个位置(P1=Q1=R1),因此单目相机无法分辨成的像是远的那个点还是近的那个点,但是它们在一旁的相机C2的投影却位于图像中三个不同位置P2、Q2、R2,因此通过两个相机的观察可以唯一确定到底是空间中的哪一个点。
了解了双目立体视觉的原理,可能还有人会问,那为什么还要再投影散斑结构光呢?很简单,前文中已经提及,想要得到深度信息,必须两只眼睛从两个不同的视角观察到同一个目标点。人眼是个非常神奇的光学系统,它具有“无特征聚焦”的能力,就比如一面白墙,仍然可以对墙上没有任何特征的任意位置聚焦成像。而相机却远没有那么智能了。假设所要测量的物体是一个白色墙面,用两个相机从不同的角度拍摄了如图18所示的两幅图片,计算机是无法判断左图中物体上的A点对应于右图中墙面上的哪个点的。
有了散斑后情况就完全不一样了。由于散斑图案的随机性能够保证局部特征的唯一性,它为场景中的任何一个空间点都打上了一个唯一的标记,如图19所示。通过对左右相机的散斑图像进行局部匹配,就能够建立左右相机的像素一一对应关系,从而可以计算得到物体的视差分布。最终根据视差分布与相机的几何标定参数就能够计算得到物体每个像素的位置和深度信息,进而复原整个三维空间。
-
通过3.1节了解到典型散斑结构光3D传感器首先由红外激光投射器(IR projector)投射出近红外波段的激光散斑,经过物体(如人手或人脸等)反射发生形变后的图案被红外图像传感器接收,最终由算法基于拍摄的图片计算出目标物所处的深度位置。因此,散斑结构光3D传感器至少需要具备散斑投射与接收装置。在基于人机交互的终端产品上,3D传感器还应考虑人体安全和功耗控制等因素,如具备自动开启、人体安全距离感应等功能。图20给出了一个终端红外散斑结构光3D传感器的内部结构实物图,其主要器件从左至右依次为红外散斑投射器(IR dot projector)、距离探测器(Distance detection)、泛光灯(Flood LED)、彩色相机(Color camera),红外相机(IR camera)。相比较技术已经非常成熟的红外/可见光图像传感器,红外散斑投射器是随着散斑结构光3D视觉的发展而出现的新型结构光投射器件[117]。这些器件与后端的3D算法处理器件一起组成了具有3D传感功能的完整设备。
-
红外光投射部分是3D传感器实现3D测量的发起端,负责提供核心的近红外光源,其投射的结构光图像(通常为散斑)的质量对测量结果至关重要。结构光投影器件也是结构光3D测量技术不同于传统被动式3D测量技术的关键所在。正是有了结构光投影器件,使得传统的基于机器视觉的三维测量方法在非接触测量的特性之上,额外增加了全视场、高精度等优点。在数字投影设备出现之前,特殊的编码图案只能通过使用光源照射加工的透明掩膜实现,例如使用二值罗奇光栅实现近似正弦分布的条纹图案投影[119]。这类投影方式限制了结构光投影图案的灵活性。随着数字投影技术的发展,数字投影仪可以将投影图案以图片的形式发送并投射出来。然而数字投影仪成本高昂,体积庞大,并不适于小型化集成。
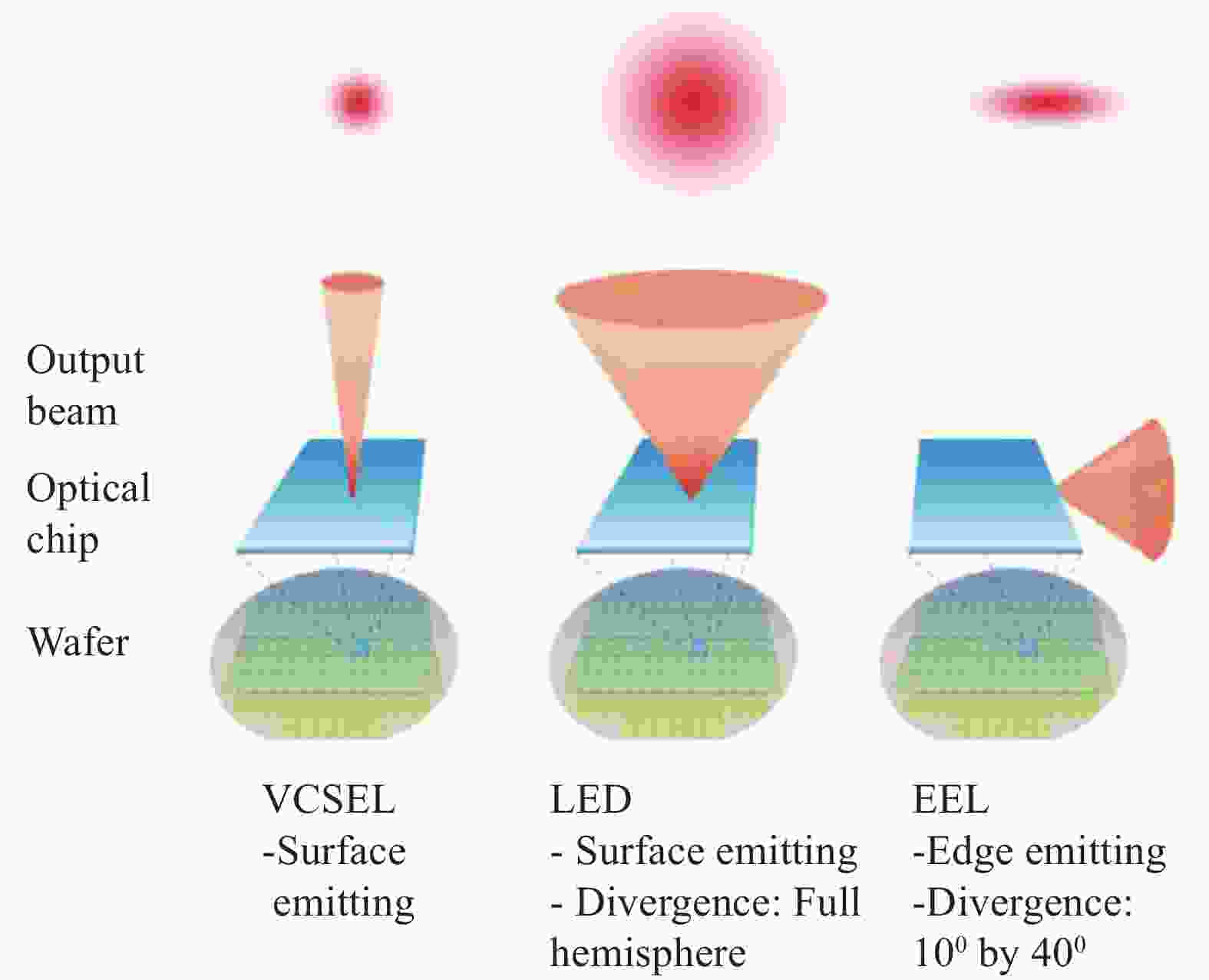
在消费终端设备上,可实现的小型化的红外投射器件多基于半导体激光器开发。与红外发光二极管(LED)相比,红外半导体激光器(Semiconductor laser)具有光发散角小,光能转换效率高,数据传输快等优点[120]。图21给出了三种常见的半导体激光器结构示意图,根据使用的半导体激光器的种类不同,可将红外散斑投射器分为基于垂直共振腔面射型激光器(Vertical-Cavity Surface-Emitting Laser, VCSEL)的投影器件(如图21(a)所示)和基于边发射激光器(Edge Emitting Laser, EEL)的投影器件[121]。其中EEL主要分为分布式反馈型发射激光器(Distributed Feedback EEL, DFB EEL)(如图21(b)所示)和法布里-珀罗型发射激光器(Fabry–Pérot EEL)(如图21(c)所示)两种。将红外发光二极管、红外VCSEL、红外EEL三种类型器件的出光图案进行对比。如图22所示,由于EEL的出射光从器件的侧面出射,光束通常呈椭圆形分布,因此相比之下其光束的均匀性不如VCSEL的出光图案。而LED的发散角较大,因此其出光的单向性不满足结构光的要求。VCSEL是目前最常用的一种激光器类型。红外散斑投射器中除了激光光源外,还包括准直镜和光学衍射器件(Diffractive Optical Element, DOE)。基于EEL的和基于VCSEL的两种投射器中,除了激光光源的种类不同以外,实现散斑投射的方式也是不一样的。EEL投射器的图案由DOE上刻蚀的图案决定,而EEL本身只提供相干光源。VCSEL投射器的图案则是在VCSEL激光器的表面加工形成。DOE的作用是将VCSEL上有限个数的散斑点进行复制并扩散。下面分别介绍基于EEL的和基于VCSEL的两种投射器。

图 21 三种半导体激光器模型(a)VCSEL;(b)分布式反馈型发射激光器;(c)法布里-珀罗型发射激光器
Figure 21. Three semiconductor lasers models (a) VCSEL; (b) DFB EEL; (c) Fabry–Pérot EEL
EEL投射器的激光具有较好的时间相干性与空间相干性。基于光学衍射理论,可以通过DOE的相位调制实现远场光场的强度调制[122-123],如图23(a)所示。

图 23 (a) DOE衍射示意图;(b) EEL散斑投射器示意图
Figure 23. (a) Schematic diagram of DOE diffraction; (b) Schematic diagram of an EEL dot projector
一个EEL投射器的模型如图23(b)所示,EEL的出射光先经过光束整形器扩束,从而使激光束的横截面积可以覆盖后面的衍射元件,再经过准直元件将扩束之后的激光重新调成平行光,随后经过DOE在特定的距离形成所需的光学图案。但由于EEL是侧发光器件,因此在尺寸敏感的产品设计中使用EEL投射器需要使用矫正光路将光线出射方向以及形状进行调整。通常该矫正光路也同时具有准直光路的功能。EEL投影器件的设计难点或者成本主要在于DOE的设计。受制于微加工技术的精度与成本,DOE通常设计成台阶形式,无法实现连续相位的调制。DOE图案的刻蚀阶数越多,衍射图案质量越高,但设计成本也随之增高。另外,由于EEL侧发光的特性导致其性能测试无法在晶圆阶段完成,必须进行切割之后才能检测其质量,故其生产成本相对VCSEL较高。目前EEL投射器在移动端产品或者设备上已经难觅踪影。
VCSEL与EEL所不同的是其激光垂直于顶面射出,且具有极好的均匀性[124]。通过在VCSEL顶层特定位置开孔,可以控制激光出射处的光强分布[125-126]。基于此特性可以将所需散斑图的亮点分布刻蚀在VCSEL的顶层。由于散斑点的密度很大程度上影响3D测量精度,开孔的数量应尽可能多且密。实际上,VCSEL上开孔的尺寸同时受到两方面的制约:一方面,开孔要足够大以保证通光量,提升散斑亮度。另一方面,开口过大将导致开孔平面无法实现稳定的谐振。这样看来,似乎只能增大VCSEL的面积以实现更多的散斑点。然而VCSEL的成本颇受VCSEL的尺寸所影响,增大VCSEL的面积的方式在实际设计生产中并不符合成本要求。
VCSEL投射器获得更多的散斑点其实可以使用具备光束复制功能的DOE来实现。如图24(a)所示的是DOE的光束复制示意图,需要的复制数量可以通过特定的DOE结构实现。VCSEL投射器模型如图24(b)所示。VCSEL顶层开孔处的出射光被准直后照射到DOE上,随后DOE衍射出与入射光完全相同的,照射角度分散的若干个子光线,最终实现散斑点数量的增加。这一方式无疑大大降低了整个投影器件的设计成本。此外,VCSEL和红黄光LED同属于GaAs材料体系,使得厂家可以大幅缩短开发周期。现在移动设备中3D传感的爆发式发展也引发了VCSEL的空前需求。VCSEL被迅速推广和采用的另外一个原因在于每个投射器(或投射器阵列)都可以在晶圆划片之前进行制造和测试。这是VCSEL相比EEL的另一大优势,因为它极大地简化了后端组装测试流程,具有大批量生产的优势[127]。
回到小型化加工这一特定需求,相应的投射器中所需的镜头也需要小型化。因为不论哪种投影器件的激光发出的红外光都需要经过准直镜头,准直镜头利用光的折射原理,将波瓣较宽的衍射图案校准汇聚为窄波瓣的近似平行光。准直镜头可以采用晶元级镜头(Wafer Level Optics, WLO)。所谓WLO是指晶元级镜头制造技术和工艺,用半导体工艺批量复制加工镜头,多个镜头晶圆压合在一起,然后切割成单颗镜头,如图25所示。其具有尺寸小、高度低、一致性好等特点,光学透镜间的位置精度达到nm级,是未来标准化的光学透镜组合的最佳选择。根据传统光学镜头和WLO的性能对比,WLO成本更低、生产效率更高、镜头一致性更好,更适合用于制造准直镜头[128]。
-
在结构光3D传感中,红外摄像头模组用于接收被物体反射的红外光。红外传感器目前主要基于红外CMOS器件,其使用与可见光传感器十分类似。目前结构光3D传感通常使用的红外传感器分辨率在100万像素至200像素之间,相机帧率在30帧每秒,可满足实时测量的条件。实际应用中,红外相机模组的分辨率与最终输出的深度图的分辨率之间存在一定的倍数关系,3D深度图的数据量通常小于原始红外图像的分辨率,一方面原因是由于计算压力较大,高分辨率的3D实时处理需要消耗较多的硬件资源;另一方面是目前3D数据在应用端只当作活体检测的参考,因此其分辨率在原始图像分辨率的基础上进一步压缩也可满足需求。
摄像头所配备光学镜头相比较其他模组也是一个相对比较成熟的部件,其主要参数包含光圈、焦距、景深、视场角等。其需要配合红外窄带滤光片将光线限制在较窄的范围内以排除其他波段,如可见光的串扰。其次是相机镜头的发散角应该与投射器保持一致以保证散斑图充满相机视场的同时,能够在任何深度位置都能拍摄到相同的散斑密度。总体而言,接收端除窄带滤波片较特殊,制造难度较高外,红外传感器和镜头都是较成熟的器件。
-
结构光3D传感器的辅助器件包括彩色相机、距离探测器、泛光灯等。彩色相机的作用主要包括两个方面,一是在消费端作为人脸识别的数据源,二是对输出的3D结果进行色彩渲染。在一些涉及人机交互的3D传感应用中,例如人脸探测与识别,需要使用距离传感器件实现有人靠近时打开设备的功能,这与手机识别人脸靠近从而自动关闭屏幕显示是一个原理。当有人靠近时,距离探测器投射的红外光被人脸反射后被接收器接收。如果反射光强超过了预设的阈值,则开启3D传感功能。传感器上的辅助器件本身不对3D数据产生影响,但可丰富3D传感器的功能,提升使用安全性,降低设备功耗。
-
如上文所述,散斑结构光三维传感器在实现深度测量时有如下三方面的核心步骤:首先,需要设计较为理想的散斑图案向待测场景中投射;然后,对拍摄到的两张散斑图像进行逐像素点匹配;最终,根据匹配结果与标定相机所得到的几何参数计算每个像素的深度,从而获得深度图。下文中详细介绍了这三个方面所涉及到的核心算法:散斑图案设计,散斑相关(视差估计)与三维重建。
-
对于基于散斑投影的三维重建技术,散斑图案的设计是至关重要的。散斑图案的质量会影响后续的散斑相关法的稳定性及三维重构的点云密度及空间分辨率。散斑图案的设计方法可以根据编码域分为:空间编码(单次拍摄)和时间编码(多次拍摄)的方案。市面上大多数流行的3D结构光传感器所采用的散斑图案设计方法都属于空间编码,因为基于空间编码的散斑图案具有天生的全局唯一性,从而使基于散斑投影的三维重建技术具有单幅重建的优势。因此,基于空间编码的散斑图案设计方法的关键性思想是如何保证局部编码在全局图像中的唯一性。空间编码方法有非正规码[42-43],M-array码[44]和De Bruijn编码[39–41]。非正规编码是最早的一类空间编码方法,该方法通常使用繁琐的蛮力搜索算法根据不同的约束以保证图案的唯一性从而生成投影图案。图26显示了根据两种不同的约束生成的投影图。如图26(a)所示,投影图案由白色随机点和一系列长度不同的黑色狭缝组成,其中随机点在每个狭缝上随机分布的切口处形成用于识别每个黑色狭缝。因此,每个狭缝被分成许多小的线段,在相机捕获的图像和待投影的图案之间执行线段匹配即可获得3D数据[43]。如图26(b)所示,投影图案由三种具有不同亮度的像素组成,包括255级灰度,0级灰度和127级灰度。使用不同数量且不同亮度的像素可以产生多种编码序列。例如,一个由72像素组成的序列BWG,WBG,WGB,GWB,GBW,BGW,其中,B、G和W分别由四个0级、127级和255级灰度的像素组成,以便可以容易地依据相关性实现图像匹配,继而重复此72个像素的序列即可创建投影图案[129]。由于没有使用任何正式、标准的编码理论来定义编码图案中每个邻域所表示的码字,因此根据不同的约束,这些编码方法所生成的图案中每个邻域的视觉特征上也是不同的。此外,因缺乏合理的编码原理,基于这种方法所生成的图案可能出现重复的邻域,即不能确保码字的唯一性,因此该类方法缺乏鲁棒性,无法获得理论上的最佳投影图案。
为了解决这一问题,一些研究人员提出基于De Bruijn序列的空间邻域编码方法。De Bruijn序列可表示为
$B(k,n)$ ,是由$k$ 个长度为$n$ 的子序列构成的循环序列,其中每个长度为$n$ 的子序列仅在循环序列中出现一次,如图27所示。基于这种一维的编码规则,许多基于De Bruijn序列的编码方法已经被提出并用来生成具有伪随机特性的投影图案,如多缝(由黑间隙分隔的窄条)[130],多条带(相邻条)[131]和网格图案[132]等。此外,由于投影图案是二维的,因此不限于一维的De Bruijn序列编码规则,二维的De Bruijn序列编码规则也能被用于投影图案设计,即M-array编码,如图28所示。待投影的图案可表示为
$M$ ,其为尺寸为$u \times v$ 的矩阵,其中每个元素均由$m \times n$ 个码字随机组成。为了使$M$ 矩阵具有局部唯一性,即应使每个大小为$m \times n$ 的不同元素恰好仅在$M$ 矩阵中出现一次,则$M$ 矩阵是理想的伪随机图案。基于这些优点,这类基于M-array编码的伪随机图案已被广泛用于基于散斑投影的三维重建技术。接下来,文中针对市面上散斑结构光传感器产品的投影图案进行分析。图29给出了三种市面上散斑结构光传感器所投射出的散斑图案。从这些散斑图案中可以发现一些共同点,如散斑图案的整体亮度较为均匀,具有较好的全局唯一性,每个散斑点之间的间隔有一定的规则。此外,如图29(a)中所示,该散斑图中没有明显的重复子图案,因此该散斑图是基于全局唯一性的编码方式生成的,图案编码的设计规则较为复杂。如图29(b)中所示,该散斑图中由类似九宫格状的子散斑图组成,九宫格中每个格子的子散斑图是相同的,因此该散斑图仅需保证子散斑图具有唯一性。如图29(c)中所示,该散斑图呈明显的重复块状子图案交错分布,每个块状子图案中的散斑图是唯一的,但是由于块状子散斑图呈交错形式排列,因此基于类似M-array编码的方式仍能保证整体散斑图的全局唯一性。此外在M-array编码的基础上,还应根据实际的系统结构来设计散斑图案,如基线距离、相机焦距和工作距离等系统参数可以共同确定测量系统的视差约束,这些编码规则都将促进生成高质量的散斑图案。
-
常见的散斑结构光传感器具有两种系统结构:单相机(单目,即只有一个红外摄像头)与双相机(双目,即有两个红外摄像头)。对于双目结构的基本原理之前已经进行了详细讨论。由于可以同时拍摄物体获取左右原始散斑图,因此可以直接对两张散斑图像进行逐像素点匹配来获得它们之间的视差图。上述过程中所涉及到的核心算法就是基于局部窗口的图像相关技术。如图30所示,对于左图中的一个像素点(左图中红色方框中心),在右图中从左到右用一个同尺寸局部窗口内的像素和它计算相似程度,相似度的度量有很多种方法,常用的相关函数有零均值归一化互相关函数(ZNCC)、零均值归一化差平方和函数(ZNSSD)等,它们的计算公式见表1和表2[133]。图30中下方的ZNCC曲线显示了相关计算结果,相关度最大的位置对应的像素点就是最佳的匹配结果。
值得注意的是,基于局部窗口的图像相关技术的运算过程是比较复杂耗时的,因为里面涉及到元素的多次相乘与累加。如果对于每个图像点的搜索都要完全遍历另一幅图像整个二维视场,那么算法的整体计算量更是难以想象。通常解决这一问题的方式是让两个相机尽可能地水平放置(比如在同一平面上左右放置),使得两个视图的散斑图像处于同一水平线上,从而直接采用一维行搜索即可,不仅大幅缩减了匹配算法的搜索区间,还降低了误匹配的概率。当然由于制造工艺、加工装调精度所限,两个相机之间可能难以保持完全水平。因此,通常还可以通过对双目立体视觉系统进行标定,利用标定数据对采集到的散斑图像进行极线校正,使得两个视图的散斑图像处于同一极线上,从而也可使二维搜索简化为一维搜索,如图31所示。假设已知正确的对应参考点,则参考点与待匹配点之间的关系为:
$$({x_r} + d,{y_r}) = ({x_t},{y_t})$$ (1) 式中:
$d$ 代表参考点与待匹配点之间的视差值。表 1 基于互相关准则的匹配函数
Table 1. Matching function based on cross-correlation criteria
CC correlation criterion Definition Cross-correlation (CC) ${C_{CC}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {[f({x_i},{y_i})g(x_i',y_j')]} } $ Normalized cross-correlation (NCC) ${C_{NCC}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {[\dfrac{{f({x_i},{y_i})g(x_i',y_j')}}{{\bar f\bar g}}]} } $ Zero-normalized cross-correlation (ZNCC) ${C_{ZNCC}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {\left\{ {\dfrac{{\left[ {f({x_i},{y_i}) - {f_m}} \right] \times \left[ {g(x_i',y_j') - {g_m}} \right]}}{{\Delta f\Delta g}}} \right\}} } $ 表 2 基于SSD相关准则的匹配函数
Table 2. Matching function based on SSD-correlation criteria
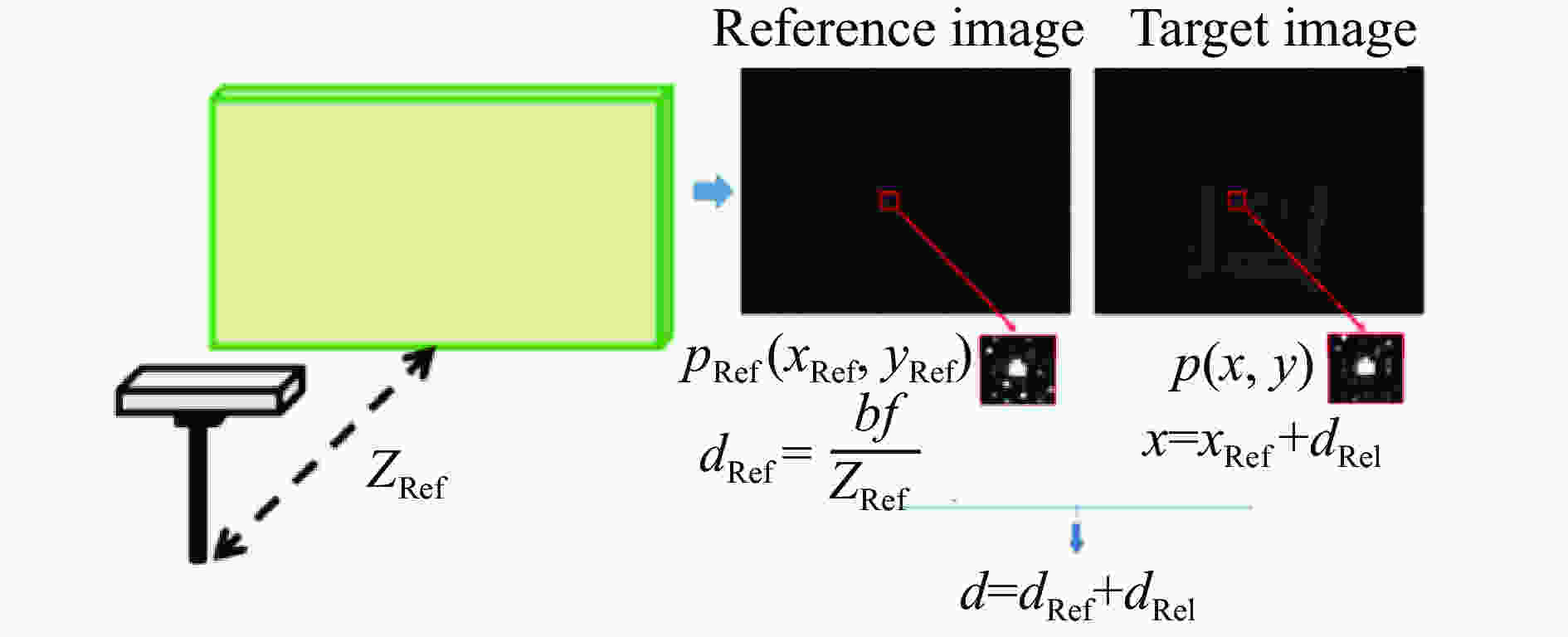
SSD correlation criterion Definition Sum of squared differences (SSD) ${C_{SSD}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {{{[f({x_i},{y_i}) - g(x_i',y_j')]}^2}} } $ Normalized sum of squared differences (NSSD) ${C_{NSSD}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {{{\left[ {\dfrac{{f({x_i},{y_i})}}{{\bar f}} - \dfrac{{g(x_i',y_j')}}{{\bar g}}} \right]}^2}} } $ Zero-normalized sum of squared differences (ZNSSD) ${C_{ZNSSD}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {{{\left[ {\dfrac{{f({x_i},{y_i}) - {f_m}}}{{\Delta f}} - \dfrac{{g(x_i',y_j') - {g_m}}}{{\Delta g}}} \right]}^2}} } $ 对于单目相机系统,理解起来可能要稍微麻烦一点。仅能获得单一视角的散斑图,那么该如何进行双目匹配呢?根据光路可逆原理,可以将散斑投射器看作是一个“逆相机”,设计好的投影散斑图就是这个逆相机所能拍摄到的图像,而物体其实可以理解为表面被喷涂上了扭曲的散斑。如果把散斑投射器换成光学系统完全一致的相机,它所拍摄到的恰好是那幅设计好的没有扭曲的投影散斑图。所以只需要将投影仪当作逆向的相机来进行标定,然后将单幅测量得到的散斑图与所设计的投影散斑图相匹配即可。但这种方式存在两方面问题:(1) 一般考虑到成本、体积等因素,结构光3D传感器里的散斑投射器并不算是一个完整的数字投影仪,因此散斑投射器的成像模型很难以参数化的形式表示,从而对其标定起来往往比较困难,难以获得散斑投射器的标准标定参数。由于这些原因,因此散斑投射器一般很难完美地等效于一个“逆相机”,即单目相机系统不能近似为双目相机系统,所以不能利用双目相机系统的原理计算得到被测场景的深度信息。(2) 由于光学系统离焦、物体表面反射率等影响,设计的散斑图与实际拍摄的散斑图往往存在一定差异,比如分辨率,畸变,像素尺寸等等。这些因素都会导致十分糟糕的匹配结果,从而影响到最终的深度测量结果。因此,另一种可行的方案是预先在所测量的深度范围内沿着z轴平移以获取一系列参考散斑图像,然后将相机所获取的散斑图像与这些已知距离的标准平板散斑图像之间进行直接匹配,如图32所示。在这种情况下,在恒定且已知的距离
${Z_{\rm{Ref}}}$ 所获取的散斑图像称为参考图像,因此可以按以下公式计算参考图的参考视差值${d_{\rm{Ref}}}$ :$${d_{\rm{Ref}}} = \frac{{bf}}{{{Z_{\rm{Ref}}}}}$$ (2) 
图 31 双目立体视觉系统中一维匹配的原理与流程。(a) 基本原理;(b) 匹配流程
Figure 31. Principle and process of one-dimensional matching in binocular stereo vision system. (a) Basic principle; (b) Matching process
然后,同样地对于相机捕获的目标图像中每一个有效的匹配点
$p(x,y)$ ,通过相关函数可以在参考图像中找到相关值最大的对应参考点${p_{\rm{Ref}}}({x_{\rm{Ref}}},{y_{\rm{Ref}}})$ ,$p(x,y)$ 与${p_{\rm{Ref}}}({x_{\rm{Ref}}},{x_{\rm{Ref}}})$ 之间的关系为:$$(x,y) = ({x_{\rm{Ref}}} + {d_{\rm{Rel}}},{y_{\rm{Ref}}})$$ (3) 式中:
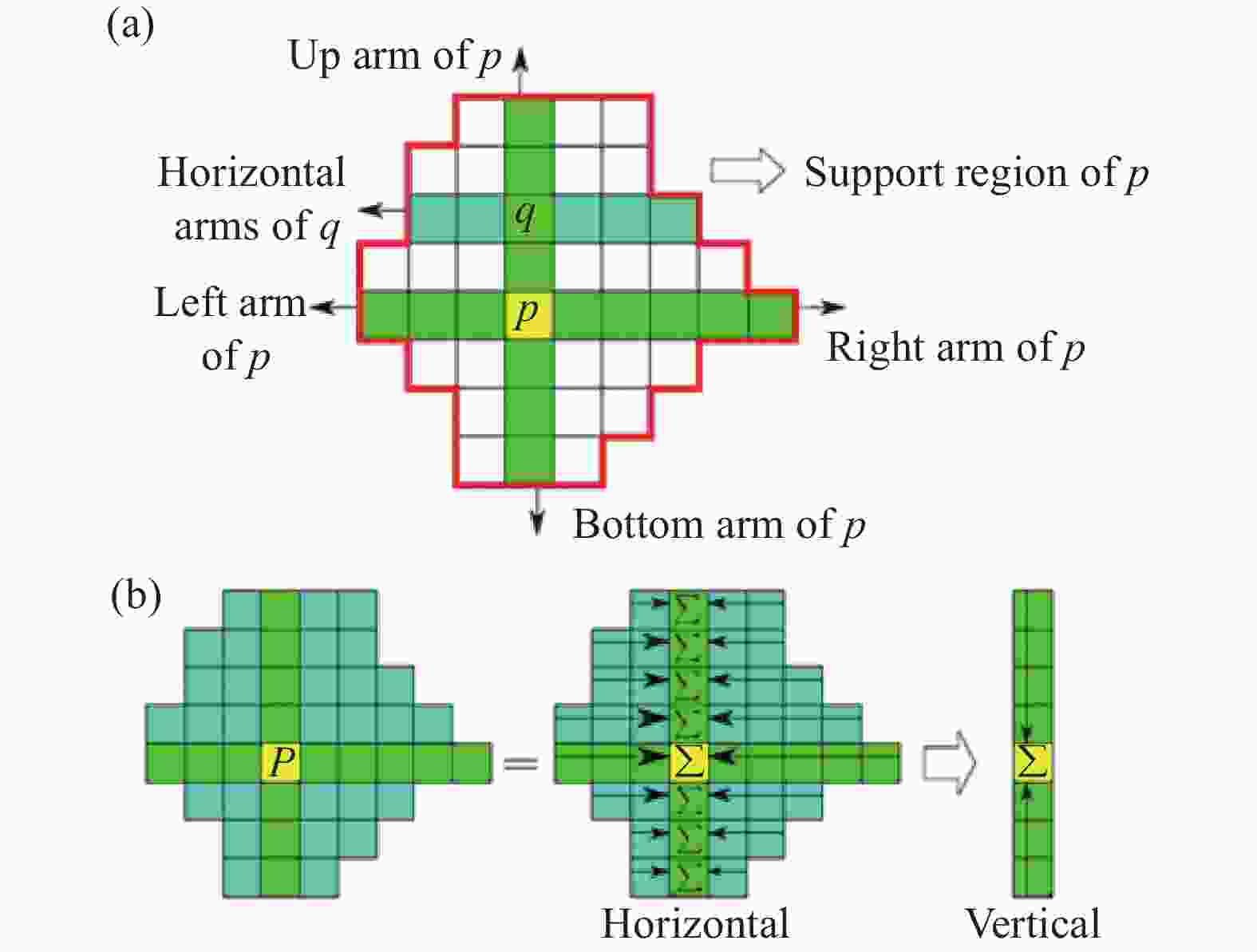
${d_{\rm{Rel}}}$ 为目标图像相对于参考图像的相对视差值。从而可以以这一方式获得每个有效目标点的实际视差值$d$ :$$d = {d_{\rm{Ref}}} + {d_{\rm{Rel}}}$$ (4) 上述算法在具体操作中还有很多实际问题值得注意,例如:通过相关函数仅能计算出具有整像素精度的视差值,这在一定程度上限制了深度量化分辨率。因此,可以通过诸多子像素优化技术来改善这些估计,尽管它们增加了计算复杂度,如成本聚合[134-135]、半全局匹配[136]、五点拟合算法[137]和左右一致性检验。如图33所示,通常在基于局部图像的匹配算法之后,对一个支持窗口内的匹配成本进行聚合从而得到参考图像上一点
$p$ 在视差$d$ 处的累积成本$CA(p,d)$ ,这一过程称为成本聚合。通过匹配成本聚合,可以降低异常点的影响,提高视差图的信噪比进而提高匹配精度。代价聚合策略通常是局部匹配算法的核心,策略的好坏直接关系到最终视差图的质量。如图34所示,在执行匹配成本聚合后,为了进一步减轻匹配的歧义性,应采用具有平滑度约束的多方向扫描线优化方法,即半全局匹配。这里考虑使用参考图像上一点$p$ 的邻域视差数据来构造惩罚函数以增加视差图的平滑性。在半全局匹配方法中,一般地,使参考图像上一点$p$ 的单个方向上能量最小化,并在多个方向上重复(一般是四个方向或十六个方向),然后通过平均得出最终结果。另一方面,局部窗口尺寸选择也是很有讲究的[138]。图35显示了不同尺寸的局部窗口对深度图计算结果的影响。从图中也不难发现:小尺寸的窗口:精度更高、细节更丰富,但是对噪声特别敏感;大尺寸的窗口:精度不高、细节不够,但是对噪声比较鲁棒。此外,窗口越大,计算量也会相应的增加,从而大大延长运算时间。此外,不同匹配代价的处理能力也各自不同,而复合代价能够使它们相互补充,提高算法稳定性。例如,对于基于census变换的匹配函数,它容易在具有重复局部结构的区域中产生错误的匹配,而基于AD的匹配函数无法处理大型无纹理区域。而复合的ADcensus匹配函数能成功减少由单个匹配函数引起的误差[134]。但是,如何确定各个匹配成本的权重依然是一个值得考虑的问题。

图 35 不同尺寸的局部窗口对视差图计算结果的影响
Figure 35. Effect of local windows with different sizes on the calculation results of disparity maps
除了基于局部窗口的立体匹配方法外,另一种比较主流的方法是全局立体匹配的方法。全局立体匹配算法主要是采用了全局的优化理论方法估计视差,建立一个全局能量函数,其包含一个数据项和平滑项,通过最小化全局能量函数得到最优的视差值。其中图割(Graph Cuts, GC)[139]、置信传播(Belief Propagation,BP)[140]、动态规划(Dynamic Programming, DP)[141-142]等优化算法都是常用的求解能量最小化的方法。全局匹配算法一般定义如下能量函数:
$$\begin{gathered} E(d) = {E_{\rm data}}(d) + {E_{\rm smooth}}(d) \\ = \sum\limits_{p \in R} {C(p,d)} + \sum\limits_{q,p \in R} {P({d_q} - {d_p})} \\ \end{gathered} $$ (5) 式中:
${E_{\rm data}}(d)$ 描述了匹配程度;平滑项${E_{\rm smooth}}(d)$ 体现了场景的平滑约束;$C(p,d)$ 是匹配成本;$P({d_q} - {d_p})$ 是点$p$ 和$q$ 的视差之间的函数,一般称之为惩罚项,当点$p$ 和$q$ 的视差不相等时,$P({d_q} - {d_p}) > 0$ ,且与两者差值越大,$P({d_q}\! -\! {d_p})$ 值越大。当点$p$ 和$q$ 的视差相等时,$P({d_q} \!-\! {d_p})\! =\! 0$ 。由于全局匹配算法在数学上是一个能量函数的优化问题,因此可以找到最优解。但是,这个问题被证明在二维空间是NP-hard的。因此,虽然全局算法具有准确性较高的优点,但其计算速度非常慢,在实时性要求高的场合不适合使用全局立体匹配算法。 -
无论是双目系统还是单目系统,一旦相机捕获到的目标图像中的所有有效像素的视差值被计算得到,就可以执行三维重建操作实现计算深度图。首先,从理想的双目相机成像模型开始分析:假设左右两个相机位于同一平面(光轴平行),且相机参数(如焦距
$f$ )一致。在获取到具有亚像素精度的视差图后,通过三角测量关系如图36所示,可获得三维目标点$P(X,Y,Z)$ 的深度值$Z$ :
图 36 基于双目视觉系统的三角测量模型示意图
Figure 36. Schematic diagram of triangulation measurement model based on binocular vision system
$$Z = \frac{{Bf}}{d}$$ (6) 式中:
$B$ 为测量系统的基线距离;$f$ 为相机的焦距。对于双目相机系统,基线距离为两个相机的物体光心之间的水平距离。对于单目相机系统,基线距离则为相机和点阵投射器的物体光心之间的水平距离。这些参数可以通过相机标定获得。接下来介绍相机的标定模型。相机是基于结构光的3D成像系统的重要设备。图37所示即为相机的针孔模型,在该模型中,总共存在四个坐标系:图像像素坐标系
$O{\rm{ - }}uv$ ,图像物理坐标系$O'{\rm{ - }}xy$ ,相机坐标系${O_c}{\rm{ - }}{x_c}{y_c}{z_c}$ 以及世界坐标系${O_w}{\rm{ - }}{X_w}{Y_w}{Z_w}$ 。图像像素坐标系是以相机CCD面阵左上角的像素为坐标原点,单位是pixel;图像物理坐标系一般是以相机CCD面阵中间的某一个点为坐标原点,单位为mm;相机坐标系以光学镜头的中心作为坐标原点,光轴经过坐标原点${O_C}$ 垂直于镜头平面;世界坐标系则是在标定过程中自定义出来的一个坐标系,单位是mm。假设在世界坐标系下有一个点
$P$ ,其在世界坐标系下的坐标为$({x_w},{y_w},{z_w})$ ,其在相机相机坐标系下的坐标为$({x_c},{y_c},{z_c})$ 。根据针孔成像模型,点$P$ 在CCD面阵平面上的透视投影点${P'}$ 为该点与透镜中心点${O_C}$ 的连线跟CCD面阵平面的交点。点${P'}$ 在图像像素坐标系和图像物理坐标系下的坐标分别$(u,v)$ 、$(x,y)$ 。它们存在如下关系:$$\left[ \begin{gathered} u \\ v \\ 1 \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{s_x}}&0&{{u_0}} \\ 0&{{s_y}}&{{v_0}} \\ 0&0&1 \end{array}} \right]\left[ \begin{gathered} x \\ y \\ 1 \\ \end{gathered} \right]$$ (7) 式中:
${s_x}$ 和${s_y}$ 为图像像素坐标系下分别在$u$ 轴和$v$ 轴方向上的像素密度,单位为pixel/mm。$({u_0},{v_0})$ 为光轴与相机CCD平面交点${O'}$ 的像素坐标系坐标,表示两个坐标系之间的偏移量。在利用标定板标定相机时,会自定义一个三维空间中的世界坐标系,该坐标系的X-Y平面就是标定板所在的平面,垂直于标定板平面的方向即是该坐标系下的Z轴方向。假设该世界坐标系变换到相机坐标系的旋转矩阵和平移矩阵分别为
$R$ 、$T$ ,则点$P$ 的世界坐标系坐标$({x_w},{y_w},{z_w})$ 转化为相机坐标系坐标$({x_c},{y_c},{z_c})$ 的转换关系可表示为:$$\left[ \begin{gathered} {x_c} \\ {y_c} \\ {z_c} \\ 1 \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} R&T \\ 0&1 \end{array}} \right]\left[ \begin{gathered} {x_w} \\ {y_w} \\ {z_w} \\ 1 \\ \end{gathered} \right]$$ (8) 通过针孔成像模型的比例关系获得:
$${z_c}\left[ \begin{gathered} x \\ y \\ 1 \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} f&0&{{u_0}}&0 \\ 0&f&{{v_0}}&0 \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R&T \\ 0&1 \end{array}} \right]\left[ \begin{gathered} {x_w} \\ {y_w} \\ {z_w} \\ 1 \\ \end{gathered} \right]$$ (9) 联立以上三个公式,不难得出世界坐标系跟图像像素坐标系之间的数学转换关系:
$${z_c}\left[ \begin{gathered} x \\ y \\ 1 \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{f_x}}&0&{{u_0}}&0 \\ 0&{{f_y}}&{{v_0}}&0 \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R&T \\ 0&1 \end{array}} \right]\left[ \begin{gathered} {x_w} \\ {y_w} \\ {z_w} \\ 1 \\ \end{gathered} \right]$$ (10) 式中:
${f_x} = f{s_x}$ ,${f_y} = f{s_y}$ ,旋转矩阵$R$ 和平移矩阵$T$ 是外部参数,由相机的空间位置和标定过程中自定义的世界坐标系的空间位置之间的相对位置决定。因此,对于双目立体视觉系统,当已知两个相机的标定参数和两个相机之间每个像素的匹配点对后,由于每一匹配点对对应着世界坐标系中同一点,因此可以通过公式(10)求解出物体的三维信息。 -
前面几个小节已对结构光3D传感器的相关原理、关键器件、核心算法进行了介绍。器件的设计与选型需要基于测量的原理来设计,而算法的顺畅运行则需要合适的算法平台作为支撑。此节对小型化结构光3D传感器算法平台所涉及的硬件系统架构进行介绍。
一个典型的3D结构光传感器的系统构架如图38所示,可以根据具体功能划分为以下四个主要部分:彩色相机、红外相机、红外投射器、算法平台。算法平台以外的部分文中已经谈及,此节主要针对算法平台进行介绍。
算法平台主要负责将获取的散斑图或者其他包含结构光信息的图片进行处理以获取场景的3D深度信息。其主要完成三个功能:一是驱动彩色相机、红外相机,以及红外投射器正常工作(参考图38中的链路关系);二是接收彩色相机和红外相机数据进行深度图像处理;三是将计算出来的深度数据输出。
目前主流的移动端结构光3D传感器多基于散斑相关算法求解深度信息,因此3D数据的获取都需要大量的运算。基于PC端的算法计算可以通过GPU并行计算实现加速。如今面对市场上移动端设备对3D测量的需求,3D传感器厂家设计研发了专用的ASIC芯片以专门支持基于散斑图相关的算法,如奥比中光的MX系列芯片、华捷艾米的IMI系列芯片等。围绕自主设计研发的3D感知芯片,配合相应的数据传输接口即组成了算法平台所涉及的完整硬件系统架构。
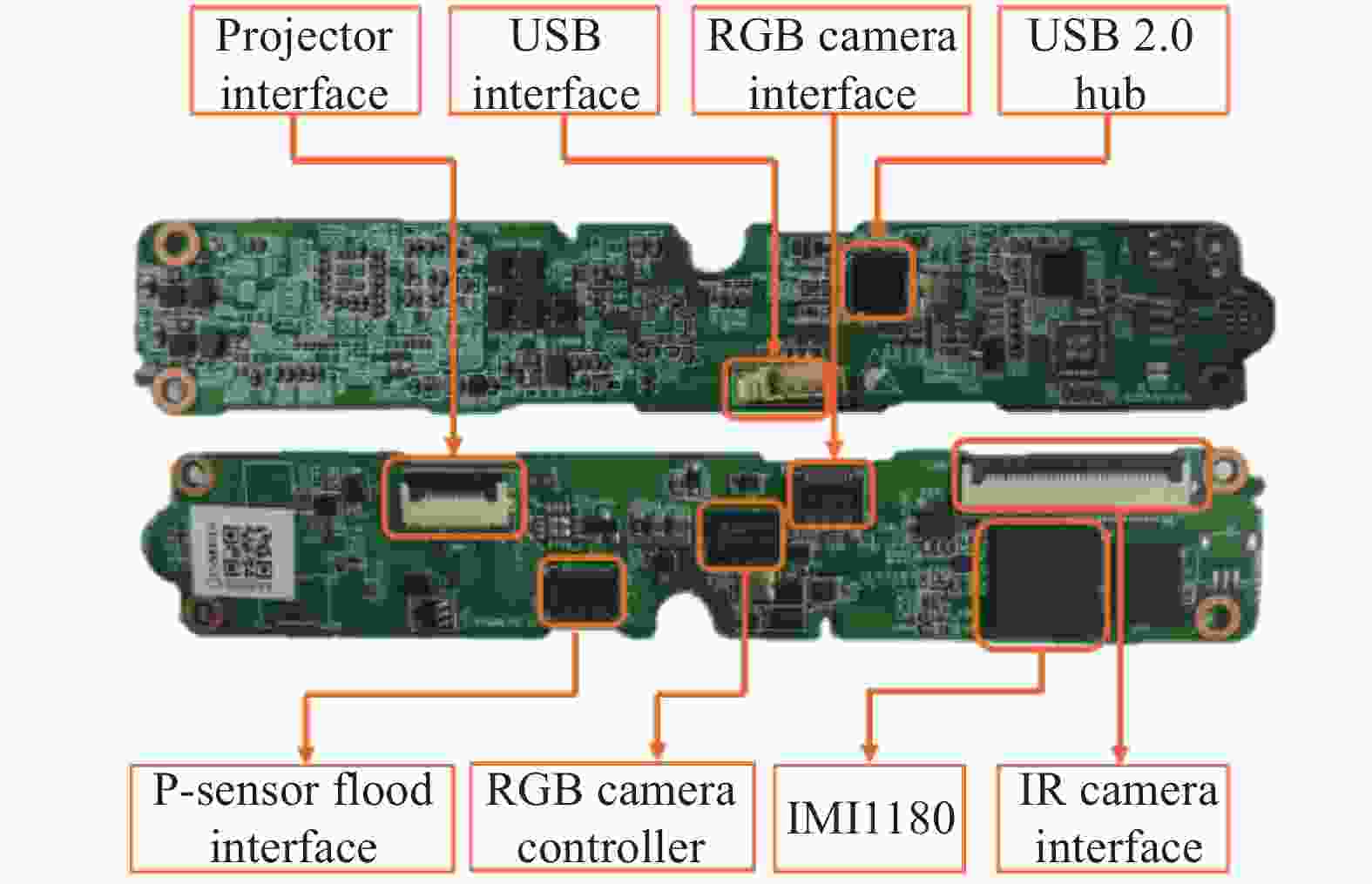
文中以华捷艾米的一款产品为例介绍其硬件系统架构,如图39所示。其中IMI1180是针对深度图像处理算法设计的芯片,该芯片不仅支持红外与彩色摄像头数据输入,而且集成了USB2.0控制器,能够驳接不同的硬件平台。硬件平台输出的数据通过USB Hub传出,方便后续功能开发使用。随着3D传感器市场的逐渐扩大,其相关设备的出货量也稳步增长,芯片研发的高投入也将获得回报。
此外通用的开发平台,如FPGA同样可以实现3D实时的运算处理,但由于其成本较高以及芯片供应依赖进口等问题限制了基于该平台的3D传感器的大批量生产的能力。当然,面对快速发展的3D传感器市场,选取通用开发平台进行前期验证与小规模打样仍然是一种普遍的选择。此外,小型企业也可以通过通用的硬件平台快速实现移动端设备的开发。以如图40所示的图漾科技的一款设备为例,其使用了FPGA芯片作为算法运行的硬件平台。与自主研制的专用算法芯片相比,由于通用硬件平台往往具备可重复编程的功能,因此算法具有可升级的可能。从图40中可以看出,该款设备使用了Intel公司的飓风5代FPGA芯片作为算法平台,该平台内嵌了通用的相机驱动接口,故IR Camera与RGB Camera可以直接连接到FPGA的通用I/O上。这不仅省去了专用相机驱动芯片的成本,也大大减轻了硬件开发人员的工作量。由于FPGA本身不具备与其他硬件平台通信的能力,故需要配合USB 2.0控制器(如CY68013A等)将算法输出的结果传出。
-
3D传感技术的主要特征在于不仅可以获取被测对象的平面图像,还可以获取到被测对象的深度信息,即三维的尺寸信息及具体位置,通过3D相机获取到的数据,能准确知道图像中每个点离摄像头距离,这样再加上该点在2D图像中的横向坐标,就能获取图像中每个点的三维空间坐标。通过三维坐标就能还原真实场景,实现场景建模等应用,其通常的组成结构为多个摄像头+深度传感器。3D摄像头可实现实时三维信息采集,为消费电子终端加上了物体感知功能,从而能被应用于多个“痛点型应用场景”,包括人脸识别、手势识别、人体骨架识别、三维测量、环境感知、三维地图重建等数十项功能,可广泛运用于电视、手机、机器人、无人机、物流、VR/AR、智能家居安防、汽车驾驶辅助等领域。
自2012年以来,3D视觉便受到全球各大科技巨头的重视,包括苹果、微软、英特尔、谷歌、索尼、三星等公司,如2012年左右,微软收购了3D-ToF相机公司canesta和3dv;2013年,英特尔推出RealSense实感技术,谷歌推出Project Tango项目,苹果收购结构光先驱PrimeSense;2015年索尼收购了3D视觉综合技术供应商SoftKinetic,Facebook旗下Oculus 收购3D手势识别公司Pebbles,苹果先后收购了Linx、Faceshift、Emotient、Flyby Media、RealFace等多家公司。作为全球消费电子的王者,苹果公司在3D视觉各个方面都进行了深度的布局,一方面收购行业内优秀的公司,进行技术布局和生态建设,另一方面不断优化技术,发布专利,进行专利布局。笔者等认为苹果移动端3D视觉技术已经进入成熟期,具备了大规模进入移动终端的基础,在苹果等科技巨头的带动下,3D视觉将打开消费级市场,行业进入加速趋势,特别是人脸识别、人机交互、场景建模典型应用将率先脱颖而出,市场空间有望迎来爆发式增长!根据研究机构Zion Research预测数据,3D摄像头市场规模将从2015年的12.5亿美元增长到2021年的78.9亿美元,年均增长率达35%!按2021年18亿部智能手机40%的渗透率来算已经超过100亿美元市场空间,加上在AR、自动驾驶、机器人等领域应用,整个3D摄像头市场空间实际有望超过200亿美元[145]。该节介绍了散斑结构光三维传感技术的典型应用。
-
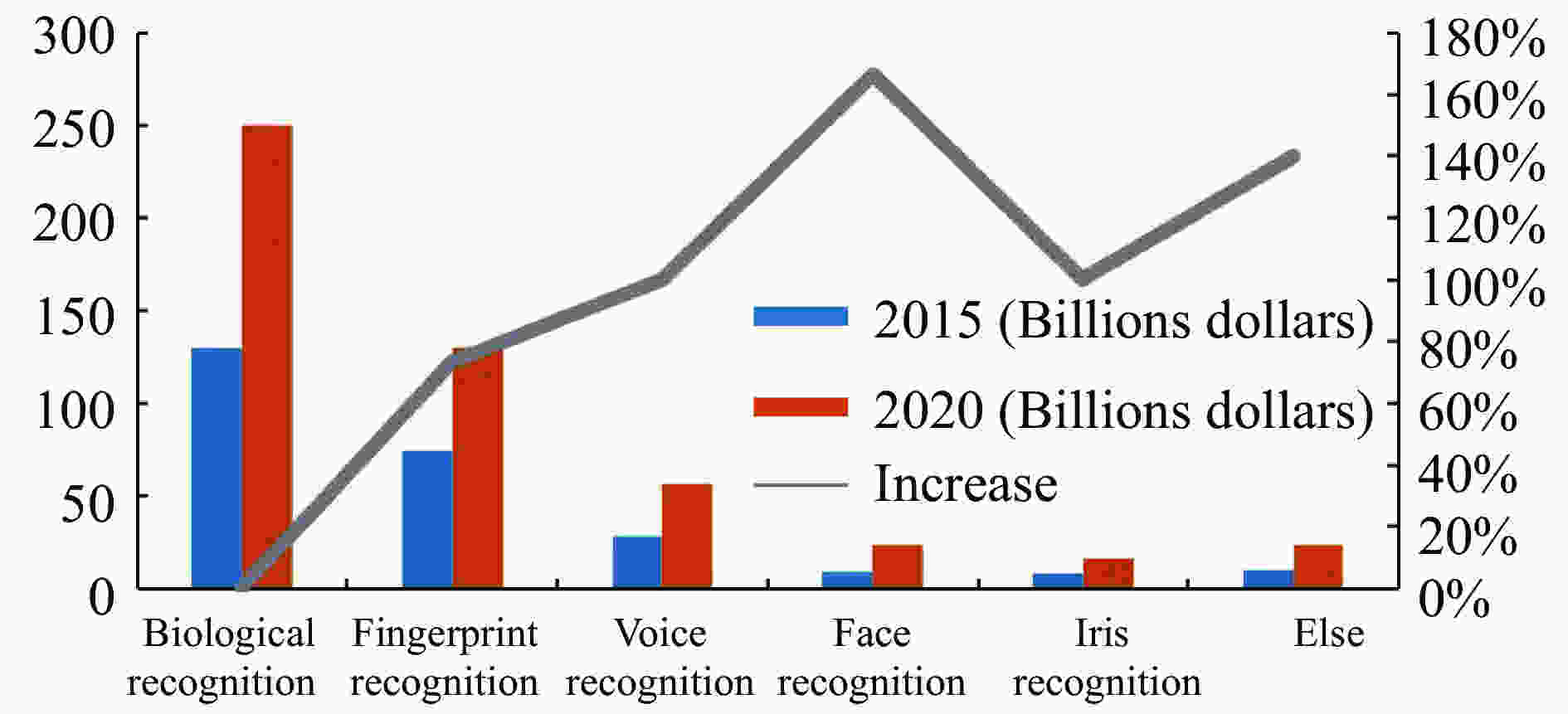
苹果公司于2013年发布苹果系列首款指纹识别功能手机iPhone 5s,并引发追随,大量手机厂商开始搭载指纹识别技术;三星公司于2016年发布首款搭载虹膜识别手机Samsung Note7。至此,应用于智能手机终端的生物特征识别技术趋于多元化,应用覆盖面进一步扩大。从指纹识别到虹膜识别,生物识别被更多的消费电子厂商采用,大家对于技术的探讨进入白热化,但技术的比较意义不大,市场才能说明一切。根据2016~2022年中国人脸识别市场现状分析及未来发展趋势报告可知,2007~2013年六年期间,生物识别技术的全球市场规模年均增速为21.7%,这在全球大部分行业增长率不到5%的对比下实属罕见。2015年生物识别技术全球市场规模将达到130亿美元,2020年将达到250亿美元,5年内平均增速约14%[146]。
2015~2020年,各细分行业市场规模增幅率分别为:指纹(73.3%)、语音(100%)、人脸(166.6%)、虹膜(100%)、其他(140%)[147](见图41)。由于指纹识别技术起步最早,因此占领着生物识别技术的绝大多数市场份额。但是,随着其他生物识别技术的快速发展,指纹识别的市场占有率整体呈下降趋势,在这众多生物识别技术中人脸识别在增幅上居于首位,预计如果终端消费电子厂商大量采用脸部识别,两年内能够接近指纹识别的市场占比。
从商业角度看,支付宝、券商、银行为主的金融服务机构已经开始大量采用脸部识别开户、转账、付款等,截至目前,可以举例多家机构在脸部识别方面的应用。2015年3月15日,在德国汉诺威国际信息及通信技术博览会开幕式上,阿里巴巴集团董事局主席马云展示了SmiletoPay扫脸技术,利用“刷脸支付”从淘宝网上购买了1948年汉诺威纪念邮票。腾讯紧随其后,在4月腾讯财付通与中国公安部所属的全国公民身份证号码查询服务中心达成人像比对服务的战略合作。2015年10月15日,招商银行15日宣布推出“ATM刷脸取款”业务,将“刷脸”应用到ATM渠道。此外脸部识别也已经渗透银联、京东钱包等重要客户。
目前人脸识别市场的解决方案主要是二维人脸识别,但由于人的脸部并非平坦,因此二维人脸识别在将三维人脸信息平面化投影的过程中存在特征信息损失。三维人脸识别使用三维人脸立体建模方法,可最大程度保留有效信息,因此三维人脸识别技术更为合理并拥有更高精度。以散斑结构光为代表的3D摄像头技术与人脸识别技术需求最为匹配。首先,3D摄像头采用红外线作为发射光线,能够解决可见光的环境光照影响问题。传统的2D识别技术在环境光照发生变化时,识别效果会急剧下降,无法满足实际系统的需要。比如拍照时遇到侧光时出现的“阴阳脸”现象(见图42),这样可能导致无法正确识别。而3D摄像头技术进行拍摄时采集得到人脸图像深度信息,能够获取更多的特征信息在传统人脸识别技术基础上大幅提升识别准确率,如图43所示。3D人脸识别能够采集眼角距、鼻尖点、鼻翼点、两个太阳穴之间的距离、从耳到眼的距离等深度特征信息,并且这些参数一般不会随着一个人整容、换发型而发生较大变化,因而3D人脸识别能够在用户特征发生变化时继续保持极高的识别准确率。
-
回顾人机交互发展,它实际上是一段不断改造机器解放人的历程。现如今,大尺寸触控显示屏已经是大多数智能终端的标配。但是,触控显示屏的局限性非常明显:手指必须接触于屏幕表面,无法离开屏幕工作,这极大地限制了用户的使用空间和灵活性。语音识别可以完全解放双手,但是在人机互动方面的应用场景有一定的局限性,对于游戏娱乐、VR/AR等领域,这些必须有用户肢体参与的场景,语音交互无法满足的需求。要实现体感交互,最重要的是手势识别。而三维传感器技术正响应了手势输入的需求,利用3D摄像头获取影像深度信息,通过算法处理对用户手势进行识别,从而实现用户手势输入。
在电影《少数派报告》中,汤姆·克鲁斯扮演的角色站在虚拟屏幕前,不用触摸任何实质的东西,仅靠一个特殊手套就能隔空操控数据。虽说电影中的场景是虚构的,但“隔空操控”的人机交互场景,却可以真实发生在我们身边。2013年,手势识别初创公司Leap Motion发布了体感控制器产品,引发了无数科技爱好者的追捧[149-150],如图44所示。2015年初,微软发布了Hololens头显[151],其中的手势交互设计令人惊艳,在用户体验和应用场景方面带来了颠覆性的改变。
随着更多的商业化应用案例的出现,手势识别以及无触碰感知系统预计将达到最快的增长速度。市场分析公司Markets and Markets发表报告称,“手势识别和无触碰感知”市场到2024年将达到340亿美元的市值[152]。报告显示手势识别市场的增长主要还是依靠智能手机来驱动。目前,已经有一些手机开始集成这方面的功能,比如华为的Mate30。上下挥手滑动浏览页面,隔空一抓即刻截取屏幕,可以让用户无需接触显示屏的情况下,便可通过挥手等对手机进行各种操作。
-
虚拟现实(Virtual Reality, VR)和增强现实(Augmented Reality, AR)的出现打破了真实与虚拟的界限,人们不仅希望能够体验电脑模拟的奇幻虚拟场景,也希望足不出户就能领略世界各地的美景。VR通过复制现实世界构建与外界隔断的虚拟空间,而AR将虚拟信息与真实世界融合将文字、图像、音乐、视频等虚拟信息放入真实世界。近来大热电影《头号玩家》就是一种在虚拟现实中用真实场景塑造的沉浸式体验。随着VR/AR技术的不断成熟,以及VR/AR产品的不断普及。2017年全球VR/AR的投资总额受VR/AR的迅速发展所带动达到了29亿美元[153],如图45所示。全球VR/AR行业也在资本加持中发展壮大。到2021年,全球VR/AR市场规模将达到1 080亿美元[153]。
不管是VR还是AR,都需要将实体场景进行数字化,这需要借助摄像头扫描现实物体,从而构建虚拟的图像画面。基于传统的2D摄像头通过不同角度的二维图像重建场景中的三维模型,真实感低;传统的三维建模需要较高的时间及人力成本。而3D摄像头的出现则解决了以上问题,使得三维重建效率、效果有了很大提升。3D摄像头能同时获得场景的色彩信息和深度数据,并基于此进行三维重建。目前,3D场景建模,在房产、旅游、电商等行业已经逐渐开始应用。图46所示的是众趣科技团队基于3D传感技术研发的一款消费级3D相机—“空间猎者N500”[154]。该产品可以在数十分钟内完成一套三居室的数据采集。用户可以通过手机步入房间任意漫游,体验虚拟入住。

图 45 2013~2017年全球VR/AR行业投资规模统计(单位:亿美元)
Figure 45. Statistics of global VR/AR industry investment in 2013-2017 (Unit: USD 100 million)
当然,3D结构光传感器技术不仅局限于这三个方面,其还能够被应用于实时监控车上所有人员的生命体征,防驾驶人瞌睡,让行车更安全。当检测驾驶员有困倦或注意力不集中时能立即做出响应,甚至启动紧急制动系统,此外配合雷达,还可以提供精准的路面状况信息,避免车祸的发生。利用高精度3D结构光传感器技术也可以实现高精度3D表面和几何检测,检测到小型电子元器件的微小特征,在高速生产过程中实现三维质量控制等,由于篇幅原因这里就不再举例赘述。
-
目前为止,散斑结构光三维测量的基本原理与理论问题都已得到了较好的解决,发展到了成熟阶段,算法层面引入的较大计算量也可以通过专用的处理芯片解决。在笔者看来,现如今散斑3D结构光传感器在消费级市场的进一步发展与应用主要面临以下几个方面的挑战。
-
散斑结构光相关方法的核心技术在于局部窗口匹配,即选取合适的窗口尺寸,基于窗口内的强度分布在其他图片中搜寻匹配区域。正如之前所讨论的,窗口的选取很大程度上影响匹配精度。我们知道,由于3D测量的对象本身会导致照射在其表面的散斑发生形变,特别是在3D结构陡变或者细节丰富的部位,由于不同视角下拍摄的形变散斑图不再具有高度的相似性,导致窗口内的子图像不再具有相似性,从而会导致误匹配,如图47所示,所以在测量3D对象时图像窗口不能太大。
那么反过来考虑:是否选取足够小的窗口就可以了呢?为了避免3D物体本身引入窗口图像变形,理论上应该选取非常小,极限状况下是单一像素组成的一个子窗口,如图48所示。显而易见,这不满足全局唯一匹配的要求,因为每个亮点都可以成为匹配点,这显然背弃了散斑相关方法的核心优势。因此,散斑结构光全局唯一性与空间分辨率之间的矛盾是限制其精度的一大关键技术瓶颈。实际上,目前也有许多算法针对该问题进行了改进优化,如根据不同的区域自适应地选取的窗口大小来在分辨率与测量鲁棒性上保持良好的折衷。但是回到本章开头提到的3D结构光传感器在消费级市场的发展,实际的挑战在于将PC端的成熟算法移植到移动端平台;又因为要在实际应用中需要保证匹配结果比较鲁棒,所以算法中会增加大量的错误剔除策略,因此进一步增加了可靠商用的难度。
-
对于双目立体视觉三维测量原理,基线与视差近似成正比,因此基线越大所对应的深度测量的敏感性越高,三维测量精度也就越高。如图49所示,文中分析了具有不同基线长度的三款双目3D传感器在同一场景下的测量精度(标准平板检验)。结果可见:随着基线增加,测量的RMS误差逐渐较小,验证了基线越大,测量精度越高的这一结论。对于单目结构的3D传感器来说也是相同的道理。但是若又回到本章开头提到的3D结构光传感器在消费级市场的发展,特别是手机这种移动设备,由于尺寸的限制,3D传感器的尺寸无法做大,尤其是在目前流行的“刘海屏”下设计的传感器的基线将进一步受到制约。
另一方面,文中在第3.2节已经介绍到,由于3D结构光传感器涉及较多的硬件部分,需要红外发射激光器、红外接收摄像头、可见光摄像头、图像处理芯片四大部分的协同合作。特别是红外光的发射与接收之间的匹配,对整个3D视觉方案的识别效果和准确度至关重要,因此整个系统模组的封装和集成是非常关键的。其难度主要体现在:(1)发射端含有的DOE和WLO等精密光学元件,在组装时需要非常高的精确度,采用高难度的同轴度调整;(2)发射端含有的VCSEL激光器,需要进行光谱检测和校准;(3)发射端、接收端和可见光摄像头是彼此独立的,三者在空间位置上的准确度和稳定性对于最终3D成像效果而言非常关键,需要高难度的匹配和校准。
在算法硬件平台方面,虽然目前已经较多的国内厂家向市场投入了几款通用的投影组件,但其标准化的投影图案并不能满足所有用户的需求,特别是在算法上有具体要求的客户。另外,全定制化ASIC具有较高的技术壁垒,全球范围内可以提供ASIC芯片方案的公司只有少数的几家。实际上,有许多供应链厂家可以根据客户需求订制某个零部件,但是一个模组的设计先后要经历整套光学参数设计,性能仿真,散斑设计。如果想根据自主需求订制特殊的投影模组,则需要足够专业的团队与供应链上下游协同配合。每个部件的开模打样费用都是一笔不菲的开销,在整体成本上也需要严格管控。这也是很多算法厂家的设备大多数基于通用模组来进行后期产品开发的原因。
-
自从苹果iPhone X问世并受到广泛认同后,对其的质疑声也如同潮水一般涌来。声称利用三维人脸扫描技术的Face-ID与Animoji动画功能经测试后在遮挡掉红外摄像头与投射器后仍然能够正常工作。而且即使在工作状态下,泛光照明器和点阵投影器也仅仅以2 Hz的左右的频率闪烁,这说明其无法重建出实时的3D人脸模型。更重要的是,在进行Face-ID人脸识别时,遮住泛光照明器后系统并不能正常进行识别工作(泛光照明器其实就是的一个红外LED灯,其作用是向人脸投射均匀的红外光,让红外摄像头得到面部的平面照片)。这意味着仅仅依靠红外结构光所获得的3D信息无法进行三维人脸识别,而泛光照明器照明下所拍摄的2D图像是实现Face-ID的必要条件。实际上,iPhone X所拍摄到的3D人脸并不是我们想象的那般“3D”,而只是一个充满阶梯状的低分辨率的人脸轮廓而已,如图50所示。这也可以解释为什么到现在为止,所有声称标配“3D”摄像头的厂家(不仅仅是苹果,还包括华为、OPPO等)从来不去向用户去展示用该摄像头所拍摄到的原始图像,因为这个模型实在是太粗糙了!单单利用这个三维模型是不可能进行精准的人脸识别的。
实际上,现阶段我们所提及的3D人脸识别实际上仅仅是2D人脸识别与3D活体检测的结合体。主要进行人脸识别的是泛光照明器照射下的2D人脸图片,其具有更高的分辨率与信噪比。而3D结构光技术仅仅用来判断手机前的是不是真正的人脸而不是照片。这也解释了为什么3D人脸识别能够有效防止照片欺骗的原因。但据美国《财富》杂志近日报道,美国圣地亚哥的一家人工智能公司Kneron用高清3D面具和照片,在世界多地成功欺骗了人脸识别系统,其中包括了中国的支付宝和微信[155],如图51所示。这说明这种2D人脸识别+3D活体检测的方式并不能很好地预防3D面具的欺骗。尽管3D面具的制作过程比照片要复杂,需要使用各种专业设备,经过相当复杂的工序才可以完成,但不得不说这的确存在某种隐患。我们理想中的3D人脸识别技术应该是以高精度三维几何数据为基础进行特征提取与身份验证的,而现实和这一理想还存在一定的差距。
-
自从2017年9月,苹果推出基于3D结构光传感技术的iPhone X以后,很多厂家纷纷开始效仿,如OPPO Find X(供应商是奥比中光)、小米8等(供应商是以色列的Mantisvision)。不过随着全面屏时代的来临,华为等厂商也在探索手机前置ToF技术,如Mate30pro等。原理方面,其3D结构光投射的是散斑图案,接收模组需要拍摄到清晰的图案才能计算出深度。而随着距离的增加,投出的图案可能会出现模糊的情况,也可能会出现亮度上的衰减,从而导致获得的深度图不完整,测量精度低,所以3D结构光不适用于远距离深度信息采集。此外,文中已经分析了结构光的精度和基线距离有关,基线间隔越长精度就越高,所以iPhone X的长刘海其实也是不得已而为之的设计。反观ToF技术,其投射的不是散斑图案,而是发散的面光源,在一定距离内光信息不会出现大量的衰减,从而可以应用在远距离测量。同时ToF测量系统首发同源,不存在基线尺寸的限制,因此模组在尺寸上会更加紧凑。
在算法方面,结构光的算法需要运算大量的数据,使得普通的便携设备在具备功耗低、发热低、尺寸小的前提下无法胜任。相对于结构光算法,ToF的3D数据直接来源于图像传感器,算法层面相对结构光则简单很多。在生产方面,3D结构光的投射器主要包括了VCSEL、准直镜头、DOE等精密复杂的器件,制造成本较高。此外,结构光模组基于几何原理进行测量,因此对组装精度要求也极高。相比之下,ToF的投射器并不需要投影复杂的图案,所使用到的Diffuser的设计制作难度相对于散斑投射器使用的DOE也简单的多。ToF技术正是凭借以上几点优势获得了众多国内手机厂商的青睐。图52所示的是全球首个实现ToF技术商用的手机OPPO R17 Pro。
ToF的产业链与结构光比较一致,主要包括ToF传感器芯片、模组、算法及VCSEL、DOE等元器件。但ToF技术对光学传感芯片要求更高,而目前国外传感器芯片厂商在国内ToF产业链中占据着主导地位。据了解,国内超过一半的手机ToF相机方案都是采用的索尼感光芯片。索尼2015年收购了擅长于ToF影像技术的Softkinetic公司,之后逐渐凭借手机摄像头市场已有的领先地位,在国内占据了大部分市场份额。除了索尼,ADI是国内被选择最多的芯片商之一。据了解,其ToF的感光芯片研发技术比较成熟,比如ADI早就研发出VGA(分辨率达到640 pixel× 480 pixel)感光芯片,只是近年随着3D应用的兴起才又将其从“箱底”启用。在ToF相机模组的封装与测评方面,舜宇光学、欧菲光、威豪等国内厂商都凭借各自的垂直领域优势占据着龙头地位。国内ToF三维传感方案产业链中的部分玩家以华为Mate 30 Pro为例,其ToF相机模组就选用了索尼的ToF传感器芯片,并选择舜宇光学和欧菲光作为摄像头模组的一供、二供。据“摄像头观察”报道,立景创新、丘钛科技也参与了Mate30 Pro的摄像机模组供应,VCSEL由纵慧、Lumentum和Ams供应,Diffuser 由 Viavi、舜宇光学供应。另外,华为还使用自己的标定系统来提高标定效率。
下面更具体地比较一下二者的测量精度。如图53所示的ToF与结构光在测量不同深度时的误差对比。ToF的误差在近距离较大,在标定面前后的误差曲线近似是直线,而结构光的误差曲线是个下凹的曲线。在一定距离以内,结构光还是有精度优势的。这个距离范围由优势点P决定,且与结构光系统的基线大小有关。结构光基线距离越大精度越高,最近可工作距离越远。一般P点在2 m左右。结构光的红外摄像头在泛光照明下还可以作为一个普通摄像头使用来采集场景或人脸纹理信息。ToF很大的软肋在深度分辨率上,VGA以上的高分辨率传感器技术目前还不成熟。

图 53 ToF与结构光在测量不同深度时的误差对比
Figure 53. Error comparison between ToF and structured-light at different measurement depths
综合来看,结构光和ToF技术并没有优劣之分,只有适用场景的不同。结构光技术功耗小,深度图分辨率较高,适合短距离场景(特别在1 m内有很大优势),可兼容输出二维纹理图,但结构较为复杂、尺寸较大,在应用上更适于前摄。ToF方案尺寸小、干扰性较好,视角较宽(中长距离使用),缺陷是功耗高,精度及深度图分辨率较低,比较适合于选择作后摄。目前手机端配备的ToF传感器芯片主要来自于国外几大厂商。在此笔者也期待国内企业自主研发的ToF传感器能够早日占领市场,并能够提供高分辨率、高精度的3D数据。
-
结构光投影技术因其非接触、高精度、全场测量、点云重建效率高等优点,已成为目前三维传感技术中的主流光学方法。有趣地是,结构光三维传感技术的科学研究与产业应用二者并不是并驾齐驱或紧密联结的。相反,二者其实存在一定的“割裂”与“鸿沟”:学术界,结构光三维传感技术一直向着“更高、更快、更强”的目标继续迈进,而产业界却不断呼唤着“更简单、更小巧、更便宜”的三维传感技术。现在国内的结构光三维传感器公司大多执着于最简单实用或者有过成功应用先例的技术,而大学里三维结构光传感技术的研究人员似乎只是在乎技术是否具有展示度,而并不是十分关心技术的实用性与转化价值。所以要谈到结构光三维传感技术未来方向,很难将学术界与产业界混为一谈,因为二者是有些矛盾的。我们当然期望“更高、更快、更强”能够以“更简单、更小巧、更便宜”的方式去实现,但是很抱歉的是现在这似乎并不是短时间所能达到的。因此,笔者等作为本行业的研究人员,在该节里将以更“学院派”的方式去对该技术的未来进行展望,但是值得注意的是“更简单、更小巧、更便宜”同样也一定是未来的发展方向,且甚至需要更多的重视。
-
这里的实时化特指多帧图像的高精度结构光三维传感技术,如条纹投影轮廓术,而非单帧的散斑结构光投影技术(单帧技术的实时性仅仅取决与算法的执行速度)。对于条纹投影轮廓术,现有研究工作大多集中在静态物体或缓变场景的形貌测量上,通过投影多组光栅条纹并结合格雷码/时间相位展开方法以获取绝对相位信息。这不可避免地延长了数据获取的时间,使其难以对动态物体或者变化场景达到快速响应。如何快速、准确、无歧义地获取动态物体或瞬态变化场景的三维形貌信息是条纹投影轮廓术领域的一个亟待解决的问题。该问题直接制约着数字光栅投影技术的适用对象与应用范围,也逐渐成为该领域的研究热点之一。目前,为实现实时动态三维测量,基于传统条纹投影轮廓术,学者们主要从三个方面进行了优化:
第一个方面:减少三维重建所需的图像数量。Zhang等[40]利用De Bruijn序列对彩色条纹进行空域编码,实现了基于单幅拍摄的实时三维重建。肯塔基大学的Liu等[157]人将利用空间编码复用原理,通过向五步相移光栅条纹引入额外频率的辅助光栅,实现了快速实时三维成像。2012年,笔者所在课题组基于2+2 PSP法与现场可编程门阵列电路(FPGA)构建了120 Hz实时光栅投影三维成像系统[158],采用低成本成像装置,仅利用四幅光栅图像即可实现针对复杂动态场景的快速无歧义三维轮廓测量[158],如图54所示。
第二个方面:通过增加观察视角。为了提升三维测量效率,应减少使用或不使用额外的用于相位展开的辅助光栅。为此,Weise等[159]与Li[160]等人提出了利用多视角极线约束为条件,通过使用额外的相机进行视角约束,实现了条纹级次的绝对展开。在此基础之上,为实现更高精度的实时三维测量,笔者所在课题组提出了一种基于多视角的三角波空域叠加复用的相移轮廓术[161]。该方法针对传统三步相移光栅引入三角波信号,其优势在于借助于三角波信号空域定位,可提升多视角极线约束相位展开的稳定性,进而可准确求解高频光栅的条纹级次。还提出的基于立体相位展开技术的四目实时三维成像系统(见图55)可在45 Hz的刷新速率下实时获取精度优于45 μm的彩色三维轮廓数据[162-163]。

图 55 基于立体相位展开法的四目三维测量系统。(a)系统外观;(b)系统内部结构俯视图;(c)系统测量场景
Figure 55. Quad-camera 3D measurement system based on SPU. (a) Appearance of the system; (b) Top view of the internal structure of the system; (c) System measurement scenario
第三个方面:解决运动引入的测量误差。该问题通常存在于基于多帧光栅图像投影的三维测量方法,如常用的三步相移法。如前所述,由于物体的运动引入了额外的相移分量,因此在重建的三维轮廓表面,通常会存在一定频率的波纹误差。为了排除补偿此类运动误差,Weise等[159]提出利用泰勒展开,拟合并补偿运动误差。Liu等[164]人建议从两帧3D图像之间的差异来估计物体的运动。然后,利用投影机的针孔模型,从估计的运动中确定运动引起的相移误差。笔者所在课题组推导了N步相移法的运动相位误差理论模型,并基于光栅图像的全局统计规律,提出了运动相位误差自适应补偿动态三维测量技术[165]。此外还有学者通过融合傅里叶变换法与相移轮廓术,结合二者的优势以使算法能够同时适应动态物体与静态物体的测量[166, 167, 162]。
-
几乎现有的基于单个投影仪和单个相机的三维光学传感器单次只能获取被测物一个视角的三维形貌信息。为了对具有复杂表面的对象进行360°全方位3D形貌测量,需要从不同的视角执行多次测量。现有的方法大多需要使用转台[168, 169],机械臂[170]或平面镜[171–173]。将对象放置在转台上,并在将对象旋转到不同视角时获取3D数据。或者将测量系统安装在可移动的机器人手臂上,以围绕对象执行多次测量。扫描后,使用复杂且耗时的点云配准算法(如迭代最近点算法ICP)将所有扫描数据融合在一起[174-175]。这些方法需要复杂的机械系统,且测量过程较为复杂耗时。针对这一问题,笔者所在课题组提出了一种高分辨率的实时360°3D模型重建方法,该方法可以手动旋转对象并在扫描过程中看到不断更新的3D模型[176]。该方法可以在任意旋转下重建复杂对象的高精度完整3D模型,而无需任何仪器辅助和复杂的后处理算法,一个典型的全方位360°三维测量结果如图56所示。

图 56 配准后的David模型的结果。 (a) 点云结果;(b) 三角化显示结果
Figure 56. Results of the David model after registration. (a) Point cloud results; (b) Triangulation results
与上述方法不同,还有类全景三维测量的方法是基于平面镜反射原理。该方法可以同时从多个不同的角度捕获被测对象的变形条纹图像(例如,通过一个真实的相机和借助平面镜实现的两个虚拟相机),从而可实现高速全景3D形貌测量。Mariottini等[177]系统地研究了反射镜的反射折射,提出了一个理想的反射折射模型。该模型有助于将反射镜反射的虚拟表面转换为真实位置。按照这个想法,Chen等[173]提出了一种简单的标定方法,通过测量平面镜上预制的两个散斑图案的3D数据来获得平面镜的标定数据。该方法要求平面镜具有前表面反射,否则应考虑平面镜的厚度[178]。针对这一问题,笔者所在课题组针对具有两个平面镜的条纹投影轮廓术系统提出了一种灵活的标定技术(系统结构如图57所示),它可以简单地标定反射镜的空间位置而无需使用散斑图案[179]。只需要相机观察一组特征点对(包括实点和虚点)即可生成平面镜的反射矩阵的解,并依次执行反射矩阵的初始估计和使用具有光束平差策略的Levenberg-Marquardt算法实现精确标定。实验结果证明了该方法能够以65.122 μm的精度进行全景3D形貌测量,如图58所示。
-
作为一种基于图像分析的三维形貌测量技术,条纹投影轮廓术通常假设被测表面呈现漫反射特征,而将测量环境中低反射(深色)区域和镜面反射(反光)区域视为异常值[180–183]。对于深色表面,拍摄的条纹图案对比度往往不高。而对于反光表面,由于反射光过于强烈,容易致使像素饱和。因此很难捕捉到重建这两种表面所需的理想条纹图案。然而在现实世界中,许多物体并非理想的朗伯体,它们可能同时具有低反射面和高反射面。传统条纹投影轮廓术的漫反射假设条件限制了其实际应用的范围。
为了解决反光表面的测量问题,一种最为直接的方式为向高亮区域喷涂一层薄粉作为显影剂,即人为地改变测量表面的反射特性。这种方法通常只适用于喷涂层厚度对测量精度的影响可以忽略时才被使用。因此为了在不改变物体原有外观的情况下准确测量物体,研究人员开发了各种高动态范围(High Dynamic Range, HDR)条纹投影技术。这些HDR技术可分为两类:基于设备调节的技术和基于算法优化的技术。这两类方法对于如何从拍摄的图像中获取几何信息,具有不同的处理方式。对于基于设备调节的一类技术[184–211],它们的重点是找到所用设备的最佳参数,例如相机的最佳曝光时间或投影光的最佳亮度,以便为低反射和高反射表面捕获理想的条纹图像。而另一方面,对于基于算法优化的一类技术[69, 212–219],它们不需要捕获理想的光栅图像。它们不对硬件设备进行任何调整,仅仅依靠精心设计的算法即可从原始的条纹图像中提取准确的相位信息。
由于现有的HDR条纹投影轮廓术中,基于设备调节的技术整体数量多于基于算法优化的技术。因此,根据调节设备的不同,对基于设备调节的技术进行了近一步的细分。它们可被分为:基于摄像机调节的技术[184–192]、基于投影机调节的技术[193–203]、基于附加设备的技术[204–207]和混合技术[208–211]。对于基于相机调节的技术,HDR三维成像是通过更改相机的曝光时间或通过调整相机的拍摄位置来捕获所需的条纹图像来实现的。基于投影机调节的技术依则赖于条纹投影轮廓术是一种主动的三维测量方法,因此通过适当调整投影光强度,将有利于拍摄理想的条纹图像。此外,也可以通过在条纹投影系统中引入额外的辅助设备来进行HDR三维测量,如图59所示,通过使用偏振片去除镜面反射的干扰[205]。混合技术是基于上述策略组合而成的一类方法。例如对于复杂场景,不仅调整相机与投影仪的参数,而且引入额外的辅助设备,共同作用以拍摄理想的光栅图像[208]。关于HDR条纹投影轮廓术更为详细的理论分析与实验效果对比,可见参考文献[220]。
-
如前所述,相移法通常具有更高精度且能够实现像素级的高分辨率相位测量。然而由于需要采集多张条纹图像,这类方法容易受到物体运动/环境振动等外界干扰的影响。相比之下,空域相位解调法由于仅通过单幅条纹图像实现相位解调,它具有更好的振动/运动鲁棒性。但是其不足之处在于对条纹陡变、不连续以及物体细节丰富的区域较为敏感,难以实现高精度、高分辨率的相位测量。此外空域相位解调算法一般具有较多的参数需要调节、难以完全实现全自动化操作。因此,目前在光学相位测量领域,亟需一种能够同时满足高精度、高效率、全自动化的条纹图案分析技术。
在此背景下,笔者所在课题组首次将深度学习技术应用在条纹分析中,并有效提升了条纹投影轮廓术的三维测量精度[221]。该方法的思想在于仅采用一张条纹图像作为输入,利用深度神经网络来模拟相移法的相位解调过程。如图60所示,通过构建两个卷积神经网络(Convolutional Neural Network,CNN1和CNN2),CNN1负责从输入条纹图像(I)中提取背景信息(A)。随后CNN2利用提取的背景图像和原始输入图像生成所需相位的正弦部分(M)与余弦部分(D)。最后,将该输出的正余弦结果带入反正切函数计算得到最终的相位分布。相比于傅里叶变换法(FT)与加窗傅里叶变换法(WFT),该方法能够更为准确地提取相位信息,特别是针对具有丰富细节的物体表面,相位精度可提升50%以上。该技术已被成功应用于高速三维成像[222]。
-
条纹投影轮廓术是用于光学3D形貌测量的成熟技术。然而在许多应用中,人们期望以非常高的速度进行3D测量,尤其是对于快速移动或形貌迅速变化的物体。目前由于相机的拍摄速度已经普遍超过了投影仪的投影速度,因此投影仪的工作速度成为了限制数字光栅投影系统测量效率提升的瓶颈。
在光栅投影轮廓术中,光栅条纹图像一般由计算机生成,通过数字投影设备投射至被测物体表面。相机采集变形的光栅图像,经过相位分析等算法处理后恢复物体的三维信息。相比于基于LCD技术的数字投影仪,基于数字光处理DLP技术的数字投影仪在速度、对比度、亮度等方面具有先天优势。DLP投影系统中的核心元件是一个称为数字微镜器件(Digital Mirror Device, DMD)的光学半导体芯片,如图61所示。DMD实际上是一种二元光学器件(非亮即暗),而想要实现具有不同灰阶的光强分布信号必须借助于对入射光进行二元时间脉冲宽度调制来实现。即在每一帧的时间内,某一像素处于两种状态的占空比决定了该像素的灰阶。所以为了显示灰阶数为
${2^8} = 256$ 的灰度图像,需要引入八个时分位平面,共需要占据255个DMD的最小时钟周期。虽然DMD的工作频率可以高达20 000 Hz以上,但因其内在的二元时间脉冲宽度调制机理,投影一幅传统的八位灰度光栅条纹图像的速度通常情况下只能达到120 Hz。因此DMD的这种基于时间积分的灰度投影机理成为其制约结构光条纹投影速度的关键性因素。
图 61 基于数字光处理DLP(Digital Light Processing)技术的数字投影仪基本结构及其核心部件DMD
Figure 61. Basic structure of a digital projector based on Digital Light Processing (DLP) technology and its core component DMD
为了解决这一问题,Zhang等[223]于2009年提出利用投影仪散焦投影二值条纹的方法来模拟正弦条纹的投影,该方法将256级灰阶投影变成了两级灰阶的投影从而提高了DLP投影仪的工作速度。但由于离焦二值条纹的正弦性不好,该方法的测量精度较低。为了提高散焦二值条纹的正弦性,学者提出了正弦脉冲宽度调制技术[224–226](SPWM)、最优脉冲宽度调制技术[225, 227](OPWM)、二进制抖动技术[228]和优化抖动技术[229–232]等,通过预先抑制原始方波中高次谐波分量,使投影仪投射更逼近理想正弦的光栅。二值离焦技术再搭配高速相机,可将三维测量的速度提升至近kHz[233, 234]级别甚至10 kHz级别[235]。2018年,笔者所在课题组基于高速DLP投影与微频移傅里叶变换法(μFTP)在国际上首次实现了速度高达10 000 Hz的瞬态三维传感,实现了气枪子弹出膛、气球爆炸瞬间等瞬态场景的三维重构[235]。图62给出了对气枪发射子弹过程的三维重建及跟踪结果。

图 62 对气枪发射的子弹的三维测量与跟踪[235]
。(a)不同时间点的相机图像;(b)相应3D重建结果;(c)枪口区域的3D重建(对应于图(b)中所示的盒装区域)以及在飞行过程中的三个不同时间点的子弹(7.5 ms,12.6 ms和17.7 ms)的3D重建。插图显示在17.7 ms处穿过飞行子弹中心的水平(x-z)和垂直(y-z)轮廓;(d)最后时刻(135 ms)场景的3D点云,彩色线显示130 ms长的子弹轨迹。插图为子弹速度-时间的图 Figure 62. 3D measurement and tracking a bullet fired from a toy gun. (a) Camera images at different time points; (b) Corresponding 3D reconstructions; (c) 3D reconstruction of the muzzle region (corresponding to the boxed region shown in (b)) as well as the bullet at three different points of time over the course of flight (7.5 ms, 12.6 ms, and 17.7 ms). The insets show the horizontal (x–z) and vertical (y-z) profiles crossing the body center of the flying bullet at 17.7 ms; (d) 3D point cloud of the scene at the last moment (135 ms), with the colored line showing the 130 ms long bullet trajectory. The inset plots the bullet velocity as a function of time
除了上述通过离焦二值技术提高DLP工作速度进而提高三维测量速度的手段以外,还有一些学者使用其他投影仪技术以实现高速三维测量。Zhang等[236]使用频闪结构光的投影方案和傅里叶轮廓术实现了对转速为1080转/分钟的旋转叶片的三维测量。Schaffer等[237–239]提出相干激光散斑投影技术,通过声光反射器(AOD)改变入射激光束方向来产生不同的散斑图案,可实现20 kHz的投影速度。Grosse等[239, 240]通过高速旋转的转镜将投影仪所投图案以不同角度入射到物表面,并基于立体视觉法实现速度高于700 Hz的三维测量。Fujigaki等[241]开发了一种采用光源步进法(LSSM)的紧凑型线性LED器件,配合光栅板可实现快速条纹投影。Heist等[242]提出阵列投影仪进行三维形状测量,该阵列投影仪由27个LED构成,每三个为一组,可投射九种非周期正弦条纹图案。通过该系统可以3 kHz的投影帧速实现了3D帧速大于330 Hz的三维测量。2016年他们提出使用GOBO(Goes Before Optics)投影法[243],通过在投影仪前放置高速旋转的带有一定镂空图案的转轮,再由离焦技术可高速“投影”出有一定结构编码的条纹图案。最近他们还通过GOBO技术实现了5D高光谱成像和高速热成像[244-245],其系统及典型实验结果如图63所示。

图 63 5D高光谱成像系统、结果及高速热成像系统及结果[244, 245]。(a) 5D高光谱成像系统;(b)高速热成像系统;(c) 5D高光谱成像结果:对柑橘植物的吸水性的测量;(d) 高速热成像结果:不同时间对篮球运动员的测量
Figure 63. Systems and results of 5D hyperspectral imaging and high speed thermal imaging[244, 245]. (a) 5D hyperspectral imaging system; (b) High speed thermal imaging system; (c) 5D hyperspectral imaging results: the measurement of water absorption by a citrus plant; (d) High-speed thermal imaging results: the measurement of a basketball player at different times
-
作为一项三维传感技术,如果所获得的三维数据不具有准确性,那么在很多应用中“三维”就丧失了其本身的意义。正如在3D人脸识别中,如果三维传感技术只能够获得人脸粗略的轮廓信息并作为活体检测手段,而不以高精度三维几何数据为基础进行特征提取与身份验证,那该项技术严格来说就不能称作“三维人脸识别”。在“高精度”的前提下保证“高速”,“小体积、低成本”是该领域的一大挑战。在第5.2与5.3节已经讨论过这些现存问题,笔者所在课题组曾经也构建了一套快速高精度三维人脸扫描系统FaceScan,其是基于多频移相的条纹投影轮廓术技术。通过FPGA控制电路控制低成本的商用投影仪实现了快速条纹投影,投影帧率为60 Hz,并且通过该控制电路完成了相机与投影仪之间的同步。相机采集到条纹图后,将其传输给计算机,计算机中的软件通过对条纹图的分析解码得到高精度、稠密的三维人脸点云数据。软件通过和数据库中的三维人脸数据进行比对最后给出识别结果。该系统在算法上通过最优条纹序列设计方法[246]在提高采集速度的同时保证了测量精度,得到的三维人脸数据精度达到0.05 mm,为后续三维人脸识别提供了精确的数据。此外,该系统通过两个相机从左右双视角对人脸三维数据进行采集,并利用ICP迭代算法进行拼接,从而能实现三维人脸数据的快速以及高精度扫描,为三维人脸识别提供了强有力的保障。图64展示了FaceScan的操作界面以及人脸扫描的结果。从中可以看出,FaceScan系统扫描出来的人脸细节部分保持得非常完整,脸上的斑点清晰可见。
对于人脸识别而言,最为关键的是要能够准确无误地提取人脸刚性区域的特征。所谓刚性区域,是指较少受到表情、姿态以及年龄影响的区域,比如人脸的鼻根、鼻尖、左右鼻翼以及颏下等位置。通过在软件上进行操作,逐次利用鼠标点击这五个特征点:鼻根点(P1)、左鼻翼点(P2)、鼻尖点(P3)、右鼻翼点(P4)、颏下点(P5),如图65所示,可以获得这些点的三维坐标。根据这些特点的坐标,可以计算出一共8条线段的长度作为特征数据集。基于FaceScan系统可以非常迅速的建立一个三维人脸数据库。为三维人脸识别的研究以及相关的应用产品提供最初的高精度的原始数据。根据图65中的三维人脸鼻根、左鼻翼、鼻尖、右鼻翼、颏下等特征点以及这些特征点之间的距离,利用三维人脸识别的融合算法,逐一跟数据库进行匹配查找,就能从三维人脸数据库中识别出所检测的人脸。
最终不得不提及的是,FaceScan虽然解决了三维人脸采集的“高速”与“高精度”问题,但其基于商用投影仪与工业相机构建,成本高昂体积庞大,难以集成于移动作为终端系统广泛采用。但想象一下目前的身份验证系统,当人们去公安局办身份证,总会有一台体积庞大的证件照系统为你拍摄一幅高清的二维人脸图作为“存根”。但是实际验证的终端系统,如高铁站、飞机场、银行ATM机器等所配备的2D摄像头达不到这么高的清晰度(但也足够使用了)。就目前而言,FaceScan其作为一个高精度人脸采集装置是绰绰有余的,但体积成本因素致使其并不适合作为一台验证终端来使用。而现在人们手机里的散斑结构光传感器或者是类似于Kinect 的深度摄像头,所能提供的三维数据不足以支撑三维人脸识别验证的需求。它们与基于高精度条纹投影技术所得到的三维数据之间的精度与空间分辨率差甚至高达两个数量级。如何在小型化、低成本的平台上实现快速高精度(亚毫米,百微米)级精度的三维数据获取,准确还原出人脸的生物特征与细节仍然是 “三维人脸识别”中最大的技术瓶颈。
-
随着人脸识别、AR/VR等应用在生活中的不断深入,结构光三维传感技术必将迎来爆发期。它们有望真正成为机器甚至智能手机的眼睛,使它们能够更准确地感知环境,识别使用者。但是目前3D结构光模组相对较为复杂,成本也相对较高,且小基线与单幅散斑的投影重建方式导致其三维重建精度在毫米甚至厘米级,这导致3D结构光的应用受到很大的限制,如手机解锁、辅助人脸识别(活体检测)、手势交互及类似Animoji的一类娱乐应用。而高精度结构光三维传感技术,如条纹投影轮廓术大多还停留在工业应用甚至实验室阶段,难以实现小型化与低成本是该项技术难以向消费电子类应用的一大障碍。而ToF技术体积小、成本低,可支持较远距离的3D扫描,应用面也相对较广。除了能够支持3D结构光的应用之外,还可以进行自动对焦、虚化、测距、AR等应用。并且ToF模组的成本可能也将会比3D结构光更低。但是其在近距离时的测量精度甚至还要比结构光更低。
因此,“3D”的时代其实并没有真正的到来,也并没有真正地那么触手可及。在笔者脑中所构想的3D时代应该是这样一番景象:包含有高精度三维人脸信息的“三维身份证”,无处不在的真三维人脸识别与身份验证,随时随地掏出手机一拍就能获取场景的高精度三维照片,对着物体扫一圈就能对其进行三维建模,这些3D照片与模型可以通过裸眼3D技术呈现在人们的眼前,并与人们的环境融为一体,可通过人们的肢体自由地去操控、展示与交互等,正如同图66所描绘的那样。就目前而言,距离这个目标,似乎还有不小的距离。
就人脸识别而言,世界上没有绝对的安全,人脸识别也是如此。人脸识别技术是一项包含光学、计算机视觉、图像处理、神经网络、人工智能等学科,同时非常具有挑战性的多学科交叉技术,这种技术现在处于不断发展的过程中。在这个过程中,必然会受到各种挑战。“3D人脸识别”带来的是对未来的无限憧憬,但是“3D活体检测”的确让人们残忍地面对现实。期待未来强大的三维光学传感技术能够进一步提升人脸识别系统的安全性,使其不但可以抵御照片攻击、还可以识别易容化妆过,甚至可以甄别出分辨双胞胎与高分辨人脸面具。不管是照片还是面具仅仅是这一系列攻防挑战的一部分,只有不断的接受挑战,技术才会得到不断的进步。
可以预见的未来,3D传感技术在大众消费电子领域将面临两种可能性:一方面技术屈服于大众审美,即手机厂商着力去解决饱受诟病的“刘海屏”问题,而不再着力以提升3D测量精度为主要驱使力,利用更小巧更易于集成的ToF传感器。到时也许就将进入真全面屏时代了,但是“真3D”将可能会离我们越来越远。结构光技术将会被ToF所取代,高性能低成本ToF芯片传感器技术将会是未来3D技术各大厂商所争夺的焦点。另一种可能性是大众需求受技术所引导,结构光三维传感技术在精度得到进一步突破的同时仍然能够保持低成本甚至可以做地更加小型化,用户为了能够获得更加真实准确的3D影像、更加安全的认证方式而可以接受手机上多出那么一点点小小的“累赘”;机场、超市、ATM机器上的3D摄像头能够随着光学传感技术的不断成熟与完善输出足够精度的三维人脸模型用于可靠的身份认证,那么可能的3D时代就将真正到来。
文中的作者贡献如下:陈钱、左超负责全文构思与引言撰写,第1章由左超撰写;第2章由张晓磊、郑晶、左超联合撰写;第3章由胡岩、尹维、沈德同、左超联合撰写;第4章由沈德同、胡岩、钟锦鑫联合撰写;第5章由左超、胡岩、沈德同联合撰写;第6章由左超、尹维联合撰写;文中的图片资料与统计数据由张晓磊、郑晶、沈德同采集或者收集。第7章由左超撰写。左超、胡岩负责全文整理、排版与定稿。感谢为文中撰写提供测试样品的众多三维传感器、器件供应链、集成方案厂家,文中不一一列举。特别感谢卢林芃为此文手绘图66。
Has 3D finally come of age? ——An introduction to 3D structured-light sensor
-
摘要: 三维成像与传感技术作为感知真实三维世界的重要信息获取手段,为重构物体真实几何形貌及后续的三维建模、检测、识别等方面提供了数据基础。近年来,计算机视觉和光电成像技术的发展以及消费电子与个人身份验证对3D传感技术日益增长的需求促进了三维成像与传感技术的蓬勃式发展。2D摄像头向3D传感器的转变也将成为继黑白到彩色、低分辨率到高分辨率、静态图像到动态影像后的“第四次影像革命”。《红外与激光工程》本期策划组织的“光学三维成像与传感”专题,共包含高水平稿件20篇,其中综述论文15篇,研究论文5篇。这些论文系统介绍了光学三维成像传感领域热点专题的研究进展与最新动态,主题全面涵盖了当前三维光学成像领域的前沿研究方向:结构光三维成像、条纹投影轮廓术、干涉测量技术、相位测量偏折术、三维立体显示技术(全息显示、集成光场显示等)、三维成像传感技术与计算成像相关交叉领域(如三维鬼成像)等。而此文作为本期专栏的引子,概括性地综述了典型的三维传感技术,并着重介绍了三维结构光传感器技术的发展现状、关键技术、典型应用;讨论了其现存问题、并展望了其未来发展方向,以求抛砖引玉。Abstract: Three-dimensional (3D) imaging and sensing technologies, as valuable information acquisition tools for perceiving the real 3D world, provide data bases for the reconstruction of the geometric shape of objects and subsequent 3D modeling, detection, and recognition. Recently the development of computer vision and optoelectronic imaging technology, as well as the growing demand for 3D technologies in consumer electronics and personal authentication, have promoted the thriving growth of 3D imaging and sensing technologies. After the imaging revolution from monochrome to color, low resolution to high resolution, and static image to dynamic video, the transition of the camera from 2D to 3D will become the new "fourth imaging revolution." This issue of "Infrared and Laser Engineering" organizes a special topic on "Optical 3D Imaging and Sensing", which contains 20 high-quality articles, including 15 review papers and 5 research papers. These papers systematically introduce the research progress or trends of the cutting-edge research topics in the field of optical 3D imaging and sensing, and their themes comprehensively cover the current hot research directions in the field of 3D optical imaging: structured-light 3D imaging, fringe projection profilometry, interferometry, phase measuring deflectometry, 3D display technologies (such as holographic display, and integral/light field display), and the interdisciplinary fields of 3D sensing technologies and computational imaging technologies (such as 3D ghost imaging). As the preface of this issue, this paper summarizes the typical 3D sensing technologies and focuses on the current status, key technologies, and typical applications of the 3D structured-light sensor technologies, discusses its existing challenges, and looks forward to its future development directions.
-
Key words:
- structured-light /
- 3D imaging /
- 3D measurement /
- 3D structured-light sensor
-
图 62 对气枪发射的子弹的三维测量与跟踪[235]
。(a)不同时间点的相机图像;(b)相应3D重建结果;(c)枪口区域的3D重建(对应于图(b)中所示的盒装区域)以及在飞行过程中的三个不同时间点的子弹(7.5 ms,12.6 ms和17.7 ms)的3D重建。插图显示在17.7 ms处穿过飞行子弹中心的水平(x-z)和垂直(y-z)轮廓;(d)最后时刻(135 ms)场景的3D点云,彩色线显示130 ms长的子弹轨迹。插图为子弹速度-时间的图 Figure 62. 3D measurement and tracking a bullet fired from a toy gun. (a) Camera images at different time points; (b) Corresponding 3D reconstructions; (c) 3D reconstruction of the muzzle region (corresponding to the boxed region shown in (b)) as well as the bullet at three different points of time over the course of flight (7.5 ms, 12.6 ms, and 17.7 ms). The insets show the horizontal (x–z) and vertical (y-z) profiles crossing the body center of the flying bullet at 17.7 ms; (d) 3D point cloud of the scene at the last moment (135 ms), with the colored line showing the 130 ms long bullet trajectory. The inset plots the bullet velocity as a function of time
图 63 5D高光谱成像系统、结果及高速热成像系统及结果[244, 245]。(a) 5D高光谱成像系统;(b)高速热成像系统;(c) 5D高光谱成像结果:对柑橘植物的吸水性的测量;(d) 高速热成像结果:不同时间对篮球运动员的测量
Figure 63. Systems and results of 5D hyperspectral imaging and high speed thermal imaging[244, 245]. (a) 5D hyperspectral imaging system; (b) High speed thermal imaging system; (c) 5D hyperspectral imaging results: the measurement of water absorption by a citrus plant; (d) High-speed thermal imaging results: the measurement of a basketball player at different times
表 1 基于互相关准则的匹配函数
Table 1. Matching function based on cross-correlation criteria
CC correlation criterion Definition Cross-correlation (CC) ${C_{CC}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {[f({x_i},{y_i})g(x_i',y_j')]} } $ Normalized cross-correlation (NCC) ${C_{NCC}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {[\dfrac{{f({x_i},{y_i})g(x_i',y_j')}}{{\bar f\bar g}}]} } $ Zero-normalized cross-correlation (ZNCC) ${C_{ZNCC}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {\left\{ {\dfrac{{\left[ {f({x_i},{y_i}) - {f_m}} \right] \times \left[ {g(x_i',y_j') - {g_m}} \right]}}{{\Delta f\Delta g}}} \right\}} } $ 表 2 基于SSD相关准则的匹配函数
Table 2. Matching function based on SSD-correlation criteria
SSD correlation criterion Definition Sum of squared differences (SSD) ${C_{SSD}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {{{[f({x_i},{y_i}) - g(x_i',y_j')]}^2}} } $ Normalized sum of squared differences (NSSD) ${C_{NSSD}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {{{\left[ {\dfrac{{f({x_i},{y_i})}}{{\bar f}} - \dfrac{{g(x_i',y_j')}}{{\bar g}}} \right]}^2}} } $ Zero-normalized sum of squared differences (ZNSSD) ${C_{ZNSSD}} = \displaystyle\sum\limits_{i = - M}^M {\displaystyle\sum\limits_{j = - M}^M {{{\left[ {\dfrac{{f({x_i},{y_i}) - {f_m}}}{{\Delta f}} - \dfrac{{g(x_i',y_j') - {g_m}}}{{\Delta g}}} \right]}^2}} } $ -
[1] 央视315晚会幕后: 揭秘人脸识别破解始末[EB/OL]. [2020-01-09]. http://science.china.com.cn/2017-03/15/content_9390265.htm. [2] CIS 2019 网络安全创新大会[EB/OL]. [2020-01-09]. https://cis.freebuf.com/. [3] Woodham R J. Photometric method for determining surface orientation from multiple images [J]. Optical Engineering, 1980, 19(1): 191139. [4] Christensen P H, Shapiro L G. Three-dimensional shape from color photometric stereo [J]. International Journal of Computer Vision, 1994, 13(2): 213−227. doi: 10.1007/BF01427152 [5] Deresiewicz H, Skalak R. On uniqueness in dynamic poroelasticity [J]. Bulletin of the Seismological Society of America, 1963, 53(4): 783−788. [6] Coleman Jr E N, Jain R. Obtaining 3-dimensional shape of textured and specular surfaces using four-source photometry [J]. Computer Graphics and Image Processing, 1982, 18(4): 309−328. doi: 10.1016/0146-664X(82)90001-6 [7] Park J S, Tou J T. Highlight separation and surface orientations for 3-D specular objects[C]//10th International Conference on Pattern Recognition. IEEE, 1990, 1: 331–335. [8] Ikeuchi K. Determining surface orientations of specular surfaces by using the photometric stereo method [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1981(6): 661−669. [9] Wu T P, Tang C K. Dense photometric stereo using a mirror sphere and graph cut[C] //2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), 2005, 1: 140–147. [10] Mozerov M G, van de Weijer J. Accurate stereo matching by two-step energy minimization [J]. IEEE Transactions on Image Processing, 2015, 24(3): 1153−1163. doi: 10.1109/TIP.2015.2395820 [11] Geiger A, Roser M, Urtasun R. Efficient large-scale stereo matching[C]//Asian Conference on Computer Vision, 2010: 25–38. [12] Tan X, Sun C, Wang D, et al. Soft cost aggregation with multi-resolution fusion[C]//European Conference on Computer Vision, 2014: 17–32. [13] Yang Q, Yang R, Davis J, et al. Spatial-depth super resolution for range images[C]// 2007 IEEE Conference on Computer Vision and Pattern Recognition, 2007: 1–8. [14] Yoon K J, Kweon I S. Adaptive support-weight approach for correspondence search [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006(4): 650−656. [15] Hosni A, Rhemann C, Bleyer M, et al. Fast cost-volume filtering for visual correspondence and beyond [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 35(2): 504−511. [16] Yang Q, Wang L, Yang R, et al. Stereo matching with color-weighted correlation, hierarchical belief propagation, and occlusion handling [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 31(3): 492−504. [17] Klaus A, Sormann M, Karner K. Segment-based stereo matching using belief propagation and a self-adapting dissimilarity measure[C]//18th International Conference on Pattern Recognition (ICPR’06), 2006, 3: 15–18. [18] Bertozzi M, Broggi A. GOLD: A parallel real-time stereo vision system for generic obstacle and lane detection [J]. IEEE Transactions on Image Processing, 1998, 7(1): 62−81. doi: 10.1109/83.650851 [19] Loop C, Zhang Z. Computing rectifying homographies for stereo vision[C]//1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149), 1999, 1: 125–131. [20] Gehrig S K, Eberli F, Meyer T. A real-time low-power stereo vision engine using semi-global matching[C]//International Conference on Computer Vision Systems, 2009: 134–143. [21] Dorrington A A, Kelly C D B, McClure S H, et al. Advantages of 3D time-of-flight range imaging cameras in machine vision applications[C]//16th New Zealand Conference (ENZCon), 2009: 18–20. [22] Ganapathi V, Plagemann C, Koller D, et al. Real time motion capture using a single time-of-flight camera[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2010: 755–762. [23] Hsu S, Acharya S, Rafii A, et al. Advanced Microsystems for Automotive Applications 2006[M]. Berlin: Springer, 2006: 205–219. [24] Shim H, Lee S. Performance evaluation of time-of-flight and structured light depth sensors in radiometric/geometric variations [J]. Optical Engineering, 2012, 51(9): 094401. [25] Hahne U, Alexa M. Depth imaging by combining time-of-flight and on-demand stereo[C]//Workshop on Dynamic 3D Imaging, 2009: 70–83. [26] Schuon S, Theobalt C, Davis J, et al. High-quality scanning using time-of-flight depth superresolution[C]//2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, 2008: 1–7. [27] Cui Y, Schuon S, Thrun S, et al. Algorithms for 3d shape scanning with a depth camera [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 35(5): 1039−1050. [28] Zhang Zuxun, Zhang Jianqing. Solutions and core techniques of city modeling[D]. Wuhan: Wuhan University, 2003. (in Chinese) [29] Wang Jizhou, Li Chengming, Lin Zongjian. A survey on the technology of three dimensional spatial data acquisition[D]. Beijing: Chinese Academy of Surveying and Mapping, 2004. (in Chinese) [30] Yu Lewen, Zhang Da, Yu Bin, et al. Research of 3D laser scanning measurement system for mining [J]. Metal Mine, 2012, 436: 101−103. (in Chinese) [31] Gao Zhiguo. The research of terrestrial laser scanning data processing and modeling[D]. Xi'an: Chang'an University, 2010. (in Chinese) [32] Fang Wei. Research on automatic texture mapping of terrestrial laser scanning data combining photogrammetry techniques[D]. Wuhan: Wuhan University. (in Chinese) [33] Nayar S K, Watanabe M, Noguchi M. Real-time focus range sensor [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(12): 1186−1198. doi: 10.1109/34.546256 [34] Watanabe M, Nayar S K. Rational filters for passive depth from defocus [J]. International Journal of Computer Vision, 1998, 27(3): 203−225. doi: 10.1023/A:1007905828438 [35] Kou L, Zhang L, Zhang K, et al. A multi-focus image fusion method via region mosaicking on Laplacian pyramids [J]. PloS One, 2018, 13(5): e0191085. doi: 10.1371/journal.pone.0191085 [36] Bailey S W, Echevarria J I, Bodenheimer B, et al. Fast depth from defocus from focal stacks [J]. The Visual Computer, 2015, 31(12): 1697−1708. doi: 10.1007/s00371-014-1050-2 [37] Geng J. Structured-light 3D surface imaging: a tutorial [J]. Advances in Optics and Photonics, 2011, 3(2): 128−160. doi: 10.1364/AOP.3.000128 [38] Zuo C, Feng S, Huang L, et al. Phase shifting algorithms for fringe projection profilometry: A review [J]. Optics and Lasers in Engineering, 2018, 109: 23−59. doi: 10.1016/j.optlaseng.2018.04.019 [39] Boyer K L, Kak A C. Color-encoded structured light for rapid active ranging [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987(1): 14−28. [40] Zhang L, Curless B, Seitz S M. Rapid shape acquisition using color structured light and multi-pass dynamic programming[C]//First International Symposium on 3D Data Processing Visualization and Transmission, 2002: 24–36. [41] Pages J, Salvi J, Collewet C, et al. Optimised De Bruijn patterns for one-shot shape acquisition [J]. Image and Vision Computing, 2005, 23(8): 707−720. doi: 10.1016/j.imavis.2005.05.007 [42] Ito M, Ishii A. A three-level checkerboard pattern (TCP) projection method for curved surface measurement [J]. Pattern Recognition, 1995, 28(1): 27−40. doi: 10.1016/0031-3203(94)E0047-O [43] Maruyama M, Abe S. Range sensing by projecting multiple slits with random cuts [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(6): 647−651. doi: 10.1109/34.216735 [44] Morita H, Yajima K, Sakata S. Reconstruction of surfaces of 3d objects by m-array pattern projection method[C]//Second International Conference on Computer Vision, 1988: 468–473. [45] Posdamer J L, Altschuler M. Surface measurement by space-encoded projected beam systems [J]. Computer Graphics and Image Processing, 1982, 18(1): 1−17. doi: 10.1016/0146-664X(82)90096-X [46] Caspi D, Kiryati N, Shamir J. Range imaging with adaptive color structured light [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(5): 470−480. doi: 10.1109/34.682177 [47] Sansoni G, Corini S, Lazzari S, et al. Three-dimensional imaging based on gray-code light projection: characterization of the measuring algorithm and development of a measuring system for industrial applications [J]. Applied Optics, 1997, 36(19): 4463−4472. doi: 10.1364/AO.36.004463 [48] Zhang Z. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques [J]. Optics and Lasers in Engineering, 2012, 50(8): 1097−1106. doi: 10.1016/j.optlaseng.2012.01.007 [49] Je C, Lee S W, Park R-H. High-contrast color-stripe pattern for rapid structured-light range imaging[C]//European Conference on Computer Vision, 2004: 95–107. [50] Geng Z J. Rainbow three-dimensional camera: new concept of high-speed three-dimensional vision systems [J]. Optical Engineering, 1996, 35(2): 376−384. doi: 10.1117/1.601023 [51] Salvi J, Pagès J, Batlle J. Pattern codification strategies in structured light systems [J]. Pattern Recognition, 2004, 37(4): 827−849. doi: 10.1016/j.patcog.2003.10.002 [52] Gorthi S S, Rastogi P. Fringe projection techniques: Whither we are? [J]. Optics & Lasers in Engineering, 2010, 48(2): 133−140. [53] Reich C, Ritter R, Thesing J. 3-D shape measurement of complex objects by combining photogrammetry and fringe projection [J]. Optical Engineering, 2000, 39(1): 224−232. doi: 10.1117/1.602356 [54] Huang P S, Zhang C, Chiang F-P. High-speed 3-D shape measurement based on digital fringe projection [J]. Optical Engineering, 2003, 42(1): 163−169. doi: 10.1117/1.1525272 [55] Pan B, Kemao Q, Huang L, et al. Phase error analysis and compensation for nonsinusoidal waveforms in phase-shifting digital fringe projection profilometry [J]. Optics Letters, 2009, 34(4): 416−418. doi: 10.1364/OL.34.000416 [56] Quan C, He X, Wang C, et al. Shape measurement of small objects using LCD fringe projection with phase shifting [J]. Optics Communications, 2001, 189(1-3): 21−29. doi: 10.1016/S0030-4018(01)01038-0 [57] Zhang Z, Towers C E, Towers D P. Time efficient color fringe projection system for 3D shape and color using optimum 3-frequency Selection [J]. Optics Express, 2006, 14(14): 6444−6455. doi: 10.1364/OE.14.006444 [58] Wang Z, Nguyen D A, Barnes J C. Some practical considerations in fringe projection profilometry [J]. Optics & Lasers in Engineering, 2010, 48(2): 218−225. [59] Pan J, Huang P S, Chiang F-P. Color-coded binary fringe projection technique for 3-D shape measurement [J]. Optical Engineering, 2005, 44(2): 023606. doi: 10.1117/1.1840973 [60] Kühmstedt P, Munckelt C, Heinze M, et al. 3D shape measurement with phase correlation based fringe projection[C]//SPIE, 2007, 6616: 66160B. [61] Liu H C, Halioua M, Srinivasan V. Automated phase-measuring profilometry of 3-D diffuse objects [J]. Applied Optics, 1984, 23(18): 3105. doi: 10.1364/AO.23.003105 [62] Takeda M, Ina H, Kobayashi S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry [J]. JOSA, 1982, 72(1): 156−160. doi: 10.1364/JOSA.72.000156 [63] Su X, Chen W. Fourier transform profilometry: a review [J]. Optics and Lasers in Engineering, 2001, 35(5): 263−284. doi: 10.1016/S0143-8166(01)00023-9 [64] Su X, Zhang Q. Dynamic 3-D shape measurement method: A review [J]. Optics and Lasers in Engineering, 2010, 48(2): 191−204. [65] Kemao Q. Two-dimensional windowed Fourier transform for fringe pattern analysis: principles, applications and implementations [J]. Optics and Lasers in Engineering, 2007, 45(2): 304−317. doi: 10.1016/j.optlaseng.2005.10.012 [66] Kemao Q. Windowed Fourier transform for fringe pattern analysis [J]. Applied Optics, 2004, 43(13): 2695−2702. doi: 10.1364/AO.43.002695 [67] Zhong J, Weng J. Spatial carrier-fringe pattern analysis by means of wavelet transform: wavelet transform profilometry [J]. Applied Optics, 2004, 43(26): 4993−4998. doi: 10.1364/AO.43.004993 [68] Malacara D. Optical Shop Testing[M]. New York: John Wiley & Sons, 2007. [69] Bruning J H, Herriott D R, Gallagher J, et al. Digital wavefront measuring interferometer for testing optical surfaces and lenses [J]. Applied Optics, 1974, 13(11): 2693−2703. doi: 10.1364/AO.13.002693 [70] Su X Y, Bally G V, Vukicevic D. Phase-stepping grating profilometry: utilization of intensity modulation analysis in complex objects evaluation [J]. Optics Communications, 1993, 98(1-3): 141−150. doi: 10.1016/0030-4018(93)90773-X [71] Li J, Hassebrook L G, Guan C. Optimized two-frequency phase-measuring-profilometry light-sensor temporal-noise sensitivity [J]. Journal of the Optical Society of America A , 2003, 20(1): 106−15. [72] Zhang S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques [J]. Optics and Lasers in Engineering, 2010, 48(2): 149−158. [73] Van der Jeught S, Dirckx J J. Real-time structured light profilometry: a review [J]. Optics and Lasers in Engineering, 2016, 87: 18−31. doi: 10.1016/j.optlaseng.2016.01.011 [74] Su X, Chen W. Reliability-guided phase unwrapping algorithm: a review [J]. Optics and Lasers in Engineering, 2004, 42(3): 245−261. doi: 10.1016/j.optlaseng.2003.11.002 [75] Gutmann B, Weber H. Phase unwrapping with the branch-cut method: role of phase-field direction [J]. Applied Optics, 2000, 39(26): 4802−4816. doi: 10.1364/AO.39.004802 [76] Zappa E, Busca G. Comparison of eight unwrapping algorithms applied to Fourier-transform profilometry [J]. Optics and Lasers in Engineering, 2008, 46(2): 106−116. doi: 10.1016/j.optlaseng.2007.09.002 [77] Ghiglia D C, Romero L A. Minimum Lp-norm two-dimensional phase unwrapping [J]. JOSA A, 1996, 13(10): 1999−2013. doi: 10.1364/JOSAA.13.001999 [78] Trouve E, Nicolas J-M, Maitre H. Improving phase unwrapping techniques by the use of local frequency estimates [J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(6): 1963−1972. doi: 10.1109/36.729368 [79] Zebker H A, Lu Y. Phase unwrapping algorithms for radar interferometry: residue-cut, least-squares, and synthesis algorithms [J]. JOSA A, 1998, 15(3): 586−598. doi: 10.1364/JOSAA.15.000586 [80] Huntley J M, Saldner H. Temporal phase-unwrapping algorithm for automated interferogram analysis [J]. Applied Optics, 1993, 32(17): 3047−3052. doi: 10.1364/AO.32.003047 [81] Gushov V, Solodkin Y N. Automatic processing of fringe patterns in integer interferometers [J]. Optics and Lasers in Engineering, 1991, 14(4-5): 311−324. doi: 10.1016/0143-8166(91)90055-X [82] Sansoni G, Carocci M, Rodella R. Three-dimensional vision based on a combination of gray-code and phase-shift light projection: analysis and compensation of the systematic errors [J]. Appl Opt, 1999, 38(31): 6565−6573. doi: 10.1364/AO.38.006565 [83] Zhao H, Chen W, Tan Y. Phase-unwrapping algorithm for the measurement of three-dimensional object shapes [J]. Applied Optics, 1994, 33(20): 4497−4500. doi: 10.1364/AO.33.004497 [84] Cheng Y-Y, Wyant J C. Two-wavelength phase shifting interferometry [J]. Applied Optics, 1984, 23(24): 4539−4543. doi: 10.1364/AO.23.004539 [85] Creath K, Cheng Y Y, Wyant J C. Contouring aspheric surfaces using two-wavelength phase-shifting interferometry [J]. Optica Acta: International Journal of Optics, 1985, 32(12): 1455−1464. doi: 10.1080/713821689 [86] Burke J, Bothe T, Osten W, et al. Reverse engineering by fringe projection[C]// SPIE, 2002, 4778: 312–325. [87] Ding Y, Xi J, Yu Y, et al. Recovering the absolute phase maps of two fringe patterns with selected frequencies [J]. Optics Letters, 2011, 36(13): 2518−2520. doi: 10.1364/OL.36.002518 [88] Falaggis K, Towers D P, Towers C E. Algebraic solution for phase unwrapping problems in multiwavelength interferometry [J]. Applied Optics, 2014, 53(17): 3737−3747. doi: 10.1364/AO.53.003737 [89] Petković T, Pribanić T, Jonlić M. Temporal phase unwrapping using orthographic projection [J]. Optics and Lasers in Engineering, 2017, 90: 34−47. doi: 10.1016/j.optlaseng.2016.09.006 [90] Xing S, Guo H. Temporal phase unwrapping for fringe projection profilometry aided by recursion of Chebyshev polynomials [J]. Applied Optics, 2017, 56(6): 1591−1602. doi: 10.1364/AO.56.001591 [91] Li Z, Shi Y, Wang C, et al. Accurate calibration method for a structured light system [J]. Optical Engineering, 2008, 47(5): 053604. doi: 10.1117/1.2931517 [92] Saldner H O, Huntley J M. Temporal phase unwrapping: application to surface profiling of discontinuous objects [J]. Applied Optics, 1997, 36(13): 2770−2775. doi: 10.1364/AO.36.002770 [93] Martinez-Celorio R A, Davila A, Kaufmann G H, et al. Extension of the displacement measurement range for electronic speckle-shearing pattern interferometry using carrier fringes and a temporal-phase-unwrapping method [J]. Optical Engineering, 2000, 39(3): 751−758. doi: 10.1117/1.602423 [94] Huang L, Asundi A K. Phase invalidity identification framework with the temporal phase unwrapping method [J]. Measurement Science and Technology, 2011, 22(3): 035304. doi: 10.1088/0957-0233/22/3/035304 [95] Tian J, Peng X, Zhao X. A generalized temporal phase unwrapping algorithm for three-dimensional profilometry [J]. Optics and Lasers in Engineering, 2008, 46(4): 336−342. doi: 10.1016/j.optlaseng.2007.11.002 [96] Pedrini G, Alexeenko I, Osten W, et al. Temporal phase unwrapping of digital hologram sequences [J]. Applied Optics, 2003, 42(29): 5846−5854. doi: 10.1364/AO.42.005846 [97] Zuo C, Huang L, Zhang M, et al. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review [J]. Optics and Lasers in Engineering, 2016, 85: 84−103. [98] wii_百度百科[EB/OL]. [2020-01-10]. https://baike.baidu.com/item/wii/2285107?fr=aladdin. [99] 便携Wii概念-芭蕾体感掌机激发游戏潮[EB/OL]. [2020-01-12]. http://tech.hexun.com/2011-02-20/127427010.html. [100] Kinect[J]. Wikipedia, 2019. [101] Kinect销量60天破800万应用范围超越游戏[EB/OL]. [2020-01-08]. http://it.sohu.com/20110117/n278914946.shtml. [102] Techweb. 鲍尔默: Kinect上市60天销量达800万台[EB/OL]. [2020-01-08]. http://www.techweb.com.cn/world/2011-01-06/736155.shtml. [103] 家用游戏机越走越近[EB/OL]. [2020-01-12]. http://games.ifeng.com/pcgame/detail_2012_11/21/19381973_2.shtml. [104] Xbox | 官方网站[EB/OL]. [2020-01-10]. https://www.xbox.com/zh-CN. [105] Kinect终于停产了: 它是怎样最终失败的?[EB/OL]. [2020-01-10]. www.sohu.com/a/200412330_624619. [106] iPhoneX和三星Note8哪个值得买?[EB/OL]. [2020-01-12]. https://www.jb51.net/shouji/576894_3.html. [107] 买不起 iPhone X?你还可以选择 iPhone X ”青春版“[EB/OL]. [2020-01-12]. www.sohu.com/a/223349103_114837. [108] 支付宝刷脸设备补贴30亿取消, 新政策“不设上限上不封顶[EB/OL]. [2020-01-08]. https://weibo.com/ttarticle/p/show?id=2309404425892335058965#related. [109] 三维视觉终于火了!两年内从Face ID到刷脸支付, 下一个风口到了[EB/OL]. [2020-01-10]. https://xueqiu.com/9919963656/132900079. [110] 刷脸支付发展史, 微信、支付宝两大巨头的重金力推[EB/OL]. [2020-01-12]. www.sohu.com/a/341173479_120295819. [111] 坐地铁、取快递、领养老金……刷脸时代真的来了[EB/OL]. [2020-01-08]. www.sohu.com/a/308339470_395108. [112] “刷脸”时代来临: 坐地铁、取快递、领养老金[EB/OL]. [2020-01-08]. http://muji.bandao.cn/a/228954.html. [113] 双眼视觉和立体视觉[EB/OL]. [2020-01-10]. http://amuseum.cdstm.cn/AMuseum/perceptive/page_3_eye/page_3_2b-16.htm. [114] Snavely N, Seitz S M, Szeliski R. Photo tourism: exploring photo collections in 3D[C]//ACM SIGGRAPH 2006 Proceedings, Association for Computing Machinery, 2006: 835-846. [115] Snavely N, Seitz S M, Szeliski R. Modeling the world from internet photo collections [J]. International Journal of Computer Vision, 2008, 80(2): 189−210. doi: 10.1007/s11263-007-0107-3 [116] Westoby M J, Brasington J, Glasser N F, et al. 'Structure-from-Motion' photogrammetry: A low-cost, effective tool for geoscience applications [J]. Geomorphology, 2012, 179: 300−314. doi: 10.1016/j.geomorph.2012.08.021 [117] 想了解3D结构光, 看这份拆解就对了![EB/OL]. [2020-01-10]. https://www.jianshu.com/p/4365145add77. [118] 蚂里奥发布全新毫米级3D人脸感知解决方案[EB/OL]. [2020-01-12]. http://www.eepw.com.cn/article/201903/398768.htm. [119] Su X Y, Zhou W S, von Bally G, et al. Automated phase-measuring profilometry using defocused projection of a Ronchi grating [J]. Optics Communications, 1992, 94(6): 561−573. doi: 10.1016/0030-4018(92)90606-R [120] Beck M, Hofstetter D, Aellen T, et al. Continuous wave operation of a mid-infrared semiconductor laser at room temperature [J]. Science, 2002, 295(5553): 301−305. doi: 10.1126/science.1066408 [121] OSA | Recent Advances of VCSEL Photonics[EB/OL]. [2020-01-08]. https://www.osapublishing.org/jlt/abstract.cfm?uri=jlt-24-12-4502. [122] Swanson G J, Veldkamp W B. Diffractive optical elements for use in infrared systems [J]. Optical Engineering, 1989, 28(6): 286605. [123] Wyrowski F. Diffractive optical elements: iterative calculation of quantized, blazed phase structures [J]. JOSA A, 1990, 7(6): 961−969. doi: 10.1364/JOSAA.7.000961 [124] Wiedenmann D, Grabherr M, Jäger R, et al. High volume production of single-mode VCSELs[C]//SPIE, 2006, 6132: 613202. [125] VCSEL amplifier dot projector with folded-path slow-light waveguide for 3D depth sensing[EB/OL]. [2020-01-08]. https://ieeexplore.ieee.org/abstract/document/8516183. [126] Morinaga M, Gu X, Shimura K, et al. Compact dot projector based on folded path VCSEL amplifier for structured light sensing[C]//Conference on Lasers and Electro-Optics (2019), Optical Society of America, 2019: SM4N. 4. [127] VCSEL为何突然火了?[EB/OL]. [2020-01-10]. http://www.sohu.com/a/295863707_256868. [128] 前置3D成像将以结构光为主流四大部件难度各异[EB/OL]. [2020-01-10]. www.sohu.com/a/154077271_99935473. [129] Durdle N G, Thayyoor J, Raso V J. An improved structured light technique for surface reconstruction of the human trunk[C]//Conference Proceedings. IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No. 98TH8341), 1998, 2: 874–877. [130] Chen C S, Hung Y P, Chiang C C, et al. Range data acquisition using color structured lighting and stereo vision [J]. Image and Vision Computing, 1997, 15(6): 445−456. doi: 10.1016/S0262-8856(96)01148-1 [131] MacWilliams F J, Sloane N J A. Pseudo-random sequences and arrays [J]. Proceedings of the IEEE, 1976, 64(12): 1715−1729. doi: 10.1109/PROC.1976.10411 [132] Salvi J, Batlle J, Mouaddib E. A robust-coded pattern projection for dynamic 3D scene measurement [J]. Pattern Recognition Letters, 1998, 19(11): 1055−1065. doi: 10.1016/S0167-8655(98)00085-3 [133] Pan B, Qian K, Xie H, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review [J]. Measurement Science and Technology, 2009, 20(6): 062001. doi: 10.1088/0957-0233/20/6/062001 [134] Mei X, Sun X, Zhou M, et al. On building an accurate stereo matching system on graphics hardware[C]// 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), 2011: 467–474. [135] Zhang Ke, Lu Jiangbo, Lafruit G. Cross-based local stereo matching using orthogonal integral images [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2009, 19(7): 1073−1079. doi: 10.1109/TCSVT.2009.2020478 [136] Hirschmuller H. Accurate and efficient stereo processing by semi-global matching and mutual information[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), 2005, 2: 807–814. [137] Zhou P, Zhu J, Jing H. Optical 3-D surface reconstruction with color binary speckle pattern encoding [J]. Optics Express, 2018, 26(3): 3452. doi: 10.1364/OE.26.003452 [138] Pan B, Xie H, Wang Z, et al. Study on subset size selection in digital image correlation for speckle patterns [J]. Optics Express, 2008, 16(10): 7037. doi: 10.1364/OE.16.007037 [139] Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222−1239. doi: 10.1109/34.969114 [140] Sun J, Zheng N N, Shum H Y. Stereo matching using belief propagation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(7): 14. [141] Jae Chul Kim, Kyoung Mu Lee, Byoung Tae Choi, et al. A dense stereo matching using two-pass dynamic programming with generalized ground control points[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), 2005, 2: 1075–1082. [142] Forstmann S, Kanou Y, Jun Ohya, et al. Real-time stereo by using dynamic programming[C]// 2004 Conference on Computer Vision and Pattern Recognition Workshop, IEEE, 2004: 29–29. [143] 体感设备-北京华捷艾米科技有限公司[EB/OL]. [2020-01-12]. http://www.hjimi.com/?pro/tgsb/. [144] 产品参数信息 – 图漾科技-存在即被感知[EB/OL]. [2020-01-12]. https://www.percipio.xyz/dev_detail/?model_id=276. [145] 电子行业智能手机走向存量时代, 关注新技术渗透带来的投资机会系列十: TOF, 海外市场发展迅速, 国内产业链机会来临[R]. 广州: 广发证券, 2016. [146] 电子行业深度研究报告: 科技红利大时代8~3D摄像创新十年最夯, VCSEL引领激光应用里程碑[R]. 贵州: 华创证券, 2017. [147] 电子元器件行业: 为什么现在需要重视脸部识别[R]. 深圳: 安信证券, 2016 . [148] 技术剖解: 人脸识别三大优势与前景分析[EB/OL]. [2020-01-12]. http://tech.sina.com.cn/roll/2013-04-25/00592729625.shtml. [149] 2017百家VR公司巡礼[EB/OL]. [2020-01-12]. www.sohu.com/a/195441916_104421. [150] 佚名. 跑步进入未来?谈Leap Motion与人机交互[EB/OL]. [2020-01-12]. https://acc.pconline.com.cn/437/4375916.html. [151] 微软Hololens_百度百科[EB/OL]. [2020-01-10]. https://baike.baidu.com/item/%E5%BE%AE%E8%BD%AFHololens/16690972?fromtitle=Microsoft%20HoloLens&fromid=16630317. [152] 手势识别也是香饽饽[EB/OL]. [2020-01-10]. https://yq.aliyun.com/articles/599214. [153] 2018年全球VR/AR行业投资现状分析中国是重要投资目的地[EB/OL]. [2020-01-10]. https://www.qianzhan.com/analyst/detail/220/180606-41ef69ab.html. [154] 众趣科技只需90分钟就能为你克隆3D实景[EB/OL]. [2020-01-10]. www.sohu.com/a/228724895_99985415. [155] 美国公司制作3D面具成功骗过微信支付宝等人脸支付[EB/OL]. [2020-01-12]. https://www.shangyexinzhi.com/article/details/id-387726/. [156] 全球首款TOF手机来袭[EB/OL]. [2020-01-10]. www.sohu.com/a/247788268_115037. [157] Liu K, Wang Y, Lau D L, et al. Dual-frequency pattern scheme for high-speed 3-D shape measurement [J]. Optics Express, 2010, 18(5): 5229−5244. doi: 10.1364/OE.18.005229 [158] Zuo C, Chen Q, Gu G, et al. High-speed three-dimensional profilometry for multiple objects with complex shapes [J]. Optics Express, 2012, 20(17): 19493−19510. doi: 10.1364/OE.20.019493 [159] Weise T, Leibe B, Van Gool L. Fast 3D Scanning with automatic motion compensation[C]//Computer Vision and Pattern Recognition, 2007. CVPR ’07. IEEE Conference on, 2007: 1–8. [160] Li Z, Zhong K, Li Y F, et al. Multiview phase shifting: a full-resolution and high-speed 3D measurement framework for arbitrary shape dynamic objects [J]. Optics Letters, 2013, 38(9): 1389−1391. doi: 10.1364/OL.38.001389 [161] Tao T, Chen Q, Da J, et al. Real-time 3-D shape measurement with composite phase-shifting fringes and multi-view system [J]. Optics Express, 2016, 24(18): 20253−20269. doi: 10.1364/OE.24.020253 [162] Qian J, Tao T, Feng S, et al. Motion-artifact-free dynamic 3D shape measurement with hybrid Fourier-transform phase-shifting profilometry [J]. Optics Express, 2019, 27(3): 2713. doi: 10.1364/OE.27.002713 [163] Tao T, Chen Q, Feng S, et al. High-precision real-time 3D shape measurement based on a quad-camera system [J]. Journal of Optics, 2018, 20(1): 014009. doi: 10.1088/2040-8986/aa9e0f [164] Liu Z, Zibley P C, Zhang S. Motion-induced error compensation for phase shifting profilometry [J]. Optics Express, 2018, 26(10): 12632−12637. doi: 10.1364/OE.26.012632 [165] Feng S, Zuo C, Tao T, et al. Robust dynamic 3-D measurements with motion-compensated phase-shifting profilometry [J]. Optics and Lasers in Engineering, 2018, 103: 127−138. doi: 10.1016/j.optlaseng.2017.12.001 [166] Zhang Y, Xiong Z, Yang Z, et al. Real-time scalable depth sensing with hybrid structured light illumination [J]. IEEE Transactions on Image Processing, 2013, 23(1): 97−109. [167] Li B, Liu Z, Zhang S. Motion-induced error reduction by combining Fourier transform profilometry with phase-shifting profilometry [J]. Optics Express, 2016, 24(20): 23289. doi: 10.1364/OE.24.023289 [168] Liu X, Peng X, Chen H, et al. Strategy for automatic and complete three-dimensional optical digitization [J]. Optics Letters, 2012, 37(15): 3126. doi: 10.1364/OL.37.003126 [169] Song L, Ru Y, Yang Y, et al. Full-view three-dimensional measurement of complex surfaces [J]. Optical Engineering, 2018, 57(10): 1. [170] Nießner M, Zollhöfer M, Izadi S, et al. Real-time 3D reconstruction at scale using voxel hashing [J]. ACM Transactions on Graphics, 2013, 32(6): 1−11. [171] Epstein E, Granger-Piche M, Poulin P. Exploiting mirrors in interactive reconstruction with structured light[C]//Vision, Modeling, and Visualization, 2004: 125-132. [172] Lanman D, Crispell D, Taubin G. Surround structured lighting: 3-D scanning with orthographic illumination [J]. Computer Vision and Image Understanding, 2009, 113(11): 1107−1117. doi: 10.1016/j.cviu.2009.03.016 [173] Chen B, Pan B. Mirror-assisted panoramic-digital image correlation for full-surface 360-deg deformation measurement [J]. Measurement, 2019, 132: 350−358. doi: 10.1016/j.measurement.2018.09.046 [174] Holz D, Ichim A E, Tombari F, et al. Registration with the point cloud library: A modular framework for aligning in 3-D [J]. IEEE Robotics & Automation Magazine, 2015, 22(4): 110−124. [175] Mohammadzade H, Hatzinakos D. Iterative closest normal point for 3D face recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(2): 381−397. doi: 10.1109/TPAMI.2012.107 [176] Qian J, Feng S, Tao T, et al. High-resolution real-time 360° 3D model reconstruction of a handheld object with fringe projection profilometry [J]. Optics Letters, 2019, 44(23): 5751. doi: 10.1364/OL.44.005751 [177] Mariottini G L, Scheggi S, Morbidi F, et al. Planar mirrors for image-based robot localization and 3-D reconstruction [J]. Mechatronics, 2012, 22(4): 398−409. doi: 10.1016/j.mechatronics.2011.09.004 [178] Wang P, Wang J, Xu J, et al. Calibration method for a large-scale structured light measurement system [J]. Applied Optics, 2017, 56(14): 3995. doi: 10.1364/AO.56.003995 [179] Yin W, Feng S, Tao T, et al. Calibration method for panoramic 3D shape measurement with plane mirrors [J]. Optics Express, 2019, 27(25): 36538. doi: 10.1364/OE.27.036538 [180] Feng S, Chen Q, Zuo C, et al. Automatic identification and removal of outliers for high-speed fringe projection profilometry [J]. Optical Engineering, 2013, 52(1): 013605−013605. doi: 10.1117/1.OE.52.1.013605 [181] Lu J, Mo R, Sun H, et al. Invalid phase values removal method for absolute phase recovery [J]. Applied Optics, 2016, 55(2): 387−394. doi: 10.1364/AO.55.000387 [182] Lu J, Mo R, Sun H, et al. Simplified absolute phase retrieval of dual-frequency fringe patterns in fringe projection profilometry [J]. Optics Communications, 2016, 364: 101−109. doi: 10.1016/j.optcom.2015.11.022 [183] Wang H, Kemao Q, Soon S H. Valid point detection in fringe projection profilometry [J]. Optics Express, 2015, 23(6): 7535−7549. doi: 10.1364/OE.23.007535 [184] Yau S T. High dynamic range scanning technique [J]. Optical Engineering, 2009, 48(3): 033604. doi: 10.1117/1.3099720 [185] Qi Z, Wang Z, Huang J, et al. Improving the quality of stripes in structured-light three-dimensional profile measurement [J]. Optical Engineering, 2016, 56(3): 031208. doi: 10.1117/1.OE.56.3.031208 [186] Long Y, Wang S, Wu W, et al. Accurate identification of saturated pixels for high dynamic range measurement [J]. Optical Engineering, 2015, 54(4): 043106. doi: 10.1117/1.OE.54.4.043106 [187] Zhang B, Ouyang Y, Zhang S. High dynamic range saturation intelligence avoidance for three-dimensional shape measurement[C]//IEEE, 2015: 981–990. [188] Ekstrand L. Autoexposure for three-dimensional shape measurement using a digital-light-processing projector [J]. Optical Engineering, 2011, 50(12): 123603. doi: 10.1117/1.3662387 [189] Zhong K, Li Z, Zhou X, et al. Enhanced phase measurement profilometry for industrial 3D inspection automation [J]. The International Journal of Advanced Manufacturing Technology, 2015, 76(9-12): 1563−1574. doi: 10.1007/s00170-014-6360-z [190] Rao L, Da F. High dynamic range 3D shape determination based on automatic exposure selection [J]. Journal of Visual Communication and Image Representation, 2018, 50: 217−226. doi: 10.1016/j.jvcir.2017.12.003 [191] Song Z, Jiang H, Lin H, et al. A high dynamic range structured light means for the 3D measurement of specular surface [J]. Optics and Lasers in Engineering, 2017, 95: 8−16. doi: 10.1016/j.optlaseng.2017.03.008 [192] Feng S, Chen Q, Zuo C, et al. Fast three-dimensional measurements for dynamic scenes with shiny surfaces [J]. Optics Communications, 2017, 382: 18−27. doi: 10.1016/j.optcom.2016.07.057 [193] Waddington C, Kofman J. Saturation avoidance by adaptive fringe projection in phase-shifting 3D surface-shape measurement[C]// IEEE, 2010: 1–4. [194] Waddington C, Kofman J. Modified sinusoidal fringe-pattern projection for variable illuminance in phase-shifting three-dimensional surface-shape metrology [J]. Optical Engineering, 2014, 53(8): 084109. doi: 10.1117/1.OE.53.8.084109 [195] Zhang L, Chen Q, Zuo C, et al. High dynamic range 3D shape measurement based on the intensity response function of a camera [J]. Applied Optics, 2018, 57(6): 1378. doi: 10.1364/AO.57.001378 [196] Li D, Kofman J. Adaptive fringe-pattern projection for image saturation avoidance in 3D surface-shape measurement [J]. Optics Express, 2014, 22(8): 9887. doi: 10.1364/OE.22.009887 [197] Chen C, Gao N, Wang X, et al. Adaptive pixel-to-pixel projection intensity adjustment for measuring a shiny surface using orthogonal color fringe pattern projection [J]. Measurement Science and Technology, 2018, 29(5): 055203. doi: 10.1088/1361-6501/aab07a [198] Lin H, Gao J, Mei Q, et al. Adaptive digital fringe projection technique for high dynamic range three-dimensional shape measurement [J]. Optics Express, 2016, 24(7): 7703. doi: 10.1364/OE.24.007703 [199] Lin H, Gao J, Mei Q, et al. Three-dimensional shape measurement technique for shiny surfaces by adaptive pixel-wise projection intensity adjustment [J]. Optics and Lasers in Engineering, 2017, 91: 206−215. doi: 10.1016/j.optlaseng.2016.11.015 [200] Chen S, Xia R, Zhao J, et al. Analysis and reduction of phase errors caused by nonuniform surface reflectivity in a phase-shifting measurement system [J]. Optical Engineering, 2017, 56(3): 033102. doi: 10.1117/1.OE.56.3.033102 [201] Babaie G, Abolbashari M, Farahi F. Dynamics range enhancement in digital fringe projection technique [J]. Precision Engineering, 2015, 39: 243−251. doi: 10.1016/j.precisioneng.2014.06.007 [202] Sheng H, Xu J, Zhang S. Dynamic projection theory for fringe projection profilometry [J]. Applied Optics, 2017, 56(30): 8452. doi: 10.1364/AO.56.008452 [203] Qi Z, Wang Z. Highlight removal based on the regional-projection fringe projection method [J]. Optical Engineering, 2018, 57(04): 1. [204] Ri S, Fujigaki M, Morimoto Y. Intensity range extension method for three-dimensional shape measurement in phase-measuring profilometry using a digital micromirror device camera [J]. Applied Optics, 2008, 47(29): 5400. doi: 10.1364/AO.47.005400 [205] Chen T, Lensch H P A, Fuchs C, et al. Polarization and phase-shifting for 3D scanning of translucent objects[C]// IEEE, 2007: 1–8. [206] Salahieh B, Chen Z, Rodriguez J J, et al. Multi-polarization fringe projection imaging for high dynamic range objects [J]. Optics Express, 2014, 22(8): 10064. doi: 10.1364/OE.22.010064 [207] Cai Z, Liu X, Peng X, et al. Structured light field 3D imaging[J]. Optics Express, 2016, 24(18): 20324-20334. [208] Feng S, Zhang Y, Chen Q, et al. General solution for high dynamic range three-dimensional shape measurement using the fringe projection technique [J]. Optics and Lasers in Engineering, 2014, 59: 56−71. doi: 10.1016/j.optlaseng.2014.03.003 [209] Liu G, Liu X Y, Feng Q Y. 3D shape measurement of objects with high dynamic range of surface reflectivity [J]. Applied Optics, 2011, 50(23): 4557. doi: 10.1364/AO.50.004557 [210] Jiang H, Zhao H, Li X. High dynamic range fringe acquisition: A novel 3-D scanning technique for high-reflective surfaces [J]. Optics and Lasers in Engineering, 2012, 50(10): 1484−1493. doi: 10.1016/j.optlaseng.2011.11.021 [211] Zhao H, Liang X, Diao X, et al. Rapid in-situ 3D measurement of shiny object based on fast and high dynamic range digital fringe projector [J]. Optics and Lasers in Engineering, 2014, 54: 170−174. doi: 10.1016/j.optlaseng.2013.08.002 [212] Yin Y, Cai Z, Jiang H, et al. High dynamic range imaging for fringe projection profilometry with single-shot raw data of the color camera [J]. Optics and Lasers in Engineering, 2017, 89: 138−144. doi: 10.1016/j.optlaseng.2016.08.019 [213] Jiang C, Bell T, Zhang S. High dynamic range real-time 3D shape measurement [J]. Optics Express, 2016, 24(7): 7337. doi: 10.1364/OE.24.007337 [214] Wang M, Du G, Zhou C, et al. Enhanced high dynamic range 3D shape measurement based on generalized phase-shifting algorithm [J]. Optics Communications, 2017, 385: 43−53. doi: 10.1016/j.optcom.2016.10.023 [215] Chen Y, He Y, Hu E. Phase deviation analysis and phase retrieval for partial intensity saturation in phase-shifting projected fringe profilometry [J]. Optics Communications, 2008, 281(11): 3087−3090. doi: 10.1016/j.optcom.2008.01.070 [216] Hu E, He Y, Chen Y. Study on a novel phase-recovering algorithm for partial intensity saturation in digital projection grating phase-shifting profilometry [J]. Optik-International Journal for Light and Electron Optics, 2010, 121(1): 23−28. doi: 10.1016/j.ijleo.2008.05.010 [217] Chen B, Zhang S. High-quality 3D shape measurement using saturated fringe patterns [J]. Optics and Lasers in Engineering, 2016, 87: 83−89. doi: 10.1016/j.optlaseng.2016.04.012 [218] Qi Z, Wang Z, Huang J, et al. Error of image saturation in the structured-light method [J]. Applied Optics, 2018, 57(1): A181−A188. doi: 10.1364/AO.57.00A181 [219] Zhang L, Chen Q, Zuo C, et al. High dynamic range 3D shape measurement based on time domain superposition [J]. Measurement Science and Technology, 2019, 30(6): 065004. [220] Feng S, Zhang L, Zuo C, et al. High dynamic range 3D measurements with fringe projection profilometry: a review [J]. Measurement Science and Technology, 2018, 29(12): 122001. doi: 10.1088/1361-6501/aae4fb [221] Feng S, Chen Q, Gu G, et al. Fringe pattern analysis using deep learning [J]. Advanced Photonics, 2019, 1(2): 025001. [222] Feng S, Zuo C, Yin W, et al. Micro deep learning profilometry for high-speed 3D surface imaging [J]. Optics and Lasers in Engineering, 2019, 121: 416−427. doi: 10.1016/j.optlaseng.2019.04.020 [223] Lei S, Zhang S. Flexible 3-D shape measurement using projector defocusing [J]. Optics Letters, 2009, 34(20): 3080−3082. doi: 10.1364/OL.34.003080 [224] Ayubi G A, Ayubi J A, Di Martino J M, et al. Pulse-width modulation in defocused three-dimensional fringe projection [J]. Optics Letters, 2010, 35(21): 3682−3684. doi: 10.1364/OL.35.003682 [225] Zuo C, Chen Q, Feng S, et al. Optimized pulse width modulation pattern strategy for three-dimensional profilometry with projector defocusing [J]. Applied Optics, 2012, 51(19): 4477−4490. doi: 10.1364/AO.51.004477 [226] Zuo C, Chen Q, Gu G, et al. High-speed three-dimensional shape measurement for dynamic scenes using bi-frequency tripolar pulse-width-modulation fringe projection [J]. Optics and Lasers in Engineering, 2013, 51(8): 953−960. doi: 10.1016/j.optlaseng.2013.02.012 [227] Wang Y, Zhang S. Superfast multifrequency phase-shifting technique with optimal pulse width modulation [J]. Optics Express, 2011, 19(6): 5149−5155. doi: 10.1364/OE.19.005149 [228] Wang Y, Zhang S. Three-dimensional shape measurement with binary dithered patterns [J]. Applied Optics, 2012, 51(27): 6631−6636. doi: 10.1364/AO.51.006631 [229] Dai J, Zhang S. Phase-optimized dithering technique for high-quality 3D shape measurement [J]. Optics and Lasers in Engineering, 2013, 51(6): 790−795. doi: 10.1016/j.optlaseng.2013.02.003 [230] Dai J, Li B, Zhang S. High-quality fringe pattern generation using binary pattern optimization through symmetry and periodicity [J]. Optics and Lasers in Engineering, 2014, 52: 195−200. doi: 10.1016/j.optlaseng.2013.06.010 [231] Sun J, Zuo C, Feng S, et al. Improved intensity-optimized dithering technique for 3D shape measurement [J]. Optics and Lasers in Engineering, 2015, 66: 158−164. doi: 10.1016/j.optlaseng.2014.09.008 [232] Dai J, Li B, Zhang S. Intensity-optimized dithering technique for three-dimensional shape measurement with projector defocusing [J]. Optics and Lasers in Engineering, 2014, 53: 79−85. doi: 10.1016/j.optlaseng.2013.08.015 [233] Zhang S, Van D W D, Oliver J. Superfast phase-shifting method for 3-D shape measurement [J]. Optics Express, 2010, 18(9): 9684. doi: 10.1364/OE.18.009684 [234] Gong Y, Zhang S. Ultrafast 3-D shape measurement with an off-the-shelf DLP projector [J]. Optics Express, 2010, 18(19): 19743−19754. doi: 10.1364/OE.18.019743 [235] Zuo C, Tao T, Feng S, et al. Micro Fourier Transform Profilometry (μ FTP): 3D shape measurement at 10, 000 frames per second [J]. Optics and Lasers in Engineering, 2018, 102: 70−91. doi: 10.1016/j.optlaseng.2017.10.013 [236] Zhang Q, Su X, Cao Y, et al. Optical 3-D shape and deformation measurement of rotating blades using stroboscopic structured illumination [J]. Optical Engineering, 2005, 44(11): 113601. doi: 10.1117/1.2127927 [237] Schaffer M, Grosse M, Harendt B, et al. High-speed optical 3-d measurements for shape representation [J]. Optics and Photonics News, 2011, 22(12): 49−49. doi: 10.1364/OPN.22.12.000049 [238] Schaffer M, Grosse M, Harendt B, et al. High-speed three-dimensional shape measurements of objects with laser speckles and acousto-optical deflection [J]. Optics Letters, 2011, 36(16): 3097−3099. doi: 10.1364/OL.36.003097 [239] Schaffer M, Grosse M, Harendt B, et al. Statistical patterns: an approach for high-speed and high-accuracy shape measurements [J]. Optical Engineering, 2014, 53(11): 112205. doi: 10.1117/1.OE.53.11.112205 [240] Grosse M, Schaffer M, Harendt B, et al. Fast data acquisition for three-dimensional shape measurement using fixed-pattern projection and temporal coding [J]. Optical Engineering, 2011, 50(10): 100503. doi: 10.1117/1.3646100 [241] Fujigaki M, Sakaguchi T, Murata Y. Development of a compact 3D shape measurement unit using the light-source-stepping method [J]. Optics and Lasers in Engineering, 2016, 85: 9−17. doi: 10.1016/j.optlaseng.2016.04.016 [242] Heist S, Mann A, Kühmstedt P, et al. Array projection of aperiodic sinusoidal fringes for high-speed three-dimensional shape measurement [J]. Optical Engineering, 2014, 53(11): 112208. doi: 10.1117/1.OE.53.11.112208 [243] Heist S, Lutzke P, Schmidt I, et al. High-speed three-dimensional shape measurement using GOBO projection [J]. Optics and Lasers in Engineering, 2016, 87: 90−96. doi: 10.1016/j.optlaseng.2016.02.017 [244] Heist S. 5D hyperspectral imaging: fast and accurate measurement of surface shape and spectral characteristics using structured light [J]. Optics Express, 2018: 14. [245] Landmann M, Heist S, Dietrich P, et al. High-speed 3D thermography [J]. Optics and Lasers in Engineering, 2019, 121: 448−455. doi: 10.1016/j.optlaseng.2019.05.009 [246] Zhang M, Chen Q, Tao T, et al. Robust and efficient multi-frequency temporal phase unwrapping: optimal fringe frequency and pattern sequence selection [J]. Optics Express, 2017, 25(17): 20381. doi: 10.1364/OE.25.020381 -

 点击查看大图
点击查看大图
计量
- 文章访问数: 7605
- HTML全文浏览量: 2237
- 被引次数: 0






 下载:
下载: