-
光学三维成像(又称三维传感,三维测量)技术已经被广泛地运用到了机械工程、生物识别、机器视觉、智能制造等领域[1-3]。在众多的测量方法中,结构光三维成像技术由于其具有精度高和灵活性好等特点,一直是行业内的研究热点之一[4-6]。过去十余年间,随着硬件设备,如高速相机、数字光处理(Digital Light Processing, DLP) 投影仪以及图形处理器(Graphics Processing Unit, GPU)等的高速发展,较高精度的高速[7-8]以及实时[9-10]三维测量逐渐成为了主流研究方向。近两年,深度学习技术的不断成熟,使得众多学者开始探索将深度学习技术运用到结构光三维成像技术中的可能性,并取得了一系列研究进展[11-17]。
基于结构光照明的三维成像技术通常是通过投影器件投影结构光场到被测物体表面,在另一角度利用成像器件拍摄变形光场,通过解调光场信息,最终获取物体的三维形貌信息。根据调制信息的不同,结构光场可被分为强度调制光场和相位调制光场两大类。其中强度调制光场包括散斑结构光场[18-19],多线结构光场[20-21],二值结构光场(如空间编码的De Bruijn码[22-23],时间编码的格雷码[24]);相位调制光场包括单频正弦光栅[25-27]和复合正弦光栅[28-31]。
由于格雷码采用二值编码,是一种误差最小化的编码方式,因此基于格雷码图案投影的三维成像技术具有良好的鲁棒性和抗噪性,且不易受投影系统的非线性影响,被广泛地应用到工业零部件检测、逆向工程、文物数字化以及生物医学等应用领域。文中主要概述了基于格雷码图案投影的结构光三维成像技术,回顾了不同种类方法的基本原理以及研究进展,给出了课题组在基于格雷码图案投影三维成像相关原理和应用研究上的结果,分析了格雷码二值图案在三维面形测量应用中的优缺点和适用范围,并指出了该领域今后的发展动向。
-
格雷码(Gray Code)是由贝尔实验室的Frank Gray在1940年代首先提出[32]。要求在一组数的编码中,任意两个相邻的代码只有一位二进制数不同(即汉明距离为1)。另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。由于格雷码是误差最小化的可靠编码方式,它也被众多学者运用到了结构光三维成像技术当中[24, 33]。
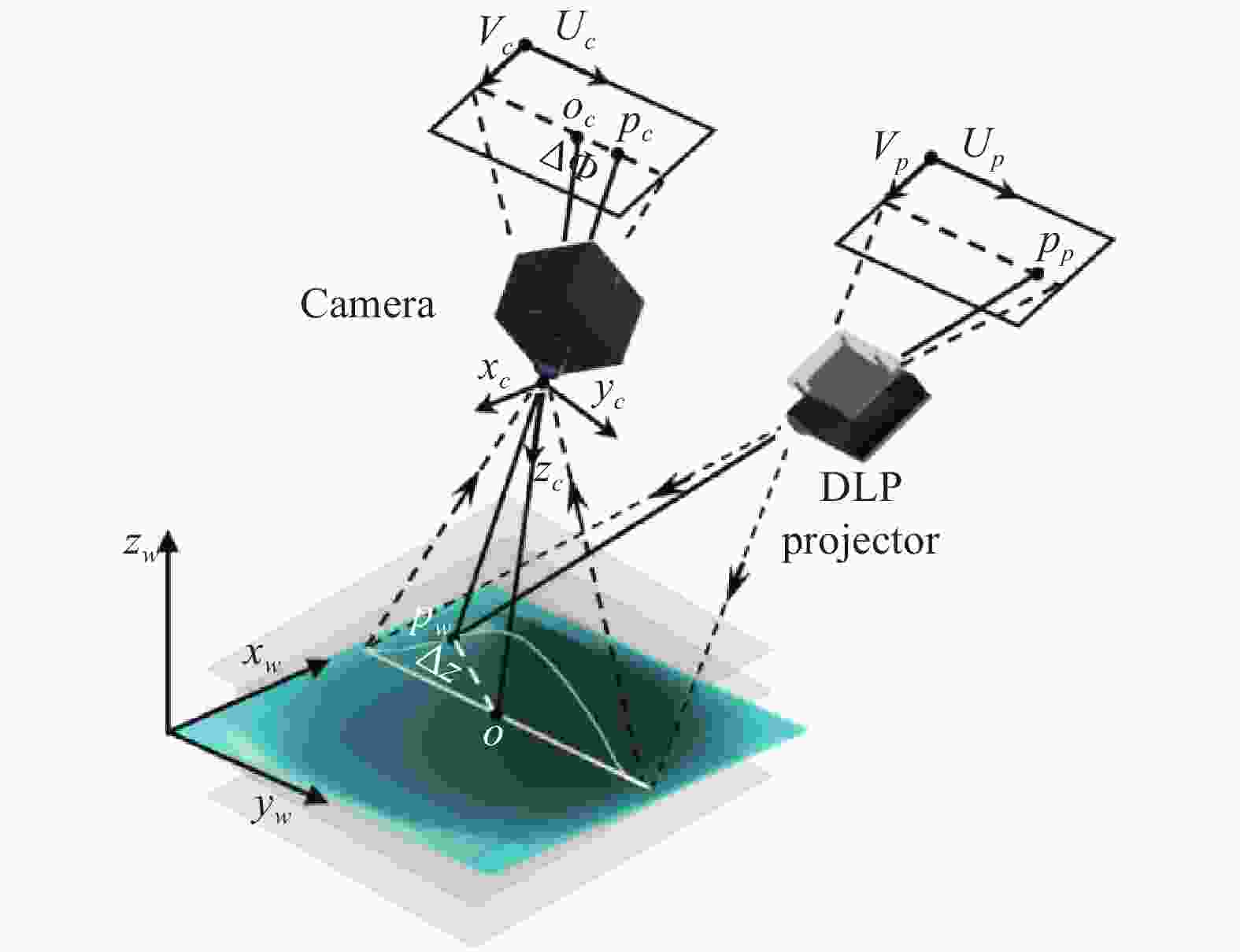
格雷码本身作为一种结构光,可以直接用来调制被测面形,也可以用来辅助其他结构光的信息获取和计算。典型的基于结构光的三维成像技术基本原理如图1所示,一系列格雷码编码图案通过投影仪依次投影到被测物体表面,在另一角度利用相机同步拍摄受物体表面高度调制的变形条纹,通过格雷码解码,提取格雷码变形前后边沿或中心位置信息,利用相机和投影仪所构建的三角几何关系可以唯一确定任一点空间几何位置,最后通过对测量系统的标定实现对物体表面形貌的三维重建。

图 1 基于格雷码图案投影的结构光三维成像技术原理图
Figure 1. Schematic diagram of 3D imaging technique based on Gray-coded structured illumination
根据格雷码在三维成像中所起作用的不同,文中将基于格雷码图案投影的结构光三维成像技术分为格雷码直接编码技术和格雷码辅助编码技术两大类,格雷码辅助编码技术下再细分为格雷码辅助线移技术、格雷码辅助条纹边沿移动技术以及格雷码辅助相移技术三个小类,后文将分别对这几种技术的原理方法,关键问题进行简要回顾。
-
格雷码图案作为一种结构光,可以直接用来调制被测面形,Inokuchi等人首先将格雷码条纹应用到形貌测量当中[24],改进了传统测量方法中用普通二进制条纹对物体进行调制的方法[34],格雷码编码方式通过投影一系列如图2(a)所示的二值格雷码码字对应图案到被测物体表面,投影图案将受到被测面形高度调制对应发生弯曲变形,记录变形格雷码图案后,其解码方式如图2(b)所示,计算过程见公式(1)和(2)。
$$ V(x,y) = \sum\limits_{i = 1}^m {G{C_i}(x,y)*{2^{(m - i)}}} $$ (1) $$ k(x,y) = i(V(x,y)) $$ (2) 式中:m代表格雷码总共幅数;i(∙)用来查找计算十进制码字V和解码码字k之间的已知关系。

图 2 格雷码直接编码技术。(a) 投影条纹;(b) 格雷码解码过程;(c) 零相交边界提取方法;(d) 正反条纹边界提取法;(e) 改进的零相交边界提取法。
Figure 2. Direct Gray-coded coding technique. (a) Projected patterns; (b) Decoding process of Gray code; (c) Zero-crossing edge detection method; (d) Positive and negative edge detection method; (e) Improved zero-crossing edge detection method
该解码示意图中可以看到,相邻两个码字之间四幅图中只有一位码字改变,可以将解码的误码率降到最低。格雷码的变形被用来解调物体的高度信息,且格雷码的编码特性可以唯一定位到每一根条纹,因此每根条纹的中心或者边界都需要被提取出来再利用三角法原理去解算物体高度。
条纹边界的提取比条纹中心具有更高的准确度,因此如何准确地提取条纹的边界是格雷码编码技术中的一个核心问题。Trobina等人在1995提出了基于格雷码编码技术的误差模型[35],并详细分析了影响此技术精度的各类因素。关于边界提取的问题,文中指出,通过额外投影全黑和全白的图像,求取拍回的两幅图像各像素灰度的平均值作为全场格雷码点对点二值化的阈值,进而获得格雷码黑白边沿。该方法能有效解决被测物体表面不同反射率导致的变形格雷码图案不均匀的二值化难题,但只能获取整像素的提取精度,要想获取亚像素级别的提取精度可以采用零相交(zero-crossing)方法或是正反条纹投影法。零相交方法是探测边沿二阶导数的过零点,如图2(c)所示,对条纹进行二阶求导操作后通过线性内插的方式找到亚像素点作为边界点,此方法的关键在于如何找到最优的梯度滤波尺寸大小。另一种方法是投影黑白翻转的两组格雷码条纹通过寻找两条剖线的交点来确定边沿点的位置,如图2(d)所示。通过实验比较,Trobina在文中总结后两种亚像素边沿提取方法的精度通常高于阈值法,而正反条纹投影法的提取精度略高于零相交方法。随后为了解决在高反射物体表面边沿提取问题,Song等人改进了零相交提取方法[36]。改进方法如图2(e)所示,当条纹投影到物体高反射区域时,条纹边沿会出现过曝的区域,因此使用以上几种方法无法找到边沿点位置。改进方法通过将正反两幅过曝的条纹图做差,再用做差结果的两个过零点均值作为条纹边沿点,此方法可有效解决在高动态测量环境中的边沿提取问题。
基于格雷码直接编码技术的测量方法因为只有格雷码边沿或中心才能解算物体形貌信息,因此测量结果都呈现离散化的“多线”分布,测量的空间分辨率不高。基于此,众多的格雷码辅助编码技术被提出来进一步提升格雷码直接编码技术的测量空间分辨率。
-
不同于格雷码直接编码技术中直接利用格雷码来重建三维形貌,格雷码也被用来辅助其他结构光的信息获取和计算,称之为格雷码辅助编码技术。因为格雷码具有鲁棒的解码特性以及无歧义性,能很好地辅助消除其他结构光的空间歧义性。根据辅助结构光类型的不同,格雷码辅助编码技术可分为格雷码辅助线移技术、格雷码辅助条纹边沿移动技术以及格雷码辅助相移技术三类。
-
由于格雷码只有边沿像素可以携带物体信息,因此要想提高测量的空间分辨率就需要通过投影更多的格雷码字来提升边沿数目,但当格雷码条纹宽度过小时,成像系统的低通滤波特性会导致格雷码的边沿更难被准确地探测定位。因此,格雷码辅助线移技术被Gühring等人研究提出[20]。原理示意图如图3(a)所示,移动的多线二值光栅被投影到物面,图中光栅周期为六个像素,其中只有宽度为一个像素的亮线强度为1,其余像素强度都为0,通过向右移动多线光栅六次,每次移动一个像素,亮线便可遍历空间上所有像素点。为了消除多线间的歧义性,格雷码用来标记多线光栅的位置,如图3(b)所示。需要说明的是,作者为了提高测量系统的鲁棒性,采用了过采样的技术,如图3(c)所示,为了标记一个亮线周期,使用了三个格雷码级次(格雷码解码码字0, 1, 2被用来标记线移条纹的第一个周期)。因为格雷码边界跳变处很容易出现解码错误,从而导致最终测量出错,理论上讲,解码出错的最大范围将是一个格雷码码字宽度,因此使用三倍采样率的做法会将原来最大六个像素的解码错误宽度范围减小到两个像素。
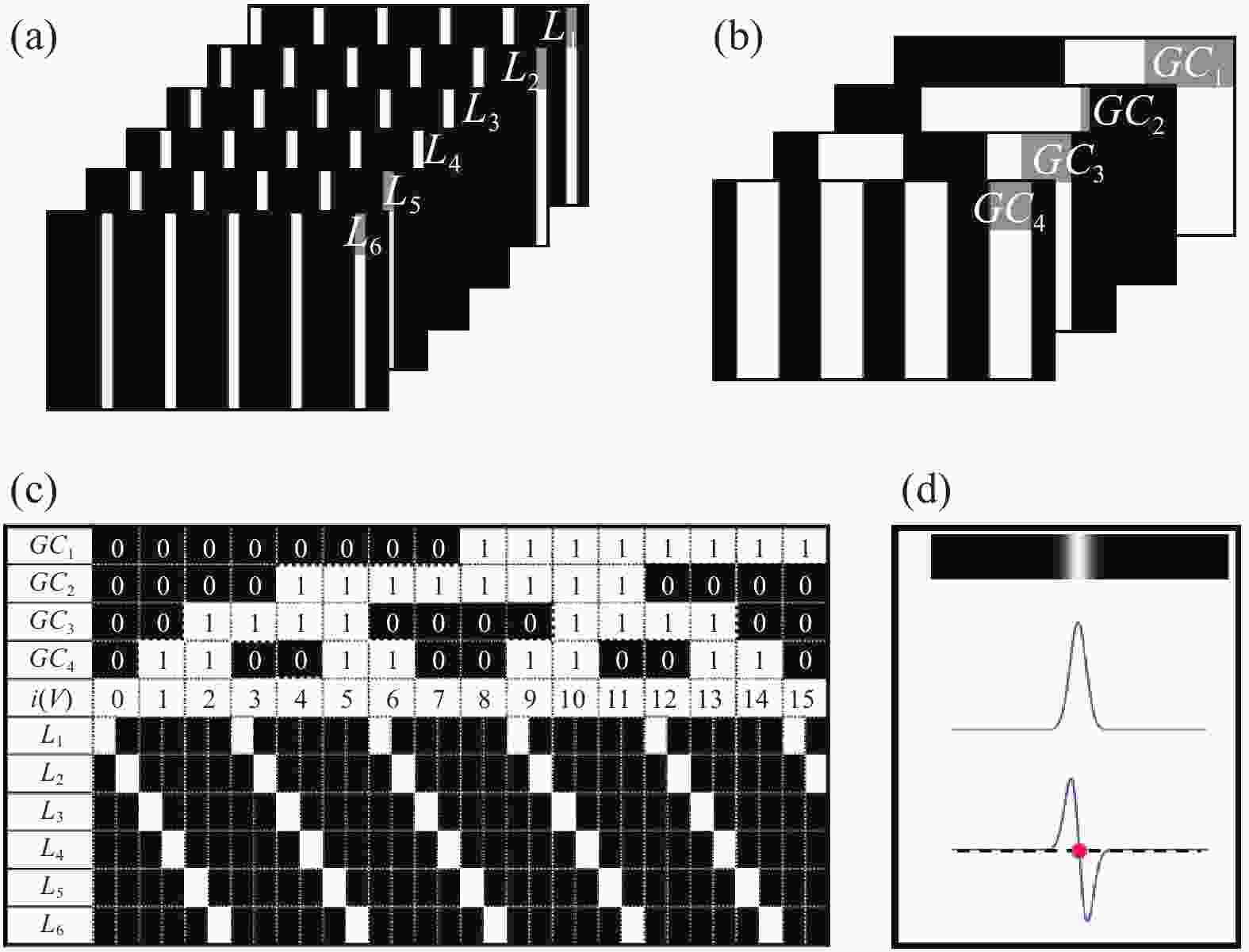
图 3 格雷码辅助线移技术。(a) 投影线移条纹;(b) 投影格雷码条纹;(c) 解码过程;(d) 亮线中心点提取
Figure 3. Gray-coded-aided line shifting technique. (a) Projected line-shifting patterns; (b) Projected Gray-coded patterns; (c) Decoding process; (d) Peak detection of the line
在多线方法中,对亮线中心点的提取精度同样也是决定了最终三维成像的精度。经系统低通滤波后,亮线的强度分布会变为高斯分布,为了实现对峰值点的亚像素探测,Blais和Rious等人提出对记录图像每行的强度分布进行一阶线性求导,然后在线性插值后找到导数的过零点即可作为亮线的亚像素峰值点[37],过程如图3(d)所示。获得亮线中心点分布后,利用前述的重建过程可以获得被测面形三维分布。
格雷码辅助线移技术利用了线结构光扫描测量精度高和格雷码编码无歧义性的优点,该两种技术手段的结合有效克服线结构光方法扫描效率低和格雷码方法测量空间分辨率低的缺点,可以很好实现高精度高分辨率的三维成像。
-
线移技术利用投影的亮线去标记物体形貌信息,亮线的宽度通常只有一个像素,因此在测量具有高反射率场景时,细线的信息很容易被高亮区域淹没或者断裂,导致无法最终正确重建对应高度。因此,Song等人提出了条纹边沿移动技术来替代传统的线移技术[36]。如图4所示,码字宽度与格雷码码字宽度相同的黑白二值条纹(罗奇光栅)边沿被用来标记物体高度信息,在一个周期内将二值条纹移动三次,每次移动一个像素来标记每个子区域。Song认为,相较于亮线,二值条纹具有更好的保边特性,因此在对高反射场景的测量中具有更好的鲁棒性。为了保证测量的准确性,文中额外投影了一组黑白翻转的码字,利用提出的边沿探测改进算法实现了效果更好的边沿亚像素定位。文中利用此方法的测量结果如图5所示,对于具有金属表面的物体,此方法能够鲁棒地精确重建完整的形貌信息,为高动态范围环境三维成像提供了一个很好的技术手段。
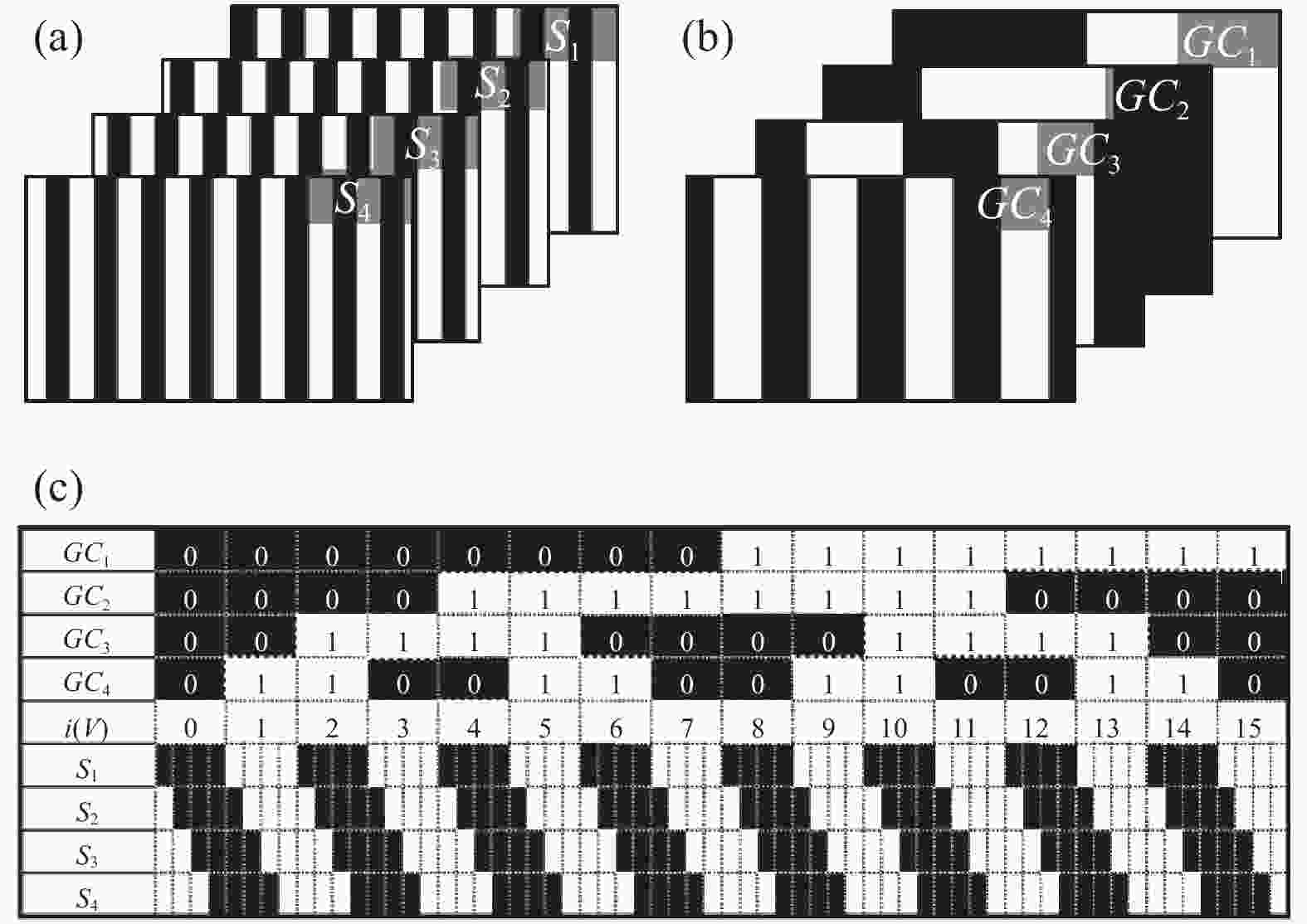
图 4 格雷码辅助条纹边沿移动技术。(a) 投影边沿移动条纹;(b) 投影格雷码条纹;(c) 解码过程
Figure 4. Gray-coded-aided stripe edge shifting technique. (a) Projected stripe-edge-shifting patterns; (b) Projected Gray-coded patterns; (c) Decoding process
为了进一步提升条纹边沿移动方法的适用性,Song结合了摄影学中的高动态范围成像技术(High Dynamic Range,HDR),提出了对相机曝光函数的估计方法,通过组合多个曝光时间下的条纹图可以得到最佳质量的条纹图[38]。参考文献[38]给出了一组实验结果如图6所示,图6(a)和6(b)分别为低曝光时间和高曝光时间下拍摄的条纹图,图6(c)为使用HDR方法组合后的条纹图,可以看到,组合后的条纹质量得到了显著的提升,最终很好地恢复具有强烈镜面反射的金属工件表面面形(如图6(d)所示)。基于格雷码辅助条纹边沿移动技术充分地利用了格雷码保边性好的优势,同时借助边沿移动的方式提高格雷码直接编码技术的测量空间分辨率。结合HDR技术,该方法能很好地测量具有非均匀反射率和高亮区域表面三维形貌,有着很好的应用前景。

图 6 改进的格雷码辅助线移技术实验结果[38]。(a) 低曝光时间下拍摄条纹;(b) 高曝光时间下拍摄条纹;(c) HDR方法合成条纹;(d) 金属表面测量结果
Figure 6. Experimental results of the improved Gray-coded-aided stripe edge shifting technique [38]. (a) Captured fringe pattern with low exposure time; (b) Captured fringe pattern with high exposure time; (c) Generated fringe pattern using HDR technique; (d) Measuring result of the metal surface
-
无论是利用格雷码来标记线移图案还是边沿移动图案,最终所投影的图案都是黑白二值条纹。由于二值条纹的离散特性,限制了测量场景重建三维点云数据的分辨率。因此,格雷码结合相移技术的测量方法[39-40]被提出。相移技术[41-42]是利用精确的相移装置(如数字投影仪)将正弦条纹在一个周期内均匀移动N(N≥3)次,每次移动2π/N的相位。投影条纹的正弦函数表达式如公式(3)所示,其中
$A\left( {x,y} \right)$ 表示背景光强,$B\left( {x,y} \right)/A\left( {x,y} \right)$ 表示条纹对比度。用这N帧变形条纹利用公式(4)计算携带物体面形信息的截断相位$\phi \left( {x,y} \right)$ 。与前述方法中的二值图案不同,该方法投影的正弦条纹具有连续的相位分布,因此利用相移技术进行三维面形测量可以有更高的空间分辨率。但在相移技术中,由于存在反正切运算,相位会截断±π之间,呈周期性分布。所以m幅格雷码图案被用来标记有2m次截断的相位级次k,并利用公式(5)展开截断相位。图7以三步相移,具有16个周期的正弦条纹为例,共需要四幅格雷码去标记条纹级次并辅助截断相位进行相位展开。得到最终的展开相位后,利用相位高度映射方法[43]以及摄像机标定[44]操作,可以最终解算物体三维形貌信息。因为投影的条纹在空间是连续分布,所以此方法的测量空间分辨率与相机的拍摄分辨率一致。$$ \begin{split} {I_n}(x,y) = & A(x,y) + B(x,y)\cos [\phi (x,y) + 2\pi (n - 1)/N], \\ &n = 1,2, \cdots,N \end{split} $$ (3) $$\phi (x,y) = \arctan \left[ {\frac{{\sum\limits_{n = 1}^N {{I_n}(x,y)\sin (2n\pi /N)} }}{{\sum\limits_{n = 1}^N {{I_n}(x,y)\cos (2n\pi /N)} }}} \right]$$ (4) $$\varPhi (x,y) = \phi (x,y) + 2\pi k(x,y)$$ (5) 
图 7 格雷码辅助相移技术。(a) 投影相移条纹;(b) 投影格雷码条纹;(c) 解码过程
Figure 7. Gray-coded-aided phase shifting technique. (a) Projected phase-shifting patterns; (b) Projected Gray-coded patterns; (c) Decoding process
由于被测物体表面反射率和背景光强度的不均匀,再加上噪声以及镜头离焦的影响,格雷码黑白边界并非锐利截止,不是理想的二值分布。因此在将图像二值化后,会出现解码级次边沿和截断相位边沿不匹配的情况,从而造成相位展开错误。为了解决这一问题,Sansoni等人提出了一种二维搜索和插补算法[40],Laughne等人也用额外投影全白和全黑的二值图像来点对点确定黑白划分阈值[45];Zheng等人通过投影仪离焦方法只利用一幅二值图像产生“0.5”灰度的图案作为阈值[46];Wu等人则直接利用相移正弦条纹的均值作为阈值,不需额外投影图像[47]。在实际测量中,以上三种方法都只能减少而并不能完全消除相位展开错误,所以额外的中值滤波[48]操作需要用来消除剩余的个别位置上相位或者重建高度错误。而Zhang等人则利用单调性假设去寻找并修正级次错误[49]。以上方法都是在得到带有局部错误数据的结果后消除或者修正误差,都属于后修正方法。这一类方法对测量静态物体形貌有很好的效果,因为在对静态场景测量时,边沿跳变误差出现的区域宽度一般较小(一~三个像素),滤波或单调性探测方法都很容易找到并消除这些错误。但当测量动态场景时,通常会利用二值离焦投影技术[50]去提高投影速率,因此对投影镜头的主动离焦以及物体本身的运动会导致边沿错误区域宽度增加,通常会达到五~十个像素左右(和投影条纹周期以及物体运动速度有关)。此时,滤波或是单调性探测的方法很难区分物体本身存在和边沿误差所带来的跳变。
针对上述问题,Sun和Zhang提出了一种提前避免误差产生的互补格雷码(Complementary Gray code)的编码方式[51-52]。如图8所示,相比于传统格雷码编码方法,该方法多投影一幅格雷码,使最后一幅格雷码的码字宽度为标记正弦条纹周期的一半。以标记16个条纹周期为例,前四幅格雷码按照传统解码方式可以得到级次k1,全部五幅格雷码可以解码得到k2。k1和k2的级次边沿正好错开,因此在展开截断相位时,公式(6)只使用k1和k2中间部分码字,从而避免使用易出现错误的级次边沿部分码字,从源头上避免了边沿跳变误差的产生。因此当边沿错误区域宽度小于半个条纹周期宽度时,误差都可以被避免,同时由于该方法属于预先避免错误产生的方法,因此当物体本身具有陡变区域时,不会影响方法的使用。但相比于后修正类型的方法,此方法需要多投影额外的一幅图案。运用传统方法和此方法对复杂风扇面形的测量结果如图9所示。

图 9 互补格雷码辅助相移方法实验结果。(a) 传统格雷码辅助相移方法测量结果;(b) 传统格雷码辅助相移方法测量结果局部放大图;(c) 互补格雷码辅助相移方法测量结果;(d) 互补格雷码辅助相移方法测量结果局部放大图
Figure 9. Experimental results of the complementary Gray-coded-aided phase shifting technique. (a) Experimental result of the traditional Gray-coded-aided phase shifting technique; (b) Partial enlargement of (a); (c) Experimental result of the complementary Gray-coded-aided phase shifting technique; (d) Partial enlargement of (c)
$$\varPhi (x,y) = \left\{ \!\!{\begin{array}{*{20}{l}} {\phi (x,y) + 2\text{π} {k_2}(x,y),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\phi (x,y) \leqslant - \text{π} /2} \\ {\phi (x,y) + 2\text{π} {k_1}(x,y),\;\;\;\;\;\; - \pi /2 < \phi (x,y) < \text{π} /2} \\ {\phi (x,y) + 2\text{π} {k_2}(x,y) - 2 \text{π} ,\;\;\;\;\;\;\;\;\;\;\;\phi (x,y) \geqslant \text{π} /2} \end{array}} \right.$$ (6) Wu等人为了将互补格雷码技术更好地应用到高速动态测量过程中,通过将传统格雷码在时间域和空间域上重新编码,设计了循环互补格雷码(Cyclic Complementary Gray code)[53]以及移动格雷码(Shifting Gray code)[47]。由于使用数字微镜器件(Digital Micro-mirror Device, DMD)的DLP数字投影仪(包括DLP Discovery, DLP Light Commander 和DLP Light Crafter等)可以以上kHz的投影速度投影二值条纹,远超过普通商用投影仪的8 bit灰度条纹120 Hz的投影速度[8],因此二值离焦投影技术[50]被广泛地运用到了高速三维形貌测量中。二值离焦投影技术是通过将8 bit的灰度正弦图像离散量化为1 bit的二值图像,再采用投影仪轻微离焦方式在成像端获得正弦条纹。主要的量化方式有一维方波二值化[49, 50],一维正弦脉宽调制[54-56]以及二维面积调制[57-59]等。典型的二值化方法如图10所示。

图 10 典型的条纹二值化方法。(a) 一维方波二值化;(b) 一维优化正弦脉宽调制;(c) 二维抖动二值化
Figure 10. Representative techniques of fringe binarization. (a) Binary square wave; (b) Optimal pulse width modulation; (c) Two dimensional dithering binarization
Wu等人采用的是二维面积调制中抖动二值化的方法[53],为了不增加互补格雷码方法中的格雷码投影数目,如图11所示,第一幅格雷码没有被投影,而是通过将传统格雷码中的第二幅格雷码第二个周期的图案(码字右半部分)在时间轴上进行循环黑白翻转,再通过对相邻两个投影序列中的第一幅投影格雷码做异或运算即可构建出未投影的格雷码,然后再利用互补格雷码方法进行解码。此方法利用互补格雷码的解码思想克服了边沿误差的问题,同时没有增加额外的投影图案数目,利用此方法以310帧/s的重建速率恢复了牛顿摆撞击过程的形貌变化,分析了撞击时左右两个单摆球的速度交换过程,如图12所示。

图 11 循环互补格雷码辅助相移方法原理图
Figure 11. Schematic diagram of the cyclic complementary Gray-coded-aided phase shifting technique
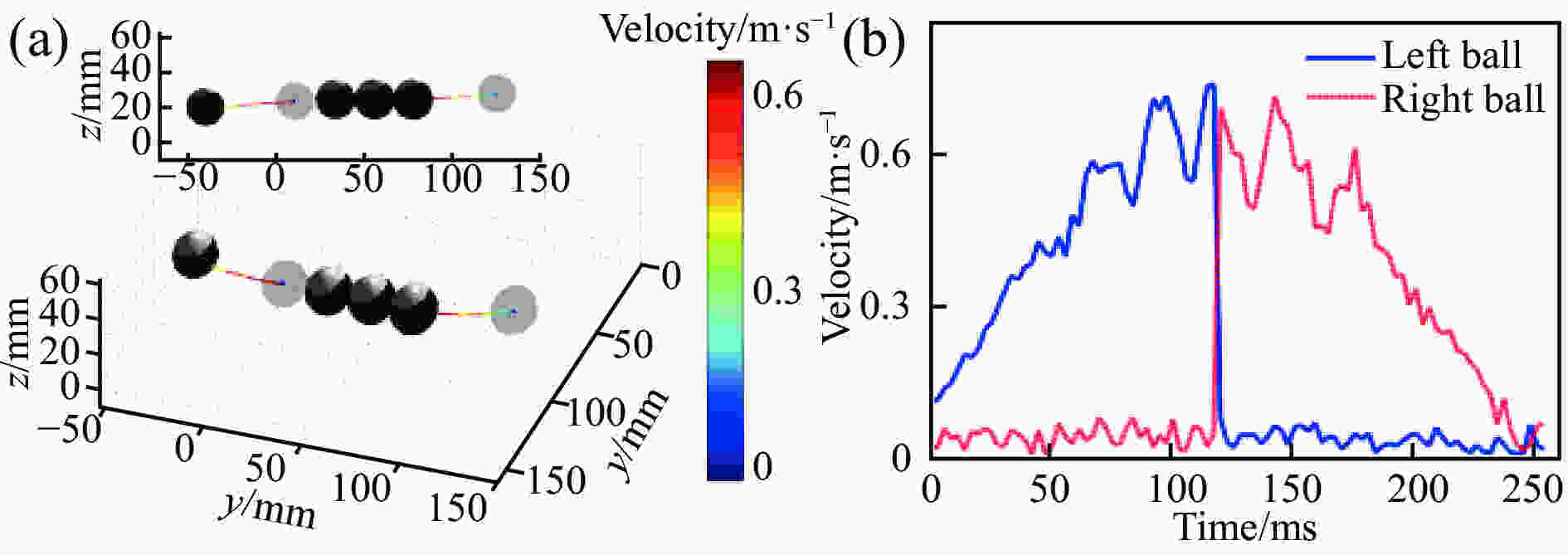
图 12 循环互补格雷码辅助相移方法实验结果。(a) 牛顿摆碰撞过程的三维重建;(b) 碰撞过程左右摆球的速度变化
Figure 12. Experimental results of the cyclic complementary Gray-coded-aided phase shifting technique. (a) 3D reconstruction of the impact process of Newton’s cradle; (b) Velocity change of the left and right balls in the impact process
此方法为格雷码辅助相移方法在高速动态测量过程中的应用提供了有效技术手段,也为使用格雷码辅助相移编码技术对动态场景测量时如何提高编码效率提供了一个思路,即可利用时间序列前后的格雷码复用的思想,充分利用每一幅格雷码图案实现高速动态三维成像。
在空间域上,Wu等人将传统的四幅格雷码条纹整体向左移动了半个条纹周期[47]以消除边沿误差的出现,原理如图13所示。

图 13 移动格雷码辅助相移方法原理图
Figure 13. Schematic diagram of the shifting Gray-coded-aided phase shifting technique
利用传统的格雷码解码方法,直接可以在相邻两个序列构建两个级次交错的解码级次,再利用互补格雷码解码方法,同样在不增加额外投影图案的前提下解决边沿跳变误差问题。相比于循环互补格雷码方法,此方法少去了异或计算,解算过程更为简单直接。如图14和图15所示,此方法被用来恢复了单摆的前后摆动过程以及积木倒塌过程的三维动态场景,为物体散裂场景的测量和分析提供了一个很好的技术手段。
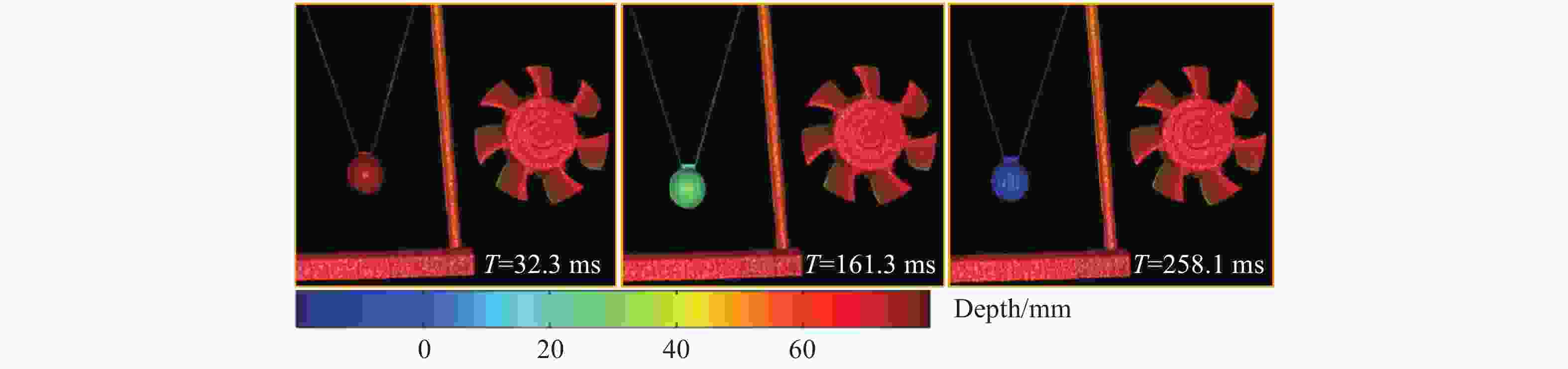
图 14 移动格雷码辅助相移方法重建单摆摆动过程实验结果
Figure 14. Experimental results of reconstructing the simple pendulum swing using shifting Gray-coded-aided phase shifting technique

图 15 移动格雷码辅助相移方法重建积木倒塌过程实验结果
Figure 15. Experimental results of reconstructing the collapsing building blocks using shifting Gray-coded-aided phase shifting technique
为了在二值离焦投影技术中进一步提高格雷码方法的编码效率,Zheng等人提出了三灰度格雷码方法[60],通过将前文提到的二值量化技术应用到格雷码图案上,可以将量化后的二值条纹通过离焦来产生“0.5”灰度码字,从而增加格雷码的编码灰度级数,提升格雷码的编码效率,其原理如图16所示。

图 16 三灰度格雷码辅助相移方法。(a) 投影三灰度格雷码;(b) 投影二值化相移条纹;(c)三灰度格雷码解码过程
Figure 16. Ternary Gray-coded-aided phase shifting technique. (a) Projected ternary Gray-coded patterns; (b) Projected binarized phase-shifting patterns; (c) Decoding process of ternary Gray-code
图16(a)和图16(b)展示的是利用抖动技术生成的二值格雷码和正弦相移条纹。通过此方法,对于m幅格雷码来说,编码的周期级次数目可以从原来的2m提高到3m。三灰度的编码和解码过程如图16(c)所示。受该思想启发,He等人将三灰度方法延伸到了四灰度编码,进一步提升编码效率[61]。此类方法可以有效地提高格雷码方法在高速测量过程的编码效率,但是增加灰度数目是以损失信噪比为代价,因此,此类方法更适用于测量低噪声环境的动态场景。
-
在前面两节阐述的四类基于格雷码的三维成像技术中,格雷码直接编码技术、格雷码辅助线移技术以及格雷码辅助边沿条纹移动技术都属于基于线或边沿调制的离散化调制技术,而格雷码辅助相移技术是属于基于相位调制的连续化调制技术。无论上述哪一种方法,如何将解算到的摄像机坐标下的像素位置信息转化到真实世界坐标下的物理三维信息都是结构光投影三维成像技术中的关键步骤。大量学者对成像系统的标定进行了研究。目前,基于格雷码图案投影的三维成像技术的标定方法主要分为三大类:光刀平面法[62-63],投影仪逆向标定法[64]以及隐式标定法[43, 65]。
-
对于离散化调制技术,最传统的系统标定方法是光刀平面法,其成像系统模型如图17所示。
XwYwZw为世界坐标,xcyczc为摄像机坐标,UcVc为图像坐标。激光器投影单线或多线结构光到被测物体表面,每条线结构光所扫过的平面被称为光刀平面。令
${p_w} = {\left( {{x_w},\;{y_w},\;{z_w},1} \right)^{\rm{T}}}$ 为光刀平面与物体表面交线上一点,${p_c} = {\left( {{u_c},\;{v_c},\;1} \right)^{\rm{T}}}$ 为对应点在成像面上的成像点。根据相机的成像模型有:$$s\left[ {\begin{array}{*{20}{c}} {{u_c}} \\ {{v_c}} \\ 1 \end{array}} \right] = {{A}}\left[ {{{R}}\;{{t}}} \right]\left[ {\begin{array}{*{20}{c}} {{x_w}} \\ {{y_w}} \\ {{z_w}} \\ 1 \end{array}} \right]$$ (7) 式中:s为尺度因子;A为相机的内参数;R和t为相机的外参数,为了方便后面的叙述,令P=A[R t],P为3×4的参数矩阵,则有:
$$s\left[ {\begin{array}{*{20}{c}} {{u_c}} \\ {{v_c}} \\ 1 \end{array}} \right] = {{P}}\left[ {\begin{array}{*{20}{c}} {{x_w}} \\ {{y_w}} \\ {{z_w}} \\ 1 \end{array}} \right]$$ (8) 另外,因为点pw在光刀平面上,因此满足光刀平面方程:
$$ a_0{x_w} + b_0{y_w} + c_0{z_w} + d_0 = 0 $$ (9) 因此,联立两式,可以得:
$$ \left\{ {\begin{array}{*{20}{c}} {s{{\left[ {\begin{array}{*{20}{c}} u&v&1 \end{array}} \right]}^t} = {{P}}{{\left[ {\begin{array}{*{20}{c}} {{x^w}}&{{y^w}}&{{z^w}}&1 \end{array}} \right]}^t}} \\ {a_0{x_w} + b_0{y_w} + c_0{z_w} + d_0 = 0} \end{array}} \right. $$ (10) 相机的内外参数通常是利用Zhang的方法[44]来进行确定,光平面方程可以通过Zhou的方法[63]来确定,在标定完成后,最终空间点坐标pw可由公式(10)解出。
-
随着DLP投影仪技术的发展,具有二维阵列DMD器件的投影越来越多地被运用到结构光投影当中,运用DLP投影仪既可以投影多线结构光,也可以投影格雷码或者相移条纹,针对运用此类投影仪的成像系统模型如图18所示。

图 18 投影仪逆向标定法标定原理示意图
Figure 18. Schematic diagram of the method based on inverse projector calibration
针对这类系统,Zhang等人提出将投影仪看作一个逆向相机来进行标定,将结构光测量系统标定问题转化为成熟的双目相机标定问题[64]。利用上一节所述相机成像模型,可以分别获得相机和投影仪的两组方程见公式(11)。
$$\left\{ {\begin{array}{*{20}{c}} {{s_c}{{\left[ {\begin{array}{*{20}{c}} {{u_c}}&{{v_c}}&1 \end{array}} \right]}^t} = {{{P}}_c}{{\left[ {\begin{array}{*{20}{c}} {{x_w}}&{{y_w}}&{{z_w}}&1 \end{array}} \right]}^t}} \\ {{s_p}{{\left[ {\begin{array}{*{20}{c}} {{u_p}}&{{v_p}}&1 \end{array}} \right]}^t} = {{{P}}_p}{{\left[ {\begin{array}{*{20}{c}} {{x_w}}&{{y_w}}&{{z_w}}&1 \end{array}} \right]}^t}} \end{array}} \right.$$ (11) 式中:相机的内外参数Pc和投影仪的内外参数Pp可以分别通过相机标定[44]和投影仪标定[64]进行获取。在标定完成后,上述六个方程需要解出
${x_w},\;{y_w},\;{z_w},$ ${s_c},{s_p},{u_p}$ 以及vp一共七个未知数。因此还需要额外的一个方程来进行求解。对于离散化调制技术,获取的是离散的位置信息,因此可以通过公式(12)来求解投影仪像面坐标up。
$${u_p} = {E_N} \times T$$ (12) 式中:EN是解算出的亮线或边沿序号,T为多线条纹或格雷码条纹一个周期内像素点个数。
对于连续化调制技术,获取的是连续的相位信息,因此可以通过公式(13)来求解投影仪像面坐标up。
$${u_p} = \varPhi \times T/(2\pi )$$ (13) 式中:Φ为解算出的相位信息,T为相移条纹一个周期内像素点个数。
-
因为相机成像镜头存在畸变,投影仪也存在非线性响应,因此光刀平面和投影仪的标定都存在一定的误差,为了将这些误差考虑到标定过程中,隐式标定法被提出,其方法示意图如图19所示。隐式标定法的核心思想是通过借助精密移动装置提前建立高度变化和亮线或边沿垂直方向像素移动量(离散化调制技术)或相移变化量(连续化调制技术)之间的关系,得到高度表达式,测量时则只需代入计算即可。此类方法的好处是将相机的畸变和投影仪的非线性都在标定过程中一起考虑,可以提高标定的精度,但缺点是需要精确知道多个平面精确相对移动位置。
对于离散化调制技术,Arold等人提出了如公式(14)所示的映射模型[65]:
$$z(n,v) = a(n,v) + b(n,v)u + c(n,v){u^2} + d(n,v){u^3}$$ (14) 式中:z为待测高度,u为多线或边沿信号垂直于条纹方向上的亚像素位置,n为亮线或边沿信号的序号数,v为条纹方向上像素坐标,通过平移装置提前测量多个已知平面,利用最小二乘法可以得到多项式拟合系数
$a\left( {n,v} \right),b\left( {n,v} \right),c\left( {n,v} \right)$ 以及$d\left( {n,v} \right)$ 。Lu等人[66]把拟合系数提高到了五阶以上,进一步提升了三维成像的精度。对于连续化调制技术,Li等人提出如公式(15)所示的相位-高度映射模型[43]:
$$\frac{1}{{z(u,v)}} = a(u,v) + \frac{{b(u,v)}}{{\Delta \varPhi (u,v)}} + \frac{{c(u,v)}}{{\Delta \varPhi {{(u,v)}^2}}}$$ (15) 笔者认为成像面每一点上的高度分布
$z\left( {u,v} \right)$ 和相位分布$\Delta \varPhi \left( {u,v} \right)$ ,二者的倒数接近二次非线性关系。同样通过测量多个已知平面,可以求解拟合系数。两类方法在完成z方向上的标定后,都可以使用相机标定[44]方法继续完成xy方向上的标定。
-
文中概述了基于格雷码图案投影的结构光三维成像技术,回顾了不同种类方法的基本原理以及研究进展。基于格雷码图案投影的结构光三维成像技术由于格雷码具有的二值编码特性及误差最小化优点,从而具有很好的鲁棒性和抗噪性,非常适用于有不确定噪声干扰、测量表面反射率不均匀或具有高光区域等复杂应用环境的三维成像。在工业零部件检测、逆向工程、文物数字化、牙科扫描、医学美容等应用领域具有极大的应用市场,是推动结构光三维成像技术走向市场应用的一类重要技术。
尽管此类技术已经被大量学者进行研究,并在不同程度上被运用到了各个领域,但随着新需求的不断提出以及技术的持续发展,基于格雷码图案投影的结构光三维成像技术将会在高速高动态范围场景表现、级次跳变误差避免或修正、编码效率提升等方面取得新的进展。同时仍面临着以下的挑战,也是我们今后工作的方向和重点。
(1) 高动态范围的动态场景三维成像:在实际的测量环境中,被测物体表面大多不是理想的漫反射表面,因此常会出现反射率不均匀,甚至存在高光区域的问题,结合格雷码本身的良好保边性和HDR技术,此问题可以得到较好的解决。但基于格雷码图案投影的测量技术的编码效率比较低,HDR技术更是会成倍地增加一次三维成像所需的投影条纹数目,使得此类技术很难在高动态范围场景动态过程(如金属表面受冲击破裂,弹片飞溅过程等)三维成像上直接运用。因此,如何在保证方法高动态范围测量环境表现的同时,提升测量的效率是今后需要迎接的一个挑战。也许,投影仪和相机的时序严格控制以及投影仪RGB三通道的颜色复用等方面的考虑某种程度上可以在该问题的解决上发挥作用。
(2) 级次跳变误差问题的解决:级次跳变问题一直是格雷码辅助编码技术中困扰学者们的一个难题,尽管大量学者就这个问题进行了深入研究,但目前常用解决方法有的存在使用局限性,有的是以额外增加投影图案或利用时间轴上的关联为代价。因此,寻找一个适用范围广,无需利用额外条纹的误差纠正方法也是学者们面临的一个挑战。该问题或许可从源头上进行消除误差和避免级次误差出现,交错构造投影序列等方面进行考虑,寻找解决方案。
(3) 进一步提高格雷码编码效率,提升高速动态三维成像表现:基于格雷码的编码技术因其二值特性和测量鲁棒性,很适用于低信噪比环境下高速动态过程三维成像。但目前该类方法编码效率低的缺点限制了其在高速动态过程三维成像中的表现。因此,如何进一步提高格雷码的编码效率,提升其在高速动态过程中的应用同样是学者们面临的一个挑战。该问题的解决可从时序复用,时空编码等思路进行考虑。
Three-dimensional imaging technique based on Gray-coded structured illumination
-
摘要: 近年来,结构光三维成像技术被深入研究和广泛应用。在众多的结构光投影三维成像方法中,基于格雷码图案投影的三维成像技术因具有良好的鲁棒性和抗噪性被广泛地应用到工业检测、文物数字化及生物医学检测等领域。投影出去的格雷码图案作为一种结构光,可以直接用来调制被测面形高度分布,也可以用来辅助其他结构光的信息获取和计算,最终达到三维成像的目的。文中概述了基于格雷码图案投影的结构光三维成像技术,回顾了不同种类方法的基本原理以及研究进展,给出了课题组相关方向上的原理及应用研究结果,分析了格雷码二值图案在三维面形测量应用中的优缺点和适用范围,并指出了该领域今后的发展动向。Abstract: Three-dimensional (3D) imaging technique based on structured illumination has been deeply studied and widely applied in recent years. Among numerous 3D imaging methods, the imaging technique based on Gray-coded structured illumination has been applied in industrial inspection, digitalization of antique, biomedicine detection and so on, owing to its robustness and anti-noise ability. To realize 3D imaging, the projected Gray-coded pattern can either be used to modulate the height information or be used to assist acquisition and computation of the height information of the tested object. In this paper, a review was given to introduce principles and progresses of the imaging techniques based on Gray-coded structured illumination and the research achievements of the author's research group about this technique were also shown. In addition, the advantages, disadvantages and application scope of binary Gray-coded patterns in 3D shape measurement were discussed and the developing trends of this technique was pointed out as well.
-
Key words:
- Gray code /
- structured light /
- three-dimensional sensing /
- fringe projection /
- dynamic 3D measurement
-
图 2 格雷码直接编码技术。(a) 投影条纹;(b) 格雷码解码过程;(c) 零相交边界提取方法;(d) 正反条纹边界提取法;(e) 改进的零相交边界提取法。
Figure 2. Direct Gray-coded coding technique. (a) Projected patterns; (b) Decoding process of Gray code; (c) Zero-crossing edge detection method; (d) Positive and negative edge detection method; (e) Improved zero-crossing edge detection method
图 6 改进的格雷码辅助线移技术实验结果[38]。(a) 低曝光时间下拍摄条纹;(b) 高曝光时间下拍摄条纹;(c) HDR方法合成条纹;(d) 金属表面测量结果
Figure 6. Experimental results of the improved Gray-coded-aided stripe edge shifting technique [38]. (a) Captured fringe pattern with low exposure time; (b) Captured fringe pattern with high exposure time; (c) Generated fringe pattern using HDR technique; (d) Measuring result of the metal surface
图 9 互补格雷码辅助相移方法实验结果。(a) 传统格雷码辅助相移方法测量结果;(b) 传统格雷码辅助相移方法测量结果局部放大图;(c) 互补格雷码辅助相移方法测量结果;(d) 互补格雷码辅助相移方法测量结果局部放大图
Figure 9. Experimental results of the complementary Gray-coded-aided phase shifting technique. (a) Experimental result of the traditional Gray-coded-aided phase shifting technique; (b) Partial enlargement of (a); (c) Experimental result of the complementary Gray-coded-aided phase shifting technique; (d) Partial enlargement of (c)
-
[1] Ford K R, Myer G D, Hewett T E. Reliability of landing 3D motion analysis: implications for longitudinal analyses [J]. Medicine & Science in Sports & Exercise, 2007, 39(11): 2021−2028. [2] Malamas E N, Petrakis E G M, Zervakis M, et al. A survey on industrial vision systems, applications and tools [J]. Image and Vision Computing, 2003, 21(2): 171−188. doi: 10.1016/S0262-8856(02)00152-X [3] Chen F, Brown G M, Song M. Overview of three-dimensional shape measurement using optical methods [J]. Optical Engineering, 2000, 39(1): 10−22. doi: 10.1117/1.602438 [4] Su Xianyu, Zhang Qican, Chen Wenjing. Three-dimensional imaging based on structured illumination [J]. Chinese Journal of Lasers, 2014, 41(02): 9−18. (in Chinese) [5] Zhang Qican, Su Xianyu. Research progress of dynamic three-dimensional shape measurement [J]. Laser & Optoelectronics Progress, 2013, 50(1): 4−17. (in Chinese) [6] Liu Dong, Yan Tianliang, Wang Daodang, et al. Review of fringe-projection profilometry and phase measuring deflectometry [J]. Infrared and Laser Engineering, 2017, 46(9): 0917001. (in Chinese) [7] Su X Y, Zhang Q C. Dynamic 3-D shape measurement method: a review [J]. Optics and Lasers in Engineering, 2010, 48(2): 191−204. doi: 10.1016/j.optlaseng.2009.03.012 [8] Zhang S. High-speed 3D shape measurement with structured light methods: A review [J]. Optics and Lasers in Engineering, 2018, 106: 119−131. [9] Zhang S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques [J]. Optics and Lasers in Engineering, 2010, 48(2): 149−158. doi: 10.1016/j.optlaseng.2009.03.008 [10] Van der Jeught S, Dirckx J J J. Real-time structured light profilometry: a review [J]. Optics and Lasers in Engineering, 2016, 87: 18−31. doi: 10.1016/j.optlaseng.2016.01.011 [11] Wang K, Li Y, Kemao Q, et al. One-step robust deep learning phase unwrapping [J]. Optics Express, 2019, 27(10): 15100−15115. doi: 10.1364/OE.27.015100 [12] Spoorthi G E, Gorthi S, Gorthi R K S S. Phasenet: A deep convolutional neural network for two-dimensional phase unwrapping [J]. IEEE Signal Processing Letters, 2018, 26(1): 54−58. [13] Feng S, Chen Q, Gu G, et al. Fringe pattern analysis using deep learning [J]. Advanced Photonics, 2019, 1(2): 025001. [14] Van der Jeught S, Dirckx J J J. Deep neural networks for single shot structured light profilometry [J]. Optics Express, 2019, 27(12): 17091−17101. doi: 10.1364/OE.27.017091 [15] Feng S, Zuo C, Yin W, et al. Micro deep learning profilometry for high-speed 3D surface imaging [J]. Optics and Lasers in Engineering, 2019, 121: 416−427. doi: 10.1016/j.optlaseng.2019.04.020 [16] Zuo Chao, Feng Shijie, Zhang Xiangyu, et al. Deep learning for computational imaging: current status, challenges and future [J]. Acta Optica Sinica, 2020, 40(1): 0111003. (in Chinese) doi: 10.3788/AOS202040.0111003 [17] Wang Fei, Wang Hao, Bian Yaoming, et al. Application of deep learning for computational imaging [J]. Acta Optica Sinica, 2020, 40(1): 0111002. (in Chinese) doi: 10.3788/AOS202040.0111002 [18] Kahn-Jetter Z L, Chu T C. Three-dimensional displacement measurements using digital image correlation and photogrammic analysis [J]. Experimental Mechanics, 1990, 30(1): 10−16. doi: 10.1007/BF02322695 [19] Sjödahl M, Synnergren P. Measurement of shape by using projected random patterns and temporal digital speckle photography [J]. Applied Optics, 1999, 38(10): 1990−1997. doi: 10.1364/AO.38.001990 [20] Gühring J. Dense 3D surface acquisition by structured light using off-the-shelf components[C] // Videometrics and Optical Methods for 3D Shape Measurement. International Society for Optics and Photonics, 2000, 4309: 220−231. [21] Ettl S, Arold O, Yang Z, et al. Flying triangulation-an optical 3D sensor for the motion-robust acquisition of complex objects [J]. Applied Optics, 2012, 51(2): 281−289. doi: 10.1364/AO.51.000281 [22] MacWilliams F J, Sloane N J A. Pseudo-random sequences and arrays [J]. Proceedings of the IEEE, 1976, 64(12): 1715−1729. doi: 10.1109/PROC.1976.10411 [23] Pages J, Salvi J, Collewet C, et al. Optimised De Bruijn patterns for one-shot shape acquisition [J]. Image and Vision Computing, 2005, 23(8): 707−720. doi: 10.1016/j.imavis.2005.05.007 [24] Inokuchi S. Range imaging system for 3-D object recognition [J]. ICPR, 1984, 1984: 806−808. [25] Su X, Chen W. Fourier transform profilometry: a review [J]. Optics and Lasers in Engineering, 2001, 35(5): 263−284. doi: 10.1016/S0143-8166(01)00023-9 [26] Kemao Q. Windowed Fourier transform for fringe pattern analysis [J]. Applied Optics, 2004, 43(13): 2695−2702. doi: 10.1364/AO.43.002695 [27] Sandoz P. Wavelet transform as a processing tool in white-light interferometry [J]. Optics Letters, 1997, 22(14): 1065−1067. doi: 10.1364/OL.22.001065 [28] Zuo C, Feng S, Huang L, et al. Phase shifting algorithms for fringe projection profilometry: A review [J]. Optics and Lasers in Engineering, 2018, 109: 23−59. doi: 10.1016/j.optlaseng.2018.04.019 [29] Liu K, Wang Y, Lau D L, et al. Dual-frequency pattern scheme for high-speed 3-D shape measurement [J]. Optics Express, 2010, 18(5): 5229−5244. doi: 10.1364/OE.18.005229 [30] Wang Y, Liu K, Hao Q, et al. Period coded phase shifting strategy for real-time 3-D structured light illumination [J]. IEEE Transactions on Image Processing, 2011, 20(11): 3001−3013. doi: 10.1109/TIP.2011.2155072 [31] Zhang Y, Xiong Z, Wu F. Unambiguous 3D measurement from speckle-embedded fringe [J]. Applied Optics, 2013, 52(32): 7797−7805. doi: 10.1364/AO.52.007797 [32] Frank G. Pulse code communication: US: 2, 632, 058[P]. 1953-03-17. [33] Yu Xiaoyang, Wu Haibin, Yin Liping, et al. 3D measurement technology based on structured light by combing Gray code with phase-shift [J]. Chinese Journal of Scientific Instrument, 2007, 12(12): 2152−2157. (in Chinese) doi: 10.3321/j.issn:0254-3087.2007.12.008 [34] Posdamer J L, Altschuler M D. Surface measurement by space-encoded projected beam systems [J]. Computer Graphics and Image Processing, 1982, 18(1): 1−17. doi: 10.1016/0146-664X(82)90096-X [35] Trobina M. Error model of a coded-light range sensor[R]. Zurich: Communication Technology Laboratory, ETH Zentrum , 1995. [36] Song Z, Chung R, Zhang X T. An accurate and robust strip-edge-based structured light means for shiny surface micromeasurement in 3-D [J]. IEEE Transactions on Industrial Electronics, 2012, 60(3): 1023−1032. [37] Blais F, Rioux M. Real-time numerical peak detector [J]. Signal Processing, 1986, 11(2): 145−155. doi: 10.1016/0165-1684(86)90033-2 [38] Song Z, Jiang H, Lin H, et al. A high dynamic range structured light means for the 3D measurement of specular surface [J]. Optics and Lasers in Engineering, 2017, 95: 8−16. doi: 10.1016/j.optlaseng.2017.03.008 [39] Sansoni G, Corini S, Lazzari S, et al. Three-dimensional imaging based on Gray-code light projection: characterization of the measuring algorithm and development of a measuring system for industrial applications [J]. Applied Optics, 1997, 36(19): 4463−4472. doi: 10.1364/AO.36.004463 [40] Sansoni G, Carocci M, Rodella R. Three-dimensional vision based on a combination of gray-code and phase-shift light projection: analysis and compensation of the systematic errors [J]. Applied Optics, 1999, 38(31): 6565−6573. doi: 10.1364/AO.38.006565 [41] Srinivasan V, Liu H C, Halioua M. Automated phase-measuring profilometry of 3-D diffuse objects [J]. Applied Optics, 1984, 23(18): 3105−3108. doi: 10.1364/AO.23.003105 [42] Halioua M, Liu H C. Optical three-dimensional sensing by phase measuring profilometry [J]. Optics and Lasers in Engineering, 1989, 11(3): 185−215. doi: 10.1016/0143-8166(89)90031-6 [43] Li W, Su X, Liu Z. Large-scale three-dimensional object measurement: a practical coordinate mapping and image data-patching method [J]. Applied Optics, 2001, 40(20): 3326−3333. doi: 10.1364/AO.40.003326 [44] Zhang Z. A flexible new technique for camera calibration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330−1334. [45] Laughner J I, Zhang S, Li H, et al. Mapping cardiac surface mechanics with structured light imaging [J]. American Journal of Physiology-Heart and Circulatory Physiology, 2012, 303(6): H712−H720. doi: 10.1152/ajpheart.00269.2012 [46] Zheng D, Da F, Huang H. Phase unwrapping for fringe projection three-dimensional measurement with projector defocusing [J]. Optical Engineering, 2016, 55(3): 034107. doi: 10.1117/1.OE.55.3.034107 [47] Wu Z, Guo W, Zhang Q. High-speed three-dimensional shape measurement based on shifting Gray-code light [J]. Optics Express, 2019, 27(16): 22631−22644. doi: 10.1364/OE.27.022631 [48] Zheng D, Da F, Kemao Q, et al. Phase-shifting profilometry combined with Gray-code patterns projection: unwrapping error removal by an adaptive median filter [J]. Optics Express, 2017, 25(5): 4700−4713. doi: 10.1364/OE.25.004700 [49] Zhang S. Flexible 3D shape measurement using projector defocusing: extended measurement range [J]. Optics Letters, 2010, 35(7): 934−936. doi: 10.1364/OL.35.000934 [50] Lei S, Zhang S. Flexible 3-D shape measurement using projector defocusing [J]. Optics Letters, 2009, 34(20): 3080−3082. doi: 10.1364/OL.34.003080 [51] Sun Xuezhen, Su Xianyu, Zou Xiaoping. Phase unwrapping based on complementary structured light binary code [J]. Acta Optica Sinica, 2008(10): 1947−1951. (in Chinese) doi: 10.3321/j.issn:0253-2239.2008.10.020 [52] Zhang Q, Su X, Xiang L, et al. 3-D shape measurement based on complementary Gray-code light [J]. Optics and Lasers in Engineering, 2012, 50(4): 574−579. doi: 10.1016/j.optlaseng.2011.06.024 [53] Wu Z, Zuo C, Guo W, et al. High-speed three-dimensional shape measurement based on cyclic complementary Gray-code light [J]. Optics Express, 2019, 27(2): 1283−1297. doi: 10.1364/OE.27.001283 [54] Ayubi G A, Ayubi J A, Di Martino J M, et al. Pulse-width modulation in defocused three-dimensional fringe projection [J]. Optics Letters, 2010, 35(21): 3682−3684. doi: 10.1364/OL.35.003682 [55] Wang Y, Zhang S. Optimal pulse width modulation for sinusoidal fringe generation with projector defocusing [J]. Optics Letters, 2010, 35(24): 4121−4123. doi: 10.1364/OL.35.004121 [56] Zuo C, Chen Q, Feng S, et al. Optimized pulse width modulation pattern strategy for three-dimensional profilometry with projector defocusing [J]. Applied Optics, 2012, 51(19): 4477−4490. doi: 10.1364/AO.51.004477 [57] Lohry W, Zhang S. 3D shape measurement with 2D area modulated binary patterns [J]. Optics and Lasers in Engineering, 2012, 50(7): 917−921. doi: 10.1016/j.optlaseng.2012.03.002 [58] Xian T, Su X. Area modulation grating for sinusoidal structure illumination on phase-measuring profilometry [J]. Applied Optics, 2001, 40(8): 1201−1206. doi: 10.1364/AO.40.001201 [59] Wang Y, Zhang S. Three-dimensional shape measurement with binary dithered patterns [J]. Applied Optics, 2012, 51(27): 6631−6636. doi: 10.1364/AO.51.006631 [60] Zheng D, Kemao Q, Da F, et al. Ternary Gray code-based phase unwrapping for 3D measurement using binary patterns with projector defocusing [J]. Applied Optics, 2017, 56(13): 3660−3665. doi: 10.1364/AO.56.003660 [61] He X, Zheng D, Kemao Q, et al. Quaternary gray-code phase unwrapping for binary fringe projection profilometry [J]. Optics and Lasers in Engineering, 2019, 121: 358−368. doi: 10.1016/j.optlaseng.2019.04.009 [62] McIvor A M. Nonlinear calibration of a laser stripe profiler [J]. Optical Engineering, 2002, 41(1): 205−213. doi: 10.1117/1.1416694 [63] Zhou F, Zhang G. Complete calibration of a structured light stripe vision sensor through planar target of unknown orientations [J]. Image and Vision Computing, 2005, 23(1): 59−67. doi: 10.1016/j.imavis.2004.07.006 [64] Zhang S, Huang P S. Novel method for structured light system calibration [J]. Optical Engineering, 2006, 45(8): 083601. doi: 10.1117/1.2336196 [65] Arold O, Ettl S, Willomitzer F, et al. Hand-guided 3D surface acquisition by combining simple light sectioning with real-time algorithms[J]. arXiv preprint arXiv: 1401.1946, 2014. [66] Lu X, Wu Q, Huang H. Calibration based on ray-tracing for multi-line structured light projection system [J]. Optics Express, 2019, 27(24): 35884−35894. doi: 10.1364/OE.27.035884 -

 点击查看大图
点击查看大图
计量
- 文章访问数: 4075
- HTML全文浏览量: 1794
- 被引次数: 0





 下载:
下载: