-
三维成像技术是对真实世界进行记录和分析的重要手段,是计算成像与几何测量领域的重要研究内容之一。在需求增长和科技进步的双重推动下,三维成像尤其是光学三维成像的研究取得了长足的进展。光学三维成像以光学传感为主要的信息获取方式,以计算机图形图像处理为主要的信息处理手段,是涉及光电技术、计算机技术、信息处理技术的新兴交叉方向。进入21世纪以来,随着高性价比光电器件的不断涌现以及计算机和嵌入式系统计算性能的持续攀升,针对光学三维成像的研究呈现出百花齐放的繁荣景象,已有的方法不断改善,新的方法时有提出[1, 2]。随着相关技术的进步,光学三维成像的应用领域日益扩大,成像的尺度范围也不断延伸。
中小尺度(mm~m)三维成像在工业、医疗和消费领域的应用最为广泛[3],其代表性技术是结构光三维成像。基于结构光的三维成像系统通常由结构光发生器和面阵相机构成,其基本工作原理是[4]:由结构光发生器产生的结构光照射目标表面时,目标表面的高低起伏(表面形貌)会对结构光进行调制,使结构光的图案产生与之相关的变形,换句话说,结构光对目标表面形貌进行了调制编码;此时用相机采集调制变形后的结构光图案,对变形图案进行解码并执行相应的三维重构算法,即可实现对目标表面形貌的三维成像。
结构光的产生机理多种多样,包括相干光干涉[5, 6]、相干光衍射[7, 8]、光栅投影[9-12]、数字投影[13-15]等。其中,以液晶显示(Liquid Crystal Display, LCD)、硅基液晶(Liquid Crystal on Silicon, LCoS)和数字微镜装置(Digital Micromirror Device, DMD)为核心器件的数字投影技术的发展和设备的普及,使研究者可以方便地通过计算机控制产生各种黑白或彩色的结构光,大大推动了基于结构光照明的三维成像技术的发展。基于结构光照明的三维成像系统结构简单,可以根据具体需求选择特定的结构光编码方案和系统硬件配置,灵活性高。一方面,针对专业级应用,可以选择高精度的结构光编码方案和高性能硬件,实现高精度的三维测量;另一方面,针对消费级应用,可以选择相对简单的结构光编码方案和低成本硬件,实现低成本的三维成像。因此,结构光三维成像技术在专业检测领域和日常消费领域均有广泛应用。
相位编码是最具特色的一种结构光编码方式[16]。由于在光学系统中相位并不是一个可以直接观测的物理量,相位编码通常以条纹结构光投影的方式实现。三维成像获取的是物体的表面形貌或者表面轮廓,因此采用相位编码的结构光三维成像技术又被称为条纹投影轮廓术(Fringe Projection Profilometry, FPP)。与其它结构光编码方式相比,相位编码有几个显著的优点:(1)本质上相位是一个独立于光强的物理量,因此相位的求解在理论上不受背景光强、物体表面的反射率、物体表面的纹理色彩等无关信息的影响,对测量时的环境光照和物体的表面材质有很好的适应性;(2)相位编码为视场中的每个像素赋予了不同的编码值,因此在进行三维重建时,根据每个像素的相位均可重建一个对应的三维空间点,对所有像素进行重建可以获得一幅具有很高数据密度的深度像;(3)连续表面所对应的相位分布是连续的,因此可以充分利用连续函数的插值和拟合来保证三维重建的精度;(4)条纹结构光产生的原理和方法多种多样,包括相干光的干涉、衍射,非相干照明的光栅投影、数字投影等,为系统的搭建提供了较多的选择余地。由此可见,FPP具有较好的普适性和灵活性,同时又能获得较高的测量精度和数据密度,因此吸引了众多学者对其各个方面展开了深入研究[17],并逐渐发展成为光学三维表面成像与测量商业化系统的主流技术。
FPP的经典系统如图1所示。投影仪将计算机生成的标准条纹图投影至目标表面;目标的表面轮廓/形貌对标准条纹图进行调制,产生变形条纹图;相机采集变形条纹图并在计算机中进行相位恢复来获得相位图;计算机利用系统模型和相位图进行三维重建,获得目标的表面轮廓/形貌。由上述基本工作过程可以分析FPP的基本要素:标准/变形条纹图及其携带的相位信息为二维信息;目标表面形貌为三维信息;系统模型描述了二维信息和三维信息之间的关系,其具体表达式取决于系统参数。如图2所示,三维成像的本质是利用参数确定的系统模型对二维信息进行计算和处理来获得三维信息,该过程称为三维重建。而在此之前,需要借助某些已知的三维信息及其对应的二维信息来估计描述模型的系统参数,该过程称为系统标定。由此可见,系统标定与系统模型密不可分,对三维成像的性能和精度有直接影响。
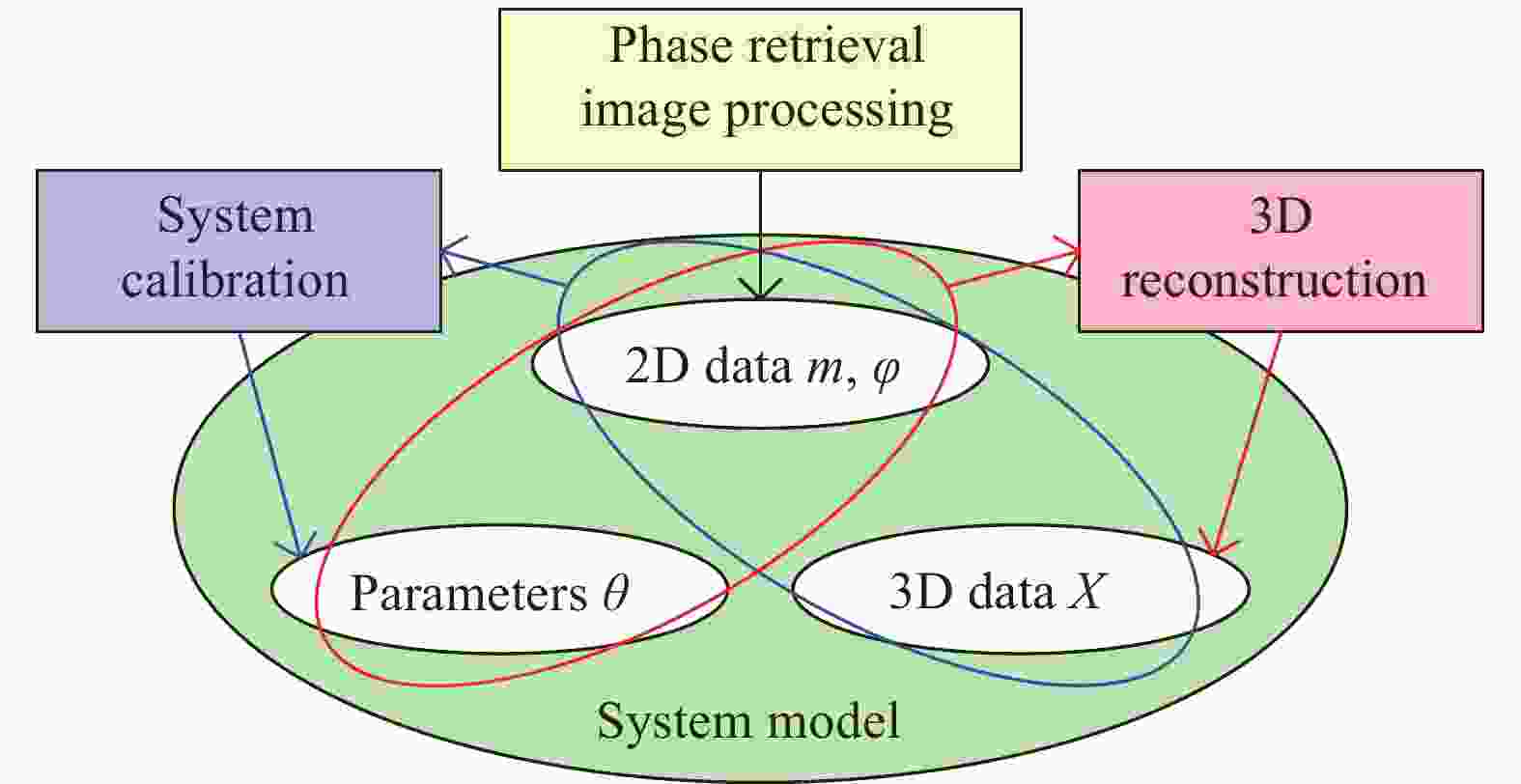
图 2 FPP的基本要素及其内在联系。其中φ表示相位图;m表示二维图像坐标;X表示三维空间坐标;θ为包含多个系统参数的参数向量
Figure 2. Basic elements of the fringe projection profilometry and their internal relations. Here φ denotes the phase distribution; m is the 2D image coordinate; X is the 3D space coordinate; θ is the parameter vector containing multiple parameters
文中将综述FPP的常用模型及其标定方法,归纳系统标定中常用的标靶与标准件,介绍常用的系统精度评估方式。
-
利用系统模型进行三维重建时,模型的输入通常是相位而不是条纹图。因此在获得相机采集的变形条纹图后,首先需要利用相位恢复算法计算相位图。根据相位恢复方法的不同,FPP通常又可分为两类:一类通过傅立叶变换、频域选择、逆傅立叶变换的过程来计算相位,称为傅立叶变换轮廓术(Fourier Transform Profilometry,FTP)[18-20];另一类通过相移算法来计算相位,称为相位测量轮廓术(Phase Measurement Profilometry, PMP)[21]或相移轮廓术(Phase-shifting Profilometry,PSP)[22]。由于相位恢复算法在数学上进行的是反正切运算,计算获得的相位呈现为[-π, π]之间的折叠分布,需要借助相位展开算法重构单调增长的展开相位[23, 24]。相位图与条纹图之间的数学关系如公式(1)所示,其中Ip为投影的标准条纹图,包含已知的标准相位图
${{\rm{\varphi}} _p}$ ;Ic为采集的变形条纹图,包含携带物体高度信息的相位图${\varphi _c}$ 。$$ \left\{ {\begin{aligned} & {{{{I}}_p} = {{{A}}_p} + {{{B}}_p}\cos\left( {{{\rm{\varphi}} _p}} \right)}\\ & {{{{I}}_c} = {{{A}}_c} + {{{B}}_c}\cos\left( {{{\rm{\varphi}} _c}} \right)} \end{aligned}} \right. $$ (1) 需要强调的是,所有的FPP系统其工作原理均基于几何光学,只考虑光的直线传播而忽略衍射效应,投影和成像镜头均等效为小孔。此时系统工作过程可以通过光线追迹的方式进行分析,其核心特点在于从投影仪发出的同一条光线上的不同点对应着投影芯片上的同一个像素,具有相同的相位值;相机接收的同一条光线(也被称为视线)上的不同点对应着相机芯片上的同一个像素。由于镜头等效为小孔,其空间位置可以由光学中心(光心)的三维坐标来描述,镜头朝向则由光轴方向来描述。系统进行三维成像在几何上对应着以投影仪发出的光线和相机接收的光线为边的三角形求顶点,因此FPP三维重建又称为三角化。有关FPP工作原理的论文不可胜数,根据原理的区别,相关的系统模型可以大致归为两类:相位-三维映射模型和立体视觉模型。
-
进行条纹投影时,物体的高度信息会对条纹图进行编码而使之发生变形。从变形条纹图解调获得的相位图包含了物体的高度信息。对于任意的条纹投影系统,相位和高度之间均存在特定的映射关系,通过系统标定估计映射关系表达式中的各项系数,由此获得与相位图中的像素一一对应的高度图,也被称为深度像。深度像仅包含了z坐标的信息,为了进一步得到完整的三维数据,需要建立相位与x和y坐标之间的映射关系,与相位-高度映射模型共同组成相位-三维映射模型。
-
以图3所示的FPP系统为例[20],相机镜头光轴与投影镜头光轴相互平行,与光轴垂直的平面定义为参考平面,也即三维直角坐标系的x-o-y平面。规定投影与相机镜头光心的连线OpOc平行于o-x轴,其长度为d。相机光心距参考平面的垂直距离为l。系统工作时,首先在参考平面处放置一个平板,投采条纹并进行相位恢复,获得参考相位图
${{\rm{\varphi}} _r}$ 。以参考平面上任意点A为观察对象,从投影仪投影至该点的相位值为${{\rm{\varphi }}_2}$ ,该点在相机中的图像坐标为${{{m}}_{c,A}} = {\left( {{u_A},{v_A}} \right)^{\rm{T}}}$ 。根据光线追迹,必定有${{\rm{\varphi }}_r}\left( {{{{m}}_{c,A}}} \right) = {{\rm{\varphi }}_2}$ 。然后放置物体,投采条纹并进行相位恢复,获得物体的变形相位图${{\rm{\varphi }}_c}$ 。假设物体表面上某点D在相机中的图像坐标同样为mc,A,且投影至该点的相位值为${{\rm{\varphi }}_1}$ 。根据光线追迹,此时有${{\rm{\varphi }}_c}\left( {{{{m}}_{c,A}}} \right) = {{\rm{\varphi }}_1}$ 。因此点D与参考平面之间的相位差为$$ \Delta {\rm{\varphi }} = {{\rm{\varphi }}_r}\left( {{{{m}}_{c,A}}} \right) - {{\rm{\varphi }}_c}\left( {{{{m}}_{c,A}}} \right) = {{\rm{\varphi }}_2} - {{\rm{\varphi }}_1} $$ (2) 根据系统的几何结构很容易推导出点D高度h的计算公式
$$ l/h = 1 + d/\overline {AB} $$ (3) 
图 3 相位-高度映射原理图。(a) 仅有参考平面的情况;(b) 对物体进行三维成像的情况
Figure 3. Schematic diagram of the phase-to-height conversion. (a) Reference plane only; (b) 3D imaging for the object
如果已知标准条纹在参考平面上的空间周期为λr,则可以根据正弦条纹相位与周期的关系计算
$\overline {AB} $ 的长度$$ \overline {AB} = \Delta {\rm{\varphi }}/2\text{π} {\lambda _r} $$ (4) 其中λr由标准条纹图的生成参数、投影仪像素尺寸、投影系统放大率等参数共同确定。公式(2)~(4)构成了一个典型的相位-高度映射模型。其中系统参数包括θ={l,d,λr},可以直接测量或通过系统标定进行估计。
上述系统结构中的平行光轴布局主要是为了保证参考平面上的条纹具有固定的空间周期,使得相位-高度映射模型可以用相对简单的数学表达式来描述。缺点在于未能充分利用有限的视场,投影仪和相机的公共(重叠)视场比较小。如果希望扩大公共视场,则通常需要偏转投影仪的镜头光轴,获得合适的光轴夹角。对于参考平面而言,此时处于倾斜投影状态,需要采用远心镜头投影[21, 25]来保证条纹周期的一致性。如果采用普通镜头进行倾斜投影,则参考平面上的条纹周期不再恒定,必然导致相位-高度映射模型的复杂化[26-34]。
-
根据系统几何结构推导相位-高度模型时,通常需要利用某些几何相似关系,因此要求相机光轴垂直于参考平面,且需要求解物体表面与参考平面的相位差值用于计算高度。这类系统模型对系统结构的特定要求降低了系统灵活性,对FPP的实际应用造成了制约。为了克服这一制约,面向任意布置的FPP系统陆续提出了各种普适的相位-高度映射模型[35-40]。
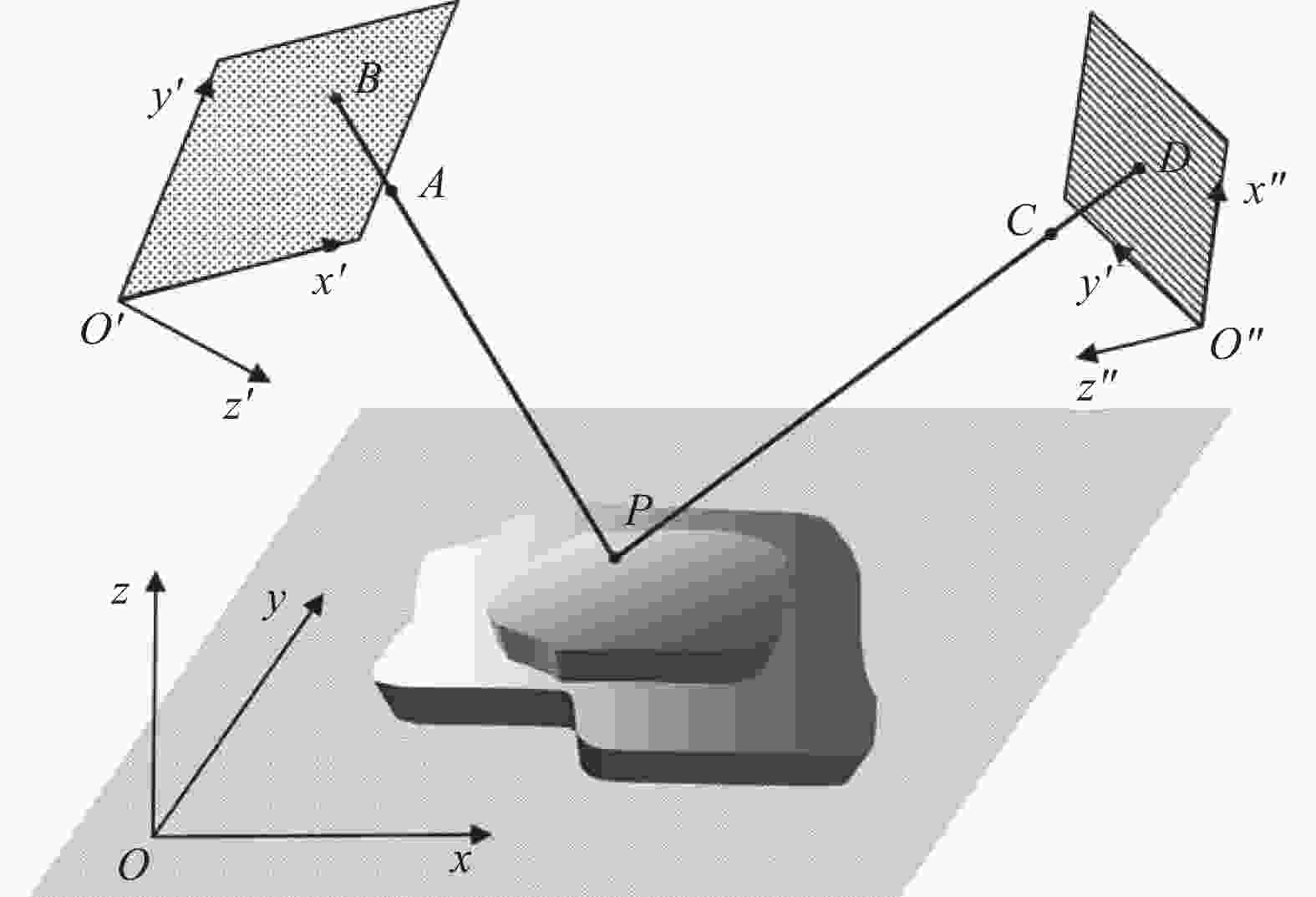
图4展示了一个任意布置的FPP系统[35],投影仪和相机的光轴方向以及光心位置可以任意设置。为了描述相机在三维空间中的任意姿态,分别建立两个坐标系:将物体所在的空间定义为世界坐标系;以相机的图像平面为x-o-y平面,相机镜头的光轴为z轴,建立相机坐标系。此时相机的位置可由其光心A在世界坐标系中的三维坐标XA来描述,方向可由世界坐标系到相机坐标系的旋转变换来描述。点B在相机图像中的二维坐标为mc,B=(uB,vB)T,在相机坐标系中的三维坐标为Xc,B=(mc,BT, 0)T,在世界坐标系中的坐标XB则由Xc,B结合世界坐标系到相机坐标系的旋转和平移变换来计算。由此,相机的姿态和相机图像中的点均可以在世界坐标系下定量表示。采用相同的机制建立投影仪坐标系,投影仪的姿态和投影图像中的点也可以在世界坐标系下定量表示。
对于投影仪而言,其标准条纹图在计算机中生成,对应的标准相位图
${\varphi_p}$ 已知。对于相机而言,由采集的变形条纹图进行相位恢复可以获得物体的变形相位图${\varphi_c}$ 。对于物体表面的某点P,可以直接由该点在相机图像中的像点坐标获取其对应的相位值${\varphi_P} = {{\rm{\varphi }}_c}\left( {{{m}_{c,B}}} \right)$ 。根据光线追迹,投影仪投影到点P的相位必定是${{\rm{\varphi }}_P}$ ,因此该点在投影平面上的投影坐标必然满足${{\rm{\varphi }}_P} = {{\rm{\varphi }}_p}\left( {{m_{p,D}}} \right)$ 。根据PAB和PCD各自的共线性,可以建立包含mc,B、mp,D、XA、XC在内的方程组,最终化简得到点P的高度表达式[35]$$ {z_P} = \frac{{{C_0} + {C_1}{\varphi_P} + \left( {{C_2} + {C_3}{\varphi_P}} \right){u_B} + \left( {{C_4} + {C_5}{\varphi_P}} \right){v_B}}}{{{D_0} + {D_1}{\varphi_P} + \left( {{D_2} + {D_3}{\varphi_P}} \right){u_B} + \left( {{D_4} + {D_5}{\varphi_P}} \right){v_B}}} $$ (5) 式中:系数
${\bf{\theta }} = \left\{ {{C_{0 - 5}},{D_{0 - 5}}} \right\}$ 取决于系统结构,其具体值可以通过系统标定进行估计。大多数相位-高度映射模型基于理想小孔成像,忽略了镜头畸变。这虽然可以简化系统模型的推导,但必然在一定程度上牺牲了系统的三维测量精度。当对系统精度要求较高时,可以在建立系统模型时引入镜头畸变[36, 39],代价是会增加系统标定的复杂度。
-
为FPP系统建立模型时,对系统结构的限定越少,考虑的普适因素越多,则系统参数越多,系统模型越复杂。原因在于必须通过增加系统参数来提高系统模型的自由度,以容纳足够多的实际系统要素。如果不追求建立全局参数一致的系统模型,而是为每个像素单独建立具有自身参数的相位-高度映射模型,则可以极大地简化模型和标定的复杂度[13, 41-48]。
应当注意到,FPP系统投影的条纹,其方向应与投影仪和相机光心连线的方向垂直。如果投影仪和相机水平放置,则投影的条纹为竖直方向的条纹。竖直条纹携带的相位在竖直方向上保持不变,在水平方向上单调增长,其在三维空间中的示意图如图5所示,空间中的相位分布形成一系列竖直的等相位面[42]。相机中的某个像素点mc对应三维空间中的一条视线(直线)。根据光线追迹原理,该视线在自由空间中会依次穿越所有的等相位面,视线与每个等相位面的交点对应着不同的高度。相位-高度映射模型可以表示为
$$ z = f\left( {{\theta_{{m_c}}};{\varphi_{c,{m_c}}}} \right) $$ (6) 式中:
${\varphi_{c,{{{m}}_c}}} = {\varphi_c}\left( {{m_c}} \right)$ 。$f\left( {{\theta_{{{m}_c}}}; \cdot } \right)$ 表示对于不同的像素点mc,映射模型虽然具有相同的数学形式,但具有不同的参数${\theta_{{m_c}}}$ 。如果FPP系统中相机的分辨率为M×N,则对应有M×N组不同的映射模型参数存储在查找表(look-up table, LUT)中。使用FPP系统对物体进行三维成像时,投采条纹并进行相位恢复,获得物体的变形相位图${{\rm{\varphi }}_c}$ 。对相位图中的每个像素,从查找表中获取其对应的模型参数,建立如公式(6)所示的相位-高度映射模型并带入该像素的相位值,即可求得该点的高度值。逐像素模型的构建可以从系统几何结构出发,按照与前两种模型的构建过程类似的方式进行分析建模[41, 43, 45];也可以根据直线(视线)与平面(等相位面)的相交等三角化的方法来进行建模[42, 44, 46]。另外,如果在建立系统模型时不考虑系统结构与模型的直接对应,仅从函数逼近的角度考虑,则可以用一般形式的高阶多项式[13, 47, 48]或有理式[49]直接表示相位与三维坐标之间的关系。
-
相位-高度映射模型的输出值是高度值,当三维直角坐标系的x-o-y平面与参考平面一致时,物体表面某点的高度值h即为该点的z坐标。从三维成像的角度看,相位-高度映射模型缺少了x和y坐标,其输出的深度像显示在三维坐标系中时,x和y轴对应着图像的像素坐标(以像素为单位)而不是真正的空间坐标(以毫米为单位)。因此深度像也被称为2.5维(2.5D)图像。为了得到完整的三维数据,需要建立相位与x和y坐标之间的映射关系,与相位-高度映射模型共同组成相位-三维映射模型[28, 30, 33-36, 39, 40, 42, 44, 47, 48, 50-60]。
相位-x、y坐标映射的立足点是相机视线(空间直线)的坐标约束关系。设相机中的某个像素mc在三维空间中的对应视线为lmc,则其一般表达式为
$$ {l_{{m_c}}}:\frac{{x - {x_0}}}{{{x_1} - {x_0}}} = \frac{{y - {y_0}}}{{{y_1} - {y_0}}} = \frac{{z - {z_0}}}{{{z_1} - {z_0}}} $$ (7) 式中:
${{{X}}_0} = {\left( {{x_0},{y_0},{z_0}} \right)^{\rm{T}}}$ 、${{{X}}_1} = {\left( {{x_1},{y_1},{z_1}} \right)^{\rm{T}}}$ 为直线${l_{{{{m}}_c}}}$ 上的任意两点。如果像素mc对应的视线方程已知,则可以由该像素对应的物体表面点的z坐标(高度值)计算其x和y坐标。 -
随着数字投影技术的发展,数字投影仪已经成为FPP系统中最常用的条纹投影装置。数字相机(以CMOS相机为例)在工作时,由物体表面发出的光经成像镜头折射后,汇聚到CMOS芯片上形成物体的像;数字投影仪(以DMD投影仪为例)在工作时,光线由DMD芯片出发,经投影镜头折射后照射到物体表面上形成特定的光强分布。比较二者的工作过程可见,数字投影仪投影恰好是数字相机成像的逆过程,这意味着可以用相机模型来描述投影仪,由此FPP系统可以借助计算机视觉中的立体视觉理论进行分析和建模[61, 62]。
-
忽略成像系统的衍射效应, 并假设相机镜头严格满足傍轴条件, 则相机镜头可视为理想成像系统。进而令镜头孔径趋于零, 则相机的成像过程等同于小孔成像, 从而得到针孔相机模型, 也称为线性相机模型。如果同时考虑镜头畸变,可以得到计算机视觉领域广泛应用的非线性相机模型
$$ \left\{ {\begin{array}{*{20}{r}} {{s_c}\widetilde {{{m}}_c'} = {{{K}}_c}\left[ {{{{R}}_c}|{{{t}}_c}} \right]\widetilde {{{{X}}_w}}\;\;\;\left(8{\rm{a}} \right)}\\ {{{{m}}_c} = {{m}}_c' + {{\delta }}\left( {{{{k}}_c};{{m}}_c'} \right)\;\;\;\;\left(8{\rm{b}} \right)} \end{array}} \right. $$ (8) 公式(8a)为针孔相机模型,描述了经过空间点Xw及其对应像点mc'的视线;公式(8b)描述了镜头畸变的影响,如图6所示。式中:Xw为空间点在世界坐标系中的三维坐标,mc为该点在相机图像中的像素二维坐标,mc'表示忽略镜头畸变时的理想像素二维坐标,
${\tilde \cdot }$ 表示齐次坐标,sc为尺度因子。Kc表示相机内参矩阵。Rc为旋转矩阵,tc为平移向量,共同组成相机外参,描述了从世界坐标系(WCS)到相机坐标系(CCS)的坐标变换。${\bf{\delta }}\left( {{{{k}}_c};{{m}}_c'} \right)$ 表示镜头畸变,其中kc为畸变系数(镜头畸变模型参数)。该模型描述了三维空间点Xw与其在相机图像中的像点mc之间的关系。由于镜头畸变为非线性函数,因此从mc恢复mc'无法直接求解,必须以迭代或者查找表的方式进行计算,从而影响数据处理的速度。因此在需要强调实时性的系统中,可以只使用针孔相机模型而不考虑镜头畸变。这样虽然会影响精度,但可以大大降低计算复杂度。
相机成像的数学本质在于确定了三维空间点到二维图像点的映射关系Xw→mc。根据光路可逆的特性,可以推测Xw与其在投影图案中的像点mp之间存在类似的关系。然而,与相机不同,投影仪只能发出光线而不能接收光线,因此无法从Xw直接得到其对应的mp。根据光线追迹,如果相机中的像点mc与投影仪中的像点mp对应于同一个空间点,则二者应始终具有相同的相位值,称二者互为同名像点。因此可令投影仪分别投射垂直和水平两个正交方向的标准条纹图序列(对应正交的标准相位图
${\rm{\varphi }}_p^u$ 和${\rm{\varphi }}_p^v$ ),而令相机采集相应的变形条纹图序列,借助恢复的正交相位(${\rm{\varphi }}_c^u$ 和${\rm{\varphi }}_c^v$ )建立mc与mp之间的对应关系。如图7所示,由于投影仪中的相位是标准分布,假设其条纹的空间周期为λp(单位为像素),零相位点的图像坐标为(u0,v0),则可根据mc点的相位确定投影图案中的像点坐标为[62-64]
图 7 利用正交相位确定投影图案中的同名像点坐标
Figure 7. Determination of the homologous image coordinate in the projection pattern according to the orthogonal phase maps
$$ {{{m}}_p} = {\left( {{u_0} + \frac{{{\rm{\varphi }}_c^u\left( {{{{m}}_c}} \right)}}{{2\text{π} }}{\lambda _p},{v_0} + \frac{{{\rm{\varphi }}_c^v\left( {{{{m}}_c}} \right)}}{{2\text{π} }}{\lambda _p}} \right)^{\rm{T}}} $$ (9) 上述过程借助相机图像和正交相位确定了三维空间点到投影仪二维图像点之间的映射关系
$$ {{{X}}_w}\mathop \to \limits^{{{{m}}_c},{\rm{\varphi }}_c^u,{\rm{\varphi }}_c^v} {{{m}}_p} $$ (10) 因此投影仪同样可以用公式(8)描述的非线性相机模型来表示,只需把对应的相机参数替换为投影仪参数即可(把表达式中的下标c替换为p)。
-
如图8所示,由于投影仪在模型上等同于相机,因此单目(相机+投影仪)结构的FPP系统原理上等同于双目系统,可以采用双目立体视觉模型来描述[61, 62]
$$ \left\{ {\begin{array}{*{20}{c}} {{{{R}}_s} = {{{R}}_p}{{R}}_c^{ - 1}\;\;\;\;\;\;\;\;\;\;\;\;\;\left(11{\rm{a}} \right)}\\ {{{{t}}_s} = {{{t}}_p} - {{{R}}_{\rm{s}}}{{{t}}_c}\;\;\;\;\;\;\;\;\;\;\;\;\left(11{\rm{b}}\right)}\\ {{{{X}}_c} = {{{R}}_c}{{{X}}_w} + {{{t}}_c}\;\;\;\;\;\;\;\;\;\;\left(11{\rm{c}} \right)}\\ {{s_c}\widetilde {{{m}}_c'} = {{{K}}_c}\left[ {{{I}}|0} \right]\widetilde {{{{X}}_c}}\;\;\;\;\;\;\left(11{\rm{d}}\right)}\\ {{{{m}}_c} = {{m}}_c' + {{\delta }}\left( {{{{k}}_c};{{m}}_c'} \right)\;\;\;\;\left(11{\rm{e}}\right)}\\ {{{\rm{s}}_p}\widetilde {{{m}}_p'} = {{{K}}_p}\left[ {{{{R}}_s}{\rm{|}}{{{t}}_s}{\rm{]}}\widetilde {{{{X}}_c}}} \right.\;\;\;\;\left(11{\rm{f}}\right)}\\ {{{{m}}_p} = {{m}}_p' + {{\delta }}\left( {{{{k}}_p};{{m}}_p'} \right)\;\;\;\left(11{\rm{g}}\right)} \end{array}\;} \right. $$ (11) 其中公式(11a)~(11b)描述了投影仪和相机之间的相对姿态,对于任意一个搭建好的系统而言,Rs和ts是确定的,称为系统的结构参数。公式(11c)~(11e)描述了相机的透视投影成像和镜头畸变,物理上对应相机接收的源于Xw的视线;公式(11f)~(11g)描述了投影仪的透视投影成像和镜头畸变,物理上对应投射到Xw的视线。三维重建实质上是从投影仪和相机的像点出发获得其各自的视线,然后在三维空间中求视线的交点。如果不考虑镜头畸变,则可以去掉公式(11e)、(11g),此时其余的公式共同组成线性双目立体视觉模型,适用于需要进行快速三维重建的情况。
相位-三维映射模型的输入是变形相位图,输出是三维数据。与之对标,双目立体视觉模型的输入也应当是变形相位图,输出是三维点云(物体表面各点的Xw)。这一意义下完整的双目立体视觉模型应由公式(9)和公式(11)组成,从而使得系统模型的输入同样是相位图。需要指出的是,公式(9)的输入是方向正交的两个相位图,对于FPP的三维重建而言存在信息冗余。通过引入极线约束[65-67]或分析线性双目立体视觉模型的显式解[68]可以发现,进行三维重建并不需要完整的mp信息(对于投影仪-相机水平摆放的FPP系统,仅需up而无需vp;反之,对于投影仪-相机竖直摆放的FPP系统,仅需vp而无需up),从而仅需要输入单一方向(竖直或水平)的相位图,与相位-三维映射模型的输入保持了一致。
由于投影仪和相机在模型上的等价性,基于立体视觉的条纹投影系统对投影仪和相机的数量没有理论限制。任意M(M≥1)个投影仪和N(N≥1)个相机均可以自由组合为一套FPP系统[6, 69, 70]。立体视觉模型的数学表达式与二维/三维空间坐标深度耦合,且内在包含了三维空间的刚体变换,因此可以方便的进行系统扩展。例如,FPP系统的另外一种典型配置是相机-投影仪-相机的双目结构[71-74]。一方面,该系统中的两个相机构成经典的双目立体视觉系统,投影仪可仅用于提供相位特征以实现双目间的同名点匹配,有助于提高系统的整体稳定性;另一方面,每个相机都可以与投影仪组成单目FPP系统,可以从两个不同的视点进行三维成像,提高了数据完整性[75]。
应当注意到,公式(8)和公式(11)描述的是相机/投影的透视投影,在物理过程上与一般的非广角、非远心镜头的光路特性相对应。而在小视场FPP系统中,有时会采用远心镜头进行投影和成像。从远心镜头的光路特性可以,其成像过程应当用正射投影来描述,此时相机/投影仪模型以及对应的立体视觉模型均需进行修正[76-80]。另外,相机成像过程是将空间物点发出的光束经主透镜汇聚到像点,是物点到像点的投影;而三维重建过程则是将像点进行反向投影,恢复空间物点。前者称为正向投影,后者称为反向投影[63]。采用反向投影模型对系统建模,能够避免相机标定与三维重建的不一致性,有助于提高系统精度[49, 81]。
-
如前所述,相位-三维映射模型中,相位与x、y坐标之间的映射关系本质上依赖于相机视线内在的空间直线约束。如果采用针孔相机模型来描述相机视线,一方面可以与三维空间的刚体变换无缝衔接,便于进行相关的模型分析和表达式推导;另一方面可以利用计算机视觉领域成熟的相机标定技术,便于进行系统标定。因此绝大多数相位-三维映射模型在建模分析时有意识地引入了针孔相机乃至非线性相机模型[28, 30, 33, 34, 36, 39, 40, 47-51, 53, 54, 56-60, 82]。考虑到
${{{X}}_w} = {\left( {x,y,z} \right)^{\rm{T}}}$ ,混合模型的三维重建分成两步进行,第一步利用相位-高度映射模型计算z坐标,第二步将z坐标带入相机模型公式(8)计算x、y坐标。 -
系统标定是为了确定系统模型中的未知参数,其执行策略与具体的系统模型密切相关,因此分别讨论相位-三维映射模型标定和立体视觉模型标定。
-
相位-三维映射模型标定通常分为两步进行。第一步仅对相位-高度映射模型进行标定,也称为离面标定。第二步对相位与x和y坐标之间的映射关系进行标定,称为面内标定或横向标定。
-
全局一致的相位-高度映射模型可以抽象为
$$ z = f\left( {{\rm{\theta }};{{\rm{\varphi }}_{c,{{m}_c}}},{{{m}}_c}} \right) $$ (12) 式中:f定义了模型的数学形式,θ为模型参数。需要强调的是,像点坐标mc也应视为模型的输入变量,一方面mc用于从整幅相位图中准确提取对应于该像点的相位值
${{\rm{\varphi }}_{c,{{{m}}_c}}}$ ,另一方面模型需要mc直接参与高度计算。理论上只要提供足够多组已知的输入↔输出组合,也即提供足够多组$\left( {{{{m}}_c},{{\rm{\varphi }}_{c,{{{m}}_c}}}} \right) \leftrightarrow z$ 数据,即可利用最小二乘优化比较准确地估计模型参数,完成系统标定。基于上述推论,相位-高度映射模型标定在数据获取环节的关键是获取多组像点坐标及其对应的相位值和高度值。典型的标定数据获取如图9所示[47],采用具有黑底白点的平面作为标靶。白色圆点作为标志点,可以利用圆心拟合算法精确估计其图像坐标mc。其对应的相位值
${{\rm{\varphi }}_{c,{{{m}}_c}}}$ 可以从相位图${{\rm{\varphi }}_c}$ 中进行插值获取。将标靶沿z轴方向多次平移,则可以获得不同的高度值z。通过平移点阵标靶可以获取足够多组标定数据,由此对模型参数θ进行估计。具体制定标定方案时,也可以选择其他形式的标志点,如棋盘格[34]或者正交光栅[55]。标靶的精确平移需要借助于精密导轨。而如果考虑用计算机视觉中的非线性相机模型描述相机,则平面标靶的姿态可以由单独的相机标定来进行估计。此时可以通过任意改变标靶姿态提供不同的高度数据[29, 39, 51, 53, 54, 56-58],无需借助精密导轨。标靶上需要有标志点图案用于图像坐标定位,常用的标志点图案包括棋盘格[39, 51, 53]和点阵[29, 54, 56, 58]。当使用无图案的白色平面标靶时,需要在标靶上另外固定一些可识别特征用于姿态估计[57]。多次改变标靶姿态可以提供充足的标定数据,有利于保证标定的稳定性。标靶姿态变化的次数也可以进一步减少,例如仅采集两个平行姿态和一个倾斜姿态的数据,而通过数据处理合成多组平行的虚拟中间姿态[50];甚至可以仅计算一个倾斜姿态的z分布,从而由一个标靶姿态标定相位-高度映射[27]。
对于相位-高度映射模型标定而言标志点并不是必须的。即使不存在标志点,对于任意的图像坐标mc,总是可以由相位图获得其相位值
${{\rm{\varphi }}_{c,{{m}_c}}}$ 。此时只要再确定其对应的高度值z,即可将相关数据用于进行标定。因此,具有不同高度的标准块可以用于系统标定[36, 38, 52],不同高度的区域可以借助阴影和相位跳变进行分割,从而可以按照分割区域确定mc和z的对应关系。用于系统标定的典型标准块如图10所示[52]。由公式(6)可知,逐像素相位-高度映射模型对于每个像素mc均具有不同的参数
${\theta}_{m_c}$ ,因此参数估计需要对每个像素分别进行,这就要求对每个像素均需要提供多组${{\rm{\varphi }}_{c,{{m}_c}}} \leftrightarrow z$ 数据。此时平移平面标靶成为首选的标定方式[41-46, 48, 49, 59, 83]。通过N次标靶平移可以对每个像素提供N组${\rm{\varphi }} \leftrightarrow z$ 数据,理论上只要N不小于${\theta}_{m_c} $ 中的参数个数,标靶平移提供的数据就足以完成逐像素相位-高度映射模型标定,为所有像素对应的模型参数生成参数查找表(LUT)。如果仅进行相位-高度映射模型标定,仅使用无图案的白色平面标靶即可。如果希望同时进行横向标定,则需要有标志点图案用于图像坐标定位。 -
横向标定是为了建立相位与x和y坐标之间的映射关系。借助于相机视线内在的空间直线约束,如果相机视线的直线方程已知,则可以由z坐标直接计算x和y坐标。而相机模型公式(8)恰好给出了相机视线的直线方程。在相位-三维映射模型中引入相机模型后,即可采用混合模型对FPP系统进行建模,此时横向标定可以由相机标定来完成[84]。混合模型下包含相位-高度映射标定和横向标定在内的完整系统标定流程通常如图11所示。标靶一般为印有标志点图案的平面标靶,在数据采集过程中需要多次改变姿态,以提供不同的高度值。在每个姿态下,需要分别采集两组图像,一组是条纹投影模式下的条纹图,另一组是均匀照明模式下的标靶图。从标靶图中提取特征点的图像坐标mc,结合已知的特征点空间坐标信息Xw,即可进行相机标定。相机标定一方面等同于横向标定,提供了由z坐标计算x和y坐标的模型;另一方面根据可以获得相机外参,从而生成相机坐标系中标志点的高度信息。从条纹图中利用相位恢复算法可以得到标靶的绝对相位图
${{\rm{\varphi }}_c}$ 。结合相机标定提供的高度信息,即可进行相位-高度映射模型标定。最终,由两部分标定结果可以组合为完整的相位-三维映射模型$$ \left( {x,y,z} \right) = g\left( {{{\rm{\theta }}_h};{{\rm{\varphi }}_{c,{m_c}}},{m_c}} \right) $$ (13) 需要注意的是,图11中的示例图像中,标靶的背景是黑色的,相位图中仅在白色的标志点区域中才存在有意义的相位值。使用黑色背景的标靶图案不能获得所有像素的相位值,因此只适用于标定全局一致的相位-高度映射模型。如果标定逐像素相位-高度映射模型,需要确保相位图中每个像素均有相位值,此时通常需要使用白色背景的标靶或者红蓝棋盘格标靶[34, 48, 53, 61, 83]。
如果系统模型中未引入相机模型,则需要单独进行横向标定。当采用平面标靶时,由于缺少相机标定,因此不能任意改变标靶姿态,只能由导轨进行精确平移。相关工作中曾经使用过的标靶图案包括分别对应两个正交方向的两帧正弦光栅[42]或单帧正交光栅[55]。另外,也可以不采用平面标靶而自行特殊设计标靶,由标靶提供的几何约束估计系统参数[30]。
-
立体视觉模型公式(11)中包含了众多参数。为了后续表达上的简便,引入简化的符号系统
$$ \left\{ {\begin{array}{*{20}{l}} {\left( {{{{K}}_{c/p}},{{{k}}_{c/p}}} \right) \to {{\rm{\theta }}_{c/p}}}\\ {\left( {{{{r}}_{c/p/s}},{{{t}}_{c/p/s}}} \right) \to {{{\Theta }}_{c/p/s}}} \end{array}} \right. $$ (14) 式中:r为3×1的旋转向量,用于取代3×3的旋转矩阵R,保证系统参数之间的线性无关特性。使用立体视觉模型进行三维重建,是在参数
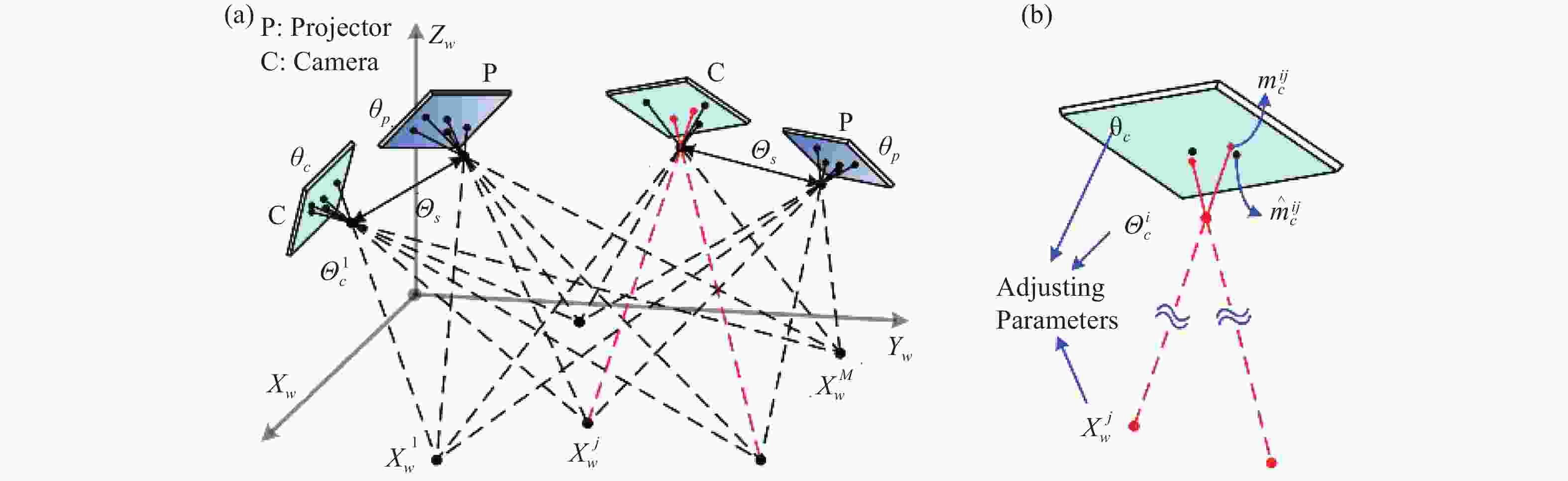
${{\rm{\theta }}_{c/p}}$ 、${{\bf{\varTheta }}_{c/p/s}}$ 已知的情况下,根据给定的mc/p,联立模型的方程组求解Xw。而标定过程则是通过给定一组标志点的Xw和mc/p,根据系统模型来估计未知的系统参数${{\rm{\theta }}_{c/p}}$ 和${{\bf{\varTheta }}_{c/p/s}}$ [61, 62, 85-90]。参数估计的过程大致分为两步:初值估计和最小二乘优化。立体视觉模型的系统标定一般流程如图12所示。系统标定之前,需要分别获得相机的标志点信息mc↔Xw和投影仪的标志点信息mp↔Xw作为输入,数据采集过程与2.1.2节中混合相位-三维模型的系统标定类似,区别在于立体视觉模型标定在采集标靶的条纹图时需要两个正交方向的条纹图,投影仪的标志点信息借助于正交相位通过公式(10)获取。首先分别估计相机和投影仪的线性模型参数,作为后续参数优化的初值。然后基于非线性模型分别对相机和投影仪参数进行最小二乘优化。优化的目标函数为
$$ \cos t\left( \tau \right) = \mathop \sum \nolimits {\left\| {{{{m}}_{c/p}} - {{{{\hat m}}}_{c/p}}\left( {{{\rm{\theta }}_{c/p}},{{\bf{\varTheta }}_{c/p}}} \right)} \right\|^2} $$ (15) 式中:
$\tau = \left\{ {{{\rm{\theta }}_{c/p}},{{\bf{\varTheta }}_{c/p}}} \right\}$ 为待优化的参数向量;${{{{\hat m}}}_{c/p}}$ 为根据线非性模型公式(8)和相应的模型参数进行重投影获得的标志点在相机和投影仪中的图像坐标。公式(15)计算了输入标志点坐标和重投影标志点坐标之间的欧氏距离误差,又称为重投影误差函数。参数取值越准确,重投影误差越小。参数的最小二乘估计即通过最小化重投影误差函数来实现。最后,根据${{\bf{\varTheta }}_{c/p}}$ 计算${{\bf{\varTheta }}_s}$ 作为初值,根据立体视觉模型定义总体优化的目标函数,将所有的参数一起进行联合优化[62, 85, 91]。联合优化的目标函数为$$ \cos t\left( \tau \right) = \mathop \sum \nolimits \left\{ {{{\left\| {{{{m}}_c} - {{{{\hat m}}}_c}\left( {{{\rm{\theta }}_c},{{\bf{\varTheta }}_c}} \right)} \right\|}^2} + {{\left\| {{{{m}}_p} - {{{{\hat m}}}_p}\left( {{{\rm{\theta }}_p},{{\bf{\varTheta }}_c},{{\bf{\varTheta }}_s}} \right)} \right\|}^2}} \right\} $$ (16) 式中:待优化的参数向量为
$\tau = \left\{ {{{\rm{\theta }}_c},{{\rm{\theta }}_p},{{\bf{\varTheta }}_c},{{\bf{\varTheta }}_p},{{\bf{\varTheta }}_s}} \right\}$ 。获取投影仪的标志点信息mp↔Xw时,其根本出发点是借助正交相位图建立投影仪与相机之间的同名像点对应关系,将相机中的信息映射到投影仪中。实际执行中根据实现策略的不同,具体可以分为图像映射和标志点映射两类。由正交相位建立逐像素的映射关系[61, 89]或者估计单应矩阵[86],可以将相机图像映射为投影仪图像,进而从投影仪图像中提取特征点坐标用于标定。也可以先从相机图像中提取特征点坐标,然后借助正交相位将坐标映射至投影仪中,直接获得投影仪中的标志点坐标[62, 75, 87, 92, 93]。
对标定过程进行分析可以发现,标志点在相机和投影仪中的观测图像坐标mc/p精度和标志点的三维坐标Xw精度均影响最终的参数估计精度。在通常的标定方法中,Xw是作为已知量直接输入的。此时Xw与其真实位置之间的偏差(可能是由于标靶面不是理想平面、标志点图案印制误差等多种因素导致)会引入系统误差,降低了标定结果的可靠性。解决这一问题可以从改善标靶精度入手,例如采用更精密的加工工艺制作标靶、利用检测设备对标志点的坐标进行逐点测量等,但需要较高的成本。而从算法角度考虑,可以通过在标定中引入光束平差(bundle adjustment, BA)来消除输入坐标Xw的误差带来的不利影响[62, 80, 91, 94],如图13所示。光束平差通过最小化模型的误差函数实现对三维结构(标志点的世界坐标)和相机参数的联合最优估计[95]。与一般标定的优化目标函数公式(16)相比,区别在于光束平差将Xw作为待优化的变量。Xw将在光束平差优化的过程中调整为更准确的值。
如果更进一步,在系统标定时不输入三维坐标Xw而仅输入图像坐标mc/p,则相当于在未知标靶的情况下进行标定,称为系统自标定[66, 69, 96, 97]。与光束平差优化相比,自标定需要在算法内部自行估计标志点的三维坐标初值。光束平差和自标定时,Xw被视为变量进行调整,其最终结果与真实的三维坐标之间满足几何上的相似关系,但丢失了绝对尺度,因此需要通过标准球等已知物体作为尺度基准确定绝对尺度[91, 97]。
-
标靶是系统标定的参照物和基准数据来源,不同的系统模型和标定方法对标靶有不同的要求。对于相位-高度映射模型标定而言,其输入应当是成组的
$\left( {{{{m}}_c},{{\rm{\varphi }}_{c,{{m}_c}}}} \right) \leftrightarrow z$ 数据,从而要求标靶易于获得相位和高度。因此相位-高度模型标定常用白色的标准平面作为标靶[28, 41, 42, 57],可以通过平移变化高度,投影条纹的对比度整体均匀,便于计算相位。另外,对于全局一致的相位-高度映射模型标定,也常用不同高度的标准块组成三维标靶[36, 38, 52],可以从一幅相位图中获得多个不同的高度,减少数据采集的工作量。对于立体视觉模型标定和相位-三维映射模型横向标定而言,从易用性和算法成熟度考虑,平面标靶具有绝对优势[84]。这两类标定的输入是成组的
$\left( {{{{m}}_c},{{\rm{\varphi }}_{c,{{{m}}_c}}}} \right) \leftrightarrow {{{X}}_w}$ 数据,图像坐标mc不仅要与z坐标对应,还要与x、y坐标对应,因此平面标靶上必须有易于提取标志点的图案。主流的标靶图案分为棋盘格[34, 39, 48, 51, 53, 61, 86]和圆点阵[58, 59, 62, 75, 85, 87-90, 93, 97]两大类。其它非常规的标靶图案,如正弦光栅[42]、正交光栅[55]、方点阵[66, 82]等,也有相关的应用案例。棋盘格的优点是标志点(角点)定位算法简单成熟,与计算机视觉中相机标定的兼容性高。尤其是红蓝棋盘格图案[34, 48, 53, 61],当使用单色相机采集图像时,在白光照明下图案不可见,适合采集条纹图进行相位恢复;在红光或蓝光均匀照明下相当于经典的黑白棋盘格,适合采集图像进行标志点提取,尤其适用于相位-三维映射模型的横向标定。
圆点阵的优点是抗离焦能力强,定位精度高,在高精度标定中应用广泛。为了提高标定的自动化程度,实现标志点图像坐标mc与三维坐标Xw的自动对应,需要对提取的标志点进行自动编码。为此提出了各种点阵的编码方案,如图14所示。其中图14(a)为编码标志点阵方案[85],每个点均可以通过其周围的圆环进行自动编码;图14(b)~14(c)为均匀点阵加定位点方案[91, 97],通过定位点之间的位置关系可以识别标靶的方位,实现自动编码;图14(d)为对具有14(c)中图案的标靶进行自动编码结果。
-
FPP系统的三维重建精度受到相位精度、标定精度、系统结构等多个因素的综合影响。其中单一环节的精度分析,例如相位误差、标定误差等,不能准确反应最终的三维重建误差。因此对FPP系统进行三维重建的精度评估时,通用的做法是将系统测得的三维数据与已知的标准数据或第三方系统测量的数据进行对比分析。
-
标准平面是精度评估常用的一类标准件。对标准平面进行测量后用测得的数据拟合一个理想平面,拟合残差可以表征三维测量的局部误差[33, 36, 53, 61, 86, 87]。测量精确移动前后的平面[41, 50]、标准块的表面[36, 48, 51, 56, 82]、标准台阶的表面[28, 29, 58, 97],然后将测得的高度差与标准高度值进行比较,可以获得三维重建的绝对误差。典型的平面拟合残差[61]和标准台阶[60]测量结果如图15所示。
标准球是精度评估常用的另一类标准件[12, 49, 59, 62, 68, 70, 72, 74, 91, 98, 99]。对标准球的测量数据进行球面拟合,拟合残差可以表征三维测量的局部误差,拟合的球半径以及一对标准球之间的球心距均可用来表征三维重建的绝对误差。典型的一对标准球及其测量结果如图16所示。
除了上述两类常用标准物体,其它特征尺寸已知的物体也可以作为精度评估的标准件,例如标准圆柱面[61]、精密加工的有沟槽的平面[69]、两个垂直的平面[86]、已知高度的物体[45]等。另外,也可以将系统的测量结果与其它商业化的成熟三维测量系统的测量结果进行对比来评估系统精度,例如与坐标测量机[30, 42]、激光线扫描仪[50]、商用三维扫描仪[85]的结果进行对比。
-
德国在条纹投影三维成像技术的研究方面一直居于前列,目前用于工业检测的高端条纹投影三维扫描系统大多是德国品牌。德国工程师协会(VDI)积极推动光学三维测量的认证工作,其下属的德国测量与自动控制学会(GMA)组织相关领域的专家制定了光学三维测量领域的技术标准VDI/VDE 2634[100]。该标准的第二部分(VDI/VDE 2634 Part 2 - Optical 3D measuring systems: Optical systems based on area scanning)面向基于区域扫描的光学系统[101],在相关领域得到了广泛的认可和应用。此节简单介绍其核心的验收测试规则,为评估FPP系统精度提供参考。
验收测试定义了3个质量参数来评估测量精度,分别是:探测误差、球间距误差、平面度测量误差。其中探测误差描述了测量体积内小部分区域面扫描的特征误差。设测量体积长方体的体对角线长度为L0,评估探测误差使用具有漫反射表面的标准球,球直径推荐为(0.1~0.2)L0。将标准球在测量体积内随机均匀改变不少于10个位置并进行测量,对每次测得的球面数据进行无约束球面拟合,将拟合的球半径与标准值进行比较。
球间距误差验证系统的长度测量能力,并确保可溯源性。评估球间距误差使用具有漫反射表面的哑铃球,球直径推荐为(0.1~0.2)L0,球心距不小于0.3L0。将哑铃球在测量体积内放置不少于7个不同的位置进行测量,如图17所示。对每次测得的哑铃球数据进行半径约束的球面拟合,根据拟合获得的球心坐标计算球心距,并与标准值进行比较。
评估平面度测量误差使用长方形漫反射平面,长方形的宽度不小于50 mm,长度不小于0.5L0。将长方形面在测量体积内放置不少于6个不同的位置进行测量,每个位置下长方形面应近似垂直于x-o-z平面,如图18所示。对每次测得的长方形面数据进行最小二乘平面拟合,计算每次测得的数据距离各自拟合平面的符号距离范围,即为平面度测量误差。
从上一节总结的FPP系统精度评估方式可知,精度评估最常用的标准件是标准平面和标准球,这与VDI/VDE 2634 Part 2标准推荐的标准件不谋而合。但是,许多报道的精度评估实验并未像图17、图18一样保证采样位置分布的均匀性,而这正是该标准值得借鉴的地方。
-
条纹投影轮廓术能较好地兼顾系统灵活性与测量精度,是当前光学三维成像与测量的主流技术。分析FPP的基本工作过程与核心要素可知,系统标定与系统模型密不可分,对三维成像的性能和精度有直接影响。文中对FPP的主流系统模型和系统标定技术进行综述,并简要总结系统精度评估的方法和依据。
FPP的三维重建在几何上相当于求解投影仪发出的视线和相机接收的视线之间的空间交点。投影仪发出的视线由相位确定,相机接收的视线由图像坐标确定,因此三维重建可视为输入图像坐标和相位并输出三维坐标的映射函数,由此发展出一系列相位-三维映射模型。而如果用透视投影为相机和投影仪建模,则模型方程直接描述相机和投影仪的视线,三维重建相当于联立相机和投影仪的模型方程,由此建立双目立体视觉模型。对于一个新的FPP系统而言,其模型中的参数未知,需要通过系统标定来估计这些未知的模型参数。标定方法和执行策略与具体的系统模型密切相关,因此针对相位-三维映射和立体视觉这两类不同的工作原理,分别对系统模型和系统标定进行了综述。
总体而言,相位-三维映射和立体视觉这两类不同的模型呈现出逐渐融合的趋势,在相位-三维映射模型的建立和标定过程中,越来越多的工作引入立体视觉中的相机模型。一方面,相机模型利用透视投影变换和三维刚体变换来描述系统,在数学上较为精确简练,引入相机模型有助于提高相位-三维映射模型的表述一致性和规范性。另一方面,相机模型在标定时能够同时估计平面标靶的外参,从而可以摆脱对精密导轨等定位装置的依赖,提高了相位-三维映射模型标定的灵活性。
FPP系统的三维重建精度受到相位精度、标定精度、系统结构等多个因素的综合影响,单一环节的精度分析不能准确反应最终的三维重建误差,因此需要直接对三维重建的结果进行精度评估。文中综述了常用的精度评估方式,并介绍了德国工程师协会制定的光学三维测量领域的技术标准VDI/VDE 2634 Part 2,作为FPP系统精度评估的参考。标准平面和标准球是最常用的精度评估标准件,为了使评估结果更严谨可靠,推荐按照VDI/VDE 2634标准确定评估数据的采样位置。
随着FPP相关理论和方法的成熟,基于FPP的光学三维扫描仪已经实现了商品化并在工业检测等领域得到了广泛应用。目前对FPP技术的研究主要集中于实时/动态场景和透明/反光等特殊表面的三维成像。不同的系统模型在三维重建算法的复杂度上存在巨大差异,对三维成像的速度和实时性有很大影响。通过建立合适的系统模型,在保证三维重建精度的前提下尽量提高计算效率,是一个值得研究的问题。将系统模型与条纹图处理、相位计算进行深度耦合,在单纯的相位恢复算法之外为条纹图和相位的计算处理提供额外约束,在提高条纹图编码效率、提升特殊表面成像质量等方向均具有较大的发展潜力。
Review of the system model and calibration for fringe projection profilometry
-
摘要: 条纹投影轮廓术能较好地兼顾系统灵活性与测量精度,是光学三维表面成像与测量的主流技术。利用条纹投影轮廓术进行三维成像,首先需要建立合适的系统模型,然后通过系统标定来确定描述模型的系统参数,最后利用标定的系统模型进行三维重建,获得物体的三维表面形貌。由此可见,系统标定与系统模型密不可分,对三维成像的性能有直接影响。根据相位-三维映射和双目立体视觉两类不同的工作原理,对条纹投影轮廓术的系统模型和系统标定方法进行了综述,并简要总结了评估系统精度的方法和依据。Abstract: Fringe projection profilometry (FPP) can well balance the system flexibility and the measurement accuracy, which is the mainstream technology of optical 3D imaging and shape measurement. When working with FPP, first an appropriate system should be established, and then the system parameters describing the system model should be determined via system calibration, finally the 3D shape is generated with 3D reconstruction by using the calibrated system model. System calibration and system model are tightly coupled, which have a direct impact on the performance of 3D imaging. The principle of FPP can be divided into two categories, i.e. the phase-3D mapping and the binocular stereo vision. This paper reviewed the system model and calibration strategy of FPP, which corresponded to the above two categories. Finally the method and basis for the accuracy evaluation of FPP were summarized.
-
图 2 FPP的基本要素及其内在联系。其中φ表示相位图;m表示二维图像坐标;X表示三维空间坐标;θ为包含多个系统参数的参数向量
Figure 2. Basic elements of the fringe projection profilometry and their internal relations. Here φ denotes the phase distribution; m is the 2D image coordinate; X is the 3D space coordinate; θ is the parameter vector containing multiple parameters
-
[1] Chen F, Brown G M, Song M. Overview of three-dimensional shape measurement using optical methods [J]. Optical Engineering, 2000, 39(1): 10−22. doi: 10.1117/1.602438 [2] Tutsch R, Petz M, Fischer M. Optical three-dimensional metrology with structured illumination [J]. Optical Engineering, 2011, 50(10): 101507. doi: 10.1117/1.3578448 [3] Sansoni G, Trebeschi M, Docchio F. State-of-the-art and applications of 3D imaging sensors in industry, cultural heritage, medicine, and criminal investigation [J]. Sensors, 2009, 9(1): 568−601. doi: 10.3390/s90100568 [4] Geng J. Structured-light 3D surface imaging: A tutorial [J]. Advances in Optics and Photonics, 2011, 3(2): 128−160. doi: 10.1364/AOP.3.000128 [5] Peng X, Tian J, Zhang P, et al. Three-dimensional vision with dual acousto-optic deflection encoding [J]. Optics Letters, 2005, 30(15): 1965−1967. doi: 10.1364/OL.30.001965 [6] Guan Y, Yin Y, Li A, et al. Dynamic 3D imaging based on acousto-optic heterodyne fringe interferometry [J]. Optics Letters, 2014, 39(12): 3678−3681. doi: 10.1364/OL.39.003678 [7] Zhang J, Zhou C, Wang X. Three-dimensional profilometry using a dammann grating [J]. Applied Optics, 2009, 48(19): 3709−3715. doi: 10.1364/AO.48.003709 [8] Miao Y, Zhao Y, Ma H, et al. Design of diffractive optical element projector for a pseudorandom dot array by an improved encoding method [J]. Applied Optics, 2019, 58(34): G169−G176. doi: 10.1364/AO.58.00G169 [9] Iwata K, Sando Y, Satoh K, et al. Application of generalized grating imaging to pattern projection in three-dimensional profilometry [J]. Applied Optics, 2011, 50(26): 5115−5121. doi: 10.1364/AO.50.005115 [10] Fujigaki M, Oura Y, Asai D, et al. High-speed height measurement by a light-source-stepping method using a linear led array [J]. Optics Express, 2013, 21(20): 23169−23180. doi: 10.1364/OE.21.023169 [11] Heist S, Dietrich P, Landmann M, et al. GOBO projection for 3D measurements at highest frame rates: A performance analysis [J]. Light: Science & Applications, 2018, 7(1): 71. [12] Hyun J-S, Chiu G T C, Zhang S. High-speed and high-accuracy 3D surface measurement using a mechanical projector [J]. Optics Express, 2018, 26(2): 1474−1487. doi: 10.1364/OE.26.001474 [13] Sitnik R, Kujawinska M, Woznicki J. Digital fringe projection system for large-volume 360-deg shape measurement [J]. Optical Engineering, 2002, 41(2): 443−449. doi: 10.1117/1.1430422 [14] Zhang S, Yau S-T. Three-dimensional shape measurement using a structured light system with dual cameras [J]. Optical Engineering, 2008, 47(1): 013604. doi: 10.1117/1.2835686 [15] Guo W, Wu Z, Xu R, et al. A fast reconstruction method for three-dimensional shape measurement using dual-frequency grating projection and phase-to-height lookup table [J]. Optics & Laser Technology, 2019, 112: 269−277. [16] Salvi J, Fernandez S, Pribanic T, et al. A state of the art in structured light patterns for surface profilometry [J]. Pattern Recognition, 2010, 43(8): 2666−2680. doi: 10.1016/j.patcog.2010.03.004 [17] Gorthi S S, Rastogi P. Fringe projection techniques: Whither we are? [J]. Optics and Lasers in Engineering, 2010, 48(2): 133−140. doi: 10.1016/j.optlaseng.2009.09.001 [18] Su X, Chen W. Fourier transform profilometry: A review [J]. Optics and Lasers in Engineering, 2001, 35(5): 263−284. doi: 10.1016/S0143-8166(01)00023-9 [19] Zhang Z H. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques [J]. Optics and Lasers in Engineering, 2012, 50(8): 1097−1106. doi: 10.1016/j.optlaseng.2012.01.007 [20] Takeda M, Mutoh K. Fourier transform profilometry for the automatic measurement of 3-D object shapes [J]. Applied Optics, 1983, 22(24): 3977−3982. doi: 10.1364/AO.22.003977 [21] Srinivasan V, Liu H C, Halioua M. Automated phase-measuring profilometry of 3-D diffuse objects [J]. Applied Optics, 1984, 23(18): 3105−3108. doi: 10.1364/AO.23.003105 [22] Zuo C, Feng S, Huang L, et al. Phase shifting algorithms for fringe projection profilometry: A review [J]. Optics and Lasers in Engineering, 2018, 109: 23−59. doi: 10.1016/j.optlaseng.2018.04.019 [23] Su X, Chen W. Reliability-guided phase unwrapping algorithm: A review [J]. Optics and Lasers in Engineering, 2004, 42(3): 245−261. doi: 10.1016/j.optlaseng.2003.11.002 [24] Zuo C, Huang L, Zhang M, et al. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review [J]. Optics and Lasers in Engineering, 2016, 85: 84−103. doi: 10.1016/j.optlaseng.2016.04.022 [25] Quan C, Tay C J, Huang Y H. 3-D deformation measurement using fringe projection and digital image correlation [J]. Optik, 2004, 115(4): 164−168. doi: 10.1016/S0030-4026(08)70004-4 [26] Mao X, Chen W, Su X. Improved fourier-transform profilometry [J]. Applied Optics, 2007, 46(5): 664−668. doi: 10.1364/AO.46.000664 [27] Tavares P J, Vaz M A. Linear calibration procedure for the phase-to-height relationship in phase measurement profilometry [J]. Optics Communications, 2007, 274(2): 307−314. doi: 10.1016/j.optcom.2007.02.038 [28] Zhang Z, Towers C E, Towers D P. Uneven fringe projection for efficient calibration in high-resolution 3D shape metrology [J]. Applied Optics, 2007, 46(24): 6113−6119. doi: 10.1364/AO.46.006113 [29] Zhang Z, Ma H, Zhang S, et al. Simple calibration of a phase-based 3D imaging system based on uneven fringe projection [J]. Optics Letters, 2011, 36(5): 627−629. doi: 10.1364/OL.36.000627 [30] Yu C, Peng Q. A unified-calibration method in ftp-based 3D data acquisition for reverse engineering [J]. Optics and Lasers in Engineering, 2007, 45(3): 396−404. doi: 10.1016/j.optlaseng.2006.07.001 [31] Chen L, Quan C. Fringe projection profilometry with nonparallel illumination: A least-squares approach [J]. Optics Letters, 2005, 30(16): 2101−2103. doi: 10.1364/OL.30.002101 [32] Wang Z, Du H, Bi H. Out-of-plane shape determination in generalized fringe projection profilometry [J]. Optics Express, 2006, 14(25): 12122−12133. doi: 10.1364/OE.14.012122 [33] Gonzalez A, Meneses J. Accurate calibration method for a fringe projection system by projecting an adaptive fringe pattern [J]. Applied Optics, 2019, 58(17): 4610−4615. doi: 10.1364/AO.58.004610 [34] Lu P, Sun C, Liu B, et al. Accurate and robust calibration method based on pattern geometric constraints for fringe projection profilometry [J]. Applied Optics, 2017, 56(4): 784−794. doi: 10.1364/AO.56.000784 [35] Du H, Wang Z. Three-dimensional shape measurement with an arbitrarily arranged fringe projection profilometry system [J]. Optics Letters, 2007, 32(16): 2438−2440. doi: 10.1364/OL.32.002438 [36] Huang L, Chua PS, Asundi A. Least-squares calibration method for fringe projection profilometry considering camera lens distortion [J]. Applied Optics, 2010, 49(9): 1539−1548. doi: 10.1364/AO.49.001539 [37] Xiao Y, Cao Y, Wu Y. Improved algorithm for phase-to-height mapping in phase measuring profilometry [J]. Applied Optics, 2012, 51(8): 1149−1155. doi: 10.1364/AO.51.001149 [38] Fu Y, Wang Y, Wang W, et al. Least-squares calibration method for fringe projection profilometry with some practical considerations [J]. Optik, 2013, 124(19): 4041−4045. doi: 10.1016/j.ijleo.2012.12.041 [39] Lu J, Mo R, Sun H, et al. Flexible calibration of phase-to-height conversion in fringe projection profilometry [J]. Applied Optics, 2016, 55(23): 6381−6388. doi: 10.1364/AO.55.006381 [40] Hu Y, Chen Q, Tao T, et al. Absolute three-dimensional micro surface profile measurement based on a greenough-type stereomicroscope [J]. Measurement Science and Technology, 2017, 28(4): 045004. doi: 10.1088/1361-6501/aa5a2d [41] Asundi A, Wensen Z. Unified calibration technique and its applications in optical triangular profilometry [J]. Applied Optics, 1999, 38(16): 3556−3561. doi: 10.1364/AO.38.003556 [42] Liu H, Su W-H, Reichard K, et al. Calibration-based phase-shifting projected fringe profilometry for accurate absolute 3D surface profile measurement [J]. Optics Communications, 2003, 216(1-3): 65−80. doi: 10.1016/S0030-4018(02)02290-3 [43] Guo H, He H, Yu Y, et al. Least-squares calibration method for fringe projection profilometry [J]. Optical Engineering, 2005, 44(3): 033603. doi: 10.1117/1.1871832 [44] Su W-H, Liu H. Calibration-based two-frequency projected fringe profilometry: A robust, accurate, and single-shot measurement for objects with large depth discontinuities [J]. Optics Express, 2006, 14(20): 9178−9187. doi: 10.1364/OE.14.009178 [45] Wen Y, Li S, Cheng H, et al. Universal calculation formula and calibration method in fourier transform profilometry [J]. Applied Optics, 2010, 49(34): 6563−6569. doi: 10.1364/AO.49.006563 [46] Liu K, Wang Y, Lau DL, et al. Dual-frequency pattern scheme for high-speed 3-D shape measurement [J]. Optics Express, 2010, 18(5): 5229−5244. doi: 10.1364/OE.18.005229 [47] Léandry I, Brèque C, Valle V. Calibration of a structured-light projection system: Development to large dimension objects [J]. Optics and Lasers in Engineering, 2012, 50(3): 373−379. doi: 10.1016/j.optlaseng.2011.10.020 [48] Merner L, Wang Y, Zhang S. Accurate calibration for 3D shape measurement system using a binary defocusing technique [J]. Optics and Lasers in Engineering, 2013, 51(5): 514−519. doi: 10.1016/j.optlaseng.2012.10.015 [49] Cai Z, Liu X, Li A, et al. Phase-3D mapping method developed from back-projection stereovision model for fringe projection profilometry [J]. Optics Express, 2017, 25(2): 1262−1277. doi: 10.1364/OE.25.001262 [50] Anchini R, Leo G D, Liguori C, et al. A new calibration procedure for 3-D shape measurement system based on phase-shifting projected fringe profilometry [J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(5): 1291−1298. doi: 10.1109/TIM.2009.2012952 [51] Vo M, Wang Z, Hoang T, et al. Flexible calibration technique for fringe-projection-based three-dimensional imaging [J]. Optics Letters, 2010, 35(19): 3192−3194. doi: 10.1364/OL.35.003192 [52] Wang Z, Nguyen D A, Barnes J C. Some practical considerations in fringe projection profilometry [J]. Optics and Lasers in Engineering, 2010, 48(2): 218−225. doi: 10.1016/j.optlaseng.2009.06.005 [53] Zappa E, Busca G, Sala P. Innovative calibration technique for fringe projection based 3D scanner [J]. Optics and Lasers in Engineering, 2011, 49(3): 331−340. doi: 10.1016/j.optlaseng.2010.10.007 [54] Zhang Z, Ma H, Guo T, et al. Simple, flexible calibration of phase calculation-based three-dimensional imaging system [J]. Optics Letters, 2011, 36(7): 1257−1259. doi: 10.1364/OL.36.001257 [55] Villa J, Araiza M, Alaniz D, et al. Transformation of phase to (x, y, z)-coordinates for the calibration of a fringe projection profilometer [J]. Optics and Lasers in Engineering, 2012, 50(2): 256−261. doi: 10.1016/j.optlaseng.2011.08.005 [56] Vo M, Wang Z, Pan B, et al. Hyper-accurate flexible calibration technique for fringe-projection-based three-dimensional imaging [J]. Optics Express, 2012, 20(15): 16926−16941. doi: 10.1364/OE.20.016926 [57] Xu J, Douet J, Zhao J, et al. A simple calibration method for structured light-based 3D profile measurement [J]. Optics & Laser Technology, 2013, 48: 187−193. [58] Zhang Z, Huang S, Meng S, et al. A simple, flexible and automatic 3D calibration method for a phase calculation-based fringe projection imaging system [J]. Optics Express, 2013, 21(10): 12218−12227. doi: 10.1364/OE.21.012218 [59] Zuo C, Tao T, Feng S, et al. Micro fourier transform profilometry (μFTP): 3D shape measurement at 10, 000 frames per second [J]. Optics and Lasers in Engineering, 2018, 102: 70−91. doi: 10.1016/j.optlaseng.2017.10.013 [60] Chen C, Yu J, Gao N, et al. High accuracy 3D calibration method of phase calculation-based fringe projection system by using lcd screen considering refraction error [J]. Optics and Lasers in Engineering, 2020, 126: 105870. doi: 10.1016/j.optlaseng.2019.105870 [61] Zhang S, Huang P. Novel method for structured light system calibration [J]. Optical Engineering, 2006, 45(8): 083601. doi: 10.1117/1.2336196 [62] Yin Y, Peng X, Li A, et al. Calibration of fringe projection profilometry with bundle adjustment strategy [J]. Optics Letters, 2012, 37(4): 542−544. doi: 10.1364/OL.37.000542 [63] Hartley R, Zisserman A. Multiple View Geometry In Computer Vision[M]. Cambridge: Cambridge University Press, 2003: 655. [64] Szeliski R. Computer Vision: Algorithms and Applications[M]. Berlin: Springer, 2010: 812. [65] Zhang S. High-speed 3D shape measurement with structured light methods: A review [J]. Optics and Lasers in Engineering, 2018, 106: 119−131. [66] Tian J, Ding Y, Peng X. Self-calibration of a fringe projection system using epipolar constraint [J]. Optics & Laser Technology, 2008, 40(3): 538−544. [67] Zhang R, Guo H, Asundi A K. Geometric analysis of influence of fringe directions on phase sensitivities in fringe projection profilometry [J]. Applied Optics, 2016, 55(27): 7675−7687. doi: 10.1364/AO.55.007675 [68] Feng S, Zuo C, Yin W, et al. Micro deep learning profilometry for high-speed 3D surface imaging [J]. Optics and Lasers in Engineering, 2019, 121: 416−427. doi: 10.1016/j.optlaseng.2019.04.020 [69] Schreiber W, Notni G. Theory and arrangements of self-calibrating whole-body three-dimensional measurement systems using fringe projection technique [J]. Optical Engineering, 2000, 39(1): 159−169. doi: 10.1117/1.602347 [70] Jiang C, Lim B, Zhang S. Three-dimensional shape measurement using a structured light system with dual projectors [J]. Applied Optics, 2018, 57(14): 3983−3990. doi: 10.1364/AO.57.003983 [71] Reich C, Ritter R, Thesing J. 3-D shape measurement of complex objects by combining photogrammetry and fringe projection [J]. Optical Engineering, 2000, 39(1): 224−231. doi: 10.1117/1.602356 [72] Yin Y, Peng X, Liu X, et al. Calibration strategy of optical measurement network for large-scale and shell-like objects [J]. Optics Communications, 2012, 285(8): 2048−2056. doi: 10.1016/j.optcom.2011.12.100 [73] Zhao H, Liang X, Diao X, et al. Rapid in-situ 3D measurement of shiny object based on fast and high dynamic range digital fringe projector [J]. Optics and Lasers in Engineering, 2014, 54: 170−174. doi: 10.1016/j.optlaseng.2013.08.002 [74] Qian J, Feng S, Tao T, et al. High-resolution real-time 360o 3D model reconstruction of a handheld object with fringe projection profilometry [J]. Optics Letters, 2019, 44(23): 5751−5754. doi: 10.1364/OL.44.005751 [75] Gai S, Da F, Tang M. A flexible multi-view calibration and 3D measurement method based on digital fringe projection [J]. Measurement Science and Technology, 2019, 30(2): 025203. doi: 10.1088/1361-6501/aaf5bd [76] Li D, Liu C, Tian J. Telecentric 3D profilometry based on phase-shifting fringe projection [J]. Optics Express, 2014, 22(26): 31826−31835. doi: 10.1364/OE.22.031826 [77] Li B, Zhang S. Flexible calibration method for microscopic structured light system using telecentric lens [J]. Optics Express, 2015, 23(20): 25795−25803. doi: 10.1364/OE.23.025795 [78] Peng J, Wang M, Deng D, et al. Distortion correction for microscopic fringe projection system with scheimpflug telecentric lens [J]. Applied Optics, 2015, 54(34): 10055−10062. doi: 10.1364/AO.54.010055 [79] Rao L, Da F, Kong W, et al. Flexible calibration method for telecentric fringe projection profilometry systems [J]. Optics Express, 2016, 24(2): 1222−1237. doi: 10.1364/OE.24.001222 [80] Liu H, Lin H, Yao L. Calibration method for projector-camera-based telecentric fringe projection profilometry system [J]. Optics Express, 2017, 25(25): 31492−31508. doi: 10.1364/OE.25.031492 [81] Gu F, Zhao H, Ma Y, et al. Camera calibration based on the back projection process [J]. Measurement Science and Technology, 2015, 26(12): 125004. doi: 10.1088/0957-0233/26/12/125004 [82] Chen L C, Liao C C. Calibration of 3D surface profilometry using digital fringe projection [J]. Measurement Science and Technology, 2005, 16(8): 1554−1566. doi: 10.1088/0957-0233/16/8/003 [83] Zhang X, Lin Y, Zhao M, et al. Calibration of a fringe projection profilometry system using virtual phase calibrating model planes [J]. Journal of Optics A: Pure and Applied Optics, 2005, 7(4): 192−197. doi: 10.1088/1464-4258/7/4/007 [84] Zhang Z. A flexible new technique for camera calibration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330−1334. doi: 10.1109/34.888718 [85] Legarda-Sáenz R, Bothe T, Jüptner W. Accurate procedure for the calibration of a structured light system [J]. Optical Engineering, 2004, 43(2): 464−471. doi: 10.1117/1.1635373 [86] Gao W, Wang L, Hu Z. Flexible method for structured light system calibration [J]. Optical Engineering, 2008, 47(8): 083602. doi: 10.1117/1.2969118 [87] Li Z, Shi Y, Wang C, et al. Accurate calibration method for a structured light system [J]. Optical Engineering, 2008, 47(5): 053604. doi: 10.1117/1.2931517 [88] Chen X, Xi J, Jin Y, et al. Accurate calibration for a camera–projector measurement system based on structured light projection [J]. Optics and Lasers in Engineering, 2009, 47(3): 310−319. [89] Huang Z, Xi J, Yu Y, et al. Accurate projector calibration based on a new point-to-point mapping relationship between the camera and projector images [J]. Applied Optics, 2015, 54(3): 347−356. doi: 10.1364/AO.54.000347 [90] Chen R, Xu J, Chen H, et al. Accurate calibration method for camera and projector in fringe patterns measurement system [J]. Applied Optics, 2016, 55(16): 4293−4300. doi: 10.1364/AO.55.004293 [91] Liu X, Cai Z, Yin Y, et al. Calibration of fringe projection profilometry using an inaccurate 2d reference target [J]. Optics and Lasers in Engineering, 2017, 89: 131−137. doi: 10.1016/j.optlaseng.2016.05.025 [92] Huang S, Xie L, Wang Z, et al. Accurate projector calibration method by using an optical coaxial camera [J]. Applied Optics, 2015, 54(4): 789−795. doi: 10.1364/AO.54.000789 [93] Zhang W, Li W, Yu L, et al. Sub-pixel projector calibration method for fringe projection profilometry [J]. Optics Express, 2017, 25(16): 19158−19169. doi: 10.1364/OE.25.019158 [94] Zhao H, Wang Z, Jiang H, et al. Calibration for stereo vision system based on phase matching and bundle adjustment algorithm [J]. Optics and Lasers in Engineering, 2015, 68: 203−213. doi: 10.1016/j.optlaseng.2014.12.001 [95] Triggs B, McLauchlan P F, Hartley R I, et al. Bundle adjustment: A modern synthesis[M]. Bill Triggs, Andrew Zisserman, Richard Szeliski, eds. Vision Algorithms: Theory and Practice. Springer, 2000: 298-372. [96] Xiao Y L, Xue J, Su X. Robust self-calibration three-dimensional shape measurement in fringe-projection photogrammetry [J]. Optics Letters, 2013, 38(5): 694−696. doi: 10.1364/OL.38.000694 [97] Chen R, Xu J, Zhang S, et al. A self-recalibration method based on scale-invariant registration for structured light measurement systems [J]. Optics and Lasers in Engineering, 2017, 88: 75−81. [98] Bräuer-Burchardt C, Heinze M, Schmidt I, et al. Underwater 3D surface measurement using fringe projection based scanning devices [J]. Sensors, 2016, 16(1): 13. doi: 10.1109/JSEN.2015.2468082 [99] Zhong K, Li Z, Li R, et al. Pre-calibration-free 3D shape measurement method based on fringe projection [J]. Optics Express, 2016, 24(13): 14196−14207. doi: 10.1364/OE.24.014196 [100] Beraldin J A, Mackinnon D, Cournoyer L. Metrological characterization of 3D imaging systems: Progress report on standards developments [J]. International Congress of Metrology, 2015: 13003. [101] VDI/VDE Society of Measuring and Automation Techniques. VDI/VDE 2634 part 2: Optical 3D measuring systems - optical systems based on area scanning[S]. Düsseldorf, 2002. -

 点击查看大图
点击查看大图
计量
- 文章访问数: 4561
- HTML全文浏览量: 4984
- 被引次数: 0






 下载:
下载: