下载:
-
图像具有直观、生动和涵盖信息量大的特性，在信息化社会运用极为广泛，其安全性也受到越来越多学者的关注。光学具有高速并行和多维参数的特点被广泛运用到图像加密中。Javidi和Ref.regier在1995年提出了基于傅里叶变换的双随机相位编码光学加密系统[1]，开启了光学图像加密先河。但其第一块模板不敏感，系统安全性低。参考文献[2]引入纯相位编码解决了第一块相位模板不敏感问题。许多学者将傅里叶变换推广到分数傅里叶[3-4]、菲涅耳变换[5-6]、Gyrator变换[7-8]、Mellin变换[9-10]等，增加密钥空间，提高系统安全性。其他成像系统，如电脑鬼成像[11-12]、数字全息[13-14]、非相干成像[15-16]等被相继提出，得到的密文为实数，便于密文的接收与传输。但上述算法均属线性运算易被选择明文[17-20]、已知明文[21]和唯密文[22-24]攻破。2010年Peng和Qin[25]提出来一种基于相位剪切的非对称、非线性加密方式，加解密过程使用不同的密钥，能有效抵御以上攻击。但在加密密钥作为公钥的情况下被迭代相位恢复算法破解[26-27]。对此许多学者对非线性或非对称加密做了进一步研究[28-33]，参考文献[28]将非线性薛定谔方程引入双随机相位编码系统，但其光路需要加入晶体和电场而使得光路复杂不易实现。参考文献[29]使用相位迭代算法进行加密，加密安全性与迭代次数有关，加密时间长且加解密都无法用光学元器件实现。参考文献[30-31]将参考文献[25]中的傅里叶变换推广到菲涅耳变换，增加了光学密钥，以增加加密系统抗攻击能力，但还是被参考文献[34]破解。参考文献[32]将矢量分解、Gyrator变换和相位剪切结合提出一种非对称的加密方式，增加了抗选择明文攻击能力，但不是每个解密密钥都能随明文变化。参考文献[33]将傅里叶、离散余弦变换、立方运算以及相位剪切运用到加密系统，用立方进一步破坏算法的线性，安全性更高。但以上非对称加密算法中明文对解密密钥以及密文的敏感性不够高，在解密过程中解密密钥的敏感性弱，密文分布不够均匀。
文中明文经过正反傅里叶变换、矢量分解和相位剪切，将信息有效隐藏在密文中。矢量分解过程中产生的解密密钥与明文关联性强，提高了明文对解密密钥和密文的敏感性，也提升了解密密钥的敏感性。相位剪切的引入扩大了解密密钥空间，进一步增强加密算法的安全性。实验表明：该算法是一种实现简单、安全性高的非对称光学图像加密方法。
-
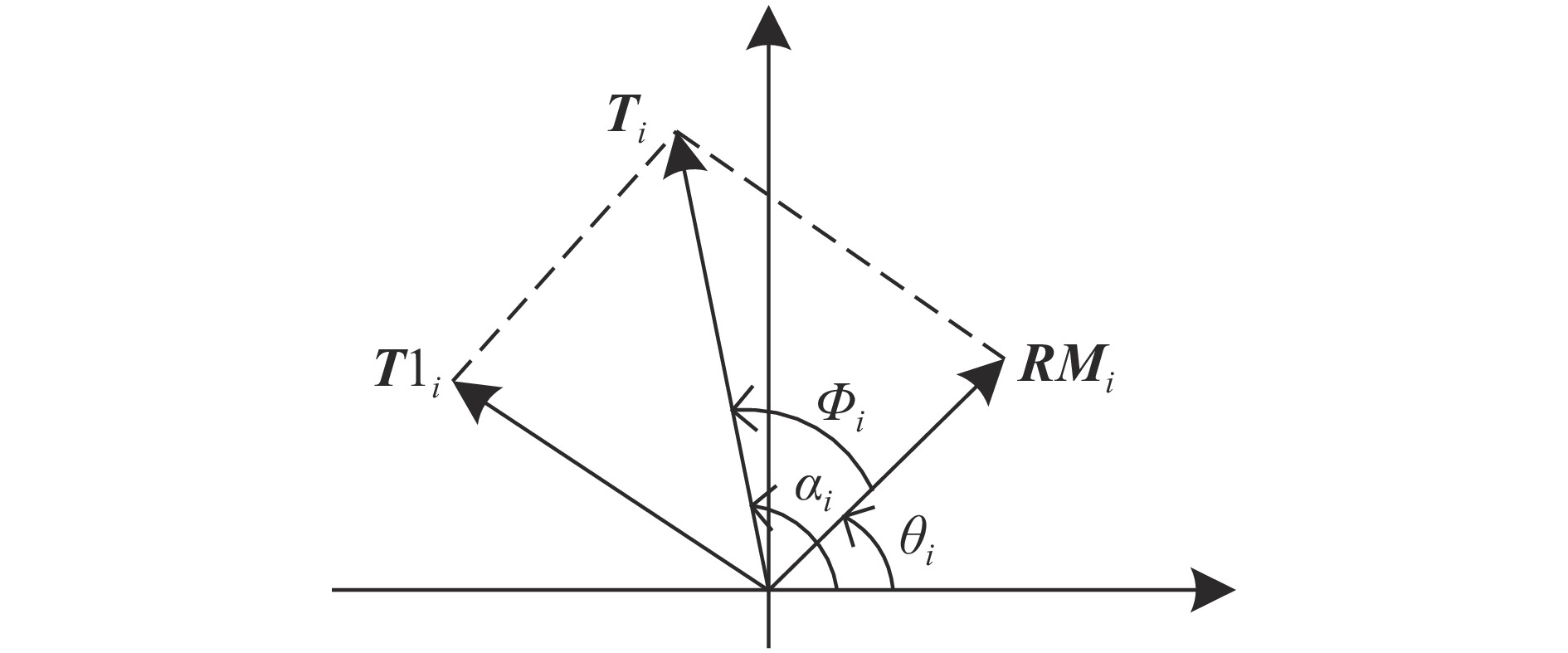
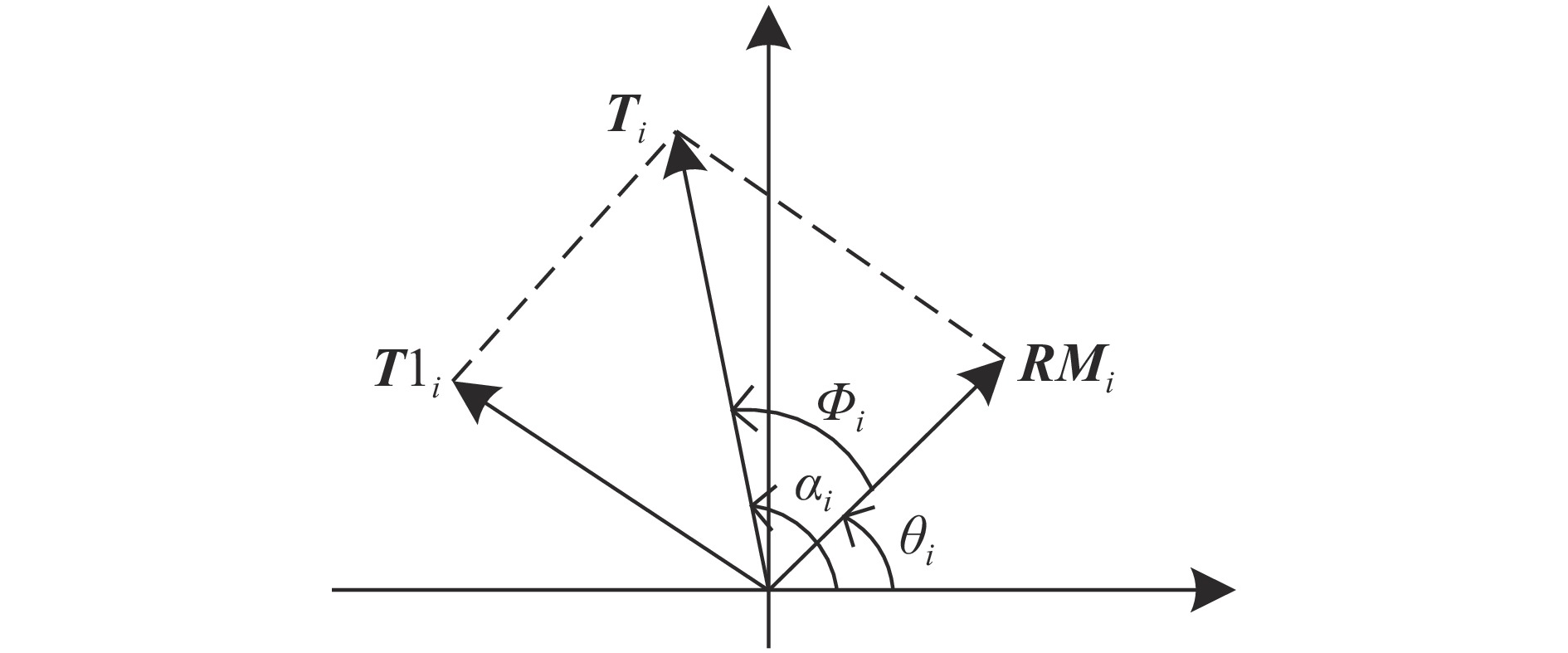
每个复数均可表示为复数坐标中的一个向量。文中在矢量分解过程中，让随机向量（解密密钥）和矢量分解结果模的最大值不超过待分解量（含有明文信息）模的最大值，使得产生的解密密钥与明文产生强关联，明文对解密密钥和密文变得更为敏感。矢量分解原理图如图1所示：
图 1 矢量分解原理
Figure 1. Vector decomposition schematic
图1中
${{{T}}_i}$ 为待分解向量，${{T}}{1_i}$ 为矢量分解结果，${{R}}{{{M}}_i}$ 为随机向量，${\phi _i}$ 为向量${{R}}{{{M}}_i}$ 到向量${{{T}}_i}$ 的夹角，${\theta _i}$ 、${\alpha _i}$ 分别为向量${{R}}{{{M}}_i}$ 和${{{T}}_i}$ 的向量角。矢量分解关系如公式（1）所示：$${{T}}{1_i} = {{{T}}_i} - {{R}}{{{M}}_i}$$ (1) 式中：
${{R}}{{{M}}_i}$ 的振幅和相位，理论上可取任何值，文中为使随机模板与明文信息产生关联，规定${{R}}{{{M}}_i}$ 和${{T}}{1_i}$ 向量的模值范围不能超过${{T}}$ 模最大值，即$\left| {{{R}}{{{M}}_i}} \right| \leqslant \max \left| {{T}} \right|$ 、$\left| {{{T}}{1_i}} \right| \leqslant \max \left| {{T}} \right|$ ，${{RM}}$ 的模$AM$ 取其值范围内的随机数，则$\theta $ 将受到约束：$${\theta _i} = {\alpha _i} - {\phi _i}$$ (2) 在向量
${{R}}{{{M}}_i}$ 、${{{T}}_i}$ 和${{T}}{1_i}$ 构成的三角形中运用余弦定理：$${\left| {{{T}}{1_i}} \right|^2} = {\left| {{{{T}}_i}} \right|^2} + {\left| {{{R}}{{{M}}_i}} \right|^2} - 2\left| {{{{T}}_i}} \right|\left| {{{R}}{{{M}}_i}} \right|\cos ({\phi _i})$$ (3) 要
$\left| {{{T}}{1_i}} \right| \leqslant \max \left| {{T}} \right|$ ，且$\cos ({\phi _i})$ 在[-1,1]之间，则$\cos ({\phi _i})$ 的范围如公式（4）所示：$$\cos {\phi _i} \in \left[ \begin{gathered} \max \left(\frac{{{{\left| {{{{T}}_i}} \right|}^2} + {{\left| {{{R}}{{{M}}_i}} \right|}^2} - {{\left[ {\max (\left| {{T}} \right|)} \right]}^2}}}{{2\left| {{{{T}}_i}} \right|\left| {{{R}}{{{M}}_i}} \right|}}, - 1\right), \\ \min \left(\frac{{{{\left| {{{{T}}_i}} \right|}^2} + {{\left| {{{R}}{{{M}}_i}} \right|}^2}}}{{2\left| {{{{T}}_i}} \right|\left| {{{R}}{{{M}}_i}} \right|}},1\right) \\ \end{gathered} \right]$$ (4) 式中：
${\left| {{{{T}}_i}} \right|^2} + {\left| {{{R}}{{{M}}_i}} \right|^2} \geqslant 2\left| {{{{T}}_i}} \right|\left| {{{R}}{{{M}}_i}} \right|$ ，且${\phi _i} \in {\rm{( - \pi ,\pi ]}}$ ，则${\phi _i}$ 的范围为：$${\phi _i} \in \left[ \begin{gathered} - {\rm{arccos}}\left\{ {\max \left(\frac{{{{\left| {{{{T}}_i}} \right|}^2} + {{\left| {{{R}}{{{M}}_i}} \right|}^2} - {{\left[ {\max (\left| {{T}} \right|)} \right]}^2}}}{{2\left| {{{{T}}_i}} \right|\left| {{{R}}{{{M}}_i}} \right|}}, - 1\right)} \right\}, \\ {\rm{arccos}}\left\{ {\max \left(\frac{{{{\left| {{{{T}}_i}} \right|}^2} + {{\left| {{{R}}{{{M}}_i}} \right|}^2} - {{\left[ {\max (\left| {{T}} \right|)} \right]}^2}}}{{2\left| {{{{T}}_i}} \right|\left| {{{R}}{{{M}}_i}} \right|}}, - 1\right)} \right\} \\ \end{gathered} \right]$$ (5) ${\phi _i}$ 取其值范围内的随机数，并通过公式（2）可知$\theta $ ，但向量角在$( - \pi ,\pi ]$ 需要对$\theta $ 进一步处理：$${\theta _i} = \left\{ {\begin{array}{*{20}{c}} {2{\text{π}} + {\alpha _i} - {\phi _i}\begin{array}{*{20}{c}} {}&{{\alpha _i} - {\phi _i} \leqslant - {\text{π}} } \end{array}} \\ {{\alpha _i} - {\phi _i}\begin{array}{*{20}{c}} {}&{ - {\text{π}} < {\alpha _i} - {\phi _i} < {\text{π}} } \end{array}} \\ { - 2{\text{π}} + {\alpha _i} - {\phi _i}\begin{array}{*{20}{c}} {}&{{\alpha _i} - {\phi _i} \geqslant {\text{π}}} \end{array}} \end{array}} \right.$$ (6) ${\theta _i}$ 为正时与x轴成逆时针旋转，为负时成顺时针旋转。用$A{M_i}$ 和${\theta _i}$ 构成${{R}}{{{M}}_i}$ ：$${{R}}{{{M}}_i}{\rm{ = }}A{M_i} \times \exp (j \times {\theta _i})$$ (7) 式中：
$j$ 为虚数单位，将${{R}}{{{M}}_i}$ 代入公式（1）完成矢量分解。 -
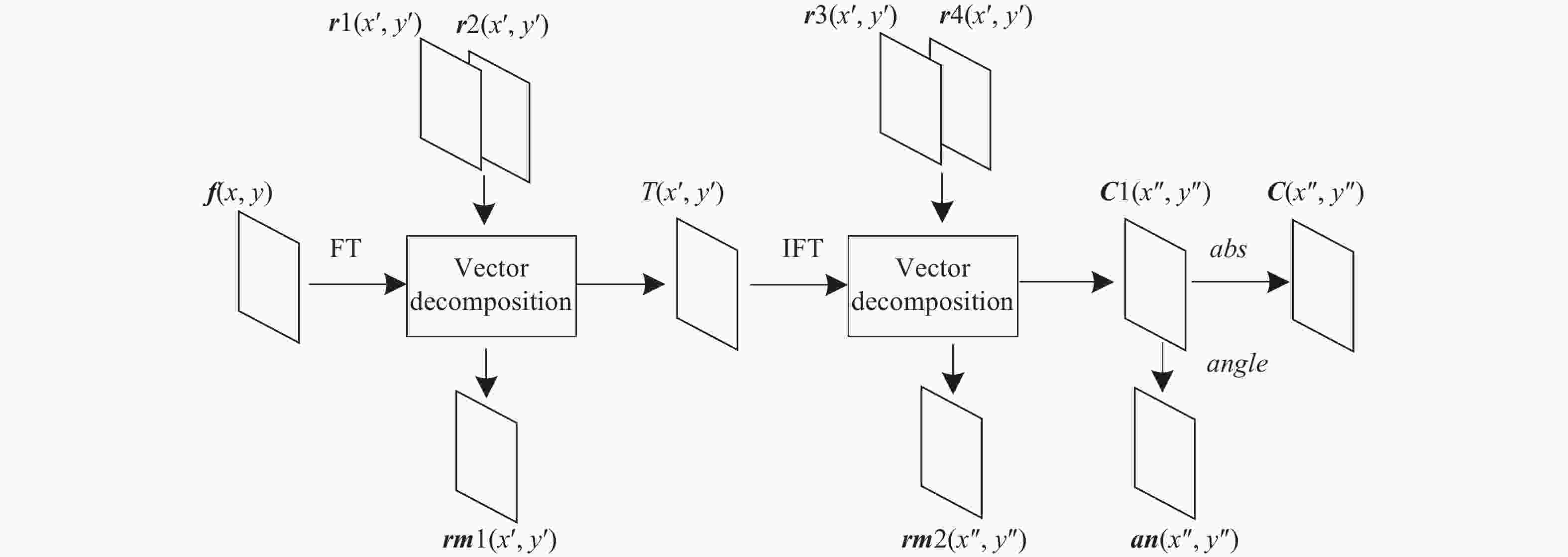
加密过程如图2所示，将图像进行傅里叶变换、矢量分解、反傅里叶变换、矢量分解和相位剪切，得到振幅密文
${{C}}$ 。其中${\rm{FT} }$ 、${\rm{IFT} }$ 为傅里叶变换和反变换，abs、angle为相位剪切和取相角变换，${{r1}}$ 、${{r2}}$ 、${{r3}}$ 、${{r4}}$ 为随机均匀分布在$[0,1]$ 的加密密钥，${{rm1}}$ 、${{rm2}}$ 、${{an}}$ 为加密过程产生的解密密钥，具体加密步骤如下：
图 2 加密过程
Figure 2. Encryption process
（1） 读取一个大小为
$M \times N$ 的待加密图像${{f}}(x,y)$ ，并生成4个$M \times N$ ，均匀分布在[0,1]的随机矩阵${{r1}}$ 、${{r2}}$ 、${{r3}}$ 、${{r4}}$ 。（2 ） 将
${{f}}(x,y)$ 进行傅里叶变换，得到${{{f}}'}(x',y'):$ $$\begin{split} {{{f}}'}(x',y') = & {\rm{FT}}\left[ {{{f}}(x,y)} \right] = \\ & \frac{1}{{MN}}\sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {{{f}}(x,y){e^{ - i2{\rm{\pi (}}x'x/M + y'y/N{\rm{)}}}}} } \end{split} $$ (8) （3） 将
${{r1}}$ 代入 公式（9）作为${{rm1}}$ 的模$AM1$ 。将$AM1$ 和${{{f}}^{{'}}}$ 代入公式（5）中求出两向量对应夹角$\phi $ 的范围$[{\phi _{\min }},{\phi _{\max }}]$ 。$$AM1(x',y') = {{r1}}(x',y') \times \max (\left| {{{{f}}^{{'}}}(x',y')} \right|)$$ (9) （4） 将
${{r2}}$ 根据公式（10）求出$\phi (x',y')$ 。$$ \phi (x',y') ={{r2}}(x',y') \times \frac{{{\phi _{\max }}(x',y') - {\phi _{\min }}(x',y')}}{{2\pi }} +{\phi _{\min }}(x',y') $$ (10) （5） 将
$\phi $ 代入公式（6）得到$\theta $ ，结合$AM1$ 运用公式（7）得到${{rm1}}$ 。用公式（11）得到${{T}}$ 。$${{T}}(x',y') = {{{f}}'}(x',y') - {{rm1}}(x',y')$$ (11) （6） 将
${{T}}$ 运用公式（12）进行反傅里叶变换得到${{{T}}^{{'}}}$ ，再用${{r3}}$ 、${{r4}}$ 进行步骤（3）~（5）的矢量分解得到中间密文${{C1}}$ 和解密密钥${{rm2}}$ 。$$\begin{array}{l} {{{T}}'}(x'',y'') = {\rm{IFT}}\left[ {{{T}}(x',y')} \right] \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} = \sum\limits_{x' = 1}^M {\sum\limits_{y' = 1}^N {{{T}}(x',y'){e^{i2{\rm{\pi (}}x'x''/M + y'y''/N{\rm{)}}}}} } \\ \end{array} $$ (12) （7 ）
${{C1}}$ 进行相位剪切得到密文${{C}}$ ，提取相位角得到解密密钥${{an}}$ 。$${{C}} = abs({{C1}}),{{an}} = angle({{C1}})$$ (13) -
在计算机中运用公式（14）解密
$${{f}}(x,y){\rm{ = IFT}}\left\{ {\operatorname{FT} \left\{ \begin{gathered} {{rm2}}(x'',y'') + \\ \left\{ \begin{gathered} {{C}}(x'',y''). \\ \exp [j \times {{an}}(x'',y'')] \\ \end{gathered} \right\} \\ \end{gathered} \right\} + {{rm1}}(x',y')} \right\}$$ (14) 也可运用光的干涉原理和凸透镜的傅里叶变换原理用光学器件进行解密，解密过程原理图如下：
图3中
${{rm1}}$ 、${{rm2}}$ 和${{an}}$ 为加密过程中产生的解密密钥，${{C}}$ 为密文。解密图像用一个工业摄像机${\rm{CCD}}$ 接收。值得注意的是S和M必须成${45^o}$ 摆放，路程${{{r}}_2} = $ ${{{r}}_6} = 2f $ 、${{{r}}_1} \!=\! {{{r}}_5} \!=\! {{{r}}_9}\! =\! {{{r}}_{10}}\! =\! {{{r}}_3} + {{{r}}_4} + {{{r}}_8} = {{{r}}_7} + {{{r}}_8} \!=\! f$ ，$f$ 为透镜的焦距。
图 3 解密原理图
Figure 3. Decryption schematic diagram
-
文中采用MATLAB R2016a作为仿真平台，同时选取256×256的灰度图lean和107×122的二值图像logo作为实验对象。加解密结果以及加解密密钥如图4所示。
图 4 加解密结果和密钥
Figure 4. Result and key encryption and decryption
从图4中可以看出：无论是加密普通的灰度图还是二值图像，文中提出的加密算法的密文完全看不出明文信息，解密图像和明文肉眼看不出差距，说明该算法加解密效果良好。
-
利用控制变量法，设置不同类型的错误密钥，当其中一类错误，其他密钥为正确密钥。文中笔者在解密密钥中用公式（15）引入噪声来改变解密密钥，同时采用平均均方误差（MSE），和相关系数（CC）来具体评价解密质量。
$$rm = rm \times (1 + kG)$$ (15) $$MSE = \frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[F(x,y) - f(x,y)]}^2}} } $$ (16) $$CC = \frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {[f(x,y) - \overline f ][F(x,y) - \overline F ]} } }}{{\sqrt {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[f(x,y) - \overline f ]}^2}} } } \sqrt {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[F(x,y) - \overline F ]}^2}} } } }}$$ (17) 式中：
$k$ 为控制参数；$G$ 为均值为0、方差为1的高斯噪声；$f(x,y)$ 为明文；$F(x,y)$ 为解密图；$\overline f $ 和$\overline F $ 为对应图像像素值的均值。$MSE$ 越小、$CC$ 越接近1说明解密精度越高，原始图像的还原质量越好，图像失真越少。对于参考文献[31]k1、k2为解密密钥，参考文献[32]θ和M2为解密密钥，参考文献[33]DK1和DK2为解密密钥。lean图像$CC$ 和$MSE$ 的对比如图5所示。
图 5 解密密钥错误时解密图像与原图的CC和MSE
Figure 5. CC and MSE of the decrypted image and plaintext when the decryption key is wrong
通过图5中对比参考文献[31-33]可以看出：当密钥加入少量噪声时，该算法的解密图像与明文的平均均方误差和相关系数变化更加迅速、程度更深，说明该算法相对于其他的非对称加密算法密钥敏感性更高，为更清楚观察到加入噪声密钥的解密效果，给出图5中一些k值点的解密图像如图6所示。
图 6 密钥错误后的解密图
Figure 6. Decrypted image after key error
由图6可见：明文为lean、
$k = 0.05$ 时，该算法解密图像基本上看不出明文图像，而对比文献的解密图还能清晰看到明文，甚至比在$k = 0.01$ 时更清晰说明该算法的密钥敏感性更高。 -
文中的解密密钥在加密过程中产生，矢量分解和相位剪切过程所得解密密钥与明文有关，使得解密密钥能随明文自适应变化，同时明文对密文也极其敏感。文中采用像素值变化率（NPCR）和归一化平均变化强度（UACI）来描述密文对解密密钥和密文的敏感性。将明文、明文第一个像素点加k和明文前k个和倒数k个像素点依次交换位置的图像分别进行加密，计算明文为lean时改变后与未改变图像在加密过程中生成解密密钥和密文间的NPCR和UACI的值，如图7所示。NPCR和UACI公式如下：
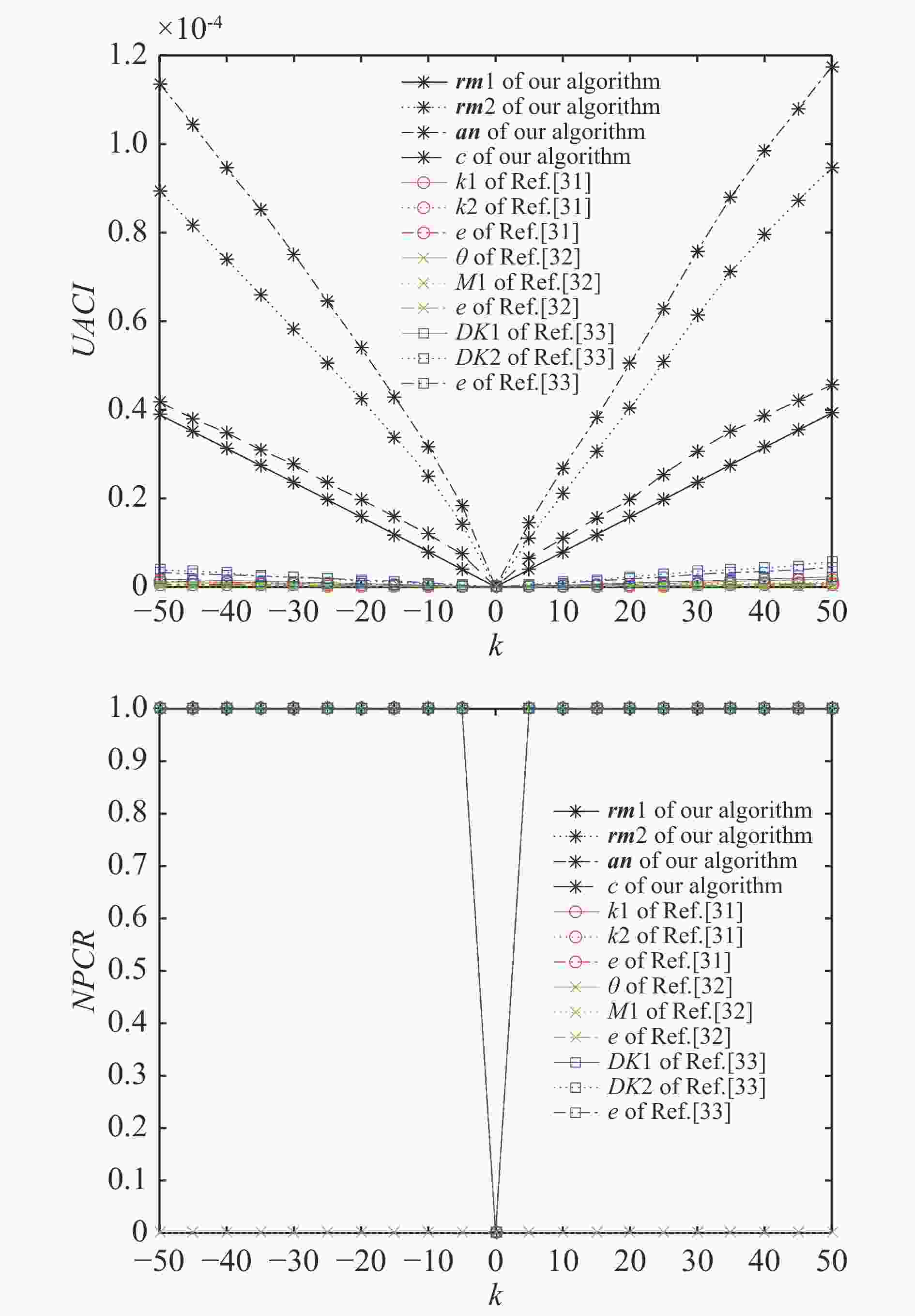
图 7 改变明文第一点像素值大小的UACI和NPCR对比图
Figure 7. UACI and NPCR comparison diagram of changing the pixel value size of the first point in plaintext
$$NPCR = \frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {p(i,j)} } }}{{M \times N}}$$ (18) $$UACI = \frac{1}{{M \times N}}[\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {C1(i,j) - C2(i,j)} } ] \times 100\% $$ (19) 式中：当
$C1(i,j) = C2(i,j)$ 时，$p(i,j) = 0$ ，否则$p(i,j) = 1$ 。同时为了便于计算和与其他文献比较，文中将公式中的$C1$ 和$C2$ 都进行归一化，复数都取实部。从图7、8可以看出：当文中的明文的像素值稍作改变时，解密密钥、密文的像素值全部都得到了改变。同时归一化平均变化强度也随着明文像素继续变大而变大。通过对比分析文中提出的算法明文的变换对解密密钥和密文相对于参考文献[31-33]敏感度得到了极大的提升。
图 8 交换明文像素点位置的UACI和NPCR对比图
Figure 8. Comparison of UACI and NPCR for exchanged plaintext pixel position
-
通常情况下，针对加密系统的攻击主要有已知明文攻击、选择明文攻击、选择密文攻击、唯密文攻击。由于选择明文攻击对加密系统最有威胁，如果加密系统能够抵抗选择明文攻击，则可以抵抗另外3种攻击[32]。因此，文中用选择明文攻击来进一步测试系统的安全性。选择明文攻击，即攻击者已经知道加密和解密算法，并且可以任意选择明文，并利用公钥获取相应的密文。文中利用上文中提到的lean文明第一位置的像素值加5和交换第一像素点和倒数第一像素点位置的两个图像作为攻击图像，放入加密系统中得到对应的解密密钥。密文用攻击图像得到的加密密钥的解密，结果如图9所示。
图 9 抗选择明文攻击分析
Figure 9. Anti-selective plaintext attack analysis
由图9可见：文中提出的加密算法在明文只稍微改变一个像素点的像素值和改变两个像素值不同的两像素点位置作为选择明文攻击图像时得到的破解图像完全看不出明文信息，而参考文献[31-33]可以清晰看见明文图像，可见文中提出的加密算法在选择明文攻击更具有抵御能力。
-
文中主要从两个方面对统计特性进行分析，一是图像像素值的分布情况和值的混乱程度，即直方图和信息熵，另一个是相邻像素的相关程度。
-
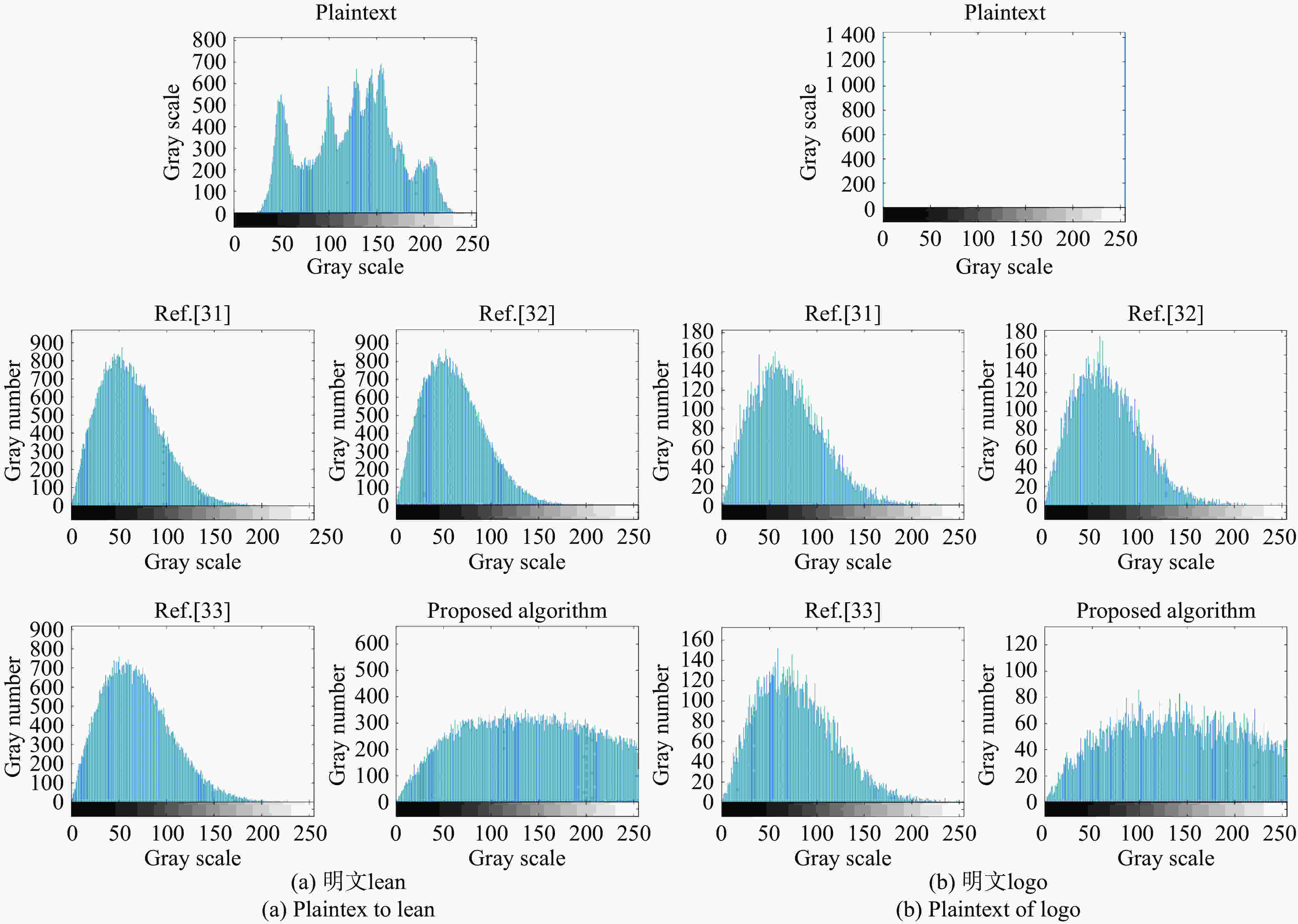
直方图能直观反映图像灰度值分布，给出文中的密文和参考文献[31-33]密文的直方图，如图10所示。为更精确地对比分析密文的统计特性，文中计算出它们的信息熵：
图 10 直方图
Figure 10. Histogram
$$en = - \sum\limits_{i = 1}^{256} {{p_i} \times \log 2({p_i})} $$ (20) 信息熵对比如表1所示。式中
${p_i}$ 为对应像素值出现的概率，为了便于比较，文中将不同加密方法的密文都归化到$\left\{ {0 \leqslant C(i,j) \leqslant 255|C(i,j) \in {N^*}} \right\}$ ，$C(i,j)$ 为密文像素值、${N^*}$ 为正整数。信息熵是度量信息有序性的一个重要手段，一个系统越是混乱信息熵就越高，在int8型数据下理想值为8。表 1 信息熵对比
Table 1. Information entropy comparison
由图10和表1可见，该加密方法明密文之间的直方图和信息熵完全不同，像素值得到很好地改变。密文的灰度值分布比明文更均匀更混乱，很好地隐藏了明文图像的灰度信息，留给密码分析者空间很小。通过对比分析可以得出：文中提出的加密方法的直方图更平滑，信息熵更接近8，说明加密效果更好。
-
一个好的加密方法应该显著破坏相邻像素的相关性。文中用公式（17）计算出明密文的水平、垂直、对角方向的相邻像素的相关系数，如表2所示。明密文在水平方向上的相邻像素相关性图如图11所示。
表 2 相邻像素相关系数
Table 2. Correlation coefficients of adjacent pixels
图 11 lena图水平方向相邻像素分布图
Figure 11. lena horizontal adjacent pixel distribution map
由图11可知：明文lean的相邻像素主要分布在对角线上，说明相邻两点像素几乎相等，明文logo主要在四点上，一眼就看出了这是一个二值图像。该加密算法的密文图像相邻像素分布更为均匀，相邻像素值差别较大。通过表2也可看出：明文的相邻相关系数接近1，而加密图像的接近于0，说明明文的统计特征已经扩散到随机的密文中。对比可知：文中的密文相邻像素间具有更小的相关系数，水平方向上的相关性图分布更加均匀，说明文中更能抵御统计特性攻击。
-
文中通过矢量分解和相位剪切，使得加密密钥与解密密钥不同，实现非对称加密，同时让解密密钥与明文产生较强关联，使其能随明文自适应变换。通过对比分析：该算法明文敏感性更高，当明文像素值发生微小变化时，密钥和密文像素变化率达到1，归一化变化强度变化更为迅速、幅度更大，抗选择明文攻击的抵御能力更强；密文分布均匀信息熵更接近理想值8，相邻像素相关性低，更有效的抵御统计攻击；解密密钥敏感性高，当引入少量加性噪声时，解密图像与明文的相关系数以及均方误差都急剧变化。相比于传统的非对称算法，具有更高安全性和实用性。
Asymmetric optical image encryption based on vector decomposition and phase-truncated
-
摘要: 结合矢量分解和相位剪切提出一种新的非对称光学图像加密算法，明文经过4个密钥加密得到分布均匀的密文和3个解密密钥。解密密钥在加密过程中产生，不同于加密密钥,实现了非对称加密,增加了系统的安全性。在矢量分解过程中产生的解密密钥与明文关联强，比现有光学非对称加密算法中明文对密文和解密密钥更为敏感，抵御选择明文攻击能力更强，同时也提高了解密密钥的敏感性。相位剪切的引入扩大了密钥空间,增强算法安全性，产生实数密文更便于传输。实验分析表明：该算法密文分布均匀、相邻像素相关性低，解密密钥、明文对解密密钥和密文敏感性高，抵御各种攻击能力强，有更好光学图像加密效果。Abstract: A new asymmetric optical image encryption algorithm was proposed, which combined vector decomposition and phase-truncated. The plaintext was encrypted by four keys to obtain uniformly distributed ciphertext and three decryption keys. The decryption key was generated in the encryption process, which was different from the encryption key. It realized asymmetric encryption and increased the security of the system. The decryption key generated in the process of vector decomposition was strongly related to plaintext. Compared with the existing optical asymmetric encryption algorithms, plaintext was more sensitive to ciphertext and decryption keys. The system was more resistant to selective plaintext attack. At the same time, it also improved the sensitivity of decryption keys. The introduction of phase-truncated enlarged the key space and enhanced the security of the algorithm. Moreover real number ciphertext was produced for easier transmission. The experimental results show that the algorithm has uniform ciphertext distribution and low correlation between adjacent pixels. The decrypted keys and the plaintext to decrypted keys and ciphertext are highly sensitive. This algorithm has strong ability to resist various attack and better optical image encryption effect.
-
Key words:
- optical image encryption /
- asymmetric system /
- vector decomposition /
- phase-truncated
-
图 5 解密密钥错误时解密图像与原图的CC和MSE
Figure 5. CC and MSE of the decrypted image and plaintext when the decryption key is wrong
图 7 改变明文第一点像素值大小的UACI和NPCR对比图
Figure 7. UACI and NPCR comparison diagram of changing the pixel value size of the first point in plaintext
图 8 交换明文像素点位置的UACI和NPCR对比图
Figure 8. Comparison of UACI and NPCR for exchanged plaintext pixel position
-
[1] Refregier P, Javidi B. Optical image encryption using input 排plane and Fourier plane random encoding [J]. Optics Letters, 1995, 20(7): 767−769. doi: 10.1364/OL.20.000767 [2] François Goudail, Bollaro F, Javidi B, et al. Influence of a perturbation in a double phase-encoding system [J]. J Opt Soc Am A, 1998, 15(10): 2629−2638. doi: 10.1364/JOSAA.15.002629 [3] Hennelly B, Sheridan J T. Optical image encryption by random shifting in fractional Fourier domains [J]. Optics Letters, 2003, 28(4): 269−271. doi: 10.1364/OL.28.000269 [4] Unnikrishnan G, Joseph J, Singh K. Optical encryption by double-random phase encoding in the fractional Fourier domain [J]. Optics Letters, 2000, 25(12): 887−889. doi: 10.1364/OL.25.000887 [5] Hennelly B M, Sheridan J T. Random phase and jigsaw encryption in the Fresnel domain [J]. Optical Engineering, 2004, 43(10): 2239−2249. doi: 10.1117/1.1790502 [6] Situ G, Pedrini G, Osten W. Strategy for cryptanalysis of optical encryption in the Fresnel domain [J]. Applied Optics, 2010, 49(3): 457−462. doi: 10.1364/AO.49.000457 [7] Xu L, Ahmad M A, Guo Q, et al. Double image encryption by using iterative random binary encoding in gyrator domains [J]. Optics Express, 2010, 18(11): 12033−12043. doi: 10.1364/OE.18.012033 [8] Singh H, Yadav A K, Vashisth S, et al. Fully phase image encryption using double random-structured phase masks in gyrator domain [J]. Appl Opt, 2014, 53(28): 6472−6481. doi: 10.1364/AO.53.006472 [9] Zhou N, Li H, Di W, et al. Image compression and encryption scheme based on 2D compressive sensing and fractional Mellin transform [J]. Optics Communications, 2015, 343: 10−21. doi: 10.1016/j.optcom.2014.12.084 [10] Zhou N, Wang Y, Gong L. Novel optical image encryption scheme based on fractional Mellin transform [J]. Optics Communications, 2011, 284(13): 3234−3242. doi: 10.1016/j.optcom.2011.02.065 [11] Zafari M, Kheradmand R, Ahmadikandjani S. Optical encryption with selective computational ghost imaging [J]. Journal of Optics, 2014, 16(10): 105405. doi: 10.1088/2040-8978/16/10/105405 [12] Clemente P, Durán V, Torrescompany V, et al. Optical encryption based on computational ghost imaging [J]. Optics Letters, 2010, 35(14): 2391−2393. doi: 10.1364/OL.35.002391 [13] Hua Lili, Xu Ning, Yang Geng. An encryption scheme based on phase-shifting digital holography and amplitude-phase disturbance [J]. Chinese Physics B, 2014, 23(6): 206−211. [14] Javidi B, Nomura T. Securing information by use of digital holography [J]. Optics Letters, 2000, 25(1): 28−30. doi: 10.1364/OL.25.000028 [15] Zang J, Xie Z, Zhang Y. Optical image encryption with spatially incoherent illumination [J]. Optics Letters, 2013, 38(8): 1289−12891. doi: 10.1364/OL.38.001289 [16] Wang Q, Xiong D, Alfalou A, et al. Optical image encryption method based on incoherent imaging and polarized light encoding [J]. Optics Communications, 2018, 415: 56−63. doi: 10.1016/j.optcom.2018.01.018 [17] Yuan S, Yao J, Liu X, et al. Cryptanalysis and security enhancement of optical cryptography based on computational ghost imaging [J]. Optics Communications, 2016, 365: 180−185. doi: 10.1016/j.optcom.2015.12.013 [18] Cheremkhin P A, Evtikhiev N N, Rodin V G, et al. Method of attack on schemes of optical encryption with spatially incoherent illumination[C]//Electro-Optical and Infrared Systems: Technology and Applications, 2017. [19] Carnicer A, Montes-Usategui M, Arcos S, et al. Vulnerability to chosen-cyphertext attacks of optical encryption schemes based on double random phase keys [J]. Optics Letters, 2005, 30(13): 1644−1646. doi: 10.1364/OL.30.001644 [20] Peng X, Wei H, Zhang P. Chosen-plaintext attack on lensless double-random phase encoding in the Fresnel domain [J]. Optics Letters, 2006, 31(22): 3261−3263. doi: 10.1364/OL.31.003261 [21] Peng X, Zhang P, Wei H, et al. Known-plaintext attack on optical encryption based on double random phase keys [J]. Optics Letters, 2006, 31(8): 1044−1046. doi: 10.1364/OL.31.001044 [22] Liao M, He W, Lu D, et al. Ciphertext-only attack on optical cryptosystem with spatially incoherent illumination: from the view of imaging through scattering medium [J]. Scientific Reports, 2017(7): 41789. doi: 10.1038/srep41789 [23] Zhang C, Liao M, He W, et al. Ciphertext-only attack on a joint transform correlator encryption system [J]. Optics Express, 2013, 21(23): 28523−28530. doi: 10.1364/OE.21.028523 [24] Liu X, Wu J, He W, et al. Vulnerability to ciphertext-only attack of optical encryption scheme based on double random phase encoding [J]. Optics Express, 2015, 23(15): 18955−18968. doi: 10.1364/OE.23.018955 [25] Qin W, Peng X. Asymmetric cryptosystem based on phase-truncated Fourier transforms [J]. Optics Letters, 2010, 35(2): 118−120. doi: 10.1364/OL.35.000118 [26] Dai C, Zhao D, Wang X, et al. Discussion and a new attack of the optical asymmetric cryptosystem based on phase-truncated Fourier transform [J]. Applied Optics, 2014, 53(2): 208−213. doi: 10.1364/AO.53.000208 [27] Wang Y, Quan C, Tay C J. Improved method of attack on an asymmetric cryptosystem based on phase-truncated Fourier transform [J]. Applied Optics, 2015, 54(22): 6874−6881. doi: 10.1364/AO.54.006874 [28] 侯俊峰, 黄素娟, 司徒国海. 非线性光学图像加密[J]. 光学学报, 2015, 35(8): 0807001. Hou Junfeng, Huang Sujuan, Situ Guohai. Nonlinear optical image encryption [J]. Acta Optica Sinica, 2015, 35(8): 0807001. (in Chinese) [29] 陈翼翔, 汪小刚. 一种基于迭代振幅-相位恢复算法和非线性双随机相位编码的图像加密方法[J]. 光学学报, 2014, 34(8): 119−124. Chen Yixiang, Wang Xiaogang. Image encryption based on iterative amplitude-phase rretrieval and nonlinear double random phase encoding [J]. Acta Optica Sinica, 2014, 34(8): 119−124. (in Chinese) [30] Wang Y, Quan C, Tay C J. Optical color image encryption without information disclosure using phase-truncated Fresnel transform and a random amplitude mask [J]. Optics Communications, 2015, 344: 147−155. doi: 10.1016/j.optcom.2015.01.045 [31] Yadav P L, Singh H. Enhancement of security using structured phase masked in optical image encryption on Fresnel transform domain[C]//2nd International Conference On Condensed Matter And Applied Physics (ICC 2017), 2018. [32] 姚丽莉, 袁操今, 强俊杰, 等. 基于gyrator变换和矢量分解的非对称图像加密方法[J]. 物理学报, 2016, 65(21): 214203. doi: 10.7498/aps.65.210201 Yao Lili , Yuan Caojin, Qiang Junjie, et al. Asymmetric image encryption method based on gyrator transform and vector operation [J]. Acta Physica Sinica, 2016, 65(21): 214203. (in Chinese) doi: 10.7498/aps.65.210201 [33] Khurana M, Singh H. An asymmetric image encryption based on phase truncated hybrid Transform [J]. 3D Research, 2017, 8(3): 28. doi: 10.1007/s13319-017-0137-8 [34] Rajput S K, Nishchal N K. Known-plaintext attack-based optical cryptosystem using phase-truncated Fresnel transform [J]. Applied Optics, 2013, 52(4): 871. doi: 10.1364/AO.52.000871 -
点击查看大图
图(11) / 表(2)
计量
- 文章访问数: 2291
- HTML全文浏览量: 741
- PDF下载量: 32
- 被引次数: 0
