-
机载脉冲激光测距机采取非相干直接探测方式,目标的检出需要在一定的可检测信噪比下实现。单脉冲机载激光测距机通常采用模拟信号处理方式,只能在幅度信噪比大于6.7时工作,探测目标距离10~20 km。与电磁雷达早在20世纪90年代就已开始数字化不同,采用数字信号处理技术实现多脉冲回波积累检测的数字体制激光测距机在21世纪初才开始兴起。目前,数字体制三脉冲激光测距机在每个脉冲串重复周期连续发射三个激光脉冲,在目标未及移出激光脉冲距离分辨单元的情况下获得三次回波,经高速A/D转换后由DSP处理器实施直接累加积累[1]。数字化多脉冲激光测距机作用距离相比模拟单脉冲激光测距机提高了一倍以上[1]。数字体制多脉冲激光测距机为采用复杂信号处理算法解决远程目标探测提供了平台。
与近程激光测距机采用波形前沿鉴别不同,远程多脉冲激光测距机通常采用峰值点检测确定目标所在位置的距离数值。影响多脉冲激光测距精度的主要因素包括发射激光脉冲宽度的距离分辨率、大气传播及目标反射特性造成的波形展宽、回波信号接收处理通道的非线性相频特性等。激光测距要求准确判决目标回波波形峰值点位置。这一问题可以看作是从含噪的回波波形中估计目标波形的峰值点位置。针对远距离低信噪比目标,多脉冲激光测距机通常采用数字化处理体制,测距精度还受到数字化采样率的影响,而激光目标回波信号滤波、目标波形提取、峰值点判决等数字信号处理环节引入目标距离判定误差也不容忽视[2-3]。
文中针对脉冲激光目标回波波形进行建模,并对比分析现有数字化激光回波信号处理算法对定位精度的影响。针对激光目标回波信号的数字化处理,文中基于经验模态分解(Empirical Mode Decomposition,EMD)研究可减小波形失真的数字化降噪算法进而对脉冲激光测距机目标回波信号进行降噪处理,以实现准确探测目标和精确提取目标峰值点位置,进而改善激光测距机的目标定位精度。
-
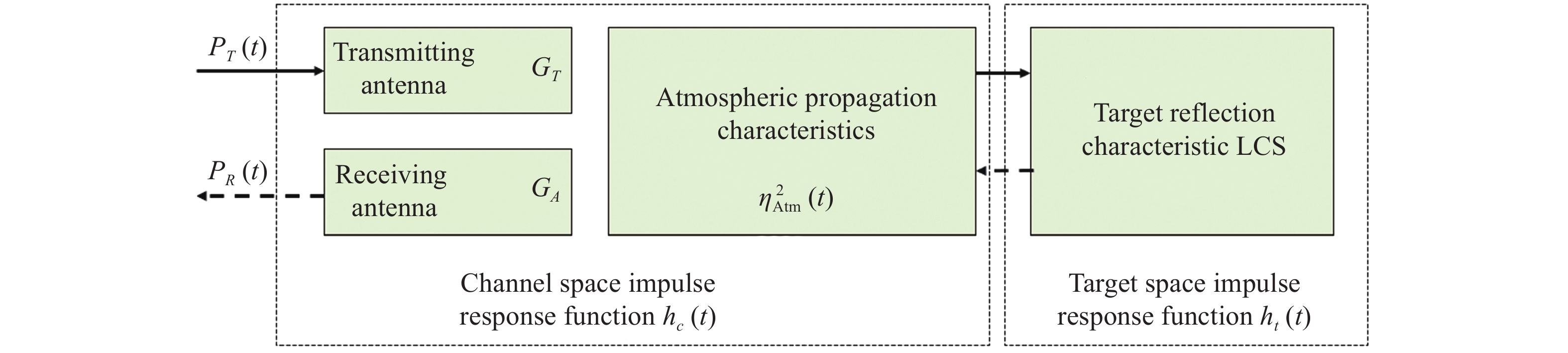
对于脉冲激光测距机,其接收光功率可看作发射脉冲信号经过大气传播信道,在距离为R处的目标反射后得到的响应,如图1所示[1]。
APD探测器接收信号与由激光测距机、大气环境、目标组成的系统之间存在传递函数关系为:
$$ \mathop P\nolimits_{\det } (t) = \mathop P\nolimits_t (t)*\mathop h\nolimits_c (t)*\mathop h\nolimits_t (t) $$ (1) 式中:时刻t=2R/c(c为光速),则距离为R处的目标反射光功率可由下述公式描述[4]:
$$ \begin{split} \mathop P\nolimits_{\det } (R) =& \mathop C\nolimits_A \int\limits_{{t'} = 0}^{2R/c} {\mathop P\nolimits_t ({t'})\mathop h\nolimits_c (R - c{t'}/2)\mathop h\nolimits_t (R - c{t'}/2){\rm d}{t'}} = \\ & \mathop C\nolimits_A \mathop P\nolimits_t (R)*\mathop h\nolimits_c (R)*\mathop h\nolimits_t (R) \\ \end{split}$$ (2) 式中:CA为脉冲激光测距机接收孔径及接收光路损耗,可由
${C_A} = \dfrac{c}{2} \times \dfrac{{\pi {D_R}^2}}{4} \times {\tau _0}$ 加以计算,DR为接收光学天线孔径,τ0为发射与接收光学系统总透过率。由公式(2)可知,脉冲激光目标回波信号的波形可由发射信号、大气传播脉冲响应函数、目标反射特性脉冲响应函数等环节卷积获得。
-
激光发射波形通常有矩形脉冲、高斯脉冲以及负抛物线脉冲等模型[5]。最简单的是矩形脉冲的形状,如公式(3)所示:
$$ \mathop P\nolimits_t (t) = \frac{{\mathop E\nolimits_t }}{{\mathop p\nolimits_w }} \times rect\left(\frac{t}{{\mathop p\nolimits_w }}\right) $$ (3) 式中:Pt(t)为激光脉冲峰值功率;Et为激光能量;pw为脉冲时间宽度。
矩形脉冲模型是一个近似实际的脉冲激光辐射产生的形状。实际应用中,大部分激光器发射脉冲可以用高斯函数表示[5]:
$$ \mathop P\nolimits_t (t) = \frac{{\mathop E\nolimits_t }}{{\mathop \sigma \nolimits_w \sqrt {2\pi } }}\mathop {\rm exp}\nolimits\left({\frac{{ - \mathop t\nolimits^2 }}{{2\mathop \sigma \nolimits_w^2 }}}\right) $$ (4) 式中:σw为高斯脉冲波形的宽度参数,以s为单位。
相比矩形脉冲,这个形状提供了一个更加真实的激光发射机的能量图形。
用于描述激光发射器输出功率的另一种模型是负抛物线模型。在该模型中,激光功率建模为倒置抛物线。负抛物线模型中,脉冲宽度为pw,如公式(5)所示:
$$ \mathop P\nolimits_t (t) = \frac{{3\mathop E\nolimits_t }}{{2\mathop p\nolimits_w }}\left(1 - \frac{{4\mathop t\nolimits^2 }}{{\mathop p\nolimits_w^2 }}\right)rect\left(\frac{t}{{\mathop p\nolimits_w }}\right) $$ (5) 该函数的缩放保证脉冲中的能量等于参数Et。矩形函数用于限制脉冲幅度的严格正值。
如图2所示为实际激光辐射器发射采样信号的示波器显示波形。可以看出,当发射脉冲宽度为5 ns时,信号波形为高斯脉冲;当脉冲宽度变大,10 ns及更宽发射激光脉冲的波形为近似矩形。工程实现中通常采取矩形函数表示发射信号[1]:
$$ \begin{split} \\ \mathop P\nolimits_t (t) = \left\{ {\begin{array}{*{20}{c}} {{P_0},}&{0 \leqslant t \leqslant {\tau _H}} \\ {0,}&{\rm else} \end{array}} \right. \end{split} $$ (6) 式中:τH为发射激光的半功率脉冲宽度;P0为发射脉冲激光的峰值功率。
-
机载激光测距机发射0.2~0.5 mrad的脉冲激光,通过光学镜头辐射至大气传播路径,再被远程目标反射回接收光学系统。这一过程发射激光功率变化的脉冲响应函数hc(R)可表示为[1]:
$$ {h_c}(R) = \frac{{\mathop \tau \nolimits_a^2 (t)}}{{\pi \mathop R\nolimits^4 \mathop \theta \nolimits_t^2 }} $$ (7) 式中:R为激光探测目标的距离,是随时间t变化的函数;τa(t)为反映单方向大气传播随时间t变化的函数,其在激光测距机单个发射周期内可视为常数,则有[1]:
$$ {h_c}(R) = \frac{{\mathop \tau \nolimits_a^2 }}{{\pi \mathop R\nolimits^4 \mathop \theta \nolimits_t^2 }} $$ (8) 式中:hc(R)为脉冲激光测距机发射激光信号经大气路径往返传播的光功率的变化。公式(7)主要适用于远程小目标测距。
-
机载平台脉冲激光测距机对远程目标照射时,目标完全处于激光光斑范围内或者部分位于光斑范围之内,后向反射的激光功率可由目标所在处的激光功率和激光目标截面积加以确定,目标反射过程的脉冲响应函数ht(R)可由一定入射角度下朗伯散射点目标的激光反射截面积得到[1]:
$$ {h_t}(R) = 4\beta {\rm d}{A_o}{\rho _{pt}} $$ (9) 式中:β为目标朗伯反射系数;dAo为脉冲激光目标反射面积,其数值与沿照射方向的目标几何尺寸变化有关,是目标距离R的函数;ρpt为远程飞机目标的反射率。
-
将公式(6)、(8)、(9)代入公式(2)可得目标探测器接收的回波光功率:
$$ \begin{split} \mathop P\nolimits_{\det } (R) =& {C_A}{P_0}{\tau _R}*{h_c}(R)*{h_t}(R) = \\ & \left[\left(\beta \frac{{{D_R}^2}}{{\pi {R^4}\theta _t^2}}\tau _a^2{\tau _0}{P_0}\right) \times \frac{{c{\tau _R}}}{2}\right]*{A_C}(R) \\ \end{split} $$ (10) 经雪崩二极管光电转换后的光电流信号表示为:
$$ \begin{split} {i_{\rm signal}} = &\mathop P\nolimits_{\det } (R)\eta e/h\nu =\\ & {C_A}{P_0}{\tau _R}*{h_c}(R)*{h_t}(R)\eta e/h\nu = \\ & \left[\left(\eta e\beta \frac{{{D_R}^2}}{{\pi h\nu {R^4}\theta _t^2}}\tau _a^2{\tau _0}{P_0}\right) \times \frac{{c{\tau _R}}}{2}\right]*{A_C}(R) \\ \end{split} $$ (11) 经前置放大电路、差分放大电路处理后的电压信号表示为[1]:
$$ \begin{array}{l} {u_{\rm signal}} = \left[{{\textit{z}}_{\rm circuit}} \left(\eta e\beta \dfrac{{D_R^2}}{{\pi h\nu {R^4}\theta _t^2}}\tau _a^2{\tau _0}{P_0}\right) \times \dfrac{{c{\tau _R}}}{2}\right]*{A_C}(R) \end{array} $$ (12) 式中:zcircuit为接收电路的阻抗,反映接收电路的相频特性。
当机载平台多脉冲激光测距机系统参数确定,并且大气传播特性稳定,特定目标距离R处的接收激光回波信号波形可由发射脉冲激光τR和激光目标反射截面积AC(R)的卷积关系决定。对于远程飞机目标来说,目标被激光光束覆盖,目标外形的各组成部分均可反射激光回波信号,因此,激光目标回波波形中就包含有目标的几何外形反射激光特性[1]。
-
公式(12)给出了脉冲激光目标的回波信号波形的数学模型。考虑到脉冲宽度τH的发射激光脉冲信号距离分辨率为dR=(cτH)/2(c为光速)。由
dR可将目标反射激光的面积AC(R)和发射脉冲信号τ(R)加以离散化,进一步再利用有限长序列线性卷积可以得到激光目标波形的离散序列表示[1]。 设激光入射方向与目标径向的夹角为θ,目标径向长度为l。发射脉冲激光经大气路径,照射远程飞机目标的激光脉冲光束时宽为τH,距离分辨单元dR。沿目标的径向距离方向,该脉冲光束可看作M个宽度dR、功率P0
的多个脉冲激光的叠加τ(R)。将光功率归一化,τ(R)的离散序列τ(n)表示为[1]: $$ \tau (n) = \left\{ {\mathop \tau \nolimits_n = 1} \right\},n = 1, \cdots ,M $$ (13) 机载激光测距机发射激光脉冲信号离散化的序列长度M=cτH/
dR。因此,不同脉宽的发射信号都可以表示为 $\tau \left( n \right) = \left\{ {1,1} \right\}$ 。发射脉冲信号的脉宽决定着回波信号的目标分辨率[1]。依据脉冲激光的目标距离分辨单元
dR,对激光目标的几何外形沿着径向进行离散化表示,目标反射截面积AC(R)的离散化后的点数N可由公式(14)表示[1]: $$ N = [l\cos \theta /{\rm d}R] $$ (14) 以dR为最小分辨单元,沿着目标几何外形径向计算目标外形面积的N点离散化面积序列Ac’(n),再结合目标的姿态,将目标外形面积Ac’(n)向径向进行投影,可得到脉冲激光目标的反射截面积为[1]:
$$ \mathop A\nolimits_c (n){\rm{ = }}\left\{ {A'\left( n \right)\cos \theta } \right\},n = 1,\cdots,N $$ (15) 脉冲激光测距机针对远程飞机目标的回波波形数字信号离散序列可通过有限长序列线性卷积计算得到[1]:
$$ \begin{array}{l} s(n) = \tau (n)*\mathop A\nolimits_c (n) = \displaystyle\sum\limits_{k = 0}^\infty {\tau (k)\mathop A\nolimits_c } (n - k) \\ \end{array} $$ (16) Ac(n)为N点序列,τ(n)为2点定长序列,则目标波形s(n)为L=N+M−1=N+1点序列。脉冲激光目标回波的数字化序列可由矩阵相乘加以计算。发射激光脉冲以及目标反射面积均是以发射脉冲的距离分辨率(脉冲宽度的一半)进行离散化的,实际模拟回波信号的离散化采样间隔τs并非就是发射脉冲的半脉宽τH/2。因此,要完整采样到目标波形像,必须满足:
$$ {\tau _s} \leqslant {\tau _H}/2 $$ (17) -
模拟体制的激光测距机采用模拟比较器电路及时间测量芯片实现目标距离输出,作用距离近、信噪比高,主要利用目标回波波形的上升沿实现输出判决。数字体制的激光测距机采用目标回波的能量最大峰值点作为目标距离输出,主要利用目标回波波形的极大值点。在激光回波数字信号处理过程中,通常采用数字滤波对波门内的回波信号进行降噪,再提取目标波形,检测波形峰值点位置,估计目标的精确距离。回波数字信号处理能够改善信噪比,但降噪算法不具备线性相频特性,引起回波波形波峰值点位置发生偏移,这将影响激光测距机输出目标距离的精度[6]。
激光回波信号能量主要集中于低频,高频信息中的有用信息较少。在时域,数字滤波采用隔样本点差分及平滑滤波算法。为了与脉冲激光探测目标的发射激光脉冲信号宽度匹配,取K=M[6],其中差分间隔样本点数为M、平滑窗口宽度为K。平滑滤波过程可由公式(18)给出:
$$ y(n) = \frac{1}{K}\sum\limits_{i = 0}^{K - 1} {[x(n + i) - x(n + i - M)]} $$ (18) 在小波域,对信号进行离散小波分解后的大部分高频系数可作为噪声删除,利用低频系数重构回波的方法进行降噪。时域平滑与低频系数重构小波降噪算法均属于低通滤波算法。EMD方法也可以依不同频率成分对波形进行分解,再通过重构实现降噪,这一方法更适合非平稳过程的信号处理[7-8]。数字平滑滤波算法在滤除高频噪声时,脉冲激光目标的回波波形的峰值点位置容易发生较大的偏移[6]。因此,研究既能保波形特征实现目标精确定位的降噪算法非常迫切。
-
针对脉冲激光目标回波信号降噪,可采用小波分解得到信号的低频及高频系数,通过设定适合软硬阈值,将认为是噪声产生的小波系数删除,而把认为是目标回波波形的小波系数保留。基于Donoho软阈值处理的小波降噪算法结合激光回波波形和噪声的小波系数,在固定阈值基础上采用随噪声状况及小波分解尺度改进的软阈值[9]:
$$ {T_{LW}} = \frac{{\gamma \sigma \sqrt {2\ln {N_j}} }}{{\ln (j + 1)}} $$ (19) 式中:波形序列长度为N;噪声强度为σ;噪声状况评估参数为γ。根据回波信号中的噪声/杂波类型评估参数γ进行调整,脉冲为非高斯杂波时,γ数值小于1,高斯白噪声设成1。小波尺度为j的波形序列长度为Nj,当j增大时,噪声/杂波的小波系数随之减小,阈值下调。
$$ d_{j,k}' = {T_h}({d_{j,k}},\lambda ) = \left\{ {\begin{array}{*{20}{c}} {0,}&{\left| {{d_{j,k}}} \right| < \lambda } \\ {{d_{j,k}},}&{\left| {{d_{j,k}}} \right| \geqslant \lambda } \end{array}} \right. $$ (20) 由公式(20),对脉冲激光测距机目标回波信号进行小波分解,其中的高频系数dj,k做阈值化处理,结合小波分解的低频系数cj,k实施回波信号波形重构,能够较好地去除回波信号中的噪声及杂波。
-
EMD是由Huang等人提出的一种信号驱动的自适应信号分解方法[10-11]。该方法是希尔伯特-黄变换(Hilbert-Huang Tansform,HHT)的重要组成部分,尤其适用于非线性系统、非平稳信号的信号处理[10]。在自适应分解信号过程中,EMD方法根据信号的幅频特性将信号分解为若干本征模态函数(Intrinsic Mode Function,IMF)和残差项[10, 12]。其中,IMF是一个由局部极大值和极小值定义的零点对称函数,具有相等数目的极值点和包络过零点;残差项为一个常数或单调函数或单极值点函数[10-11]。EMD方法简述如下[10-11]:
1)针对原始脉冲激光目标回波信号,求取IMF项。首先寻找信号波形中具有等量极值点和包络过零点并包络线零点对称的分量,作为信号EMD分解的第1个IMF项。
2)将激光回波信号
$x(t)$ 与步骤1)中得到的第1个IMF项${c_1}(t)$ 求差,作为第1个残差项${r_1}\left( t \right)$ ,如公式(21)所示:$$ {r_1}\left( t \right) = x(t) - {c_1}(t) $$ (21) 3)将步骤2)中得到的残差项视作下一步EMD分解的新原始信号,不断循环步骤1)和2),得到若干IMF项和残差项,如公式(22)所示:
$$ \left\{ \begin{array}{l} {r_2}\left( t \right) = {r_1}(t) - {c_2}(t) \\ {\rm{ }} \vdots \\ {r_n}\left( t \right) = {r_{n - 1}}(t) - {c_n}(t) \\ \end{array} \right. $$ (22) 式中:n为迭代次数;
${c_2}\left( t \right)\sim {c_n}\left( t \right)$ 为激光回波信号的第2~n个IMF项;${r_2}\left( t \right)\sim {r_n}\left( t \right)$ 分别表示激光回波的第2~n个残差项。4)不断重复步骤3)中信号分解过程,直至残差项
${r_n}\left( t \right)$ 为一个常数或单调函数或单极值点函数,则EMD分解过程终止。最后,EMD方法将原始激光回波信号分解为若干IMF项和一个残差项(即分解过程中的最后一个残差项),如公式(23)所示:$$ x\left( t \right) = \sum\limits_{i = 1}^n {{c_i} + {r_n}} $$ (23) 机载平台脉冲激光目标波门内的数字采样回波信号f(k)为含噪声的序列[6]:
$$ f(k) = s(k) + n(k),k = 1 - N $$ (24) 式中:s(k)为目标波形序列;n(k)为随机高斯白噪声;信号f(k)为脉冲激光目标检测波门内的信号。针对脉冲激光目标回波信号进行EMD分解,得到一系列IMF项和残差项,尺度i=0~J, 序列长度k=1~N。再结合噪声IMF项与信号IMF项选择,与残差项重构时域离散目标回波波形序列f’(k)。这时就得到降噪后的激光回波信号。
-
脉冲激光目标精确定位算法的核心在于如何减小波形畸变,因此EMD分解重构算法的降噪性能及峰值点位置偏移情况需要加以仿真验证[6]。另外,开展外场实验可以获取在接近真实应用条件下的数据,对目标精确定位算法的性能加以实验验证。下面实验主要针对单帧回波信号降噪及峰值点位置提取开展仿真实验。
实验1:基于EMD的激光回波降噪
将单帧脉冲激光目标回波信号以一定的信噪比与高斯白噪声进行叠加,得到待处理的含噪回波信号。使用EMD方法对含噪回波信号进行处理,并对选择EMD分解得到的若干IMF项及残差项进行重构,得到降噪后的波形。其中,IMF项及残差项波形如图3所示,脉冲激光回波信号EMD降噪结果如图4所示。图5给出了不同降噪算法的处理结果。
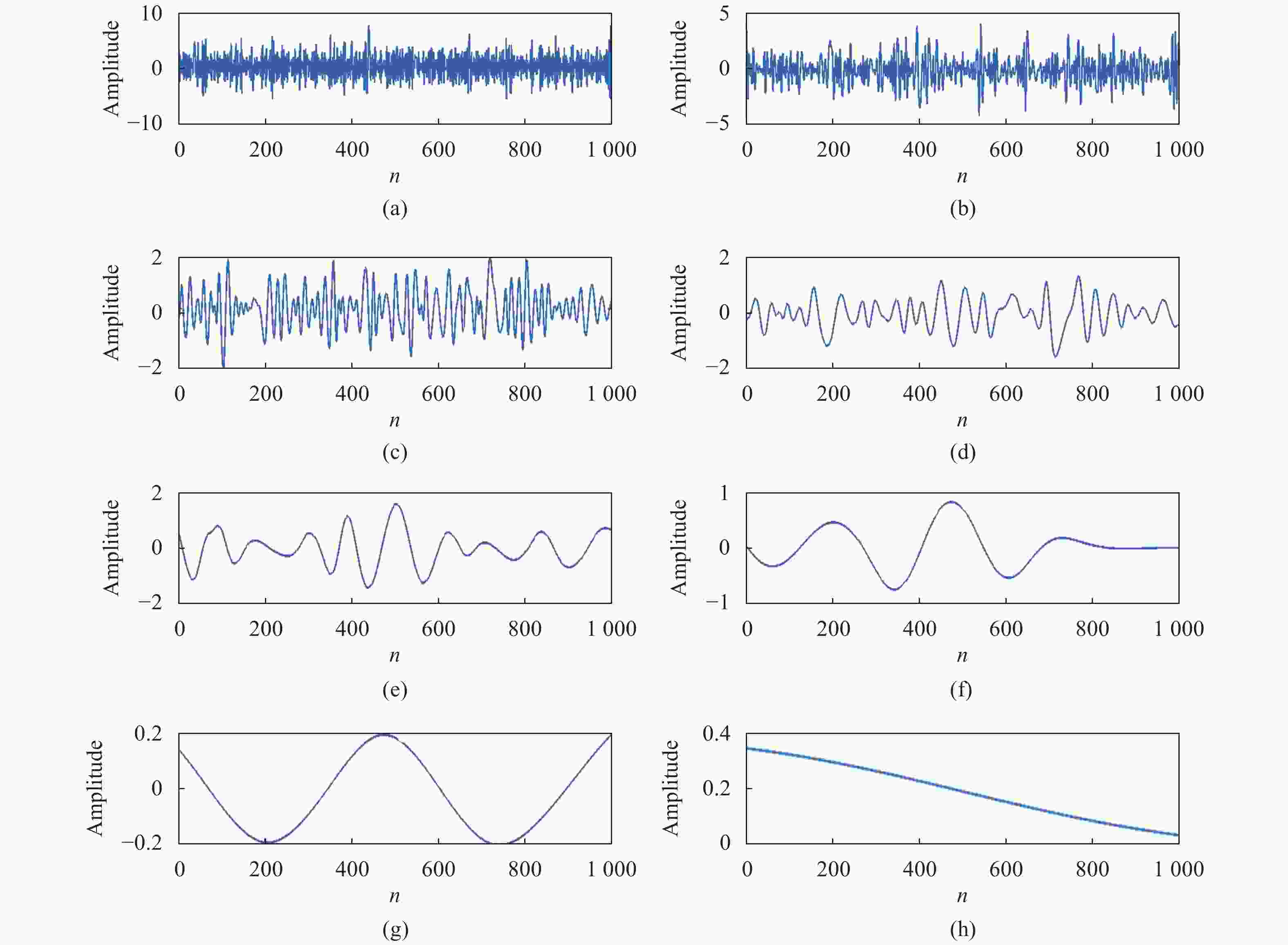
图 3 脉冲激光回波信号经验模态分解。 (a) IMF-1; (b) IMF-2; (c) IMF-3; (d) IMF-4;(e) IMF-5; (f) IMF-6; (g) IMF-7; (h) 残差
Figure 3. Empirical Mode Decomposition of the pulse laser echo signal. (a) IMF-1; (b) IMF-2; (c) IMF-3; (d) IMF-4; (e) IMF-5; (f) IMF-6; (g) IMF-7; (h) Residual

图 4 回波信号EMD降噪结果。 (a) 发射激光波形; (b) 回波信号; (c) 回波信号EMD算法降噪结果
Figure 4. Results of the echo signal denoised by EMD. (a) Emitting laser waveform; (b) Echo signal; (c) Result of the echo signal denoised by EMD algorithm

图 5 SNR=−15 dB时回波信号经不同降噪算法得到的波形。 (a) 发射信号; (b) 回波信号; (c) 回波信号SF算法降噪结果; (d) 回波信号WRD算法降噪结果; (e) 回波信号EMD算法降噪结果
Figure 5. Results of the echo signal denoised at SNR=−15 dB by various denoising methods. (a) Emitting signal; (b) Echo signal; (c) Result of the echo signal denoised by SF algorithm; (d) Result of the echo signal denoised by WRD algorithm; (e) Result of the echo signal denoised by EMD algorithm
实验2:针对单帧激光回波信号降噪,几种常用数字滤波算法性能对比
机载多脉冲激光测距机接收的目标回波脉冲波形的宽度为20 ns,依照对数幅度信噪比−15 dB混合高斯白噪声。采用数字平滑滤波(Smoothing Filter,SF)算法、小波降噪(Wavelet Reconstruction Denoising,WRD)算法、EMD降噪(Empirical Mode Decomposition Denoising,EMDD)算法进行100次回波信号降噪处理,统计回波信号的最小可检测信噪比。
表1给出了最小可检测信噪比的统计结果。可以看出,经窗口宽度为10点的平滑滤波,其最小可检测信噪比稍逊于窗口宽度为15点的SF算法。而WRD算法的信噪比改善效果明优于SF算法。而与SF和WRD算法相比,文中提出的EMDD算法的可检测信噪比改善效果更优。
表 1 不同降噪算法的最小可检测信噪比
Table 1. The least SNR detected by various denoising algorithms
Algorithms SF(M=10) SF(M=15) WRD EMDD SNR/dB −10 −12 −15 −17 实验3:针对降噪后的单帧激光回波信号波形,几种常用数字处理算法峰值点位置偏移情况对比
采用三种降噪算法滤波后直接检测峰值点的位置并进行对比。表2给出了不同信噪比时不同算法针对单帧回波信号进行目标检测后的峰值点位置与真实值的误差点数,其中统计次数为100次平均,X表示无结果。
表 2 不同信号处理算法的峰值点位置估计误差
Table 2. The estimation error of the peak point position by different signal processing algorithms
Algorithms SF(M=10) SF(M=15) WRD EMDD SNR=−10 dB 15 9 5 2 SNR=−12 dB X 11 5 3 SNR=−15 dB X X 6 3 由表2可以看出,随着回波信号信噪比不断降低,SF、WRD和文中EMDD算法的目标位置估计偏移量不断增大;另外,文中EMDD算法的目标位置估计偏移量在不同回波信号信噪比情况下均小于对比算法(SF和WRD算法),且当回波信号信噪比为−10 dB时,文中EMDD算法的目标位置估计偏移量达到了两个点,进一步改进了对比方法目标位置估计偏移量过大的问题。文中提出的EMDD激光回波降噪数字处理方法不仅有较好信噪比改善性能,且处理后得到的回波波形峰值点位置更接近真实值。
图6为脉冲激光测距机消光比法测距机性能的外场评估结果。采用文中算法研究开发的测距机在中国计量科学研究院外场打靶测试,靶面位置不动(靶面距定位孔27.5 cm),测距机分别放置在不同的测距台上,出光口到定位孔的距离为25 cm。测试前先用校准好的枪瞄瞄准目标,然后加合适倍率的衰减片完成距离测量,用于绝对距离的校准及测距精度的分析。记录完数据后,逐渐增加衰减倍率,直到不能稳定得到回波数据,用于评估测距性能。中国计量科学研究院标定距离分别为:431.027 m (5号靶)、623.049 m (6号靶)、863.040 m (7号靶)、1 175.0611 m (8号靶),测距机实测距离分别为:430.502 m、622.524 m、862.515 m和1 174.535 m。
-
文中针对机载平台多脉冲激光测距目标回波信号的数字化降噪,提出了基于EMD分解重构的降噪算法,兼具较好的信噪比改善与目标波形峰值点位置保持特性,可用于改善远程目标定位精度。经仿真实验证明,采用EMD降噪后,激光目标最小可检测信噪比降至−17 dB,检测峰值点的定位精度明显优于数字平滑滤波及小波降噪算法。在实际研制的机载多脉冲激光测距机外场消光比法打靶实验中,采用EMD降噪的多脉冲激光目标定位精度改善至0.5 m,优于现有采用低通数字平滑滤波的远程激光测距机定位精度。
Target echo denoising algorithm of airborne platform multi pulse laser rangefinder under low SNR
-
摘要: 针对远距离飞机目标,机载多脉冲激光测距机通常采用数字化处理体制,影响其测距精度的因素包括发射激光脉冲宽度的距离分辨率、大气传播及目标反射特性造成的波形展宽、回波信号接收处理通道的非线性相频特性等。数字化采样率、回波信号降噪、目标峰值点位置估计等数字化处理过程引起较大的目标距离定位误差。提出了基于经验模态分解(Empirical Mode Decomposition,EMD)和重构的回波降噪方法,首先对脉冲激光目标回波波形进行建模,然后分析了现有数字化回波降噪算法的性能及其对定位精度的影响。实验结果表明,所提方法可以准确提取目标峰值点位置,改善激光测距机的目标定位精度。Abstract: For long-distance aircraft targets, airborne multi pulse laser rangefinders usually adopt digital processing system. The factors that affect the ranging accuracy include the range resolution of emitting laser pulse width, the waveform broadening caused by atmospheric propagation and target reflection characteristics, the nonlinear phase frequency characteristics of echo signal receiving and processing channel, etc. Digital sampling rate, echo signal denoising and target waveform peak point position estimation usually cause large target range positioning error. In this paper, an echo denoising method based on Empirical Mode Decomposition(EMD) and reconstruction was proposed. Firstly, the echo waveform of pulse laser target was modeled, and then the performance of existing digital echo denoising algorithms and its influence on positioning accuracy were analyzed. The experimental results show that the proposed method can accurately extract the target peak point position and improve the target positioning accuracy of laser rangefinder.
-
图 5 SNR=−15 dB时回波信号经不同降噪算法得到的波形。 (a) 发射信号; (b) 回波信号; (c) 回波信号SF算法降噪结果; (d) 回波信号WRD算法降噪结果; (e) 回波信号EMD算法降噪结果
Figure 5. Results of the echo signal denoised at SNR=−15 dB by various denoising methods. (a) Emitting signal; (b) Echo signal; (c) Result of the echo signal denoised by SF algorithm; (d) Result of the echo signal denoised by WRD algorithm; (e) Result of the echo signal denoised by EMD algorithm
表 1 不同降噪算法的最小可检测信噪比
Table 1. The least SNR detected by various denoising algorithms
Algorithms SF(M=10) SF(M=15) WRD EMDD SNR/dB −10 −12 −15 −17 表 2 不同信号处理算法的峰值点位置估计误差
Table 2. The estimation error of the peak point position by different signal processing algorithms
Algorithms SF(M=10) SF(M=15) WRD EMDD SNR=−10 dB 15 9 5 2 SNR=−12 dB X 11 5 3 SNR=−15 dB X X 6 3 -
[1] Sun Junling, Ma Pengge, Sun Guangmin, et al. Multi-pulse laser radar target signal simulation based on target echo waveform model [J]. Infrared and Laser Engineering, 2016, 45(7): 0726006. (in Chinese) doi: 10.3788/IRLA201645.0726006 [2] Cheng P F. Research on key technologies of high dynamic range and high precision laser ranging[D]: Shanghai: Graduate University of Chinese Academy of Sciences (Shanghai Institute of Technical Physics), 2014. (in Chinese) [3] Wang Dan, Zhao Xin, Zhou Yonggang, et al. Research on filtering algorithm based on laser ranging system [J]. Laser and Optoelectronics Progress, 2016, 53(10): 101402. (in Chinese) [4] Zhao Y Z, Lea T K, Schotland R M. Correction function for the lidar equation and some techniques for incoherent CO(2) lidar data reduction [J]. Applied Optics, 1988, 27(13): 2730-2740. doi: 10.1364/AO.27.002730 [5] Jelalian A V. Laser Radar System[M]. Boston, USA: Artech House, 1992. [6] Sun J L, Sun G M, Ma P G, et al. Laser target localization based on symmetric wavelet denoising and asymmetric gauss filtering [J]. Chinese Journal of Lasers, 2017, 44(6): 0604001. (in Chinese) [7] Xiao S P, He Y Y. An improved signal denoising algorithm of EMD image [J]. Modern Electronics Technique, 2016, 39(16): 91-93. (in Chinese) [8] Kopsinis Y, McLaughlin S. Development of EMD-based denoising methods inspired by wavelet thresholding [J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1351-1362. doi: 10.1109/TSP.2009.2013885 [9] Wang R, Zhang Y C. New threshold function in wavelet threshold de-noising [J]. Computer Engineering and Appli-cations, 2013, 49(15): 215-218. (in Chinese) doi: 10.3778/j.issn.1002-8331.1211-0364 [10] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. doi: 10.1098/rspa.1998.0193 [11] Piñeiro-Ave J, Blanco-Velasco M, Cruz-Roldán F, et al. Target detection for low cost uncooled MWIR cameras based on empirical mode decomposition [J]. Infrared Physics & Technology, 2014, 63: 222-231. [12] Blanco-Velasco M, Weng B W, Barner K E. ECG signal denoising and baseline wander correction based on the empirical mode decomposition [J]. Computers in Biology and Medicine, 2008, 38(1): 1-13. doi: 10.1016/j.compbiomed.2007.06.003 -







 下载:
下载: