-
结构光三维测量技术主要有散斑结构光投影法和条纹投影轮廓术。散斑结构光投影技术首先投影散斑图案到物体表面,然后将拍摄到的散斑图案进行极线校正和相关匹配,最后通过三角测量原理得到物体三维形貌,重建仅需投影单帧散斑图案,投影效率高;但是单目散斑结构光对散斑投射器具有很高要求,且匹配结果受到光学系统离焦、物体表面反射率、分辨率、畸变等多种因素影响,从而影响重建精度[1]。条纹投影轮廓术主要有傅里叶变换轮廓术(Fourier Transform Profilometry,FTP)和相移测量轮廓术(Phase Shifting Profilometry,PSP)两种典型方法[2]。FTP方法通常采用单张编码图像求解相位并重建,但是空间信息的使用使其对表面不连续的物体难以精确重建[3-4]。在复杂建模的高精度重建中更多采用PSP方法[2, 5]。PSP方法需要采用多张条纹编码图像,具有稳定性好、精度高等特点,但存在投影效率低的问题。
PSP方法主要包括包裹相位求解和相位展开两个部分。为了获取包裹相位,大量的算法被提出[6-11]。其中,标准
$N$ 帧相移算法[9]对任意阶次的谐波噪声不敏感以及对图像获取设备的非线性响应具有极佳的抑制作用,被广泛用于获取包裹相位。为了提高系统测量的速度,采用三步相移算法是一个合适的选择。当获取了包裹相位后,为了得到全场范围不重复的相位值,需要对相位进行展开。因此,须明确相位所处的周期,即相位级数。多频外差的方法被广泛用来进行相位展开[12-13],通过这种方法获取展开相位具有精度高,能抵抗多种不同的误差源的优点[2]。将$N$ 帧相移算法与多频外差相结合,即多频多步相移算法,进行相位展开需要投影大量的条纹图像。若采用三频三步相移算法[14],则共需要投影9张图像,虽然具有较高精度,但系统的整体投影效率会受到影响。为了提高投影效率,Liu等人[6]提出了双频移相算法(Dual-frequency phase-shifting approach),条纹图中包含两个不同振幅、频率和相移的正弦分量,高频用于得到包裹相位,低频用于相位展开,但是测量精度和相位展开的可靠性会受到条纹振幅分配的影响[2]。Zuo等人[8]提出了“3+2”相移算法(Bi-frequency phase-shifting approach),通过高频的三步相移图像得到包裹相位和背景光强,然后应用单频的两步相移图像与前面得到的背景光强求得单频的相位,用于相位展开,相位展开的可靠性受到条纹频率的影响[15]。Zuo等人[7]还提出了一种“2+2”相移算法(2+2 phase shifting algorithm),仅需两幅相移为π的高频图像和两幅光强斜率呈线性增加或减少的光强图像分别得到包裹相位和无包裹的相位图。但是此方法仅适用于条纹频率较低的情况,当求解包裹相位的图像频率较高时,由于离焦效应的影响,条纹的对比度减弱,斜率线性增长的图像由于非常低的频率受到离焦效应的影响较小,导致两种频率的图像之间调制相位有较大的差异[2]。针对以上问题,文中提出了一种改进的三频三步相移算法,该方法在继承原有算法优势的基础上,提高了系统的整体效率。该方法与传统三频三步算法均需要三种频率的正弦条纹图,但条纹图数量只需5张,即最高频率光栅图3张,另外两种频率的各1张。该算法首先通过3种频率中最高频率的3张图像,应用三步相移算法得到精度最高的包裹相位。其次将最高频率的3张图像计算出背景光强和调制光强,代入剩下两张条纹图即可得到另外两个频率的三角包裹相位。最后将最高频率的3张图像求得的包裹相位进行相位展开得到展开相位,从而进行三维重建。通过4组实验验证了该算法的重建精度、重建复杂及不连续物体的能力、不同光照强度下重建的稳定性以及对彩色物体的重建能力。结果证明了该算法在有效提高测量速度的同时保证了与传统三频三步算法一致的精度和适应性。
-
改进的三频三步相移算法需要3种频率
$\left( {{f_1} > {f_2} > {f_3}} \right)$ 共5张条纹图像,包括3张频率为${f_1}$ 的图像,和频率为${f_2},{f_3}$ 的图像各1张。5张条纹图像的光强表达式表示如下:$${I_1}\left( {x,y} \right) = A\left( {x,y} \right) + B\left( {x,y} \right)\cos \left[ {{\varPhi _1}\left( {x,y} \right)} \right]$$ (1) $${I_2}\left( {x,y} \right) = A\left( {x,y} \right) + B\left( {x,y} \right)\cos \left[ {{\varPhi _1}\left( {x,y} \right) - \frac{{2\pi }}{3}} \right]$$ (2) $${I_3}\left( {x,y} \right) = A\left( {x,y} \right) + B\left( {x,y} \right)\cos \left[ {{\varPhi _1}\left( {x,y} \right) - \frac{{4\pi }}{3}} \right]$$ (3) $${I_4}\left( {x,y} \right) = A\left( {x,y} \right) + B\left( {x,y} \right)\cos \left[ {{\varPhi _2}\left( {x,y} \right)} \right]$$ (4) $${I_5}\left( {x,y} \right) = A\left( {x,y} \right) + B\left( {x,y} \right)\cos \left[ {{\varPhi _3}\left( {x,y} \right)} \right]$$ (5) 式中:
${I_i}\left( {x,y} \right)$ 表示第$i$ 张编码的正弦条纹图像的光强值,$i = 1,2,3,4,5$ ,$\left( {x,y} \right)$ 表示图像像素坐标点;$A\left( {x,y} \right)$ 和$B\left( {x,y} \right)$ 分别为背景光强和调制光强值;${\varPhi _1}\left( {x,y} \right)$ ,${\varPhi _2}\left( {x,y} \right)$ 和${\varPhi _3}\left( {x,y} \right)$ 分别为满足传统多频外差算法[12]的3种不同频率$\left( {{f_1} > {f_2} > {f_3}} \right)$ 的图像对应的相位值。对于横向编码的条纹图像,其表达式如下:$${\varPhi _j}(x,y) = 2\pi {f_j}x{\rm{ }}\;\;\;\;\;\;\;\;\;\;j = 1,2,3$$ (6) 一般采用条纹周期数
${T_j} = {f_j} \times width$ 衡量频率,$width$ 是投影图像的宽度。例如当${T_1} = 70$ ,${T_2} = 64$ ,${T_3}{\rm{ = }}59$ , 有如图 1所示的条纹图像。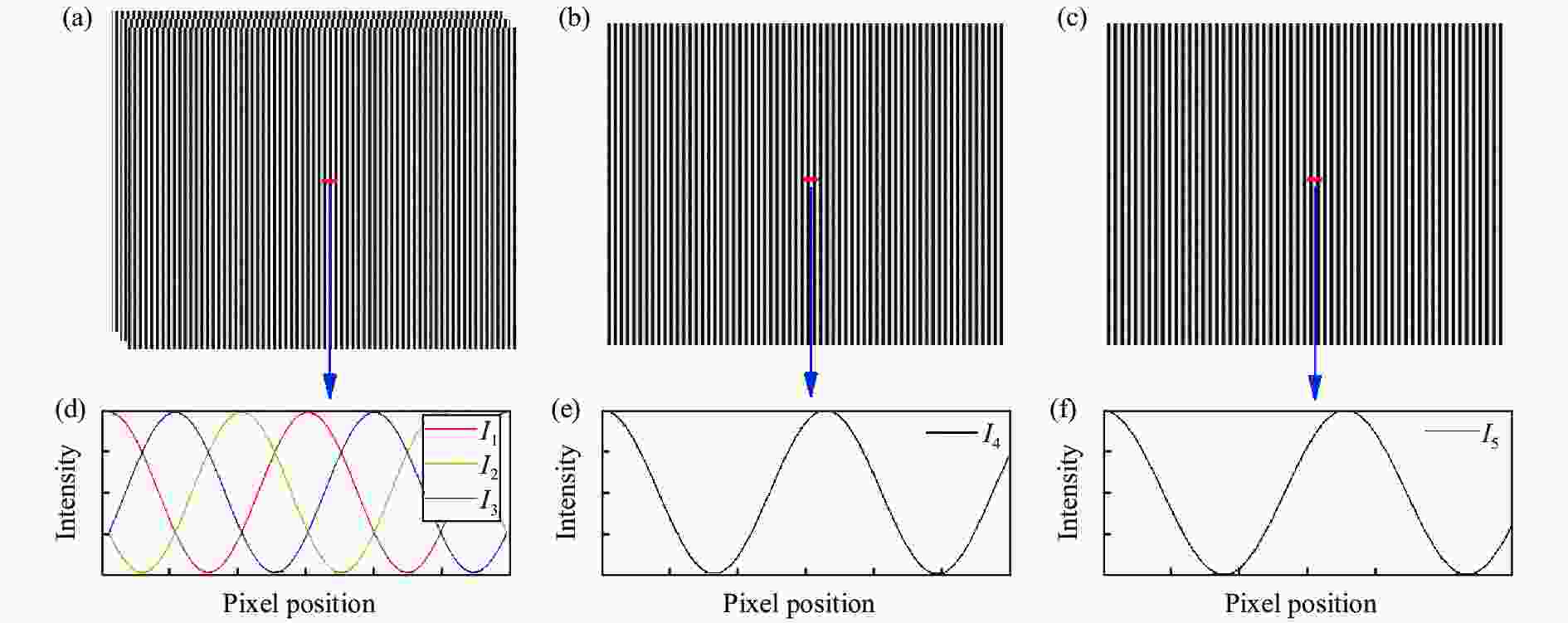
图 1 投影的5张正弦条纹图。(a)频率为
${f_1}$ 的3张正弦条纹图$ {I}_{1},{I}_{2},{I}_{3}$ ;(b)频率为${f_2}$ 的正弦条纹图${I_4}$ ;(c)频率为${f_3}$ 的正弦条纹图${I_5}$ ;(d)~(f) 图1(a)~(c)中红色划线像素位置的光强值Figure 1. Projected five sinusoidal fringe patterns. (a) Three sinusoidal fringe patterns
${I_1}$ ,${I_2}$ , and${I_3}$ with frequency${f_1}$ ; (b) Sinusoidal fringe pattern${I_4}$ with frequency${f_2}$ ; (c) Sinusoidal fringe pattern${I_5}$ with frequency${f_3}$ ; (d)-(f) Intensity at the red line pixel position in Fig. 1(a)-(c) respectively首先,根据频率为
${f_1}$ 的3张图像(公式(1)~(3))得到$A\left( {x,y} \right)$ ,$B(x,y)$ 和包裹相位${\varphi _1}(x,y)$ :$$A\left( {x,y} \right) = \frac{1}{3}\left[ {{I_1}\left( {x,y} \right) + {I_2}\left( {x,y} \right) + {I_3}\left( {x,y} \right)} \right]$$ (7) $$\begin{split}&B\left( {x,y} \right) = \frac{1}{3}·\\& \sqrt {{{\left[ {2{I_1}\left( {x,y} \right) - {I_2}\left( {x,y} \right) - {I_3}\left( {x,y} \right)} \right]}^2} + 3{{\left[ {{I_2}\left( {x,y} \right) - {I_3}\left( {x,y} \right)} \right]}^2}} \end{split}$$ (8) $${\varphi _{1o}}\left( {x,y} \right) = {\rm arctan }\left\{ {\frac{{\sqrt 3 \left[ {{I_2}\left( {x,y} \right) - {I_3}\left( {x,y} \right)} \right]}}{{2{I_1}\left( {x,y} \right) - {I_2}\left( {x,y} \right) - {I_3}\left( {x,y} \right)}}} \right\}$$ (9) $${\varphi _1}(x,y) = \left\{ {\begin{array}{*{20}{c}} {\varphi _{1o}}(x,y) & & {\varphi _{1o}}(x,y) \geqslant 0 \\ {\varphi _{1o}}(x,y) + 2\pi & & {\varphi _{1o}}(x,y) < 0 \\ \end{array}} \right.$$ (10) 公式(9)中由反正切函数计算出的初始包裹相位
${\varphi _{1o}}\left( {x,y} \right)$ 范围在[−π, π),通过转换公式(10)将其转换到[0,2π)范围。为了得到${\varphi _1}\left( {x,y} \right)$ 的展开相位,需要求得另外两个频率的包裹相位,再通过三频外差算法计算${\varphi _1}\left( {x,y} \right)$ 对应的条纹级数。由于频率为${f_2}$ 和${f_3}$ 的条纹图像均为一张,要得到该频率下的包裹相位,需先求得图像${I_4}$ 、${I_5}$ 的背景光强值${A_2}$ 、${A_3}$ 和调制光强值${B_2}$ 、${B_3}$ 。图 2(a)所示为在同等实验条件下相机拍摄得到的不同频率的三步相移条纹图像,对应的条纹周期数分别为70、64、59、1。图 2(b)、(c)分别为通过三步相移图像计算得到的各个频率的背景光强和调制光强。背景光强相差不大,由于投影仪离焦效应的影响,投影得到的不同频率条纹图像的调制光强值会发生变化。从图 2(c)可以看出,频率越低,调制光强的幅值变化越大,对于频率相近的高频图像来说,不同图像间的调制光强差距较小。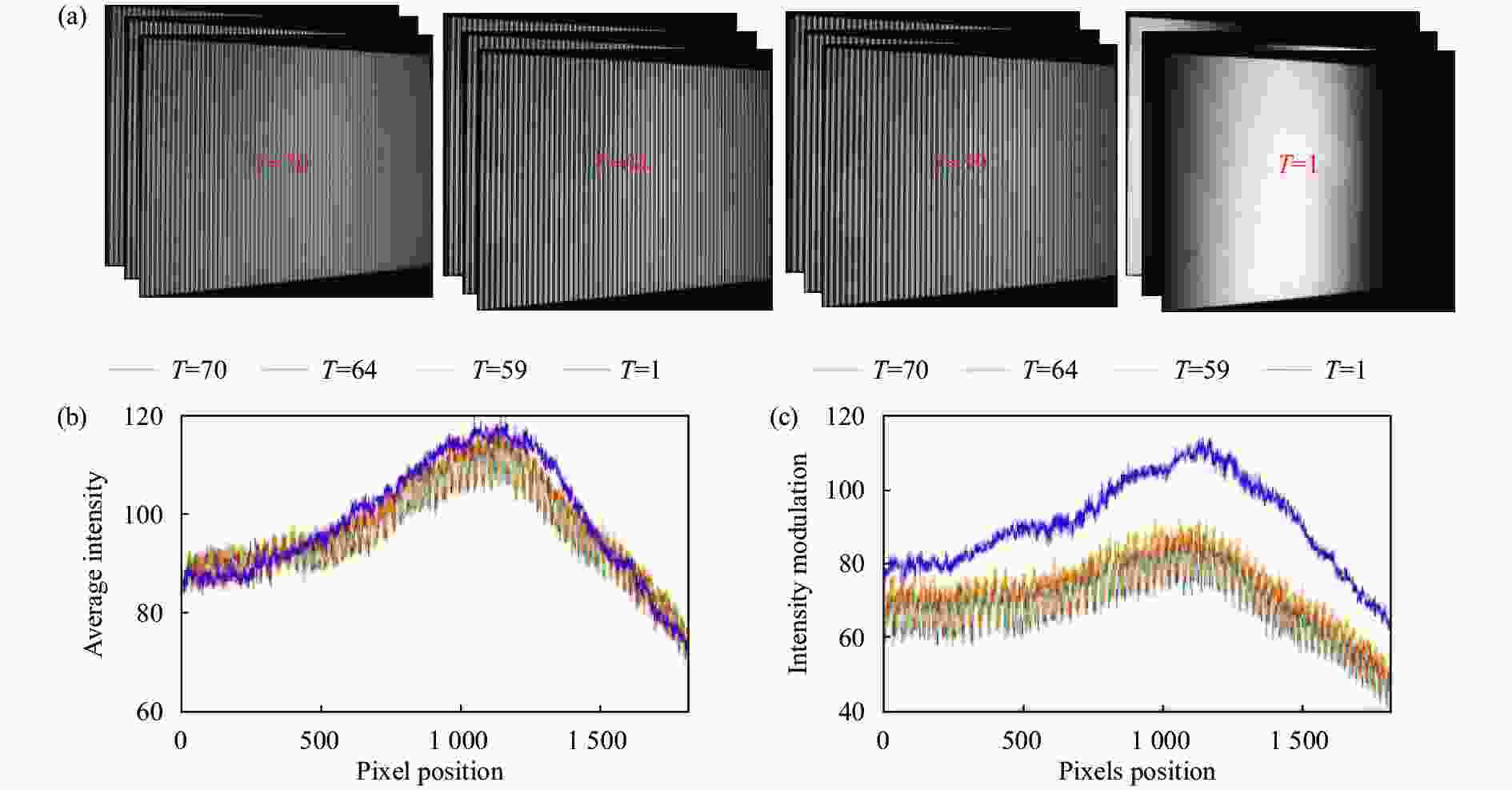
图 2 条纹周期分别为70、64、59、1的正弦条纹图像光强实验。(a) 实验得到的三步相移图;(b) 对应的背景光强;(c) 对应的调制光强
Figure 2. Light intensity experiment of sinusoidal fringe patterns with fringe periods of 70, 64, 59, 1. (a) Three-step phase-shifting patterns obtained from the experiment; (b) Average intensity obtained from the experiment; (c) Intensity modulation obtained from the experiment
为了减小不同频率之间由于离焦效应对调制光强的影响,同时保持高精度,3种图像频率均为高频,且频率相近[2]。则有:
$$\left\{ \begin{gathered} {A_2}(x,y) \approx A(x,y) \\ {A_3}(x,y) \approx A(x,y) \\ {B_2}(x,y) \approx B(x,y) \\ {B_3}(x,y) \approx B(x,y) \\ \end{gathered} \right.$$ (11) 将计算得到的背景光强
$A\left( {x,y} \right)$ 和调制光强$B\left( {x,y} \right)$ 代入公式(4)~(5)求解三角包裹相位${\varphi _2}\left( {x,y} \right)$ 和${\varphi _3}\left( {x,y} \right)$ :$${\varphi _2}\left( {x,y} \right) = {\rm arccos}\left[ {\frac{{{I_{\rm{4}}}\left( {x,y} \right) - A\left( {x,y} \right)}}{{B\left( {x,y} \right)}}} \right]$$ (12) $${\varphi _3}\left( {x,y} \right) = {\rm arccos}\left[ {\frac{{{I_{\rm{5}}}\left( {x,y} \right) - A\left( {x,y} \right)}}{{B\left( {x,y} \right)}}} \right]$$ (13) 由于反余弦函数的限制,三角包裹相位
${\varphi _2}\left( {x,y} \right)$ 和${\varphi _3}\left( {x,y} \right)$ 的变化范围为$0$ ~$\pi $ 。为了适应三频外差算法用于相位展开,需根据三角包裹相位像素坐标斜率变化将其转换到$0$ ~$2\pi $ 范围。转换公式如下:$${\varphi _{ju}}\left( {x,y} \right) = \left\{ \begin{gathered} {\varphi _j}\left( {x,y} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm if}\;\;{k_{jx}}\left( {x,y} \right) \geqslant 0 \\ 2\pi - {\varphi _j}\left( {x,y} \right)\;\;\;\;\;\;\;\;\;{\rm if}\;\;{k_{jx}}\left( {x,y} \right) < 0 \\ \end{gathered} \right.$$ (14) 式中:
${\varphi _{ju}}\left( {x,y} \right)$ 为三角包裹相位${\varphi _j}$ 转换后得到的标准包裹相位,$j = 2,3$ ;${k_{jx}}\left( {x,y} \right)$ 为三角包裹相位${\varphi _j}\left( {x,y} \right)$ 在$x$ 方向的斜率,可根据邻近像素点之间的相位关系求解。通过比较斜率的正负特性,得到从$0$ ~$2\pi $ 变化的标准包裹相位${\varphi _{2u}}\left( {x,y} \right)$ 和${\varphi _{3u}}\left( {x,y} \right)$ ,如图 3所示。再由上述得到的包裹相位${\varphi _1}\left( {x,y} \right)$ ,${\varphi _{2u}}\left( {x,y} \right)$ 和${\varphi _{3u}}\left( {x,y} \right)$ 通过三频外差算法[12]获取条纹级数${N_j}(x,y)$ ,$j{\rm{ = }}1,2,3$ 。由3个频率的包裹相位求得的条纹级数在一个周期内保持一致,需要通过取整来进一步计算,当偏差导致取整前的级数误差小于0.5时,不会影响级数正确求解[16],同时可通过常规方法对级数进行矫正[17]。最终通过精度最高的包裹相位${\varphi _1}\left( {x,y} \right)$ 和条纹级数${N_1}(x,y)$ 得到展开相位${\varPhi _1}\left( {x,y} \right)$ :
图 3 通过反余弦函数计算得到的包裹相位φ1和三角包裹相位φ2、φ3以及三角包裹相位φ2、 φ3转换得到的包裹相位φ2u、φ3u
Figure 3. Wrapped phase
${\varphi _1}$ and triangular wrapped phases${\varphi _2}$ and${\varphi _3}$ which are obtained by arc cosine functions, wrapped phase${\varphi _{2u}}$ and${\varphi _{3u}}$ which are phases transformed by triangular wrapped phases${\varphi _2}$ and${\varphi _3}$ $${\varPhi _1}(x,y) = 2\pi {N_1}(x,y) + {\varphi _1}(x,y)$$ (15) 利用以上展开相位结果对结构光测量系统中的投影仪和相机图像平面坐标点进行匹配,结合系统内外参数重建得到物体的空间三维信息。
-
结构光测量系统由一个计算处理单元、一个DLP投影仪和一个CCD相机组成。DLP投影仪采用Acer型号为H7850的投影仪,分辨率为1024×768,CCD相机采用AVT型号为Manta G-505B的工业摄像机,分辨率为2452×2056,工作温度为5~45 ℃。将计算处理单元生成的重建所需条纹图像通过投影仪投射到待测物体表面,相机同步采集经过物体表面调制后发生变形的条纹图,最后由计算处理单元通过解相和重建算法对图像进行处理得到物体三维形貌。下面通过4个实验分别就算法的测量精度、对不连续物体的重建能力以及算法对不同光强的重建稳定性和重建彩色物体的鲁棒性进行验证。文中采用的3种高频图像条纹周期数为70、64、59[12]。
-
首先为了检验算法的重建精度,对哑铃型陶瓷标准球棒进行重建,并与传统三频三步算法进行对比。哑铃型陶瓷标准球棒的标准值通过三坐标测量仪测量得到。标准球棒两陶瓷球球心距为100.0343 mm,测量结果的不确定度为2.0 μm;球A和球B的直径分别为50.8070 mm和50.8048 mm,测量不确定度均为1.0 μm。重建结果点云数据通过Geomagic Studio软件进行后处理分析。为了验证实验的一致性,进行了10组三维重建实验,测量系统如图 4(a)所示。图 4(b)、(c)为其中一组实验重建结果。

图 4 哑铃型陶瓷标准球棒实验。(a) 结构光测量系统;(b) 相机采集的被标准球棒调制的正弦条纹图像;(c) 标准陶瓷球的重建结果和对应的拟合球面
Figure 4. Experiment of the standard dumbbell-shaped ceramic sphere bat. (a) Structured light measurement system; (b) Camera captures a sinusoidal fringe image modulated by a standard sphere bat; (c) Reconstructed results of the standard ceramic sphere and corresponding fitted sphere surface
陶瓷标准球棒的测量值如图 5所示。通过对数据的分析可以得出,对于A球,文中算法和传统算法三维重建出的直径误差分别为0.0167 mm和0.0142 mm;对于B球,文中算法和传统算法三维重建出的直径误差分别为0.0160 mm和0.0236 mm;对于A、B两球球心距,文中算法和传统算法三维重建出的直径误差分别为0.0039 mm和0.0019 mm;图 5中,误差棒表示测量值的波动范围,可以看出文中算法三维重建一致性良好。从以上结果中可以看出,文中算法具有较高的重建精度,与传统的三频三步算法接近,且仅需5张投影图像,图像投影效率较传统算法提升44.44%。

图 5 传统算法与文中算法得出的哑铃型陶瓷标准球棒测量值。(a)标准陶瓷球A、B的直径;(b)标准陶瓷球A、B的球心距
Figure 5. Values of the standard dumbbell-shaped ceramic sphere bat measured by traditional algorithm and proposed algorithm. (a) Diameters of standard ceramic spheres A and B; (b) Center-to-center distance of the standard ceramic spheres A and B
-
为了验证算法对具有较大梯度变化的复杂物体的重建能力,将折叠后具有较大梯度变化的纸张进行重建,如图 6所示,将编码图像投影到待测物体表面,得到如图 6(b)所示的条纹图像,通过改进算法重建得到图 6(c)所示的折纸。图 6(b)中红色划线像素位置轮廓重建结果如图 6(d)所示,轮廓坡度被完整重建,实验证明算法重建的有效性。
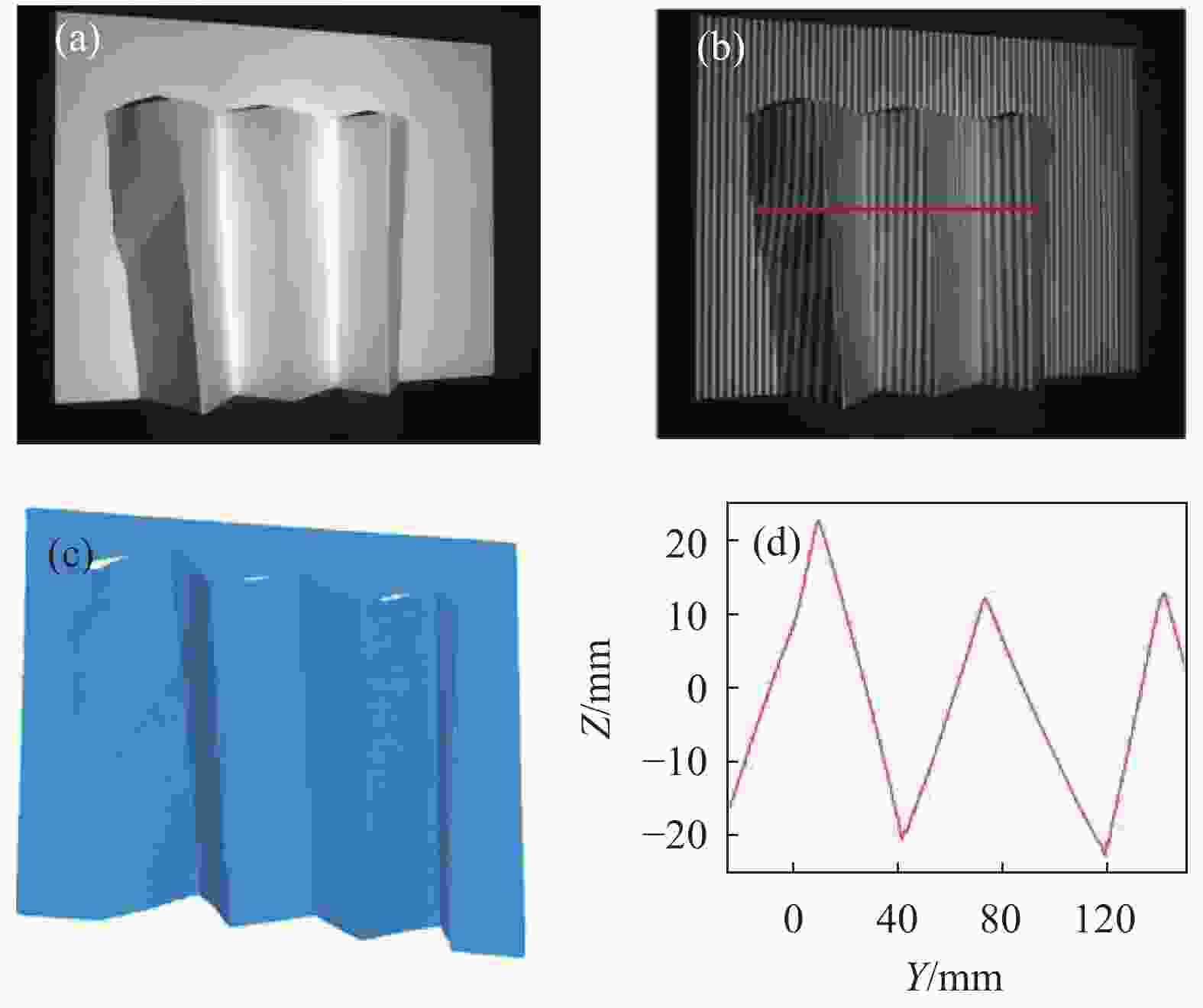
图 6 折纸重建实验。(a) 折纸原始图像;(b) 被折纸调制后的条纹图像;(c) 折纸重建结果;(d) 在图(b)中红色划线像素位置处的重建轮廓
Figure 6. Paper folding reconstruction experiment. (a) Original image of paper folding; (b) Fringe pattern modulated by paper folding; (c) Paper folding reconstruction result; (d) Reconstructed contour at the red-line pixel position in Fig.(b)
为了验证文中提出的算法对表面不连续物体的重建能力,通过实验对两个独立的物体进行三维测量,其结果如图 7所示。图 7(a)为相机捕获的一张不连续物体的图像,图 7(b)表示在图 7(a)中正弦条纹图的红色划线部分图像像素位置的光强值,通过文中算法得到的包裹相位和对应的条纹级数,图 7(c)表示重建物体的点云图。通过实验结果可以看出,不连续物体的三维形貌被很好地重建了出来。

图 7 不连续物体测量结果。(a) 相机采集的被不连续物体调制的正弦条纹图像;(b) 在图(a)中图像红色划线像素位置的光强、对应的包裹相位和相位级数;(c)重建的不连续物体的点云图
Figure 7. Measured results of the discontinuous objects. (a) Sinusoidal fringe pattern modulated by discontinuous objects with camera captured; (b) Light intensity, corresponding wrapped phase and phase order at the red line pixel position in Fig.(a); (c) Point cloud map of the reconstructed discontinuous objects
-
为了验证算法的稳定性,对同一物体在不同光强条件下进行了实验。结果如图 8所示。

图 8 文中3种不同光强情况下的物体三维重建结果;图像列从左到右分别表示低(图(a)、(d)、(g))、中(图(b)、(e)、(h))、高(图(c)、(f)、(i))3种光强情况,图像行从上到下分别代表捕获的南瓜面具像(图(a)~(c))、捕获图像的光强信息(图(d)~(f))、南瓜面具的重建结果(图(g)~(i))
Figure 8. 3D reconstructed results of the objects in three different light intensities using the proposed algorithm. The rows from left to right show the results in low(Fig.(a), (d), (g)), moderate(Fig.(b), (e), (h)) and high(Fig.(c), (f), (i)) light intensities respectively. The columns from top to bottom show the captured patterns of pumpkin mask(Fig.(a)-(c)), the light intensity of the captured patterns(Fig.(d)-(f)) and reconstructed results of pumpkin object(Fig.(g)-(i)) respectively
图 8(a)~(c)分别表示在不同光强情况下获取的经过物体表面调制的条纹图像。从图 8(d)~(f)中可以看出,南瓜面具在低光照强度、一般光照强度和强光照3种不同情况下进行实验,颜色条表示光强强度大小,图像从左到右表示光强从低到高。根据提出的算法,在低光照、一般光照和强光照3种不同光强情况下的南瓜面具三维重建结果如图 8(g)~(i)所示,在每种情况下面具均得到了正确完整的重建。图 9(a)表示图 8(a)~(c)红色划线位置处条纹图像的光强值,图 9(b)所示为图 8(a)~(c)红色划线位置所在横截面的重建南瓜面具高度信息。蓝色、黑色和红色的曲线分别代表重建南瓜面具在低、中、高3种光强情况下的重建高度信息,3种情况下获得的轮廓曲线相互重叠。在此组实验中,在3种光强情况下均能对空间物体进行有效重建,不同光强环境下算法的稳定性得以验证。

图 9 不同光强情况下的重建南瓜面具横截面的高度信息。(a) 图9(a)~(c)红色划线位置处的光强值;(b) 图9(a)~(c)红色划线位置所在横截面的重建南瓜面具的高度信息
Figure 9. Height information of cross section the reconstructed pumpkin mask in different light intensity. (a) Light intensity at the red-line position in Fig.9 (a)-(c); (b) High information of reconstructed pumpkin mask of the cross section at the red-line position in Fig.9 (a)-(c)
-
为了验证算法对彩色物体的重建能力,在实验中将黑白相机AVT Manta G-505B换成彩色相机AVT Manta G-505C,其余实验条件不变,对带有多种颜色的狼面具进行了一组实验。如图 10所示。

图 10 彩色狼面具测量结果。(a) 相机采集的被彩色狼面具调制的正弦条纹图像;(b) 在图(a)中图像红色划线像素位置的光强、对应的包裹相位和相位级数;(c) 重建的彩色狼面具的点云图
Figure 10. Measured results of the colorful wolf mask. (a) Sinusoidal fringe pattern modulated by colorful wolf mask with camera captured; (b) Light intensity, corresponding wrapped phase and phase order at the red line pixel position in Fig.(a); (c) Point cloud map of the reconstructed colorful wolf mask
图 10(a)展示了一张相机捕获的彩色狼面具。图 10(b)表示捕获图像红色划线部分图像像素位置的光强强度、对应的包裹相位和条纹级数。包裹相位和条纹级数被正确解出。如图 10(c)所示,彩色狼面具的三维形貌被正确重建,面具表面的细节如图 11所示的疤痕信息得以清晰呈现。实验证明提出的算法对彩色物体重建的鲁棒性良好。
-
文中提出了一种改进的三频三步相移算法,并详细介绍了该算法的原理。与传统三频三步算法存在相同点,该算法需要3种高频率的正弦条纹图像;不同的是所需图像从9张减少到5张,较传统算法图像投影及拍摄效率提高44.44%。重建所需包裹相位由3张最高频的条纹图直接求得,另外两个频率的图像用于对包裹相位进行展开。由于相移算法的最终精度由最高频的相位确定,文中提出的算法理论上与传统三频三步算法具有相同的精度。从4个方面分别对算法的性能进行验证。通过第1个标准球实验对算法精度进行验证。通过复杂模型重建实验验证算法重建不连续物体重建能力。通过第3个不同光强情况下的物体重建实验验证算法稳定性,最后通过彩色物体的实验验证了算法对不同颜色物体的鲁棒性。在将传统三频三步算法所需图像由9张减少到5张提高算法速度的情况下,提出的算法保持了与传统算法相同的精度。因此,文中算法在三维测量系统的精度和速度中取得了很好地平衡。
Modified three-dimensional reconstruction based on three-frequency three-step phase shifting algorithm
-
摘要: 针对结构光三维重建中的传统三频三步相移方法需要投影过多编码图像、效率低的问题,提出了改进的三频三步相移结构光三维重建方法。该方法与传统三频三步方法均需要3种频率的正弦条纹图,但条纹图数量只需5张,即最高频率的条纹图3张,但初始相位不同,剩余频率的条纹图各1张。较传统方法的9张条纹图投影效率提高44.44%。随后推导了该方法的求解原理,由最高频的3张条纹图直接求得重建所需包裹相位,另外两张条纹图用于对包裹相位进行展开,理论上该方法与传统三频三步算法具有相同的精度。最后进行了4组实验,验证了该方法的重建精度、复杂不连续模型重建能力、不同光照环境中的重建稳定性以及对彩色物体重建能力。结果证明该方法在有效提高测量速度的同时保证了和传统三频三步方法一致的精度和适应性。Abstract: Aiming at the problem that the traditional three-frequency three-step phase shifting algorithm in structured light three-dimensional measurement needed to project too many fringe patterns and has low efficiency, the modified three-frequency three-step phase shifting algorithm was proposed. The proposed algorithm and traditional one both required sinusoidal fringe patterns of three frequencies, but the number of fringe patterns was reduced to 5, that was, 3 fringe patterns of the highest frequency, and one for each of the other two frequencies. Compared with 9 fringe patterns of the traditional algorithm, the projection and capture efficiency was increased by 44.44%. The principle of the proposed algorithm was derived. Three fringe patterns of the highest frequency were used to directly obtain the wrapped phase, and the other two fringe patterns were used to unwrap the phase. In theory, the proposed algorithm owned the same accuracy as the traditional one. Finally, four sets of experiments were conducted to verify the reconstruction accuracy of the algorithm, the reconstruction ability of complex discontinuous models, the reconstruction stability in different illuminations, and the reconstruction ability of color objects. The experimental results prove that the algorithm can effectively improve the measurement speed while maintaining the accuracy and adaptability consistent with the traditional three-frequency three-step phase shifting algorithm.
-
图 1 投影的5张正弦条纹图。(a)频率为
${f_1}$ 的3张正弦条纹图$ {I}_{1},{I}_{2},{I}_{3}$ ;(b)频率为${f_2}$ 的正弦条纹图${I_4}$ ;(c)频率为${f_3}$ 的正弦条纹图${I_5}$ ;(d)~(f) 图1(a)~(c)中红色划线像素位置的光强值Figure 1. Projected five sinusoidal fringe patterns. (a) Three sinusoidal fringe patterns
${I_1}$ ,${I_2}$ , and${I_3}$ with frequency${f_1}$ ; (b) Sinusoidal fringe pattern${I_4}$ with frequency${f_2}$ ; (c) Sinusoidal fringe pattern${I_5}$ with frequency${f_3}$ ; (d)-(f) Intensity at the red line pixel position in Fig. 1(a)-(c) respectively图 2 条纹周期分别为70、64、59、1的正弦条纹图像光强实验。(a) 实验得到的三步相移图;(b) 对应的背景光强;(c) 对应的调制光强
Figure 2. Light intensity experiment of sinusoidal fringe patterns with fringe periods of 70, 64, 59, 1. (a) Three-step phase-shifting patterns obtained from the experiment; (b) Average intensity obtained from the experiment; (c) Intensity modulation obtained from the experiment
图 3 通过反余弦函数计算得到的包裹相位φ1和三角包裹相位φ2、φ3以及三角包裹相位φ2、 φ3转换得到的包裹相位φ2u、φ3u
Figure 3. Wrapped phase
${\varphi _1}$ and triangular wrapped phases${\varphi _2}$ and${\varphi _3}$ which are obtained by arc cosine functions, wrapped phase${\varphi _{2u}}$ and${\varphi _{3u}}$ which are phases transformed by triangular wrapped phases${\varphi _2}$ and${\varphi _3}$ 图 4 哑铃型陶瓷标准球棒实验。(a) 结构光测量系统;(b) 相机采集的被标准球棒调制的正弦条纹图像;(c) 标准陶瓷球的重建结果和对应的拟合球面
Figure 4. Experiment of the standard dumbbell-shaped ceramic sphere bat. (a) Structured light measurement system; (b) Camera captures a sinusoidal fringe image modulated by a standard sphere bat; (c) Reconstructed results of the standard ceramic sphere and corresponding fitted sphere surface
图 5 传统算法与文中算法得出的哑铃型陶瓷标准球棒测量值。(a)标准陶瓷球A、B的直径;(b)标准陶瓷球A、B的球心距
Figure 5. Values of the standard dumbbell-shaped ceramic sphere bat measured by traditional algorithm and proposed algorithm. (a) Diameters of standard ceramic spheres A and B; (b) Center-to-center distance of the standard ceramic spheres A and B
图 6 折纸重建实验。(a) 折纸原始图像;(b) 被折纸调制后的条纹图像;(c) 折纸重建结果;(d) 在图(b)中红色划线像素位置处的重建轮廓
Figure 6. Paper folding reconstruction experiment. (a) Original image of paper folding; (b) Fringe pattern modulated by paper folding; (c) Paper folding reconstruction result; (d) Reconstructed contour at the red-line pixel position in Fig.(b)
图 7 不连续物体测量结果。(a) 相机采集的被不连续物体调制的正弦条纹图像;(b) 在图(a)中图像红色划线像素位置的光强、对应的包裹相位和相位级数;(c)重建的不连续物体的点云图
Figure 7. Measured results of the discontinuous objects. (a) Sinusoidal fringe pattern modulated by discontinuous objects with camera captured; (b) Light intensity, corresponding wrapped phase and phase order at the red line pixel position in Fig.(a); (c) Point cloud map of the reconstructed discontinuous objects
8 文中3种不同光强情况下的物体三维重建结果;图像列从左到右分别表示低(图(a)、(d)、(g))、中(图(b)、(e)、(h))、高(图(c)、(f)、(i))3种光强情况,图像行从上到下分别代表捕获的南瓜面具像(图(a)~(c))、捕获图像的光强信息(图(d)~(f))、南瓜面具的重建结果(图(g)~(i))
8. 3D reconstructed results of the objects in three different light intensities using the proposed algorithm. The rows from left to right show the results in low(Fig.(a), (d), (g)), moderate(Fig.(b), (e), (h)) and high(Fig.(c), (f), (i)) light intensities respectively. The columns from top to bottom show the captured patterns of pumpkin mask(Fig.(a)-(c)), the light intensity of the captured patterns(Fig.(d)-(f)) and reconstructed results of pumpkin object(Fig.(g)-(i)) respectively
图 9 不同光强情况下的重建南瓜面具横截面的高度信息。(a) 图9(a)~(c)红色划线位置处的光强值;(b) 图9(a)~(c)红色划线位置所在横截面的重建南瓜面具的高度信息
Figure 9. Height information of cross section the reconstructed pumpkin mask in different light intensity. (a) Light intensity at the red-line position in Fig.9 (a)-(c); (b) High information of reconstructed pumpkin mask of the cross section at the red-line position in Fig.9 (a)-(c)
图 10 彩色狼面具测量结果。(a) 相机采集的被彩色狼面具调制的正弦条纹图像;(b) 在图(a)中图像红色划线像素位置的光强、对应的包裹相位和相位级数;(c) 重建的彩色狼面具的点云图
Figure 10. Measured results of the colorful wolf mask. (a) Sinusoidal fringe pattern modulated by colorful wolf mask with camera captured; (b) Light intensity, corresponding wrapped phase and phase order at the red line pixel position in Fig.(a); (c) Point cloud map of the reconstructed colorful wolf mask
-
[1] Zuo C, Zhang X L, Hu Y, et al. Has 3D finally come of age?—An introduction to 3D structured-light sensor [J]. Infrared and Laser Engineering, 2020, 49(3): 0303001. (in Chinese) doi: 10.3788/IRLA202049.0303001 [2] Zuo C, Feng S, Huang L, et al. Phase shifting algorithms for fringe projection profilometry: A review [J]. Optics and Lasers in Engineering, 2018, 109: 23-59. doi: 10.1016/j.optlaseng.2018.04.019 [3] Van der Jeught S, Dirckx J J J. Real-time structured light profilometry: A review [J]. Optics and Lasers in Engineering, 2016, 87: 18-31. doi: 10.1016/j.optlaseng.2016.01.011 [4] Chen Y, Pan Y Q, Liu B C, et al. Linear phase error suppression technique based on window Fourier transform [J]. Optics and Precision Engineering, 2020, 28(6): 1314-1322. (in Chinese) doi: 10.3788/OPE.20202806.1314 [5] Zhang S H, Yang Y X, Qin Q M. A fast blind denoising method for grating image [J]. Chinese Optics, 2021, 14(3): 596-604. (in Chinese) doi: 10.37188/CO.2020-0166 [6] Liu K, Wang Y, Lau D L, et al. Dual-frequency pattern scheme for high-speed 3-D shape measurement [J]. Opt Express, 2010, 18(5): 5229-5244. doi: 10.1364/OE.18.005229 [7] Zuo C, Chen Q, Gu G, et al. High-speed three-dimensional profilometry for multiple objects with complex shapes [J]. Opt Express, 2012, 20(17): 19493-19510. doi: 10.1364/OE.20.019493 [8] Zuo C, Chen Q, Gu G, et al. High-speed three-dimensional shape measurement for dynamic scenes using bi-frequency tripolar pulse-width-modulation fringe projection [J]. Optics and Lasers in Engineering, 2013, 51(8): 953-960. doi: 10.1016/j.optlaseng.2013.02.012 [9] Xing S, Guo H. Temporal phase unwrapping for fringe projection profilometry aided by recursion of Chebyshev polynomials [J]. Appl Opt, 2017, 56(6): 1591-1602. doi: 10.1364/AO.56.001591 [10] Shang W Q, Zhang W X, Wu Z, et al. Three-dimensional measurement system based on full-field heterodyne interferometry [J]. Optics and Precision Engineering, 2019, 27(10): 2097-2104. (in Chinese) doi: 10.3788/OPE.20192710.2097 [11] Fu Y J, Han Y H, Chen Y, et al. Research progress of 3D measurement technology based on phase coding [J]. Infrared and Laser Engineering, 2020, 49(3): 0303010. (in Chinese) doi: 10.3788/IRLA202049.0303010 [12] Carsten R, Reinhold R, Jan T. White light heterodyne principle for 3D-measurement[C]//SPIE, 1997, 3100: 236-244. [13] Qiao N S, Sun P. The influence of CCD nonlinearity effect on the three-dimensional shape measurement of dual frequency grating [J]. Chinese Optics, 2021, 14(3): 661-669. (in Chinese) doi: 10.37188/CO.2020-0143 [14] Zhang S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques [J]. Optics and Lasers in Engineering, 2010, 48(2): 149-158. doi: 10.1016/j.optlaseng.2009.03.008 [15] Xu Y, Liang Y, Zou Y, et al. Fast phase extraction of a synthetic wavelength from a dual-wavelength interferogram through Hilbert transformation [J]. Appl Opt, 2021, 60(5): 1440-1447. doi: 10.1364/AO.402801 [16] Liu Fei, Li Jiaxin, Lai Junlin, et al. Full-frequency phase unwrapping algorithm based on multi-frequency heterodyne principle [J]. Laser & Optoelectronics Progress, 2019, 56(1): 011202. (in Chinese) [17] Zheng D, Da F, Kemao Q, et al. Phase-shifting profilometry combined with Gray-code patterns projection: unwrapping error removal by an adaptive median filter [J]. Opt Express, 2017, 25(5): 4700-4713. doi: 10.1364/OE.25.004700 -




















 下载:
下载:


























































































