-
光纤布拉格光栅(Fiber Bragg Grating, FBG)由于其轻巧、规模小、不受电磁干扰和复用能力的影响等优点,已在NIR范围内广泛用于监视结构健康[1],机械运行[2],航空航天[3]和其他领域[4-5]。在实际应用中,对FBG进行解调对于快速准确地捕获温度、压力和应变等参数的变化至关重要[6],可以通过分析FBG的波长偏移来获得测量的参数。目前,已经开发出各种方法来解调FBG的波长偏移,包括CCD光谱仪、匹配光栅方法、可调法布里-珀罗(Fabry-Perot)滤波器方法、边缘滤波方法以及频谱分析方法[7-8]。在这些方法中,可调谐的Fabry-Perot滤波器方案在准确性、容量和成本之间取得了良好的平衡,并已广泛应用于实际测量。
使用光纤光栅和光纤可调滤波器来检测光纤光栅波长的可调滤波器方法被提出以来,立刻成为开发低成本解调系统的主流方法[9]。由于光信号在1550 nm处的衰减系数最低[10],因此许多研究工作已在1550 nm范围内使用FBG传感器来测量动态响应,这需要可调扫描激光(TSL)的范围处于近红外(NIR)区域。在TSL的解调系统中,扫描滤波器通常使用由压电换能器(PZT)驱动的Fabry-Perot可调光纤(FFP-TF)和正弦驱动信号来使PZT高频谐振。迄今为止,已经报道了几种基于TSL的FBG传感系统[11]。但是,正弦波扫描波形在边缘扫描区域周围遭受强烈的非均匀波长间隔响应。实际上,非线性激光波长调谐将导致测量误差和分辨率降低。
目前,提出了各种解决方案来校准激光扫描过程中的非线性和漂移。干涉仪产生的电子触发信号(k触发器)用于改善A/D时钟[11]。该解决方案效果很好,但是它增加了系统的总成本。另一种方法是使用参考校准方法。基于自标记氰化氢(HCN),吸收光谱作为绝对频率参考,获得了3.6~5 pm的解调精度。但是使用HCN气室会导致存储困难。此外,HCN光谱的吸收线深度较浅,并且由光强度引起的基线漂移(BW)导致解调过程的复杂性。另外还可以使用一些找到特定FBG反射轮廓的峰值的方法来提高解调精度,例如高阶多项式函数、曲线拟合方法、质心方法、微分方法、光谱相关(SC)方法、径向基函数网络方法[12]和高斯拟合方法[13-14]。在这些算法中,高斯拟合算法更适合于高精度的波长解调,且通过实验获得20 pm的波长精度[15]。同时有必要在确保解调方法的简单性和所用设备的轻便性的基础上进一步提高解调精度。
文中提出了一种光纤法布里-珀罗标准具(FFPE)的高精度标定方法。自行设计的FFP-TF和FFPE分别为59.5 mm (长)×26 mm (宽)×11.2 mm (高)和98 mm (长)×74 mm (宽)×14 mm (高)。TSL在NIR区域对解调系统进行扫描,其中一个FFPE用作波长标记以提取波长。细分波长扫描范围以实现分段线性解调。通过分析5 Hz扫描频率下的解调精度、波长分布和解调数据分布,提出了一种波长优化算法,进一步提高了解调精度。实验结果表明,在波长范围为1525~1565 nm的近红外扫描激光条件下,系统的解调精度为±0.5 pm。
-
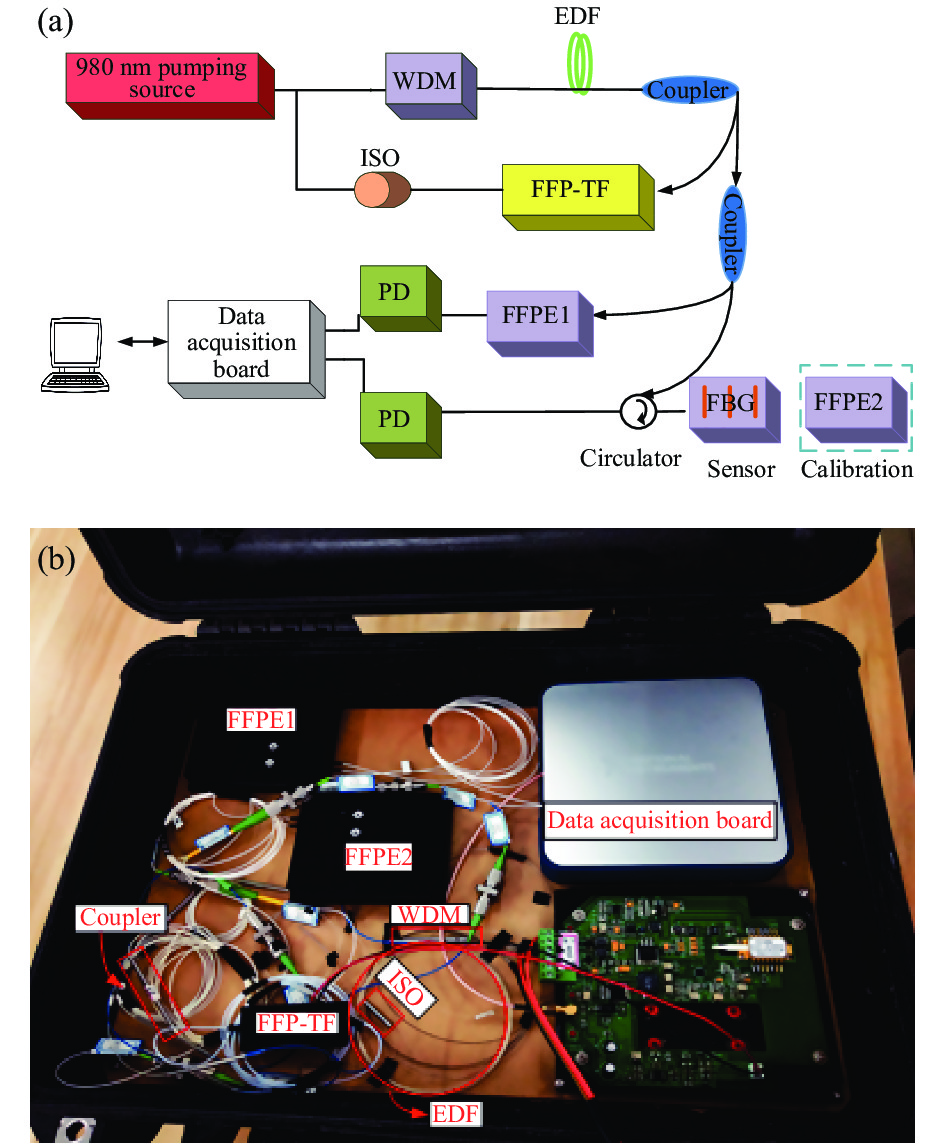
文中设计的FBG解调系统如图1(a)所示,该解调系统的NIR扫频激光器主要由可调谐激光源,参考通道、感应通道以及信号采集和解调单元组成。环形光路依次连接到波分复用器(WDM)、用作增益介质的吸收系数为−18.4 dB/m的14 cm掺杂光纤(EDF)、输出功率为1.4 mW的980 nm激光二极管、3 dB耦合器、精细度(F-P滤波器能够分辨的最小波长的指标,精度越高,F-P滤波器感知的波长变化越小,可用公式表示为
${{F}} = \dfrac{{{{FSR}}}}{{{{BW}}}}$ )为1000且自由光谱范围(FSR)为50 nm的FFP-TF和隔离器(ISO)。ISO用于防止由双向操作引起的空间孔烧伤,从而实现更稳定的单频操作。同时可以阻止来自系统输出端口的反馈。宽带可调光源的调谐带宽为1525~1565 nm,单个激光束的3 dB带宽约为0.05 nm,通过TSL循环依次进行,光功率为1.4 mW。
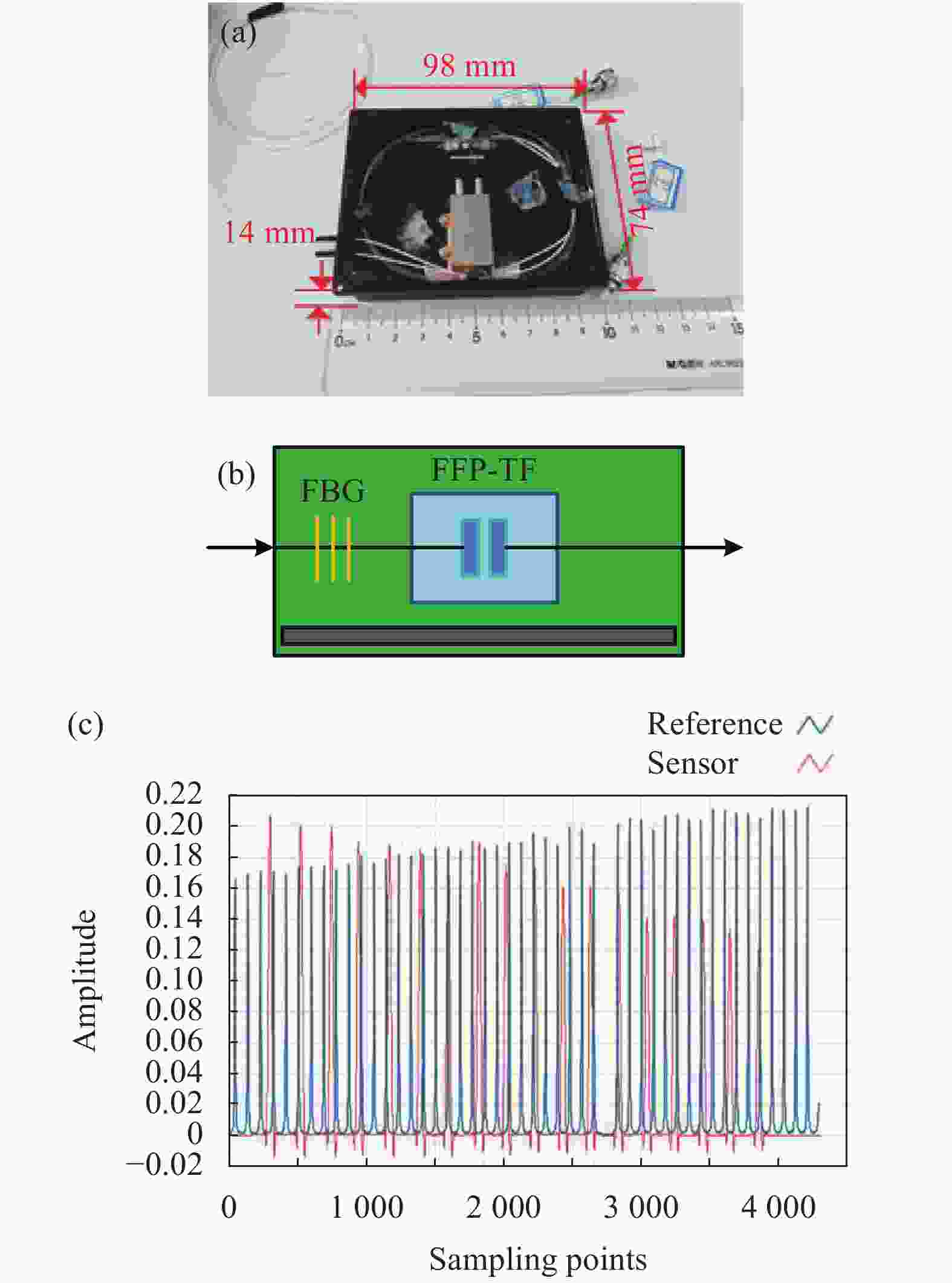
图 1 (a) FBG解调系统方案;(b) 校准解调系统实物图
Figure 1. (a) Scheme of FBG demodulation system; (b) Photograph of calibrating demodulation system
激光输出通过另一个3 dB耦合器分为两部分。一束光束被引入名为FFPE1的法布里-珀罗标准具(FFPE)光纤,其FSR为107 GHz (0.8 nm),波长范围为1525~1565 nm,插入损耗为4 dB。另一束光束被导入传感器。通过两个光电检测器(PD)检测通过传感和FFPE1通道的光,并通过一个数据采集板(PCI-6251,美国国家仪器公司)将光电压电平数字化。用计算机记录光电压水平。当光源波长在FBG的中心波长上扫描时,反射光的功率将在峰值反射功率上相应地变化。
与光纤F-P滤波器解调和匹配光栅解调法相比,TSL解调技术能够有效克服上述两种方法的缺点。TSL技术利用F-P滤波器产生连续的单束可调谐激光,将滤波器放入宽带光源内,扫描激光分为两部分,分别进入传感、校准通道。其中,校准通道目的是利用高精度、稳定的光纤标准具,对光的波长进行标定。该标准具投射波长几乎不受环境变化的影响,故可以产生宽带梳状波。当波长变化量很小时,F-P滤波器与线性滤波效果基本相同,因此使用这种方法将各个不同发射波长的光进行分段后线性解调,可以在取得较好解调效果的同时,避免了迟滞效应和非线性因素对解调精度的影响。
-
确保校准解调系统的实际精度需要用于校准的中心参考波长具有较高的稳定性。然而,由于光纤光栅传感器对各种环境因素敏感,波长偏移很大,无法完成pm级的校准。因此,提出了FFPE来代替传感器。由于FFPE使用特殊精度的机械和光学结构,因此可以确保参考波长的稳定性。同时,FFPE在整个频带中产生44个峰值,波长间隔为0.8 nm。如图1所示,提出了另一个名为FFPE2的FFPE来代替传感器,以获得系统中的高精度校准解调器。校准解调系统的照片如图1(b)所示。FFPE1和FFPE2分别连接在参考通道和测量通道中。在每个扫描周期中,实时动态获取FFPE1和FFPE2的透射反射波长。
-
在FBG解调系统中,环境参数的变化通常很小,当传感器的反射波长发生变化时,反射信号将小于或等于数十pm。FFP-TF的性能直接影响解调系统的检测精度。FFP-TF的实物如图2(a)所示。该模块的尺寸为59.5 mm (长)×26 mm (宽)×11.2 mm (高)。文中使用的FFP-TF的结构示意图主要包括压电陶瓷、两个高反射透镜、定位结构和单模光纤,如图2(b)所示。根据多光束干扰的原理,当宽带光束进入FFP-TF谐振器时,它将在F-P谐振器上反射多次,合格的光将射出。压电陶瓷的微小变形改变了两个透镜之间的距离,从而实现了FFP-TF腔的过滤效果。
-
系统中使用FFPE1作为校准标准具,而FFPE2作为测量标准具。图3(a)所示为FFPE的实物图。该模块的设备尺寸为98 mm (长)×74 mm (宽)×14 mm(高)。标准具的结构示意图如图3(b)所示。它由一个光学F-P腔和一个用于波长校准的FBG组成。箭头标记的方向是光波的传播方向。校准光栅滤出透射波长并在梳状波长中产生间隙以用于解调系统的波长校准。如图3(c)所示,数据采集卡被用来收集校准的标准具和测量的标准具的反射光谱。蓝色波形是经过校准的标准具的反射波,红色波形是所测量的标准具的反射波。选用日本横河电机的AQ6151光学波长仪来校准校准标准仪器的每个峰值波长。波长计的精度高达±0.3 pm,采集时间为15 min。将15 min内的数据取平均值,以获得一组平均数据,可用作测量的真实值。峰值波长数据被输入到反射光谱。
-
压电陶瓷的内部极化状态随施加电压的变化而变化。当极化状态的变化与电压的变化不一致时,会导致电压上升和下降过程的曲线不一致,并存在反冲现象,称为磁滞现象。磁滞与材料、压电元件结构、电压变化和负载有关。除磁滞外,蠕变是另一个影响压电陶瓷定位精度的特性。由于极化后内部分子的摩擦力,变形无法及时完成,它需要一个滞后时间。当施加的电压保持不变时,位移会随时间缓慢变化,并在一段时间后可以达到稳定。当施加的驱动电压不同时,达到稳定性的时间也不同。由于压电陶瓷固有的磁滞和蠕变特性,可调F-P滤波器的膨胀和电压之间存在非线性关系,即透射峰的位置和F-P滤波器的电压是非线性的。为了解决FFP-TF的非线性问题,提出了以下FBG波长解调和波长优化算法。实际上,非线性激光波长调谐将导致测量误差和分辨率降低。
-
FFPE的方案似乎相对简单,但是解调需要高精度和稳定性。理想的波长梳是由间隔隔开的一组离散的等距波长分量。但是,由于TSL的非线性,由采集卡收集的梳状滤波器峰值是不均匀的。对于光纤传感器的绝对测量,必须固定每个元件的位置,这可以通过先前的校准来完成。选择了日本横河电机的AQ6151光波长仪来校准FFPE的每个梳状滤波器峰值,波长计的精度高达±0.3 pm。通过AQ6151在15 min内测量44个梳状滤波器峰值的每个波长,并将相应的平均值设置为校准的NIR波长,该波长可用作测量的真实值,从而减少FFP-TF非线性的影响。因此,为了提高测量精度,使用线性插值法对FFPE的每个峰进行了连续校准,以校准每个采样点的波长。
一旦得出了上升扫描过程中FBG的时间,就可以直接确定每个FBG信号两侧的两个最近的FFPE梳。如图4所示,两个最接近的梳齿的采样时间分别为
${t_n}$ 和${t_{n + 1}}$ 。${\lambda _n}$ 和${\lambda _{n + 1}}$ 是对应于${t_n}$ 和${t_{n + 1}}$ 的参考通道的已知波长。在梳状滤波器峰值校准之后,将FFPE的光谱分为43个部分,分离出的光谱区域可用于线性查询。线性拟合可以提高解调的准确性,而FBG中心波长${\lambda _{{\rm{FBG}}}}$ 可以描述为:$${\lambda _{{\rm{FBG}}}} = {\lambda _n} + \frac{{{t_{{{\rm{FBG}}}}} - {t_n}}}{{{t_{n + 1}} - {t_n}}}({\lambda _{n + 1}} - {\lambda _n})$$ (1) -
以上方法仅削弱了FFP-TF非线性在解调系统中的影响。下面的算法可用于进一步优化解调数据。在综合监视系统中,可以将解调系统的信号假定为相对于采样点或时间((
${T_i}$ ,${\lambda _i}$ ),$i = 1,2\cdots , n$ )的记录波长数据的序列。将数据采样的步长设置为$\Delta T$ 时,将在瞬间生成第i个数据点:$${T_i} = \Delta T \cdot \left( {i - 1} \right)$$ (2) 第m个最小二乘拟合多项式为:
$$P({\lambda _i}) = \sum\nolimits_{k = 0}^{m - 1} {{c_k}T} _i^k$$ (3) 每个数据点的偏差为:
$$\left. {\left| {{\varepsilon _i}} \right.} \right| = \left. {\left| {{\lambda _i} - P({\lambda _i})} \right.} \right|$$ (4) 为了最小化偏差平方的总和,使用多项式最小二乘曲线拟合数据:
$$ S={\sum\limits_{i=1}^{n}({\lambda }_{i}}{{-P}({\lambda }_{\rm{i}}))}^{2}=\sum\limits_{i=1}^{n}\left({\lambda }_{i}-{{\sum }_{k=0}^{m-1}{c}_{k}}{T}_{i}^{k}\right)^{2}$$ (5) 当公式(5)结果达到最小值时,多个函数值条件指示:
$$\frac{{\partial S}}{{\partial {C_k}}} = 2\sum\limits_{i = 1}^n {\left[ {{\lambda _i} - \sum\nolimits_{k = 1}^n {{C_k}T_i^k} } \right]} \cdot T_i^k$$ (6) 在公式(6)中引入内积简化后,可以得到多项式(7):
$$A = \left[ {\begin{array}{*{20}{c}} {{C_1}} \\ \ldots \\ {{C_m}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} n\;{\displaystyle\sum\limits_{i = 1}^n {{T_i}} }\; \ldots \;{\displaystyle\sum\limits_{i = 1}^n {T_i^m} } \\ {\displaystyle\sum\limits_{i = 1}^n {{T_i}} }\;{\displaystyle\sum\limits_{i = 1}^n {T_i^2} }\; \ldots \;{\displaystyle\sum\limits_{i = 1}^n {T_i^{m + 1}} } \\ {\displaystyle\sum\limits_{i = 1}^n {T_i^m} }\;{\displaystyle\sum\limits_{i = 1}^n {T_i^{m + 1}} }\; \ldots \;{\displaystyle\sum\limits_{i = 1}^n {T_i^{2m}} } \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^n {{\lambda _i}} } \\ {\displaystyle\sum\limits_{i = 1}^n {{T_i}{\lambda _i}} } \\ {\displaystyle\sum\limits_{i = 1}^n {T_i^m{\lambda _i}} } \end{array}} \right]$$ (7) 然后获得数据点
$\left( {{T_i},P({\lambda _i})} \right)\left( {i = 1,2 \cdots n} \right)$ 的值。均方根为${\varepsilon _x} = \sqrt {\dfrac{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{\lambda _i} - P({\lambda _i})} \right)}^2}} }}{{n - 1}}} $ 。根据拉吉达准则,将总错误阈值设置为$3{\varepsilon _x}$ ,相应的置信度为97%。$$\left. {\left| {{\lambda _i} - P({\lambda _i})} \right.} \right| > 3{\varepsilon _x}$$ (8) 满足公式(8)的数据是总误差,需要消除然后替换。当需要替换单个点时,
${\lambda _i}$ 是一个严重错误,替换值为:$${\lambda _i} = \frac{{{\lambda _{i - 1}} + {\lambda _{i - 2}} + {\lambda _{i + 2}} + {\lambda _{i + 1}}}}{4}$$ (9) 当需要对附近的两个点进行插值时,都是严重误差,则替换值为:
$${\lambda _i} = \frac{{{\lambda _{i - 1}} + {\lambda _{i - 2}} + {\lambda _{i + 2}}}}{3}$$ (10) 粗差处理的流程图如图5所示。将参考部分中的初始值设置为整个粗略误差数据估计的第一值,然后估计下一点的状态值。比较估计值和实际值之间的差异,如果该差异较小,则估计该估计值是合理的。否则,该点被认为是严重错误,需要更换。当参考零件向后移动一个点时,其第一个值将被删除,并由参考零件中的相邻值代替。如此循环直到数据处理完成,然后继续下一步。在上一轮中替换的数据将确定该轮数据中是否存在新的总差额。如果不是,则计算完成。否则,循环执行上述操作。
-
FFP-TF由三角波的上升沿驱动。NIR波长由采集卡的内部驱动器模块生成,这有利于增强可调F-P滤波器的扩展和电压之间的同步。该实验是通过波长范围为1525~1565 nm的激光进行的,结果如图6所示。
图6显示了测量值的线性拟合。蓝点是测量数据的平均值,采用图6左上角的误差棒形式表示。红线是测量数据平均值的线性拟合,线性可以达到0.998。图中所示的双空格空白是由于标准具本身的结构所致,该标准具用于标记中心波长。实验时选取了1525~1565 nm之间的45个不同真实中心波长的梳状滤波器峰值测量,得到的误差均在±0.5 pm之间。以表现出1531.8302 nm真实中心波长的梳状滤波器峰值为例详细展示。所选波长的误差线显示50 s的测量数据,如图6误差棒所示,平均值为1531.8324 nm,最大值为1531.8367 nm,最小值为1531.8320 nm。第3节中给出的多项式最小二乘曲线拟合算法可以进一步提高解调系统的精度。根据以上算法,得到了解调后的数据。
对以上数据的分析表明,测得的波长范围为1531.8300~1531.8305 nm。如图7所示,相对误差主要集中在0.2~0.3 pm。为了验证解调系统的准确性,选择了全部梳状峰的波长用于验证性实验。最终得到了非常有优异的结果,解调系统的精度为±0.5 pm。
-
综上,文中设计并制作了一种基于NSL区域中TSL的精确FBG波长解调系统。通过使用带有波长标记的FFPE梳状滤波器,减少了扫描非线性的问题。然后,FFPE梳将细分范围细分为进一步的非线性校准,并解决了分段线性解调的精度校准问题。自行设计的FFP-TF和FFPE的尺寸分别为59.5 mm(长)×26 mm (宽)×11.2 mm (高)和98 mm (长)×74 mm(宽)×14 mm (高)。对NIR波长采样点分布的分析表明,绝大多数波长是集中的。通过消除系统的总误差并使用中心极限定理来减少由FFP-TF的非线性引起的误差,在近红外区域提高了FBG传感和解调系统的调谐精度和稳定性。该系统的整体性能测试表明,基于可调谐扫描激光的高精度FBG传感的解调精度和稳定性为±0.5 pm。通过这种方式,可以在NIR波长扫频激光范围内以高精度高效地解调实时FBG波长。
High-precision FBG demodulation system using near-infrared wavelength scanning laser
-
摘要: 光纤布拉格光栅(FBG)由于其轻巧、规模小、不受电磁干扰和复用能力的影响等优点,广泛用于监视结构健康、机械运行、航空航天和其他领域。引入可调谐扫描激光(TSL)来研制近红外(NIR)范围内的精确光纤布拉格光栅(FBG)波长解调系统,实现高速度、宽范围、高精度的解调。采用一种光纤法布里-珀罗标准具(FFPE)用作波长标记以提取波长在细分波长扫描范围内实现分段线性解调,解决可调扫描激光器带来的非线性问题。引入了另一种光纤法布里–珀罗标准具,实现解调的高精度校准。提出一种多项式最小二乘曲线拟合算法,进一步提高解调的准确性和稳定性,利用了波长范围为1525~1565 nm的近红外波长扫频激光器,得到了非常优异的结果,解调系统的精度为±0.5 pm,实现了高精度、简易化和小型化。
-
关键词:
- FBG解调 /
- 光纤传感 /
- 近红外 /
- 可调谐扫描激光 /
- 光纤法布里-珀罗标准具
Abstract: Fiber Bragg grating (FBG) has been widely used in monitoring structural health, mechanical operation, aerospace field, and other physical parameters due to its advantages of being lightweight, tiny scale, immune to electromagnetic interference and multiplexing capability.Tunable scanning laser (TSL) was introduced to fabricate an accurate FBG wavelength demodulating system in the near infrared range (NIR) to achieve high-speed, wide-range, and high-precision demodulation. One fiber Fabry–Perot etalon (FFPE) was used as a wavelength marker to extract wavelength. The wavelength scanning range was subdivided to implement piecewise linear demodulation, which solves the nonlinear problem brought about by tunable scanning laser. Another fiber Fabry–Perot etalon was introduced to realize high-accuracy calibration of the demodulation. A polynomial least square curve fitting algorithm was proposed to further enhance demodulation accuracy and stability. This work has been utilizing a near-infrared wavelength scanning laser with a wavelength range of 1525-1565 nm. It showed a very promising result whereby the accuracy of the demodulating system exceeds ±0.5 pm, which achieves high accuracy, simplification and miniaturization. -
-
[1] Zhu M, Murayama H. Fast demodulation of OFDR based long length FBG sensing system for noisy signals [J]. Optics Express, 2018, 26: 19804-19814. doi: 10.1364/OE.26.019804 [2] Zhou Z D, Quan L, Ai Q S, et al. Intelligent monitoring and diagnosis for modern mechanical equipment based on the integration of embedded technology and FBGS technology [J]. Measurement, 2011, 44: 1499-1511. doi: 10.1016/j.measurement.2011.05.018 [3] Fan X, Jiang J, Zhang X, et al. Self-marked HCN gas based FBG demodulation in thermal cycling process for aerospace environment [J]. Optics Express, 2018, 26: 22944-22953. doi: 10.1364/OE.26.022944 [4] An Jianchang, Jiang Junfeng, Xu Zhongyuan, et al. Design of composite intrusion detection system based on optical fiber sensor and infrared video [J]. Infrared and Laser Engineering, 2020, 49(5): 20190446. (in Chinese) [5] Zhang Cui, Tao Yuan, Tong Xinglin, et al. Monitoring system of railway track based on identity weak fiber Bragg grating array [J]. Infrared and Laser Engineering, 2019, 48(6): 0622001. (in Chinese) [6] Wang J, Zhu W, Ma C, et al. FBG wavelength demodulation based on a radio frequency optical true time delay method [J]. Optics Letters, 2018, 43: 2664-2667. doi: 10.1364/OL.43.002664 [7] Loranger S, Gagné M, Lambin-Iezzi V, et al. Rayleigh scatter based order of magnitude increase in distributed temperature and strain sensing by simple UV exposure of optical fibre [J]. Scientific Reports, 2015, 5: 11177. doi: 10.1038/srep11177 [8] Díaz C A R, Marques C A F, Domingues M F F, et al. A cost-effective edge-filter based FBG interrogator using catastrophic fuse effect micro-cavity interferometers [J]. Measurement, 2018, 124: 486-493. doi: 10.1016/j.measurement.2018.03.067 [9] Ashrafi A, Adhami R. A direct digital frequency synthesizer utilizing quasi-linear interpolation method [J]. IEEE Transactions on Circuits & Systems I Regular Papers, 2010, 57: 863-872. [10] Hafizi Z M, Epaarachchi J, Lau K T. Impact location determination on thin laminated composite plates using an NIR-FBG sensor system [J]. Measurement, 2015, 61: 51-57. doi: 10.1016/j.measurement.2014.08.040 [11] Ribeiro B A, Werneck M M, Gonçalves M N, et al. A Bragg grating tunable filter based on temperature control system to demodulate a voltage sensor[C]//24th International Conference on Optical Fibre Sensors, 2015: 963444. [12] Li Kai, Xin Jingtao, Meng Fanyong, et al. Sensing demodulation system using US-FBG spectral linear region [J]. Optics and Precision Engineering, 2018, 26(1): 31-37. (in Chinese) doi: 10.3788/OPE.20182601.0031 [13] Mei Jiawei, Xiao Xiaosheng, Yang Changxi. Optimization of sweeping nonlinearity of wavelingth-swept laser and its application in FBG demodulation [J]. Optics and Precision Engineering, 2014, 22(11): 2888-2893. (in Chinese) doi: 10.3788/OPE.20142211.2888 [14] Wu Jing, Wu Hanping, Huang Junbin, et al. Research progress in signal demodulation technology of fiber Bragg grating sensors [J]. Chinese Optics, 2014, 7(4): 519-531. (in Chinese) [15] Ma Z Y, Li D W, Dong F W. Gross error elimination based on the polynomial least square method in integrated monitoring system of subway [J]. Telkomnika Indonesian Journal of Electrical Engineering, 2014, 12: 415-421. -






 下载:
下载: