-
光纤光栅传感器在航空航天、道路桥梁、石油电力、安全监测等诸多领域具有重要的应用[1]。2008年,NASA[2]利用光纤光栅传感器测量系统对Ikhana无人机机翼形状进行了测试,每个机翼布置了1440个传感器。在大规模航空航天飞行器的结构检测中,需要在飞行器表面布置大量光纤光栅传感器,因此需要大量的解调任务。采用传统的寻峰算法解调FBG中心波长时,单一通道上复用的FBG数目受到带宽的限制。单纯增加传感器数目,相邻FBG的光谱会产生混叠,无法用常规寻峰算法精确解调。因此,研究混叠光谱解调算法可很好的解决解调通道有限和解调容量大之间的矛盾,为大容量机载传感网络解调技术提供技术支持。
随着现代信息技术的发展,人们发现可以借鉴数学工具为研究光谱信号的重叠峰分离提供新的思路[3]。基于小波理论在混叠光谱解析中的应用也取得了许多进展。2019年,海军工程大学Peng Ding 等[4]提出了一种基于连续小波变换(CWT)的多峰FBG反射谱分割方法。选择合适尺度的一阶高斯或墨西哥帽小波基函数进行连续小波变换。利用处理后的信号中的极值点对原始信号进行分割。模拟了无重叠峰和有噪声、部分重叠峰和有噪声两种情况下的多峰FBG谱。
人工神经网络对非线性信号有良好的逼近能力。2014年,Jing Chen等[5]出了一种基于最小二乘支持向量回归的光栅传感网络(LS-SVR)解调算法,中心波长解调均方根误差(RMS)为3.955 pm,计算解调时间为0.0736 s。
近年来,深度学习模型的应用领域越来越广泛。将深度学习模型部署在混叠光纤光栅光谱解调算法中会有更高的准确率,并取得更好的效果。2019年,Jiang H 等[6]提出了一种基于长短期记忆(LSTM)网络的光纤布拉格光栅(FBG)传感器网络波长检测方法。中心波长解调均方根误差(RMS)为0.674 pm,计算解调时间为0.0736 s。2020年,江灏等[7]针对光纤布拉格光栅(FBG)传感网络中重叠光谱的中心波长解调问题,提出一种基于门控循环单元(GRU)网络的波长检测方法,RMS为0.8325 pm。Yibeltal Chanie Manie等[8]提出了基于强度波分复用(IWDM)的自修复光纤光栅传感器网络的深度学习算法,也提出了一种门控循环单元(GRU)深度学习算法,提升了一些解调精度。RMS为0.067 pm,解调计算时间0.342 s。使用深度学习技术解调混叠光谱的中心波长的技术已经取得一些进展,面对实际工程需要,特别在算力有限的情况下,解调精度和速度很难满足应用需求。开展兼顾精度和速度的混叠光谱解调技术具有重要的研究价值。
混叠光谱的解调是一种非线性回归问题,CNN是近年来深度学习应用于计算机视觉领域的重要部分。2020年,Hao Yan等[9]提出一种基于拉曼光谱和深度学习技术的CNN框架,用于识别人舌鳞状细胞癌组织。此方法有着较高的精度,CNN模型在拉曼光谱分类识别的领域有较大潜力。CNN可以学习和识别在不同混叠情况下的光谱特征。在文中提出的CNN模型中,对输入的长序列光谱数据的特征提取可由卷积层自动完成,将光谱数据转换成一维(1D)数据,提升了检测效率,获得了更高的解调精度。
文中提出一种利用深度学习技术一维卷积神经网络(CNN)来解调光纤光栅混叠光谱的布拉格波长的方法,搭建了一种用于构造光纤光栅混叠光谱数据自动采集系统,包括混叠驱动装置和光谱数据自动采集系统。之后分别与其他解调算法进行了解调精度和测试时间对比,提供了一种在并联光栅结构中解调混叠光谱的办法,实验结果表明,解调模型均方根误差结果为0.08258 pm,解调计算时间为0.338 s。提出的一维卷积神经网络模型文件可保存为pb (protocol, buffer)格式文件,是一种表示神经网络模型结构的二进制文件,大小总计在400 kB以下,所需设备算力较小,模型文件可部署在小型嵌入式设备中,而同样的长短期记忆模型(LSTM),门控循环单元(GRU)等网络模型的大小为4.78 MB,2.1 MB,对设备的算力需求比CNN模型更多。研究结果表明,采用卷积神经网络模型对于混叠光谱中心波长解调结果的准确性具有合理性,同时对不同混叠程度下多组光谱数据同时使用解调模型算法进行中心波长值的对比并进行误差分析。提升了解调精度,为大规模结构健康检测提供了一种新的方案。
-
构建混叠光谱解调算法之前,需要有训练数据,因此设计光谱数据采集系统来采集光谱数据,形成深度学习模型所需训练集测试集。混叠驱动装置,用于构建出两个或多个光纤光栅光谱在波长漂移时从分离到混叠的全过程。利用准分子激光光纤光栅刻写系统,设计了两组光纤光栅,用于构建混叠光谱。混叠光谱的数据由三角悬臂梁实验结构的应变产生。将光纤光栅分别贴在三角悬臂梁之上。之后设计一组三角悬臂梁支持结构,通过改变三角悬臂梁的应变,来进行光谱的波长漂移。其中一组使用步进电机进行弯曲,可实现定量波长漂移。电机控制系统使用大恒光电的GCD-0401 M系列电控台控制器控制步进电机。另外一组使用固定平台,应变梁的尾部固定端变为可移动的滑块,可改变应变梁的长度,增大光纤光栅波长漂移量的范围。在三角应变梁的支撑装置在上下同时安装微分头施加应变力,可以再增加应变范围,增大光纤光栅波长漂移量的范围,使得光谱数据量更加丰富,并提升训练精度。
光纤光栅传感网络中各组光栅光路连接方式有两种,串联结构和并联结构。串联结构为几组光纤光栅在同一光纤上,但采集光谱数据时,光开关要置于两光栅之间,不易采集混叠光谱的原光谱数据。并联结构,则是通过耦合器将两列光栅进行混合,通过多路光开关切换混叠及未混叠的光谱,在光路上较为容易。图1为并联结构混叠光谱数据采集系统示意图,光源通过耦合器分别进入光谱仪和八通道光开关。以获得光纤光栅的反射谱,未混叠的光谱由1、2通道控制。混叠光谱由FBG1、FBG2的另一端连接耦合器,至光开关的通道3。三个通道的光谱形状及数据可由光谱仪连接至上位机,通过虚拟仪器软件显示。数据可随着悬臂梁的应变自动采集。混叠光谱数据采集系统实验装置图总体包括有贴有光纤光栅的三角悬臂梁,八通道采集光开关,光谱仪等。实验使用AQ6370 D光谱仪采集光谱并连接PC端,将数据保存。
光谱仪通过网络TCP/IP协议连接至上位机,同时上位机通过电平指令控制光开关的通道数。上位机程序将读取到的光谱数据分通道扫描并进行显示,之后将数据进行保存,包含波长和强度信息。图2为混叠光谱数据采集上位机程序框图。程序开始运行之后,首先确定光通道的开启情况,并获得光开关的指令,与此同时进行光谱仪的初始化。

图 2 混叠光谱数据采集上位机程序框图
Figure 2. Program block diagram of the upper computer of the aliasing spectrum data acquisition
随后进入参数设置,包括波长范围设置,反射率,分辨率,采样点,采样间隔设置,可输出包含横纵坐标的光谱数据。设置好路径之后,写入文件,即可保存文件。之后就可进入到电机控制环节,首先设置上升距离,系数,脉冲数,步进方向指令等参数,发送指令就可以完成电机上升。上位机显示界面可分别显示,当前正在扫描保存的光谱,两个原始光谱及混叠光谱的形状。波长范围可调整,以适应中心波长不同的光纤光栅光谱数据采集。数据保存完成后,进入电机控制部分,使用步进电机及控制系统以0.005 mm的步长上升,控制端前面板可实时显示移动距离,运行状态,停止运行的距离高度。图3(a)~图3(e)为上位机显示界面中光谱由完全分离到逐渐重叠,再到完全重叠,之后恢复完全分离情况的示意图。数据采集系统的带宽范围是1532~1540 nm,对2 001个点进行采样。

图 3 上位机显示界面中光谱的重叠过程
Figure 3. Overlap process of the spectrum in the display interface of the host computer
在采集过程中,为获得更多数据,在一次步进电机行程结束之后,改变步进距离,多次进行采集。当电机上升并到达预定距离之后,采集完成,采集系统会自动停止运行,光谱数据包含通道信息,横坐标为波长值,纵坐标为光谱强度,以文本型文件保存,便于之后进行模型的调用及数据预处理工作。
-
混叠光谱的解调是一种非线性回归问题,文中提出的CNN模型能够处理混叠光谱非线性序列模型问题。CNN是近年来深度学习应用于计算机视觉领域的重要部分,也逐渐在自然语言处理、信号分析等领域中使用。文中提出了一种CNN深度学习算法,用于解决大型光纤光栅传感器并联传感网络中混叠光谱不可准确识别出中心波长的问题,CNN可以通过反射光谱序列的特征,学习和识别在不同混叠情况下的光谱特征。在文中提出的CNN模型中,对输入的长序列光谱数据的特征提取可由卷积层自动完成,因此,将光谱数据转换成一维(1D)数据,提升了检测效率,获得了更高的解调精度。在CNN模型训练完成后,可以从FBG重叠谱中解调出每个FBG的中心波长。在混叠光谱解调算法构建之前,首先要进行数据的预处理,归一化可以有效降低损失函数,由于特征向量中不同特征的取值相差较大,会导致目标函数变形。这样在进行梯度下降的时候,梯度的方向就会偏离最小值的方向,会导致训练时间过长。归一化后加快了梯度下降求最优解的速度。
首先,需要训练一个可复用的光纤光栅对波长检测模型。对于网络训练,测试样本是从OSA (optical spectrum analyzer)中收集到的光谱数据,一组数据采集2001个像素点,共采集11000组数据。训练前,频谱归一化为0~1,光谱序列数据设为以模型输入,通过CNN学习的特征学习输出向量FBG1和FBG2光谱的中心波长。CNN网络在TensorFlow深度学习框架中实现。迭代数epoch被设定为1000,学习率为0.1。
在深度学习框架中搭建好模型结构之后,将归一化完成之后的光谱数据进行训练,训练的CPU为Intel Core i7-8550 U CPU,训练完成之后的CNN模型可进行波长检测训练。经过良好训练的CNN模型可以直接应用于在线检测。经过训练的模型, 不需要高水平配置的计算机,便可以达到的毫秒级响应,同时也可以方便地移植到嵌入式系统。
程序部分包括数据加载部分,模型训练部分,混叠光谱模型解调结果输出部分。数据加载部分首先将数据顺序打乱,并划分训练集和测试集。
之后进行神经网络的搭建,首先设置三层卷积层三层池化层,激活函数为ReLu函数。由于输出结果为两个数值,因此在这里设置两个分支,再分别进行一层卷积层和池化层,之后设置一个输出层,为全连接层,激活函数为sigmoid函数。之后设置损失函数,以均方根误差和平均值误差代表。训练时使用Adam随机优化算法,该算法提升了计算效率,减小了噪声和稀疏性。最后将模型保存。图4为该卷积神经网络模型的结构示意图。该设计提出的一维卷积神经网络模型文件可保存为pb(protocol, buffer)格式文件,是一种表示神经网络模型结构的二进制文件,大小总计在400 kB以下,所需设备算力较小。在大规模结构健康检测的应用中,测量精度高、测点范围分布广、数量大。需实现大容量光纤光栅混叠光谱实时解调。因此,模型大小应进行控制,而同样的长短期记忆模型(LSTM),门控循环单元(GRU)等网络模型的大小为4.78 MB,2.1 MB,模型所占内存更大,对设备的算力需求比CNN模型更多。因此,基于一维卷积神经网路的混叠光谱解调模型具有优势。
-
在模型找到最优解之前,CNN算法进行了若干次训练,在模型训练部分主函数程序,经过1000次模型迭代训练,损失函数结果接近最优值。使用均方根误差(RMS)和平均值误差(MAE)来评估光纤光栅传感器混叠光谱测量信号的误差指标。RMS可计算为:
$$ {\rm{RMS}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - \overline y } \right)}^2}} } $$ (1) 式中:n表示样本数量;
$ {y}_{i} $ 为当前误差值;$ {\overline y} $ 为误差平均值。为了验证CNN模型的有效性,进一步评价模型的性能,将该方法与极限学习机(ELM)、最小二乘支持向量回归(LS-SVR)和粒子群优化(PSO)、LSTM,GRU等算法[5-6,8,10-11]进行了比较,通过RMS、MAE来评估模型的预测性能。MAE可计算为:$$ {\rm{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_i} - \overline y } \right|} $$ (2) 式中:n表示样本数量;
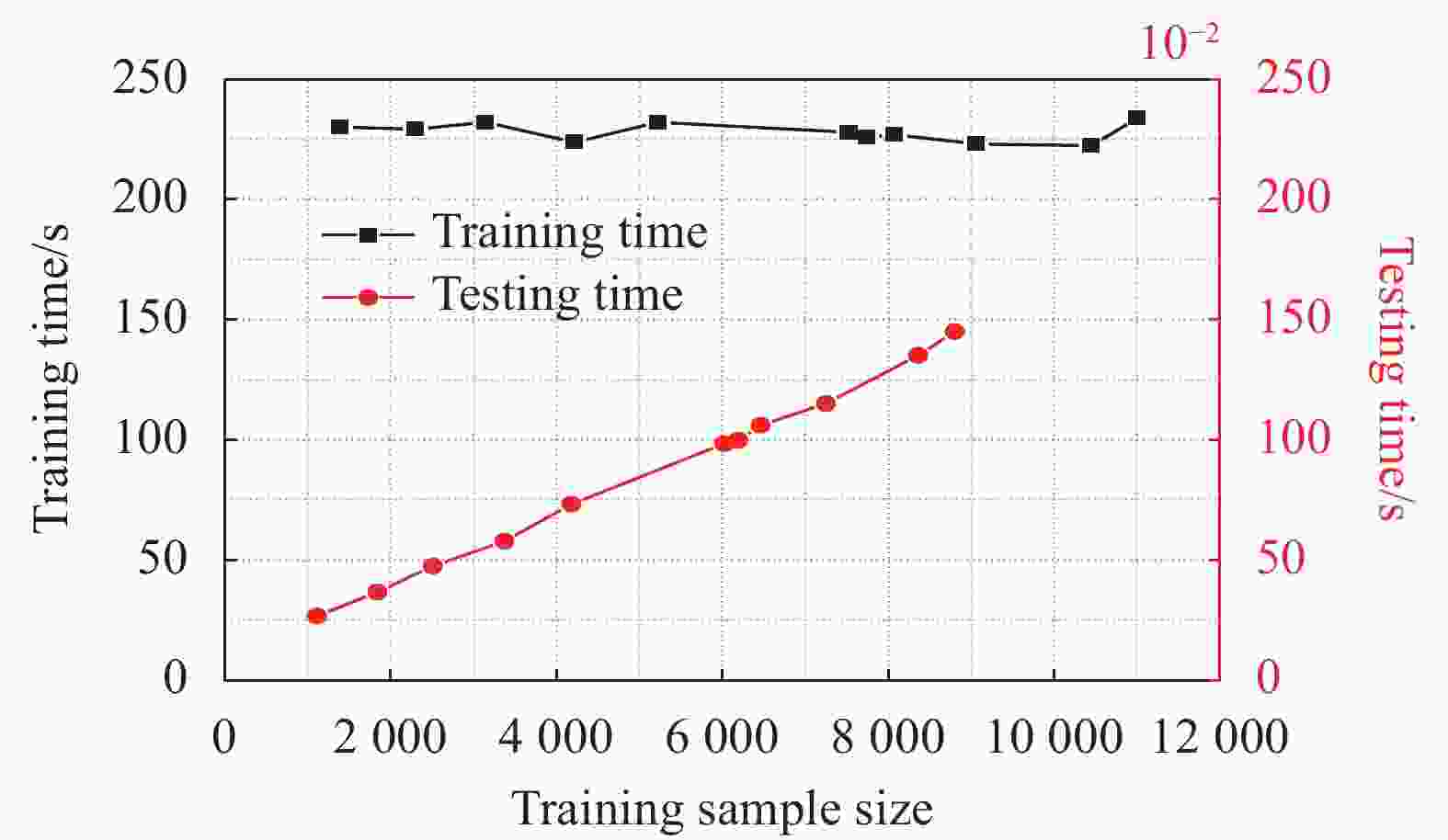
$ {y}_{i} $ 为当前误差值;$ {\overline y} $ 为误差平均值。传感器网络参数与实验环境参数保持一致。与以往的机器学习算法相比,卷积神经网络具有更高的准确度,优于ELM和LS-SVR。LSTM (长短期记忆网络),GRU (门控循环单元)等算法更适合波长序列特征,能够学习FBG光谱间的高阶表示和长期相关性。CNN深度网络结构的使用增强了学习能力,擅长对光谱形状的特征学习,是一种良好的寻峰算法,可以获得较高的寻峰检测精度。将CNN的性能与其他算法进行比较,以评价其性能,如表1所示,表中也给出了各种算法模型的解调计算时间,文中提出算法的解调计算时间明显低于其他算法。为更好的评价模型的性能,将模型的一些具体参数(数据样本量、迭代次数)进行调整,观测其损失函数的变化。从图5可以看出,批次大小在100、1000次迭代次数下,随着训练样本和测试样本的增加,训练的时间普遍在200 s以上,测试时间逐步增加。图6为模型训练的损失函数下降情况,训练集和测试集的损失函数为RMS (均方根误差),结果基本保持一致,在迭代次数达到400以上趋于平稳。表 1 不同算法之间的比较
Table 1. Comparison between different algorithms
-
模型在训练完成之后进行保存,可进行混叠光谱的快速解调。混叠光谱解调算法模型在训练集的均方根误差为0.0867 pm,在测试集上的均方根误差为0.0826 pm,结果优于同级别设备或解调算法。图7(a)~(d)为光谱不同混叠程度解调模型解调结果,可以看出在往左右各方向混叠时的情况。图7(a)和图7(c)为两光谱部分重叠的情况, 图7(a)中显示的两个FBG的中心波长差值为0.697 nm,根据光谱形状,仍然可分辨出两个峰值,此时的模型解调精度均方根误差以达到0.05 pm以下。图7(c)中的FBG1和FBG2的中心波长的中心波长差值为−0.391 nm,和图7(a)的情况相比,两FBG之间的距离更近,由此可以看出两个FBG左右交换位置后,模型解调出的中心波长值和FBG仍然有良好的匹配性。图7(b)中,FBG1和FBG2的中心波长差值为1.004 nm,可以明显地区分出两个峰值,图7(d)为两个光纤光栅光谱完全重叠的情况,可以看出该解调算法有着良好的解调结果。对于这四种情况的RMS为0.0322、0.0319、0.0148、0.0301 pm。在8000个样本数据中,RMS达到0.050 pm,有92.1%样本的均方根误差在0.1 pm以下。样本数据包含了不同混叠程度的光谱数据,以及未混叠下的光谱数据,解调结果并无明显差别,如表2所示。因此,进一步地验证了该混叠光谱解调模型的准确度和适应性。
表 2 不同混叠程度的解调结果
Table 2. Demodulation results with different degrees of aliasing
Case FBG1/nm FBG2/nm Δλ/nm RMS/pm a 1536.8488 1536.1514 0.6974 0.0322 b 1537.1559 1536.1521 1.0038 0.0319 c 1535.7527 1536.1434 −0.3907 0.0148 d 1536.1317 1536.1549 −0.0232 0.0301 -
文中设计了新的混叠光谱解调方法,在数据采集方面,设计了一种混叠光谱数据采集装置,包括应变传递梁实验装置、增加了应变的范围,在此基础上通过光开关的切换,可同时构造出混叠光谱,以及其对应的单个光谱。各光谱数据可通过上位机自动采集,形成深度学习神经网络模型的训练集和测试集。之后搭建一个适合的深度学校网络模型,通过实验调整其超参数,以得到合适的解调结果。实验结果表明,该模型的均方根解调误差高达0.082 6 pm、解调时间为0.338 s、并且具有高精度、高重复性的特点。模型文件可部署在小型嵌入式设备中,在大规模机载传感网络,结构健康监测中有良好的应用价值。
Demodulation method of overlapping spectrum based on convolutional neural network
-
摘要: 研究了一种基于深度学习的光纤光栅混叠FBG光谱解调方法。利用卷积神经网络(Convolutional Neural Networks, CNN)模型处理混叠光谱非线性序列模型问题,通过一维卷积神经网络预测识别混叠光谱中心波长,并搭建了并联结构的混叠光谱数据自动采集实验系统,验证了混叠光谱的中心波长高精度解调。实验分析了训练样本、迭代次数对训练时间、测试时间、解调精度的影响,并对训练完成后的模型进行了解调时间测试。分别与其他解调算法进行了解调精度和测试时间对比,同时对同一组光谱数据使用解调模型算法及最高点寻峰算法进行中心波长值的对比并进行误差分析。实验结果表明:解调模型均方根误差结果为0.082 58 pm,使用Intel(R) Core(TM) i7-8550U CPU (Central Processing Unit)的解调计算时间为0.338 s。研究结果表明:采用卷积神经网络模型对于混叠光谱中心波长解调结果的准确性具有合理性,与其他算法相比,文中的解调算法在解调精度和时间上具有优势,模型大小在400 kB以下,所需算力较小,可部署在小型嵌入式设备中,在大规模机载传感网络,结构健康监测中有良好的应用前景。Abstract: An FBG spectral demodulation method based on deep learning was studied. The Convolutional Neural Networks(CNN) model was used to deal with the nonlinear sequence model of the overlapping spectrum, and the central wavelength of the overlapping spectrum was predicted and identified through a one-dimensional convolutional neural network. And a parallel structure of the overlapping spectrum data automatic acquisition experimental system was built to verify the high-precision demodulation of the center wavelength of the overlapping spectrum. The experiment analyzes the effects of training samples and epoch times on training time, testing time, and demodulation accuracy, and tests the computational demodulation time of the model after training. The demodulation accuracy and test time were compared with other demodulation algorithms. At the same time, the demodulation model algorithm and the peak finding algorithm at the highest point were used to compare the center wavelength value and analyze the error for the same set of spectral data. The experimental results show that the root means square error of the demodulation model is 0.082 58 pm, and the demodulation calculation time is 30.886 ms, which is used Intel(R) Core (TM) i7-8550U CPU. The research results show that the convolutional neural network model is reasonable for the accuracy of the central wavelength demodulation results of the overlapping spectrum. Compared with other algorithms, the demodulation algorithm in this article has advantages in demodulation accuracy and time. The model size is less than 400 kB, and the required computing power is small. It can be deployed in small embedded devices. It has good application prospects in large-scale airborne sensor networks and structural health monitoring.
-
表 1 不同算法之间的比较
Table 1. Comparison between different algorithms
表 2 不同混叠程度的解调结果
Table 2. Demodulation results with different degrees of aliasing
Case FBG1/nm FBG2/nm Δλ/nm RMS/pm a 1536.8488 1536.1514 0.6974 0.0322 b 1537.1559 1536.1521 1.0038 0.0319 c 1535.7527 1536.1434 −0.3907 0.0148 d 1536.1317 1536.1549 −0.0232 0.0301 -
[1] Xu G Q, Xiong D Y. Applications of fiber Bragg grating sensing technology in engineering [J]. Chinese Optics, 2013, 6(3): 306-317. (in Chinese) [2] Wang W J, Xue J F, Zhang M J. Application progress and prospect of optical fiber sensor in aircraft structural health monitoring [J]. Aeronautical Science & Technology, 2020, 31(7): 95-101. [3] Tao W L, Liu Y, Wang X P, et al. Implementation of overlapping peak separation algorithm for absorption spectra by fractal dimension analysis intime-frequency domain [J]. Spectroscopy and Spectral Analysis, 2017, 37(12): 3664-3669. (in Chinese) [4] Ding P, Huang J, Tang J. Multi-peak FBG reflection spectrum segmentation based on continuous wavelet transformation [J]. Optical Fiber Technology, 2019, 50: 250-255. doi: 10.1016/j.yofte.2019.04.003 [5] Chen J, Jiang H, Liu T, et al. Wavelength detection in FBG sensor networks using least squares support vector regression [J]. Journal of Optics, 2014, 16(4): 045402. doi: 10.1088/2040-8978/16/4/045402 [6] Jiang H, Zeng Q, Chen J, et al. Wavelength detection of model-sharing fiber Bragg grating sensor networks using long short-term memory neural network [J]. Optics Express, 2019, 27(15): 20583. doi: 10.1364/OE.27.020583 [7] Jiang H, Wang Y G, Chen J, et al. Wavelength detection of overlapping spectra in FBG sensor network based on gated recurrent unit network [J]. Acta Optica Sinica, 2020, 40(7): 0706001. (in Chinese) [8] Manie Y C, Peng P C, Shiu R K, et al. Enhancement of the multiplexing capacity and measurement accuracy of FBG sensor system using IWDM technique and deep learning algorithm [J]. Journal of Lightwave Technology, 2020, 38(6): 1589-1603. doi: 10.1109/JLT.2020.2971240 [9] Yan H, Yu M, Xia J, et al. Diverse region-based cnn for tongue squamous cell carcinoma classification with Raman spectroscopy [J]. IEEE Access, 2020, 8: 127313. doi: 10.1109/ACCESS.2020.3006567 [10] Qi Y, Li C, Jiang P, et al. Research on demodulation of FBGs sensor network based on PSO-SA algorithm [J]. Optik, 2018, 164: 647-653. doi: 10.1016/j.ijleo.2018.03.088 [11] Jiang H, Chen J, Liu T. Wavelength detection in spectrally overlapped FBG sensor network using extreme learning machine [J]. IEEE Photonics Technology Letters, 2014, 26(20): 2031-2034. doi: 10.1109/LPT.2014.2345062 -







 下载:
下载: