-
天基红外成像技术一直是世界各航天大国发展的重要方向,因其具有全天时昼夜成像、判断目标工作状态、伪装目标和隐蔽目标的发现能力,在国民经济和军事领域发挥着重要作用。然而,适用于空间应用的大阵列长波红外焦平面(Infrared focal plane arrays, IRFPA)器件一直是世界难题,从而限制了天基长波红外遥感能力的建设。随着碲镉汞单层外延材料等关键技术的突破,天基红外遥感技术得到快速发展。然而,受材料、制造工艺水平等因素的影响,IRFPA各探测单元响应特性普遍存在着非一致性,即响应非均匀性(Non-uniformity),影响成像信噪比和温度分辨率等关键技术指标[1]。因此,通过非均匀性校正(Non-unifor-mity correction, NUC)技术有效地减小或去除非均匀性成为提高天基红外成像质量的关键。
非均匀性校正方法可分为两类,基于场景技术和基于标定技术的算法。其中,基于场景技术的算法利用场景统计特性[2],获得每个探测单元的校正系数,其不需要专用的定标机构,成像的同时即可获取校正系数。近年来,基于帧间配准技术的场景类非均匀性校正算法已经突破了算法快速收敛等关键难题[3],具有较好的应用效果,然而基于场景类的校正算法由于无法定量获取黑体辐射通量,因此仅能实现相对辐射校正,无法实现绝对辐射校正,难以满足天基红外定量化遥感应用的需求。因此,卫星在轨通常采用基于定标技术的非均匀性校正方法[4],该方法通过周期性的停机,对不同温度点的均匀黑体进行一次或多次成像,实现对IRFPA的标定,并利用线性或分段线性响应模型计算出每个像元的增益和偏移系数,实现非均匀性校正。
然而,通常星载长波成像系统在轨工作动态范围大,达到100 K以上。研究表明,红外探测器在大动态范围条件下具有强烈的非线性[5-6],若要提升校正质量,则要求必须设置密集的黑体定标温度点,多次的黑体结构切换、黑体控温及成像造成一次定标耗时长达数小时,严重影响天基遥感成像获取的时效性。另一方面,基于IRFPA探测单元线性响应模型进行非均匀性校正必然引起由于模型失配造成的非均匀性校正残差。
因此,笔者认为提升星载长波红外探测器非均匀性校正精度的关键在于:在不改变现有星载黑体定标机构和定标模式的条件下,以尽量少的黑体定标温度点,减弱或消除长波红外探测器在大动态范围条件下表现出的强非线性对非均匀性校正精度的影响。鉴于此,文中提出一种基于改进伽马曲线的星载长波红外成像通道非均匀性校正算法,该算法采用非线性的伽马曲线模拟探测器响应特性,采用非线性压缩映射和逆映射方法提升线性化校正算法对探测器非线性响应模式的适配性,以获取更稳定更准确的校正效果。理论分析和数据处理结果表明,该算法动态范围大,校正精度高,满足卫星在轨使用要求。
-
理论研究表明,红外探测器的电信号响应输出和入射红外辐射功率是连续单调递增函数关系,可表示为:
$$ {{V(T) = R}}\int_{{\lambda _1}}^{{\lambda _2}} {L{\rm{(}}\lambda {{,T)}}\eta {\rm{(}}\lambda {\rm{)d}}\lambda } {\rm{ + }}D $$ (1) 式中:
${{R = }}{\tau _{eff}}{t_{{\rm{int}}}}\left[ {\pi {{\cos }^4}\theta /4{F^2}{\rm{ + }}1} \right]A$ ,$ {\tau _{eff}} $ 为光学系统透过率,${{{t}}_{\rm{int} }}$ 为积分时间,θ为像元相对出射光轴的偏轴角,F为成像光学系统的F数,A为像元有效面积;$ {\lambda _{\rm{1}}} $ 、$ {\lambda _{\rm{2}}} $ 分别为光学系统截止波长的上下限;η为像元量子效率;D为像元暗电荷,$L{\rm{(}}\lambda {{,T)}}$ 为物空间单元在温度T下的光谱光子辐射功率,根据普朗克定律,其有如下函数关系:$${{L(}}\lambda {{,T) = }}2h{c^2}{\lambda ^{{\rm{ - }}5}}/\left[ {\exp {\rm{(}}hc/k\lambda T{\rm{) - 1}}} \right]$$ (2) 式中:h为普朗克常量;c为光速。
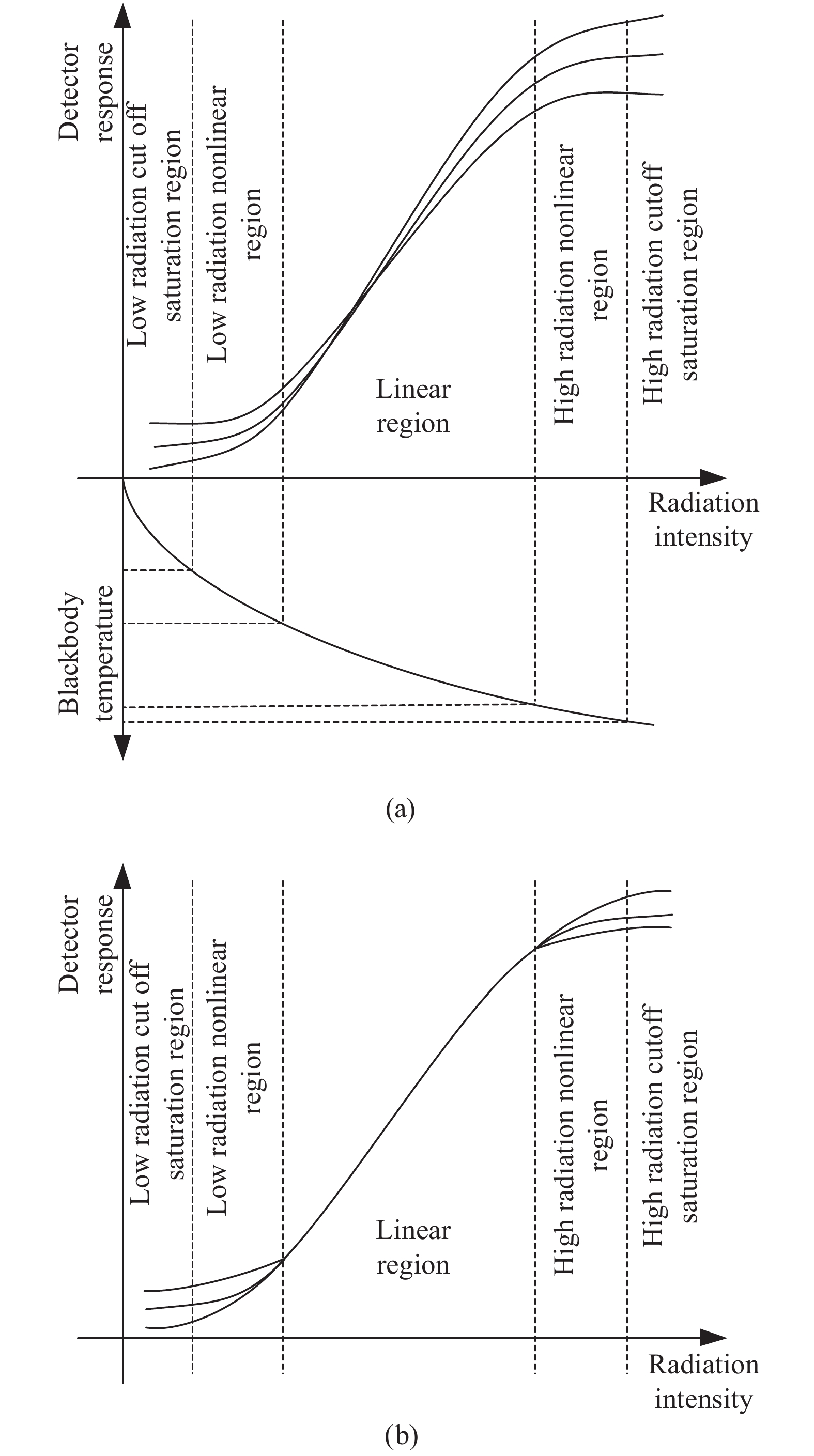
由公式(1)、(2)可见,黑体温度、红外辐射强度和探测器响应的关系可用图1(a)所示曲线表示,红外探测器响应与光谱光子辐射是非线性对应关系,仅在较窄的特定动态范围内可近似为准线性关系[7]。而在动态范围较大时,IRFPA探测元的输出响应信号与入射辐照度之间的非线性特性表现突出,表现为强非线性关系[8]。进一步研究表明,实际探测元对红外辐射信号响应都有一个由截止到饱和的过程,响应曲线一般经历由截止到缓慢上升,准线性增长直到饱和,即响应曲线服从“S”型非线性分布[9-10]。归纳而言,可将探测单元的曲线分为低辐射截止饱和区、低辐射非线性区、线性工作区、高辐射非线性区和高辐射截止饱和区五个区域[11]。
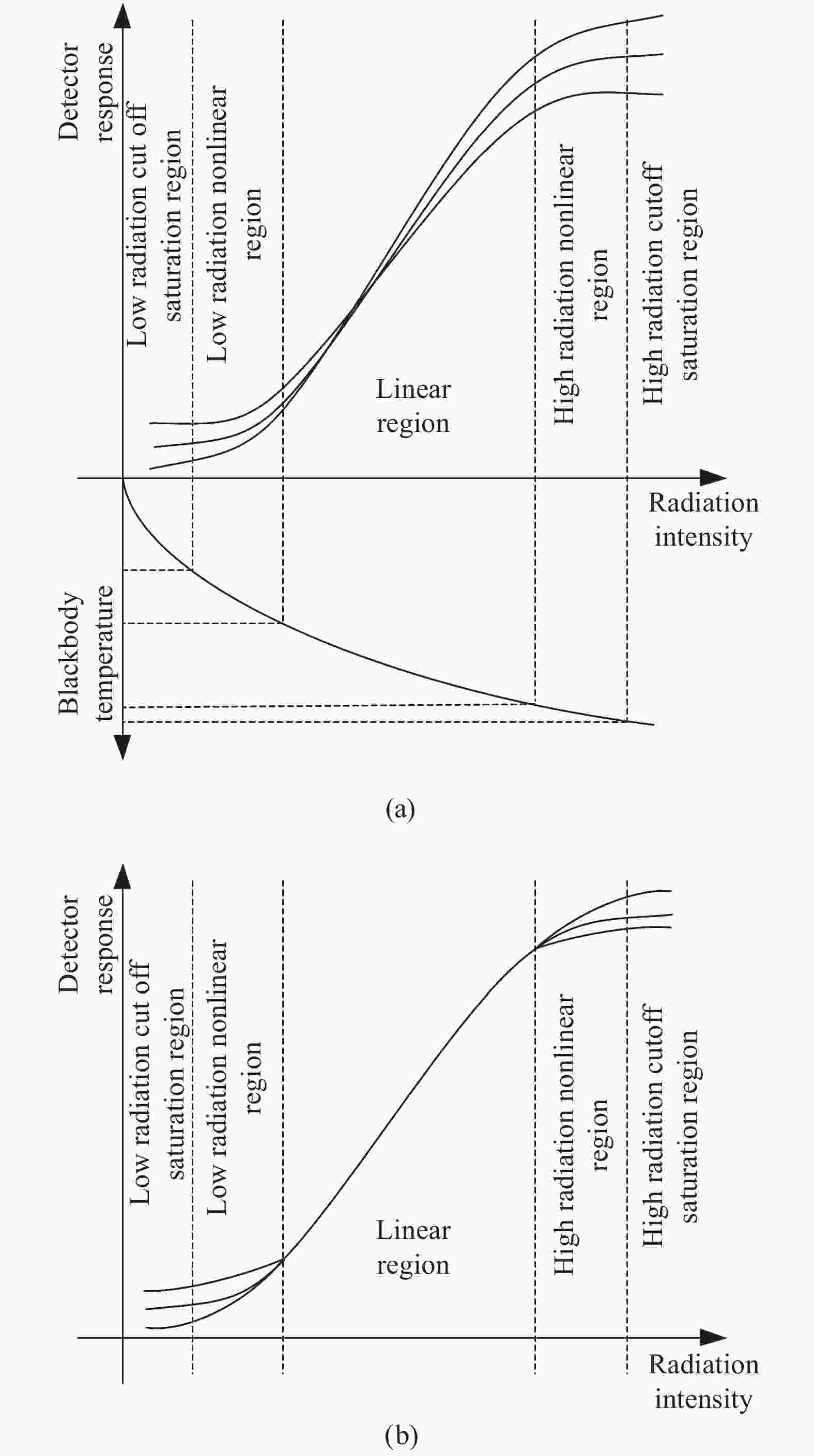
图 1 (a) IRFPA探测器原始响应特性曲线示意图;(b) 传统线性校正算法校正后响应特性曲线示意图
Figure 1. (a) Schematic diagram of the original response characteristic curves of the IRFPA detector; (b) Schematic diagram of response characteristic curves after correcting by traditional linear correction algorithm
从图1(b)可以看出,由于传统的星载非均匀性校正算法是建立在IRFPA探测元的响应是线性定常的假设之上的,经过非均匀性校正后,线性区域内的像元通过斜率和偏置的校正可达到一致,校正后的图像可以很好地保证线性区内的成像质量,然而在非线性区内,像元间的非均匀性难以消除,从而产生校正误差。
-
典型的“S”型曲线是伽马曲线[12],也称为通用Logistic曲线,最早由比利时科学家P.E.Vehulst导出其数学模型,它是一个广泛使用而且灵活的函数,该函数及其改进形式已被应用于政治学、种群动态、林木生长等多领域的模型建立[13]。可通过函数参数配置拟合典型的“S”型曲线,曲线的拐点及拐点处的增长速率均可控制,其函数形式如下式所示:
$$ {y_{\rm{i}}}{\rm{ = }}{{{A}}_i}{\rm{ + }}\frac{{{B_i}}}{{1{\rm{ + }}\exp {\rm{(}}{{{C}}_i}{{ - }}{{{D}}_i} \cdot {{{x}}_i}{\rm{)}}}} $$ (3) 式中:yi和xi为函数的变量和自变量;Ai为低端渐近线数值;Bi为高端渐近线数值;Ci为
控制最大增长位置(拐点);Di为控制拐点速度。然而,将Gamma曲线直接用于红外探测器响应曲线拟合存在一定局限性,由于Gamma函数关于拐点对称,会导致不能够结合实际的探测器响应特性对强非线性区域进行增强描述。笔者课题组对大量实验室和在轨数据的统计特性进行分析,结果表明在高辐射非线性区,红外探测器响应的非线性程度明显强于低辐射非线性区。可见,传统的Gamma模型的拐点对称特性无法准确模拟实际红外探测器响应在高辐射区和低辐射区非线性程度的不同。因此,需要找到一种改进的“S”型曲线模拟红外探测器的响应模型。归纳而言,该模型应满足如下条件: (1)函数不能是拐点对称的,从而可以分别描述低端温度和高端温度区域的非线性,且非线性程控可通过参数控制。
(2)通过调整模型参数可控制函数的斜率、截距、非线性区域范围、值域和定义域,从而定量化描述红外探测器输出增益、偏置、非线性工作区间、输出图像灰度值、输入动态范围。
(3)模型的函数结构形式简单,易于通过非线性压缩方法实现线性域和非线性域之间的映射和逆映射。
经过综合分析比较,在经典Gamma曲线4参数模型的基础上,增加参数t表征瞬时增长率(密度制约参数),公式(3)函数模型演化成如下非线性响应曲线:
$$ {{{y}}_{{i}}} = {{{A}}_i} + \frac{{{{{B}}_i}}}{{{{{{[1}} + {{t}} \times \exp {{(}}{{{C}}_i}{\rm{ - }}{{{D}}_i} \times {{{x}}_i}{\rm{)]}}}^{{{1/t}}}}}} $$ (4) 式中:yi和xi分别表示探测像元i的辐照输入和响应输出;新增的参数t的取值范围为[0, ∞],用于控制曲线在截止区和饱和区的非线性程度,使其具有表征像元非线性响应特性更好的适应性,同时可控制最大增长出现在低端还是高端;系数Ai的物理意义是探测器响应的最低值,表征探测器响应偏置,系数(Ai,Bi)共同决定探测器单元响应的动态范围;系数Ci控制探测器响应的非线性区起点位置;Di决定曲线的增长速度,物理意义是探测器的广义增益。
-
传统的星载红外非均匀性校正算法建立在探测器的线性或分段线性响应模型基础之上,其基本原理是通过定期辐射定标获取密集温度点的定标图像数据,利用线性校正算法抑制像元间的响应不一致性。文中拟采用改进伽马曲线模型更真实地模拟探测器的实际响应特性,因此,若要借助星载线性化校正算法实现校正参数的估计和更新,则必须首先完成对非线性响应模型的线性化。图2所示的流程图给出了文中算法实现过程中的信息流示意,其中,如图2(a)和(b)所示,算法首先运用非线性映射(取对数运算)方法处理红外探测器的输出图像,将图像响应特性线性化;而后,如图2(c)所示,对线性化后的图像实施基于线性校正算法的非均匀性校正,获取均匀的响应图像;最后,如图2(d)所示,通过对线性化图像的校正图像进行逆-非线性映射(取指数运算)还原出红外探测器输出图像。

图 2 (a) 算法步骤1:获取探测元原始输出;(b) 算法步骤2:非线性映射;(c) 算法步骤3:线性非均匀性校正;(d) 算法步骤4:逆-非线性映射
Figure 2. (a) Algorithm flow step 1: get raw output of detector unit; (b) Algorithm step 2: non-linear mapping; (c) Algorithm step 3: linear non-uniformity correction; (d) Algorithm step 4: inverse non-linear mapping
由于IRFPA探测元响应具有时间漂移特性,因此需要通过周期性的黑体定标更新校正参数矩阵,用于消除模型参数时移引起的非均匀性校正残差。然而,黑体定标会导致星载红外成像停机,从而影响卫星在轨红外成像的重访能力和应急成像能力,因此,笔者希望尽可能降低每次黑体定标的时长。文中算法的创新性还在于可大幅降低黑体定标时采样温度点的数量,从而达到降低黑体定标时长的目的。
传统黑体定标方法无差别的设置密集定标温度点获取探测元的响应曲线特征,然而在线性区设置多个定标温度点对校正精度并无有效提升。文中算法采用提取IRFPA探测元响应曲线特征点的方式确定黑体定标温度点,特征点定义为曲线变化率最大的位置,即曲线的两个拐点,其物理意义分别是低辐射非线性区至线性区、线性区至高辐射非线性区的工作温度转换点。通过该方法,配合所建立的改进伽马曲线模型,采用更少的定标温度点即可实现对探测器响应曲线的准确拟合,同时,考虑到校正算法对黑体定标温度点附近的工作温度范围具有更好的校正效果,该方式还能够进一步消除建模误差,从而提升校正精度。
-
通过数学推导的方式来详细描述文中算法实现过程。文中算法可归纳为四个步骤,首先,对图像进行线性化变换;其次,在变换域采用线性校正算法完成非均匀性校正;同时,提取伽马曲线特征点作为下一节拍黑体定标温度点;最后,通过逆-非线性变换还原出实际的校正输出图像。图3所示的算法原理图直观地反映了文中算法完整的实施流程。
首先,通过非线性压缩方法对公式(4)两端进行移项及取对数运算,完成对IRFPA探测元输出信号的线性化:
$$ {{{y'}}_{{i}}} = {\rm ln}{\left[ {\left( {\frac{{{{{B}}_{{i}}}}}{{{{{y}}_{{i}}}{\rm{ - }}{{{A}}_{{i}}}}}} \right){\rm{ - 1}}} \right]^t} = {\rm{ - }}{D_i} \cdot {{{x}}_i} + \left[ {{\rm ln}{{(t)}} + {{{C}}_{{i}}}} \right] $$ (5) 由此可以看出,对探测元响应近似满足S形曲线的输出图像采用公式(5)进行线性化处理后,非线性响应
${{{y}}_{{i}}}$ 转化为线性响应的${{{y'}}_{{i}}}$ 。其次,在变换域对探测元进行线性非均匀性校正,校正输出
${{{\hat Y}}_{{i}}}$ 可表示为:$$ \begin{split} \\ {{{\hat Y}}_{{i}}} = {{W}}_{{i}}^{\rm{T}} \cdot {{{X}}_{{i}}} \end{split} $$ (6) 式中:
${{{X}}_{{i}}} = {\left[ {{{{{y'}}}_{{i}}}{{,}}1} \right]^{\rm T}}$ 为观测矩阵;${{{W}}_{{i}}} = {\left[ {{{{{\hat g}}}_{{i}}}{{,}}{{{{\hat o}}}_{{i}}}} \right]^{\rm T}}$ 为校正参数矩阵,其中${{{\hat g}}_{{i}}}$ 和${{{\hat o}}_{{i}}}$ 为校正系数的增益和偏移参数,${{{\hat g}}_{{i}}}$ 和${{{\hat o}}_{{i}}}$ 由高低温黑体辐射定标图像经公式(5)非线性变换后由以下公式获取:$$ {{{\hat g}}_{{i}}} = \frac{{\overline {{{DN}}} {{(}}{T_2}{\rm{) - }}\overline {{{DN}}} {{(}}{T_1}{{)}}}}{{D{N_{{i}}}{{(}}{T_2}{{) - D}}{{{N}}_i}{{(}}{T_1}{{)}}}} $$ (7) $$ {{{\hat o}}_{{i}}} = \frac{{D{N_{{i}}}{{(}}{T_2}{{)}} \cdot \overline {{{DN}}} {{(}}{T_1}{{) - }}D{N_{{i}}}{{(}}{T_1}{{)}} \cdot \overline {{{DN}}} {{(}}{T_2}{{)}}}}{{D{N_{{i}}}{{(}}{T_2}{{) - D}}{{{N}}_i}{{(}}{T_1}{{)}}}} $$ (8) 式中:
$\overline {{{DN}}} {{(}}{T_1}{{)}}$ 和$\overline {{{DN}}} {{(}}{T_{{2}}}{{)}}$ 分别表示在${{{T}}_1}$ 和${{{T}}_2}$ 温度点获取的黑体定标图像经公式(5)进行非线性化压缩后图像的均值,相应的${{D}}{{{N}}_i}{{(}}{T_1}{{)}}$ 和${{D}}{{{N}}_i}{\rm{(}}{T_{\rm{2}}}{\rm{)}}$ 为对应的第i个像元在${{{T}}_1}$ 和${{{T}}_2}$ 温度点获取的数值。将${{{\hat g}}_{{i}}}$ 和${{{\hat o}}_{{i}}}$ 代入公式(6)即可获得线性化图像的校正输出${{{\hat Y}}_{{i}}}$ 。同时,获取伽马曲线的特征作为黑体定标温度点。令伽马曲线二阶导数为0,可得下一节拍高低温黑体定标温度点
${{{T}}_{\rm{H}}}$ 和${{{T}}_{\rm{L}}}$ 如下式所示:$$ {{{T}}_{\rm{H}}} = {\rm{ - }}C{\rm{/}}t $$ (9) $$ {{{T}}_{\rm{L}}} = B{\rm{/(1}} + {{t}}{{\rm{)}}^{{{1/t}}}} $$ (10) 最后,利用公式(6)中获得的线性化图像的校正输出
${{{\hat Y}}_{{i}}}{{(k)}}$ 可看做${{{y'}}_{{i}}}{{(k)}}$ 的估计值,因此,将${{{\hat Y}}_{{i}}}{{(k)}}$ 代入公式(5),并对等式各项进行逆-非线性变换,采用公式(11)即还原出实际的图像输出:$$ {{{\hat y}}_{{i}}} = {A_i} + \frac{{{{{B}}_{{i}}}}}{{\exp {\rm{(}}{{{{y'}}}_{{i}}}^{^{{{1/t}}}}{\rm{)}} + {\rm{1}}}} $$ (11) -
为了检验星载长波红外成像通道在轨大动态范围工作条件下文中算法对空间非均匀性的抑制效果,将文中算法与传统的基于探测器线性响应模型的多点定标非均匀性校正算法进行对比,多点定标算法的黑体定标温度点选取10个,采用分段线性法校正原始图像。同时,还给出了典型的基于曲线拟合的非均匀性校正算法[14]作为对比。测试数据分别采用了实验室定标黑体图像序列数据和基于在轨实际非均匀性特性提取的半实景图像序列数据,通过性能指标定量化分析和视觉效果两方面验证文中算法针对国产化大阵列红外探测器强非线性非均匀性校正的效果。
-
校正效果定量化性能评价指标采用国家标准规定的非均匀性指标[15]
${{{U}}_r}$ 和图像粗糙度指标[2]$\; \rho $ 。其中,指标${{{U}}_r}$ 为红外探测器各像元响应均方根偏差与平均响应的百分比,表达式如下:$$ {{{U}}_{{r}}} = \frac{1}{{\bar R}} \cdot \sqrt {\frac{1}{{M \cdot N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left[ {{R_{{{ij}}}}{{ - \bar R}}} \right]}^2}} } } \cdot 100 {\text{%}} $$ (12) 式中:
$ \bar R $ 和${R_{{{ij}}}}$ 分别表示红外探测器输出图像的全局平均值和i像元j时刻响应输出值。指标
$\; \rho $ 用于衡量给定图像的粗糙程度,其表达式为:$$ \rho = \frac{{{{\left\| {{{{h}}_{\rm{1}}}{\rm{*}}f} \right\|}_1} + {{\left\| {{{{h}}_{\rm{2}}}{\rm{*}}f} \right\|}_1}}}{{{{\left\| {{f}} \right\|}_1}}} $$ (13) 式中:
${{{h}}_{\rm{1}}}$ 为水平差分模板[1,−1];${{{h}}_{\rm{2}}} = {{{h}}_{\rm{1}}}^{\rm T}$ 表示垂直差分模板;$ {\left\| \cdot \right\|_1} $ 表示${{{L}}_{\rm{1}}}$ 范数。指标${{{U}}_r}$ 和$\; \rho $ 的取值越小,表示图像的响应一致性越好,表明校正后图像的残留非均匀性越小,校正效果越好。 -
采用实验室黑体辐射定标系统采集不同黑体温度条件下的定标图像,分别采用文中算法和传统星载多点校正算法完成辐射校正,并对比两种校正算法在大动态范围信号输入条件下的校正性能。为充分模拟空间环境,辐射定标在真空低温环境下进行,真空罐真空度小于10−3 Pa,热沉温度小于100 K,定标黑体模拟240~340 K范围相机入瞳处的辐射亮度。校正参数采用270 K和300 K黑体图像进行计算,待校正图像选取动态范围内240、275、305、340 K共4个温度点,校正前后图像灰度值见图4,其中图4(a)为校正前4个温度点图像灰度分布,图4(b)为采用文中算法的校正结果,图4(c)为采用传统算法的校正结果,量化对比结果如表1所示。
表 1 不同算法对人工黑体图像非均匀校正后的性能参数
Table 1. Performance parameters of artificial blackbody images non-uniformity corrected by different algorithms
Parameter Blackbody temperature/K Image before correction Image after correction Proposed algorithm Curve fitting based algorithm Multipoint correction algorithm Ur 340 22.86% 0.41% 0.59% 1.27% 305 14.40% 0.33% 0.31% 0.93% 275 9.86% 0.38% 0.39% 0.77% 240 8.23% 0.49% 0.44% 1.46% $ \rho $ 340 0.4800 0.0685 0.0739 0.0991 305 0.2851 0.0396 0.0411 0.0570 275 0.1843 0.0288 0.0251 0.0361 240 0.1687 0.0245 0.0260 0.0324 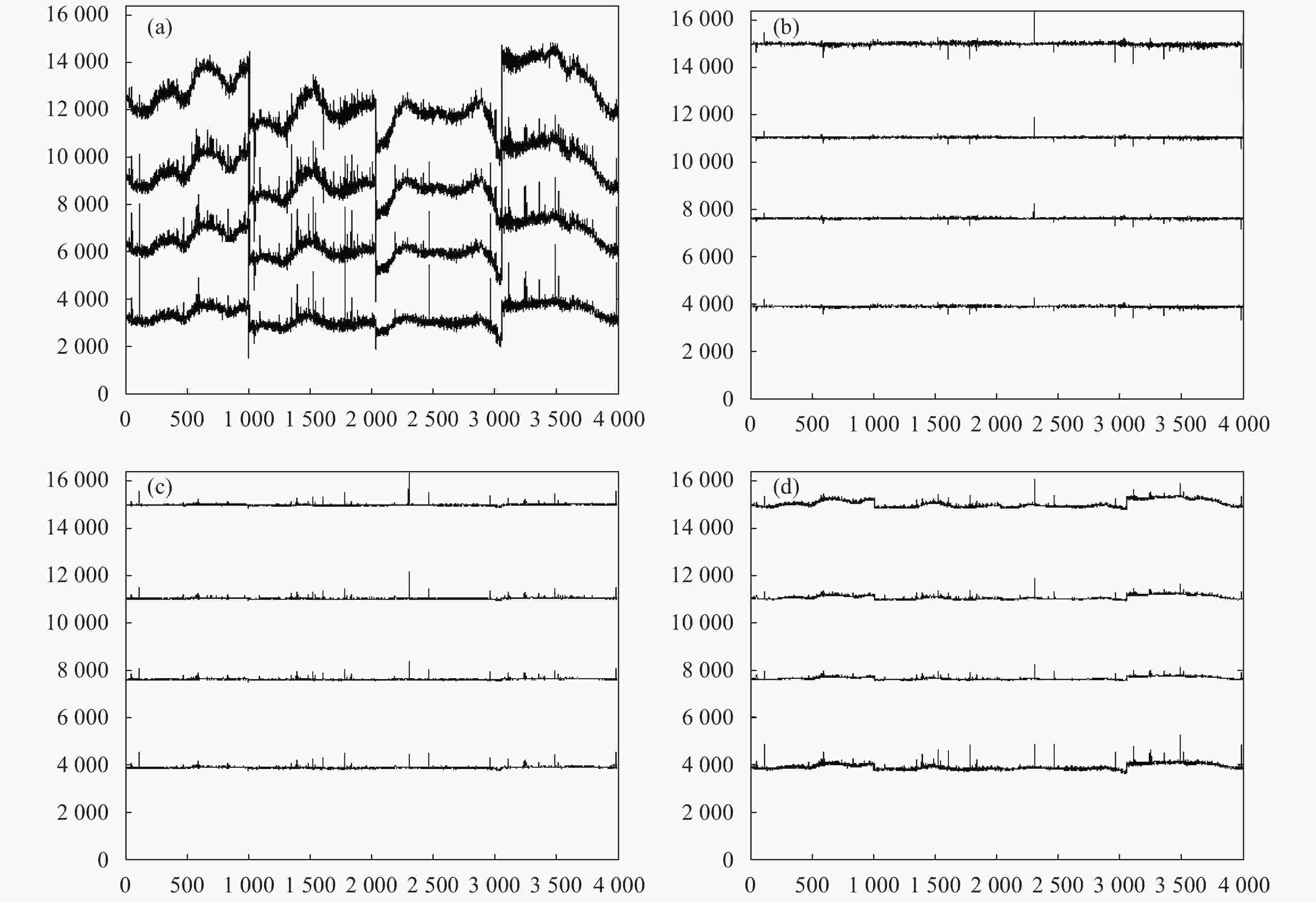
图 4 (a) 校正前图像灰度分布;(b) 文中算法非均匀性校正结果;(c) 典型曲线拟合算法非均匀性校正结果;(d) 多点校正算法非均匀性校正结果
Figure 4. (a) Image gray distribution before correction; (b) Result for NUC of the proposed algorithm; (c) Result for NUC of typical curve fitting based algorithm;(d) Result for NUC of multi-point correction algorithm
采用非均匀性指标
${{{U}}_r}$ 和图像粗糙度指标$\; \rho $ 量化比较两种算法对黑体图像的校正结果如表1所示。从黑体定标实验验证结果可以看出,传统的星载多点校正算法由于模型失配的原因,校正效果不理想,残留分均匀性较大。而经过文中和参考文献[14]所述的曲线拟合算法校正后,在中等温度区域,两种算法均能得到较好的校正效果;然而,参考文献[14]应用场景为地面热成像,工作动态范围相对较低,在天基红外遥感应用领域具有一定局限性,表现为探测器响应非线性程度更强的高度温度区域校正效果不佳。文中算法通过改进的5参数S曲线模型,以其更好的自由度实现了对于探测器高温区域强非线性的准确拟合,从而具有更好的校正效果,表现了文中算法对探测器响应强非线性的良好适应性。
-
将卫星红外成像通道在轨实际获取的非均匀性特性叠加在一幅典型的标准长波红外遥感图像上,分别采用文中算法、参考文献[14]算法和传统星载多点校正算法完成辐射校正,并对比分析校正效果,校正效果如图5所示。从视觉效果的对比而言,相对于传统星载多点校正算法,文中和参考文献[14]所述的曲线拟合算法对表现为条纹图案的非均匀性噪声抑制效果更好,校正后的图像场景细节更加平滑清晰。文中算法的优势还在于拟合探测器响应曲线所需的黑体定标温度点数量相对更少,从而可以大幅降低星载遥感红外相机停机定标时间。

图 5 (a) 校正前的半实景红外遥感图像;(b) 文中算法非均匀性校正结果;(c) 曲线拟合算法非均匀性校正结果;(d) 多点校正算法非均匀性校正结果
Figure 5. (a) Semi-real infrared remote sensing image before correction; (b) Result for NUC of the proposed algorithm; (c) Result for NUC of curve fitting based algorithm; (d) Result for NUC of multi-point correction algorithm
此外,再次借助参数
${{{U}}_r}$ 和$ \;\rho $ 量化对比上述两种校正算法对实景红外图像的校正效果。表2所示的实验结果表明经文中算法校正后的红外图像具有相对较小的粗糙度和残余非均匀性,校正效果更好。表 2 不同算法半实景红外遥感图像非均匀校正后的性能参数
Table 2. Performance parameters of semi-real infrared remote sensing image non-uniformity corrected by different algorithms
Parameter Image before correction Image after correction Proposed algorithm Curve fitting based algorithm Multipoint correction algorithm Ur 13.69% 11.33% 11.62% 12.17% $ \rho $ 0.1193 0.0847 0.0893 0.1028 -
星载红外探测器的非线性响应特性是当前天基红外遥感非均匀性校正中亟待解决的技术难题。传统的星载非均匀性校正算法能在一定程度上消除红外探测器非均匀性,然而,传统算法是基于探测元的线性响应模型导出的,天基应用要求红外探测器工作在大动态范围,探测元实际响应的非线性势必会引起较大的校正误差。为此,提出一种基于动态伽马函数的星载红外非均匀性校正算法,该算法采用更接近于探测器实际响应特性的改进伽马曲线模型以拓宽信号响应的动态范围,然后利用非线性压缩运算将校正过程映射为基于线性化模型的校正参数估算,同时根据模型参数动态确定黑体定标温度点,最终获得准确的校正输出。针对黑体图像和实景图像的实验结果表明,文中算法具有动态范围大、校正精度高和黑体定标效率高的优点。
Non-uniformity correction algorithm of space-borne long-wave infrared focal plane arrays based on improved Gamma curve
-
摘要: 随着长波红外探测器技术的进步,通过选用宇航级大阵列长波红外探测器,天基红外遥感卫星技术得到快速发展。长波红外探器响应强非线性导致传统的基于线性模型的非均匀性校正算法校正误差大,从而影响卫星在轨使用效能。针对该问题,结合大量实验室数据和卫星在轨数据的统计分析结果,建立了一种新的长波红外探测器非线性响应模型,据此提出了一种基于改进伽马曲线的非均匀性校正算法,以有效克服探测器响应强非线性对校正精度的影响。该算法首先建立基于改进伽马曲线的探测器非线性响应模型,依据此模型对获取图像进行非线性压缩映射,实现探测器响应的线性化,然后利用星载基于定标技术的线性化算法实施非均匀性校正,同时,定标温度点根据所建立模型参数动态更新,最后通过逆非线性化压缩映射还原出实际的非均匀校正后的图像。基于人造黑体和在轨实景红外图像的实验结果表明,该算法有效解决了探测器响应强非线性对校正精度的影响,校正后图像的视觉效果和定量化指标均优于传统的星载非均匀校正算法。Abstract: With the progress of long-wave infrared detector technology, space-based infrared remote sensing satellite technology has developed rapidly by selecting Aerospace large array long-wave infrared detector. The response of long-wave infrared detectors is strongly nonlinear, which leads to large correction errors in traditional non-uniformity correction algorithms based on linear models, thereby affecting the effectiveness of the satellite in orbit. Aiming at this problem, combing the statistical analysis results of a large number of laboratory data and satellites in orbit data, a new long-wave infrared detector nonlinear response model was established, and an new non-uniformity correction algorithm based on improved Gamma curve was proposed accordingly, which was in order to effectively overcome the influence of the strong nonlinear response of infrared detector on the correction accuracy. Firstly, the nonlinear response model based on improved Gamma curve for infrared detector was established, and the nonlinear compression mapping operation on the original image data was completed to achieve linearization of the infrared detector response. Secondly, the linearization algorithm was used to implement non-uniformity correction based on space-borne calibration technology. Meanwhile, the calibration temperature point was dynamically updated according to the established model parameters. Finally, the actual image after non-uniformity correction was restored by inverse nonlinear compression mapping. The experimental result based on artificial blackbody and on orbit real infrared images show that the proposed algorithm can effectively solve the influence of strong nonlinearity of infrared detector response on the correction accuracy, and the visual effect and quantitative index of the corrected image are better than the traditional space-borne non-uniformity correction algorithm.
-
图 5 (a) 校正前的半实景红外遥感图像;(b) 文中算法非均匀性校正结果;(c) 曲线拟合算法非均匀性校正结果;(d) 多点校正算法非均匀性校正结果
Figure 5. (a) Semi-real infrared remote sensing image before correction; (b) Result for NUC of the proposed algorithm; (c) Result for NUC of curve fitting based algorithm; (d) Result for NUC of multi-point correction algorithm
表 1 不同算法对人工黑体图像非均匀校正后的性能参数
Table 1. Performance parameters of artificial blackbody images non-uniformity corrected by different algorithms
Parameter Blackbody temperature/K Image before correction Image after correction Proposed algorithm Curve fitting based algorithm Multipoint correction algorithm Ur 340 22.86% 0.41% 0.59% 1.27% 305 14.40% 0.33% 0.31% 0.93% 275 9.86% 0.38% 0.39% 0.77% 240 8.23% 0.49% 0.44% 1.46% $ \rho $ 340 0.4800 0.0685 0.0739 0.0991 305 0.2851 0.0396 0.0411 0.0570 275 0.1843 0.0288 0.0251 0.0361 240 0.1687 0.0245 0.0260 0.0324 表 2 不同算法半实景红外遥感图像非均匀校正后的性能参数
Table 2. Performance parameters of semi-real infrared remote sensing image non-uniformity corrected by different algorithms
Parameter Image before correction Image after correction Proposed algorithm Curve fitting based algorithm Multipoint correction algorithm Ur 13.69% 11.33% 11.62% 12.17% $ \rho $ 0.1193 0.0847 0.0893 0.1028 -
[1] Dong Liquan, Jin Weiqi, Sui Jing. Summarize on the scene-based Nonuniformity correction algorithms for IRFPA[C]//Proceedings of the SPIE, 2005, 5881: 1-10. [2] Torres S N, Hayat M M. Kalman filtering for adaptive nonuniformity correction in infrared focal plane arrays [J]. J Opt Soc Am A, 2003, 20: 470-480. doi: 10.1364/JOSAA.20.000470 [3] Zuo C, Chen Q, Gu G, et al. Scene-based nonuniformity correction algorithm based on interframe registration [J]. JOSA A, 2011, 28(6): 1164-1176. doi: 10.1364/JOSAA.28.001164 [4] Perry D L, Dereniak E L. Linear theory of nonuniformity correction in infrared staring sensors [J]. Opt Eng, 1993, 32: 1854-1859. doi: 10.1117/12.145601 [5] Zhou Huixin, Lai Rui, Liu Shangqian, et al. New improved nonuniformity correction for infrared focal plane arrays [J]. Opt Com, 2005, 245: 49-53. doi: 10.1016/j.optcom.2004.09.077 [6] Wilhelm Isoz. Thomas Svensson, Ingmar Renhorn. Nonuniformity correction of infrared focal arrays[C]//Proceedings of SPIE, 2005, 5783: 949-960. [7] Greg Matis, Jack Grigor, Jay James, et al. Radiance calibration of target projectors for infrared testing[C]//Proceedings of SPIE, 2006, 6207: 62070N1. [8] Shi Yan, Zhang Tianxu, Cao Zhiguo, et a1. A feasible approach for nonuniformity correction in IRFPA with nonlinear response [J]. Infrared Physics & Technology, 2005, 46: 329-337. [9] Qu Huiming, Chen Qian, Zhang Canlin. Accurate noneffective pixel detection and replacement based on multi-temperature matching[C]//Proceedings of SPIE, 2007, 6279: 62796X. [10] Zhu Ruifei, Wang Chao, Wei Qun, et al. Manufacture of nonuniformity correction system for infrared detector [J]. Infrared and Laser Engineering, 2013, 42(3): 1669-1673. (in Chinese) [11] Qu Huiming, Chen Qqian. A theoretical model on infrared focal panel arrays binary nonlinear nonuniformity [J]. Acta Electronica Sinica, 2008, 36: 2150-2153. (in Chinese) [12] Wang Fuhua. Demand forecast of the logistic park based on the curve of growth theory [C]//IEEE International Conference on Interlligent Computing and Intelligent System, 2009: 57-61. [13] Georgios G. Techno-economic evaluation of 3rd generation mobile system[D]. London: University College London, 2003: 34-36. [14] Zuo C, Chen Q, Gu G. Nonuniformity correction based on unified photoresponse characteristics of infrared focal plane arrays [J]. Acta Photonica Sinica, 2011, 40(6): 926-932. (in Chinese) doi: 10.3788/gzxb20114006.0926 [15] Country Engineering Supervision Bureau. The Technique Norms for Measurement and Test of Characteristic of China (GB/T 17444-1998)[S]. Beijing: Standards Press of China, 1998. (in Chinese) -






 下载:
下载: