-
光电稳定平台是一种光、机、电高度集成的精密设备[1],由光电载荷、陀螺仪和执行机构组成。主要完成目标捕获、跟踪和定位等任务,广泛应用在各种军事和民用领域[2]。光电稳定平台用于对载体运动进行隔离,是一种高精度的伺服系统。在飞机飞行过程中,机体受到的载体扰动会引起平台视轴的抖动,严重影响平台的稳像精度[3]。所以如何提高光电平台的抗干扰能力,是改善平台性能、提高稳像精度的关键[4]。
光电稳定平台所受的扰动很多,有摩擦、质量不平衡、载体振动、导线牵拉和风阻等[5],其中以摩擦干扰对平台伺服系统的影响最大,所以对摩擦干扰进行有效补偿是提高平台稳像精度的关键。为了提高平台的稳像精度,研究者采取了许多扰动补偿措施,但对于摩擦扰动都没有较好的解决办法,比如参考文献[6]中提出的自抗扰方法由于其补偿过程较为复杂,响应时间慢,观测器带宽较低使得无法对较高频的扰动进行补偿;参考文献[7]中提出的
$DOB$ 方法因为基于平台伺服系统的传递函数,依赖待补偿的控制系统模型,对系统辨识准确率要求较高,同样无法对无规律的摩擦扰动进行有效补偿。所以针对摩擦干扰,文中提出了一种基于最小二乘法估计的摩擦补偿方法,并经仿真验证,证明该方法可以有效抑制平台伺服系统所受的摩擦干扰,改善平台性能。文中方法先对机构实际角加速度利用最小二乘估计方法进行观测,然后将这个观测值与控制电流期望机构产生的角加速度值进行对比,得到伺服系统受摩擦干扰影响所损失的角加速度,据此计算获得机构受摩擦影响所消耗的力矩,最终得到需要补偿的电流值。文中利用LuGre动态摩擦模型对平台所受摩擦扰动进行建模,然后提出补偿原理和角加速度估计算法,在Matlab/simulink中建立仿真平台,验证基于机构角位置信息的加速度估计摩擦补偿方法的有效性。最后,在实际稳定平台上进行实验,实验结果表明,此方法能切实改善平台的稳像精度,提升平台的稳定性能。 -
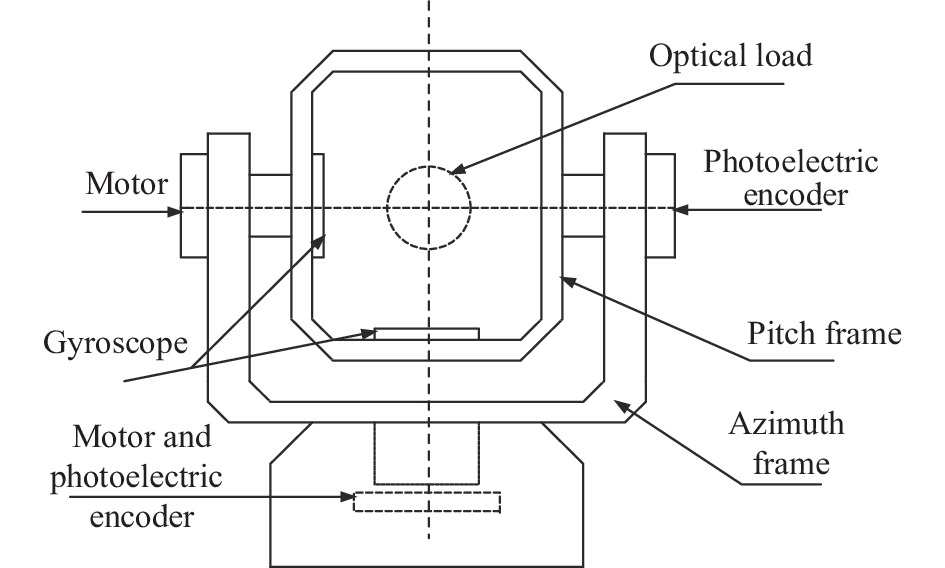
文中针对的是两轴两框架的光电稳定平台,这种平台机械强度高、运动精度易实现[8],是一种应用较广且技术比较成熟的光电稳定平台。图1为某型两轴两框架光电稳定平台结构示意图,其内部有两套电机驱动平台运转,包含方位与俯仰两个轴系[9],陀螺与光电编码器分别负责测量机构的角速度与角位置值。
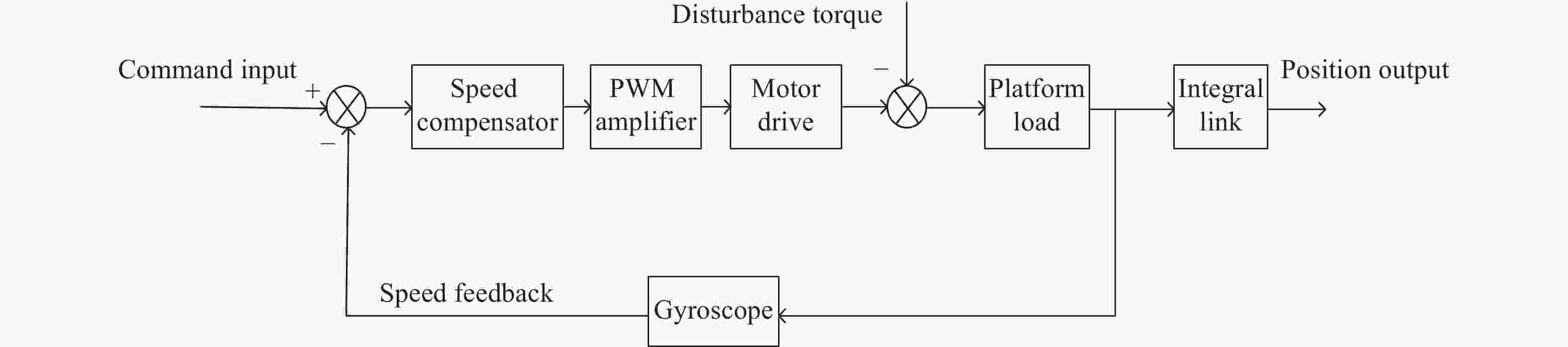
光电稳定平台伺服系统采用闭环控制,通过陀螺仪来实时反馈机构角速度,达到光电稳定平台隔离扰动,保持相对稳定的作用。图2所示是光电稳定平台单轴回路控制框图,主要结构包含控制器、功率放大器、驱动电机、负载、陀螺仪[10]。
-
摩擦力矩是影响视轴稳定的一个重要扰动因素,电机带动机构运动的过程会将连接轴的摩擦力耦合在传感器视轴上,使视轴指向偏差预定值,摩擦力矩模型分为经典静态摩擦模型和动态摩擦模型[11]。
静态摩擦模型有库伦摩擦模型,库伦+粘滞摩擦模型,静摩擦+库仑摩擦+粘滞摩擦模型,Stribeck 模型[12];动态摩擦模型常用的是LuGre模型,由于LuGre模型可以在低速且高精度的控制系统中较准确描述一些复杂的动静态特性,是一个较为完善的动态摩擦模型,能够比较准确的反映实际工程中电机角速度与系统摩擦力矩之间的动态关系,所以文中利用LuGre模型进行仿真工作。
LuGre模型可以表示为:
$$ \frac{ {\rm d}z}{{\rm d}t}={\omega }_{l}-\frac{\left|{\omega }_{l}\right|}{g\left({\omega }_{l}\right)}z\text{,}{\omega }_{l}=\frac{{\omega }_{m}}{i} $$ (1) 公式(1)表示两个接触面鬃毛的平均形变量
$\dfrac{ {\rm d}z}{{\rm d}t}$ 与负载转速${\omega _l}$ 通过传动比$i$ 与电机转速${\omega _m}$ 的关系,$z$ 表示鬃毛的平均形变量。非线性函数$g\left( {{\omega _l}} \right) > 0$ 表示不同的摩擦效应[13]。$$ \text{ } {\sigma }_{0}g\left({\omega }_{l}\right)={T}_{c}+\left({T}_{s}-{T}_{c}\right) $$ (2) 式中:
${T_c}$ 为库伦摩擦力矩;${T_{{s}}}$ 为最大静摩擦力矩;${\omega _s}$ 为$Stribeck$ 速度。摩擦力矩${T_f}$ 用下式表示:$$ \text{ } {T}_{f}={\sigma }_{0}z+{\sigma }_{1}\frac{{\rm d}z}{{\rm d}t}+{\sigma }_{2}{\omega }_{l} $$ (3) 式中:
${\sigma _0}$ 为鬃毛的刚度系数;${\sigma _1}$ 为鬃毛的阻尼系数;${\sigma _2}$ 为粘滞摩擦系数。 -
在对稳定平台进行扰动补偿的过程中,注意到参考文献[6]中提到的自抗扰控制在实际补偿时存在带宽较低的问题,对较高频的扰动或者其他非线性扰动补偿效果不明显,尤其对于毫无规律的摩擦扰动,自抗扰控制效果不是特别理想。所以针对其不足,文中考虑设计一种新型补偿方法,期望可以提高观测器的带宽,对摩擦力矩也能够进行有效补偿。由于机构是连续运动的,也就是机构运动不会突变的特性,所以在极小时间点内对机构运动情况进行连续采样,可以认为机构的角加速度是恒定的。根据角度传感器输出的数据,经最小二乘角加速度估计算法可得到机构的实际角加速度,又由机构内控制器输出控制电流值可得到机构的期望角加速度,两个角加速度的差值就是扰动力矩所带来的角加速度扰动。根据扰动角加速度,可反算出扰动力矩,进一步得到所需的补偿电流值。
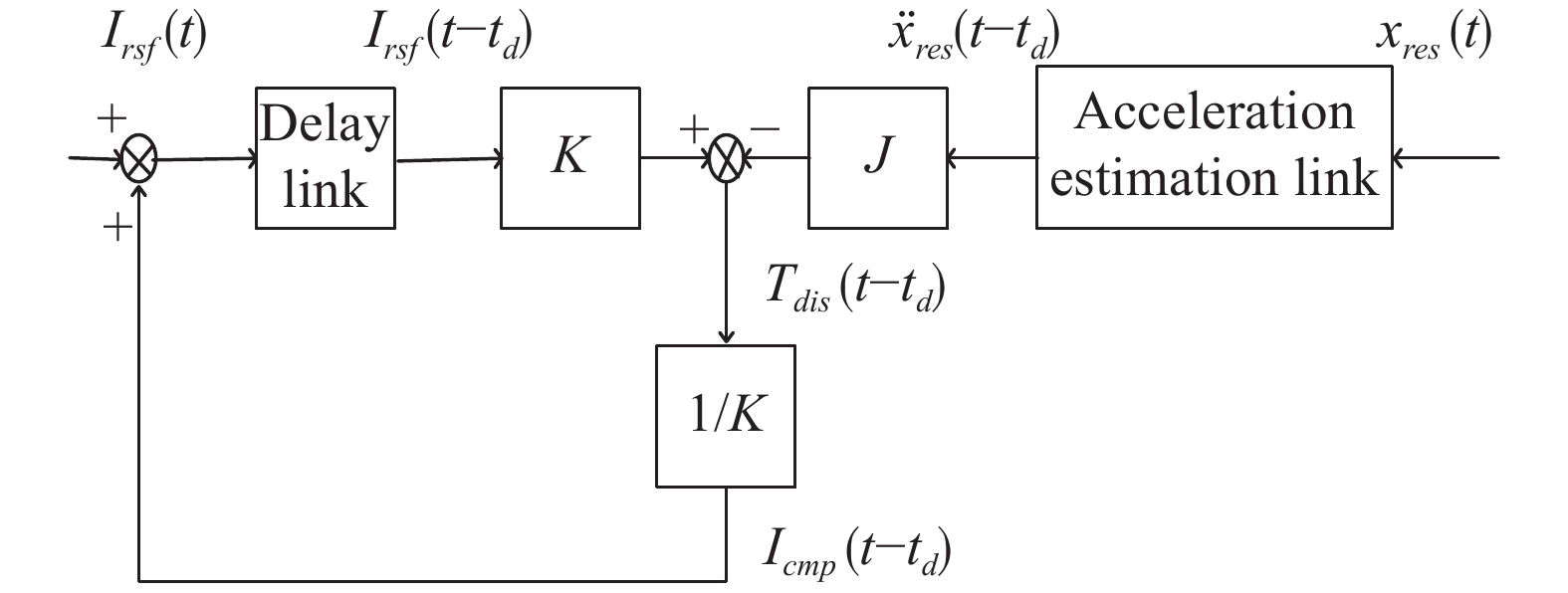
该方法是设计一个观测器来估计干扰或模型不确定性,然后根据观测器的输出进行补偿[14]。摩擦力矩
${T_f}$ 可以通过1.1节提出的LuGre摩擦模型得到。补偿过程是通过获得控制器输出的控制电流${I_{ref}}$ ,让其与转矩系数$K$ 相乘得到机构所受力矩的理论值;然后设计角加速度估计算法得到机构实际角加速度${\ddot x_{res}}$ ,让${\ddot x_{res}}$ 与转动惯量$J$ 相乘得到机构实际转动所需力矩,机构所受力矩理论值与机构实际所需力矩作差就是机构受扰动影响损失的力矩,可以认为是机构所受到的摩擦力矩。通过图3中扰动观测器计算得到损失力矩大小,然后让其除以转矩系数$K$ 就可以得到需要补偿的电流值${I_{cmp}}$ ,将该电流值${I_{cmp}}$ 补偿到系统控制器输出端最终达到摩擦补偿的效果。图3描述了稳定平台加速度补偿的基本结构:
其中,
$\rm Signal$ 是摩擦模型输入的扰动信号;${I_{ref}}$ 是控制电流;K是转矩系数,相对误差为10%;${T_{f}}$ 是摩擦力矩;$J$ 是转动惯量;${\ddot x_{res}}$ 是机构实际角加速度;$s$ 表示拉普拉斯算子;${x_{res}}$ 是机构实际转动角度;${I_{cmp}}$ 是通过扰动观测器计算得到的补偿电流值。下标$ref$ 表示参考值,下标$res$ 表示响应值,下标$cmp$ 表示补偿值。如图3所示,考虑到摩擦力矩为扰动力矩的主体,有实际补偿过程如下所示:
$$ \text{ }{T}_{f}={I}_{ref}K-J{\ddot{x}}_{res} $$ (4) $$ \text{ } {I}_{cmp}={T}_{f}/K $$ (5) -
根据1.3节提供的补偿原理可知,文中提供的补偿方法的关键点就是如何根据机构转动角度准确估计机构实际角加速度。
估计机构实际角加速度需要知道机构运动位置的变化情况,文中采用光电编码器进行机构位置的测量,通过将传感器与电机转轴相连来测得机构在任意时刻的位置,任意时刻时,机构位置如下式所示:
$$ x_{res}^i = E\left[ i \right] $$ (6) 式中:
$x_{res}^i$ 代表机构在时间${t_i}$ 的位置;$E\left[ i \right]$ 是传感器在时间${t_i}$ 测得的机构位置。同理$E\left[ {i + 1} \right]$ 是传感器在时间${t_{i + 1}}$ 测得的机构位置,机构位置传感器采样原理如图4所示,先假设采样数$n = 7$ ,则采样周期$T = {t_n} -{t_{n - 1}}$ 。然后根据描述的机构运动位置图估计机构运动轨迹公式,机构运动轨迹由二阶多项式公式近似表示:
$$ \begin{array}{c} {\widehat{x}}_{res}^{i}=\alpha {\left(iT\right)}^{2}+\beta \left(iT\right)+\gamma =\\ \left(\alpha {T}^{2}\right){i}^{2}+\left(\beta T\right)i+\gamma \end{array} $$ (7) $T$ 是采样周期,机构实际角加速度估计值$\hat{ \ddot x}_{res}^{i}$ 计算如下:$$ {\hat {\ddot x}}_{res}^{i} = 2\alpha $$ (8) 这个机构实际角加速度估计值
$ {\hat {\ddot x}}_{res}^i $ 在采样时间${t_0}$ 到${t_{n - 1}}$ 之间是恒值,这个方法当且仅当采样样本数小且采样周期较短时有效。式中的$ \alpha ,\beta ,\gamma $ 采用最小二乘法计算如下:$$ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} {i^4}}&{2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} {i^3}}&{2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} {i^2}} \\ {2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} {i^3}}&{2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} {i^2}}&{2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} i} \\ {2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} {i^2}}&{2\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} i}&{2n} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\alpha {T^2}} \\ {\beta T} \\ \gamma \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} R\left( {E\left[ i \right] + E\left[ i \right] + 1} \right){i^2}} \\ {\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} R(E\left[ i \right] + E\left[ i \right] + 1)i} \\ {\displaystyle\mathop \sum \limits_{i = 0}^{n - 1} R(E\left[ i \right] + E\left[ i \right] + 1)} \end{array}} \right] \\ \end{gathered} $$ (9) 最小二乘法可以用数字FIR滤波器来描述,该数字FIR滤波器的输入是传感器采样得到的机构位置
$E\left[ i \right]$ 和$E\left[ {i + 1} \right]$ ,输出是估计的机构角加速度参数$\alpha $ 。电机加速度参数
$\alpha $ 计算如下所示:$$ \alpha = H\left( z \right)\left( {E\left[ {n - 1} \right] + E\left[ {n - 1} \right] + 1} \right) \\ = H\left( z \right)\left( {2E\left[ {n - 1} \right] + 1} \right) $$ (10) 其中
$H\left( z \right)$ 计算过程如下:$$ H\left( z \right) = \frac{1}{D}\mathop \sum \limits_{i = 0}^{n - 1} {c_i}{z^{ - \left( {n - 1 - i} \right)}}$$ (11) $$ \begin{split} {c_i} =& \left( {\mathop \sum \limits_{i = 0}^{n - 1} {i^2} - \frac{{\displaystyle\mathop \sum \nolimits_{i = 0}^{n - 1} i\displaystyle\mathop \sum \nolimits_{i = 0}^{n - 1} {i^3}}}{{\displaystyle\mathop \sum \nolimits_{i = 0}^{n - 1} {i^2}}}} \right)+ \left( {\frac{{n\displaystyle\mathop \sum \nolimits_{i = 0}^{n - 1} {i^3}}}{{\displaystyle\mathop \sum \nolimits_{i = 0}^{n - 1} {i^2}}} - \mathop \sum \limits_{i = 1}^{n - 1} i} \right)i + \\ & \left( { - n + \frac{{{{(\displaystyle\mathop \sum \nolimits_{i = 0}^{n - 1} i)}^2}}}{{\displaystyle\mathop \sum \nolimits_{i = 0}^{n - 1} {i^2}}}} \right){i^2} = \left( {\frac{{n\left( {n - 1} \right)\left( {2n - 1} \right)}}{6} - \frac{{3{n^2}{{\left( {n - 1} \right)}^2}}}{{4\left( {2n - 1} \right)}}} \right) +\\ & \left( {\frac{{n\left( {n + 1} \right)}}{{2\left( {2n - 1} \right)}}\left( {i\left( {n - 1} \right) - {i^2}} \right)} \right) \end{split} $$ (12) $$\begin{split} D=2{T}^{2}\{\{{\left({\displaystyle \sum }_{i=0}^{n-1}{i}^{2}\right)}^{2}-n\left({\displaystyle \sum }_{i=0}^{n-1}{i}^{4}\right)-2{\displaystyle \sum }_{i=0}^{n-1}i{\displaystyle \sum }_{i=0}^{n-1}{i}^{3}+\\ \frac{{({{\displaystyle \sum }}_{i=0}^{n-1}i)}^{2}}{{{\displaystyle \sum }}_{i=0}^{n-1}{i}^{2}}{\displaystyle \sum }_{i=0}^{n-1}{i}^{4}+ \frac{n}{{{\displaystyle \sum }}_{i=0}^{n-1}{i}^{2}}{\left({\displaystyle \sum }_{i=0}^{n-1}{i}^{3}\right)}^{2}\} \end{split} $$ (13) 由于实际响应时间存在延时,所以应考虑增加延时环节,根据数字FIR滤波器相关概念,延时时间
${t_d}$ 与采样样本数$n$ 之间关系如下[15]:$$ {t_d} = \frac{{n - 1}}{2}T $$ (14) 就是计算角加速度的数字FIR滤波器的时间延时是
$\dfrac{{n - 1}}{2}T$ 。下面估计FIR滤波器的精度与其时间延时的关系:
假设FIR滤波器估计的精度有
$\Delta a$ 的误差,引起传感器在每个采样周期产生的位置误差$\Delta {x_i}$ 如下:$$ \Delta {x_i} = \frac{1}{2}\Delta a{\left( {iT} \right)^2} $$ (15) 传感器的位置误差
$\Delta {x_i}$ 应比其分辨率$R$ 要小。故FIR滤波器精度误差$\Delta a$ 与样本数$n$ 、采样周期$T$ 之间关系如下:$$ \Delta a=\frac{2\Delta {x}_{i}}{{\left(\left(n-1\right)T\right)}^{2}} < \frac{2R}{{\left(\left(n-1\right)T\right)}^{2}}={\varepsilon }_{a} $$ (16) -
首先对所要仿真的稳定平台进行建模,稳定平台以陀螺仪、光电编码器作为反馈元件,控制器输出控制信号给负载电机,然后通过负载电机来带动机构的运动。
由于采用FIR滤波器估计角加速度方法有
${t_d}$ 的延时时间,所以还需要增加延时环节来同步观测器所需要估计的机构角加速度${\hat {\ddot x}}_{res}^i$ 。计算的扰动观测器的精度由FIR滤波器的估计精度决定,并且要求的精度取决于机构的控制信号的大小[16],该扰动观测器用于平台伺服系统中所具有的精度是
$ \varepsilon _{a} $ ,精度$ \varepsilon _{a} $ 、采样周期$T$ 、传感器分辨率$R$ 之间关系如下所示:$$ n=\frac{1}{T}\sqrt{\frac{2R}{{\varepsilon }_{a}}}+1 $$ (18) 观测器模型如图5所示。
令延时环节传递函数为
$ {G_1}\left( s \right) $ ,角加速度估计环节传递函数为${G_2}\left( s \right)$ ,观测器输入为机构控制电流值${X_1} = {I_{ref}}$ 和机构受摩擦力矩作用转动角度${X_2} = {x_{res}}$ ,输出值为平台伺服系统需要补偿的电流值$Y = {I_{cmp}}$ 。所以得到该观测器传递函数如下:
$$ Y = \frac{{{G_1}\left( s \right)K{X_1} - J{G_2}\left( s \right){X_2}}}{K} $$ (19) -
实验在两轴两框架小型光电稳定平台上进行,采用LuGre摩擦模型对扰动信号进行处理,转化为扰动摩擦力矩,使摩擦扰动可以根据不同的输入信号进行转化,目的是减小摩擦扰动对光电平台造成的影响,先进行Matlab/simulink仿真验证,然后搭建实验平台,在光电平台上进行实验,根据实验数据证实该方法可以有效减小摩擦力矩对平台伺服系统造成的影响。
参考需要仿真的稳定平台的结构参数,设置观测器与稳定平台伺服系统各参数取值如表1所示。
表 1 平台参数取值
Table 1. Parameter selection of platform
Item Parameters Value Sample period T/ms 0.1 Rotate inertia J/(kg·m2) 0.086 Torque coefficien K/(N·m·A−1) 0.718 Peak voltage U/V 12.2 Peak current I/A 17 Resistance R/Ω 1.8 Inductance L/mH 5.4 经过对文中所研究的光电稳定平台进行离线辨识,测量有关数据,然后参考LuGre摩擦模型的数学结构,设置LuGre摩擦模型各参数取值如表2所示。
表 2 LuGre摩擦模型参数取值
Table 2. Parameter selection of LuGre friction model
${\sigma _0}$ ${\sigma _1}$ ${\sigma _2}$ ${T_s}$ ${T_c}$ 200 8 0.01 0.15 0.06 考虑到在稳定平台实际应用过程中,低频大幅扰动可以通过调整平台伺服系统稳定回路相关增益进行扰动隔离,且有较好效果;高频小幅扰动通过稳定平台自身的惯性稳定和安装减震器方法也可以进行很好的隔离,而中频段是稳定平台控制系统较为薄弱的频段,故文中选择对
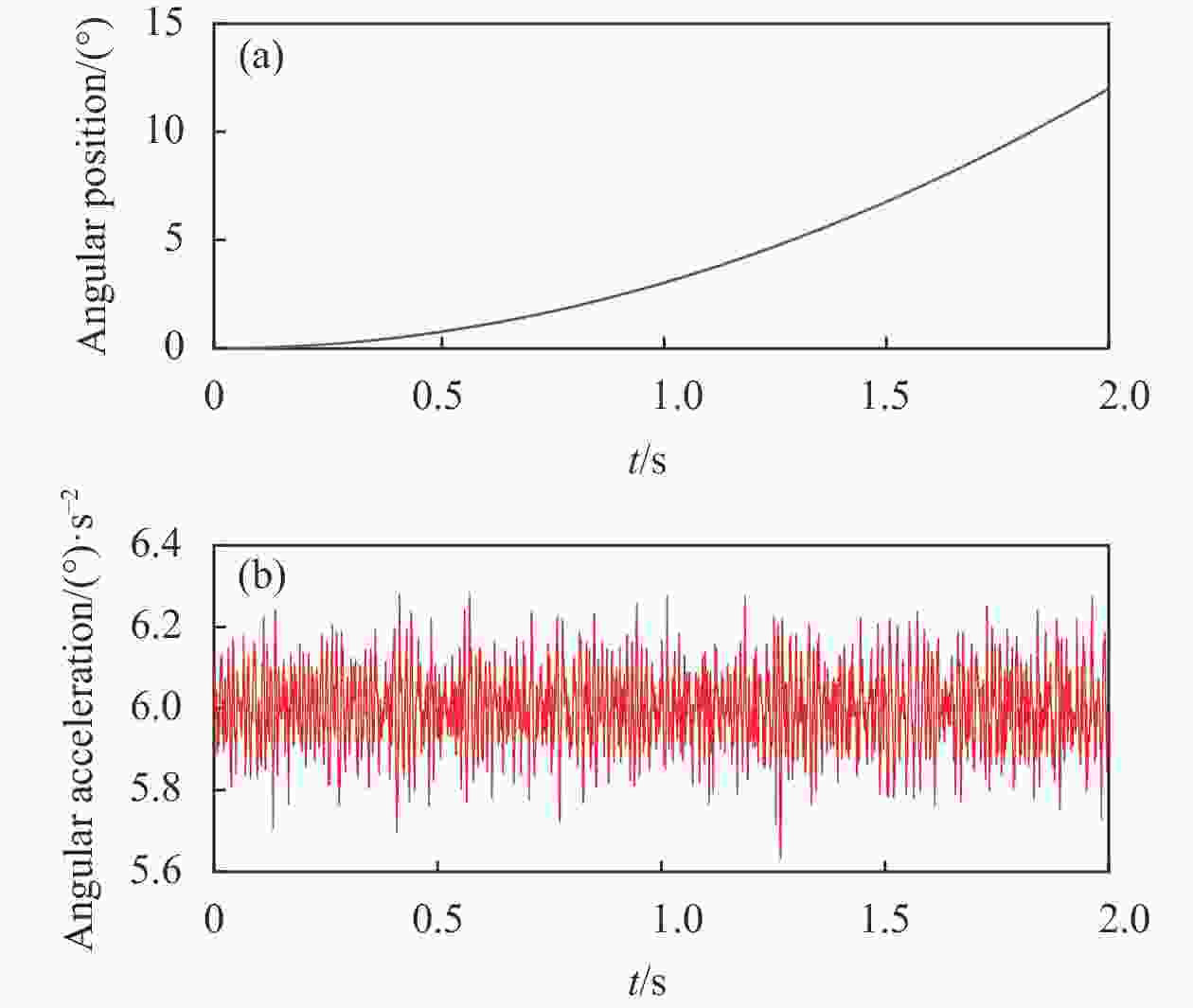
$ 10\;{\rm{Hz}},{0.03}^{°} $ 的中频扰动进行扰动补偿研究。为了提高仿真结果的准确程度,先验证文中提出的最小二乘角加速度估计算法的有效性,根据实际系统配置,将加速度估计环节输入信号设置为
$y = 3{t^2} + \omega $ ,其中$\omega $ 为白噪声信号,由于文章实验选用19位分辨率的DS-130光电编码器,经实测统计,得到该编码器的白噪声幅值为1×10−5 rad。输入信号如图6蓝线所示,经最小二乘角加速度估计之后的曲线如图6红线所示。可以看到,在经过二次微分引起的噪声放大影响后, FIR滤波器加速度估计环节的精度误差为$ \Delta a = 6.98\times{10^{ - 3}}\;{\rm{rad}}/{{\rm{s}}^2} $ ,根据公式(16),求出FIR滤波器的精度$ {\varepsilon}_{a}=0.167\;{\rm{rad}}/{{\rm{s}}}^{2} $ ,满足公式(16)提出的精度要求。图7蓝色部分表示将
$ 10\;{\rm{Hz}},{0.03}^{°} $ 的中频扰动信号输入给LuGre摩擦模型使其产生对应的摩擦力矩,该力矩加入稳定平台伺服系统时平台的速度响应图;红色部分表示经稳定平台角位置信息摩擦补偿之后的平台速度响应图。
图 7 10 Hz,0.03°扰动施加时补偿前后负载速度响应图
Figure 7. Load speed response diagram before and after compensation when 10 Hz,0.03° disturbance is applied
由图7可以看出,摩擦力矩作用于机构使得机构响应速度幅值为
$6.1\times{10^{ - 3}}\;{\rm{rad}}/{\rm{s}}$ ,但采用角加速度估计补偿之后,平台伺服系统的抗干扰能力有了很大的提升。经补偿后机构响应速度幅值仅为$2.5\times{10^{ - 3}}\;{\rm{rad}}/{\rm{s}}$ ,可见对$ 10\;{\rm{Hz}},{0.03}^{°} $ 的中频扰动产生的摩擦干扰该方法能实现很好的抑制效果。 -
由仿真验证结果,基于机构角位置信息的摩擦补偿可以有效抑制平台受到的摩擦扰动。为了进一步验证摩擦补偿方法在稳定平台中的实际应用效果,需要在实验平台上进行验证。
实验平台选择某两轴两框的稳定平台,针对平台方位轴系进行实验。该机构方位轴系转动惯量为0.315 kg·m2,方位电机选用直流有刷力矩电机,陀螺组件选择STM210型陀螺,方位测角元件选择绝对式光电编码器DS-130。陀螺与光电编码器的特性由表3、表4进行说明。
表 3 STM210陀螺主要技术指标
Table 3. Main technical specifications of STM210 gyro
Parameters Value Measuring range/(°)·s−1 −400-400 Zero bias ≤20 Zero bias stability/(°)·h−1 ≤0.5 Bandwidth/Hz 131 表 4 DS-130光电编码器主要技术指标
Table 4. Main technical specifications of DS-130 photoelectric encoder
Parameters Value Resolution/(") 2.47 Precision/(") 9.89 Acquisition delay/ms 0.25 Data update cycle/ms 0.1 文中对摩擦扰动的抑制能力的好坏直接关系到平台视轴稳像精度,所以实验以摩擦补偿方法对平台视轴稳像精度的提升程度为基准进行研究。
实验时,将稳定平台固定于模拟转台上方,给模拟转台输入
$ 10\;{\rm{Hz}},{0.03}^{°} $ 中频扰动信号,采样时间设置为0.04 s,统计20 s的稳定平台实验数据,图8(a)是在$ 10\;{\rm{Hz}},{0.03}^{°} $ 的信号作用下,平台方位轴系的稳像精度图:图8(b) 是在10 Hz,0.03°的信号作用下,平台方位轴系通过最小二乘加速度估计进行摩擦补偿后的稳像精度图。

图 8 10 Hz,0.03°扰动信号输入时摩擦补偿 前后平台的稳像精度
Figure 8. Image stabilization accuracy of the platform before and after friction compensation when 10 Hz,0.03° disturbance signal is input
经过对实验数据进行分析处理,绘制平台受摩擦力矩影响的稳像精度图,对平台输入
$ 10\;{\rm{Hz}},{0.03}^{°} $ 扰动信号,经计算,得到补偿前平台稳像精度是26$\text{μ} {\rm{rad}}$ ,基于机构角位置信息进行加速度估计摩擦补偿之后,平台稳像精度达到了17$\text{μ} {\rm{rad}}$ ,性能提升了34.6%。实验结果表明,文中提供的扰动补偿方法可以切实提高稳定平台稳像精度,提升整体性能。 -
文中以光电稳定平台所受的摩擦力矩扰动作为研究重点,提出了一种新型补偿方法,基于光电平台机构运行的角位置信息来进行加速度估计,设计了一种基于最小二乘法的加速度估计算法,以此建立扰动观测器,对整个回路进行建模仿真,最后,将该模型应用到两轴两框架的稳定平台系统中,模拟转台以10 Hz的频率做正弦运动时,通过对比加入摩擦补偿前后的平台输出实验数据,计算对应的稳像精度。
实验结果表明,未经摩擦补偿时,稳定平台在10 Hz频率下稳定运作的稳像精度是26
$\text{μ} {\rm{rad}}$ ,在经过文中提出的摩擦补偿之后,平台稳像精度达到了17$\text{μ} {\rm{rad}}$ ,稳像精度降低9$\text{μ} {\rm{rad}}$ ,性能整体提升了34.6%,仿真与实验结果表明,使用设计摩擦模型进行摩擦力矩拟合,以此为基础进行机构角位置加速度估计,进行摩擦补偿,可以有效增强平台伺服系统的抗干扰能力,增强系统稳定性能。
Friction observation compensation technology based on angular position information of photoelectric platform
-
摘要: 为了提高光电伺服稳定平台的稳像精度,根据平台所受摩擦扰动作用原理,提出一种基于机构运行角位置信息的摩擦观测补偿方法。首先,建立光电伺服平台精确控制模型,并运用LuGre摩擦模型对平台所受摩擦力矩进行分析;然后,基于机构运行的角位置信息,采用最小二乘法进行加速度估计,设计基于机构运行角位置信息的扰动观测器进行摩擦观测补偿;最后,在Matlab/simulink中建立系统仿真平台,进行仿真及实验验证。将稳定平台安装于模拟转台上进行实验,给转台施加10 Hz正弦信号,对平台摩擦观测补偿前后的实验数据进行对比分析,实验结果表明,该补偿方案在模拟飞行转台以10 Hz频率做正弦运动的情况下,摩擦观测补偿前后,平台稳像精度由26 μrad减小到17 μrad,性能提升34.6%,该方法可以有效增强系统的抗干扰能力,提高系统稳定性能。Abstract: In order to improve the image stability accuracy of the photoelectric servo stabilization platform, a compensation method of friction observation based on the running angle position information of the mechanism was proposed according to the principle of friction disturbance on the platform. Firstly, the precise control model of the photoelectric servo platform was established, and the friction torque of the platform was analyzed by using LuGre friction model, and then, the acceleration was estimated by the least square method based on the angular position information of the mechanism, and a disturbance observer based on the angular position information of the mechanism was designed to compensate the friction observation. Finally, the system simulation platform was established to perform simulation and experimental verification in Matlab/simulink. During the experiment, the mirror mechanism was installed on the simulation turntable, and a 10 Hz sinusoidal signal was applied to the turntable to compare and analyze the before/after experimental data of friction observation compensation. The experimental results show that when the simulation flight turntable moves sinusoidal at 10 Hz frequency, at friction observation of the before/after compensation, the image stabilization accuracy of the platform is reduced form 26 μrad to 17 μrad, and the performance is improved by 34.6%. This method can effectively enhance the anti-interference ability of the system, and improve the stability of the system.
-
表 1 平台参数取值
Table 1. Parameter selection of platform
Item Parameters Value Sample period T/ms 0.1 Rotate inertia J/(kg·m2) 0.086 Torque coefficien K/(N·m·A−1) 0.718 Peak voltage U/V 12.2 Peak current I/A 17 Resistance R/Ω 1.8 Inductance L/mH 5.4 表 2 LuGre摩擦模型参数取值
Table 2. Parameter selection of LuGre friction model
${\sigma _0}$ ${\sigma _1}$ ${\sigma _2}$ ${T_s}$ ${T_c}$ 200 8 0.01 0.15 0.06 表 3 STM210陀螺主要技术指标
Table 3. Main technical specifications of STM210 gyro
Parameters Value Measuring range/(°)·s−1 −400-400 Zero bias ≤20 Zero bias stability/(°)·h−1 ≤0.5 Bandwidth/Hz 131 表 4 DS-130光电编码器主要技术指标
Table 4. Main technical specifications of DS-130 photoelectric encoder
Parameters Value Resolution/(") 2.47 Precision/(") 9.89 Acquisition delay/ms 0.25 Data update cycle/ms 0.1 -
[1] Zheng Chunyan, Zhang Honggang, Feng Xingwei, et al. ADRC of airborne electro-optical stabilized platform [J]. Electronics Optics & Control, 2017, 24(2): 51-54. (in Chinese) [2] Hu Hongjie, Wang Yuanzhe. Composite compensation control scheme for airborne opto-electronic platform [J]. Optics and Precision Engineering, 2012, 20(6): 1272-1281. (in Chinese) doi: 10.3788/OPE.20122006.1272 [3] Zhou Xiangyang, Yang Chao, Cai Tongtong. A model reference adaptive control/PID compound scheme on disturbance rejection for an aerial inertially stabilized platform [J]. Journal of Sensors, 2016, 17(4): 1-11. (in Chinese) [4] Song Xiaoru, Chen Hua, Xue Yonggang. Stabilization precision control methods of photoelectric aim-stabilized system [J]. Optics Communications, 2015, 351: 115-120. doi: 10.1016/j.optcom.2015.04.056 [5] Zhang Mingyue, Liu Hui, Chu Hairong, et al. Double integral sliding mode control based on ESO for stabilized platform of seeker [J]. Infrared and Laser Engineering, 2018, 47(8): 0817009. (in Chinese) doi: 10.3788/IRLA201847.0817009 [6] Chen Zengqiang, Liu Junjie, Sun Mingwei. Overview of a novel control method: active disturbance rejection control technology and its practical applications [J]. CAAI Transactions on Intelligent Systems, 2018, 13(6): 865-877. (in Chinese) [7] Chen Xiaogang, Cai Meng, Dai Ning. A DOB based disturbance suppression method for airborne photoelectric stabilized platform [J]. Electronics Optics& Control, 2020, 27(1): 98-101. (in Chinese) doi: 10.3969/j.issn.1671-637X.2020.01.020 [8] Shi Lei, Xu Yongsen, Tian Dapeng, et al. Design of stable aviation platform operated by cable drive [J]. Optics and Precision Engineering, 2020, 28(6): 1245-1253. (in Chinese) doi: 10.3788/OPE.20202806.1245 [9] Li Hongguang, Peng Fulun, Jiang Xu, et al. Stabilization platform of complex axes embedded into optical path for optics-electricity system with upside mirror [J]. Optics and Precision Engineering, 2019, 27(10): 2224-2232. (in Chinese) doi: 10.3788/OPE.20192710.2224 [10] Ren Yan, Niu Zhiqiang. Application of new terminal sliding mode in photoelectric stabilized platform [J]. Infrared and Laser Engineering, 2018, 47(6): 0617005. (in Chinese) doi: 10.3788/IRLA201847.0617005 [11] Zhang Zhiyong, Li Zhiqiang, Zhou Qingkun, et al. Application in prestiction friction compensation for angular velocity loop of inertially stabilized platforms [J]. Chinese Journal of Aeronautics, 2014, 27(3): 655-662. doi: 10.1016/j.cja.2014.04.026 [12] Al-bender Farid, Swevers Jan. Characterization of friction force dynamics [J]. IEEE Control Systems Magazine, 2008, 28(6): 64-81. doi: 10.1109/MCS.2008.929279 [13] Yao Jianyong, Jiao Zongxia, Yao Bin. Robust control for static loading of electro-hydraulic load simulator with friction compensation [J]. Chinese Journal of Aeronautics, 2012, 25: 954-962. doi: 10.1016/S1000-9361(11)60467-6 [14] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance observer-based control and related methods–An overview [J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1083-1095. doi: 10.1109/TIE.2015.2478397 [15] 吴镇扬. 数字信号处理[M]. 北京: 高等教育出版社, 2004: 134-143 Wu Zhenyang. Digital Signal Processing[M]. Beijing: Higher Education Press, 2004: 134-143. ( in Chinese) [16] Sun Liteng, Dong Limin, Tang Chao. Design of electron wave Tilters in monolayer grapheme with velocity modulations [J]. Chin Phys B, 2013, 22(4): 1-5. -







 下载:
下载: