-
自2004年光子多普勒测速仪[1-2](Photonic Doppler Velocimetry, PDV)提出以来,光子多普勒测速技术因其非接触测量、成本低、使用方便、响应快、量值溯源性好、频响高、动态性能好等优点,被广泛应用于高速冲击[3]、材料高应变率动态力学性能测试[4-5]、动高压技术加载飞片[6]等研究领域中。普通光子多普勒测速系统的数据通过电学高带宽示波器进行采集,因为数模转换技术的带宽限制,将直接导致光子多普勒测速系统范围受到限制。目前,国际上较为成熟的高性能示波器能达到32 GHz带宽,PDV的测速上限因此能达到24.8 km/s,而国内市场较为成熟示波器带宽上限为5 GHz,PDV的测速上限能达到3.9 km/s。面对更高速度的测量需求,使用更高性能示波器将带来更高的成本和技术瓶颈限制。
随着皮秒、飞秒和阿秒激光产生技术的发展,超快测量成为国内外热门研究领域[7]。时间拉伸技术是利用超快激光脉冲在色散介质中的群速色散特性,通过两级色散光纤构成拉伸因子,实现信号频率降低。由于电信行业的发展带来的光纤激光技术的飞速进步,时间拉伸方法被广泛应用与高带宽实时光采样[8]、距离测量[9]、光谱测量[10]、实时光成像[11]等领域[12]。在瞬态高速测量领域,时间拉伸技术是光子多普勒测速系统突破电学数模转换技术瓶颈新型解决方案之一,近两年开始在国外开展研究,国内相关研究较少,尚处于理论研究阶段[13-14]。
2019年,美国内达华国家实验室Mance J G等人提出时间拉伸光子多普勒测速系统(Time-Stretched Photonic Doppler Velocimetry, TS-PDV)。该系统通过脉冲选择器选择单个脉冲,使用色散补偿光纤作为色散器件完成150 ns时间拉伸,拉伸倍数为0.276,在Z机器上测量的爆聚速度达到44 km/s[15]。但是,该方法一方面光源与采集器件需要合适的触发条件,保证在脉冲到达时刻能采集到速度信号;另一方面速度信号仅能在有脉冲时刻被有效采集,测量时间决定于脉冲拉伸宽度,因此测量有效时间受到较大限制。
文中提出改进TS-PDV,飞秒脉冲直接经过一级色散光纤进行拉伸,在时域上完全铺满,避免了采样间断;在信号解调上引入位移误差补偿算法,减小了因为位移引入的系统误差从而增加有效记录时间。
-
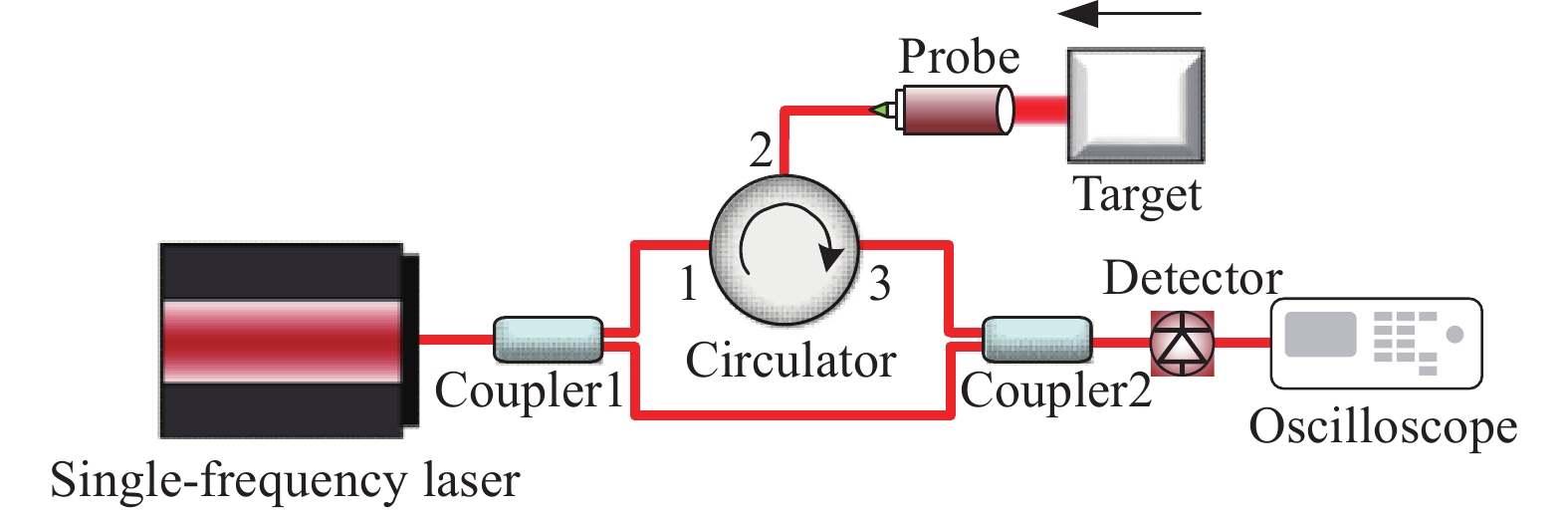
光子多普勒测速系统采用光外差干涉探测技术,如图1所示,通过窄线宽单频激光器产生单频激光,信号光在耦合器1分为频率
$ {\omega _0} $ 的探测光和参考光。探测光从3端口环形器端口进入,从2端口输出到光纤探头上。光信号透射在运动速度为$ \mu (t) $ 目标物体表面,反射回的探测光因目标物体的运动产生多普勒频移。探测光多普勒频移大小与目标物体运动速度成正比,频率为$ {\omega _0} + 2\mu (t)/{\lambda _0} $ 。光强为$ {E_1} $ 探测光与$ {E_2} $ 参考光在耦合器进行混频后,光电探测器将多普勒频移信号转换为可探测的射频信号。目前,常用的光电探测器不能响应光波频率,其他与光频接近或更高频率信息,因为超过光电探测器的响应带宽而被滤去,所以最终检测信号Esignal可表示为:$$ {E_{signal}} = \frac{{E_1^2 + E_2^2}}{2} + {E_1}{E_2}\cos \left[ {\frac{{4\pi }}{\lambda }\mu (t)t + \Delta \varphi } \right] $$ (1) 式中:
$ \Delta \varphi $ 为初始探测光与参考光相位差,相位差固定不变时,探测信号表现为频率随时间变化的瞬态信号。因此,通过短时傅里叶变换、小波变换等时频分析算法可以将目标物体的速度信息解调出来。对于更高测速需求场景,目前工程领域主要通过两种方法实现测速范围的扩展。(1)采用多个不同波长激光器,通过级联方式实现测速范围扩展,该系统称为Leapfrog-PDV。该方法采用多个不同波长的光源作为级联通道参考信号,不同通道通过提高参考光频率基准来降低拍频频率 [16];(2) TS-PDV将采集到的速度信号利用飞秒激光的时间拉伸原理在光域内进行降频处理,可以直接通过控制一级色散光纤长度
$ {L_1} $ 与二级色散光纤长度$ {L_2} $ 的比例来控制降频因子$ M = {L_1}/({L_1} + {L_2}) $ ,降低了光电信号采集与电学数模转换技术带宽压力,理论上可以将PDV测速范围扩展为原来的10倍。Leapfrog-PDV光源为普通连续激光,继承了PDV能不间断测量和测量准确度高的优点,但Leapfrog-PDV方法需要配备多个激光器和光电探测器,这种级联方式让系统变得更为复杂,对于更高测速需求不可能继续通过叠加激光器来解决。 -
时间拉伸光子多普勒测速系统光源使用飞秒激光器,飞秒激光脉冲一般脉冲宽度在fs级别,光谱宽度能够达到几十nm。飞秒激光脉冲在色散介质中传输过程中,不同光谱成分将会因为自身传播速度不同被映射在时域不同的时间点,因此可以通过色散介质控制不同光谱成分时频分布,达到降频目的。
时间拉伸光子多普勒测速系统结构图如图2所示,锁模激光器使用50 MHz飞秒激光,经过滤波器筛选出合适的波长范围,可调衰减器减小飞秒脉冲功率,减弱飞秒激光脉冲在单模光纤中的非线性效应。单模光纤配合光纤反射镜实现双倍色散量,达到双倍长度单模光纤的拉伸效果。一级拉伸通过SMF1配合光纤反射镜的使用,实现L1=200 km的色散拉伸,二级拉伸是SMF2采用同样方式实现L2=100 km拉伸效果。探测光和参考光在SMF1和SMF2中进行拉伸时,两者还没有分离,此时参考光频率等于探测光频率
$ {\omega _{ref}} = {\omega _{sig}} $ 。经过SMF1后,光脉冲进行了充分的时间拉伸,从飞秒级时间长度脉冲展宽到时间长度为纳秒级,不同频率分量的信号在时域上展开分布形成啁啾脉冲信号。耦合器1将光信号分为探测光$ {\omega _{sig}} $ 和参考光$ {\omega _{ref}} $ ,此时$ {\omega _{sig}} = {\omega _{ref}} $ ,探测光通过掺铒光纤放大器EDFA进行功率放大至1 W。经过目标物体反射回的带有速度信息的频率为$ {\omega _{shift}} $ 频移信号与频率为$ {\omega _{ref}} $ 的参考信号在耦合器2进行混频,因为目标物体速度$ u $ 远远小于光速$ c $ ,可以将探测光频率与参考光频率关系近似处理为$ {\omega _{ref}} \approx {\omega _{shift}}(1 - 2 u/c) $ 。频率
$ \omega $ 的光信号通过长度为$ L $ 的光纤线路传播,$ \;{\beta _i} $ 值为相位传播常数。信号相对于频率$ {\omega _0} $ 在光纤中的传播时间可记为:$$ \mathop t\limits^{} = {\beta _1}L + {\beta _2}L(\omega - {\omega _0}) + \frac{1}{2}{\beta _2}L{(\omega - {\omega _0})^2} + \cdot \cdot \cdot $$ (2) 忽略高阶色散项,探测光和参考光相对于中心频率
$ {\omega _0} $ 光信号的传输时间$ {t_{sig}} $ 和$ {t_{ref}} $ 可以概括为:$$ \begin{split} {t_{ref}} =& {\beta _1}({L_1} + {L_2}) + {\beta _2}({L_1} + {L_2})({\omega _{ref}} - {\omega _0}) +\\ &\frac{1}{2}{\beta _3}({L_1} + {L_2}){({\omega _{ref}} - {\omega _0})^2} \end{split} $$ (3) $$ \begin{split} {t_{sig}} =& {\beta _1}L + {\beta _2}{L_1}({\omega _{shift}}(1 - 2u/c) - {\omega _0}) + {\beta _2}{L_2}({\omega _{shift}} - {\omega _0}) + \\ &\frac{1}{2}{\beta _3}{L_1}{({\omega _{shift}}(1 - 2u/c) - {\omega _0})^2} + \frac{1}{2}{\beta _3}{L_2}{({\omega _{shift}} - {\omega _0})^2}\\[-8pt] \end{split} $$ (4) 调节延时器使参考路与探测路光程相等,因此两路信号在初始状态时频分布完全相同。在拍频时刻参考光和探测光的传输时间相等
$ {t_{sig}} = {t_{ref}} $ ,因此由公式(3)和公式(4)可以得到:$$ {\omega _{ref}} = {\omega _{shift}}\left(1 - \frac{{{L_1}}}{{{L_1} + {L_2}}}\frac{{2u}}{c}\right) $$ (5) 其中
$ \lambda $ 为激光波长,因此光电探测器探测到的差频可表示为:$$ {\omega _d} = {\omega _{shift}} - {\omega _{ref}} = {\omega _{ref}}\frac{{{L_1}}}{{{L_1} + {L_2}}}\frac{{2u}}{c} = \frac{{{L_1}}}{{{L_1} + {L_2}}}\frac{{2u}}{\lambda } $$ (6) 依据公式(6),光脉冲经过SMF3第二次时域展宽,探测光与参考光频率差被降低为
$ M = {L_1}/ ({L_1} + {L_2}) $ 倍。示波器使用纳秒激光器Q-Switch作为触发信号,将示波器延时至触发后500 µs开始采集。由于目标物体位移引起信号臂和参考臂中啁啾脉冲引入相位差,探测器拍频信号中包含了位移引入的系统误差信号。系统色散总长度为L1+L2=300 km,色散系数D=16.7 ps/(nm·km),锁模光源通过滤波器后,光谱起始波长
$ {\lambda _s} = 1\;550 $ nm和终止波长$ {\lambda _e} = 1\;560 $ nm ,$ \Delta T $ 为拉伸的脉冲宽度,可表示为:$$ \Delta T = D({L_1} + {L_2})({\lambda _s} - {\lambda _e}) $$ (7) $ \Delta T $ 在第一级单模光纤后脉冲宽度为20 ns,信号在整个时域被完全铺满。此时飞秒脉冲被拉伸为准连续光,避免了目标物体速度信息丢失。调节参考臂和信号臂长相等,目标物体运动位移$ x $ 后,其因位移产生两臂相位时延为$ \Delta t = x/c $ 。由于距离较短,忽略高阶项,此时不同频率的光在时域上被认为线性分布,位移产生的频差信号可表示为:$$ {\omega _d} = 2 \cdot \frac{x}{c} \cdot \frac{{c/{\lambda _s} - c/{\lambda _e}}}{{\Delta T}} = 2 \cdot \frac{x}{{{\lambda _s}{\lambda _e}({L_1} + {L_2})D}} $$ (8) 式中:c为光在空气中传播速度。在文中的系统实验中,随着目标物体的移动,飞片被记录的位移约为5 mm,因位移产生的频差能达到约600 MHz,因此必须通过误差补偿的算法进行补偿。
-
目前,瞬态高速测量环境主要由以下5类:气炮、化学爆炸、电脉冲、磁驱动和激光驱动[17]。激光驱动飞片是一种更为安全、成本更低和测量效率更高的测速环境[18]。该方案中高速目标由纳秒激光驱动铝膜产生,该系统中纳秒激光器使用vlite-200,输出波长532 nm,单脉冲能量200 mJ,飞片材料采用3 µm厚铝金属膜,汇聚焦斑直径2 mm。纳秒激光器发出纳秒脉冲经过透镜汇聚作用于铝膜表面,铝膜表面被烧蚀部分经过熔化、气化、电离过程而产生高温高压等离子体,表面后未被烧蚀部分在等离子体作用下沿激光入射方向加速运动,形成高速飞片被发射出去。
PDV是常用的速度诊断工具,测速精度小于1%,实验使用PDV测量结果作为速度曲线参考真值。由于飞片速度曲线重复性较好,图3中测速系统采用PDV和TS-PDV分离独立测量方式以获得更高信噪比频移信号。通过PDV和TS-PDV测量时频图分布如图4所示,时频图在飞片加速阶段后呈现较为分散状态,主要原因是纳秒激光驱动金属膜时,发射的金属膜并非是完整的飞片,而是由多个小碎片组成,不同位置的小碎片携带不同频率多普勒频移信号,时频图呈现较为分散状态。

图 3 高速飞片产生与速度测量系统原理图
Figure 3. Schematic diagram of high-speed flyer generation and velocity measurement system
速度曲线需要通过图像处理算法进行能量脊线提取。首先通过阈值处理对时频图进行预处理,然后通过膨胀腐蚀标记区域,使用骨架提取、筛选和连通算法提取出能量脊线。如图5所示,黄色轮廓是通过图像处理选取出区域,中间黄色曲线通过骨架提取算法提取出能量脊线,提取出能量脊线坐标后,通过插值拟合和平滑处理得到最终多普勒频移曲线,如图5中红色虚线所示。

图 5 不同系统测量时频脊线提取对比图
Figure 5. Comparison of the time-frequency ridge extraction diagram measured by different systems
提取到的速度曲线通过标定算法完成多普勒频移到速度信号的转化。但该速度信号中仍然包含因位移产生的系统误差。位移通过梯形公式对速度积分,
$\Delta {{{t}}_{\text{0}}}$ 为采样间隔,$ a $ 为位移误差常数,可由公式(7)得到。时刻1目标物体静止,初始速度$ {v_1} $ 与位移$ {x_1} $ 为0,$ {f_1} $ 为0。不同时刻的速度$ V({v_1},{v_2},{v_3}\cdots{v_t}) $ 、位移$ X({x_1},{x_2},{x_3}\cdots{x_t}) $ 和采样数据$ F({f_1},{f_2},{f_3}\cdots{f_t}) $ 可用公式(9)表示。$ v $ 为其中唯一未知量,通过上述方法,求解出消除位移误差的速度$ V({v_1},{v_2},{v_3}\cdots{v_t}) $ 。$$ \begin{gathered} \\ {v_1} = {f_1} = 0\begin{array}{*{20}{c}} {}&{{x_1} = 0} \end{array} \\ {v_2} + a{x_2} = {f_2}\begin{array}{*{20}{c}} {}&{{x_2} = {x_1} + \dfrac{{\Delta {t_0} \cdot ({v_1} + {v_2})}}{2}} \end{array} \\ {v_3} + a{x_3} = {f_3}\begin{array}{*{20}{c}} {}&{{x_3} = {x_2} + \dfrac{{\Delta {t_0} \cdot ({v_2} + {v_3})}}{2}} \end{array} \\ \cdots \\ \end{gathered} $$ (9) 式中:
$ v $ 表示速度;$ x $ 表示位移;$ f $ 表示通过TS-PDV采集直接转换的速度数据。 -
通过图像处理提取算法后得到如图6(a)所示速度曲线,PDV测量结果作为TS-PDV参考值,通过与参考值相比较,随着目标飞片飞行时间增大,因位移带来的系统误差越来越大,因位移带来动态系统误差占比最终达到40% (如图6(b)所示,而经过位移误差补偿算法补偿后,与PDV参考测量速度系统误差明显减小,其动态误差明显降低。从总体趋势上来看,通过位移误差算法补偿,在1.2 µs测量时间内,时间拉伸光子多普勒测速系统与普通光子多普勒测速系统动态误差能稳定在5%以内,实验效果较好。产生动态误差主要原因是在时频脊线的提取算法过程中。时频图中能量分布较为分散,图像处理操作的区域骨架提取算法受到较大影响,因此动态误差在5%范围内进行波动。
实验中飞秒脉冲经过第一次时间拉伸后,脉冲时间20 ns,经过第二次时间拉伸后,脉冲拉伸为30 ns。相邻脉冲间混叠时间10 ns,而示波器相邻采样时间间隔为25 ps,短时傅里叶变换时间窗长1200,在时频信号分析最小时间分辨为30 ns,混叠时间小于最小时间分辨,因此该混叠时间可以忽略。实验中拉伸倍数受到了第二级色散器件的影响,若增大拉伸倍数还需要增加第二级光纤长度,此次实验受限于单模光纤长度,继续增加单模光纤长度,会增强光脉冲在光纤传输的非线性效应,系统频谱成分变得非常复杂,所以要增大拉伸倍数在色散器件上还有很大优化空间。
-
文中提出了一种改进时间拉伸光子多普勒测速系统,飞秒激光经过一级色散光纤进行充分拉伸铺满整个时域,避免了信号采样间断和锁模光源触发条件限制;通过后端位移误差补偿算法,减小因位移产生的系统误差,延长系统有效记录时间。该系统通过飞秒激光时间拉伸原理实现信号在光域中实现降频处理,完成了在1.2 µs测量时间内,将3.6 GHz的多普勒频移信号降低为2.4 GHz、拉伸倍数为2/3的激光驱动飞片测速实验验证,通过与PDV进行比对测量,测速动态误差在5%以下。
文中对时频图上因激光器相邻脉冲采集速度信号的重叠影响进行了忽略,该系统时间分辨能力局限在纳秒分辨能力的场景下。在高时间分辨能力、拉伸倍数、位移补偿等技术上还有较大优化空间。改进的TS-PDV适用于高功率脉冲激光、磁驱动、电爆炸、化学爆炸等动高压加载飞片速度测量领域,丰富瞬态高速领域测量手段。该系统在时间拉伸倍数上可以灵活调节拉伸倍数,理论上能够将频率降低为原来10倍,在超高速目标飞片速度测量中具有更加明显优势。
Research on time-stretched photon Doppler velocimetry
-
摘要: 在瞬态高速测速场景中,目标物体在几十ns时间内能加速到几~几十km/s,因此光子多普勒测速系统中电学数模转换器件带宽要求达到GHz甚至上百GHz。时间拉伸光子多普勒测速系统利用飞秒激光时间拉伸特性,在光域中完成信号降频处理,降低了光电信号探测器件和电学数模转换器件带宽压力。提出了改进的时间拉伸光子多普勒测速系统,飞秒脉冲经过第一级色散器件充分展宽铺满整个时域,避免了速度信号的采样间断;信号解调上采用误差补偿算法对频移信号进行补偿,减小了因为位移引入的系统误差,从而增加了有效记录时间。实验使用纳秒激光驱动铝膜产生高速飞片,测试了文中测速系统在记录时间1.2 µs内的实验效果。实验使用重频50 MHz飞秒光源,第一级和第二级色散器件分别使用200 km和100 km单模光纤,构成比例因子2/3。最终实验表明系统将3.6 GHz的多普勒频移信号降低为2.4 GHz,通过与光子多普勒测速系统进行结果比对,实验动态误差小于5%。该系统将能够应用于多种动高压技术加载飞片场景下的速度进行测量,为瞬态高速测量领域提供了新的测量手段。Abstract: In the transient high-speed velocity measurement scene, the target accelerates to several-tens of km/s in tens of ns. Therefore, the Doppler frequency shift can reach GHz or even hundreds of GHz. The velocity measurement range of photon Doppler velocimetry was limited by the current electrical digital to analog conversion technology. The time-stretched photon Doppler velocimetry used the time-stretched characteristic of femtosecond laser to reduce the signal frequency in the optical domain, which reduced the pressure of photoelectric signal detector and electrical digital-to-analog conversion device. An improved time-stretched photon Doppler velocimetry system was proposed in this paper. The femtosecond pulse was fully widened and spread over the whole time domain through the first stage dispersion fiber, in order to avoid the sampling interruption of velocity signal; In signal demodulation, error compensation algorithm was used to compensate the frequency shift signal, which reduced the system error caused by displacement and increased the effective recording time. Nanosecond laser was used to drive the aluminum film to produce high-speed flyer in the experiment, and the experimental results of the paper speed system were tested in the recording time of 1.2 µs. The repetition frequency 50 MHz femtosecond laser was used in the experiment. The first and second stage dispersion devices used 200 km and 100 km single-mode fiber, forming a scale factor of 2/3. In the end, the experiment showed that the Doppler shift signal of 3.6 GHz was reduced to 2.4 GHz, which was compared with the photon Doppler velocimetry system, and the experimental error was less than 5%. The system will be able to apply velocity measurement under dynamic high pressure technology loading flyer scene, and provides new measures for transient high-speed measurement area.
-
-
[1] Strand O T, Berzins L V, Goosman D R, et al. Velocimetry using heterodyne techniques [J]. International Congress on High-Speed Imaging and Photonics, 2005, 77(8): 083108. [2] Wu L Z, Chen S J, Ye Y H, et al. Photonic Doppler velocimetry used for instant velocity measurement of high-speed small flyer [J]. Infrared and Laser Engineering, 2016, 45(12): 1217001. (in Chinese) [3] Weng J D, Li Y L, Chen H, et al. Application of all-fiber displacement interferometry in SHPB experimental measurement [J]. Chinese Journal of High Pressure Physics, 2018, 32(1): 94-99. [4] Wang C H, Lee H, Hsu Y H, et al. Photonic Doppler velocimetry for high-speed fragment generator measurements. [J]. Optics Express, 2020, 28(3): 3864-3878. doi: 10.1364/OE.377832 [5] Dolan D H. Extreme measurements with Photonic Doppler Velocimetry (PDV). [J]. The Review of Scientific Instruments, 2020, 91(5): 051501. doi: 10.1063/5.0004363 [6] Stanley B, Allan C, Micheal K, et al. Measurement and characterization of nanosecond laser driven shockwaves utilizing photon Doppler velocimetry [J]. J Appl Phys, 2021, 129(20): 205101. [7] Fortier T, Baumann E. 20 years of developments in optical frequency comb technology and applications [J]. Communications Optics, 2019, 3(1): 1-27. [8] Li Y H, Zhu K, Kang Z, et al. CMOS-compatible high-index doped silica waveguide with an embedded silicon-nanocrystal strip for all-optical analog-to-digital conversion [J]. Photonics Research, 2019, 7(10): 1200-1208. doi: 10.1364/PRJ.7.001200 [9] Zhao L J, Zhao C B, Xia C Q, et al. Nanometer precision time-stretch femtosecond laser metrology using phase delay retrieval [J]. Journal of Lightwave Technology, 2021, 39(15): 5156-5162. [10] 章振. 基于飞秒激光时域拉伸的超快光谱学技术[D]. 中国科学技术大学, 2021. Zhang Z. Ultrafast spectroscopy based on femtosecond time-stretch technique[D]. Hefei: University of Science and Technology of China, 2021. (in Chinese) [11] Goda K, Tsia K K, Jalia B. Serial time-enconded amplified imaging for real-time observation of fast dynamic phenomena [J]. Nature, 2009, 458: 1145-1149. [12] Mahjoubfar A, Churkin D V, Barland S, et al. Time stretch and its applications [J]. Nat Photonics, 2017, 11(6): 341-351. doi: 10.1038/nphoton.2017.76 [13] Lv L J, Wu T F, Han J B, et al. Research status and prospect of transient high-speed Photon Doppler Velocimetry [J]. Metrology & Measurement Technology, 2021, 41(2): 64-72. (in Chinese) doi: 10.11823/j.issn.1674-5795.2021.02.07 [14] Wu T F, Lv L J, Han J B, et al. Simulation of time-stretched photon Doppler velocimetry[C]//Sixteenth National Conference on Laser Technology and Optoelectronics, 2021, 11907: 119072Z. [15] Mance J G, La Lone B M, Dolan D H, et al. Time-stretched photonic Doppler velocimetry [J]. Optics Express, 2019, 27(18): 25022-25030. doi: 10.1364/OE.27.025022 [16] Dolan D H, Lemke R W, McBride R D, et al. Tracking an imploding cylinder with photonic Doppler velocimetry [J]. Rev Sci Instrum, 2013, 84(5): 055102. doi: 10.1063/1.4803074 [17] Luo B Q, Zhang X P, Hao L, et al. Advances on the techniques of ultrahigh-velocity launch above 7 km/s [J]. Explosion and Shock Waves, 2021, 41(2): 5-15. (in Chinese) [18] Wang Z H, Li Y, Qin W Z, et al. Research progress in the flight characteristics of laser-driven flyer [J]. Chinese Journal of Energetic Materials, 2019, 27(3): 255-264. (in Chinese) doi: 10.11943/CJEM2018235 -







 下载:
下载: