-
倾斜和非平面表面上的微结构有独特的光、机、电、热特性[1-5],因此广泛应用于微光学、微电子学、微流体等领域。例如,与自适应光学的传统方法相比,在弯曲折射表面上添加衍射微结构可以起到简化消色差光学系统的作用[6];植入式神经探针侧壁上的微结构是记录三维神经信号的有效方法[7];微流控通道垂直方向的表面微纳加工可以显著提高其性能[8]。
传统的平面光学投影光刻[9],将光掩模图案通过投影物镜成像到涂有光刻胶的硅衬底上,具有很高的效率和分辨率,然而,由于成像光学的限制,很难实现对斜面或曲面的光刻。双光子激光直写光刻[10-11]、电子束离子束直写光刻[12-15]等直写式光刻技术是当前用于斜面和曲面微结构加工的主要技术。但是由于采用的是逐点扫描加工的方式,所以加工效率低,不适合应用于大批量加工。
利用计算机生成全息图将目标图案直接投影到光刻胶表面进行曝光[16],无需投影物镜,不受光学成像限制,加工效率也大大提升,是实现斜面、曲面甚至三维光刻的一种可行方案。Maxim Shusteff等[17]利用从相互垂直的三个方向射入的平面全息光场叠加而成的三维光场实现了一些特殊三维结构的光固化,然而基底会遮挡三面光场的叠加,不能用于斜面和曲面的光刻。王鹏等[18]使用改进的直接二元搜索算法,设计并制作了一个三维衍射相位掩膜,利用该掩膜形成的三维光场实现了斜面和多平面的光刻,但该方法形成的全息光场质量较差,存在许多散斑,光场层与层之间的间隔也较大,光刻效果并不理想,而且衍射相位掩膜的制作成本高、加工难度大,一个掩膜也只能加工单一产品,灵活性受限。
为实现灵活、快速的斜面和曲面光刻,文中提出了基于液晶空间光调制器的计算全息光刻法,用空间光调制器取代传统的物理掩膜,从而实现了计算机实时可控的任意结构光刻,降低了成本,同时也增强了光刻的灵活性。此外,为了提高光场质量,针对斜面和曲面采用了不同的计算全息算法,利用多幅随机相息图在空间光调制器上快速切换的方法使得光场更加均匀,大大减少了斑点噪声的影响。
-
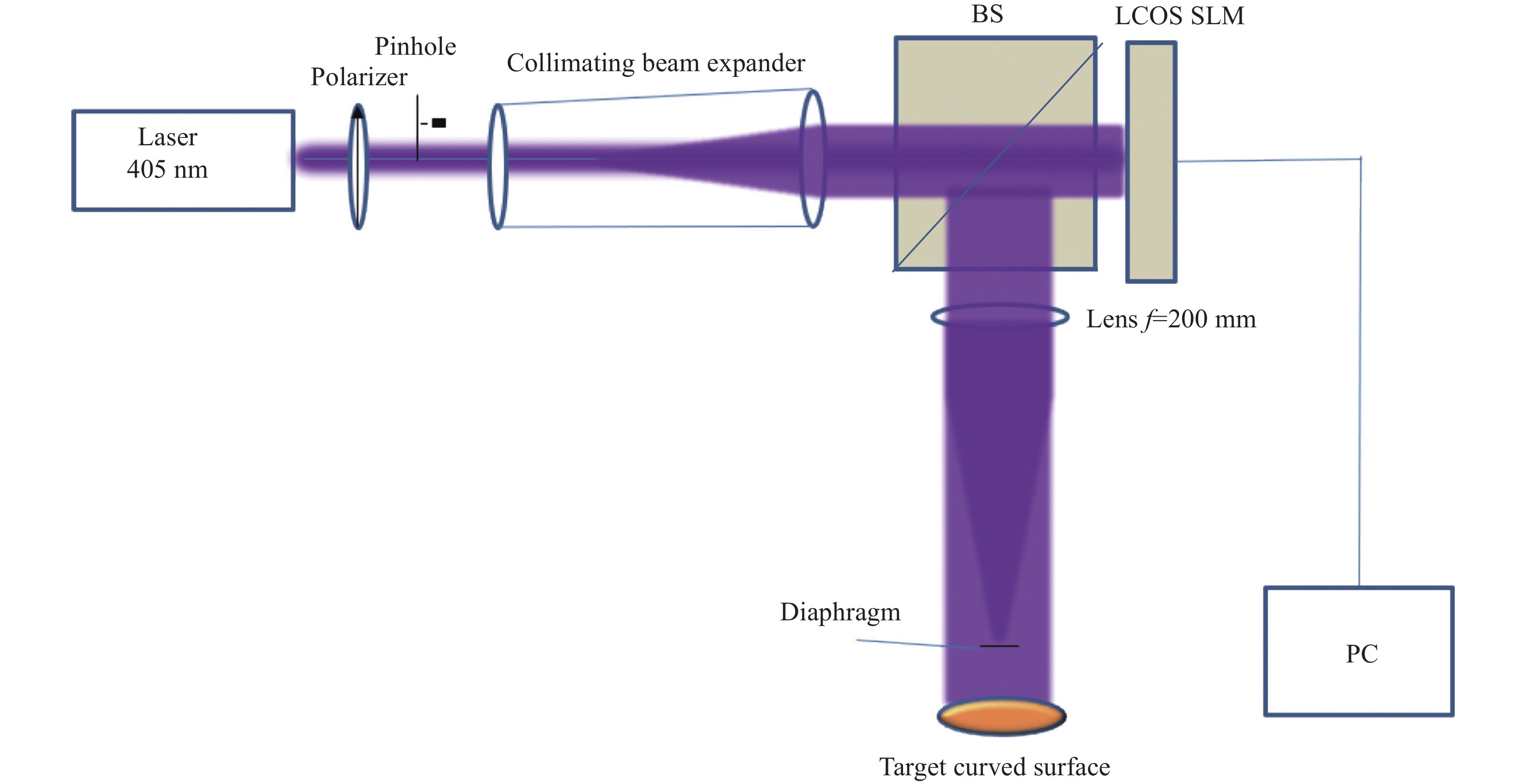
图1为光刻系统的结构示意图,激光出射后经小孔扩束匀化器件后,平行入射到加载了纯相位全息图的液晶空间光调制器上,对入射光进行调制,经过透镜后得到目标三维光场,实现对目标曲面表面光刻胶的曝光。由于空间光调制器的填充率并非100%,因此,并非所有入射光都能被调制,这些未被调制的光经过透镜后会汇聚到其焦点处,控制目标光场成像在透镜焦点之后,再放置一个光阑在透镜焦面即可排除这些未被调制的光。
-
纯相位空间光调制器理论上有更高的衍射效率,因此,纯相位全息图是当前计算机生成全息图的主流编码方式。Gerchberg-Saxton(GS)[19]算法及其改进算法[20-23]是计算全息迭代算法中运用最多的算法,在该类算法中,根据全息图平面与重建图像平面振幅分布,通过迭代进行正逆向的光波传递以及施加在两个平面上的限制条件,进而求得全息平面中光场的相位信息。
-
根据角谱衍射理论,空间平面上的光场可以利用傅里叶变换分解为不同方向传播的平面波。因此,如果能够通过频率空间的坐标变换,将原先表示在某空间平面的这些平面波在与原平面不平行的新坐标系中重新表示,则能通过新坐标系中的傅里叶逆变换求出在新坐标平面下的光波场,实现平面到斜面的正逆向衍射运算,Matsushima等[24]就利用这一原理实现了斜面投影,然而其实现的是由全息面直接到目标斜面的投影。在文中的光刻系统中,为了去除未被空间光调制器调制的杂散光,需要在全息面后使用一个凸透镜。如图2所示,其光路传播过程可分解为,目标斜面
${x}_{\rm t}{y}_{\rm t}$ 传播到与全息面平行的平面${x}_{\rm p}{y}_{\rm p}$ ,再由${x}_{\rm p}{y}_{\rm p}$ 平面到透镜焦面,最后,透镜焦面经透镜传播到全息面。若设目标图像的振幅为t(${x}_{\rm t}$ ,${y}_{\rm t}$ ),则其频谱如下:$$T\left({f}{x}_{\rm t},{f}{y}_{\rm t}\right)=F\left\{{t}\left({x}_{\rm t},{y}_{\rm t}\right)\times \mathrm{exp}\left[-{i}{k}{y}_{\rm t}\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\theta }\right)\right]\right\} $$ (1) 式中:F表示傅里叶变换
$ \mathrm{\theta } $ 为斜面与平面之间的夹角;f${x}_{\rm t}$ , f${y}_{\rm t}$ 是坐标轴${x}_{\rm t}{y}_{\rm t}$ 表示的空间频谱。经过坐标变换即可得到坐标轴
${x}_{\rm p}{y}_{\rm p}$ 下的频谱,图中仅围绕x轴发生了旋转,故坐标变换矩阵M计算如下:$$ \left[\begin{array}{c}{f}{x}_{\mathrm t}\\ \begin{array}{c}{f}{y}_{\mathrm t}\\ {f}{{\textit{z}}}_{\mathrm t}\end{array}\end{array}\right]=M\left[\begin{array}{c}{f}{x}_{\mathrm p}\\ \begin{array}{c}{f}{y}_{p}\\ {f}{{\textit{z}}}_{\mathrm p}\end{array}\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& \mathrm{cos}\theta & \mathrm{sin}\theta \\ 0& -\mathrm{sin}\theta & \mathrm{cos}\theta \end{array}\right]\left[\begin{array}{c}{f}{x}_{\mathrm p}\\ \begin{array}{c}{f}{y}_{\mathrm p}\\ {f}{{\textit{z}}}_{\mathrm p}\end{array}\end{array}\right] $$ (2) 那么平行平面
${x}_{\rm p}{y}_{\rm p}$ 的频谱可以表示为:$$P\left({f}{x}_{\mathrm p},{f}{y}_{\mathrm p}\right)=T\left(\mathrm{\alpha }\left({f}{x}_{\mathrm p},{f}{y}_{\mathrm p}\right),\mathrm{\beta }\left({f}{x}_{\mathrm p},{f}{y}_{\mathrm p}\right)\right){{J}}\left|{f}{x}_{\mathrm p},{f}{y}_{\mathrm p}\right| $$ (3) 其中
$$ {{\alpha}} \left({f}{x}_{\mathrm p},{f}{y}_{\mathrm p}\right)={{f}}{x}_{\rm t}=0 $$ (4) $$ {\beta} \left({f}{x}_{\mathrm p},{f}{y}_{\mathrm p}\right)={{f}}{y}_{\rm t}={{f}}{{\textit{z}}}_{\rm p}\mathrm{cos}\theta -{f}{y}_{\mathrm p}\mathrm{sin}\theta $$ (5) 式中:
${J}$ 表示雅各比矩阵,那么平行平面${x}_{\rm p}{y}_{\rm p}$ 的复振幅分布表示为:$$ U\left({x}_{\rm p}{y}_{\rm p}\right)={F}^{-1}\left(P\left({f}{x}_{\rm p},{f}{y}_{\rm p}\right)\right) $$ (6) $ {F}^{-1} $ 表示二维傅里叶逆变换,透镜焦面到平行平面${x}_{\rm p}{y}_{\rm p}$ 之间的传播是菲涅耳衍射,透镜焦面上的复振幅经透镜傅里叶逆变换可得到全息面光场,若$ {T}_{Z} $ 表示透镜焦面到平面${x}_{\rm p}{y}_{\rm p}$ 的传播过程,$ {T}_{Z}^{-1} $ 表示平面${x}_{\rm p}{y}_{\rm p}$ 到透镜焦面的传播过程,则全息面光场分布为:$$ U\left(x,y\right)={F}^{-1}\left({T}_{Z}^{-1}U\left({x}_{\rm p}{y}_{\rm p}\right)\right)$$ (7) 经过上述过程的逆运算即可得到全息面到目标斜面的衍射计算。
-
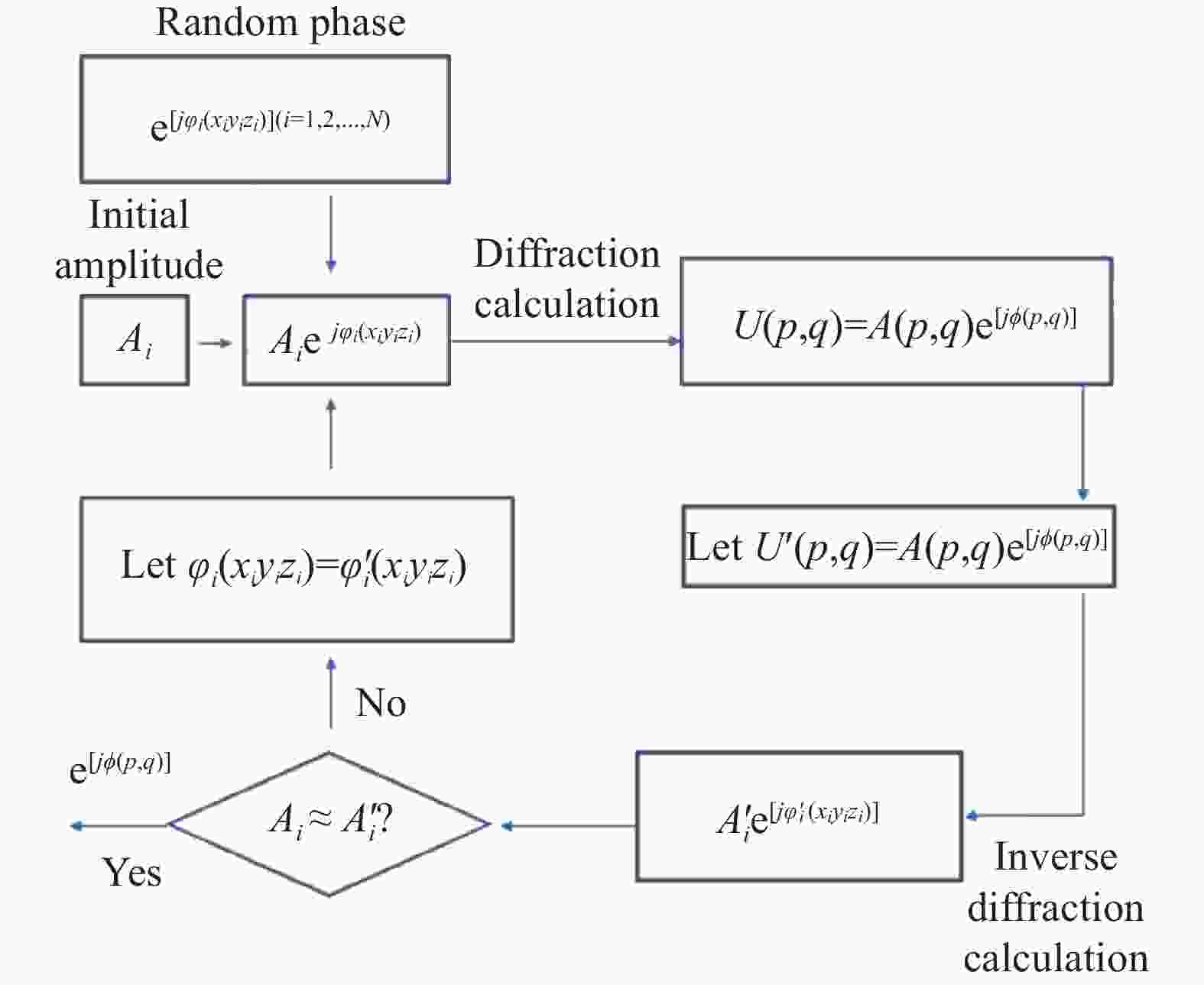
完成了正向和逆向的衍射计算推导之后,只需在全息面和目标斜面上添加振幅限制然后来回迭代运算即可实现纯相位全息图的优化。具体算法流程如图3所示。
(1)斜面初始复振幅为
${A}_{i}{\rm e}^{j{\phi }_{i}\left({x}_{i}{y}_{i}{{\textit{z}}}_{i}\right)}$ ,$ {A}_{i} $ 为目标图案振幅,${\rm e}^{j{\phi }_{i}\left({x}_{i}{y}_{i}{{\textit{z}}}_{i}\right)}$ 为随机生成的相位,计算该光场传播到全息平面的光场为$ U(p,q) $ ;(2)限制条件:实际入射到全息平面的光场是均匀的平行光,故限制全息平面振幅相等,这里限制振幅都为1,故将步骤(1)中计算得到全息平面光场
$ U(p,q) $ 振幅都置1为$ {U'}(p,q) $ ;(3)计算
$ {U'}(p,q) $ 由全息平面传播到倾斜面的光场为${{A}}'_{i}{\rm e}^{j{{\phi }}'_{i}\left({x}_{i}{y}_{i}{z}_{i}\right)}$ ;(4)判断斜面上的光场振幅与目标振幅的差距是否满足精度条件,如果是,则输出第二步中的
${U'}(p,q)$ 作为全息图,如果不是,则进入下一步;(5)限制条件:以目标图案强度替换步骤(3)中斜面光场的振幅,得到斜面光场为
${A}_{i}{\rm e}^{j{{\phi }}'_{i}\left({x}_{i}{y}_{i}{z}_{i}\right)}$ ,回到步骤(1)继续迭代,直到所得结果满足精度条件。 -
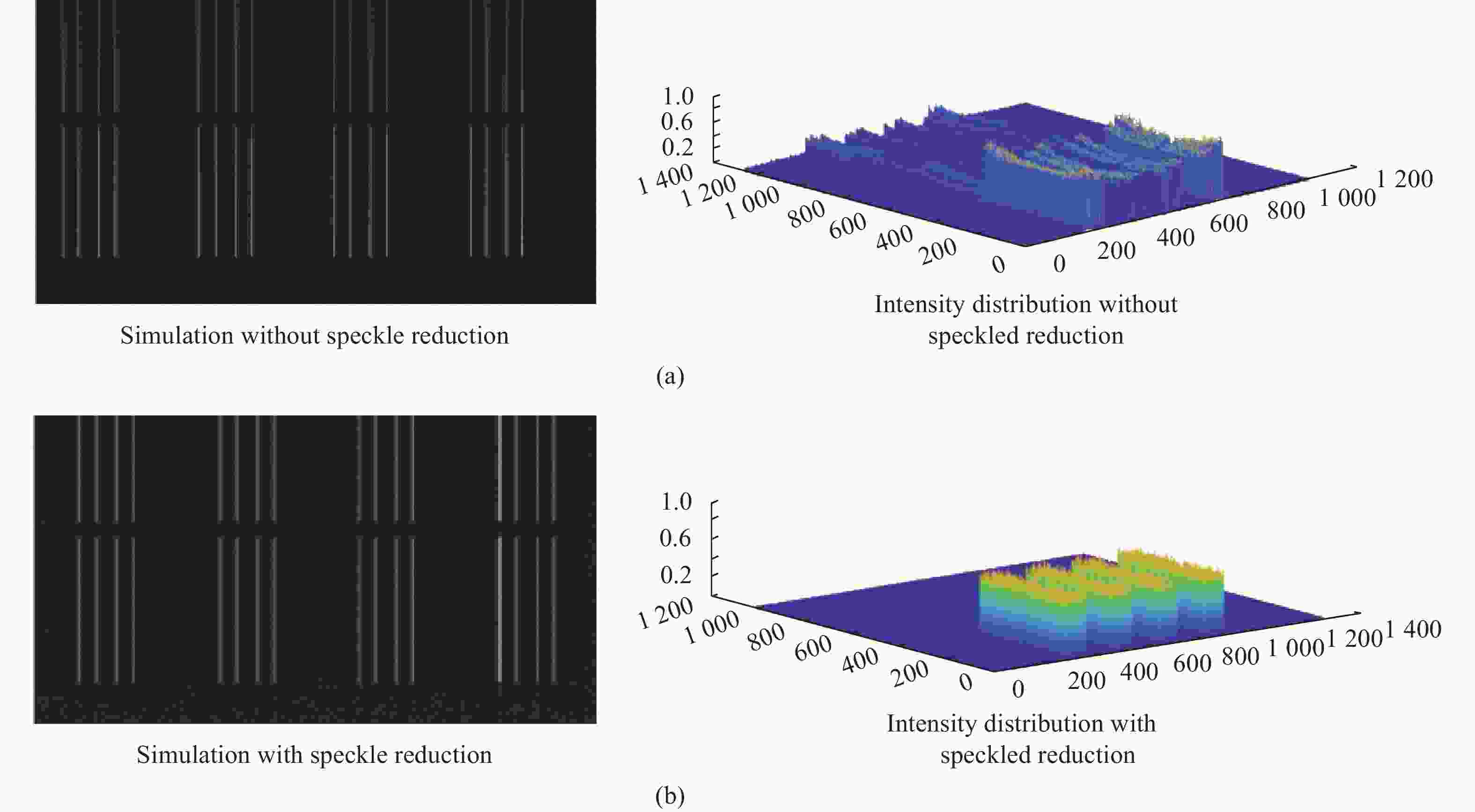
GS类算法在迭代过程中目标面上的相位不受限制,相邻点随机发生的干涉会形成斑点噪声。理论上,每幅相息图相位都是随机的,产生的斑点位置也是随机的,所以当多幅目标振幅相同的相息图快速切换时可以起到匀化光场,减弱散斑影响的作用。为了验证该方法的有效性,笔者以八组单像素条纹的目标图案为例进行了仿真,为衡量全息光场的误差,采用均方误差(RMSE)作为标准,具体定义为
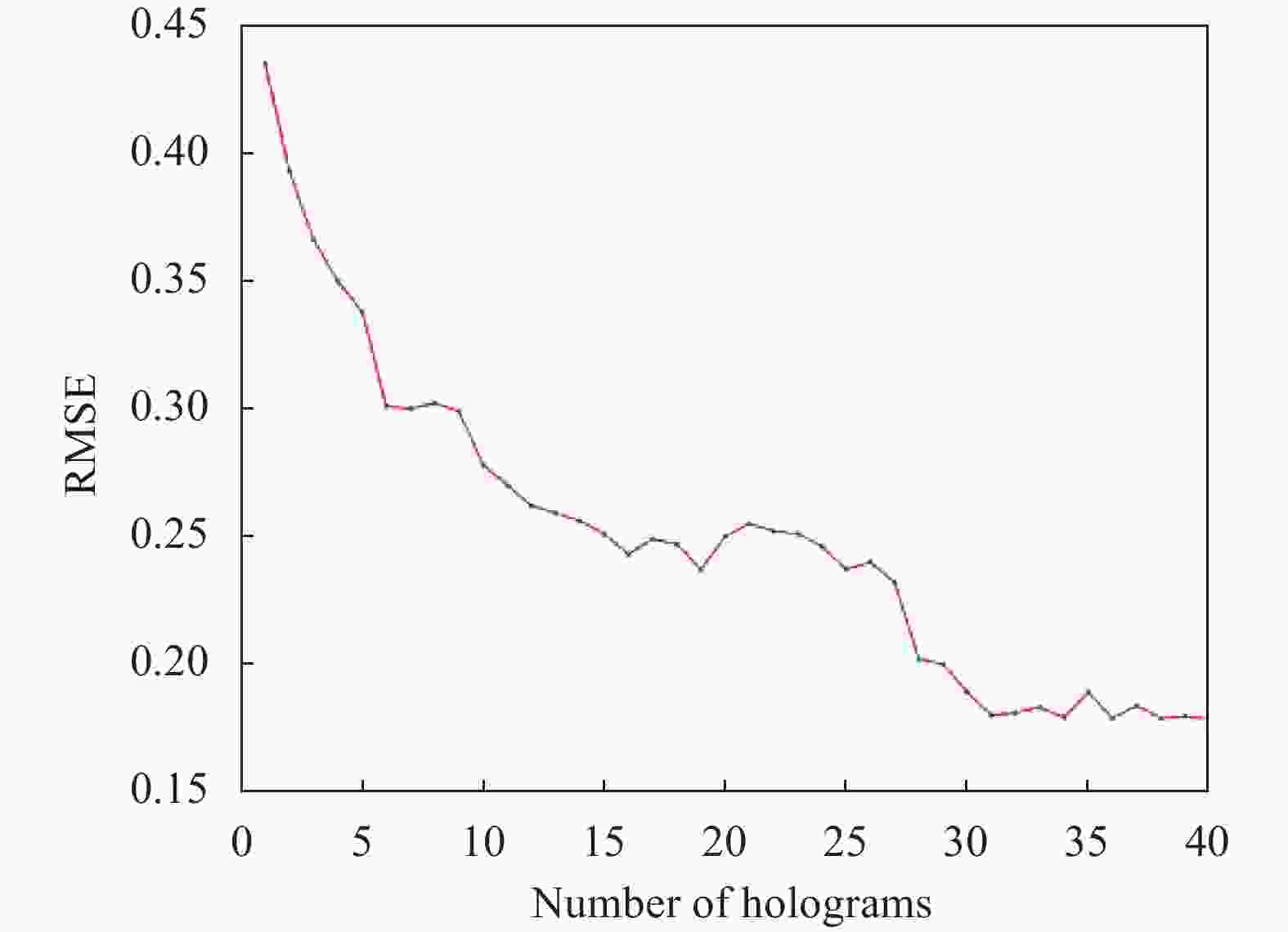
$ RMSE= \sqrt{\displaystyle\sum {({U}^{2}-{U}_{d}^{2})}^{2}\Big/\displaystyle\sum {U}_{d}^{2}} $ ,其中,U为全息光场的振幅,$ {U}_{d} $ 为目标光场的振幅,如图4所示,图4(a)是仅1幅相息图时的全息仿真和其强度分布,图4(b)是使用30幅相息图快速切换消散斑时的全息仿真和强度分布。在使用30幅消散斑后,光场散斑减少,生成的全息图与目标图的均方误差(RMSE)也由0.435下降到了0.18,进一步的探究显示,在所使用的相息图较少时,增加相息图消散斑效果显著,当相息图数量增加到一定数量后再增加相息图数量就很难起到消散斑的效果了,消散斑效果与所使用的相息图数量的二分之一次方成正比,如图5显示了相息图数量与均方差的关系。 -
为验证文中所提方法的可行性,搭建了实验系统并进行了斜面和球面光刻实验验证,如图6所示,实验系统所使用的激光器波长为405 nm,空间光调制器后的透镜焦距为200 mm,液晶空间光调制器型号为滨松下X13138具体参数如下:尺寸:12.8 mm×15.9 mm,像素数:1024×1272,单元尺寸:12.5 µm,填充率:96%。
-
仅考虑空间光调制器的衍射极限,系统的横向分辨率应为:
$$ {R}_{x}=\frac{\lambda f}{h},{R}_{y}=\frac{\lambda f}{l}$$ (8) 式中:
$ \lambda $ 为入射波长;$ f $ 为透镜焦距;$ h $ ,$ l $ 分别为空间光调制器的短边和长边;代入实际参数得Rx= 6.3281 μm,Ry=5.0943 μm。纵向分辨率为:
$$ {R}_{{\textit{z}}}=\frac{\lambda {f}^{2}}{h} $$ (9) -
将图6所示全息系统的CCD替换为如图7所示的曝光光路,将倾斜45°的硅片分别涂上AZ9260光刻胶和Lcd405光敏树脂,进行了曝光显影和光固化实验。图8(a)为光敏树脂固化结果,曝光时间为5 s,最小线宽为760 μm,图8(b)为单像素的线阵光刻胶曝光结果,曝光时间10 s,线宽为20 μm,显然这与上面讨论的横向分辨率不符,说明曝光精度受到了除空间光调制器衍射极限外其他因素的影响。
-
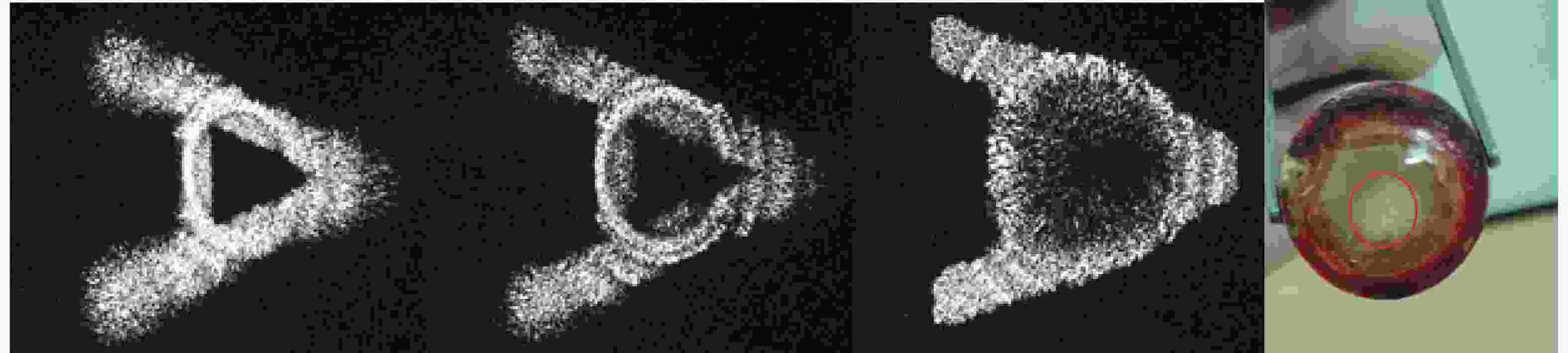
曲面光刻系统的光路如图1所示,目标曲面是涂有光刻胶(az9260)的平凸球面透镜,其球面半径为13.17 mm,实验中将球面上的目标图案A字母分割为20层,再利用多层全息算法Global gs[25]求得相息图得到目标全息光场,该光场的设计深度为0.433 mm。图9为垂直于光轴、距透镜分别为210、210.2、210.4 mm处的三个截面所截取的光场,由此可以看到不同位置光场聚焦位置不同,证明所得光场确实是一个球面光场,得到光刻结果。
-
提出了利用基于液晶空间光调制器的纯相位计算全息技术投影目标图案到斜面和曲面进行曝光的方法,利用相应算法生成了斜面和球面光场,并对光场进行了消散斑和杂散光处理,提升了光场质量。实验结果表明:该方法可以实现斜面和曲面的一步曝光,斜面光刻精度可达20 μm,且只需通过计算机控制就可实现掩膜变换,从而完成不同图案的光刻,具有加工效率高、设计灵活多变的优点。
Optical lithography on tilted and curved surfaces based on computer generated holography
-
摘要: 斜面和曲面微结构元件在微电子学、微光学、微流体学等领域有着重要的应用,为了实现快速、低成本的斜面和曲面光刻,提出了利用基于液晶空间光调制器的纯相位计算全息技术投影目标图案到斜面和曲面进行曝光的方法。生成了斜面和球面全息光场,对光场进行消散斑和杂散光去除的处理,完成了斜面和球面光刻实验验证。实验结果表明:该方法加工效率高、设计灵活多变,不受单一结构限制,是一种极具潜力的三维微纳加工方法。Abstract: Micro-structural elements on tilted and curved surfaces has important applications in microelectronics, micro-optics, micro-fluidics and other fields. In order to achieve rapid and low-cost lithography of tilted and curved surfaces, the method is proposed, in which pure phase computer generated holography technology based on liquid crystal spatial light modulator is used to project target pattern to the tilted and curved surfaces completing exposure. The tilted and curved surfaces pure phase computer generated holographic light fields are generated, and the speckle elimination and stray light removal of the optical field are processed. The experimental verification of tilted and curved surfaces lithography is completed. The experimental results show that the method has high machining efficiency, flexible design and is not limited by a single structure. It is a potential 3D micro-nano machining method.
-
[1] Shen Runlong. Study on transmission characteristics of surface plasmons in metal insulator metal structure nano waveguides[D]. Ji'nan: Shandong University of Science and Technology, 2014. (in Chinese) [2] Liu Pukun, Huang Tiejun. Terahertz surface plasmon polaritons and their applications [J]. Journal of Infrared and Millimeter Waves, 2020, 39(2): 169-190. doi: 10.11972/j.issn.1001-9014.2020.02.006 [3] Xie Huikai, Pan Yingtian, Fedder G K. A CMOS-MEMS mirror with curled-hinge comb drives [J]. Journal of Microelectro-mechanical Systems, 2003, 12(4): 450-457. [4] Bernstein J, Miller R, Kelley W, et al. Low-noise MEMS vibration sensor for geophysical applications [J]. Journal of Microelectromechanical Systems, 1999, 8(4): 433-438. doi: 10.1109/84.809058 [5] Wang F, Cheng R, Li X. MEMS vertical probe cards with ultra densely arrayed metal probes for wafer-level IC testing [J]. Journal of Microelectromechanical Systems, 2009, 18(4): 933-941. doi: 10.1109/JMEMS.2009.2021815 [6] Booth M J, Neil M A A, Juškaitis R, et al. Adaptive aberration correction in a confocal microscope [J]. Proceedings of the National Academy of Sciences, 2002, 99(9): 5788-5792. doi: 10.1073/pnas.082544799 [7] John J, Li Y, Zhang J, et al. Microfabrication of 3D neural probes with combined electrical and chemical interfaces [J]. Journal of Micromechanics and Microengineering, 2011, 21(10): 105011. doi: 10.1088/0960-1317/21/10/105011 [8] Martinez A W, Phillips S T, Whitesides G M. Three-dimensional microfluidic devices fabricated in layered paper and tape [J]. Proceedings of the National Academy of Sciences, 2008, 105(50): 19606-19611. doi: 10.1073/pnas.0810903105 [9] Ito T, Okazaki S. Pushing the limits of lithography [J]. Nature, 2000, 406(6799): 1027-1031. doi: 10.1038/35023233 [10] Leon J A, Alves E S, Elias D C, et al. Rapid fabrication of bilayer graphene devices using direct laser writing photolithography [J]. Journal of Vacuum Science & Technology B, 2011, 29(2): 021204. [11] Mitchell J I, Park S J, Watson C A, et al. Laser direct write of silicon nanowires [J]. Optical Engineering, 2011, 50(10): 104301. doi: 10.1117/1.3630225 [12] Bhuvana T, Kulkarni G U. Highly conducting patterned Pd nanowires by direct-write electron beam lithography [J]. ACS Nano, 2008, 2(3): 457-462. doi: 10.1021/nn700372h [13] Gopal V, Radmilovic V R, Daraio C, et al. Rapid prototyping of site-specific nanocontacts by electron and ion beam assisted direct-write nanolithography [J]. Nano Letters, 2004, 4(11): 2059-2063. doi: 10.1021/nl0492133 [14] Lee L P, Berger S A, Liepmann D, et al. High aspect ratio polymer microstructures and cantilevers for bioMEMS using low energy ion beam and photolithography [J]. Sensors and Actuators A: Physical, 1998, 71(1-2): 144-149. doi: 10.1016/S0924-4247(98)00177-0 [15] Gonin Y, Munnik F, Benninger F, et al. Creating sub-surface channels in PMMA with ion beam lithography in only one step [J]. Applied Surface Science, 2003, 217(1-4): 289-293. doi: 10.1016/S0169-4332(03)00534-8 [16] Dominguez-Caballero J A, Takahashi S, Barbastathis G, et al. Design and sensitivity analysis of Fresnel domain computer generated holograms [J]. International Journal of Nano-manufacturing, 2010, 6(1-4): 207-218. [17] Shusteff M, Browar A E M, Kelly B E, et al. One-step volumetric additive manufacturing of complex polymer structures [J]. Science Advances, 2017, 3(12): eaao5496. doi: 10.1126/sciadv.aao5496 [18] Wang P, Menon R. Optical microlithography on oblique and multiplane surfaces using diffractive phase masks [J]. Journal of Micro/Nanolithography, MEMS, and MOEMS, 2015, 14(2): 023507. doi: 10.1117/1.JMM.14.2.023507 [19] Gerchberg R W. A practical algorithm for the determination of phase from image and diffraction plane pictures [J]. Optik, 1972, 35: 237-246. [20] Yang G, Dong B, Gu B, et al. Gerchberg–Saxton and Yang–Gu algorithms for phase retrieval in a nonunitary transform system: A comparison [J]. Applied Optics, 1994, 33(2): 209-218. doi: 10.1364/AO.33.000209 [21] Yang G, Gu B Y, Dong B Z. Theory of the amplitude-phase retrieval in any linear-transform system and its applications[C]//Inverse Problems in Scattering and Imaging. SPIE, 1992, 1767: 457-478. [22] Kuzmenko A, Iezhov P, Kim J T. Weighting iterative Fourier transform algorithm for kinoform implemented with phase-only SLM[C]//Digital Holography and Three-Dimensional Imaging. Optical Society of America, 2011: DTuC37. [23] Wu Y, Wang J, Chen C, et al. Adaptive weighted Gerchberg-Saxton algorithm for generation of phase-only hologram with artifacts suppression [J]. Optics Express, 2021, 29(2): 1412-1427. doi: 10.1364/OE.413723 [24] Matsushima K. Formulation of the rotational transformation of wave fields and their application to digital holography [J]. Applied Optics, 2008, 47(19): D110-D116. doi: 10.1364/AO.47.00D110 [25] Piestun R, Spektor B, Shamir J. Wave fields in three dimensions: Analysis and synthesis [J]. JOSA A, 1996, 13(9): 1837-1848. doi: 10.1364/JOSAA.13.001837 -







 下载:
下载: