-
高Q值光学微腔兼具低损耗和小模式体积,是非线性光学研究与应用中的理想实验平台[1]。利用材料的三阶非线性(
$ \chi^{(3)} $ 非线性)或克尔效应(Kerr effect),可以在光学微腔中通过四波混频(Four-wave mixing,FWM)效应实现参量震荡[2-3]。而随着四波混频过程的级联,可以得到更多的频率谱线,从而构成一个光学频率梳,即所谓的微腔光频梳(microcomb)[4]。这里的光频梳是指一系列等间距分布的频率谱线,每根谱线的频率可以写为$ \nu_n=f_0+nf_r $ ($ n $ 为谱线序号,$ f_r $ 为梳齿间距,$ f_0 $ 为光频梳偏频)。它是沟通微波频率与光学频率之间的桥梁,同时也为超短脉冲的相位控制开辟了新方法[5-7]。其已在光学频率计量、超精密守时与光原子钟、超低相位噪声微波信号合成、天文光谱校准与地外行星探测、时频传递、绝对距离测量、精密光谱测量、任意光学波形产生、阿秒科学等众多领域起到了深远的影响[5-7]。传统的光频梳一般由飞秒激光器产生,通过跨倍频程光频梳的自参考锁定可以实现$ f_0 $ 和$ f_r $ 的全锁定并实现极高的频率稳定性[5-8]。飞秒激光器中的光学脉冲也可以被认为是一种耗散光学孤子[9],其中脉冲的产生是通过虚拟或者实际的可饱和吸收体实现的。而在微腔光频梳的产生过程同样也可伴随着光孤子的产生,但微腔中的锁模过程是依赖克尔效应实现的[10-12]。也正是因为微腔系统与锁模激光器的差别,微腔光孤子呈现出独有的特性。此外,受限于锁模激光器空间尺寸的限制,飞秒激光器光频梳一般难以实现很高的重频(
$ f_r=c/ (n_gL)$ ,$c$ 为真空光速,$n_g$ 为群折射率,$L$ 为往返腔长)。而利用小型化的微腔则可以实现GHz到THz的梳齿间距[13-15]。这种大间距的光频梳在天文光谱校准[16-19]、波分复用通信系统[20-22]、微波光子学[23-24]中都有着重要的应用需求[25]。目前微腔光频梳已经在氟化镁[10, 23]、氮化硅[26-28]、二氧化硅[29-30]、硅[31]、氮化铝[32]、铌酸锂[33-34]、铝镓砷[35-37]、氧化钽[38]、氮化镓[39]、磷化镓[40]、高折射率二氧化硅[41]等众多材料体系中实现。这其中很多材料平台的制备工艺是与微电子CMOS工艺兼容的;并且近年来已经实现了集成微腔与泵浦源的混合集成[42-43]和单片集成[44],这势必将在不远的未来里推动集成光频梳系统的量产和实验室外的应用。文中将讨论微腔光孤子产生过程的物理基础与孤子光频梳研究领域的最新进展,并重点介绍微腔多孤子间的相互作用。同时也将讨论基于微腔双光梳的新应用,特别是在中红外光频梳产生和双光梳光谱测量中的应用。
-
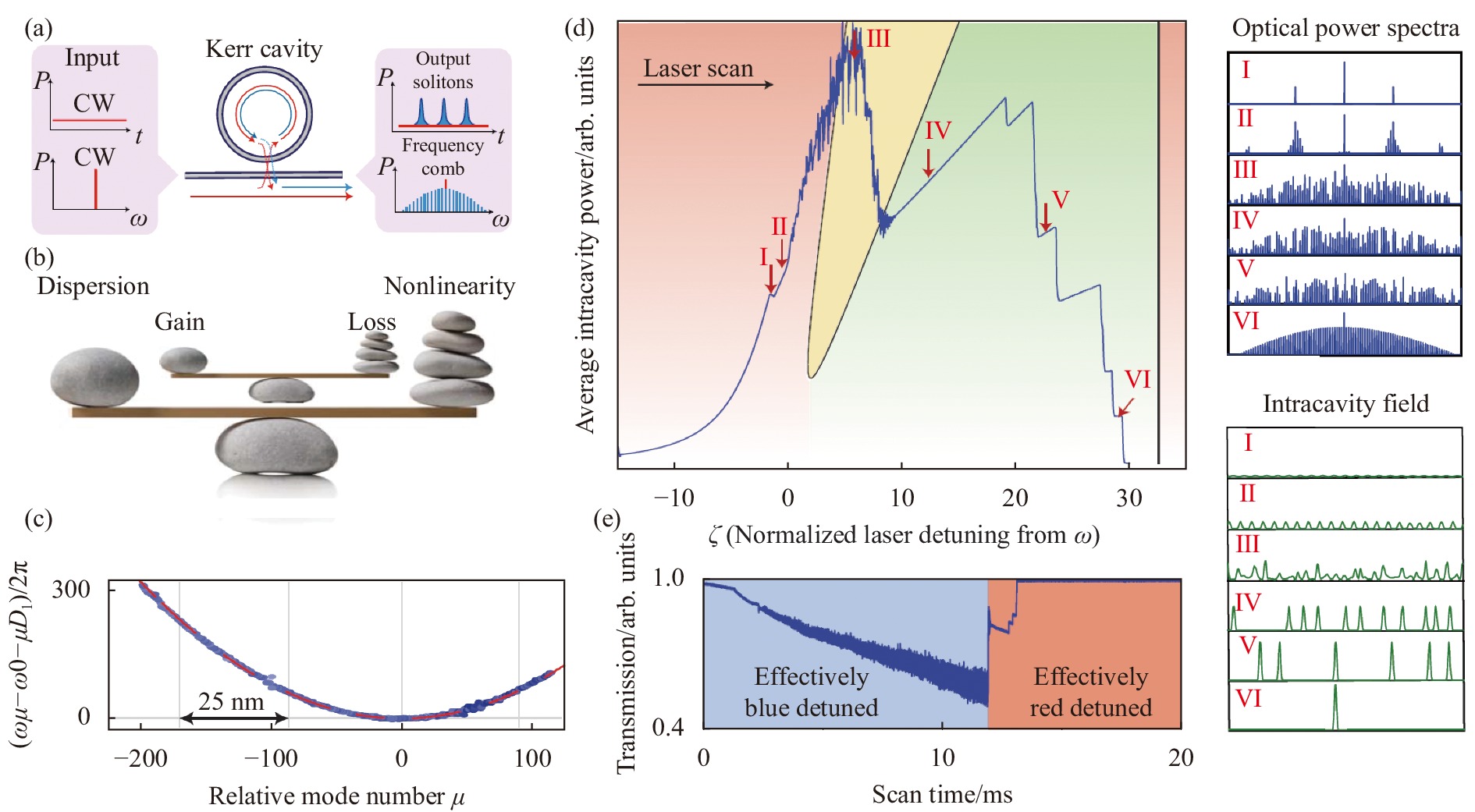
当采用连续激光对高Q微腔进行相干泵浦时,在合适的条件下,可以得到一个周期性的脉冲串的输出,这在频域上对应一个光频梳,即孤子光频梳(图1(a))。在微腔内,光孤子的稳定运转需要色散与非线性间的平衡和增益与损耗间的平衡[12](图1(b))。在反常色散区,色散将引起光频梳梳齿不同的线性相位延迟和腔模的不等间距分布(图1(c));对于一个双曲正割的sech型脉冲,这一频域上的相位变化可以通过克尔效应得到补偿[45]。而对于微腔光孤子而言,系统中不存在与增益介质对应的主动增益,微腔的损耗也要由克尔效应引起的参量增益来补偿。对于正常色散的微腔,可以通过产生暗脉冲来实现色散与非线性,增益与损耗之间的双平衡[11]。因参量增益不对应材料实际的增益峰,这也意味着微腔光频梳在大波段范围内均可以工作。
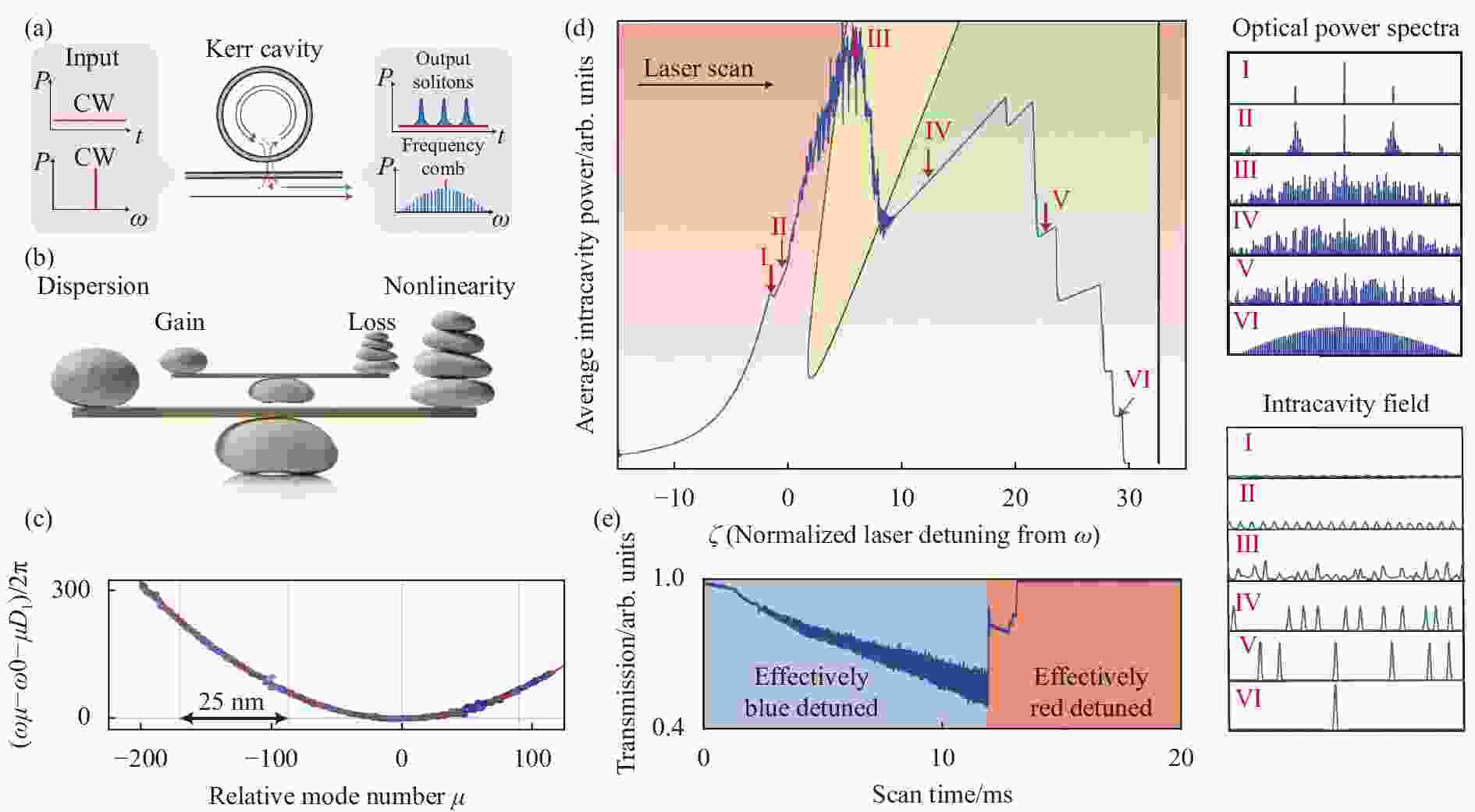
图 1 微腔光孤子产生基础:(a) 相干泵浦时微腔时域和频域输入及输出[46];(b) 微腔中耗散光孤子的产生需满足增益和损耗与色散和非线性的双平衡;(c)反常色散微腔对应的色散曲线;(d)仿真得到的腔内功率随失谐量的变化,以及不同状态下的时域和频域波形;(e) 从有效蓝失谐区域扫描到有效红失谐区域过程中测得的输出光功率的变化[10, 12]
Figure 1. Fundamental of soliton dynamics in microcavities:(a) Input and output of a coherently pumped microcavity[46]; (b) Double balance between gain and loss as well as dispersion and nonlinearity is needed to support dissipative solitons in microcavities; (c) Dispersion curve of an anomalous dispersion cavity; (d) Simulated intracavity power change when scanning the pump frequency detuning. The power change features several steps indicating soliton states; (e) Experimentally measured transmitted power when scanning the laser from blue-detuning to red-detuning[10, 12]
对于反常色散区的微腔光孤子来说,一般需要在泵浦光的红失谐状态下,才能实现上述的双平衡。因而,在微腔孤子的产生过程中,需要将泵浦光波长从蓝失谐逐渐调谐到红失谐区[10]。在蓝失谐区,微腔内可以通过调制不稳定性和级联四波混频产生光频梳齿,此时各梳齿间不一定互相干。继续调谐泵浦频率从有效蓝失谐区经过谐振峰,进入有效红失谐区时,可以观察到腔内功率呈台阶式变化,这代表在微腔内产生了高相干的微腔光孤子(见图1(d)中的仿真结果与各状态对应的波形与光谱)。同时,实验上也可在传输曲线中观察到孤子台阶(见图1(e))。然而,从混沌状态转变到光孤子状态的过程中伴随腔内功率的骤降,这会使腔模谐振频率产生比较大的蓝移,有效失谐量有可能落到孤子存在范围(soliton existence range,SER)之外[46-47]。这种由热效应引起的瞬态不稳定性使得微腔孤子光频梳的产生在实验上相对困难。
为了克服热效应的影响,人们发展出了一系列方法,已在多种高Q值微腔中产生了光孤子。2014年,Kippenberg课题组通过选择合适的泵浦频率扫描速度使微腔始终处在热平衡的状态,在氟化镁微腔中观察到了光孤子[10]。通过扫频直接产生光孤子的方法比较简单,但只适用于氟化镁这种热效应比较小的微腔。而对于热效应比较强的氮化硅、二氧化硅等微腔,这种方法可能不再适用。此后,人们采用了“Power kicking”的方法来产生微腔孤子,也就是通过电光、声光(EOM,AOM)等调制器,在孤子产生的瞬态过程中快速提升泵浦功率,以补偿孤子产生过程中腔内功率的骤降,从而实现微腔孤子的产生[26, 29]。配合Power kicking,再引进锁定环路来稳定光频梳的功率,可以实现瞬态微腔光孤子的捕获和长时间稳定[48]。而通过改进工艺,降低微腔的热效应,在氮化硅微腔中也可以通过慢速激光器的调谐,直接产生微腔孤子,此时微腔内的孤子数目将决定腔内的功率,并最终影响微腔孤子的稳定性[47]。此外,还可以对泵浦进行单边带调制,并以极快的速度对激光频率进行扫描以抑制微腔内热效应的积累,也可以实现微腔孤子的稳定产生[49]。此外,在蓝失谐区域,激光是处于热锁定状态的,因而可以引入额外一个位于蓝失谐区域的激光,通过双泵浦的方法实现微腔孤子的稳定产生[50-51]。
除了扫描泵浦频率外,也可以使泵浦光频率固定,调谐微腔谐振频率,使泵浦光进入有效红失谐区产生光孤子;例如,Gaeta课题组通过控制集成在氮化硅微腔周围的微加热器,实现了微腔孤子的稳定产生[28]。相对于扫描激光器频率,该方法可以采用更窄线宽的固定频率激光器作为泵浦源,这可用于降低微腔光频梳的噪声。除了上述这些需要扫描激光频率与谐振峰间的失谐量的方法外,通过自注入锁定(即将微腔的背向散射光耦合进泵浦激光器)[23, 52]也可以实现微腔孤子的产生,此时无需通过调谐激光频率便可实现启钥式(turnkey)微腔孤子的产生[42]。此时热效应也不会引起孤子的湮灭,可以大大简化微腔光频梳的产生系统。
微腔孤子数目的控制是微腔光频梳产生中的另一个重要问题;单孤子具有光滑的光频梳包络,更具有实际应用价值。一般微腔孤子产生的数目是随机的,且得到单孤子的概率往往很低[10]。为了实现孤子数目的控制,Kippenberg课题组提出后向调谐法,即在微腔孤子产生后,往短波长调谐泵浦激光,可以使得孤子数目依次递减直至达到单孤子状态[46]。除此以外,Weiner课题组则发现微腔空间模式耦合引起的色散波(dispersive wave,也被称为切伦科夫辐射,Cherenkov radiation)可以被动地引起单孤子的产生[53]。而在此之前色散波普遍被认为是不利于孤子产生的[54],但实际上合适强度的色散波有助于单孤子的产生。这是因为色散波是微腔孤子的一种非线性损耗,且微腔内模式耦合引起的色散波强度与孤子数目的平方成正比;则在外加泵浦一定的时候,孤子会倾向于往单孤子演化,以降低整个系统的损耗。而且色散波还可使孤子光频梳梳齿进入正常色散区,从而拓宽微腔光频梳的带宽[26]。这对于实现跨倍频程的微腔光频梳[14-15]和微腔光频梳的自参考锁定[55-56]都具有重要的意义。
微腔孤子的性质可以通过泵浦光功率和失谐量进行高精度的控制[10],这也为研究光学孤子的各种非线性动力学过程提供了良好的实验平台。例如,孤子与材料拉曼增益的相互作用,可使得微腔孤子中心频率呈现一定的红移(孤子自频移)[57-59]。而该拉曼频移可与色散波引起的光谱回波(spectral recoil)相互作用,使得总的孤子中心频率不随泵浦光频率发生明显变化,从而抑制泵浦光频率噪声往微腔孤子噪声的转化,以产生低噪声微腔光频梳[60]。而在量子噪声的作用下,微腔孤子则会发生随机游走或者类扩散运动;这也决定了微腔孤子稳定性的上限[61-64]。除了稳定的孤子态外,微腔孤子也可能工作在不稳定的状态。因相干泵浦的存在,微腔孤子每一圈都需要与泵浦发生干涉,若孤子载波与泵浦的相位差随传播圈数发生变化,孤子将会工作在不稳定的状态[65],如对应光谱周期性展宽和压缩的呼吸子状态[66]。在实验上可以通过控制泵浦光功率与失谐量(大泵浦功率、小失谐量)在微腔中产生呼吸子[67-69],且实验上可观测到光谱中心和边缘部分能量的周期性交换[67]。此外,Vahala课题组利用基于电光调制梳与微腔光梳异步采样的方法(等效于双光梳测量,见第
$4$ 节),对微腔内包含呼吸子在内的多种孤子动力学现象进行了快速测量[70]。而在正常色散区,在较小的失谐量下,微腔中也可以存在暗呼吸孤子[71]。相对于亮呼吸孤子,暗呼吸孤子呼吸深度小得多,而且各梳齿的功率变化的方式差别也较大。在正常色散区,在单晶体(如氮化铝)微腔中的窄带拉曼增益峰的作用下,微腔光频梳还可能工作在呼吸态的平顶脉冲下[72]。除泵浦条件外,微腔孤子的性质还可以通过色散的调谐进行控制[73]。上述对微腔孤子非线性动力学的实验和理论的研究,对加深光孤子性质的理解和孤子光频梳的调控都具有重要的意义。 -
上述对微腔孤子物理的研究,主要针对单孤子状态;而若微腔内存在多个孤子,则孤子间会发生相互作用,这是光孤子物理研究的基本问题之一,也是理解复杂系统动力学的关键[74]。常见的孤子间相互作用一般需要孤子脉冲的尾部存在一定的重合[74];该种短距离相互作用,可以捕获(即soliton trapping)两个不同频率(相差几十MHz)泵浦光产生的微腔孤子,从而形成异核孤子分子[75]。光孤子通过克尔效应形成的折射率势阱还可以捕获不同中心波长(相差十几THz)的脉冲,形成新型的斯托克斯孤子(Stokes solitons)[76]。在高Q值二氧化硅微腔中可以通过拉曼增益在远离泵浦光的频率处产生另一个脉冲,该脉冲与泵浦光直接形成的主脉冲隶属不同的空间横模。如果其中一个模式在拉曼增益峰附近的自由频谱程(FSR)与另一个模式在泵浦光附近的FSR相近,则拉曼增益峰内的脉冲会被主脉冲的折射率势阱捕获,产生斯托克斯孤子。当然,折射率势阱不一定要通过克尔效应产生,也可由对泵浦进行相位调制实现[77],该方法同样可以起到对微腔孤子的位置灵活操控的作用。
除了短距离相互作用外,微腔内色散波的存在,使得孤子间可以产生长程的相互作用。色散波在时域上表现为振荡拖尾,在克尔效应的作用下,也相当于一个折射率势阱,从而也可以起到束缚微腔孤子的作用[78-79]。具体来讲,如果色散波相对于泵浦光的频率为
$ \nu_{\rm{DW}} $ ,则在腔内会形成以1/$ \nu_{\rm{DW}} $ 为周期的“光学晶格”[78],多个孤子只能以晶格周期的整数倍为间隔在腔内分布。如果孤子数目足够多的时候,可以在色散波的作用下,形成“孤子晶体”。孤子晶体内部可能会存在一些缺陷;比如光学晶格最多可以支持$ N= \nu_{\rm{DW}}T_R $ 个孤子,但实际的孤子数往往少于$ N $ 。也就是说孤子并不严格以1/$ \nu_{\rm{DW}} $ 的间隔分布;这也意味着在频域上梳齿的间距仍为$ 1/T_R $ (但间隔$ \nu_{\rm{DW}} $ 的梳齿会得到增强)。而如果以较低的泵浦功率(略高于阈值功率)激发微腔孤子晶体,则可以产生孤子数目为$ N $ 的完美孤子晶体[80]。此时,孤子时域上的间隔为$ T_R/N $ ,而频域上梳齿的间隔为$ N/T_R $ ,单梳齿功率为单孤子时的对应梳齿功率的$ N^2 $ 倍(见图2(b))。
图 2 微腔孤子间的相互作用:(a) 同向传播的孤子间通过色散波产生锁定[79];(b) 完美孤子晶体(PSC),在同个微腔中存在X个等间距分布的微腔孤子[80];(c)相向传播的微腔孤子可通过微腔的瑞利背向散射引起相互作用[82];(d) 不同微腔孤子间可通过将某一微腔孤子注入另一个微腔实现两个微腔孤子间的同步[84]
Figure 2. Soliton interaction in microcavities:(a) Illustration of co-propagating (CoP) solitons trapped by dispersive wave emission[79]; (b) Perfect soliton crystals (PSC) comprising X solitons in a microcavity[80]; (c) Counter-propagating (CP) solitons interaction via Rayleigh backscattering[82]; (d) Synchronization of solitons in two different microcavities via injecting one of the solitons into the other one[84]
而对于被捕获的微腔孤子来说,一个关键问题是孤子捕获效应有多强。对于色散波势阱束缚作用的强弱,Vahala课题组曾利用平衡光互相关仪(BOC)对同向传播(Co-propagating,CoP)孤子对在时域上的运动进行了亚飞秒时间分辨率的测量,并在实验观测到被色散波束缚的CoP孤子对的相对时间抖动可以远低于单个孤子的量子极限[62],这也证明了微腔内色散波引入的孤子间的束缚作用的强度是非常强的。
而除了同向传播的多孤子外,可以通过对微腔进行双向泵浦(可将一束激光经分束、移频后产生两个方向的泵浦源),在腔内产生相向传播的孤子对,即CP solitons(counter-propagating solitons)[81]。对于高Q二氧化硅微腔,孤子对间将通过微腔的瑞利散射相互作用,并且存在两种不同的锁定状态。第一种是当两路泵浦光频率差
$ \Delta\nu_P $ 较小(0 Hz ~ 数百kHz)时,两个孤子的重复频率被锁定即$ \Delta f_r $ =0。在第二种锁定中,两路泵浦光频率差$ \Delta\nu_P $ 较大时(如几MHz),其重频差$ \Delta f_r $ 为泵浦频率差$ \Delta\nu_P $ 的整数分之一($ \Delta f_r=\Delta\nu_P/r $ ,$ r $ 为一整数)[81]。针对第一种状态,在$ \Delta\nu_P $ =0,利用BOC对输出的CP孤子对进行测量,可以看到短时间内(几微秒)的孤子扩散运动和长时间内的孤子锁定现象;且因为CP孤子对技术噪声极好的共模噪声抑制作用,短时扩散运动的幅度与量子噪声预测扩散运动的幅度相吻合[62]。而如果$ \Delta\nu_P $ 为几十或几百kHz时,BOC的测量显示CP孤子耦合出腔后并不像CoP孤子对那样严格锁定的;两个脉冲间的相对时延会发生以$ \Delta\nu_P $ 为频率的周期性运动,其运动幅度为几百fs (图2(c))[82]。这是因为相干泵浦的存在,使得CP孤子对不能完成载波的锁定(即$ f_0 $ 的锁定),而背向散射使得某一方向的梳齿耦合进另一路梳齿,并对另一路孤子的中心频率和群速度进行周期性调制,从而产生周期性的相对运动(图2(c))。而第二种锁定,因为两个孤子重频将不再一致,所以两个方向的梳齿对的频率差将会随梳齿序号发生变化;若第$ r $ 根梳齿对间的频率相差很小,则两者可以通过背向散射实现注入锁定,则此时$ \Delta f_r $ 将等于$ \Delta\nu_P/r $ 。而因为CP孤子对的泵浦频率可源自同个激光器,则第二种锁定提供了互相干性极好的双光梳光源,可用于双光梳光谱、测距等应用(详见第 4 节)[81]。此外值的一提的是Kippenberg课题组通过泵浦氟化镁微腔中的不同空间模式,在单个微腔中最多同时产生了三个微腔光孤子,且此时孤子间的重频差比泵浦泵浦同个模式时获得CP孤子对显著增大(提升一个量级以上),这也验证了单腔多光孤子在多光频梳应用中的巨大潜力[83]。除了单个微腔中引起多孤子间的相互锁定外,来自不同微谐振器中的频率梳也可以通过孤子间的相互作用实现锁定(图2(d))。例如,哥伦比亚大学的Gaeta和Lipson课题组通过光纤链路将一个氮化硅微腔光频梳输出的一小部分耦合到另一个氮化硅微腔中,实现了不同微腔光频梳间重频的锁定[84]。该方法不仅适用于亮孤子,也可适用于暗孤子光频梳[85]。这也为未来在微腔阵列中实现多路互相干的光频梳提供了可行方案。
-
双光梳测量是指利用两台重频有微小差别的光频梳间的多外差干涉,实现光频梳齿与射频梳齿间的一一映射,并通过射频谱的测量完成光谱测量的方法[86]。因为重频差的存在,一路光脉冲将周期性地扫过另一路互相干的脉冲,所以双光梳光谱也相当于一种新型的傅里叶变换光谱技术;但其利用脉冲重频差代替了机械组件完成脉冲扫描,因而可以极大地缩短测量时间,缩小系统体积,同时该方法也可实现梳齿分辨而保持极高的光谱分辨率。微腔频率梳具有单梳齿功率高、重频大的特点。而双光梳测量的最短时间为2
$ \nu_{\rm{BW}}/f_r^2 $ ($ \nu_{\rm{BW}} $ 为测量带宽)[86],因此基于微腔光频梳有望实现单芯片、小型化、高速双光梳光谱仪。微腔双光梳光谱测量的报道可以追溯到2016年,当时Vahala课题组基于高Q二氧化硅微腔在1550 nm波段实现了H 13CN气体的双光梳光谱测量(图3(a))[87]。测量系统包含两个重频接近22 GHz的二氧化硅微腔光频梳(由两台独立的连续光激光器泵浦两个微腔产生),两者的重频差为2.6 MHz。在20
$ \text{μ} $ s的测量时间内,两个自由运转光频梳保持良好的互相干性;双光梳测量结果与扫描连续光测量的结果相近,验证了芯片级双光梳光谱仪的可行性。但需指出的是受限于微腔的高重频,测得气体吸收光谱的分辨率较差[87]。2018年,哥伦比亚大学的Lipson课题组则报道了更高重频(450 GHz)和更高重频差(1.12 GHz)的片上双氮化硅微腔光频梳光源[88]。两个氮化硅微环腔集成在同一片上,并由同一个激光器经分束后同时泵浦,此光源互相干时间可达100$ \text{μ} $ s。利用该单片双光梳光源,实现了二氯甲烷液体170 nm光谱范围内的快速(20$ \text{μ} $ s)光谱测量。为了实现更好的互相干性,可以采用上文提到的CP孤子对的方法,该方法可以实现被动锁定,极大地简化了双光梳光源系统。利用CP孤子对,可以构成“游标光谱仪”(Vernier spectrometer),对连续激光进行校准,从而可以对快速扫描连续光激光器、锁模激光光谱、气体吸收谱等进行快速的测量(图3(b))[89]。
图 3 微腔光频梳在双光梳测量中的应用:(a) 微腔双光梳光谱示意图[87];(b) 单微腔双光梳游标光谱仪示意图[89];(c) 微腔双光梳成像测量[90];(d) 双微腔光频梳的快速距离测量[92]
Figure 3. Dual-microcomb applications:(a) Dual-comb spectroscopy using microcombs[87]; (b) A microcavity based vernier spectrometer[89]; (c) Dual-comb imaging using microcombs[90]; (d) Ultrafast distance measurement with dual-microcombs[92]
而为实现更精细的光谱分辨,某些场景需要降低微腔光频梳的重频;例如,2018年Vahala课题组就报道了工作于通信波段的1.86 GHz超低重频的二氧化硅微腔光频梳[13]。该微腔光频梳也被应用于了双光梳测量[90],该工作将双光梳用于快速成像而非光谱分析(图3(c))。实验中将宽谱的光频梳,经一个虚拟成像相位阵列(VIPA)和一个光栅,在二维空间上进行色散,形成一个二维点阵。则该点阵可以加载物体信息,通过双光梳光谱的测量方法,实现物体的快速成像。实验中利用9.38 GHz的双光梳和1.86 GHz的双光梳和单像素的探测器,均实现了超过100 kHz帧率的快速成像,这也显示了微腔双光梳对快速运动目标进行成像的潜力。
双光梳测距是双光梳测量的另一个重要应用领域;微腔双光梳测距仪可以实现芯片化、高速测量,同时保持亚纳米的测量精度。例如,2018年Vahala课题组便利用单个重频9 GHz二氧化硅微腔产生的CP孤子对进行了双光梳测距;利用飞行时间法对4.6 mm处的静态目标进行了测量,在500 ms测量时间内实现了200 nm的测距精度[91]。几乎同时,Kippenberg课题组则报道了利用两个100 GHz氮化硅微腔进行的超快光学测距结果[92];利用该系统实现了对150 m/s的速度高速飞行的气枪子弹的轮廓的超快测量。该实验很好地阐明了双光梳测量在高速测距上的巨大潜力(图3(d))。
-
上述的微腔光频梳主要工作在通信波段,而中红外波段( 2~20 μm)的微腔光频梳的研究相对较少。该波段存在“分子指纹”区域,分子吸收强度远超近红外波段;发展该波段的集成光频梳,特别是结合上文提到的双光梳光谱测量方法,可大大地推动微量气体检测和精密光谱分析的发展。但总体来讲,中红外激光技术相比起近红外和可见光波段仍相对不成熟,产生中红外光频梳的技术难度也相对较大[93]。目前中红外光频梳的产生方法主要包括直接的中红外相干光源(固体与光纤锁模激光器、量子级联激光器和微腔光频梳等)和非线性频率转换(光学差频DFG、
$ \chi^{(2)} $ 参量振荡器、超连续谱等)[93]两种方法。其中基于光学微腔,已经在氟化镁[94]、硅[31, 95- 96]、氮化硅[97]等多个材料平台实现了中红外光频梳的产生。2013年,Kippenberg课题组在高Q值氟化镁微腔中实现了在2.5
$\text{μ} $ m波段的光频梳,梳齿间距100 GHz,带宽超过10 THz;且验证了其中产生低噪声光频梳的可行性[94]。随后,美国康奈尔大学的Gaeta和Lipson课题组通过克服硅微腔中载流子损耗的影响实现了高Q值硅微腔,并利用中红外激光的泵浦在硅微腔中实现了2.1~3.5$\text{μ}$ m的宽带频率梳[95],并且随后在其中实现了孤子锁模与相干中红外光频梳的产生[31]。而利用两个低噪声硅微腔光频梳,该课题组实现了中红外双光梳光谱(图4(a))[96];在2900~3100 nm的光谱范围和2$ \text{μ} $ s的测量时间内实现了对丙酮样品的吸收谱的测量,光谱分辨率为127 GHz。若想提升光谱分辨率,则需要更低FSR的微腔和更高Q值的微腔(参见通信波段的GHz重频光频梳[13, 90]);目前中红外波段GHz FSR的高Q值微腔尚未见报道。
图 4 光学差频技术在分子光谱学中的应用:(a) 中红外双微腔光梳测吸收光谱[96];(b) 使用 iDFG 中红外梳对甲烷进行双梳光谱(DCS)分析[102]; (c) 脉冲内自差频技术[100];(d) 间隔光学差频(iDFG)技术[101]
Figure 4. Application of optical frequency combs for spectroscopy:(a) Scheme of mid-infrared dual-comb spectroscopy using silicon microcavities[96]; (b) Dual-comb spectroscopy (DCS) analysis of methane using iDFG mid-IR combs[102]; (c) Intrapulse difference-frequency-generation technology[100]; (d) Interleaved difference-frequency-generation (iDFG) technology[101]
而利用DFG等技术则可以将可集成近红外光频梳转换到中红外波段(图4(b)、(d))。DFG的具体原理是指把两个在近红外或可见光波段的光源作为泵浦光和信号光输入非线性晶体,在满足相位匹配的条件下可以通过晶体的二阶非线性实现闲频光的产生,闲频光的频率等于泵浦光和信号光的频率之差(
$ \nu_{\rm{idler}}= \nu_{\rm{pump}}- \nu_{\rm{signal}} $ )。目前已经有团队将可片上集成的电光光频梳与微腔光频梳,通过DFG技术转换到中红外波段。例如,2017年,Picque课题组将1.55$ \text{μ} $ m波段的电光光频梳与1.06$ \text{μ} $ m波段的连续光做差频,实现了3$\text{μ} $ m波段的中红外光频梳的产生;并在亚毫秒的时间尺度上对甲烷等气体进行了高相干的双光梳测量图4(b)[98]。而Diddams课题组则利用电光光频梳与连续激光的产品实现了10 GHz重频的中红外光频梳的产生[99]。传统的DFG中一般利用脉冲光与连续光做差频,或者两个重频一致的输入做差频(如脉冲内自差频intrapulse DFG等方法(图4(c))[100]),此时得到的中红外光频梳的重频与近红外光频梳的重频保持一致。当采用高重频的微腔光频梳作为输入,并想得到较低重频的中红外光频梳的时候,则可以使得两个输入近红外光频梳的重频存在差异(如使得
$ f_{r2}=m_2 f_{r1}/m_1 $ ,$ m_1,\; m_2 $ 为两个互质的整数),从而实现间隔光学差频(interleaved DFG, iDFG)的中红外光频梳的产生,则两个输入光频梳的相互作用只有在$ m_2/f_{r1} $ 之后才会重复,则所产生的中红外光频梳的重频将会被降低至$ f_{r1}/m_1 $ (图4(d))[101]。实验中,可利用22 GHz的微腔产生1.55$ \text{μ} $ m波段的孤子光频梳,再利用光电探测器探测其重频信号$ f_{r1} $ ,再对重频信号进行分频、混频与滤波等处理,产生$ (m_1-1)f_{r1}/m_1 $ 的微波频率,并用其驱动1.06$ \text{μ} $ m波段的电光光频梳的产生,从而得到iDFG两个输入光源。将其输入到周期性极化的非线性晶体(如PPLN)中实现GHz重频的中红外光频梳的产生;而且选取不同的分频系数$ n $ ,可以使得中红外光频梳的重频 在22/$ m_1 $ GHz各数值间分立可调[101]。需要指出的是iDFG可能使得差频过程的转换效率降低,因而更适用于双光梳测量等线性应用。而且通过采用片上薄膜波导作为非线性变换介质,有望通过更强的模场局域实现更高的转换效率。iDFG产生的GHz重频的中红外光频梳已经可以适用于窄线宽的气体吸收峰的测量。再借助上文提到的CP孤子对的互相干性,则可以实现高相干的中红外双微腔光频梳的应用[102]。通过在22 GHz的二氧化硅微腔中产生两个CP孤子,再由这对孤子经光电探测后驱动两个电光光频梳的产生(电光光频梳的种子光由同个激光器经分束后产生),则系统中所用到两对iDFG输入(总共四个光频梳)具有高的互相干性,使得高相干的中红外双光梳测量成为了可能。利用基于CP孤子和iDFG技术的双光梳光谱测量,可以实现在3.3
$ \text{μ} $ m的甲烷、乙烷的混合气体的测量,测量分辨率在2.8 GHz和1.4 GHz间可调,测量时间可以短至0.5 ms;这也显示了片上集成的中红外气体传感器的潜力(图4(b))。值得一提的是如果通过低色散微腔或者腔外扩谱的方法产生足够宽光谱的GHz微腔光频梳,则通过脉冲内自差频的方法[100]也可以产生中红外光频梳。该方法将使得中红外光频梳的偏置频率$ f_0 $ 恒为0,从而方便中红外光频梳梳齿频率的精准确定,但此时也将失去iDFG技术中重频的可调谐性。 -
光频梳自20世纪90年代末实现自参考锁定以来,引领了时间和频率计量的革命性进展。微腔的出现使光频梳系统有望实现小型化与芯片化[55]。当前微腔光频梳的发展,主要依赖于微腔的孤子锁模过程;这一过程为产生超高重频的飞秒脉冲串提供了新方法,也为研究光孤子的性质提供了新的实验平台。近年来,研究人员对于微腔光孤子的理解不断深入,在氟化镁、氮化硅、二氧化硅、硅、铌酸锂和氮化铝等多种微腔平台中产生了光孤子,并对孤子之间相互作用等非线性动力学现象进行了大量研究。并且,微腔光孤子以其小型化、低损耗、大梳齿间距、单根梳齿功率高等优势在光学频率合成、低噪声微波源产生、双光梳测量等诸多领域都取得了重要应用。利用高重频微腔光频梳可以提高双光梳光谱的采样速度,实现对燃烧、湍流等快速变化过程的光谱动态监测。而关于微腔光频梳的工作波段,拓展现有的工作波段至长波中红外、可见光乃至紫外光等波段将进一步推动其在气体传感、天文光谱[18-19]和紫外光谱[103]等领域的应用。进一步的应用的推广,要求光孤子具有更宽的光谱,微腔系统具有更高的能量转换效率和更高的光学集成度。因此,发展更先进的色散调控方法、提升微腔加工工艺与Q值以及探索新的光孤子产生方法等,都将是微腔未来的发展方向。而在微腔光频梳基础方面,光孤子的量子特性的研究则将帮助我们揭示光频梳的更基础的性质[62, 104]。
-
摘要: 光学孤子是指一种通过非线性折射率势阱维持脉冲形状不变的光波,它广泛存在于光纤、飞秒激光器、参量振荡器等系统中。近年来,人们在相干泵浦下的高Q值微腔中也观测到了光孤子,这为研究光孤子性质提供了新的实验平台。又因为微腔光孤子在频域上对应高重频的光学频率梳,微腔光孤子的诞生也极大地推动了小型化光学频率梳的发展。微腔光孤子频率梳已经可以实现自参考锁定;这使得片上集成的光频合成器、光原子钟、波分复用光源、微腔光谱仪、微腔激光雷达等众多应用成为了可能。文中介绍了微腔光孤子的产生基础,特别是光孤子相互作用相关的研究,还讨论了基于微腔的双光梳测量在高速成像与中红外气体光谱分析上的应用。Abstract: Optical solitons are wavepackets that can sustain the shape via a nonlinear refractive index potential well. They exist in a wide range of optical systems spanning optical fibers, fiber lasers and parametric oscillators. Recently, a new type optical solitons have been observed in coherently pumped high-Q microcavities. The observation of microcavity optical solitons provides a well-controlled experimental platform to study soliton physics. Microcavity optical solitons also endow an array of highly stable spectral lines in the frequency domain, which advance the miniaturization of frequency comb systems. These soliton microcombs have been self-reference stabilized and could enable many chip-based applications including optical frequency synthesizers, optical atomic clocks, data transmission, spectrometer and LiDAR in the near future. Here, the fundamental of microcavity optical solitons was introduced, with a special focus on soliton interaction dynamics. The microcavity dual-comb measurement based applications in fast imaging and mid-infrared gas spectroscopy were also discussed.
-
Key words:
- optical soliton /
- coherent pump /
- microcomb /
- dual-comb measurements
-
图 1 微腔光孤子产生基础:(a) 相干泵浦时微腔时域和频域输入及输出[46];(b) 微腔中耗散光孤子的产生需满足增益和损耗与色散和非线性的双平衡;(c)反常色散微腔对应的色散曲线;(d)仿真得到的腔内功率随失谐量的变化,以及不同状态下的时域和频域波形;(e) 从有效蓝失谐区域扫描到有效红失谐区域过程中测得的输出光功率的变化[10, 12]
Figure 1. Fundamental of soliton dynamics in microcavities:(a) Input and output of a coherently pumped microcavity[46]; (b) Double balance between gain and loss as well as dispersion and nonlinearity is needed to support dissipative solitons in microcavities; (c) Dispersion curve of an anomalous dispersion cavity; (d) Simulated intracavity power change when scanning the pump frequency detuning. The power change features several steps indicating soliton states; (e) Experimentally measured transmitted power when scanning the laser from blue-detuning to red-detuning[10, 12]
图 2 微腔孤子间的相互作用:(a) 同向传播的孤子间通过色散波产生锁定[79];(b) 完美孤子晶体(PSC),在同个微腔中存在X个等间距分布的微腔孤子[80];(c)相向传播的微腔孤子可通过微腔的瑞利背向散射引起相互作用[82];(d) 不同微腔孤子间可通过将某一微腔孤子注入另一个微腔实现两个微腔孤子间的同步[84]
Figure 2. Soliton interaction in microcavities:(a) Illustration of co-propagating (CoP) solitons trapped by dispersive wave emission[79]; (b) Perfect soliton crystals (PSC) comprising X solitons in a microcavity[80]; (c) Counter-propagating (CP) solitons interaction via Rayleigh backscattering[82]; (d) Synchronization of solitons in two different microcavities via injecting one of the solitons into the other one[84]
图 3 微腔光频梳在双光梳测量中的应用:(a) 微腔双光梳光谱示意图[87];(b) 单微腔双光梳游标光谱仪示意图[89];(c) 微腔双光梳成像测量[90];(d) 双微腔光频梳的快速距离测量[92]
Figure 3. Dual-microcomb applications:(a) Dual-comb spectroscopy using microcombs[87]; (b) A microcavity based vernier spectrometer[89]; (c) Dual-comb imaging using microcombs[90]; (d) Ultrafast distance measurement with dual-microcombs[92]
图 4 光学差频技术在分子光谱学中的应用:(a) 中红外双微腔光梳测吸收光谱[96];(b) 使用 iDFG 中红外梳对甲烷进行双梳光谱(DCS)分析[102]; (c) 脉冲内自差频技术[100];(d) 间隔光学差频(iDFG)技术[101]
Figure 4. Application of optical frequency combs for spectroscopy:(a) Scheme of mid-infrared dual-comb spectroscopy using silicon microcavities[96]; (b) Dual-comb spectroscopy (DCS) analysis of methane using iDFG mid-IR combs[102]; (c) Intrapulse difference-frequency-generation technology[100]; (d) Interleaved difference-frequency-generation (iDFG) technology[101]
-
[1] Vahala K J. Optical microcavities [J]. Nature, 2003, 424: 839-846. doi: 10.1038/nature01939 [2] Kippenberg T, Spillane S, Vahala K. Kerr-nonlinearity optical parametric oscillation in an ultrahigh-Q toroid microcavity [J]. Phys Rev Lett, 2004, 93: 083904. doi: 10.1103/PhysRevLett.93.083904 [3] Savchenkov, A A, Matsko A B, Strekalov D, et al. Low threshold optical oscillations in a whispering gallery mode CaF2 resonator [J]. Phys Rev Lett, 2004, 93: 243905. doi: 10.1103/PhysRevLett.93.243905 [4] Del’Haye, P, Schliesser A, Arcizet O, et al. Optical frequency comb generation from a monolithic microresonator [J]. Nature, 2007, 450: 1214-1217. doi: 10.1038/nature06401 [5] Udem T, Holzwarth R, Hänsch T W. Optical frequency metrology [J]. Nature, 2002, 416: 233. doi: 10.1038/416233a [6] Cundiff S T, Ye J. Colloquium: Femtosecond optical frequency combs [J]. Rev Mod Phys, 2003, 75: 325. doi: 10.1103/RevModPhys.75.325 [7] Diddams S A, Vahala K, Udem T. Optical frequency combs: coherently uniting the electromagnetic spectrum [J]. Science, 2020, 369: eaay3676. doi: 10.1126/science.aay3676 [8] Jones D J, Diddams S A, Ranka J K, et al. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis [J]. Science, 2000, 288: 635-639. doi: 10.1126/science.288.5466.635 [9] Grelu P, Akhmediev N. Dissipative solitons for modelocked lasers [J]. Nature Photonics, 2012, 6: 84-92. doi: 10.1038/nphoton.2011.345 [10] Herr T. Brasch V, Jost J D, et al. Temporal solitons in optical microresonators [J]. Nature Photonics, 2014, 8: 145-152. doi: 10.1038/nphoton.2013.343 [11] Xue X X, Xuan Y, Liu Y, et al. Mode-locked dark pulse Kerr combs in normal-dispersion microresonators [J]. Nature Photonics, 2015, 9: 594-600. doi: 10.1038/nphoton.2015.137 [12] Kippenberg T J, Gaeta A L, Lipson M, et al. Dissipative Kerr solitons in optical microresonators [J]. Science, 2018, 361: eaan8083. doi: 10.1126/science.aan8083 [13] Suh M G, Vahala K. Gigahertz-repetition-rate soliton microcombs [J]. Optica, 2018, 5: 65-66. doi: 10.1364/OPTICA.5.000065 [14] Li Q, Briles T C, Westly D A, et al. Stably accessing octave-spanning microresonator frequency combs in the soliton regime [J]. Optica, 2017, 4: 193-203. doi: 10.1364/OPTICA.4.000193 [15] Pfeiffer M H, Herkommer C, Liu J Q, et al. Octave-spanning dissipative Kerr soliton frequency combs in Si3N4 microresonators [J]. Optica, 2017, 4: 684-691. doi: 10.1364/OPTICA.4.000684 [16] Li C H, Benedick A J, Fendel P, et al. A laser frequency comb that enables radial velocity measurements with a precision of 1 cms−1 [J]. Nature, 2008, 452: 610-612. doi: 10.1038/nature06854 [17] Steinmetz T, Wilken T, Araujo-Hauck C, et al. Laser frequency combs for astronomical observations [J]. Science, 2008, 321: 1335-1337. doi: 10.1126/science.1161030 [18] Suh M G, Yi X, Lai Y H, et al. Searching for exoplanets using a microresonator astrocomb [J]. Nature Photonics, 2019, 13: 25. doi: 10.1038/s41566-018-0312-3 [19] Obrzud E, Rainer M, Harutyunyan A, et al. A microphotonic astrocomb [J]. Nature Photonics, 2019, 13: 31. doi: 10.1038/s41566-018-0309-y [20] Marin-Palomo P, Kemal J N, Karpov M, et al. Microresonator-based solitons for massively parallel coherent optical communications [J]. Nature, 2017, 546: 274. doi: 10.1038/nature22387 [21] Fülöp, A, Mazur M, Lorences-Riesgo A, et al. High-order coherent communications using mode-locked dark-pulse Kerr combs from microresonators [J]. Nature Communications, 2018, 9: 1-8. [22] Geng Y, Zhou H, Han X J, et al. Coherent optical communications using coherence-cloned kerr soliton microcombs [J]. Nature Communications, 2022, 13: 1070. doi: 10.1038/s41467-022-28712-y [23] Liang W, Eliyahu D, Ilchenko V S, et al. High spectral purity Kerr frequency comb radio frequency photonic oscillator [J]. Nature Communications, 2015, 6: 7957. doi: 10.1038/ncomms8957 [24] Marpaung D, Yao J, Capmany J. Integrated microwave photonics [J]. Nature Photonics, 2019, 13: 80-90. [25] Kippenberg T J, Holzwarth R, Diddams S A. Microresonator-based optical frequency combs [J]. Science, 2011, 332: 555-559. doi: 10.1126/science.1193968 [26] Brasch V, Geiselmann M, Herr T, et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation [J]. Science, 2016, 351: 357-360. doi: 10.1126/science.aad4811 [27] Wang P H, Jaramillo-Villegas J A, Xuan Y, et al. Intracavity characterization of micro-comb generation in the single-soliton regime [J]. Opt Express, 2016, 24: 10890-10897. doi: 10.1364/OE.24.010890 [28] Joshi C, Jang J K, Luke K, et al. Thermally controlled comb generation and soliton modelocking in microresonators [J]. Opt Lett, 2016, 41: 2565-2568. doi: 10.1364/OL.41.002565 [29] Yi X, Yang Q F, Yang K Y, et al. Soliton frequency comb at microwave rates in a high-Q silica microresonator [J]. Optica, 2015, 2: 1078-1085. doi: 10.1364/OPTICA.2.001078 [30] Xu Y, Lin Y, Nielsen A, et al. Harmonic and rational harmonic driving of microresonator soliton frequency combs [J]. Optica, 2020, 7: 940-946. doi: 10.1364/OPTICA.392571 [31] Yu M, Okawachi Y, Griffith A G, et al. Mode-locked mid-infrared frequency combs in a silicon microresonator [J]. Optica, 2016, 3: 854-860. doi: 10.1364/OPTICA.3.000854 [32] Gong Z, Bruch A, Shen Mohan, et al. High-fidelity cavity soliton generation in crystalline AlN micro-ring resonators [J]. Opt Lett, 2018, 43: 4366-4369. doi: 10.1364/OL.43.004366 [33] He Y, Yang Q F, Ling J W, et al. Self-starting bi-chromatic LiNbO3 soliton microcomb [J]. Optica, 2019, 6: 1138-1144. doi: 10.1364/OPTICA.6.001138 [34] Gong Z, Liu X, Xu Y, et al. Near-octave lithium niobate soliton microcomb [J]. Optica, 2020, 7: 1275-1278. doi: 10.1364/OPTICA.400994 [35] Pu M, Ottaviano L, Semenova E, et al. Efficient frequency comb generation in algaas-on-insulator [J]. Optica, 2016, 3: 823-826. doi: 10.1364/OPTICA.3.000823 [36] Chang L, Xie W Q, Shu H W, et al. Ultra-efficient frequency comb generation in algaas-on-insulator microresonators [J]. Nature Communications, 2020, 11: 1-8. [37] Moille G, Chang L, Xie W Q, et al. Dissipative Kerr solitons in a III-V microresonator [J]. Laser & Photonics Reviews, 2020, 14: 2000022. [38] Jung H, Yu S P, Carlson D R, et al. Tantala Kerr nonlinear integrated photonics [J]. Optica, 2021, 8: 811-817. doi: 10.1364/OPTICA.411968 [39] Zheng Y, Sun C Z, Xiong B, et al. Integrated gallium nitride nonlinear photonics[J]. arXiv, 2020: 2010.16149. [40] Wilson D J, Schneider K, Honl S, et al. Integrated gallium phosphide nonlinear photonics [J]. Nature Photonics, 2020, 14: 57-62. doi: 10.1038/s41566-019-0537-9 [41] Lu Z, Chen H J, Wang W, et al. Synthesized soliton crystals [J]. Nature communications, 2021, 12: 1-7. [42] Shen B, Chang L, Liu J, et al. Integrated turnkey soliton microcombs [J]. Nature, 2020, 582: 365-369. doi: 10.1038/s41586-020-2358-x [43] Stern B, Ji X, Okawachi Y, et al. Battery-operated integrated frequency comb generator [J]. Nature, 2018, 562: 401-405. doi: 10.1038/s41586-018-0598-9 [44] Xiang C, Liu J, Guo J, et al. Laser soliton microcombs heterogeneously integrated on silicon [J]. Science, 2021, 373: 99-103. doi: 10.1126/science.abh2076 [45] Bao C, Yang C. Mode-pulling and phase-matching in broadband Kerr frequency comb generation [J]. JOSA B, 2014, 31: 3074-3080. doi: 10.1364/JOSAB.31.003074 [46] Guo H, Karpov M, Lucas E, et al. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators [J]. Nature Physics, 2017, 13: 94-102. doi: 10.1038/nphys3893 [47] Bao C, Xuan Y, Jaramillo-Villegas J A, et al. Direct soliton generation in microresonators [J]. Optics Letters, 2017, 42: 2519-2522. doi: 10.1364/OL.42.002519 [48] Yi X, Yang Q F, Yang K Y, et al. Active capture and stabilization of temporal solitons in microresonators [J]. Optics Letters, 2016, 41: 2037-2040. doi: 10.1364/OL.41.002037 [49] Stone J R, Briles T C, Drake T E, et al. Thermal and nonlinear dissipative-soliton dynamics in Kerr-microresonator frequency combs [J]. Physical Review Letters, 2018, 121: 063902. doi: 10.1103/PhysRevLett.121.063902 [50] Zhou H, Geng Y, Cui W, et al. Soliton bursts and deterministic dissipative Kerr soliton generation in auxiliary-assisted microcavities [J]. Light: Science & Applications, 2019, 8: 1-10. [51] Zhang S, Silver J M, Del Bino L, et al. Sub-milliwatt-level microresonator solitons with extended access range using an auxiliary laser [J]. Optica, 2019, 6: 206-212. doi: 10.1364/OPTICA.6.000206 [52] Pavlov N G, Koptyaev S, Lihachev G V, et al. Narrow-linewidth lasing and soliton Kerr microcombs with ordinary laser diodes [J]. Nature Photonics, 2018, 12: 694-698. doi: 10.1038/s41566-018-0277-2 [53] Bao C, Xuan Y, Leaird D E, et al. Spatial mode-interaction induced single soliton generation in microresonators [J]. Optica, 2017, 4: 1011-1015. doi: 10.1364/OPTICA.4.001011 [54] Herr T, Brasch V, Jost J D, et al. Mode spectrum and temporal soliton formation in optical microresonators [J]. Physical Review Letters, 2014, 113: 123901. doi: 10.1103/PhysRevLett.113.123901 [55] Spencer D T, Drake T, Briles T C, et al. An integrated-photonics optical-frequency synthesizer [J]. Nature, 2017, 557: 81. [56] Newman Z L, Maurice V, Drake T, et al. Architecture for the photonic integration of an optical atomic clock [J]. Optica, 2019, 6: 680-685. doi: 10.1364/OPTICA.6.000680 [57] Karpov M, Guo H, Kordts A, et al. Raman self-frequency shift of dissipative Kerr solitons in an optical microresonator [J]. Physical Review Letters, 2016, 116: 103902. doi: 10.1103/PhysRevLett.116.103902 [58] Yi X, Yang Q F, Yang K Y, et al. Theory and measurement of the soliton self-frequency shift and efficiency in optical microcavities [J]. Optics Letters, 2016, 41: 3419-3422. doi: 10.1364/OL.41.003419 [59] Yao S, Wei Z, Guo Y, et al. Self-frequency shift of AlN-on-sapphire Kerr solitons [J]. Optics Letters, 2021, 46: 5312-5315. doi: 10.1364/OL.441696 [60] Yi X, Yang Q F, Zhang X, et al. Single-mode dispersive waves and soliton microcomb dynamics [J]. Nature Communications, 2017, 8: 1-9. [61] Matsko A B, Maleki L. On timing jitter of mode locked Kerr frequency combs [J]. Optics Express, 2013, 21: 28862-28876. doi: 10.1364/OE.21.028862 [62] Bao C, Suh M G, Shen B, et al. Quantum diffusion of microcavity solitons [J]. Nature Physics, 2021, 17: 462-466. doi: 10.1038/s41567-020-01152-5 [63] Jia K, Wang X, Kwon D, et al. Photonic flywheel in a monolithic fiber resonator [J]. Physical Review Letters, 2020, 125: 143902. doi: 10.1103/PhysRevLett.125.143902 [64] Jeong D, Kwon D, Jeon I, et al. Ultralow jitter silica microcomb [J]. Optica, 2020, 7: 1108-1111. doi: 10.1364/OPTICA.390944 [65] Bao C, Yang C. Carrier-envelope phase dynamics of cavity solitons: Scaling law and soliton stability [J]. Physical Review A, 2015, 92: 053831. doi: 10.1103/PhysRevA.92.053831 [66] Matsko A B, Savchenkov A A, Maleki L. On excitation of breather solitons in an optical microresonator [J]. Optics Letters, 2012, 37: 4856-4858. doi: 10.1364/OL.37.004856 [67] Bao C, Jaramillo-Villegas J A, Xuan Y, et al. Observation of Fermi-Pasta-Ulam recurrence induced by breather solitons in an optical microresonator [J]. Physical Review Letters, 2016, 117: 163901. doi: 10.1103/PhysRevLett.117.163901 [68] Lucas E, Karpov M, Guo H, et al. Breathing dissipative solitons in optical microresonators [J]. Nature Communications, 2017, 8: 1-11. [69] Yu M, Jang J K, Okawachi Y, et al. Breather soliton dynamics in microresonators [J]. Nature Communications, 2017, 8: 1-7. doi: 10.1038/s41467-016-0009-6 [70] Yi X, Yang Q F, Yang K Y, et al. Imaging soliton dynamics in optical microcavities [J]. Nature Communications, 2018, 9: 1-8. doi: 10.1038/s41467-017-02088-w [71] Bao C, Xuan Y, Wang C, et al. Observation of breathing dark pulses in normal dispersion optical microresonators [J]. Physical Review Letters, 2018, 121: 257401. doi: 10.1103/PhysRevLett.121.257401 [72] Yao S, Bao C, Wang P, et al. Generation of stable and breathing flat-top solitons via Raman assisted four wave mixing in microresonators [J]. Physical Review A, 2020, 101: 023833. doi: 10.1103/PhysRevA.101.023833 [73] Yao B, Huang S W, Liu Y, et al. Gate-tunable frequency combs in graphene–nitride microresonators [J]. Nature, 2018, 558: 410-414. doi: 10.1038/s41586-018-0216-x [74] Stegeman G I, Segev M. Optical spatial solitons and their interactions: universality and diversity [J]. Science, 1999, 286: 1518-1523. doi: 10.1126/science.286.5444.1518 [75] Weng W, Bouchand R, Lucas E, et al. Heteronuclear soliton molecules in optical microresonators [J]. Nature Communications, 2020, 11: 1-9. doi: 10.1038/s41467-019-13993-7 [76] Yang Q F, Yi X, Yang K Y, et al. Stokes solitons in optical microcavities [J]. Nature Physics, 2017, 13: 53-57. doi: 10.1038/nphys3875 [77] Jang J K, Erkintalo M, Coen S, et al. Temporal tweezing of light through the trapping and manipulation of temporal cavity solitons [J]. Nature Communications, 2015, 6: 1-7. [78] Taheri H, Matsko A B, Maleki L. Optical lattice trap for Kerr solitons [J]. The European Physical Journal D, 2017, 71: 1-13. doi: 10.1140/epjd/e2016-70680-8 [79] Wang Y, Leo F, Fatome J, et al. Universal mechanism for the binding of temporal cavity solitons [J]. Optica, 2017, 4: 855-863. doi: 10.1364/OPTICA.4.000855 [80] Karpov M, Pfeiffer M H P, Guo H, et al. Dynamics of soliton crystals in optical microresonators [J]. Nature Physics, 2019, 15: 1071-1077. doi: 10.1038/s41567-019-0635-0 [81] Yang Q F, Yi X, Yang K Y, et al. Counter-propagating solitons in microresonators [J]. Nature Photonics, 2017, 11: 560-564. doi: 10.1038/nphoton.2017.117 [82] Bao C, Shen B, Suh M G, et al. Oscillatory motion of a counterpropagating Kerr soliton dimer [J]. Physical Review A, 2021, 103: L011501. doi: 10.1103/PhysRevA.103.L011501 [83] Lucas E, Lihachev G, Bouchand R, et al. Spatial multiplexing of soliton microcombs [J]. Nature Photonics, 2018, 12: 699-705. doi: 10.1038/s41566-018-0256-7 [84] Jang J K, Klenner A, Ji X, et al. Synchronization of coupled optical microresonators [J]. Nature Photonics, 2018, 12: 688-693. doi: 10.1038/s41566-018-0261-x [85] Kim B Y, Jang J K, Okawachi Y, et al. Synchronization of nonsolitonic Kerr combs [J]. Science Advances, 2021, 7: eabi4362. doi: 10.1126/sciadv.abi4362 [86] Coddington I, Newbury N, Swann W. Dual-comb spectroscopy [J]. Optica, 2016, 3: 414-426. doi: 10.1364/OPTICA.3.000414 [87] Suh M G, Yang Q F, Yang K Y, et al. Microresonator soliton dual-comb spectroscopy [J]. Science, 2016, 354: 600-603. doi: 10.1126/science.aah6516 [88] Dutt A, Joshi C, Ji X, et al. On-chip dual-comb source for spectroscopy [J]. Science Advances, 2018, 4: e1701858. doi: 10.1126/sciadv.1701858 [89] Yang Q F, Shen B, Wang H, et al. Vernier spectrometer using counterpropagating soliton microcombs [J]. Science, 2019, 363: 965-968. doi: 10.1126/science.aaw2317 [90] Bao C, Suh M G, Vahala K. Microresonator soliton dual-comb imaging [J]. Optica, 2019, 6: 1110-1116. doi: 10.1364/OPTICA.6.001110 [91] Suh M G, Vahala K J. Soliton microcomb range measurement [J]. Science, 2018, 359: 884-887. doi: 10.1126/science.aao1968 [92] Trocha P, Karpov M, Ganin D, et al. Ultrafast optical ranging using microresonator soliton frequency combs [J]. Science, 2018, 359: 887-891. doi: 10.1126/science.aao3924 [93] Schliesser A, Picqué N, Hänsch T W. Mid-infrared frequency combs [J]. Nature Photonics, 2012, 6: 440-449. doi: 10.1038/nphoton.2012.142 [94] Wang C Y, Herr T, Del’Haye P, et al. Mid-infrared optical frequency combs at 2.5 μm based on crystalline microresonators [J]. Nature Communications, 2013, 4: 1-7. [95] Griffith A G, Lau R K W, Cardenas J, et al. Silicon-chip mid-infrared frequency comb generation [J]. Nature Communications, 2015, 6: 1-5. [96] Yu M, Okawachi Y, Griffith A G, et al. Silicon-chip-based mid-infrared dual-comb spectroscopy [J]. Nature Commu-nications, 2018, 9: 1-6. [97] Luke K, Okawachi Y, Lamont M R E, et al. Broadband mid-infrared frequency comb generation in a Si3N4 microresonator [J]. Optics Letters, 2015, 40: 4823-4826. doi: 10.1364/OL.40.004823 [98] Yan M, Luo P L, Iwakuni K, et al. Mid-infrared dual-comb spectroscopy with electro-optic modulators [J]. Light: Science & Applications, 2017, 6: e17076. [99] Kowligy A S, Carlson D R, Hickstein D D, et al. Mid-infrared frequency combs at 10 GHz [J]. Optics Letters, 2020, 45: 3677-3680. doi: 10.1364/OL.391651 [100] Timmers H, Kowligy A, Lind A, et al. Molecular fingerprinting with bright, broadband infrared frequency combs [J]. Optica, 2018, 5: 727-732. doi: 10.1364/OPTICA.5.000727 [101] Bao C, Yuan Z, Wang H, et al. Interleaved difference-frequency generation for microcomb spectral densification in the mid-infrared [J]. Optica, 2020, 7: 309-315. doi: 10.1364/OPTICA.382992 [102] Bao C, Yuan Z, Wu L, et al. Architecture for microcomb-based GHz-mid-infrared dual-comb spectroscopy [J]. Nature Communications, 2021, 12: 1-8. doi: 10.1038/s41467-020-20314-w [103] Cingöz A, Yost D C, Allison T K, et al. Direct frequency comb spectroscopy in the extreme ultraviolet [J]. Nature, 2012, 482: 68-71. doi: 10.1038/nature10711 [104] Guidry M A, Lukin D M, Yang K Y, et al. Quantum optics of soliton microcombs [J]. Nature Photonics, 2022, 16: 52-58. doi: 10.1038/s41566-021-00901-z -






 下载:
下载: