-
近年来,基于高品质因子光学微腔的光学频率梳技术受到国内外研究人员的广泛关注[1-4],包括微腔中的非线性光学机理、光学微腔的微纳加工工艺、以及微腔光频梳的应用都得到了极大的发展,目前已经能够实现全集成、高紧凑的光学频率梳芯片,为频率-时间计量提供大批量、高性能的激光光源。同时,微腔光频梳也被证明能够在超大容量光通信[5-6]、光学数据中心[7-8]、 激光雷达[9]、低噪声微波合成[10-11]、光子神经形态运算[12-13]等领域有着巨大的应用前景。
回音壁模式 (WGM)微腔是研究微腔光频梳技术的一个重要平台,也是最早开展此项研究的平台。至今,回音壁模式微腔,如氟化物微腔,具有高达1011的超高品质因子,以及高达107的精细度(finesse)[14]。微腔光频梳的许多经典理论和实验现象均在回音壁模式微腔中获得了验证,包括腔内的时域耗散孤子态形成[15]、孤子量化缩放[16]、孤子数目切换[17-18]、呼吸孤子态[19]、模间呼吸孤子[20]等。此外,超高品质因子的微腔也能用作超稳腔,实现具有超窄线宽的连续激光[21-22]和光频梳[23-25]。
氧化硅(SiO2)是实现WGM微腔的主要材料之一。加工SiO2 WGM微腔主要方法有高温火焰熔融,以及利用高功率二氧化碳(CO2)激光实现局部熔融。加工成型的微腔主要有石英棒微腔、光纤端的微球腔、以及基于石英套管或空芯光纤的微瓶腔。早在1989年,Braginsky等首次利用熔融SiO2材料制备出了微球腔[26],Q值高达108,讨论了降低光开关的控制阈值的可能性。1996年,Gorodetsky等用氧-氢微燃烧器制备了高纯度熔融SiO2微球[27],Q值高达3×109,并讨论了影响微腔Q值的相关因素。2007 年,Del’ Haye等通过将1550 nm连续光泵浦到石英玻璃微腔[28],首次实现微腔光频梳的产生,证明了晶体微腔光频梳的可行性。2011年, Papp等基于前人的工作,提出了一种新的制造方法,采用金刚石研磨和火焰抛光相结合的方法,在SiO2石英棒上制备了Q值高达6.2×108的微腔[29],并在1560 nm附近形成了线间距36 GHz、跨度50 nm、阈值小于10 mW的频率梳。2013年,Papp等优化了加工工艺,利用CO2激光器熔融石英棒的方式制备微腔[30-31],Q值达到了109,并实现了微梳线间距的宽带机械控制。2019年,Del’ Haye等同样利用CO2激光器熔融SiO2微棒腔[32],制备了Q值高达 3.7×108的微腔,并产生孤子微梳,为低阈值微梳系统的实现铺平了道路。2019年,肖云峰等制备了超高Q值SiO2光学微球腔[33],其Q值高达109,通过将 SSB 的基本概念扩展到有源微腔来实现对称破缺拉曼激光器。2021年,董春华等利用CO2激光器熔融石英棒,得到了Q值为2×108的微棒腔[34],通过辅助激光法产生了孤子梳,并观察到了完美孤子晶体。2021年,邱昆等利用Q值为108次方的微棒腔生成了单个耗散克尔孤子微梳[35],并通过迭代退火过程精确调整孤子重复频率。2021年,姚佰承等利用Q值为3×108的SiO2微球首次产生了多个模式家族的孤子同时输出[36],并实现了不同载频中心孤子的相互锁定。使无标记多参量气体混合物的单分子探测成为可能,为光频梳的生化精密测量提供了新的路径。根据上述研究进展,可以总结目前SiO2微腔的制备技术已经较为成熟,Q值普遍达到了108以上,且相关的延伸性研究,包括实现微腔光频梳、实现高精度传感、实现低阈值的光开关等,也已经有所发展。
文中的主要工作是基于SiO2棒制备了高品质因子的回音壁模式微腔(即石英棒微腔),并开展了微腔的特性表征和微腔光频梳产生的研究。
-
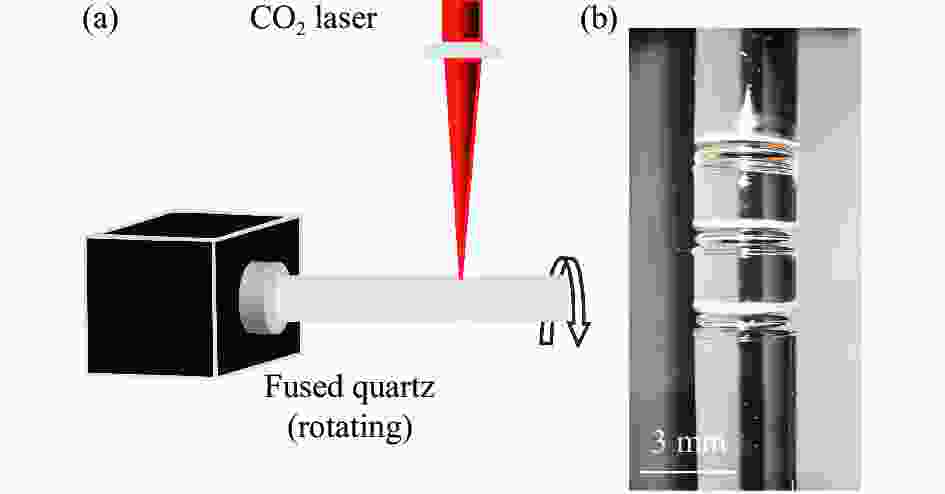
利用CO2激光器制备SiO2微腔。首先,准备了低OH−含量、高纯度的直径为3 mm的石英棒,将其安装在电机驱动的气伏马达主轴上, 此外,CO2激光束的粗对准是由一个可见共线对准的激光器支持的,通过调整CO2激光器高度,使激光束聚焦在石英棒上,如图1(a)所示;其次,将气伏马达以600 r/min的转速带动石英棒转动,同时让CO2激光沿着棒的轴向来回扫描以蒸发石英棒表层,起到清洁和预热作用;最后,通过CO2激光器对石英棒两次熔融的距离和时间的控制,得到初步的微腔结构,再对微腔表面进行最终的熔融处理,获得表面光滑的微腔,如图1(b)所示。
-
SiO2晶体微腔的品质因子Q值不仅与材料本身有关,还与其微腔表面粗糙度、清洁度以及微腔圆度有关,因此,笔者通过对微腔表面粗糙度以及微腔圆度进行表征,来确定制备的微腔的可用性,如图2所示。
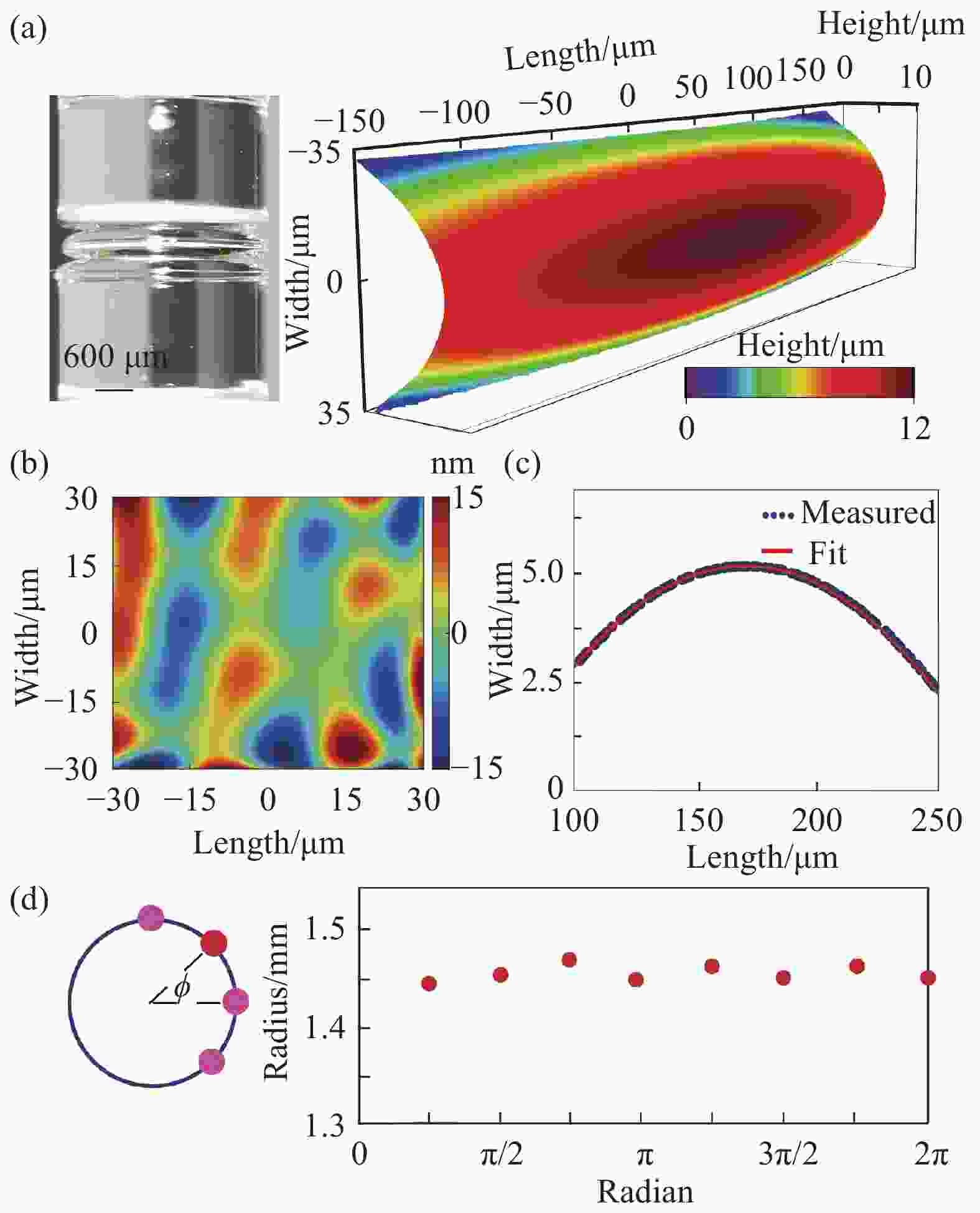
图 2 微腔形貌。(a) 微腔3D表面轮廓;(b) 微腔表面粗糙度图;(c)~(d) 微腔圆度表征
Figure 2. Morphology of microcavity. (a) 3D surface profile of the microcavity; (b) Surface roughness diagram of microcavity; (c)-(d) Characterization of microcavity roundness
首先,通过光学干涉轮廓仪对微腔的表面数据进行提取,表征出微腔的三维表面轮廓;其次,用二维多项式函数对实测轮廓进行拟合,提取表面粗糙度作为拟合的残差,最终估算其表面均方根(RMS)粗糙度低至几纳米;此外,根据实验测得的表面粗糙信息可知,存在相比RMS粗糙度更大的表面结构起伏,通常这些较大的起伏结构位于微腔外缘两侧,推测对于微腔内高阶横向模式会有影响。如图2(a)、(b)所示;最后,每隔π/4采集一组数据进行圆度表征,共采集了8组数据,对其进行圆度拟合并取平均值,计算得到腔直径上的变化约3%,如图2(c)、(d)所示,其圆率满足实验要求。
-
为了测试微腔的谐振峰特性,搭建了微腔耦合的测试系统,如图3(a)所示。系统使用可调谐连续波激光器(CTL1550_Toptica)作为光源,经过锥腰直径约为3 μm的锥形光纤波导实现SiO2微腔的耦合。通过扫描激光频率,可以在示波器(OSC)中观察微腔的透射信号,并研判谐振峰的特性。当激光频率调谐速度为2.5 GHz/s,测得的微腔透射谱如图3(b)所示,由测得的结果可知,其FSR为17.8 GHz。采用洛伦兹线形对各个谐振峰进行拟合,结果显示微腔中最佳的Q值约为3.87×108,如图3(c)所示;当激光调谐速度为350 GHz/s,实验中观察到谐振峰出现了振荡衰退(Ring down)现象,如图3(d)所示。理论上[37],一个谐振模式内腔场的时间演化可以描述为一个简单的谐振模型,即:
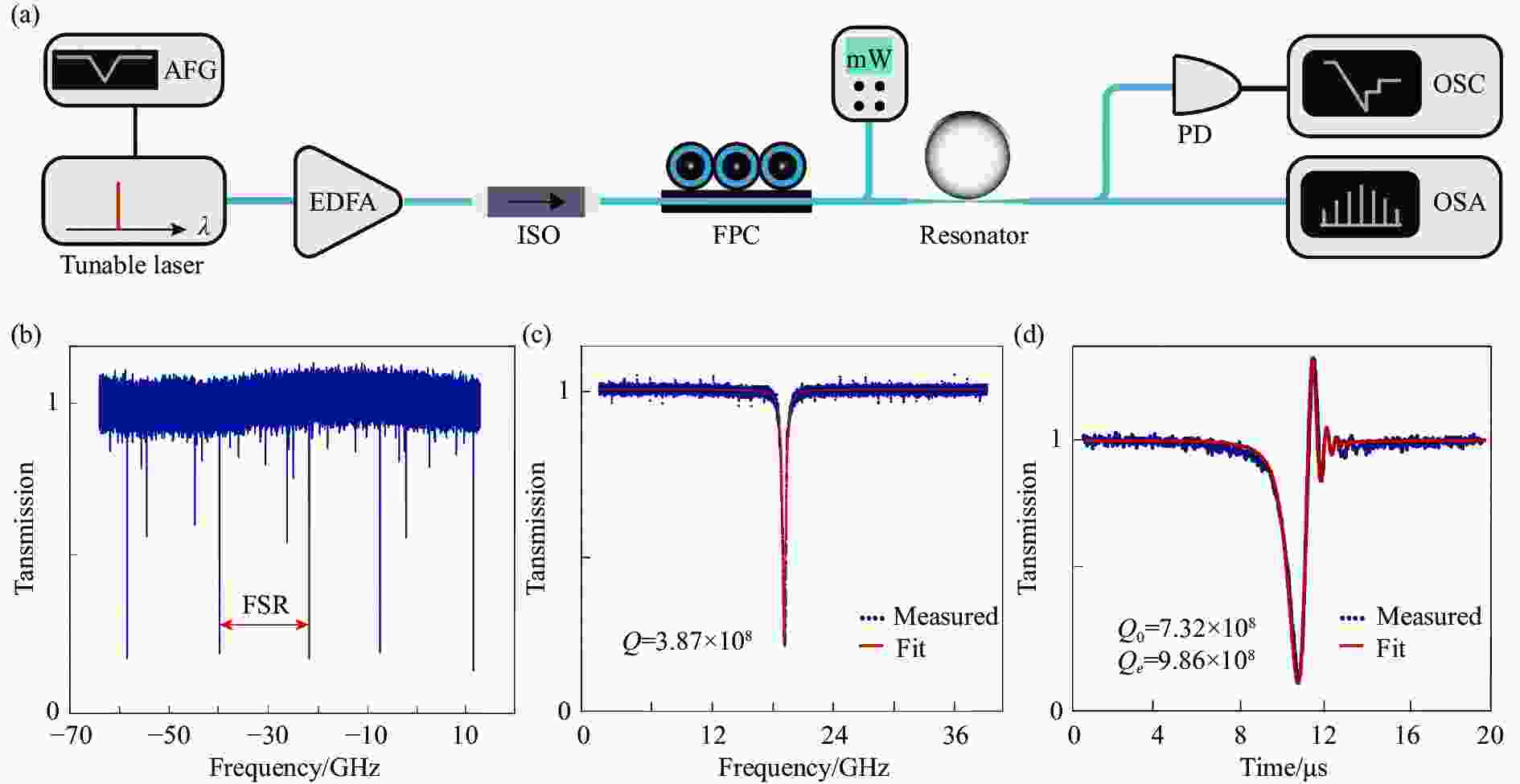
图 3 SiO2微腔谐振峰测试。(a) 微腔耦合测试示意图;(b) 微腔功率透射谱;(c) 洛伦兹拟合谱线;(d) Ringdown拟合
Figure 3. Measurement of resonant peak of SiO2 microcavity. (a) Schematic diagram of microcavity coupling test; (b) Power transmission spectrum of microcavity; (c) Lorentz fitting spectral line; (d) Ringdown fitting
$$ \frac{\partial A}{\partial t}=\mathrm{i}{\omega }_{0}A-\frac{k}{2}A+\sqrt{{k}_{ex}}\cdot {s}_{in} $$ (1) 式中:
$ {\omega }_{0} $ 为谐振角频率;$ k $ 为系统总损耗率,包括固有损耗率$ {k}_{0} $ 和耦合损耗率$ {k}_{ex} $ ,即$ k={k}_{0}+{k}_{ex} $ ;$ {s}_{in} $ 为外部源,在频率可调的连续波模式下,其变化${s}_{in}={s}_{0}{\rm exp}\left(i\phi \left(t\right)\right)$ 。在稳态形式下,即相对于其初始值$ {\omega }_{i} $ 的激光频率调谐与腔内光子寿命相比缓慢变化,笔者得到$ \phi \left(t\right)={\omega }_{i}t $ ,公式(1)的解给出了作为激光失谐$ {\delta }_{\omega }={\omega }_{i}-{\omega }_{0} $ 函数的标准洛伦兹分布。相反,在激光频率调谐与光子寿命相当的条件下,得到$ \phi \left(t\right)=\left({\omega }_{i}+\dfrac{{V}_{s}t}{2}\right)t $ ,其中,$ {V}_{s} $ 为激光频率的调谐速度。因此,设$A=a\cdot {\rm exp}\left(i\phi \left(t\right)\right)$ ,公式(1)可以变换为:$$ \frac{\partial a}{\partial t}=i\left({\delta }_{\omega }-{V}_{s}t\right)a-\frac{k}{2}a+\sqrt{{k}_{ex}}\cdot {s}_{0} $$ (2) 对上式积分可得:
$$ a=\sqrt{{k}_{ex}}\cdot {s}_{0}\cdot \mathrm{exp}\left(\mathrm{i}{\delta }_{\omega }t-\dfrac{k}{2}t\right) \times \left[f\left(t\right)-\dfrac{1}{i{\delta }_{\omega }-\dfrac{k}{2}}\right] $$ (3) 其中,
$$ \begin{split} {f\left(t\right)}=&{-\sqrt{\dfrac{i\pi }{2{V}_{s}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(i\dfrac{{\left(i{\delta }_{\omega }-\raisebox{1ex}{$k$} \left/ \raisebox{-1ex}{$2$}\right.\right)}^{2}}{2{V}_{s}}\right) \times \left[{\rm erf}\left(-i\dfrac{i({\delta }_{\omega }-{V}_{s}t)-\raisebox{1ex}{$k$} \left/ \raisebox{-1ex}{$2$}\right.}{\sqrt{2i{V}_{s}}}\right)-\right.}\\ &{ \left. {\rm erf}\left(-i\dfrac{i({\delta }_{\omega }-\raisebox{1ex}{$k$} \left/ \raisebox{-1ex}{$2$}\right.}{\sqrt{2i{V}_{s}}}\right)\right]} \end{split} $$ 式中:erf(z)为复误差函数。腔透射率可以计算为:
$$ T={\left|\frac{{s}_{0}-\sqrt{{k}_{ex}}\cdot a}{{s}_{0}}\right|}^{2} $$ (4) 注意,使用公式(4)进行拟合将确定地返回耦合率kex作为整体损耗率k的一部分,从而可以区分腔体的耦合状态(过度耦合或欠耦合)。
通过对实验观察到的Ringdown曲线进行拟合,结果显示谐振峰对应的固有品质因子为:
${Q}_{0}= {{\omega }_{0}}/{k}_{0}=7.32\times {10}^{8}$ ,耦合品质因子为$ {Q}_{e}=9.86\times {10}^{8} $ 。以及总体的品质因子Q值为:$ {1}/{{Q}_{0}}+{1}/{{Q}_{e}}=4.2\times {10}^{8} $ ,该结果与低速频率调谐下洛伦兹拟合的谐振峰Q值相似。因此,笔者验证了Q值超过108的SiO2回音壁模式微腔。 -
为了研究微腔的耦合特性,笔者通过实验测得微腔的耦合理想曲线(Ideality)。首先,通过调整光纤锥和微腔的耦合状态,找到一个耦合效率较高的位置,此时,再将光纤锥移至远离微腔的位置处;然后,将光纤锥从远处慢慢靠近微腔,在这个过程中采集同一模式下的谐振峰的数据,利用洛伦兹曲线对采集的谐振峰数据进行拟合,得到了不同耦合状态下的谐振峰数据。最后,通过拟合得到微腔谐振峰深度和线宽Ideality曲线,如图4所示。
需要说明的是,本征损耗主要由材料吸收损耗、辐射损耗和散射损耗所决定,而耦合损耗主 要与微腔和光纤锥的耦合距离有关。由结果可知,当光纤锥从远处慢慢靠近微腔直到刚出现谐振峰时,此时,耦合损耗小于本征损耗,系统处于欠耦合状态;当光纤锥逐步靠近微腔直到谐振峰深度达到最深时,此时,耦合损耗等于本征损耗,系统处于临界耦合;当光纤锥再贴近微腔直到谐振峰深度变浅时,此时,耦合损耗大于本征损耗,系统处于过耦合。 实验中测的谐振峰深度与线宽的变化,基本符合标准的Ideality曲线,证明在微腔耦合过程中,没有额外的能量损耗。
-
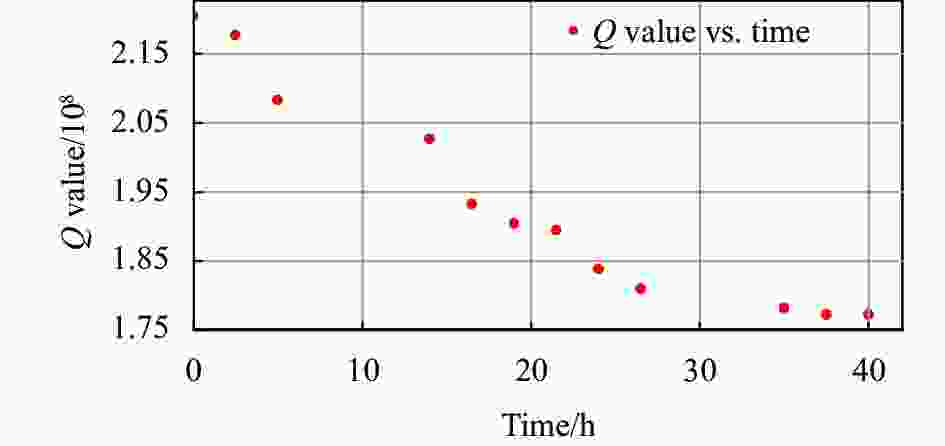
由于制备SiO2微腔材料的水羟基的存在,使其具有较强的亲水性,这也导致了SiO2微腔放置一段时间后其Q值会有所下降。为了测试其Q值随时间的变化关系,每隔一段时间对微腔的Q值进行测试,其结果如图5所示。由结果可知,微腔Q值随着时间不断降低,经过一段时间后,其Q值的变化趋于平稳,主要原因可能是由于SiO2微腔表面的水羟基饱和,导致其Q值最终变化不大。
为了能实现对制备的SiO2微腔重复使用,一是要对制备的SiO2微腔进行隔绝空气保存,二是对Q值退化的微腔进行退火处理来使微腔表面的水汽蒸发,来实现Q值的回升。处理方案主要有两种,一是利用CO2激光器对微腔进行重新熔融处理,但基于目前的微腔制备系统,无法重新找到微腔的精确位置,因此,笔者选择了另外一种方式,即利用马弗炉对已经放置一段时间的SiO2微腔进行退火处理,来验证此方法的可行性。为了比较退火前后的Q值的变化,以及Q值的恢复程度,先对刚制备的微腔的部分谐振峰Q值进行了测试,其中,Depth为0时表示此时系统处于临界耦合。一段时间后,再次对退火前后同级深度的谐振峰Q值进行了测试,其中,退火温度设置为950 ℃,退火时间设置为6 h,其结果如表1所示。由表可知,其Q值较未退火前有所提升,但未能恢复到刚制备好时的水平。由于笔者对微腔退火的研究还处于探索阶段,并没有找到最佳的退火温度和退火时间。并且在退火过程中,马弗炉内的微尘可能吸附到微腔表面,也会导致Q值恢复不明显。因此,可以通过探索最佳的退火温度和退火时间以及优化微腔退火的夹具来实现Q值的高效恢复。
表 1 退火前后微腔Q值变化
Table 1. Change of Q value of microcavity before and after annealing
Depth 0.6 0.5 0.4 0.3 0.2 0.1 0 Initial Q value - 3.23×108 - 2.14×108 1.43×108 - - Before annealing 1.78×108 1.66×108 8.57×107 6.9×107 6.1×107 5.7×107 5.96×107 After annealing 3.11×108 2.12×108 1.59×108 1.3×108 7.9×107 7.1×107 7.57×107 -
利用高Q值的SiO2微腔系统对光频梳产生过程进行研究。光频梳产生的实现系统图如图3(a)所示。采用任意信号发生器(AFG)驱动可调谐激光器来实现输出激光围绕着特定频率进行快速扫频,激光通过掺铒光纤放大器(EDFA)放大,经过隔离器(ISO)和偏振控制器(FPC)注入到SiO2微腔中,用示波器(OSC)和光谱仪(OSA)观察谐振峰状态和光频梳产生。
首先,通过调整光纤锥和微腔的耦合状态,找到一个耦合效率较高的位置;其次,对泵浦功率进行扫描,通过调节EDFA,得到的输出功率为80 mW,然后调节偏振控制器,在示波器上找到可以产生孤子梳时所出现的“台阶”,台阶长度约为1.8 MHz,如图6(a)、(b)所示。笔者控制可调谐激光,从短波长向长波长进行调谐,在调谐过程中,光频梳最先由单频的泵浦光产生第一、第二级边带,如图6(c)所示,即腔内光场形成了时域的Turing模式;继续调谐激光波长,微腔内激发的简并与非简并四波混频(FWM)作用将产生更多的梳齿,如图6(d)、(e)所示,此时,微腔进入到调制不稳定状态,即腔内的时域模式是随机不稳定的,光频梳也不具有较高相干性。目前,由于孤子台阶较短,笔者还无法获得孤子态的微腔光频梳。通过优化泵浦功率,并采用有效的热平衡技术,如辅助激光法[38]等,可以有效增加孤子台阶的长度,以此获得孤子态的微腔光频梳产生。

图 6 光频梳产生。(a) 高泵浦功率下微腔的透射谱线;(b) 图(a)的部分放大的透射谱线;(c)~(e) 光频梳的演化过程,分别对应于图(a)中微腔透射谱线的三个不同的位置
Figure 6. Optical frequency comb generation. (a) Transmission lines of microcavity at high pump power;(b) Partially amplified transmission line of Fig.(a); (c)-(e) Evolution process of optical frequency comb corresponds to three different positions of microcavity transmission line in Fig.(a)
此外,利用LLE方程描述实验中微腔光频梳的演化过程[15],设定泵浦功率Pin为100 mW,有效折射率n0为1.45、耦合线宽kex为2π×600 kHz、色散D2为2π×8000 Hz、FSR为17.8 GHz、有效模式体积Veff为9×10−12 m3、非线性系数n2为2.4×10−19 m3·W−1、中心波长λ为1550 nm,图7展示了通过仿真得到的第一、二级边带梳、子梳、调制不稳定频梳以及单孤子光频梳的光谱图和时域波形图。模拟中泵浦激光从相对于微腔模式蓝失谐区域扫描到红失谐区域,一开始随着泵浦调谐,腔内能量逐渐升高,频域开始出现初级梳齿边带,对应的时域分布表现为连续波的均匀分布,如图7(a)、(b)中I图所示;随着泵浦继续调谐,腔内能量进一步升高,频域表现为低相干的MI梳,时域表现为不规则的混沌状态,如图7(a)、(b)中II、III图所示;随着泵浦进一步调谐,光频梳进入孤子状态,频梳处于低噪态,各谱线是相干的,对应时域表现为单孤子状态,如图7(a)、(b)中IV图所示。由此可知,实验结果和仿真结果具有较好的一致性。
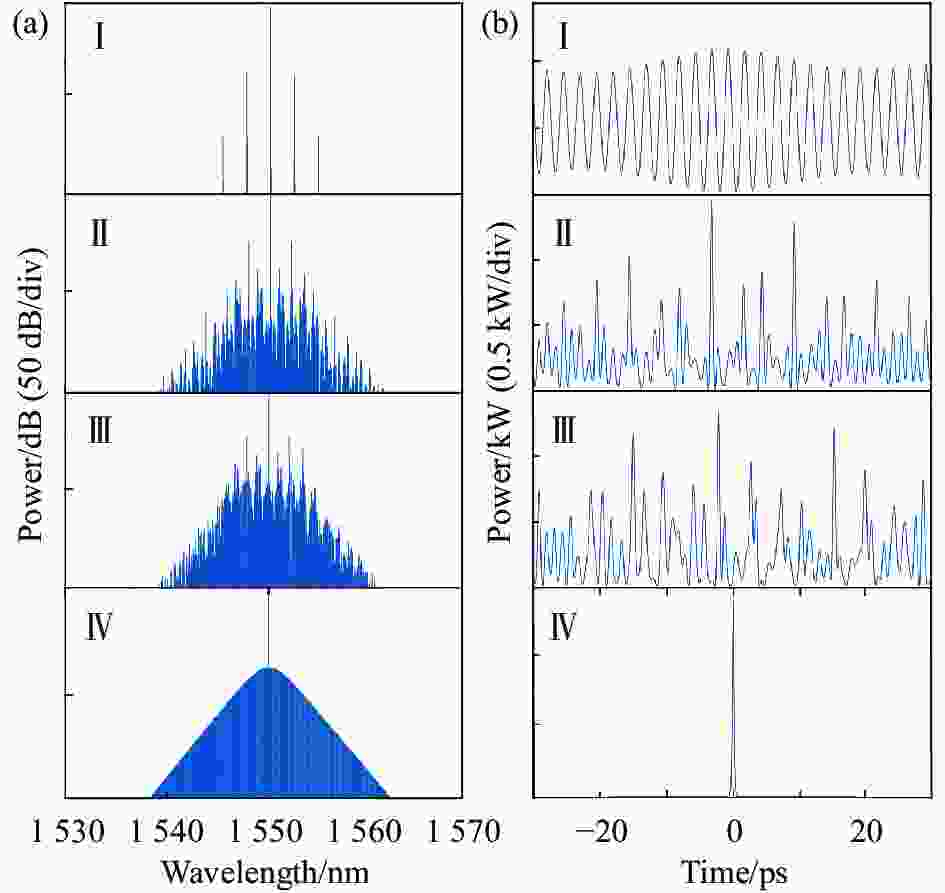
图 7 LLE仿真得到的光频梳演化过程。(a) I、II、III、IV图为光频梳的演化过程;(b) 分别对应图(a)中不同梳齿状态下的时域谱
Figure 7. Simulated optical frequency comb evolution based on LLE. (a) Figures I, II,III and IV show the evolution process of optical frequency comb; (b) Corresponding to the time-domain spectra in different comb states in Fig.(a)
-
文中利用自制的SiO2微腔系统实现了光频梳的产生。通过CO2激光器熔融石英棒制备了Q值达到3.87×108的SiO2微腔,对制备的微腔的形貌进行了表征分析,为笔者优化制备工艺提供了重要依据。同时对降低的Q值微腔进行退火处理,实现了Q值的回升,从而为微腔的可重复使用提供了可行性的条件。最后,通过激光频率调谐实现了微腔中的光学频率梳产生。实验中目前已经观察到对应低噪声、高相干孤子态光频梳的孤子台阶信号,未来将通过优化泵浦功率,改善微腔中的光热现象来激发孤子的光频梳。此外,实验中对调制不稳定状态的光频梳产生的研究也具有一定的参考价值,在光频梳演变过程中,初级边带的位置可以有效反映出微腔的色散参数;同时,调制不稳定性的梳状光谱具有低相干性,在光学断层扫描,高光谱成像等领域有着重要的应用。
Fabrication and optical frequency comb generation in high-quality factor silicon oxide microcavity (Invited)
-
摘要: 基于超高品质因子(Q值)和非线性光学微腔产生的光学频率梳(微腔光频梳)在大容量光通信、光学数据中心、光子神经形态运算以及大规模并行激光雷达等方面有着重要的应用。回音壁模式(WGM)微腔是研究微腔光频梳技术的一个重要平台,具有创纪录的超高Q值和超高精细度(Finesse),能够实现超窄线宽激光、窄线宽光学频率梳,合成超低噪声的光子微波;同时也是研究腔内孤子动力学的重要平台,对掌握孤子态的光学频率梳特性起到了重要的支撑作用。利用二氧化碳(CO2)激光器熔融氧化硅(SiO2)石英棒制备了高Q值的WGM微腔。其自由光谱范围(FSR)在10 GHz以上,Q值达到了108。对腔的谐振和耦合理想特性进行了表征,并在开放环境下观察到微腔受潮引起的Q值退化现象,通过二次退火实现了Q值的回升。在SiO2微腔中验证了基于非线性克尔(Kerr)效应的光学频率梳产生,其主要状态为调整不稳定性主导的低相干频率梳。同时,实验中也观察到了对应于全相干耗散孤子态频率梳的“阶跃”信号,表明目前制备的SiO2微腔具备实现低噪声孤子光频梳的能力,并具有微腔光频梳的应用潜力。
-
关键词:
- 光学频率梳 /
- 回音壁模式微腔 /
- 激光熔融二氧化硅微腔
Abstract: Based on ultra-high quality factor(Q) and nonlinear optical microcavities, optical microcombs(microcavity optical frequency comb) have enabled a variety of important applications including high volume optical communications, optical data center, photonic neuromorphic computation and massive parallel LIDAR. Whispering gallery mode (WGM) microcavities stand for an important platform for studying the microcavity optical frequency comb technology, particularly having record ultra-high Q factors as well as the ultra-high finesse. It can realize ultra-narrow linewidth lasers and optical frequency combs, and photonic microwaves for synthesizing ultra-low noise. Here we developed high Q WGM microcavities from a silica (SiO2) rod fused and shaped with the CO2 laser. The quality factor is above 108 with a free spectrum range at the level of 10 GHz. The cavity resonances as well as the coupling ideality have been characterized, where a degradation of Q factors in a humid environment was observed and recovered with a second annealing process. Moreover, Kerr comb generation was demonstrated in such SiO2 microcavities, which at the moment is mostly in a noisy state governed by the modulation instability regime. Yet the footprint of the cavity soliton state was experimentally observed as a “soliton step” signal. The results indicate that a low-noise and fully coherent soliton microcomb is potentially accessible in home developed SiO2 microcavities, and is readily for comb-related applications. -
图 6 光频梳产生。(a) 高泵浦功率下微腔的透射谱线;(b) 图(a)的部分放大的透射谱线;(c)~(e) 光频梳的演化过程,分别对应于图(a)中微腔透射谱线的三个不同的位置
Figure 6. Optical frequency comb generation. (a) Transmission lines of microcavity at high pump power;(b) Partially amplified transmission line of Fig.(a); (c)-(e) Evolution process of optical frequency comb corresponds to three different positions of microcavity transmission line in Fig.(a)
图 7 LLE仿真得到的光频梳演化过程。(a) I、II、III、IV图为光频梳的演化过程;(b) 分别对应图(a)中不同梳齿状态下的时域谱
Figure 7. Simulated optical frequency comb evolution based on LLE. (a) Figures I, II,III and IV show the evolution process of optical frequency comb; (b) Corresponding to the time-domain spectra in different comb states in Fig.(a)
表 1 退火前后微腔Q值变化
Table 1. Change of Q value of microcavity before and after annealing
Depth 0.6 0.5 0.4 0.3 0.2 0.1 0 Initial Q value - 3.23×108 - 2.14×108 1.43×108 - - Before annealing 1.78×108 1.66×108 8.57×107 6.9×107 6.1×107 5.7×107 5.96×107 After annealing 3.11×108 2.12×108 1.59×108 1.3×108 7.9×107 7.1×107 7.57×107 -
[1] Schibli T R, Hartl I, Yost D C. Optical frequency comb with submillihertz linewidth and more than 10 W average power [J]. Nature Photonics, 2008, 2(6): 355-359. doi: 10.1038/nphoton.2008.79 [2] Brasch V, Geiselmann M, Herr T, et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation [J]. Science, 2016, 351(6271): 357-360. doi: 10.1126/science.aad4811 [3] Chen Haojing, Xiao Yunfen. Applications of integrated microresonator-based optical frequency combs in precision measurement [J]. Infrared and Laser Engineering, 2021, 50(11): 20210560. (in Chinese) doi: 10.3788/IRLA20210560 [4] Xue Xiaoxiao, Zheng Xiaoping. Novel microwave photonic applications based on integrated microcombs (Invited) [J]. Infrared and Laser Engineering, 2021, 50(7): 20211046. (in Chinese) doi: 10.3788/IRLA20211046 [5] Marin-Palomo P, Kemal J N, Karpov M, et al. Microresonator-based solitons for massively parallel coherent optical communications [J]. Nature, 2017, 546(7657): 274-279. doi: 10.1038/nature22387 [6] Fujii S, Tanaka S, Ohtsuka T, et al. Dissipative Kerr soliton microcombs for FEC-free optical communications over 100 channels [J]. Optics Express, 2022, 30(2): 1351-1364. doi: 10.1364/OE.447712 [7] Raja A S, Lange S, Karpov M, et al. Ultrafast optical circuit switching for data centers using integrated soliton microcombs [J]. Nature Communications, 2021, 12(1): 5867. doi: 10.1038/s41467-021-25841-8 [8] Corcoran B, Tan M, Xu X, et al. Ultra-dense optical data transmission over standard fibre with a single chip source [J]. Nature Communications, 2020, 11(1): 2568. doi: 10.1038/s41467-020-16265-x [9] Riemensberger J, Lukashchuk A, Karpov M, et al. Massively parallel coherent laser ranging using a soliton microcomb [J]. Nature, 2020, 581(7807): 164-170. doi: 10.1038/s41586-020-2239-3 [10] Lucas E, Brochard P, Bouchand R, et al. Ultralow-noise photonic microwave synthesis using a soliton microcomb-based transfer oscillator [J]. Nature Communications, 2020, 11(1): 374. doi: 10.1038/s41467-019-14059-4 [11] Liu J, Lucas E, Raja A S, et al. Photonic microwave generation in the X-and K-band using integrated soliton microcombs [J]. Nature Photonics, 2020, 14(8): 486-491. doi: 10.1038/s41566-020-0617-x [12] Xu X, Tan M, Corcoran B, et al. 11 TOPS photonic convolutional accelerator for optical neural networks [J]. Nature, 2021, 589(7840): 44-51. doi: 10.1038/s41586-020-03063-0 [13] Feldmann J, Youngblood N, Karpov M, et al. Parallel convolutional processing using an integrated photonic tensor core [J]. Nature, 2021, 589(7840): 52-58. doi: 10.1038/s41586-020-03070-1 [14] Savchenkov A A, Matsko A B, Ilchenko V S, et al. Optical resonators with ten million finesse [J]. Optics Express, 2007, 15(11): 6768-6773. doi: 10.1364/OE.15.006768 [15] Herr T, Brasch V, Jost J D, et al. Temporal solitons in optical microresonators [J]. Nature Photonics, 2014, 8(2): 145-152. doi: 10.1038/nphoton.2013.343 [16] Lucas E, Guo H, Jost J D, et al. Detuning-dependent properties and dispersion-induced instabilities of temporal dissipative Kerr solitons in optical microresonators [J]. Physical Review A, 2017, 95(4): 043822. doi: 10.1103/PhysRevA.95.043822 [17] Guo H, Karpov M, Lucas E, et al. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators [J]. Nature Physics, 2017, 13(1): 94-102. doi: 10.1038/nphys3893 [18] Taheri H, Matsko A B, Maleki L, et al. All-optical dissipative discrete time crystals [J]. Nature Communications, 2022, 13(1): 1-10. doi: 10.1038/s41467-021-27699-2 [19] Lucas E, Karpov M, Guo H, et al. Breathing dissipative solitons in optical microresonators [J]. Nature Communications, 2017, 8(1): 736. doi: 10.1038/s41467-017-00719-w [20] Guo H, Lucas E, Pfeiffer M H P, et al. Intermode breather solitons in optical microresonators [J]. Physical Review X, 2017, 7(4): 041055. doi: 10.1103/PhysRevX.7.041055 [21] Alnis J, Schliesser A, Wang C Y, et al. Thermal-noise-limited crystalline Whispering-Gallery-mode resonator for laser stabilization [J]. Physical Review A, 2011, 84(1): 011804. doi: 10.1103/PhysRevA.84.011804 [22] Lim J, Savchenkov A A, Dale E, et al. Chasing the thermodynamical noise limit in Whispering-Gallery-mode resonators for ultrastable laser frequency stabilization [J]. Nature Communications, 2017, 8(1): 8. doi: 10.1038/s41467-017-00021-9 [23] Pavlov N G, Koptyaev S, Lihachev G V, et al. Narrow-linewidth lasing and soliton Kerr microcombs with ordinary laser diodes [J]. Nature Photonics, 2018, 12(11): 694-698. doi: 10.1038/s41566-018-0277-2 [24] Pavlov N G, Lihachev G, Koptyaev S, et al. Soliton dual frequency combs in crystalline microresonators [J]. Optics Letters, 2017, 42(3): 514-517. doi: 10.1364/OL.42.000514 [25] Liu G, Ilchenko V S, Su T, et al. Low-loss prism-waveguide optical coupling for ultrahigh-Q low-index monolithic resonators [J]. Optica, 2018, 5(2): 219-226. doi: 10.1364/OPTICA.5.000219 [26] Braginsky V B, Gorodetsky M L, Ilchenko V S. Quality-factor and nonlinear properties of optical whispering-gallery modes [J]. Physics Letters A, 1989, 137(7-8): 393-397. doi: 10.1016/0375-9601(89)90912-2 [27] Gorodetsky M L, Savchenkov A A, Ilchenko V S. Ultimate Q of optical microsphere resonators [J]. Optics Letters, 1996, 21(7): 453-455. doi: 10.1364/OL.21.000453 [28] Del’Haye P, Schliesser A, Arcizet O, et al. Optical frequency comb generation from a monolithic microresonator [J]. Nature, 2007, 450(7173): 1214-1217. doi: 10.1038/nature06401 [29] Papp S B, Diddams S A. Spectral and temporal characterization of a fused-quartz-microresonator optical frequency comb [J]. Physical Review A, 2011, 84(5): 053833. doi: 10.1103/PhysRevA.84.053833 [30] Papp S B, Del’Haye P, Diddams S A. Mechanical control of a microrod-resonator optical frequency comb [J]. Physical Review X, 2013, 3(3): 031003. doi: 10.1103/PhysRevX.3.031003 [31] Del'Haye P, Diddams S A, Papp S B. Laser-machined ultra-high-Q microrod resonators for nonlinear optics [J]. Applied Physics Letters, 2013, 102(22): 221119. doi: 10.1063/1.4809781 [32] Zhang S, Silver J M, Del Bino L, et al. Sub-milliwatt-level microresonator solitons with extended access range using an auxiliary laser [J]. Optica, 2019, 6(2): 206-212. doi: 10.1364/OPTICA.6.000206 [33] Cao Q T, Liu R, Wang H, et al. Reconfigurable symmetry-broken laser in a symmetric microcavity [J]. Nature Communications, 2020, 11(1): 1-7. doi: 10.1038/s41467-019-13993-7 [34] Niu R, Wan S, Wang Z Y, et al. Perfect soliton crystals in the high-Q microrod resonator [J]. IEEE Photonics Technology Letters, 2021, 33(15): 788-791. doi: 10.1109/LPT.2021.3096645 [35] Wen Q, Cui W, Geng Y, et al. Precise control of micro-rod resonator free spectral range via iterative laser annealing [J]. Chinese Optics Letters, 2021, 19(7): 071903. doi: 10.3788/COL202119.071903 [36] Tan T, Yuan Z, Zhang H, et al. Multispecies and individual gas molecule detection using Stokes solitons in a graphene over-modal microresonator [J]. Nature Communications, 2021, 12(1): 6716. doi: 10.1038/s41467-021-26740-8 [37] Dumeige Y, Trebaol S, Ghişa L, et al. Determination of coupling regime of high-Q resonators and optical gain of highly selective amplifiers [J]. JOSA B, 2008, 25(12): 2073-2080. doi: 10.1364/JOSAB.25.002073 [38] Zhou H, Geng Y, Cui W, et al. Soliton bursts and deterministic dissipative Kerr soliton generation in auxiliary-assisted microcavities [J]. Light: Science & Applications, 2019, 8(1): 1-10. -






 下载:
下载: