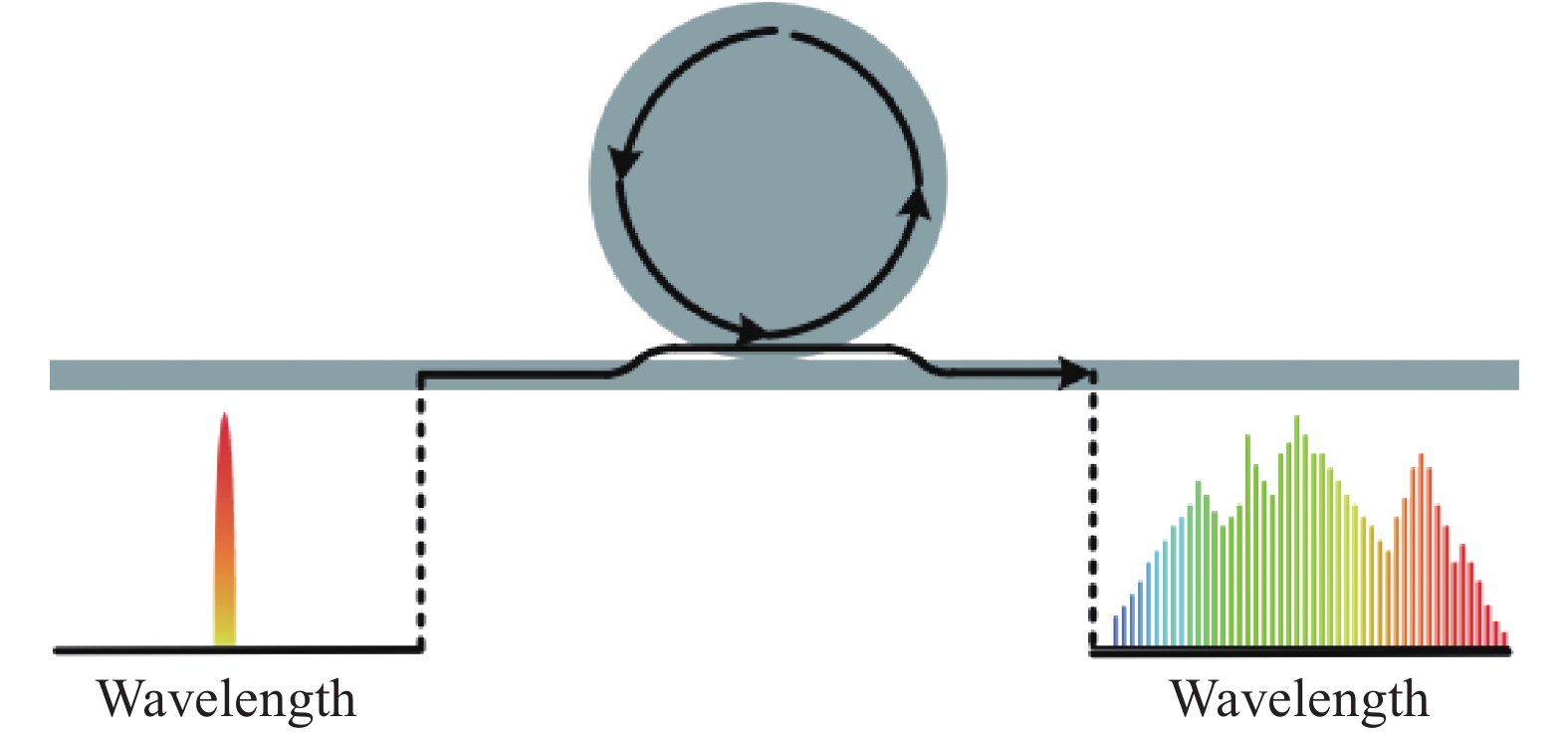
-
光学频率梳(Optical Frequency Comb,简称光频梳)是指在频谱上由一系列均匀间隔且具有相干稳定相位关系的频率分量组成的光源。自锁模光频梳被开发以来,光频梳被广泛应用于传感、光谱学、原子分子物理等领域的研究,为测量和光谱学[1-2]带来革命性的进步,在光钟、时间标准[3-6]、气体传感器[7-9]、振铃光谱[10]等方面具有重要的作用,逐步成为物理精密测量的基石。2005年诺贝尔物理学奖授予了美国国家标准技术研究院John L. Hall教授和德国马普量子光学所Theodor W. Hansch教授,以表彰其在光频梳领域做出的开创性研究工作[11-12]。
表征光频梳特性的两个关键物理量是梳齿频率间隔frep和初始偏移频率fceo,因此对应的任意梳齿的频率表示为fm =fceo+mfrep,其中m是整数用于标记第m根梳齿。偏移频率fceo描述了整个梳状结构与零频率起始梳状结构之间的偏差,这反映了载波和脉冲包络在时间输出中的相位关系。传统光频梳的主要实现方式包括锁模激光器、电光调制光频梳、非线性材料中的级联四波混频。
第一种方式是利用半导体锁模激光器产生多个波长的光,基于激光器内部增益介质或者调控介质的主动调制以及可饱和吸收等非线性效应被动实现不同波长之间的相位锁定。锁模激光器[12-13]产生的光频梳对应为时域的规则脉冲序列,因此也被应用于超短脉冲产生和超快光学研究。在时域上,frep对应于单位时间内脉冲的数目,也被称为重复频率。常见的钛宝石激光器和掺铒光纤激光器可以产生重复频率为1 GHz左右的光频梳[13-15]。第二种方式,可以通过对连续波激光器的输出进行振幅或相位上的调制,生成频谱上等间隔的梳齿或者直接产生时域上的脉冲[16],而frep由电光调制器上所加的射频源的频率决定,fceo可以通过改变输入激光频率来调节。
第三种方式是最近几年发展起来的新的途径,主要通过对腔注入一个单频连续激光并借助于非线性腔增强的级联非线性混频过程来实现。得益于回音壁模式(Whispering Gallery Mode, WGM)微腔[17]具有高品质因子、小模式体积以及几何结构可控等优势,能极大地增强光与物质的相互作用,级联四波混频产生光频梳在这一独特的平台得到了迅速的发展[8, 18-20]。2004年,T. Kippenberg等人制备了截面很小的微芯圆环腔[21],将工作频率的总色散调至大于零,实验上首次实现了克尔非线性的参量振荡过程。同年,在晶体微腔内也实现了参量振荡过程[22]。如果微腔有足够宽范围的反常色散区域,简并四波混频和非简并四波混频过程就会展宽,形成等间距的级联四波混频。基于此原理,P. Del’Haye等人在2007年首次报道了基于克尔效应的微腔光频梳[10],因此基于回音壁微腔的光频梳也称为克尔光频梳[8, 10, 23]。
基于回音壁模式微腔的四波混频光频率梳的原理见图1。回音壁模式微腔一般为圆对称的,对于给定的横向模场分布,其支持大量行波模式,其模式由轨道角动量区分且相邻模式的角动量差1并且自由光谱范围(Free Spectral Range, FSR)大致相同。由于微腔介质材料的克尔效应,当连续光耦合泵浦到某一轨道角动量为m的模式时,可以找到一对轨道角动量分别为m+n和m−n的行波模式,其频率与泵浦模式的差为+n×FSR和−n×FSR,则这一对模式与泵浦模式满足四波混频的能量和动量匹配。因此,可以在腔中发生两个泵浦光子湮灭并在m+n和m−n阶两个模式中分别产生一个光子,当泵浦光功率超过一定阈值时就会发生超参量震荡。而m+n或m−n阶的模式中的光场可以作为泵浦光场,在频谱上进一步拓展,通过级联四波混频在更多的模式中产生光,最终扩展为模式间隔为一个FSR的频率梳。
相比于传统光频梳(增益来自于传统增益介质材料),克尔光频梳仅依赖于微腔内部介质的非线性特性,而且不需要宽带激光增益介质,因此原则上可以在任何泵浦频率附近产生克尔光频梳,泵浦源仅需连续激光即可。得益于微腔的小尺寸以及由此产生的较大的自由光谱范围,克尔光频梳的梳齿间距也比传统光频梳大几个数量级,典型范围为10 GHz~1 THz[23]。从材料角度来讲,克尔光频梳对材料的选择并不挑剔,目前,在二氧化硅、掺杂二氧化硅、碳化硅、氮化铝、铌酸锂、金刚石和晶体微腔中都实现了宽带的光频梳[8, 23, 25-31]。随着近年来研究的发展,克尔光频梳已能实现一个倍频程的展宽,如图2(a)所示,这些研究是迈向f−2f自参考型微腔光频梳的关键一步[32]。

图 2 几种克尔光频梳。(a) 二氧化硅微环谐振器中倍频程频率梳[23];(b) Si3N4微环腔中单孤子光频梳[47];(c) 二氧化硅微环腔中孤子光频梳[48]
Figure 2. Several kinds of Kerr OFCs. (a) An octave-spanning frequency comb generated in a silica microtoroid [23]; (b) Spectrum of solitons comb generated in Si3N4 microtoroid[47]; (c) Spectrum of solitons comb generated in silica[48]
在一个理想的回音壁微腔中,腔模应该是严格等距的。而由于色散的存在,腔模并非严格等距,导致实际实验中频率梳谱宽度会受到限制。微腔模式色散包括几何色散(geometrical dispersion)和材料色散(material dispersion)。材料色散为材料的固有属性,不容易直接调节,因此调谐模式色散的手段一般为调节几何色散,即调节微腔的结构。最近,研究者发现适当的色散会有助于实现锁模的克尔光频梳:当泵浦光稳定在模式红失谐时,微腔达到反常色散与非线性、损耗与参量振荡增益的双平衡,可以产生耗散孤子(dissipative solitons)光频梳[1, 29, 33-35],这一结果由T. Kippenberg课题组率先报道[1]。如图2(b)~(c)所示,孤子光频梳[36]不仅可以维持宽带宽,而且其稳定性及相干性更好,因此孤子光频梳极大的推动了克尔光频梳的发展和应用[37-38]。微腔的紧凑特性也保证了集成化的克尔光频梳得以实现,2018年,M. Lipson教授课题组展示了片上(on-chip)集成的克尔光频梳,利用电泵浦半导体放大器经滤波之后产生泵浦光源,该克尔光频梳仅用七号电池即可驱动。
目前,国际上关于微腔光频梳的研究主要集中于红外波段,近年来光谱不断拓宽,至中红外和可见光波段。其中,可见光波段光频梳在诸多领域扮演不可或缺的角色,比如,基于铷和锶跃迁线的原子钟[39]、天文光谱校准[38, 40-42]以及非接触生物组织成像技术[43-44](光学相干断层扫描[45],实时相干反斯托克斯拉曼光谱[46]),可见波段微腔光频梳的高相干、低功耗及紧凑特性能为探求原子分子内部能级结构、基本物理常数测量、新一代片上原子钟及生物光学成像技术的研制提供全新测量与研究平台。然而在可见光波段,由于材料具有较大的正常色散,且瑞利散射与波长的四次方成反比,材料在该波段吸收损耗和散射损耗较大(降低微腔品质因子),因此使得可见光波段的反常色散调节及克尔光频梳的实现变得异常困难。
文中将综述可见光波段的微腔频率梳的研究,侧重实验进展,主要介绍通过材料的混合二阶与三阶非线性效应、微腔截面几何参数调节以及引入额外的横向模式的耦合效应来调控色散的方法克服可见光波段微腔正常色散的挑战。
-
为实现可见波段的光频梳,研究者提出并实现各种不同的方案,接下来分三种主要的方法详细展开介绍。第一种方式为间接产生可见光频梳方式:基于二阶与三阶混合非线性效应将近红外光频梳转换为可见光频梳。后两种方式为直接产生可见光频梳:通过调节几何色散和模式耦合效应在可见波段实现模式反常色散。
-
在近红外C波段(~1550 nm)较容易实现腔模反常色散[49],利用材料的二阶与三阶非线性效应,将在近红外产生的光频梳通过频率转换可以实现可见光波段的光频梳。
2014年,M. Lipson组在Si3N4微环腔[50]中通过二倍频、四波混频与和频效应在可见光波段产生光频梳。其产生过程如图3(a)所示,泵浦光首先利用二倍频效应在可见光波段产生二次谐波。随着腔内循环功率的增加,在近红外范围内基于四波混频效应产生光频梳。然后,光频梳与泵浦光相互作用,通过和频效应在可见波段产生光频梳,这些光频梳与近红外梳状线同时生成。要使得上述过程能顺利进行,必须设计合理的波导色散使得二倍频、四波混频与和频的相位匹配能够同时满足,基模和二次谐波模式的有效折射率必须匹配,这种相位匹配是通过对倍频光使用高阶波导模式来实现的。如图3(b)所示,三阶横电(Transverse Electric, TE)模在770 nm处与泵浦光TE基模在1540 nm处具有相同的有效折射率。四波混频的相位匹配条件在很大程度上取决于群速度色散(Group Velocity Dispersion, GVD)。其最佳条件是在泵浦频率下具有反常色散(GVD > 0),且GVD值很小,然后通过三阶非线性相位偏移对色散进行补偿,从而实现四波混频的相位匹配条件。如图3(c)所示,TE模式在一个很宽的范围内呈现反常色散。一旦四波混频与二倍频过程的相位匹配得到保证,最终和频过程将自动满足相位匹配。实验中,将17条光频梳线从近红外波长转换到可见光波长,使得可见光波段的光频梳能覆盖到767~775 nm。由于在微腔中对波导结构有严格设计要求,使其即满足反常色散条件且同时满足二倍频与和频的相位匹配条件,这是相对困难的。因此,清华大学孙长征教授课题组在AlN微环腔[51]中利用相位不匹配的基模和一阶可见光波段模式来实现宽带频率的转换。如图3(d)所示,泵浦频率下的横磁(Transverse Magnetic, TM)基模TM00与二次谐波下的TM00、TM10并未实现相位匹配,从图3(e)中的模式重叠面积也可看出二次谐波下的TM00、TM10参与的是非相位匹配的倍频与和频转换。实验中将泵浦光通过波导近场耦合到微环腔,随着腔内功率增强,发生基于三阶非线性效应的简并和非简并FWM。同时,当近红外光频梳的功率足够大时,通过二倍频与和频效应实现近可见光频梳,且近红外与可见光光谱具有相同的梳齿间距。其可见光频梳覆盖范围从720~840 nm(图3(f)),多达153根梳状线,转换效率高达2.6%。

图 3 利用二倍频、四波混频与和频效应产生可见光频梳。(a) 近红外波段光学频梳到可见光学频梳的转换过程;(b) 近红外基本TE模与可见光范围内三阶TE模的有效折射率;(c) 基本TE模的群速度色散[50];(d)近红外TM00模式与可见光TM10、TM00模式的有效折射率;(e) 归一化模态重叠因子;(f) 红外光频梳、二次谐波与可见光频梳的产生[51]
Figure 3. Visible light OFCs are generated using second harmonic generation, four-wave mixing and sum-frequency effects. (a) Generate simultaneous near IR and visible wavelength frequency comb lines; (b) The effective index of the fundamental TE mode in near IR spectral range and the third-order TE mode in the visible spectral range; (c) The group velocity dispersion (GVD) of the fundamental TE mode[50]; (d) The effective index of TM00 mode in near IR spectral range and TM10、TM00 mode in the visible spectral range; (e) Normalized modal overlap; (f) Generation of IR、second harmonics and near-visible microcombs [51]
同年,耶鲁大学的Hong X. Tang课题组也报道了在AlN芯片上利用二倍频产生的可见光频梳[52],并利用热调谐方式实现了超过一个FSR的调谐。最近,他们进一步发展这一混合二阶和三阶非线性的微腔平台,实现了在可见光泵浦或者红外光泵浦的红外-可见光波段同时发射的孤子光频梳[53-54]。由于该系统内较强的二阶非线性,其可见光波段的光频梳能量与整体出射光能的比例能达到17%的量级,光谱范围覆盖760~800 nm。
对于在更短波段的光频梳,则可以基于红外光频梳借助三倍频与和频效应来实现。2016年,John E. Bowers课题组在Si3N4环形微谐振器中[55],利用三倍频效应与和频效应将C波段克尔光频梳转换为绿光波段(508~535 nm)光频梳。微环腔中绿色光频梳的第一条光频梳线是由三倍频效应实现的,来自泵浦的三个光子相互作用,产生一个三倍频率的光子。接着,当泵浦频率逐渐调谐到共振状态,此时腔内产生四波混频,在红外波段产生光频梳。与此同时,来自红外光频梳的三个光子相互作用,通过三阶和频产生一个绿光波段的光子。上述过程也需要在满足相位匹配的条件下才会实现。对于四波混频的相位匹配,可以通过调整波导的宽度和高度,使得几何色散处于反常色散区,实现对材料色散的补偿,如图4(a)所示,TE00、TM00在泵浦频率下都处于反常色散区。当红外波段下基模的波数比绿光下高阶模式的波数小三倍时,三倍频效应的相位匹配得到满足。如图4(b)所示,泵浦频率下的TE00(或TM00)与三倍频下的18th、19th、20th(或20th、21th、22th)能实现三倍频的相位匹配。当三倍频与四波混频达到相位匹配条件时,三阶和频的相位匹配会自动满足。实验上,首先在C波段产生宽谱光频梳(图4(c)),进而利用三倍频和和频效应在508~535 nm波长范围内实现绿色的光频梳,其输出功率可达11 μW。
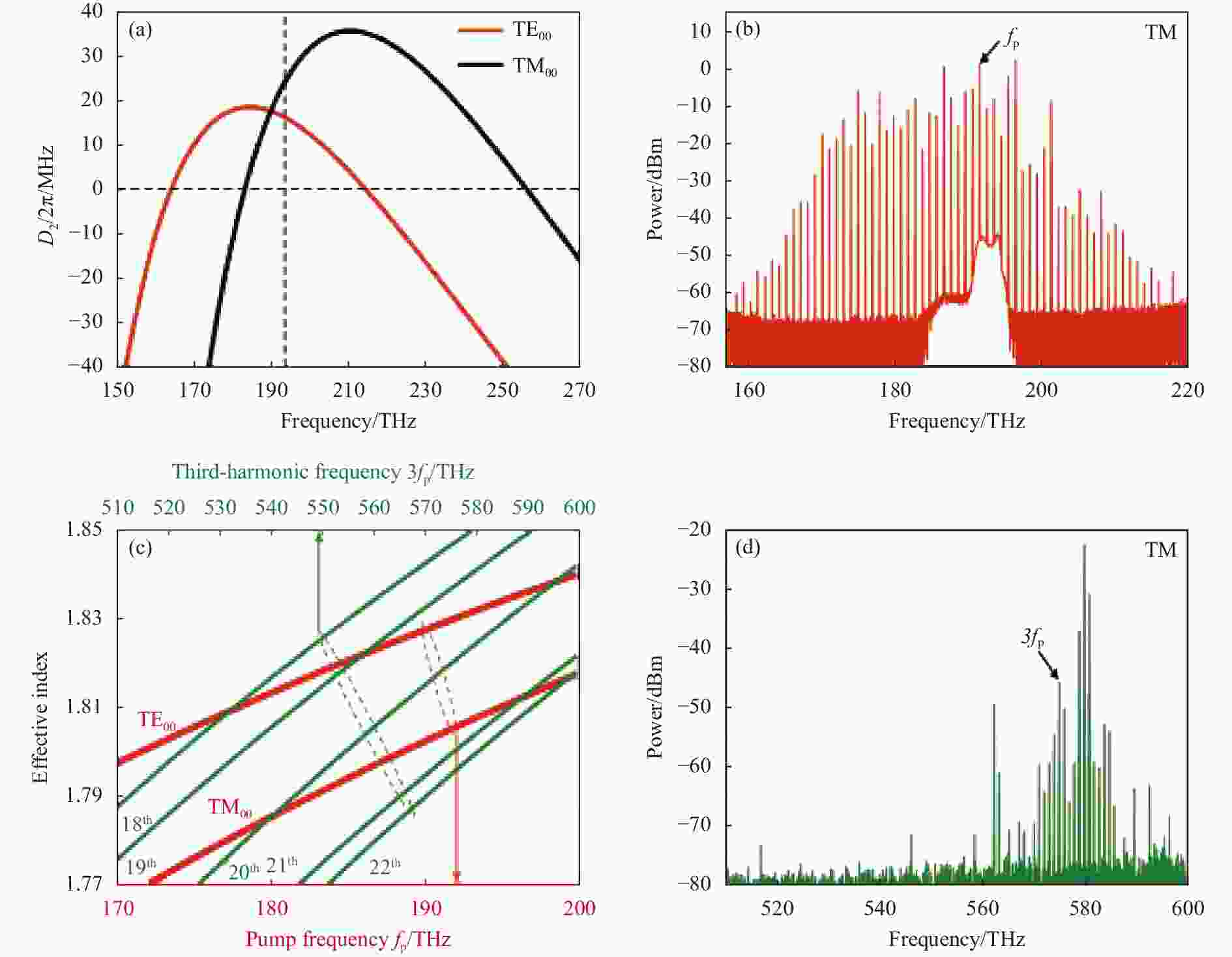
图 4 (a) TE00与TM00的二阶色散D2/(2π);(b) 泵浦频率下模式与三次谐波处的模式匹配;(c)红外波段下光频梳的产生;(d) 三次谐波与绿光光频梳的产生[55]
Figure 4. (a) The second-order dispersion D2/(2π) for the fundamental TE and TM modes; (b) The effective index for the fundamental TE、TM modes at the pump frequency and higher-order modes at the third-harmonic frequency; (c) Generation of IR microcombs; (d) Generation of third harmonics and green light comb [55]
上述方法中都需要借助材料的三阶非线性效应来实现,Karsten Buse课题组在一个毫米量级的铌酸锂微谐振器[56]中只借助二阶非线性效应在532 nm处实现绿光光频梳。这种方法依赖于级联的二阶非线性光学过程,如倍频之后光学参量的产生,然后再次导致倍频等等[57]。当泵浦光为单一偏振光(o光或e光),且满足产生二次谐波的双折射相位匹配条件时,就会产生正交偏振(e光或o光)的二次谐波。随着泵浦功率逐渐增大超过阈值时,通过一系列级联二阶非线性过程在泵浦和二次谐波处会产生光频梳。泵浦与二次谐波处的光频梳具有相同的梳齿间距416 GHz,相当于20倍的FSR,这些过程可以用调制不稳定引起的光谱展宽来解释。随着泵浦光的红移,形成了一个宽度为2 THz的近红外和绿色光频梳,包括100条单独的梳子,其梳齿间距为一个FSR。如果相位匹配伴随着泵浦光和二次谐波之间FSR的偏移而减小或消失,则可以生成孤子频梳[58-60]。
值得一提的是,基于红外光频梳产生可见光频梳的方法还面临着另外一个重要的实验挑战:由于模式在近红外C波段和可见波段有效折射率差别很大,很难同时获得近红外光频梳和可见光频梳的高效收集效率。耶鲁大学的Hong X. Tang课题组利用红外和可见波段波导倏逝场耦合的色散效应,分别设计了可见光和红外波段的微腔-波导耦合器[62],实现了两个波段同时可调的高效率耦合。另外,北京大学肖云峰教授课题组首次提出和证明了非对称微腔中(图5(a))混沌辅助光子宽带动量变换过程,实现了混沌辅助的超宽谱光频梳((图5(b))[61]。实验上首先利用FWM效应产生近红外克尔光频梳,通过表面破缺诱导二倍频效应和本征三倍频效应将近红外克尔光频梳转换为可见波段光频梳((图5(c)),整个光频梳波长范围达到450~2 000 nm。进一步通过混沌诱导动量变换通道[63],实现了微腔与耦合波导的宽带有效耦合,从而极大地增强了宽谱光频梳在全波段的收集效率。

图 5 (a) 变形微芯圆环腔电镜图;(b) 混沌辅助的标准WGMs到混沌状态的动态隧穿;(c) 近可见光频梳通过二倍频和三倍频效应转换为可见光频梳[61]
Figure 5. (a) Scanning electron microscope image of the deformed microtoroid resonator; (b) Chaos-assisted dynamical tunneling from WGMs to chaotic states; (c) Nonlinear frequency conversion from infrared combs to visible wavelengths[61]
-
通过优化回音壁模式微腔的几何尺寸来调控色散,使其在可见光波段实现模式反常色散,利用可见光(或近可见光)作为泵浦源,实现可见克尔光频梳。
2016年,Yong Yang等人在二氧化硅的空心微泡腔[64]中通过选择合适的壁厚来调控微腔基膜的色散,实现可见光频梳。当改变微泡腔壁厚时,模式强度在空气中的比例发生变化,从而改变空腔模式的有效折射率和频率分布,通过减小壁厚,零色散波长向更短的波长移动。将壁厚控制在1.4 μm时,微泡腔中TM模式的零色散波长移到764 nm处,使得在该位置处的相位匹配成为可能。实验中,在输入功率为3 mW时,观察到四波混频效应,其两根光频梳之间的间距为两倍FSR。逐渐增加功率,最终观察到14条梳状线的克尔光频梳。Nicolas Riesen课题组[65]在理论上也证实具有中空结构的微泡腔可以通过改变壁厚调控模式色散,舒方杰等人近期调控微泡腔色散获得光频梳并实现调谐[66]。
除了对基本模式进行色散调控,也可通过改变高阶模式的色散实现可见光频梳。2019年,南京大学的姜校顺教授课题组通过控制SiO2微盘腔[67]的楔形角与厚度来实现对微腔色散的调控。当把微盘腔的直径控制在80 μm,厚度1 μm,楔形角为56°时,TM10模式的色散在780 nm附近被调节为反常色散,如图6(b)所示。从图6(c)可知,当微盘腔的厚度从0.8 μm增加到1.2 μm时,该模式在780 nm处仍都处于反常色散。对于在不同楔形角的情况下,模式色散并没有太大的区别,随着楔形角的增大,零色散波长将缓慢的向短波长方向移动。对于一个直径为2 mm的圆盘腔,通过此方法使其零色散波长可以移到680 nm。如图6(d)所示,实验中选择合适的几何结构参数,在780 nm处实现反常色散,实验上产生了包含112条梳齿的可见光频梳,波长范围从700~897 nm。

图 6 楔形角调控微盘腔色散产生可见光频梳。(a) 腔体内部基本TM10模式的模式剖面图;(b) TM10、TM20、TM30模式色散(插图:TM10、TM20、TM30模式轮廓);(c) 在不同厚度与楔形角下TM10模式色散;(d) 可见克尔光频梳的产生[67]
Figure 6. Wedge angle modulation of microdisk cavity dispersion to generate visible OFCs. (a) Illustration of the mode profile for the fundamental TM10 mode inside the cavity; (b) Dispersion characteristics of the TM10, TM20, TM30 modes(Inset: simulated mode profiles of the TM10, TM20 and TM30 modes); (c) Variation of the dispersion when changing the thickness of the disk at different wedge angles; (d) Generation of near-visible Kerr OFCs [67]
2020年,基于同样的方法,Yun Zhao等人基于芯片波导的高阶模式在近可见光波长范围内实现反常GVD,在784 nm附近产生宽带克尔孤子频梳[68]。实验中制作了一个截面为730 nm×1330 nm、半径为22 μm的SiN微环腔,其TE10模式的零色散点接近760 nm,通过热调谐方法,产生了一个锁模孤子频梳。尽管高阶波导模式通常会有更大的辐射损失,实验中TE10模式的Q值可达
$7.7 \times {10^5}$ ,并通过合理的设计波导与微环腔的耦合实现了TE00模式到TE10模式有效激励[69]。克尔孤子光频梳的产生过程可分为三个状态[70-72]:最初,泵浦光被固定在共振的蓝失谐一侧,模式未被激发,此时并未收集到光频梳;随着泵浦光红移,模式被激发产生初级光频梳,产生的光频梳较少,如图7(d)所示;泵浦光进一步红移,光频梳紧接着进入混沌状态,此时光频梳数量明显变多,如图7(e);最后过渡到孤子状态,光谱的形状能用sech2曲线拟合,如图7(f)所示。在过渡到孤子状态(称为“孤子阶跃”)后,略微增加加热器电压以补偿内腔功率突然变化引起的温差,其电压变化如图7(a)所示。图7(b)描述了这几种状态下腔内功率,当处于孤子态时,腔内功率趋于平稳。图7(g)~(i)展示出三种状态下光谱的噪声特性,发现孤子态具有平坦的噪声谱和最低的射频噪声。实验中观察到四孤子态的光谱,如图7(c)所示,该状态下腔内功率接近混沌状态。该光频梳跨越了常用于时间和频率计量的几个原子跃迁线,如位于795 nm处的梳状线与85Rb的原子跃迁线一致。对于更短波长下的光频梳,通过模拟截面为400 nm×1000 nm,半径100 μm的SiO2微环腔, 发现TE20模式的零色散点位于587 nm,使用Lugiato-Lefever Equation (LLE)[73-74]模拟相应的孤子谱,实现覆盖Hg+(563 nm)和Yb(578 nm)原子光钟的孤子光频梳。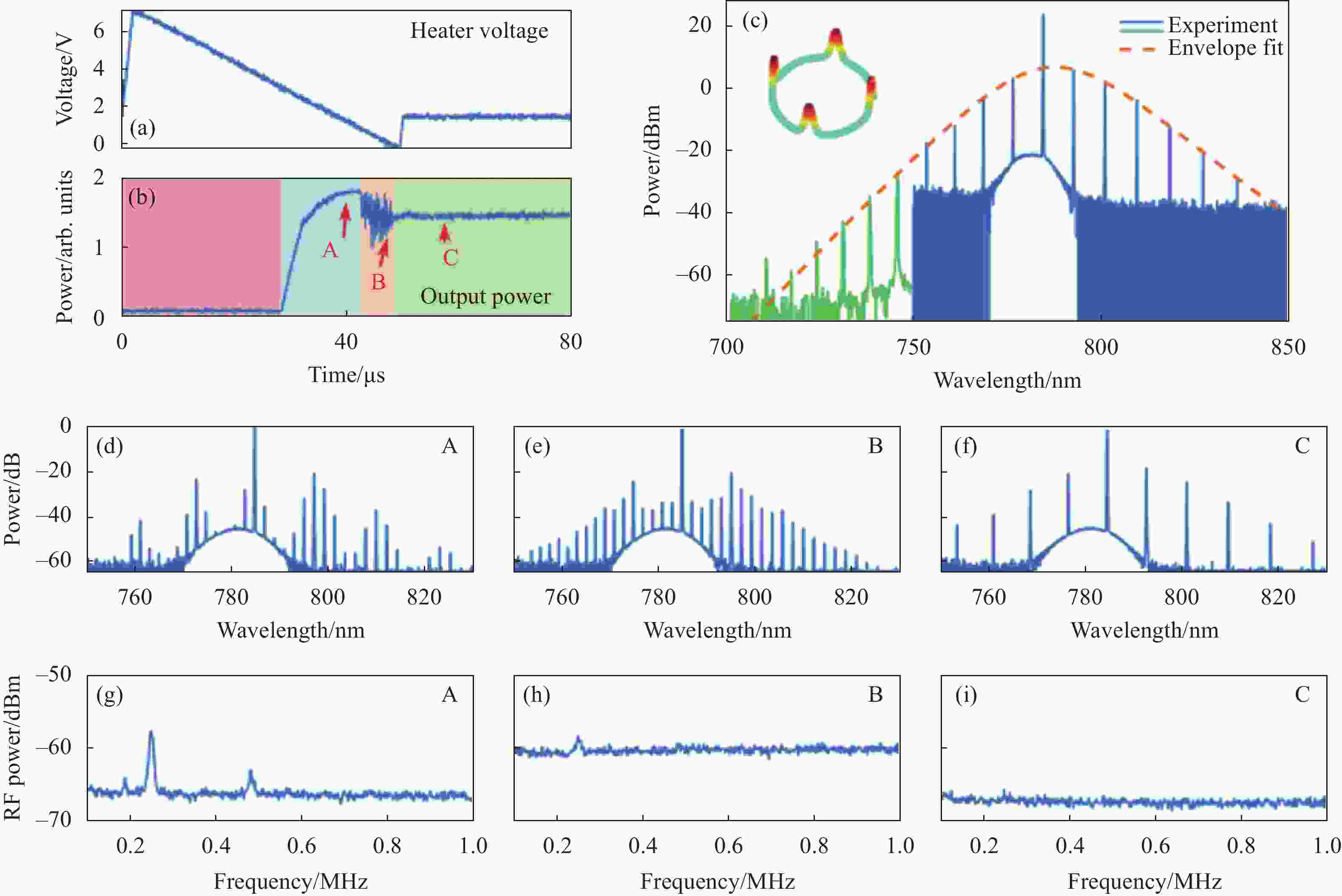
图 7 通过高阶模TE10产生可见光频梳。(a) 用于调节片上加热器的电压模式;(b) 与(a)中的模式对应的梳状功率的演变;(c) 四孤子态光谱图;(d)~(f) 图(b)中A(微梳形成)、B( 浑沌状态)、C(孤子态)对应的光谱;(g)~(i) 图(d)~(f)对应的射频噪声[67]
Figure 7. Visible OFCs generation by higher-order mode TE10. (a) Voltage pattern used to modulate the on-chip heater; (b) Evolution of comb power corresponding to the pattern in Fig.(a); (c) Comb spectrum of four-soliton state; (d)-(f) Optical spectra corresponding to point A (minicomb formation), B (chaotic state), and C (soliton state) in Fig.(b); (g)-(i) RF noise corresponding to Fig.(d)-(f)[67]
前面两种方法都是通过调控旋转对称微腔的方位角模式来实现模式的反常色散,OEwaves公司的A. Matsko等人曾报道在氟化钙椭球晶体微腔里通过曲率调节模式色散,激发轴向模式来实现可见光频梳[75]。由于在可见光波段材料具有大的正常色散,因此需要设计合适的谐振腔尺寸与形状来对材料色散进行补偿。但光频梳的重复率由谐振器尺寸决定,中心波长的选择受材料色散的限制,这就使得该方法无法在任意波长下产生具有任意重复率的频率梳。利用椭球晶体谐振器的轴向模式来激发光频梳可以消除这一限制。在完美圆形腔内,轴向模式是简并的,在其内产生的四波混频效应都是基于方向角模式(即不同的m模式,图8(a))。在椭球微腔中,尽管方位角模式在可见区域处于正常色散,但轴向模式这时是解简并的,并且可以通过调节椭球曲率将轴向模式调至反常色散,产生基于轴向模式间的四波混频效应(图8(b)),进而实现了基于轴向模式的克尔光频梳(图8(c))。频率上,基模最小,高阶模式较大(图8(b))。因此,在赤道平面上只能收集到长波长的基于基模非对称光频梳;在赤道平面外(上方或者下方)只能收集到短波长的基于高阶轴向模式的非对称光频梳(图8(c))。卢启景等人曾利用微泡腔实现了C波段基于轴向模式[76-77]的密集克尔光频梳[78],北京航空航天大学丁铭教授和中国科技大学王克逸教授课题组近期也有关于轴向模式光频梳的相关报道[79-80]。

图 8 基于轴向模式产生光频梳[75]。(a) 传统基于方位角模式的四波混频示意图;(b) 基于轴向模式的四波混频示意图;(c) 基于轴向模式产生的光频梳与收集位置的关系
Figure 8. OFC generated with axial (vertical) modes [75]. (a) Schematic of FWM with the fundamental azimuthal mode family; (b) Schematic of FWM with the axial mode family; (c) Relationship between OFC generated with aixal modes and collection positions
-
在回音壁模式微腔中,若有两个横向模式达到相位匹配条件及有足够的模场交叠,且耦合强度大于模式线宽时,模式之间可以发生强耦合,导致模式在频域和空域会重新分布并形成两个超模式(supermodes):对称模式(Symmetric Mode, SM)和反对称模式(Anti-symmetric Mode, ASM)。模式强耦合的标志是两个横向模式的不同m阶模式的波长呈现反交叉(Avoided Mode Crossing, AMX), 其中反对称模式由于模式耦合会达到反常色散,其物理机制在于模式的耦合使反对称模式的传播路径变长,其FSR随着波长的增加而减少,即实现反常色散[30, 81-85]。
2016年,M.Soltani等人[86]首次在理论上提出了超模式可以在任意波段实现反常色散,利用两个水平或垂直放置的微环腔来实现模式耦合。其耦合方程为:
$$ \frac{\rm{d}}{{{\rm d}z}}{a_1} = i\beta {a_1} + i\kappa {a_2} $$ (1) $$ \frac{\rm{d}}{{{\rm d}z}}{a_2} = i\beta {a_2} + i{\kappa ^*}{a_1} $$ (2) 式中:a、β、κ、z分别是每个波导中的场振幅、单个波导中模式的传播常数、波导之间的耦合系数、传播方向。通过求解上式的本征解,得到对称模式(β+)和反对称模式(β-)的传播常数为β± = β ± κ,相应的对称与反对称模式的色散为:
$$ {D_ \pm } = {D_0} \mp \frac{{{\omega ^2}}}{{2\pi c}}\frac{{{\rm{d}^2}\left| \kappa \right|}}{{\rm{d}{\omega ^2}}} $$ (3) 式中:
${D_0} = - \left( {{{{\omega ^2}} \mathord{\left/ {\vphantom {{{\omega ^2}} {\left( {2\pi c} \right)}}} \right. } {\left( {2\pi c} \right)}}} \right){{{\rm{d}^2}\beta } \mathord{\left/ {\vphantom {{{\rm{d}^2}\beta } {\rm{d}{\omega ^2}}}} \right. } {\rm{d}{\omega ^2}}}$ 是没有模式耦合时的单独波导的色散。由于在复合结构中波导之间的耦合取决于倏逝场,因此耦合因子与频率有关,其中|κ|~exp(−αω),α是一个常数,其值取决于波导的材料和结构。上式中耦合因子的二阶导数为正,因此D- > D0,耦合将反对称超模的GVD移向反常区域。图9(a)为双环微腔结构和对称模式及反对称模式的模场分布,任意单个微环腔模式色散在可见及近可见波段为正常色散(如图9(b)中绿色实线和虚线),通过改变两个微环腔的尺寸和间距使得外环的有效折射率小于内环的有效折射率并与环半径成反比时,模式能达到相位匹配条件发生强耦合,其中反对称模式(如图9(b)中红色实线)会形成反常色散区域,其色散曲线的峰值大小取决于单个环模式之间的群速度差;反对称模式的残余频率失谐量(Residual Frequency Detuning, RFD)如图9(c)所示,RFD的两个零点位置宽度代表了克尔光频梳的宽度[86],结果表明利用模式强耦合可实现宽带克尔光频梳。图9(d)展示出由对称模式与反对称模式产生的光频梳。
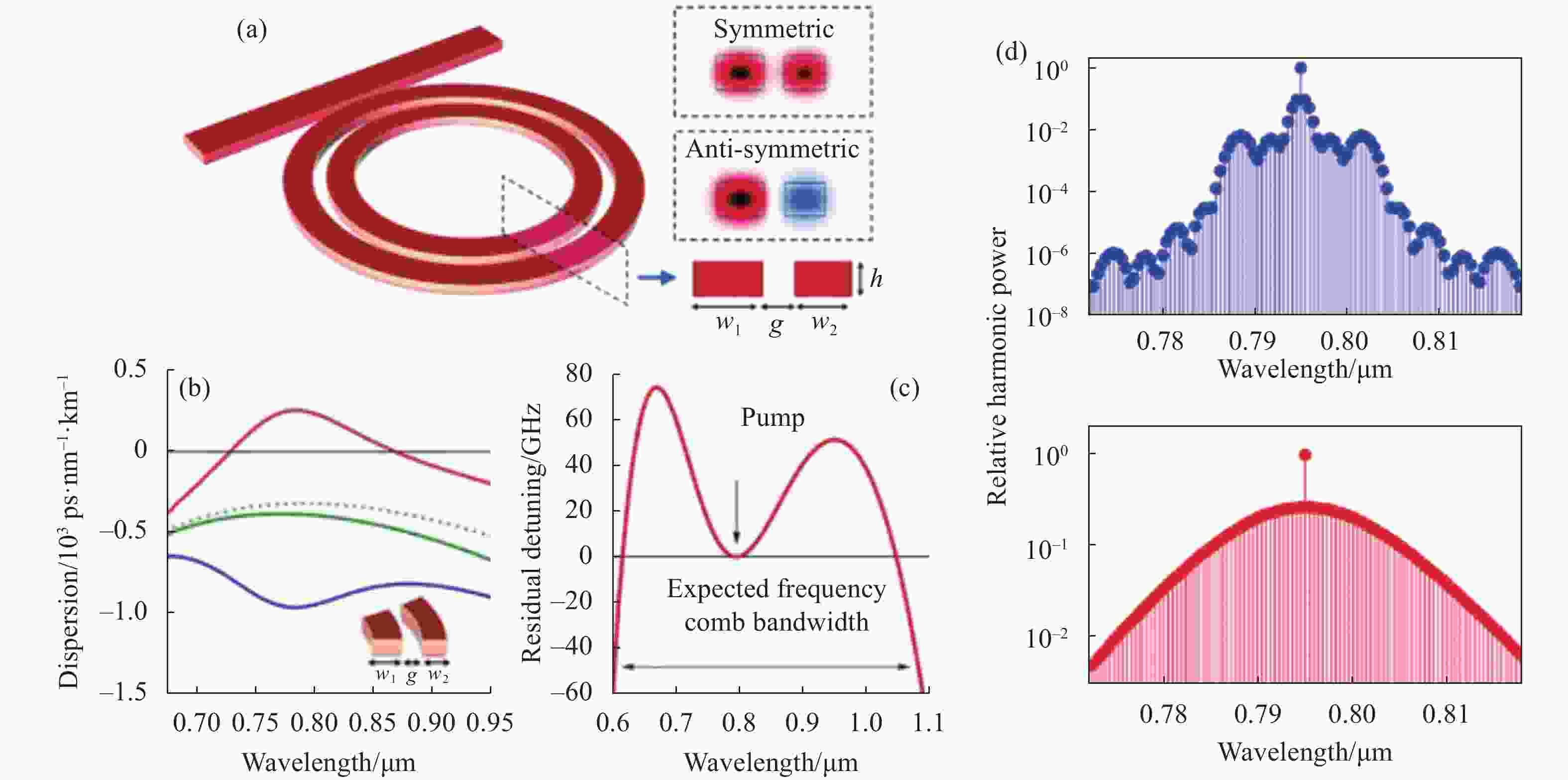
图 9 基于超模式反常色散实现可见光频梳。(a) 耦合型双环微腔结构示意图及对称模式和反对称模式场分布图;(b) 反对称模式(红线)和对称模式(蓝线)的色散;(c) 残余频率失谐量;(d) 对称模式与反对称模式下光频梳的产生[86]
Figure 9. Visible OFCs generated by supermode with anomalous dispersion. (a) Structure diagram of coupled double ring microcavity and field distribution of symmetric mode and antisymmetric mode; (b) Dispersion of antisymmetric mode (red line) and symmetric mode (blue line); (c) Residual frequency detuning; (d) OFC generation in symmetric and anit-symmetric supermodes[86]
2017年,K. Vahala课题组在一个毫米量级的SiO2微盘腔[87]中利用TM1和TE2模式相互耦合,实现孤子光频梳的产生。如图10(a)所示,当谐振器具有垂直侧壁或楔形角为90°时,由于反射对称性的存在禁止了不同偏振模式之间的相互作用,两个模式的有效折射率发生交叉,不会发生模式耦合。通过减小楔形角可以破坏谐振器的反射对称性,有效折射率简并被解除使得TM1和TE2模式发生耦合,造成局部GVD的突然改变,其色散曲线如图10(b)所示,反对称模式被调节为反常色散。如图10(d)所示,当把楔形角控制在接近30°时,混合模式在蓝光波段处于反常色散,这使得在蓝光波段产生孤子光频梳成为可能。实验中将微盘腔的楔形角控制在40°,厚度为1.47 μm,直径3.2 mm,其反对称模式处于反常色散区。在778 nm处产生重复频率为20 GHz,时间脉冲宽度为145 fs的孤子光频梳,如图10(c)所示。2020年底,该课题组再次利用同样方法产生了一种类似于量子场论狄拉克孤子的新型狄拉克光孤子[88]。
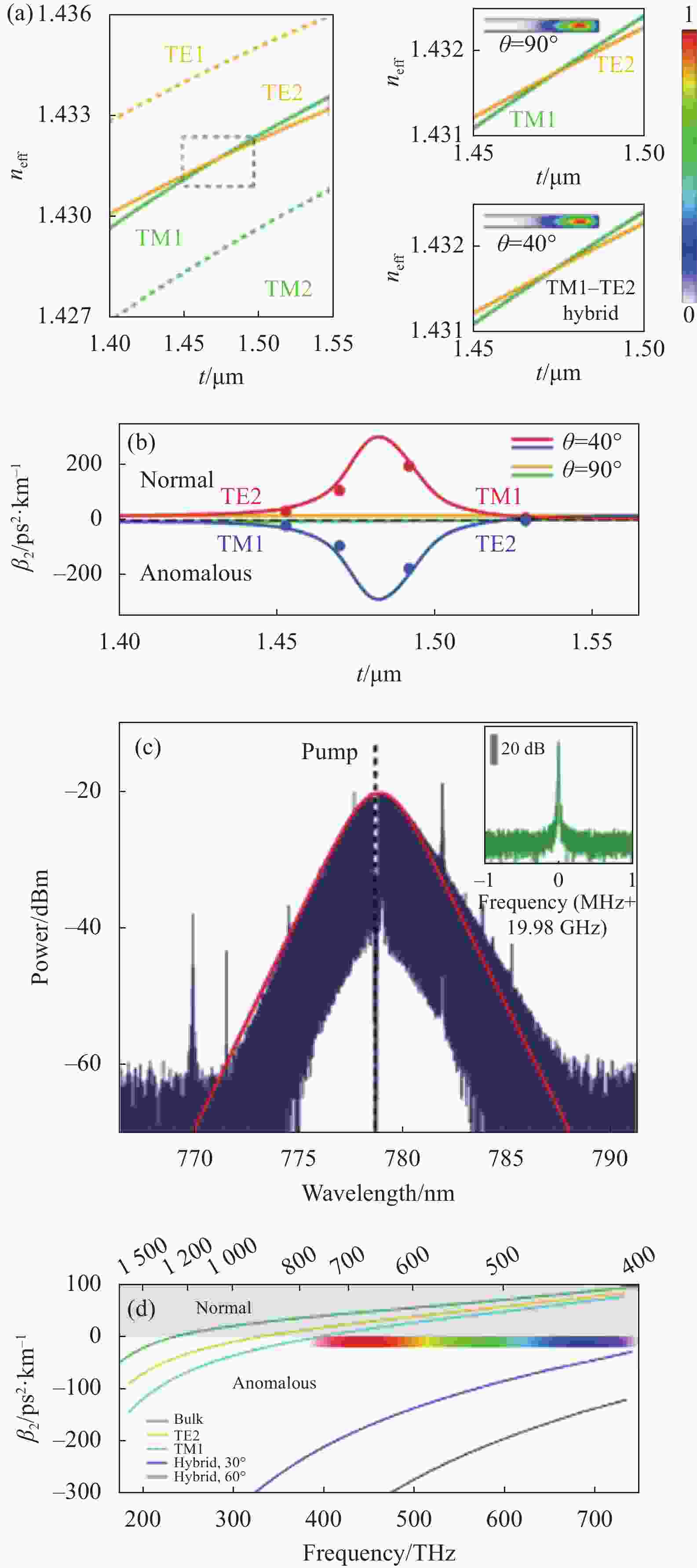
图 10 TM和TE模式耦合形成超模,产生可见光频梳。(a) 不同厚度下模式有效折射率;(b) 不同厚度下超模式的色散曲线;(c) 孤子光谱[87];(d) 超模式色散曲线[88]
Figure 10. TM and TE modes are coupled to form supermodes, generating visible frequency combs. (a) Effective refractive index under different thicknesses; (b) Dispersion curves of supermodes with different thicknesses; (c) Optical spectrum of a soliton generated[87]; (d) Dispersion curves of supermodes[88]
次年,T. Kippenberg课题组在一个微米量级的Si3N4微环腔[20]里面利用超模式,实现了带宽超过一个倍频程的耗散克尔孤子光频梳。利用TM00与TE00的耦合,使得TE模式的局部GVD发生剧烈变化,使其从正常色散(D2/2π = −32 MHz)变为高度反常色散(D2/2π = 510 MHz)。要产生耗散克尔光频梳,需要使得微腔在有效的红失谐状态下运行。其中一种实现方法为:泵浦激光从蓝失谐扫描到红失谐,并且在一个确定的泵浦共振失谐量停止。当泵浦激光位于共振的蓝失谐一侧时,腔内显示出调制不稳定性和伴随噪声的克尔光频梳。在进一步的调节泵浦失谐后,克尔光频梳向孤子光频梳过渡,光谱的形状向着
${{\rm{sech}} ^2}$ 曲线变化,以及出现孤子系统中的双峰结构。实验上观察到由几个具有不同FSR的类孤子谱组成的多孤子态,这是由模式相互作用造成的,与单孤子相比,多孤子具有很高的转换效率,因为其腔内脉冲的数量很高,在该实验中转换效率接近50%。由此产生的孤子态光谱实现了从776~1630 nm的倍频孤子频梳(图11),孤子脉冲时间宽度为18 fs。光谱在800 nm处通过孤子诱导的切伦科夫辐射产生色散波,使得孤子光谱向较短的波长延伸[89]。该波段覆盖Rb原子的D1和D2两个跃迁线[12, 90],因此,该可见孤子频梳在高精度计时中将发挥重要作用[11]。2020年,Ali Eshaghian Dorche等人在AlxGa1-xN微腔[91]中利用模式耦合在蓝光波段实现反常色散。如图12(a)所示,该谐振腔由两个矩形波导垂直堆叠而成,谐振腔衬底为AlN。通过选择几何参数和材料组成,可以调节模式耦合的波长。改变波导的宽度不会对GVD产生影响,如图12(b)所示;当增大hf1时会使得GVD的值变大且色散曲线向短波长方向移动(图12(c));增大hf2时,其效果与增大hf1相反(图12(e)),其原因是在模式耦合附近两个波导色散曲线β1和β2的斜率存在显著差异。如图12(d)所示,增大hg并不会移动色散曲线,但却显著提高了GVD的值,这是因为耦合系数κ由单个波导模式之间的重叠面积决定,增大hg会减小耦合系数从而改变GVD的值;同时还可以改变波导中Al的占比,从而改变相邻材料之间的折射率比值,并且可以稍微调整,以减少对几何参数的严格要求,从而将结构的反常色散调整到所需的区域。将泵浦光波长固定在442 nm,利用LLE数值计算光频梳的产生,其中显示位于436 nm与467 nm处的梳状线和171Yb+离子光学时钟的E2、E3能级吻合。
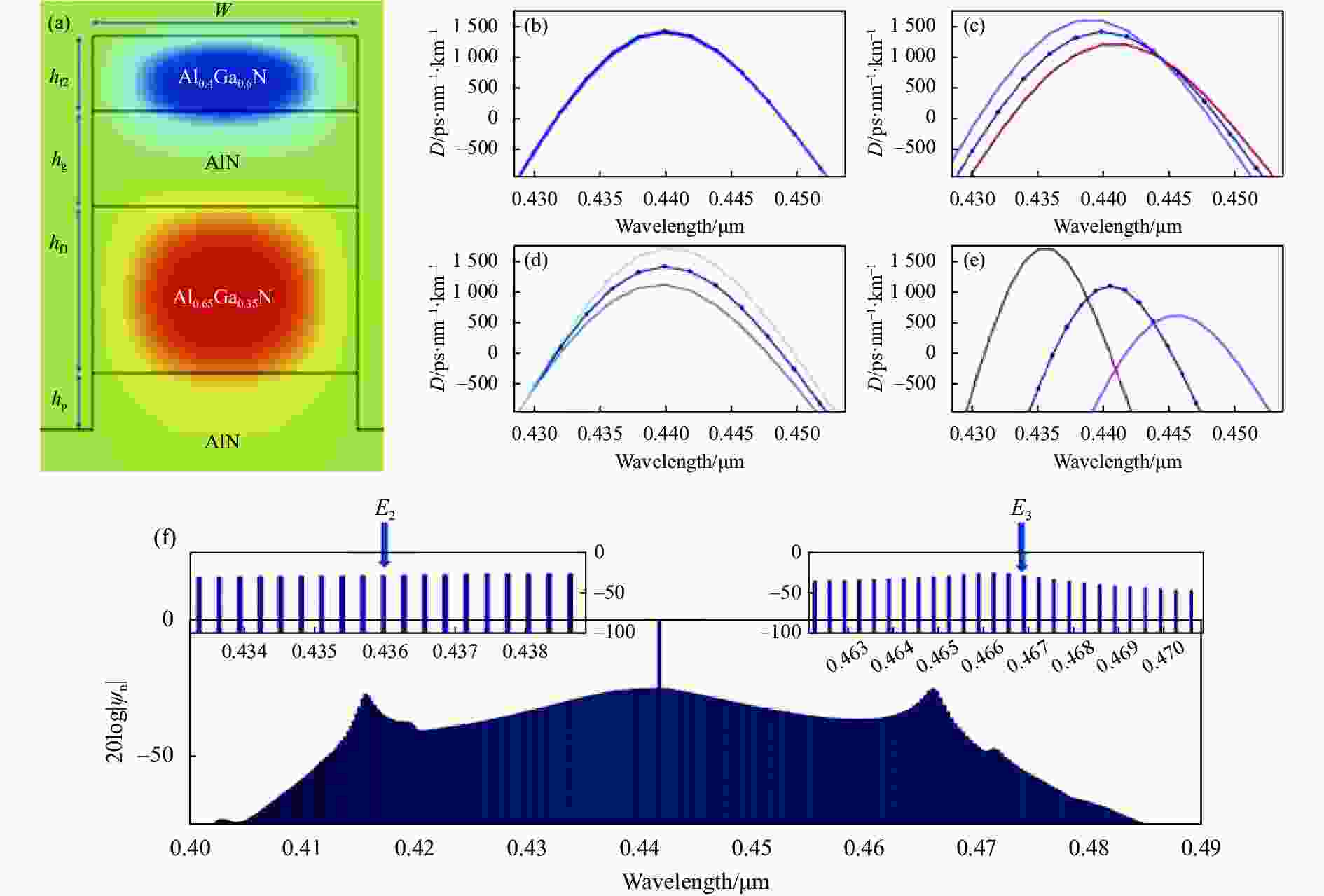
图 12 堆叠耦合超模产生可见光频梳。(a) AlGaN混合波导结构及超模式的场振幅分布;(b)~(e) 不同w、hf1、hg、hf2下的GVD;(f) 模拟光频梳的产生[91]
Figure 12. Visible OFCs generated by stacked coupled supermodes. (a) A representative AlGaN hybrid waveguide structure and the field amplitude profile of super-mode; (b)-(e) Dispersion curves of supermodes in different width w、height hf1、height hg、height hf2; (f) Simulated frequency-comb spectrum[91]
最近,Judith Su课题组在水溶液中实现基于微芯圆环腔的可见光频梳,为研究基于微腔光频梳的单分子光谱检测提供一种新思路[92]。当将微腔放置在水溶液中时,腔模色散处于正常色散区域,难以产生宽带光频梳。由于不同的光学模式有各自的模式分布、有效折射率与FSR,当微腔中存在多种模式时,这些模式会发生AMXs,使模式色散发生局部变化,达到反常色散区域。实验中制备了一个外直径为500 μm的微芯圆环腔,使得能在一个FSR内存在更多的光学模式,从而更高效的实现模式耦合。通过调整锥形光纤与微环腔的接触位置,来激发低阶模式和高阶模式实现模式耦合。将20 mW的泵浦光耦合到微腔中,观察到克尔光频梳,如图13(b)所示,其主梳(第一个生成的边带,λ>773 nm)与AMX发生的位置(λ>772 nm)具有一个微小偏差,这是由于腔体温度升高引起的频率偏移造成的。当泵浦光从高频扫频到低频时,腔内功率的增加使腔体变热,由于不同的模式可能具有不同的热灵敏度,使得频率发生偏移,从而改变AMX的位置。如图13(c)所示,当同时存在多个AMX时,主梳并不会出现在离泵浦光最近的AMX位置,而是取决于模式之间的耦合强度(图13(d))。借助远离泵浦波长的AMX产生了一个跨越300 nm的宽带光频梳。
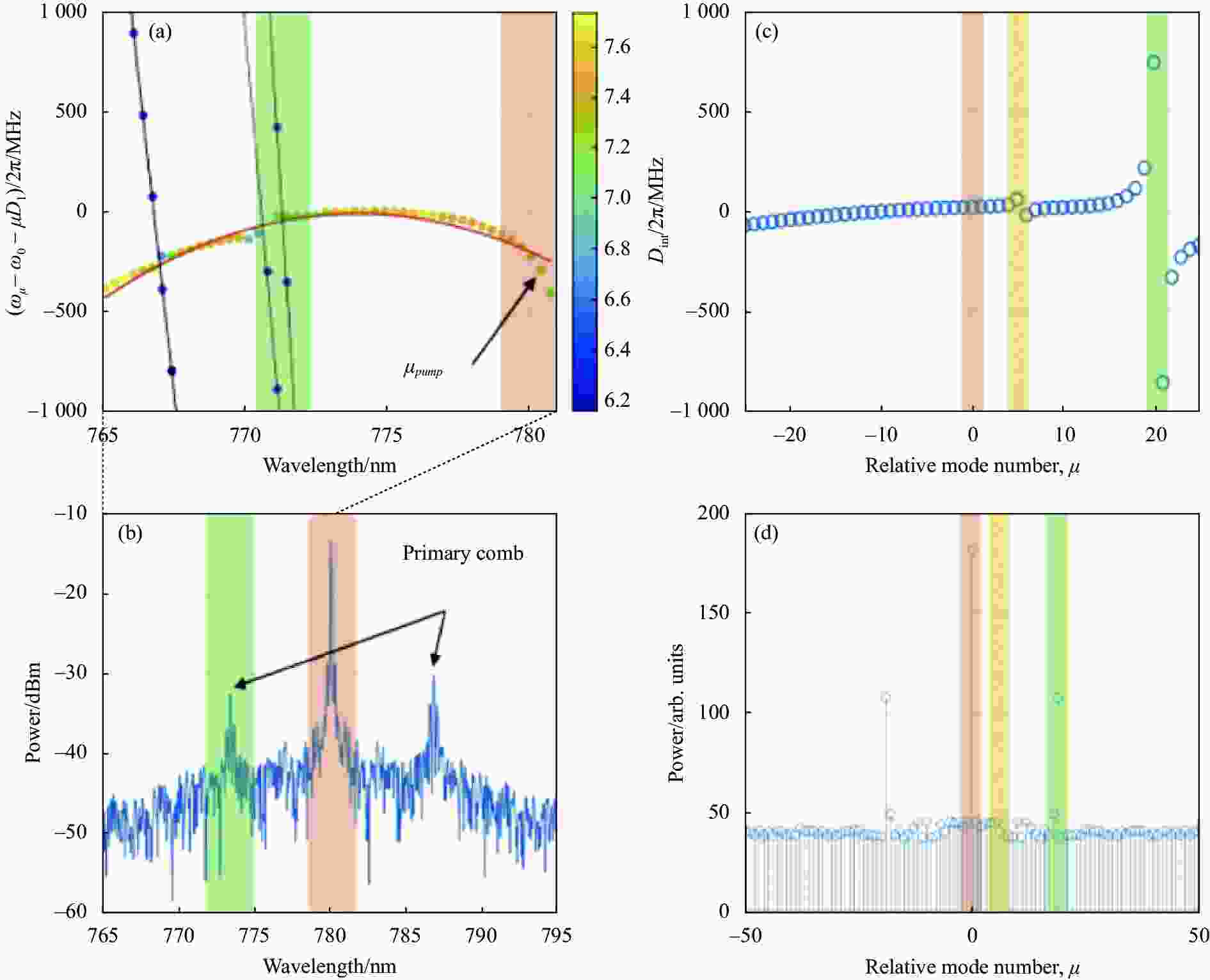
图 13 利用AMXs产生可见光频梳。(a) 模式耦合的高阶色散;(b) 图(a)情况下初级光频梳的产生;(c) 计算的模式色散;(d) 图(c)情况下初级梳状线产生[92]
Figure 13. Visible OFCs generated by AMXs. (a) Integrated dispersion of supermode; (b) Generated frequency comb when the mode indicated in (a) is pumped; (c) Simulation of the integrated dispersion; (d) Primary comb line generation when the mode indicated in (c) is pumped[92]
-
综上,可见光频梳在诸多领域有着重要作用,但材料色散使得可见光频梳的实现具有很大的实验挑战。目前解决方案主要有三种:第一种是利用材料的二阶与三阶非线性效应,将在近红外波段产生的光频梳通过倍频与和频效应,相干的转换到可见光波段,该方案在可见波段区域并没有实现微腔模式的反常色散,因此产生的光频梳带宽较窄且相干转换效率也受到限制;第二种是通过选择合适的微腔尺寸和形状,使得在可见光波段模式色散处于反常色散区,利用可见或近可见光作为泵浦源来激发光频梳的产生,该方法对微腔的尺寸和形状有严格的限定;第三种是利用模式之间的耦合效应,形成的反对称模式在可见光波段处于反常色散,从而补偿材料的正常色散,此方法还有利于孤子光频梳的产生。
尽管可见光频梳相比于C波段光频梳较难实现,但是,随着回音壁模式微腔加工技术和色散调控技术的发展,可见孤子光频梳将在不久的将来逐步成熟、走向应用。可以预期未来几年会有更多的研究投入到可见光频梳的研究中,并在以下几个方向上取得进展:一、在更短的波长上实现光频梳;二、降低阈值功率,实现可见光的孤子光频梳;三、实现可见光频梳的有效调控,并基于原子跃迁参考实现其重复频率和初始偏移频率的锁定;四、将可见光频梳应用于分子原子光谱探测、天文探测及生物医学中。
Research progress of optical frequency comb in visible light band based on whispering gallery microcavities (Invited)
-
摘要: 基于光学微腔的光频梳具有阈值低、光谱宽及结构紧凑等特点,在精密测量与传感等领域具有重要的应用前景,因此近年来微腔光频梳成为国际研究热点。目前相关的研究都聚焦于红外波段锁模光频梳的产生原理和应用探索,虽然可见光波段的光频梳在精密光谱、原子钟及生物医学等领域有特殊应用价值,但是可见光频梳的实现极具挑战性。文中在简要阐述光频梳产生原理的基础上,介绍了在可见光波段实现光频梳的主要挑战,以及目前三种实现方案的研究进展,包括利用材料的二阶与三阶非线性效应、调节微腔的几何色散和模式强耦合效应调控色散来产生可见光频梳。Abstract: Optical frequency combs (OFCs) based on optical microcavities have the characteristics of low threshold, wide spectrum, and compact structure, and have important application prospect in the fields of precision measurement, sensing and et al. Therefore, microcavity based OFC has become an international research hotspot in recent years. At present, relevant researches focus on the generation principle and application of mode-locked OFCs in the infrared band. Although the OFCs in the visible light band have special applications in the fields of precision spectroscopy, atomic clocks and biomedicine, the realization of visible light OFCs is extremely challenging. Based on a brief description of the generation principle of OFCs, this paper introduces the main challenges of realizing OFCs in the visible light band, and the current research progress of three implementation schemes, including the use of the second-order and third-order nonlinear effects of materials, the regulation of the geometric dispersion of the microcavity, and the regulation of the dispersion via modal strong coupling effect to generate visible light frequency combs.
-
图 2 几种克尔光频梳。(a) 二氧化硅微环谐振器中倍频程频率梳[23];(b) Si3N4微环腔中单孤子光频梳[47];(c) 二氧化硅微环腔中孤子光频梳[48]
Figure 2. Several kinds of Kerr OFCs. (a) An octave-spanning frequency comb generated in a silica microtoroid [23]; (b) Spectrum of solitons comb generated in Si3N4 microtoroid[47]; (c) Spectrum of solitons comb generated in silica[48]
图 3 利用二倍频、四波混频与和频效应产生可见光频梳。(a) 近红外波段光学频梳到可见光学频梳的转换过程;(b) 近红外基本TE模与可见光范围内三阶TE模的有效折射率;(c) 基本TE模的群速度色散[50];(d)近红外TM00模式与可见光TM10、TM00模式的有效折射率;(e) 归一化模态重叠因子;(f) 红外光频梳、二次谐波与可见光频梳的产生[51]
Figure 3. Visible light OFCs are generated using second harmonic generation, four-wave mixing and sum-frequency effects. (a) Generate simultaneous near IR and visible wavelength frequency comb lines; (b) The effective index of the fundamental TE mode in near IR spectral range and the third-order TE mode in the visible spectral range; (c) The group velocity dispersion (GVD) of the fundamental TE mode[50]; (d) The effective index of TM00 mode in near IR spectral range and TM10、TM00 mode in the visible spectral range; (e) Normalized modal overlap; (f) Generation of IR、second harmonics and near-visible microcombs [51]
图 4 (a) TE00与TM00的二阶色散D2/(2π);(b) 泵浦频率下模式与三次谐波处的模式匹配;(c)红外波段下光频梳的产生;(d) 三次谐波与绿光光频梳的产生[55]
Figure 4. (a) The second-order dispersion D2/(2π) for the fundamental TE and TM modes; (b) The effective index for the fundamental TE、TM modes at the pump frequency and higher-order modes at the third-harmonic frequency; (c) Generation of IR microcombs; (d) Generation of third harmonics and green light comb [55]
图 5 (a) 变形微芯圆环腔电镜图;(b) 混沌辅助的标准WGMs到混沌状态的动态隧穿;(c) 近可见光频梳通过二倍频和三倍频效应转换为可见光频梳[61]
Figure 5. (a) Scanning electron microscope image of the deformed microtoroid resonator; (b) Chaos-assisted dynamical tunneling from WGMs to chaotic states; (c) Nonlinear frequency conversion from infrared combs to visible wavelengths[61]
图 6 楔形角调控微盘腔色散产生可见光频梳。(a) 腔体内部基本TM10模式的模式剖面图;(b) TM10、TM20、TM30模式色散(插图:TM10、TM20、TM30模式轮廓);(c) 在不同厚度与楔形角下TM10模式色散;(d) 可见克尔光频梳的产生[67]
Figure 6. Wedge angle modulation of microdisk cavity dispersion to generate visible OFCs. (a) Illustration of the mode profile for the fundamental TM10 mode inside the cavity; (b) Dispersion characteristics of the TM10, TM20, TM30 modes(Inset: simulated mode profiles of the TM10, TM20 and TM30 modes); (c) Variation of the dispersion when changing the thickness of the disk at different wedge angles; (d) Generation of near-visible Kerr OFCs [67]
图 7 通过高阶模TE10产生可见光频梳。(a) 用于调节片上加热器的电压模式;(b) 与(a)中的模式对应的梳状功率的演变;(c) 四孤子态光谱图;(d)~(f) 图(b)中A(微梳形成)、B( 浑沌状态)、C(孤子态)对应的光谱;(g)~(i) 图(d)~(f)对应的射频噪声[67]
Figure 7. Visible OFCs generation by higher-order mode TE10. (a) Voltage pattern used to modulate the on-chip heater; (b) Evolution of comb power corresponding to the pattern in Fig.(a); (c) Comb spectrum of four-soliton state; (d)-(f) Optical spectra corresponding to point A (minicomb formation), B (chaotic state), and C (soliton state) in Fig.(b); (g)-(i) RF noise corresponding to Fig.(d)-(f)[67]
图 8 基于轴向模式产生光频梳[75]。(a) 传统基于方位角模式的四波混频示意图;(b) 基于轴向模式的四波混频示意图;(c) 基于轴向模式产生的光频梳与收集位置的关系
Figure 8. OFC generated with axial (vertical) modes [75]. (a) Schematic of FWM with the fundamental azimuthal mode family; (b) Schematic of FWM with the axial mode family; (c) Relationship between OFC generated with aixal modes and collection positions
图 9 基于超模式反常色散实现可见光频梳。(a) 耦合型双环微腔结构示意图及对称模式和反对称模式场分布图;(b) 反对称模式(红线)和对称模式(蓝线)的色散;(c) 残余频率失谐量;(d) 对称模式与反对称模式下光频梳的产生[86]
Figure 9. Visible OFCs generated by supermode with anomalous dispersion. (a) Structure diagram of coupled double ring microcavity and field distribution of symmetric mode and antisymmetric mode; (b) Dispersion of antisymmetric mode (red line) and symmetric mode (blue line); (c) Residual frequency detuning; (d) OFC generation in symmetric and anit-symmetric supermodes[86]
图 10 TM和TE模式耦合形成超模,产生可见光频梳。(a) 不同厚度下模式有效折射率;(b) 不同厚度下超模式的色散曲线;(c) 孤子光谱[87];(d) 超模式色散曲线[88]
Figure 10. TM and TE modes are coupled to form supermodes, generating visible frequency combs. (a) Effective refractive index under different thicknesses; (b) Dispersion curves of supermodes with different thicknesses; (c) Optical spectrum of a soliton generated[87]; (d) Dispersion curves of supermodes[88]
图 12 堆叠耦合超模产生可见光频梳。(a) AlGaN混合波导结构及超模式的场振幅分布;(b)~(e) 不同w、hf1、hg、hf2下的GVD;(f) 模拟光频梳的产生[91]
Figure 12. Visible OFCs generated by stacked coupled supermodes. (a) A representative AlGaN hybrid waveguide structure and the field amplitude profile of super-mode; (b)-(e) Dispersion curves of supermodes in different width w、height hf1、height hg、height hf2; (f) Simulated frequency-comb spectrum[91]
图 13 利用AMXs产生可见光频梳。(a) 模式耦合的高阶色散;(b) 图(a)情况下初级光频梳的产生;(c) 计算的模式色散;(d) 图(c)情况下初级梳状线产生[92]
Figure 13. Visible OFCs generated by AMXs. (a) Integrated dispersion of supermode; (b) Generated frequency comb when the mode indicated in (a) is pumped; (c) Simulation of the integrated dispersion; (d) Primary comb line generation when the mode indicated in (c) is pumped[92]
-
[1] Herr T, Brasch V, Jost J D, et al. Temporal solitons in optical microresonators [J]. Nature Photonics, 2014, 8(2): 145-152. doi: 10.1038/NPHOTON.2013.343 [2] Yang Q F, Suh M G, Yang K Y, et al. Microresonator soliton dual-comb spectroscopy[C]//Conference on Lasers and Electro-Optics (CLEO), 2017: SM4D. 4. [3] Cundiff S T, Ye J. Colloquium: Femtosecond optical frequency combs [J]. Reviews of Modern Physics, 2003, 75(1): 325-342. doi: 10.1103/RevModPhys.75.325 [4] Koke S, Grebing C, Frei H, et al. Direct frequency comb synthesis with arbitrary offset and shot-noise-limited phase noise [J]. Nature Photonics, 2010, 4(7): 462-465. doi: 10.1038/nphoton.2010.91 [5] Stern B, Ji X C, Okawachi Y, et al. Battery-operated integrated frequency comb generator [J]. Nature, 2018, 562(7727): 401-405. doi: 10.1038/s41586-018-0598-9 [6] Yao B C, Huang S W, Liu Y, et al. Gate-tunable frequency combs in graphene-nitride microresonators [J]. Nature, 2018, 558(7710): 410-414. doi: 10.1038/s41586-018-0216-x [7] Matsko A B, Savchenkov A A, Strekalov D, et al. Optical hyperparametric oscillations in a whispering-gallery-mode resonator: threshold and phase diffusion [J]. Physical Review A, 2005, 71(3): 033804. doi: 10.1103/PhysRevA.71.033804 [8] Lin G P, Coillet A, Chembo Y K. Nonlinear photonics with high-Q whispering-gallery-mode resonators [J]. Advances in Optics and Photonics, 2017, 9(4): 828-890. doi: 10.1364/AOP.9.000828 [9] Kues M, Reimer C, Lukens J M, et al. Quantum optical microcombs [J]. Nature Photonics, 2019, 13(3): 170-179. doi: 10.1038/s41566-019-0363-0 [10] Del'Haye P, Schliesser A, Arcizet O, et al. Optical frequency comb generation from a monolithic microresonator [J]. Nature, 2007, 450(7173): 1214-1217. doi: 10.1038/nature06401 [11] Udem T, Holzwarth R, Hänsch T W. Optical frequency metrology [J]. Nature, 2002, 416(6877): 233-237. doi: 10.1038/416233a [12] Jones D J, Diddams S A, Ranka J K, et al. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis [J]. Science, 2000, 288(5466): 635-639. doi: 10.1126/science.288.5466.635 [13] Spencer D T, Drake T, Briles T C, et al. An optical-frequency synthesizer using integrated photonics [J]. Nature, 2018, 557(7703): 81-85. doi: 10.1038/s41586-018-0065-7 [14] Steinmetz T, Wilken T, Araujo-Hauck C, et al. Laser frequency combs for astronomical observations [J]. Science, 2008, 321(5894): 1335-1337. doi: 10.1126/science.1161030 [15] Suh M G, Vahala K J. Soliton microcomb range measurement [J]. Science, 2018, 359(6378): 884-887. doi: 10.1126/science.aao1968 [16] Bartels A, Heinecke D, Diddams S A. 10-GHz self-referenced optical frequency comb [J]. Science, 2009, 326(5953): 681-681. doi: 10.1126/science.1179112 [17] Vahala K J. Optical microcavities [J]. Nature, 2003, 424(6950): 839-846. doi: 10.1038/nature01939 [18] Breunig I. Three-wave mixing in whispering gallery resonators [J]. Laser & Photonics Reviews, 2016, 10(4): 569-587. doi: 10.1002/lpor.201600038 [19] Strekalov D V, Marquardt C, Matsko A B, et al. Nonlinear and quantum optics with whispering gallery resonators [J]. Journal of Optics, 2016, 18(12): 123002. doi: 10.1088/2040-8978/18/12/123002 [20] Gaeta A L, Lipson M, Kippenberg T J. Photonic-chip-based frequency combs [J]. Nature Photonics, 2019, 13(3): 158-169. doi: 10.1038/s41566-019-0358-x [21] Kippenberg T J, Spillane S M, Vahala K J. Kerr-nonlinearity optical parametric oscillation in an ultrahigh-Q toroid microcavity [J]. Physical Review Letters, 2004, 93(8): 083904. doi: 10.1103/PhysRevLett.93.083904 [22] Savchenkov A A, Matsko A B, Strekalov D, et al. Low threshold optical oscillations in a whispering gallery mode CaF2 resonator [J]. Physical Review Letters, 2004, 93(24): 243905. doi: 10.1103/PhysRevLett.93.243905 [23] Kippenberg T J, Holzwarth R, Diddams S A. Microresonator-based optical frequency combs [J]. Science, 2011, 332(6029): 555-559. doi: 10.1126/science.1193968 [24] Wang Mengyu, Fan Lekang, Wu Lingfeng, et al. Research on Kerr optical frequency comb generation based on MgF2 crystalline microresonator with ultra-high-Q factor [J]. Infrared and Laser Engineering, 2021, 50(5): 20210481. (in Chinese) doi: 10.3788/IRLA20210481 [25] Agha I H, Okawachi Y, Gaeta A L. Theoretical and experimental investigation of broadband cascaded four-wave mixing in high-Q microspheres [J]. Optics Express, 2009, 17(18): 16209-16215. doi: 10.1364/OE.17.016209 [26] Okawachi Y, Saha K, Levy J S, et al. Octave-spanning frequency comb generation in a silicon nitride chip [J]. Optics Letters, 2011, 36(17): 3398-3400. doi: 10.1364/OL.36.003398 [27] Jung H, Xiong C, Fong K F, et al. Optical frequency comb generation from aluminum nitride microring resonator [J]. Optics Letters, 2013, 38(15): 2810-2813. doi: 10.1364/OL.38.002810 [28] Hausmann B J M, Bulu I, Venkataraman V, et al. Diamond nonlinear photonics [J]. Nature Photonics, 2014, 8(5): 369-374. doi: 10.1038/nphoton.2014.72 [29] Brasch V, Geiselmann M, Herr T, et al. Photonic chip-based optical frequency comb using soliton Cherenkov radiation [J]. Science, 2016, 351(6271): 357-360. doi: 10.1126/science.aad4811 [30] Kim S, Han K, Wang C, et al. Dispersion engineering and frequency comb generation in thin silicon nitride concentric microresonators [J]. Nature Communications, 2017, 8: 372. doi: 10.1038/s41467-017-00491-x [31] Wang C, Zhang M, Yu M J, et al. Monolithic lithium niobate photonic circuits for Kerr frequency comb generation and modulation [J]. Nature Communications, 2019, 10: 978. doi: 10.1038/s41467-019-08969-6 [32] Del'Haye P, Herr T, Gavartin E, et al. Octave spanning tunable frequency comb from a microresonator [J]. Physical Review Letters, 2011, 107(6): 063901. doi: 10.1103/PhysRevLett.107.063901 [33] Xue X X, Xuan Y, Liu Y, et al. Mode-locked dark pulse Kerr combs in normal-dispersion microresonators [J]. Nature Photonics, 2015, 9(9): 594-600. doi: 10.1038/NPHOTON.2015.137 [34] Yi X, Yang Q F, Yang K Y, et al. Soliton frequency comb at microwave rates in a high-Q silica microresonator [J]. Optica, 2015, 2(12): 1078-1085. doi: 10.1364/OPTICA.2.001078 [35] Yang Q F, Yi X, Yang K Y, et al. Stokes solitons in optical microcavities [J]. Nature Physics, 2017, 13(1): 53-57. doi: 10.1038/NPHYS3875 [36] Weiner A M. Frequency combs cavity solitons come of age [J]. Nature Photonics, 2017, 11(9): 533-535. doi: 10.1038/nphoton.2017.149 [37] Kippenberg T J, Gaeta A L, Lipson M, et al. Dissipative Kerr solitons in optical microresonators [J]. Science, 2018, 361(6402): eaan8083. doi: 10.1126/science.aan8083 [38] Obrzud E, Rainer M, Harutyunyan A, et al. A microphotonic astrocomb [J]. Nature Photonics, 2019, 13(1): 31-35. doi: 10.1038/s41566-018-0309-y [39] Ludlow A D, Boyd M M, Ye J, et al. Optical atomic clocks [J]. Reviews of Modern Physics, 2015, 87(2): 637-701. doi: 10.1103/RevModPhys.87.637 [40] Holzwarth R, Udem T, Hansch T W, et al. Optical frequency synthesizer for precision spectroscopy [J]. Physical Review Letters, 2000, 85(11): 2264. doi: 10.1103/PhysRevLett.85.2264 [41] Murphy M T, Udem T, Holzwarth R, et al. High-precision wavelength calibration of astronomical spectrographs with laser frequency combs [J]. Monthly Notices of the Royal Astronomical Society, 2007, 380(2): 839-847. doi: 10.1111/j.1365-2966.2007.12147.x [42] Margolis H S. Spectroscopic applications of femtosecond optical frequency combs [J]. Chemical Society Reviews, 2012, 41(15): 5174-5184. doi: 10.1039/c2cs35163c [43] Hartl I, Li X D, Chudoba C, et al. Ultrahigh-resolution optical coherence tomography using continuum generation in an air-silica microstructure optical fiber [J]. Optics Letters, 2001, 26(9): 608-610. doi: 10.1364/OL.26.000608 [44] Wilt B A, Burns L D, Ho E T W, et al. Advances in light microscopy for neuroscience [J]. Annual Review of Neuroscience, 2009, 32: 435-506. doi: 10.1146/annurev.neuro.051508.135540 [45] Fercher A F, Drexler W, Hitzenberger C K, et al. Optical coherence tomography - principles and applications [J]. Reports on Progress in Physics, 2003, 66(2): 239-303. doi: 10.1088/0034-4885/66/2/204 [46] Ideguchi T, Holzner S, Bernhardt S B, et al. Coherent Raman spectro-imaging with laser frequency combs [J]. Nature, 2013, 502(7471): 355-358. doi: 10.1038/nature12607 [47] Wan S, Niu R, Peng J L, et al. Fabrication of the high-Q Si3N4 microresonators for soliton microcombs [J]. Chinese Optics Letters, 2022, 20(3): 032201. doi: 10.3788/COL202220.032201 [48] Lu Z Z, Wang W Q, Zhang W F, et al. Deterministic generation and switching of dissipative Kerr soliton in a thermally controlled micro-resonator [J]. AIP Advances, 2019, 9(2): 025314. doi: 10.1063/1.5080128 [49] Fujii S, Tanabe T. Dispersion engineering and measurement of whispering gallery mode microresonator for Kerr frequency comb generation [J]. Nanophotonics, 2020, 9(5): 1087-1104. doi: 10.1515/nanoph-2019-0497 [50] Miller S, Luke K, Okawachi Y, et al. On-chip frequency comb generation at visible wavelengths via simultaneous second- and third-order optical nonlinearities [J]. Optics Express, 2014, 22(22): 26517-26525. doi: 10.1364/OE.22.026517 [51] Liu X W, Sun C Z, Xiong B, et al. Generation of multiple near-visible comb lines in an AlN microring via chi((2)) and chi((3)) optical nonlinearities [J]. Applied Physics Letters, 2018, 113(17): 171106. doi: 10.1063/1.5046324 [52] Guo X, Zou C L, Jung H, et al. Efficient generation of a near-visible frequency comb via Cherenkov-like radiation from a Kerr microcomb [J]. Physical Review Applied, 2018, 10(1): 014012. doi: 10.1103/PhysRevApplied.10.014012 [53] Bruch A W, Liu X, Gong Z, et al. Pockels soliton microcomb [J]. Nature Photonics, 2021, 15(1): 21-27. doi: 10.1038/s41566-020-00704-8 [54] Gong Z, Bruch A W, Yang F, et al. Quadratic strong coupling in AlN Kerr cavity solitons [J]. Optics Letters, 2022, 47(4): 746-749. doi: 10.1364/OL.447987 [55] Wang L R, Chang L, Volet N, et al. Frequency comb generation in the green using silicon nitride microresonators [J]. Laser & Photonics Reviews, 2016, 10(4): 631-638. doi: 10.1002/lpor.201600006 [56] Szabados J, Puzyrev D N, Minet Y, et al. Frequency comb generation via cascaded second-order nonlinearities in microresonators [J]. Physical Review Letters, 2020, 124(20): 203902. doi: 10.1103/PhysRevLett.124.203902 [57] Buryak A V, Di Trapani P, Skryabin D V, et al. Optical solitons due to quadratic nonlinearities: from basic physics to futuristic applications [J]. Physics Reports-Review Section of Physics Letters, 2002, 370(2): 63-235. doi: 10.1016/S0370-1573(02)00196-5 [58] Skryabin D V, Champneys A R. Walking cavity solitons [J]. Physical Review E, 2001, 63(6): 066610. doi: 10.1103/PhysRevE.63.066610 [59] Villois A, Kondratiev N, Breunig I, et al. Frequency combs in a microring optical parametric oscillator [J]. Optics Letters, 2019, 44(18): 4443-4446. doi: 10.1364/OL.44.004443 [60] Villois A, Skryabin D V. Soliton and quasi-soliton frequency combs due to second harmonic generation in microresonators [J]. Optics Express, 2019, 27(5): 7098-7107. doi: 10.1364/OE.27.007098 [61] Chen H J, Ji Q X, Wang H, et al. Chaos-assisted two-octave-spanning microcombs [J]. Nature Communications, 2020, 11(1): 1-6. doi: 10.1038/s41467-020-15914-5 [62] Guo X, Zou C L, Schuck C, et al. Parametric down-conversion photon-pair source on a nanophotonic chip [J]. Light: Science & Applications, 2017, 6(5): e16249. doi: 10.1038/lsa.2016.249 [63] Jiang X,Shao L, Zhang S X, et al. Chaos-assisted broadband momentum transformation in optical microresonators [J]. Science, 2017, 358(6361): 344-347. doi: DOI:10.1126/science.aao0763 [64] Yang Y, Jiang X F, Kasumie S, et al. Four-wave mixing parametric oscillation and frequency comb generation at visible wavelengths in a silica microbubble resonator [J]. Optics Letters, 2016, 41(22): 5266-5269. doi: 10.1364/OL.41.005266 [65] Riesen N, Zhang W Q, Monro T M. Dispersion in silica microbubble resonators [J]. Optics Letters, 2016, 41(6): 1257-1260. doi: 10.1364/OL.41.001257 [66] Shu F J, Zhang P J, Qian Y J, et al. A mechanically tuned Kerr comb in a dispersion-engineered silica microbubble resonator [J]. Science China-Physics Mechanics & Astronomy, 2020, 63(5): 254211. doi: 10.1007/s11433-019-1464-8 [67] Ma J Y, Xiao L F, Gu J X, et al. Visible Kerr comb generation in a high-Q silica microdisk resonator with a large wedge angle [J]. Photonics Research, 2019, 7(5): 573-578. doi: 10.1364/PRJ.7.000573 [68] Zhao Y, Ji X C, Kim B Y, et al. Visible nonlinear photonics via high-order-mode dispersion engineering [J]. Optica, 2020, 7(2): 135-141. doi: 10.1364/OPTICA.7.000135 [69] Luo L W, Ophir N, Chen C P, et al. WDM-compatible mode-division multiplexing on a silicon chip [J]. Nature Communications, 2014, 5: 3069. doi: 10.1038/ncomms4069 [70] Karpov M, Guo H R, Pfeiffer M H , et al. Dynamics of soliton crystals in optical microresonators[C]//Conference on Lasers and Electro-Optics (CLEO), 2017. [71] Wan S, Niu R, Wang Z Y, et al. Frequency stabilization and tuning of breathing solitons in Si3N4 microresonators [J]. Photonics Research, 2020, 8(8): 1342-1349. doi: 10.1364/PRJ.397619 [72] Wang X Y, Xie P, Wang W Q, et al. Program-controlled single soliton microcomb source [J]. Photonics Research, 2021, 9(1): 66-72. doi: 10.1364/PRJ.408612 [73] Coen S, Randle H G, Sylvestre T, et al. Modeling of octave-spanning Kerr frequency combs using a generalized mean-field Lugiato-Lefever model [J]. Optics Letters, 2013, 38(1): 37-39. doi: 10.1364/OL.38.000037 [74] Godey C, Balakireva I V, Coillet A, et al. Stability analysis of the spatiotemporal Lugiato-Lefever model for Kerr optical frequency combs in the anomalous and normal dispersion regimes [J]. Physical Review A, 2014, 89(6): 063814. doi: 10.1103/PhysRevA.89.063814 [75] Savchenkov A A, Matsko A B, Liang W, et al. Kerr combs with selectable central frequency [J]. Nature Photonics, 2011, 5(5): 293-296. doi: 10.1038/NPHOTON.2011.50 [76] Lu Q, Wu X, Liu L, et al. Mode-selective lasing in high-Q polymer micro bottle resonators [J]. Optics Express, 2015, 23(17): 22740-22745. doi: 10.1364/OE.23.022740 [77] Lu Q, Chen X, Liu X, et al. Opto-fluidic-plasmonic liquid-metal core microcavity [J]. Applied Physics Letters, 2020, 117(16): 161101. doi: 10.1063/5.0028050 [78] Lu Q J, Liu S, Wu X, et al. Stimulated Brillouin laser and frequency comb generation in high-Q microbubble resonators [J]. Optics Letters, 2016, 41(8): 1736-1739. doi: 10.1364/OL.41.001736 [79] Yin Y H, Niu Y X, Qin H Y, et al. Kerr frequency comb generation in microbottle resonator with tunable zero dispersion wavelength [J]. Journal of Lightwave Technology, 2019, 37(21): 5571-5575. doi: 10.1109/JLT.2019.2932844 [80] Jin X Y, Xu X, Gao H R, et al. Controllable two-dimensional Kerr and Raman-Kerr frequency combs in microbottle resonators with selectable dispersion [J]. Photonics Research, 2021, 9(2): 171-180. doi: 10.1364/PRJ.408492 [81] Ramelow S, Farsi A, Clemmen S, et al. Strong polarization mode coupling in microresonators [J]. Optics Letters, 2014, 39(17): 5134-5137. doi: 10.1364/OL.39.005134 [82] Carmon T, Schwefel H G L, Yang L, et al. Static envelope patterns in composite resonances generated by level crossing in optical toroidal microcavities [J]. Physical Review Letters, 2008, 100(10): 103905. doi: 10.1103/PhysRevLett.100.103905 [83] Savchenkov A A, Matsko A B, Liang W, et al. Kerr frequency comb generation in overmoded resonators [J]. Optics Express, 2012, 20(24): 27290-27298. doi: 10.1364/OE.20.027290 [84] Xue X X, Xuan Y, Wang C, et al. Thermal tuning of Kerr frequency combs in silicon nitride microring resonators [J]. Optics Express, 2016, 24(1): 687-698. doi: 10.1364/OE.24.000687 [85] Lin G, Diallo S, Saleh K, et al. Cascaded Brillouin lasing in monolithic barium fluoride whispering gallery mode resonators [J]. Applied Physics Letters, 2014, 105(23): 231103. doi: 10.1063/1.4903516 [86] Soltani M, Matsko A, Maleki L. Enabling arbitrary wavelength frequency combs on chip [J]. Laser & Photonics Reviews, 2016, 10(1): 158-162. doi: 10.1002/lpor.201500226 [87] Lee S H, Oh D Y, Yang Q F, et al. Towards visible soliton microcomb generation [J]. Nature Communications, 2017, 8: 1295. doi: 10.1038/s41467-017-01473-9 [88] Wang H, Lu Y K, Wu L, et al. Dirac solitons in optical microresonators [J]. Light: Science & Applications, 2020, 9(1): 205. doi: 10.1038/s41377-020-00438-w [89] Akhmediev N, Karlsson M. Cherenkov radiation emitted by solitons in optical fibers [J]. Physical Review A, 1995, 51(3): 2602-2607. doi: 10.1103/PhysRevA.51.2602 [90] Watanabe N, Tamura H, Musha M, et al. Optical frequency synthesizer for precision spectroscopy of Rydberg states of Rb atoms [J]. Japanese Journal of Applied Physics, 2017, 56(11): 112401. doi: 10.7567/JJAP.56.112401 [91] Dorche A E, Timucin D, Thyagarajan K, et al. Advanced dispersion engineering of a III-nitride micro-resonator for a blue frequency comb [J]. Optics Express, 2020, 28(21): 30542-30554. doi: 10.1364/OE.399901 [92] Choi G H, Gin A, Su J. Optical frequency combs in aqueous and air environments at visible to near-IR wavelengths [J]. Optics Express, 2022, 30(6): 8690-8699. doi: 10.1364/OE.451631 -







 下载:
下载: