-
得益于国内大口径反射镜制备技术的进步,越来越多的在研和在轨相机将口径提升到1.5 m以上[1-2],在极大的提升卫星观测能力的同时,也对相机光机结构提出了更苛刻的要求。在运载能力相对固定的情况下,相机口径的提高,意味着光学系统更复杂,装配公差更严格,结构轻量化要求更高。在现有的加工、制造和检测能力下,通过精巧的结构设计和合理的工艺选择,获得更高的尺寸精度和结构稳定性,成为保障相机性能的有效手段。
三反同轴系统是相机常用的光学系统结构型式[3],主承力板作为此类相机的主体承载部件,是整个支撑结构的核心。主承力板为各光学组件及其他结构提供机械接口,并保证各元件间的相对位置关系稳定,因此,主承力板对其他部件安装面的几何精度及本身的尺寸稳定性应满足系统要求。相机口径的大幅提升使得主承力板的尺寸也相应增大,而光学系统复杂性的增加又提出了更高的结构稳定性要求。以某三反同轴相机为例,主承力板外包络尺寸由800 mm增加到2 m,尺寸稳定性要求则由0.01 mm提升到0.004 mm,使得零件关键部位的尺寸和形位公差达到IT0级甚至IT01级,这对检测精度提出了更高的要求。
大尺寸结构件的高精度平面度检测方法较多,主要有水平仪法、自准直仪法、光轴法、多测头误差分离法、干涉条纹拼接法、三坐标机测量法等[4]。Fujimoto等采用三点法测量450 mm直径圆晶平面度,精度达0.3 μm[5];Liu等使用蓝光传感器搭建测量系统测试陶瓷零件表面,精度高达20 nm[6];Chen等使用多光束角传感器测量镜面平面度,精度优于12 nm[7]。主承力板在完成机械加工以及稳定性试验前后需要进行多次平面度测试以及刮研修复,考虑到产品研制周期、检测时间、测量精度、经济成本以及现有可用设备情况,选择三坐标机测量法作为平面度检测方法。
文中提出了一种大尺寸高精度主承力板的平面度检测方法,将准运动学支撑方法引入到主承力板检测结构设计中,利用有限元仿真确定了主承力板水平放置时采用逆Bipod支撑结构形式,并优化卸载方案,显著降低主承力板检测时的变形。以某在研大口径相机为工程实例,对其2 m口径主承力板进行了多种工况下的平面度检测,检测误差小于2 μm,满足产品加工研制过程中的检测要求。
-
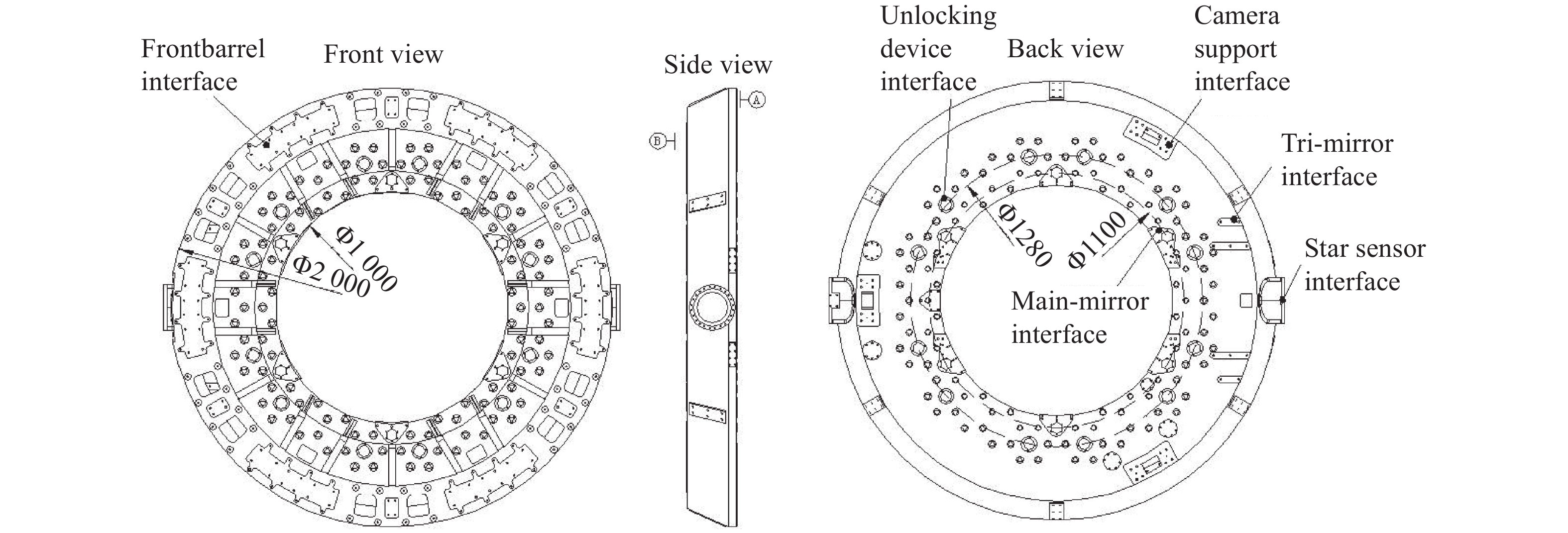
根据某大口径相机总体结构设计方案及部组件接口分布情况,结合主反射镜、前镜筒、三镜等主要光机部件的连接方式,考虑到结构的稳定性、对称性以及轻量化,主承力板采用台阶式圆盘状构型,如图1所示。主承力板使用C/SiC烧结成型,表面可进行刮研、铣磨等机械加工,可以获得较高的加工精度。主承力板外包络尺寸为2 000 mm×2 000 mm×230 mm,平均壁厚4 mm,重量90 kg,其对前镜筒安装接口环面(外径1900 mm、内径1600 mm)为基准面,背面六处凸台面组成的平面为工艺基准面,为满足系统使用要求,基准面精度要求见表1。
表 1 主承力板基准面精度要求
Table 1. Requirement of mainboard datum plane
Flatness error of front barrel mounting
interface (base A)Stability of base A’s
flatnessFlatness error of technological
datum (base B)Design requirement ≤0.012 mm ≤0.004 mm ≤0.02 mm -
三坐标机作为精密工程中广泛使用的测量仪器,目前大量应用于航天产品的检测工作,其精度一般可达微米级,按其结构形式可分为移动桥式、固定桥式、龙门式、悬臂式、立柱式等[8]。主承力板为薄壁圆盘状结构,径向刚度与轴向刚度差别大,检测时需要考虑不同放置状态下重力变形的差异。主承力板立式放置时,重力作用于被测面内,引起的法向变形很小,基本不会对平面度产生影响;而卧式放置时,重力与被测面垂直,会引起可观的法向变形,使得平面度恶化。利用有限元软件ABAQUS对此进行分析,编制Matlab程序进行后处理,去除刚体位移,计算基准面的PV值,作为平面度评价指标。从计算结果看,受重力影响,三点固支状态下,主承力板卧式放置时基准面PV值为6.8 μm,而立式放置时为0.25 μm,仅为前者的1/27。图2为主承力板立卧放置状态的重力变形对比。
然而,主承力板立式检测方案实施时受到几个因素的制约:首先,由于主承力板径向尺寸大,检测时竖直方向工作行程接近2.5 m,现有可用的桥式三坐标极限行程为1.5 m;其次,如图3所示,满足行程要求的龙门式三坐标,其测针不像桥式三坐标那样可以进行横向转接,由于测臂结构干涉,无法对直立面进行采点测量;再次,测针的接触力约为0.5 N,这相对于主承力板支撑点会产生一个弯矩,使之发生轻微变形,在零件不同位置采点时,采点处局部位移相差约0.3 μm;另外,主承力板重心高出测量台面超过1 m,若采用移动台面的测量设备,测量过程易会发生晃动,产生额外的测量误差。基于以上几点,结合现有设备的容纳能力,选择卧式放置的方案进行主承力板检测。根据仿真结果,三点固支状态下,卧式放置时重力造成的主承力板基准面平面度误差为6.8 μm,与产品所要求的平面度指标及稳定性指标在同一数量级,若能寻找一种适当的支撑方式,将重力变形降低到可接受的范围内,就可以满足使用要求。
-
主承力板平面度三坐标测量误差主要由下述几部分构成:
1)装配和装夹变形,记为U1。主承力板检测时需要通过使用支撑工装、搭压板固定、辅助粘接等方式与测量台面可靠连接,避免晃动。这会产生一些装配和装夹应力,应力通过结构传递到基准面上,会引起其平面度的变化;
2)重力变形,记为U2。主承力板轴向刚度相对较低,卧式放置时,非支撑部位对支点的重力矩会造成零件变形,此变形量与支撑结构的构型及布置方式有关;
3)设备误差,记为U3。即三坐标设备的工作误差,此部分误差由设备导轨精度以及环境决定。设备检定后,在控温控湿的试验室环境下,所选设备的工作误差可由公式(1)表示:
$${U_{\rm{3}}}{\rm{ = 1}}{.6 + L/600000}$$ (1) 式中:单位为μm,第一部分1.6 μm为系统误差,第二部分为与行程L相关的线量最大不确定度。当使用三坐标设备进行形状误差测量时,U3只取决于系统误差[8]。
分析上述三项误差的产生机理可知,U1~U3互不相关,系统测量误差U0可表示为:
$${U_{\rm{0}}} = \sqrt {\mathop \sum \nolimits_{{\rm{i = 1}}}^{\rm{3}} U_{\rm{i}}^{\rm{2}}} $$ (2) 由计量和检测相关行业标准及工程经验可知,测量误差评估值应小于被测值不确定值的1/4[9]。根据表1所列要求,主承力板基准面平面度要求为U≤0.012 mm,则测量误差U0应小于3 μm。式(2)中
$ {U_{\rm{3}}}{\rm{ = 1}}{\rm{.6\;\mu m}}$ ,U1、U2分别由检测时的装配装夹状态和支撑结构确定。 -
在力学上,根据约束状态不同可以将结构支撑分为不稳定支撑、运动学支撑、冗余支撑和准运动学支撑。运动学支撑的特点是,被支撑件所有的刚体运动刚好被完全限制,没有冗余,因此不需要知道支撑结构本身的刚度就可以求解出所有支撑点处的支反力;当环境温度变化、支撑结构运动、支撑结构间存在装配误差等情况时,被支撑件只会产生刚体位移,内部不会产生应力变化,即不会产生弹性变形。冗余支撑的结构通常存在较大的内应力,且对装配敏感。在工程应用中,由于摩擦、间隙、局部变形等因素的影响,绝对理想的运动学支撑难以实现,通常使用弱化约束的准运动学支撑来替代运动学支撑[10]。通过适当的结构设计,在运动学支撑的基础上增加少量的冗余,可以实现高精度零件的准运动学支撑。采用准运动学支撑方法,可以大幅减小主承力板检测时装配和装夹变形带来的误差。
基于Bipod (二脚架)的三点支撑结构,是一种最常用的准运动学支撑结构形式[11-12],根据其连接方式的不同,可以分为正Bipod和逆Bipod。相同条件下,选用逆Bipod构型可以将载荷分散到更多的连接点上,有利于降低主承力板的应力水平和自重变形,但装配环节相对复杂,需要通过一定的工艺方法来进行优化。
-
研究表明,无中心孔实体反射镜径向三点支撑时,最佳环向支撑位置在0.6R~0.65R之间,其中R为反射镜半径[13]。主承力板中心有一个半径0.5R的中心孔,且截面结构呈台阶状,因此其最佳支撑位置将更加靠近外边缘。为保持对称性,逆Bipod的六个支撑点应呈60°均布,从图1可以看出,在不引入辅助结构进行转接的情况下,主承力板背面可用作连接点位置的只有解锁机构安装点和主镜安装点两处,前者分布半径为0.64R,后者为0.55R。根据经验选用解锁机构安装点作为主承力板检测时的支撑接口[14-15]。
采用易装配的自润滑关节轴承作为Bipod两端的柔性环节,可减少Bipod两端的弯曲和剪切刚度冗余,实现准运动学支撑。如图4所示,Bipod两端的上、下铰板分别与主承力板及测试底板相连,扩展角取90°,轴向刚度由可调金属杆提供。装配时,应先连接上铰板与主承力板,然后通过关节轴承调整金属杆的指向,微调各组Bipod的杆长,最后连接下铰板与测试底板,以降低主承力板与检测结构间的装配应力水平。
主承力板重量90 kg,存在偏载情况下,三组Bipod下端连接点处的载荷不会超过500 N。选取GEEW14T型向心关节轴承,该轴承径向额定静载荷为128 kN,轴向额定静载荷为53 kN,静力安全裕度大于100。在扩展角90°构型下,按支撑点载荷500 N估算,金属杆轴向压力
$ {F}_{\rm{N}} $ 为346 N。金属杆横截面为外径30 mm,内径20 mm的圆环,材料为不锈钢304,其杨氏模量E为194 GPa,屈服强度${\sigma _{0.2}} $ 为205 MPa。按式(3)算得,截面正应力为0.22 MPa,远低于屈服强度。金属杆设计长度l为420 mm,按欧拉公式(4)进行压杆稳定性校核,得到分叉载荷${F_{{\rm{Pcr}}}}$ = 5541 kN,安全裕度大于15000。$${\sigma _{\rm{x}}}{\rm{ = }}{F_{\rm{N}}}{\rm{/}}\pi {\rm{(}}{{r}_{\rm{1}}}^{\rm{2}}{\rm{ - }}{{r}_{\rm{2}}}^{\rm{2}}{\rm{)}}$$ (3) $${F_{{\rm{Pcr}}}}{\rm{ = }}\frac{{{{\rm{\pi }}^{\rm{2}}}{EI}}}{{{{{(\mu l)}}^{\rm{2}}}}}$$ (4) 式中:I为截面对其形心主轴的惯性矩,对于圆管,
$I{\rm{ = }}\dfrac{{{\rm{\pi (}}{{\rm{r}}_{\rm{1}}}^{\rm{4}}{\rm{ - }}{{\rm{r}}_{\rm{2}}}^{\rm{4}}{\rm{)}}}}{{\rm{4}}}$ ;μ为长度系数,对于两端铰支的杆件,取值为1。 -
如2.1节所述,
$ U_{\rm{1}} $ 由检测结构装配以及测试时的装夹造成,可由公式(5)表示。$${U_1}{\rm{ = }}\sqrt {{\rm{6}}U_{{\rm{11up}}}^{\rm{2}}{\rm{ + }}U_{{\rm{11down}}}^{\rm{2}}{\rm{ + }}U_{{\rm{12}}}^{\rm{2}}} $$ (5) 式中:
$ U_{\rm{11up}} $ 为单处上铰板与主承力板装配引起的误差;$ U_{\rm{11down}} $ 为下铰板固定带来的误差;$ U_{\rm{12}} $ 为装夹造成的误差。建立有限元模型,评估公式(5)中的各误差项。主承力板采用壳单元S4R模拟,Bipod的挠性主结构使用梁单元B31模拟,Bipod两端的柔性使用ABAQUS特有的Connector连接器模拟,各连接器释放所有的转动自由度,只约束平动自由度。分析下铰板装配带来的误差时,模型中不加入测试底板,下铰板底角固支作为位移边界条件。分析装夹带来的误差时,下铰板与测试底板固连,约束测试底板作为边界条件,各约束点分布和定义如图5所示。

图 5 装配及装夹分析约束点位置分布
Figure 5. Constrain points location distribution of assembly and clamping analysis
根据检测结构的装配过程,三组Bipod首先通过上铰板与主承力板连接,由于装配面之间的平面度误差,此过程会产生强迫位移。上铰板平面度加工公差为0.012 mm,主承力板相应局部区域平面度公差为0.015 mm,考虑工程余量,假设该强迫位移为0.03 mm,算得
$ {U}_{\rm{11up}} $ 为1.5 nm。各支杆长度及角度调整完毕后,组件与测试底板相连,由于杆件长度偏差以及装配面局部的平面度误差,此连接过程同样存在强迫位移,考虑现有的加工及装配精度,保守估计此位移在三个方向上均达到2 mm,通过强迫位移产生位置的组合形成一系列计算工况,算得$ {U}_{\rm{11down}} $ 最大不超过18 nm,各工况计算结果见表2。表 2 下铰板强迫位移计算结果
Table 2. FEA results of forced displacement on down linkboard
Load region
(Point index)Flatness error of
base A/nm(PV)Load region
(Point index)Flatness error of
base A/nm(PV)1,2 12.66 1,2,5,6 17.34 3,4 16.14 1,4,5,6 14.04 1,2,3,4 13.42 1,2,3,4,5,6 14.99 1,4,5,8 14.05 1,2,3,4,7,8 13.86 根据主承力板尺寸及重量,三坐标测试时选择在测试底板表面均布三处压板进行装夹,装夹过程中测试底板的变形可以抽象为强迫位移的形式,仍然假定位移值为2 mm,各种不同的组合工况下,算得
$ {U}_{\rm{12}} $ 不超过14 nm,结果如表3所示。由公式(5)可得,U1<25 nm。表 3 装夹变形计算结果
Table 3. FEA results of clamping deformation
Load region
(Point index)Flatness error of base A/nm(PV) Load region
(Point index)Flatness error of base A/nm(PV) A,D 11.07 A,D,G,H 12.77 B,C 13.16 B,C,G,H 12.75 A,B,C,D 11.26 A,B,C,D,E,F 13.04 A,D,E,F 11.06 A,B,C,D,G,H 12.28 -
现已求得
${U_{\rm{1}}}{\rm{ < 0}}{\rm{.025}}\;{\rm{\mu m,}}\;{U_{\rm{3}}}{\rm{ = 1}}{\rm{.6}}\;{\rm{\mu} m}$ ,由公式(2)可得${U_{\rm{2}}} \le {\rm{2}}{\rm{.536}}\;{\rm{\mu m}}$ 时,$ {U_{\rm{0}}} \le {\rm{3}}\;{\rm{\mu m}}$ ,即重力变形造成的基准面平面度误差不得超过2.536 μm。通过仿真结果看,在现有构型下,${U_{\rm{2}}}{\rm{ = 2}}{\rm{.9}}\;{\rm{\mu m}}$ ,不满足上述要求,需要进一步对检测结构进行优化。主承力板为非完全轴对称结构,在重力场下,两端星敏接口结构的重量相对支撑环会形成一个向下的弯矩,使得主承力板前端面出现两端“下沉”、中心“拱起”的一阶弯曲状态,如图6、图7所示,若能减小此弯矩,就能改善基准面变形情况。为便于计算比对,将卸载点布置在主承力板背面的中心线上,只考察卸载力大小及施力点水平距离的影响。从图8的结果看,施力点离中心点越远,需要的卸载力越小,而各组曲线的最低值均在1.15~1.2 μm之间,差别不大。为保护正样产品,降低卸载点局部的应力水平,施力点尽量选在布有加强筋的位置,并远离中心点。图9中所示位置距中心点820 mm,为环筋与横筋交汇处,刚度最好且便于实施,在此处施加4处大小为10 N的集中力,此时${U_{\rm{2}}}{\rm{ = $ $ 1}}{\rm{.17}}\;{\rm{\mu m}}$ ,由公式(2)算得,${U_0}{\rm{ = 1}}{\rm{.99}}\;{\rm{\mu m}}$ 。 -
在上述计算及分析结果的基础上,进行了主承力板检测结构的加工及装配。根据零件检验结果,主承力板与上铰板连接处局部平面度为0.02 mm,上铰板相应区域平面度最差为0.009 mm;下铰板与测试底板连接前用塞尺确定各处间隙,最大为0.25 mm;主承力板就位后,用三个等高块垫起测试底板,测得测试底板与等高块接触区域间隙最大值为0.37 mm。根据以上数据进行仿真,得到
$ {U_{\rm{1}}}<8\;{\rm{nm}}$ 。主承力板基准面刮研、消应力试验及稳定性试验前后,均使用该结构进行了基准面平面度三坐标检测,如图10所示。在检测过程中,对检测结构的设计有效性进行了验证,从图11的结果看,在改变测试底板装夹状态时,测得基准面的平面度变化量在三坐标设备误差范围内,说明检测结构能有效的隔离装配和装夹应力;撤除卸载力后,基准面平面度变差,与仿真计算结果相符。目前,检测合格后的主承力板已经交付整机使用,主要光学部件与之装配后无异常变形情况,符合设计预期。
-
文中以某在研大口径相机主承力板检测问题为背景,提出了使用准运动学支撑方式对大尺寸高精度关键结构件进行支撑的方法,来解决零件检测过程中的重力变形问题。根据主承力板的结构特点和指标要求,结合现有测量设备的容纳能力,比对相应的仿真分析结果,最终选定了基准面平面度检测方案。通过对检测误差的详细分析,设计了主承力板检测结构工装,并确定卸载方案,使得主承力板平面度检测误差优于2 μm。该工装加工要求不高,成本低廉,装配简单易行,容错性好,从各研制环节中主承力板检测结果看,检测误差符合设计预期。
此方法适用于大尺寸扁平结构上高精度基准面的三坐标卧式检测,在大型空间相机口径普遍升级到1.5 m以上量级的情况下,拓展了现有三坐标设备的检测能力,有广泛的实际使用价值。
Design and error analysis of measurement structure for large aperture space camera mainboard
-
摘要: 主承力板作为空间相机的核心承力部件,需要具备极高的尺寸精度和结构稳定性,常规的检测方法和装夹方式无法满足产品使用要求。根据某大口径相机主承力板的结构形式和指标要求,结合现有测量设备的容纳能力,选择了卧式放置的方式进行关键部位的平面度检测;引入准运动学支撑概念,主承力板使用3个逆Bipod支撑以避免装夹变形及装配变形,设计并制造了专用检测结构;以主承力板基准面PV值为评价指标,使用ABAQUS有限元软件和Matlab软件进行仿真计算,确定检测时的卸载力位置和大小。实验结果表明,使用检测结构得出的基准面平面度检测误差小于2 μm,提升了三坐标设备的检测能力,有广泛的应用前景。Abstract: High precision and stability are demanded for mainboard as a core construction of high resolution space camera, thus, traditional measurement methods could not match the application requirements. According to the structure and specification of the mainboard used in a large aperture camera and the capability of measurement equipment, horizontal placement was adopted for flatness test of mainboard datum plane using gantry coordinate measuring machine (CMM). The concept of quasi-kinematic mount was introduced, the mainboard was supported by 3 inverted Bipods to avoid clamping and assembly deformation, a specialized measurement structure was designed and manufactured as well. The position and magnitude of unloading force were confirmed by numerical simulation based on ABAQUS and Matlab with an index of datum plane's flatness error (PV). The results show that using designed measurement structure datum plane's flatness error is less than 2 μm. This method promotes the capability of CMM for measurement of large precise objects and has widely application prospect.
-
Key words:
- mainboard /
- quasi- kinematic mount /
- inverted Bipod /
- measurement structure
-
表 1 主承力板基准面精度要求
Table 1. Requirement of mainboard datum plane
Flatness error of front barrel mounting
interface (base A)Stability of base A’s
flatnessFlatness error of technological
datum (base B)Design requirement ≤0.012 mm ≤0.004 mm ≤0.02 mm 表 2 下铰板强迫位移计算结果
Table 2. FEA results of forced displacement on down linkboard
Load region
(Point index)Flatness error of
base A/nm(PV)Load region
(Point index)Flatness error of
base A/nm(PV)1,2 12.66 1,2,5,6 17.34 3,4 16.14 1,4,5,6 14.04 1,2,3,4 13.42 1,2,3,4,5,6 14.99 1,4,5,8 14.05 1,2,3,4,7,8 13.86 表 3 装夹变形计算结果
Table 3. FEA results of clamping deformation
Load region
(Point index)Flatness error of base A/nm(PV) Load region
(Point index)Flatness error of base A/nm(PV) A,D 11.07 A,D,G,H 12.77 B,C 13.16 B,C,G,H 12.75 A,B,C,D 11.26 A,B,C,D,E,F 13.04 A,D,E,F 11.06 A,B,C,D,G,H 12.28 -
[1] 郭疆, 朱磊, 赵继, 等. 大口径空间反射镜大容差支撑结构设计与优化[J]. 光学 精密工程, 2019, 27(5): 1138-1147. doi: 10.3788/OPE.20192705.1138 Guo Jiang, Zhu Lei, Zhao Ji, et al. Design and optimize of high tolerance support structure for large aperture space mirror [J]. Optics and Precision Engineering, 2019, 27(5): 1138-1147. (in Chinese) doi: 10.3788/OPE.20192705.1138 [2] 翟岩, 梅贵, 江帆, 等. φ2020 mm口径空间红外相机主反射镜设计[J]. 发光学报, 2018, 39(8): 1170-1176. doi: 10.3788/fgxb20183908.1170 Zhai Yan, Mei Gui, Jiang Fan, et al. φ2020 mm aperture space infrared camera main reflector design [J]. Chinese Journal of Luminescence, 2018, 39(8): 1170-1176. (in Chinese) doi: 10.3788/fgxb20183908.1170 [3] 姜海滨, 罗世魁, 曹东晶, 等. “高分二号”卫星轻小型高分辨率相机技术[J]. 航天返回与遥感, 2015, 36(4): 25-33. Jiang Haibin, Luo Shikui, Cao Dongjing, et al. Technology of high-density and high-resolution camera of GF-2 satellite [J]. Spacecraft Recovery & Remote Sensing, 2015, 36(4): 25-33. (in Chinese) [4] 陈宝刚, 邵亮, 李剑锋. 大直径窄环带平面平面度的精确测量[J]. 光电工程, 2015, 42(8): 14-19. doi: 10.3969/j.issn.1003-501X.2015.08.003 Chen Baogang, Shao Liang, Li Jianfeng. Precise measurement of flatness for large diameter narrow zone annular plane [J]. Opto-electronic Engineering, 2015, 42(8): 14-19. (in Chinese) doi: 10.3969/j.issn.1003-501X.2015.08.003 [5] Fujimoto I, Nishimura K, Takatsuji T, et al. A technique to measure the flatness of next-generation 450mm wafers using a three-point method with an autonomous calibration function [J]. Precis Eng, 2012, 36: 270-280. doi: 10.1016/j.precisioneng.2011.11.001 [6] Liu Chienhung, Lin Binhung. Development of a nanometer resolution flatness measurement system for the ceramic surface by using Blue-ray optical pickup [J]. Microsystem Technologies, 2013, 19(11): 1817-1821. doi: 10.1007/s00542-013-1805-0 [7] Chen Meiyun, Takahashi Satoru, Takamasu Kiyoshi. Multi-beam angle sensor for flatness measurement of mirror using circumferential scan technology [J]. International Journal of Precision Engineering and Manufacturing, 2016, 17(9): 1093-1099. doi: 10.1007/s12541-016-0133-6 [8] 张国雄. 三坐标测量机[M].天津: 天津大学出版社, 1999. Zhang Guoxiong. Coordinate Measuring Machines[M]. Tianjin: Tianjin University Press, 1999.(in Chinese) [9] 装备计量保障通用要求检测和校准[S]. GJB 5109-2004. General requirement of metrology support for military material Test and calibration[S]. GJB 5109-2004. [10] 道尔 凯斯 B, 基恩伯格 维克托 L, 迈克尔斯 第2版. 格雷戈里 J. 光机集成分析[M]. 连华东, 王小勇, 徐鹏, 译. 北京: 国防工业出版社, 2015. Doyle K B, Genberg V L, Michels G J. Integrated Optomechanical Analysis[M]. Lian Huadong, Wang Xiaoyong, Xu Peng,Translated. 2nd ed, Beijing: National Defense Industry Press, 2015.(in Chinese) [11] Toulemont Y, Passvogel T, Pilbratt G L, et al. The 3.5-m all-SiC telescope for Herschel[C]//Proc of SPIE, 2004, 5487: 1119-1128. [12] Denis Fappani. Manufacturing & control of the spherical mirrors for the telescope of the French satellite Pleiades[C]//SPIE, 2007, 6687: 1-11. [13] Yoder P R. 光机系统设计[M]. 周海宪, 程云芳, 译. 第三版, 北京: 机械工业出版社, 2008. Yoder P R. Opto-Mechanical Systems Design[M]. Zhou Haixian, Cheng Yunfang,Translated. 3rd ed, Beijing: China Machine Press, 2008.(in Chinese) [14] 王成彬, 孙胜利, 胡亭亮, 等. 高精度反射镜组件面形检测结构设计方法[J]. 红外与激光工程, 2016, 45(1): 0117006. Wang Chengbin, Sun Shengli, Hu Tingliang, et al. Design method of high precision reflection mirror topography measurement structure [J]. Infrared and Laser Engineering, 2016, 45(1): 0117006. (in Chinese) [15] 安源, 贾学志, 张雷, 等. 基于碳纤维复合材料的空间相机高比刚度主承力板优化设计[J]. 光学 精密工程, 2013, 21(2): 416-422. doi: 10.3788/OPE.20132102.0416 An Yuan, Jia Xuezhi, Zhang Lei, et al. Optimizing design of CFRP based main backbone with high stiffness ratio for space camera [J]. Optics and Precision Engineering, 2013, 21(2): 416-422. (in Chinese) doi: 10.3788/OPE.20132102.0416 -






 下载:
下载: