-
自适应光学( adaptive optics,AO)技术对于提高光学系统性能具有重要作用[1]。一个典型的自适应光学系统包含波前探测、信号处理、波前校正等环节。当波前探测器(如哈特曼传感器)和波前校正器(如变形镜)具有更多单元数时,有助于提升AO的校正效果[2]。而随着单元数的增多,AO系统易受外部环境干扰与系统内部不确定因素影响,造成系统失稳[3],AO系统工作在失稳状态会影响系统的校正效果,甚至威胁系统安全[4]。
为降低外部扰动影响,保证AO系统稳定闭环,一般会根据应用场景调整控制器性能。当目标信号存在干扰时,通过稳定性分析得到稳定性判据,并依此调整控制器参数提高系统的误差带宽,保证系统稳定[5]。但对于复杂的工作环境与可能出现的不确定因素,控制回路不能及时更新参数,会造成系统无法稳定运行,校正后波前难以预测,影响系统中其他设备安全[6]。为保证系统安全,有必要对系统是否失稳进行实时检测。
AO系统失稳检测首先需要对系统正常工作时的信号回路进行分析,找到其中的不稳定因素。通过故障树方法进行列表查询能够实现全面检测[7],但因为系统自身集成了较多器件和单元,为提高反应速度,需要找到其中威胁系统核心部件的因素,并对经常出现的失稳因素进行主要研究。AO系统中波前探测器较敏感,波前校正器中变形镜(deformable mirror,DM)价值高且易损伤,这两个环节将作为重点监测对象。对探测器状态的检测有根据有效光斑孔径数通过神经网络提供开闭环决策[8],以及根据缺光孔径构建0-1故障模型[6]等。而对DM的监测多集成在波前控制环节中,考虑到其自身结构特性[9],有必要对其进行单独检测。
为获取AO系统不同失稳类型的异常数据,一方面需要在实际应用中采集异常数据进行分析,这需要额外的数据存储装置,实际系统中已有2.5 kHz数据记录仪对系统校正过程中的斜率电压数据进行记录,在数据记录仪主机上进行失稳检测可以不干扰校正过程。另一方面则可以通过建立对应AO系统仿真模型,经过对失稳情况进行仿真获得异常数据。国内外已经针对AO系统正常闭环开发了多款仿真平台[10-11],在已有研究基础上进行失稳仿真能近似实际系统运行情况。
利用获得的异常数据,检测失稳时可以使用不同算法进行效果对比。在设备异常检测方面,基于聚类[12]、最近邻[13]、时间序列分析[14]等机器学习方法都获得过较好的检测效果[12-13],为文中研究提供了思路。
基于上述问题,文中搭建了一套127单元AO系统失稳仿真平台以获取异常数据,并基于DM电压使用不同检测方法对系统失稳状态进行检测。
-
对于自适应光学系统,在设计时已经对系统的响应频率、控制带宽进行了理论分析,并得到大概的工作范围。但在实际应用时,需要对系统状态进行实时观测,尤其是工作环境中的不确定因素干扰,可能使系统从稳定状态开始波动,甚至达到系统极限,这对系统安全造成极大挑战。
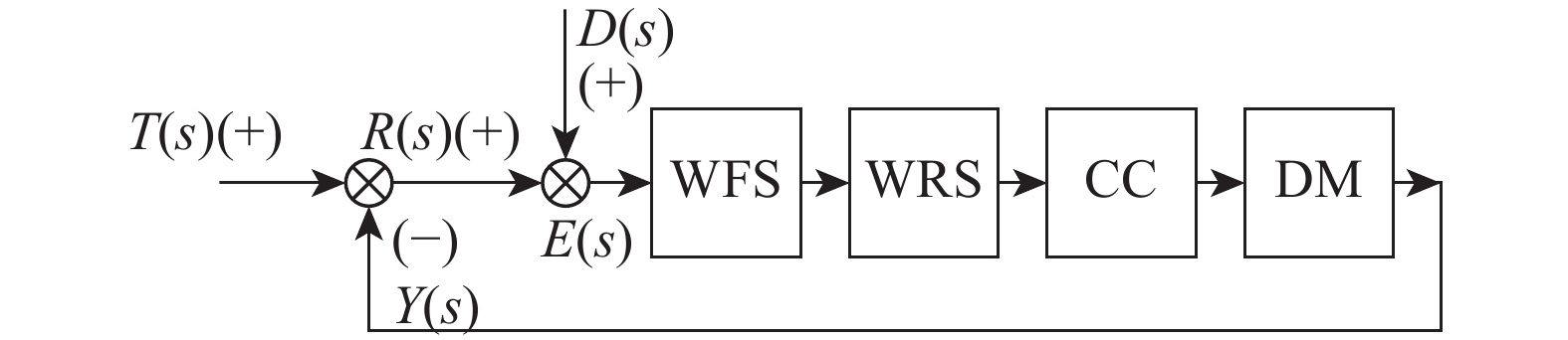
系统闭环结构如图1所示,图中T(s)为输入湍流波前,R(s)为残差波前,D(s)为干扰相差,E(s)为探测波前,Y(s)为校正镜组面型。通过分析发现AO系统中最易受到干扰的是波前传感器。当传感器出现异常时,直接影响系统的工作状态。最需要关注的是校正镜组,当校正镜组出现异常时,直接威胁到系统安全。结合实际应用中遇到的问题,建立AO系统控制回路异常状态表(如表1所示)。
表 1 自适应光学系统闭环异常状态表
Table 1. Close loop abnormal states of adaptive optical system
AO system components Abnormal phenomenon Possible causes Hartmann wavefront sensor Subaperture lack of light The spot intensity is too low to be detected Obstacles block light path Incomplete wavefront caused by pupil deviation Sub-spot saturation The spot intensity is higher than the sensor threshold The slope of subaperture changes sharply Stray light interference Background noise interference The light source flickers Mutation of work environment Sub-spot jitter Light source jitter Work platform jitter Closed-loop overshoot Overall slope mutation Optical axis offset Deformable mirror Control voltage saturation Aberrations are too large Drive units failure Control voltage oscillation Closed-loop overshoot Control voltage burr Drive unit exception Excessive voltage difference between local control units Mismatch between DM and sensor 从表1中发现,实际应用过程中,斜率异常状态大多与工作环境相关。当工作环境稳定时,通过调整光路,调试设备使系统正常工作。当工作环境发生突变时,无法通过正常方式根据斜率准确复原波前,系统无法正常工作,需要重新调试设备或等待工作环境好转使系统状态恢复。如果将AO系统失稳的检测放在哈特曼探测环节,斜率变化灵敏,但有可能将部分外界扰动误认为系统失稳,造成频繁报警。
除了斜率异常外,表1还分析了校正镜组中DM控制电压的异常状态。DM作为AO系统校正波前像差的核心部件,在闭环工作时,DM 面形受系统回路中的静态像差、待校正动态像差以及干扰噪声等多种因素影响。如果将AO系统失稳检测放在DM校正环节,通过控制电压对实际面型进行评估,则可以排除控制器已经滤除的干扰,只针对造成DM无法正常工作的情况(即失稳)进行检测。此时,失稳检测在控制环节计算控制电压后,DM驱动器执行前,可以有效保护系统安全。
文中选择对DM失稳进行检测,首先对DM失稳因素进行分析仿真,但在多种因素共同影响下,传统方法难以准确区分有用信号与失稳信号,给失稳因素的分析带来困难。为了仿真DM的失稳过程,文中结合DM自身结构特性,将DM失稳过程进行数值化处理,对4类主要失稳类型下DM控制电压变化进行仿真,如表2所示。
表 2 4类DM失稳仿真过程
Table 2. Four kinds of DM instability simulation process
Idx Instability phenomenon Simulation process Asets1 Control voltage saturation Let several random drive voltages reach the threshold Asets2 Control voltage oscillation Let the voltage difference between adjacent frames of several random
drivers exceed the normal rangeAsets3 Control voltage burr Keep several random drive voltages in the high range Asets4 Excessive voltage difference between
local control unitsThe random driver voltage is kept high, and the adjacent driver voltage is kept low -
文中用Easylaser平台仿真一套127单元AO系统,使用112孔径哈特曼探测器(探测波长633 nm,采样率2 500 Hz),单元布局见图2。仿真AO系统使用直接斜率法复原波前,通过PI控制器计算控制电压。使用符合柯尔莫哥洛夫理论的冻结大气长相屏作为系统输入大气湍流数据。仿真系统控制器原理见图3。
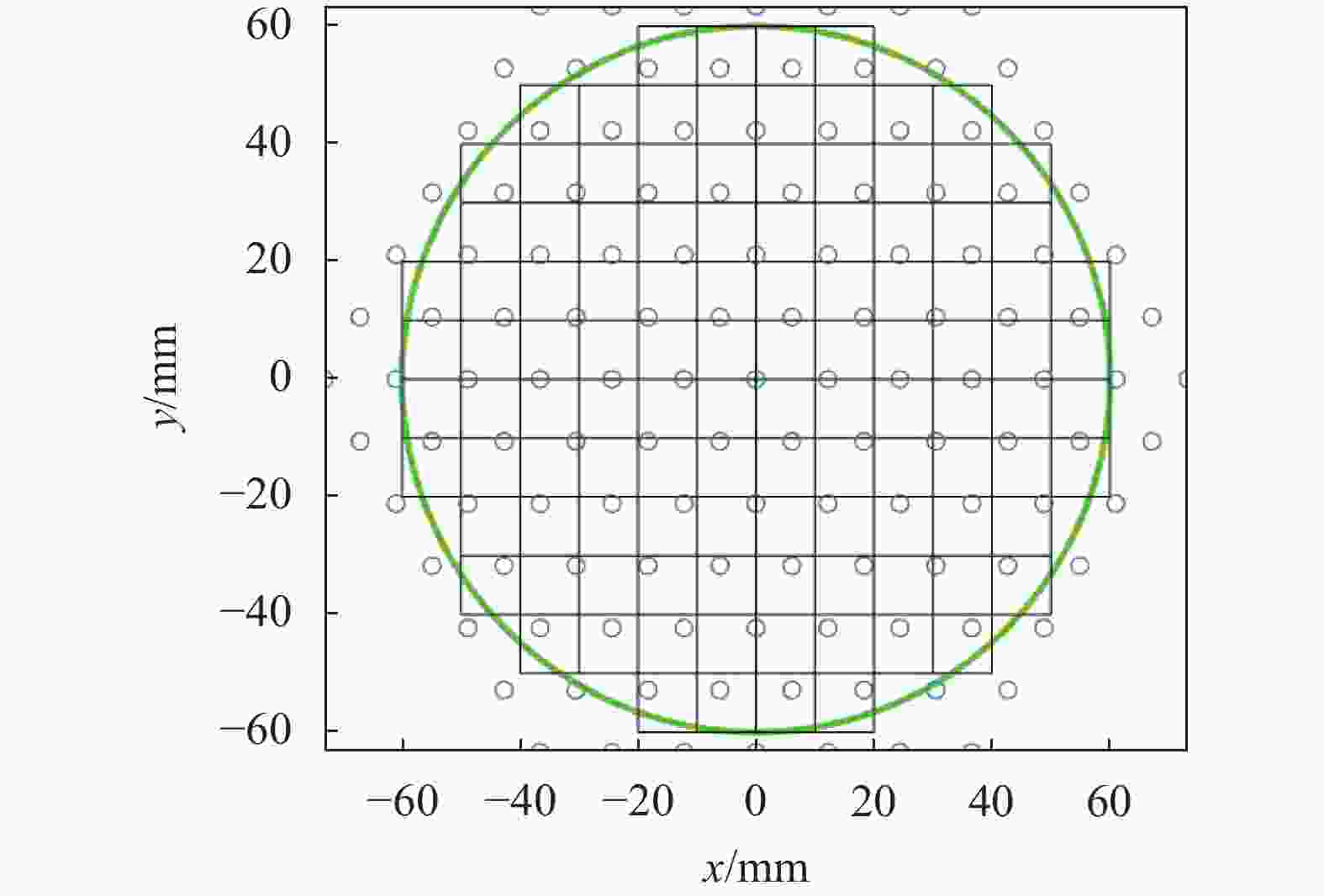
图 2 仿真系统子孔径分布与驱动器单元布局
Figure 2. Sub apertures distribution and driver units layout of simulation system
根据自适应光学理论,探测器检测到输入波前,通过微透镜阵列在CCD图像上呈现子光斑图像,使用质心提取算法获得波前斜率Gx,Gy,分别为:
$$\left\{ {\begin{array}{*{20}{c}} {{G_x} = \dfrac{{\displaystyle\sum_i {\sum\limits_j {{T_{xj}}{I_{ij}}} } }}{{\displaystyle\sum_i {\sum\limits_j {{I_{ij}}} } }}} \\ {{G_y} = \dfrac{{\displaystyle\sum_i {\sum\limits_j {{T_{yj}}{I_{ij}}} } }}{{\displaystyle\sum_i {\sum\limits_j {{I_{ij}}} } }}} \end{array}} \right.$$ (1) 使用直接斜率法,根据DM影响函数矩阵
${A_{v2g}}$ ,可计算得到复原电压。$$\left\{ {\begin{array}{*{20}{c}} {G = {A_{v2g}}{\rm{ }} \times V}\\ {V = A_{v2g}^ + {\rm{ }} \times G} \end{array}} \right.$$ (2) 复原电压通过控制器得到控制电压。复原计算过程存在时间延迟τ,大约为两倍采样时长
$\tau \approx 2T$ 。控制器使用积分控制时,转化为如下差分方程:
$$\left\{ {\begin{array}{*{20}{c}} {e(k) = u(k) - y(k - 2)}\\ {y(k) = 0.18 \times e(k - 1) + y(k - 1)} \end{array}} \right.$$ (3) 此时控制电压施加在DM上,通过影响函数计算DM面型,与此时刻湍流波前像叠加,获得的残差波前再次进入探测器,完成下一次校正计算。仿真过程整体流程如图4所示。
-
AO系统在闭环状态下出现的异常主要与DM异常相关,如不及时反应则会造成严重后果。此节针对闭环AO系统,分析斜率和电压这两种信号异常时进行的失稳信号仿真,方案如下:
(1) 在正常湍流波前输入下,运行仿真系统,得到正常的闭环运行电压和斜率数据,标记为正常数据集Nsets。
(2) 对正常闭环运行过程中施加不同程度的干扰,获得异常的运行数据,标记为异常数据集Asets。
通过Easy laser获得了畸变波前,将其作为输入经过仿真AO系统处理,获得正常情况下的闭环数据集Nsets,如图5所示。
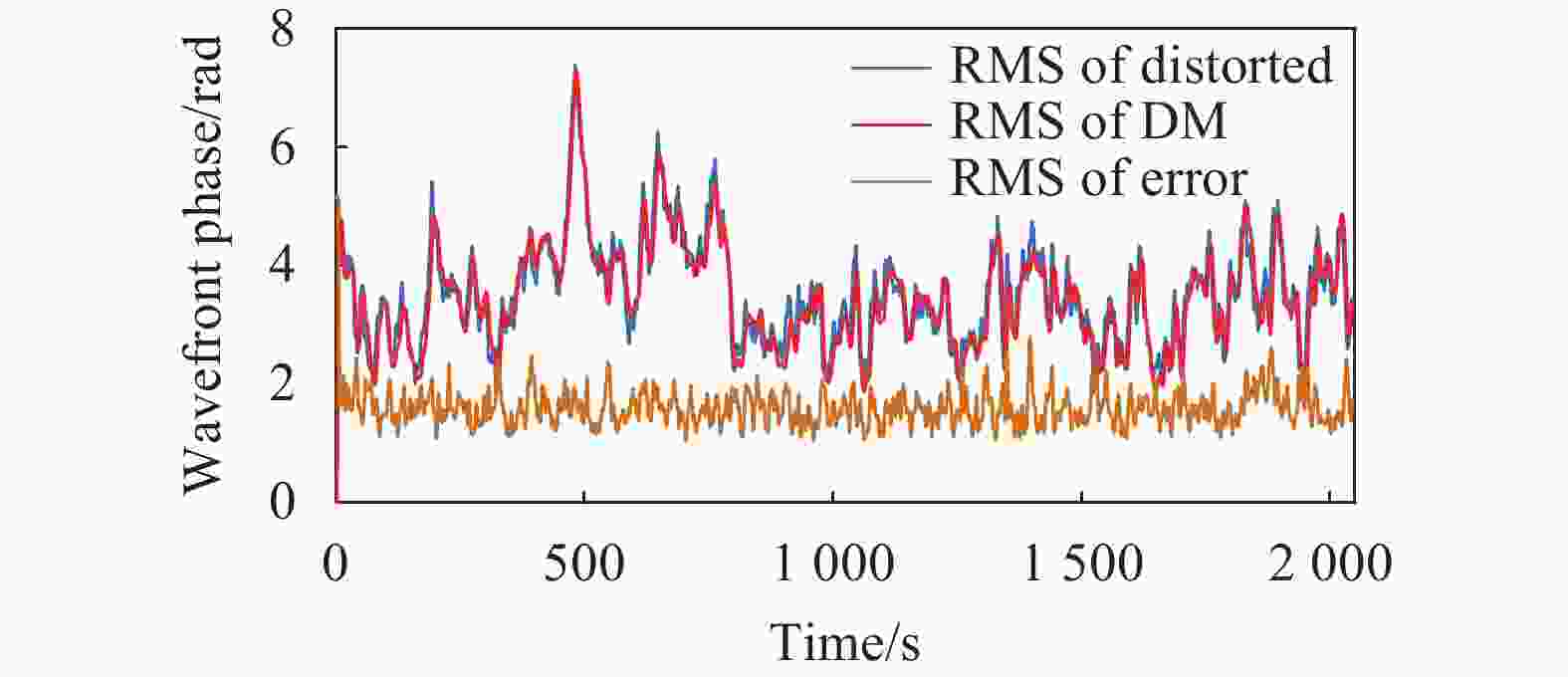
图 5 正常闭环运行时畸变波前、残差与补偿面型RMS
Figure 5. RMS of residual,distorted and compensating surface in normal closed-loop operation
正常闭环时观察DM面型斜二测画法直观图,发现表面平滑,其控制电压RMS曲线也是一条平滑的曲线,如图6所示。
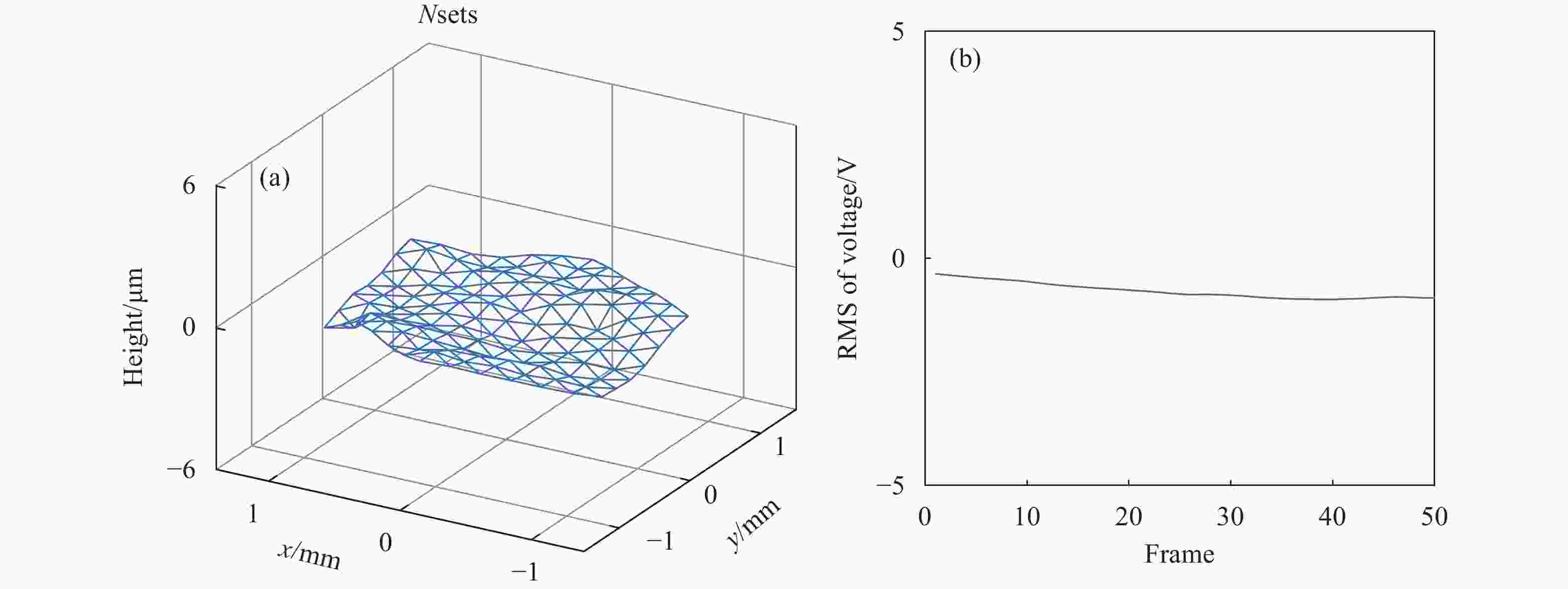
图 6 正常闭环运行时DM面形与控制电压RMS曲线
Figure 6. DM appearances and RMS curves of control voltage in normal closed loop operation
下面需要对可能存在的干扰造成的数据异常进行仿真,在1.1节中,分析了系统运行时可能出现的不确定异常,个别单元出现饱和点,可能是个别单元故障;个别单元的剧烈波动,可能是系统受到外部扰动或系统自身参数改变引起的超调;某个区域内单元出现拉扯,可能是受到外部扰动引起失配。
因此文中通过仿真随机单元数值饱和,模拟单元故障(Asets1);仿真部分随机单元时间序列剧烈波动模拟系统震荡(Asets2);特别的,对于长时间处于异常临界的单元,若持续过久也有可能存在隐患(Asets3);最后仿真区域性扰动引起的系统不稳定,例如哈特曼-DM间可能存在的耦合干扰(Asets4)。分别记录DM电压在4类失稳情形下的闭环数据,将获得4组失稳数据。
图7中绘制了选定的异常单元电压曲线,前25帧为正常闭环过程数据,后25帧为失稳状态时的电压。
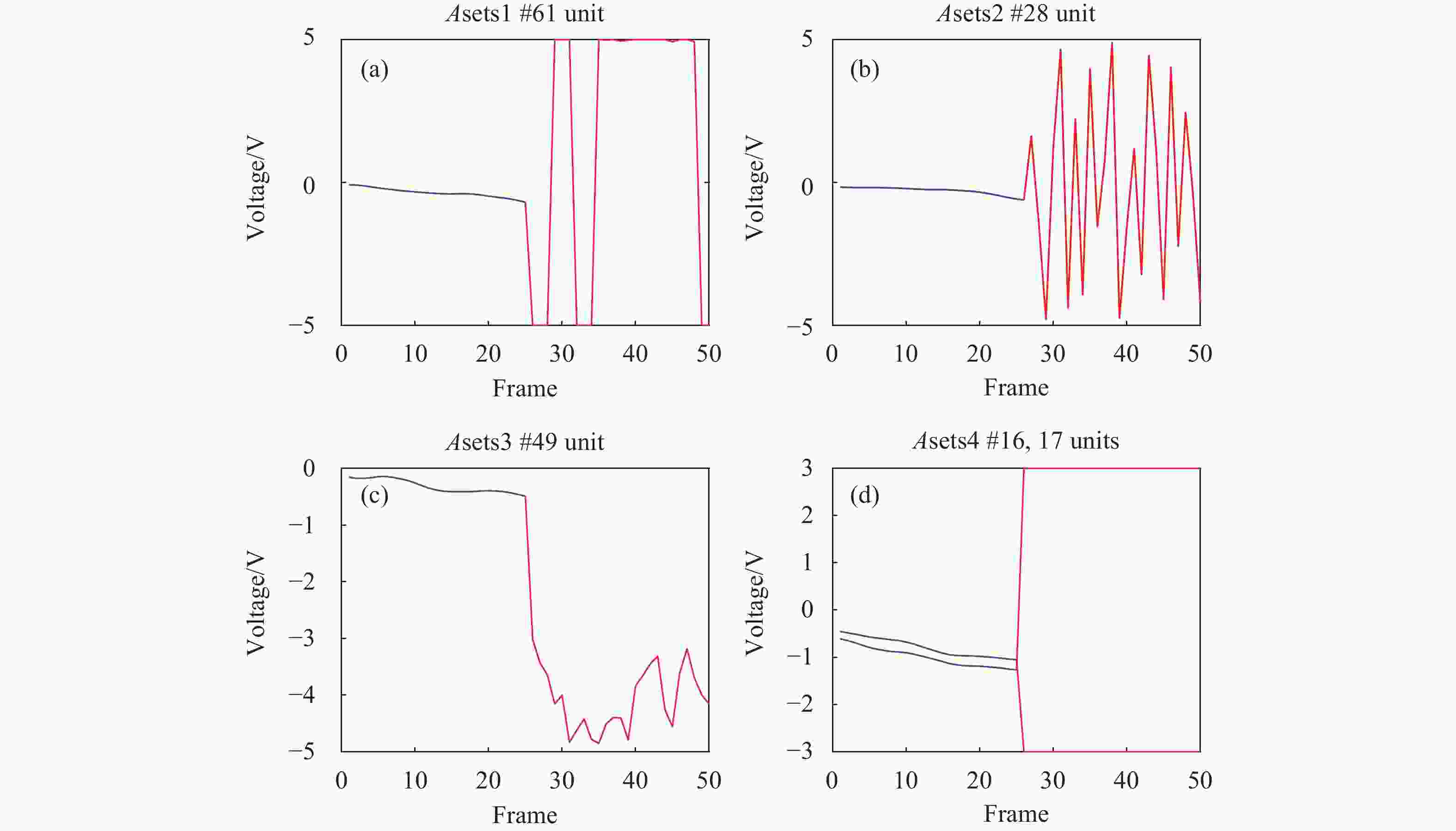
图 7 DM控制电压4类失稳情形异常单元的电压曲线
Figure 7. Voltage curves of abnormal unit under four types of DM control voltage instability
此外,不同类型失稳对系统产生影响的时间也有差别,因此对每种异常的引入持续不同时间,在2 500 Hz的采样频率下,失稳分别持续25、100、250帧对样本进行扩展。即将闭环过程分为3种时间长度,每种时间长度下都会经历一段正常运行后,加入异常。在一组校正数据中,可以扩展得到15组正常与异常样本。
图8中Asets1绘制了在驱动器电压饱和时的失稳电压RMS,对比3种时间发现受一场持续时间影响较小,一旦出现此类异常,系统立即受到影响。Asets2绘制了在驱动器震荡时的失稳电压RMS,观察可以发现,RMS曲线震荡剧烈,代表DM面型发生剧烈抖动,威胁系统安全。Asets3绘制了在驱动器长时间保持在高位区间时的电压RMS曲线,发现随着时间发展有恶化趋势,符合实际经验。Asets4绘制了随机驱动器电压保持高位,其相邻驱动器电压保持低位时的电压RMS曲线,发现短时间内变化趋势不明显,但长时间看存在跳变和抖动,不能平稳工作。

图 8 电压失稳异常出现前后电压RMS曲线
Figure 8. Voltage RMS curves before and after the appearance of voltage instability
下一步将基于这些正常与异常数据使用不同方法进行状态检测。
-
第1节对每个环节分别分析建模,探测环节与校正环节分别对应112孔径哈特曼波前传感器与127单元连续面型分立式DM。同时,因为DM是AO系统中价值较高且更易损坏的重要器件,保存了4种失稳异常下的DM控制电压RMS进行检测算法验证。
为了及时发现系统失稳,评价系统运行健康程度,文中针对AO系统多环节、多单元、时序相关的特性,尝试探索使用机器学习方法对4类失稳异常进行检测。考虑到上位机性能,为简化计算,文中检测对象选择来自数据记录仪的电压RMS时间序列,通过DM整体面型反映系统稳定性。
机器学习中的异常检测方法有很多种,常见的包括基于统计模型的方法、基于距离的方法和基于聚类的方法等。文中使用Kmeans聚类、K-NN分类与ARIMA预测方法进行失稳检测。
-
Kmeans聚类是异常检测方法中最常用的方法之一,K值代表要分的类别数。训练过程通过随机取K个质心,计算每个样本到质心间的距离,此节使用欧氏距离:
$$D(X,Y) = {\left(\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^2}} \right)^{\frac{1}{2}}}$$ (4) 欧氏距离
$D(X,Y)$ 通过对欧氏空间中两点X,Y每一维坐标xi,yi计算差值平方和后求平方根得到。距离最近的质心所代表的类别即为样本类别,并进行多次迭代,保证所有类别质心Cj位置不变即获得各类质心cj与样本xi的标签Idx。
$$Id{x_i} = \mathop {\arg \min }\limits_{i = 1,2,...,N,1 \leqslant j \leqslant K} \left\| {{x_i} - {c_j}} \right\|$$ (5) 在使用聚类方法进行数据测试时,若样本类别缺失,使用少于K类样本进行聚类将会获得错误的质心。考虑到实际测试时可能都是正常数据缺少异常数据,文中在失稳仿真数据中训练好二分类质心(电压RMS值正常与异常的质心),选择性能最佳的一组作为测试时的分类依据。
-
K近邻(K-NN)算法同样是是异常检测中常见算法之一,此处K值代表需要比较的距离数。K-NN算法将训练数据集中已带标签数据视为历史数据,利用历史数据对新输入数据进行分类。
对于新输入样本,计算其与所有历史数据的距离,并选择距离最近的K个样本,统计这K个样本标签,选择最多的标签作为新输入样本的标签。
此节使用的历史数据为失稳仿真数据样本中正常样本的四分位数和失稳样本数据的四分位数,考虑到正常样本与失稳样本距离较远且分类边界模糊,特别引入最近3帧历史数据扩充历史数据。
即历史数据库有固定点(72个)和随时间变化点(7个)两部分构成,固定点使用已知正常与异常数据的四分位点。变化点随时间进行增删,添加最新历史数据,删除最早历史数据,K值取5。
-
ARIMA算法是一类时间序列分析方法,其本身是由回归(AR)过程和移动平均(MA)过程共同作用,I代表对序列W(t)差分。ARMA模型一般写作ARMA(p,q)。下式中,Φp表示p帧前历史数据Wt-p的权重;θq表示q帧前历史误差at-q的权重。
$$\begin{array}{l} {W_t} = {\phi _1}{W_{t - 1}} + {\phi _2}{W_{t - 2}} + \cdots + {\phi _p}{W_{t - p}} + {a_t} -\\ { {\theta _1}{a_{t - 1}} - {\theta _2}{a_{t - 2}} + \cdots - {\theta _q}{a_{t - q}}} \end{array} $$ (6) q=0时,ARMA(p,q)模型退化为AR(p)模型:
$${W_t} = {\phi _1}{W_{t - 1}} + {\phi _2}{W_{t - 2}} + \cdots + {\phi _p}{W_{t - p}} + {a_t}$$ (7) p=0时,ARMA(p,q)模型退化为MA(q)模型:
$${W_t} = {a_t} - {\theta _1}{a_{t - 1}} - {\theta _2}{a_{t - 2}} + \cdots - {\theta _q}{a_{t - q}}$$ (8) 对于符合ARIMA预测模型的时间序列有良好的预测性能,因而也可被用于时间序列的异常检测。对于DM控制电压RMS时间序列,存在明显变化趋势(上升或下降),通过求差分,可以得到一个通过平稳性检验的时间序列,因此该序列可以被ARIMA模型预测。正常闭环电压RMS时序平稳性分析见表3。
只有二阶差分通过平稳性检验,因此,文中使用二阶差分序列进行序列预测。
表 3 正常闭环电压RMS时序平稳性分析
Table 3. Stability analysis of RMS for normal closed-loop voltage
Original First difference Second difference Adftest 0 0 1 Kpsstest 1 1 0 建立ARIMA模型时通过比较自相关和偏自相关系数(见图9),确定模型参数为arima (2, 2, 1),此时模型预测结果和实际情况一致。

图 9 DM电压RMS二阶差分的自相关与偏自相关系数
Figure 9. Autocorrelation and partial autocorrelation coefficients of second order difference of DM voltage RMS
根据时间序列预测误差结果,此时设置误差阈值ec,超过该阈值的样本将被标记为异常。
-
根据仿真得到的正常与异常数据,进行测试,结果如表4所示。Kmeans聚类方法对不同异常有不同聚类质心,在各组质心中,选择一组距离适中的质心,如果距离过远,会对异常不敏感,距离过近,正常数据会判定为异常。
表 4 聚类方法在异常数据训练集集上的正确率
Table 4. Accuracy of clustering method on abnormal data training sets
Anomaly duration Training sets Asets1 Asets2 Asets3 Asets4 Accuracy Clustering centroids Accuracy Clustering centroids Accuracy Clustering centroids Accuracy Clustering centroids 25 frames 0.988 0.687,4.439 0.896 0.432,1.698 0.9 0.429,2.27 0.9 0.429,1.798 100 frames 0.996 0.646,4.607 0.926 0.498,1.707 1 0.63,2.685 0.934 0.509,2.039 250 frames 0.999 0.472,4.622 1 0.466,1.854 1 0.467,2.948 1 0.467,2.432 最后,选则质心组合[0.466;1.854]进行判定,它在长时间异常组中得到充分迭代,对异常数据能够准确识别,也能保证正常数据不被误判。这一组质心在测试集中的表现也很好(如表5所示)。
表 5 聚类方法在异常数据测试集集上的正确率
Table 5. Accuracy of clustering method on abnormal data test sets
Anomaly duration Test sets Asets1 Asets2 Asets3 Asets4 25 frames 1 1 0.984 1 100 frames 1 1 0.997 1 250 frames 1 1 0.998 1 K-NN方法在训练集和测试集上都表现得很好(见表6),动态分类的原理很好理解,即在已有距离较远的已知正常与异常数据之间,使用时间最近邻进行动态调整,如果数据波动很小,最近历史数据的标签将会被继承,对于稳定变化的情况将识别为系统稳定。
表 6 K-NN方法在训练集与测试集上的正确率
Table 6. Accuracy of K-NN method in training sets and test sets
Anomaly duration Training sets Test sets Asets1 Asets2 Asets3 Asets4 Asets1 Asets2 Asets3 Asets4 25 frames 1 0.908 1 1 1 1 1 1 100 frames 1 0.999 1 1 1 1 1 1 250 frames 1 1 1 1 1 1 1 1 根据ARIMA的识别结果(见表7),笔者发现该方法在前3类异常中的识别效果显著,而在第4类异常中,算法识别度下降。错分样本都是将异常数据识别为正常,而在文中方法的判别标准中,数据绝对值大小与数据波动程度不具有一致性,即只考虑数据发展趋势是否稳定,而递增递减后造成的数值饱和无法判定。
表 7 ARIMA方法在训练集与测试集上的正确率
Table 7. Accuracy of ARIMA method on training sets and test sets
Anomaly duration Training sets Test sets Asets1 Asets2 Asets3 Asets4 Asets1 Asets2 Asets3 Asets4 25 frames 1 1 1 0.964 1 1 1 0.952 100 frames 1 1 1 0.633 1 1 1 0.628 250 frames 1 1 1 0.538 1 1 1 0.5878 从准确率上看,Kmeans方法通过训练集的质心计算后,在分类时使用“一刀切”的阈值来分类,对于大部分仿真数据都能准确判断,但当正常数据中出现大像差时,会被识别为异常,当异常发展初期影响较小时,会被识别为正常(表5中Asets3),此评价标准不够灵活。
K-NN方法引入历史数据进行距离计算后,对正常数据识别较好,但当异常数据的震荡明显但数值上与正常数据分布较近,处于临界状态时会将此情形误判为正常,对此类震荡不敏感(表6中Asets2)。
ARIMA方法通过建立正常闭环数据模型进行预测,将预测值与实际值的差值作为分类依据,若干帧的差值累积超过阈值,视为系统失稳,在前3类存在震荡的异常数据中表现良好,但对于逐渐恶化的情形,除了突变时刻误差较大,后期预测值与实际值趋于一致,差值减小导致无法准确识别(表7中Asets4)。
-
文中建立了一套127单元AO系统失稳数据仿真平台,通过该平台获得了DM单元电压饱和、震荡、毛刺以及局部拉扯4种失稳情形的异常;使用3种机器学习方法(Kmeans聚类、K-NN分类、ARIMA预测)对异常数据的变形敬电压进行识别检测。
Kmeans方法通过训练数据提取质心,在测试样本上获得99%的准确率;K-NN方法准确率同样高,ARIMA方法对第4类异常准确率低,但对前3类识别准确。识别结果说明3种稳定性检测方法对系统失稳检测均有一定的效果和适用范围,Kmeans方法可以方便快捷地识别系统失稳,K-NN和ARIMA方法计算量较大,使用时需考虑上位机性能。
文中验证了应用机器学习方法对AO系统进行失稳检测是可行的,在实现了对系统失稳的检测后,可以根据失稳数据的特点,设计改善系统性能。例如在检测到失稳后,及时报警,自动开环或者对控制回路进行自适应调整等。
Detection methods for instability of adaptive optics system
-
摘要: 自适应光学(AO)系统校正像差是提高光学系统性能的有效技术手段。为了保证AO系统长时间安全、稳定地工作,需要对AO系统运行的数据进行监测,识别系统失稳状态以提供决策建议。基于以上目的,建立了一套127单元AO系统失稳数据仿真平台,通过该平台仿真得到了4种闭环失稳异常。基于变形镜控制电压RMS指标使用Kmeans聚类、K-NN分类和ARIMA预测3种机器学习方法进行识别检测。3种方法在不同类型异常数据中的检测结果有所不同,说明3种异常检测方法对系统失稳检测均有一定的效果和适用范围,在实际使用时,可以根据需要选择一种或综合多种方法进行检测。Abstract: Applying adaptive optics (AO) system to correct aberrations is an effective technical way to improve the performance of optical systems. In order to ensure the long-term, safe and stable operation of the AO system, it is necessary to monitor the operating data of the AO system and identify the instability state of the system to provide decision making suggestions. Based on the above purpose, a set of 127 units AO system instability data simulation platform was established. The abnormal data frames were inserted into the closed-loop operation of the simulation platform, and the abnormal data sets under four kinds of closed-loop instability were obtained. Once the deformable mirror, the core component of AO system, worked abnormally, it will threaten the safety of the system. Based on the deformable mirror control voltage rms index, three machine learning methods were used:
Kmeans clustering, K-NN classification and ARIMA prediction for recognition and detection. The detection results of the three methods in different types of abnormal data are different, indicating that the three anomaly detection methods have certain effects and scope of application for system instability detection. In actual application, one or a combination of multiple methods should be selected for testing. -
Key words:
- adaptive optics /
- anomaly detection /
-
Kmeans clustering / - K-NN classification /
- ARIMA prediction
-
表 1 自适应光学系统闭环异常状态表
Table 1. Close loop abnormal states of adaptive optical system
AO system components Abnormal phenomenon Possible causes Hartmann wavefront sensor Subaperture lack of light The spot intensity is too low to be detected Obstacles block light path Incomplete wavefront caused by pupil deviation Sub-spot saturation The spot intensity is higher than the sensor threshold The slope of subaperture changes sharply Stray light interference Background noise interference The light source flickers Mutation of work environment Sub-spot jitter Light source jitter Work platform jitter Closed-loop overshoot Overall slope mutation Optical axis offset Deformable mirror Control voltage saturation Aberrations are too large Drive units failure Control voltage oscillation Closed-loop overshoot Control voltage burr Drive unit exception Excessive voltage difference between local control units Mismatch between DM and sensor 表 2 4类DM失稳仿真过程
Table 2. Four kinds of DM instability simulation process
Idx Instability phenomenon Simulation process Asets1 Control voltage saturation Let several random drive voltages reach the threshold Asets2 Control voltage oscillation Let the voltage difference between adjacent frames of several random
drivers exceed the normal rangeAsets3 Control voltage burr Keep several random drive voltages in the high range Asets4 Excessive voltage difference between
local control unitsThe random driver voltage is kept high, and the adjacent driver voltage is kept low 表 3 正常闭环电压RMS时序平稳性分析
Table 3. Stability analysis of RMS for normal closed-loop voltage
Original First difference Second difference Adftest 0 0 1 Kpsstest 1 1 0 表 4 聚类方法在异常数据训练集集上的正确率
Table 4. Accuracy of clustering method on abnormal data training sets
Anomaly duration Training sets Asets1 Asets2 Asets3 Asets4 Accuracy Clustering centroids Accuracy Clustering centroids Accuracy Clustering centroids Accuracy Clustering centroids 25 frames 0.988 0.687,4.439 0.896 0.432,1.698 0.9 0.429,2.27 0.9 0.429,1.798 100 frames 0.996 0.646,4.607 0.926 0.498,1.707 1 0.63,2.685 0.934 0.509,2.039 250 frames 0.999 0.472,4.622 1 0.466,1.854 1 0.467,2.948 1 0.467,2.432 表 5 聚类方法在异常数据测试集集上的正确率
Table 5. Accuracy of clustering method on abnormal data test sets
Anomaly duration Test sets Asets1 Asets2 Asets3 Asets4 25 frames 1 1 0.984 1 100 frames 1 1 0.997 1 250 frames 1 1 0.998 1 表 6 K-NN方法在训练集与测试集上的正确率
Table 6. Accuracy of K-NN method in training sets and test sets
Anomaly duration Training sets Test sets Asets1 Asets2 Asets3 Asets4 Asets1 Asets2 Asets3 Asets4 25 frames 1 0.908 1 1 1 1 1 1 100 frames 1 0.999 1 1 1 1 1 1 250 frames 1 1 1 1 1 1 1 1 表 7 ARIMA方法在训练集与测试集上的正确率
Table 7. Accuracy of ARIMA method on training sets and test sets
Anomaly duration Training sets Test sets Asets1 Asets2 Asets3 Asets4 Asets1 Asets2 Asets3 Asets4 25 frames 1 1 1 0.964 1 1 1 0.952 100 frames 1 1 1 0.633 1 1 1 0.628 250 frames 1 1 1 0.538 1 1 1 0.5878 -
[1] 姜文汉. 自适应光学发展综述[J]. 光电工程, 2018, 45(3): 7-21. Jiang Wenhan. Overview of adaptive optics [J]. Optoelectronic Engineering, 2018, 45(3): 7-21. (in Chinese) [2] 凡木文. 高性能压电波前校正器高压驱动技术研究[D]. 成都: 中国科学院研究生院(中国科学院光电技术研究所), 2016. (in Chinese) Fan Muwen. Research on high voltage driving technology of high performance piezowave front corrector[D]. Chengdu: Graduate School of Chinese Academy of Sciences (Institute of Optics and Electronics, Chinese Academy of Sciences), 2016. [3] 宋定安, 李新阳, 彭真明. 稳健控制在自适应光学系统中的应用[J]. 激光与光电子学进展, 2016, 53(6): 060001. doi: 060001 Song Ding'an, Li Xinyang, Peng Zhenming. Application of robust control in adaptive optical system [J]. Laser & Optoelectronics Progress, 2016, 53(6): 060001. (in Chinese) doi: 060001 [4] 谢丽, 王家秋, 钟哲强, 等. 压电陶瓷驱动器疲劳对变形镜校正带宽的影响[J]. 光子学报, 2019, 48(9): 0912005. doi: 0912005 Xie Li, Wang Jiaqiu, Zhong Zhejiang, et al. The effect of piezoelectric actuator fatigue on the correction bandwidth of deformable mirror [J]. Acta Photonica Sinica, 2019, 48(9): 0912005. (in Chinese) doi: 0912005 [5] Wang L, Chen T, Liu X Y, et al. Stability evaluation and improvement of adaptive optics systems by using the Lyapunov stability approach [J]. Journal of the Korean Physical Society, 2016, 68(3): 486-92. [6] 宋定安, 李新阳, 彭真明. 0-1故障模型在自适应光学系统中的应用[J]. 红外与激光工程, 2018, 47(11): 1111004. doi: 1111004 Song Ding'an, Li Xinyang, Peng Zhenming. Application of 0-1 fault model in adaptive optical system [J]. Infrared and Laser Engineering, 2018, 47(11): 1111004. (in Chinese) doi: 1111004 [7] Gao Guoqing, Zhou Luchun. Fault tree analysis on reliability of electronic control system of adaptive optics [J]. Laser & Optoelectronics Progress, 2016, 53(1): 010102. doi: 010102 [8] 陈忠凤. 基于HS光斑有效性检测的AO系统自动闭环判断研究[D]. 成都: 中国科学院大学(中国科学院光电技术研究所), 2017. (in Chinese) Chen Zhongfeng. Research on automatic closed loop judgment of AO system based on HS spot validity detection[D]. Chengdu: University of Chinese Academy of Sciences (Institute of Opticsand Electronics, Chinese Academy of Sciences), 2017. [9] 罗帅, 王家秋, 张彬. 压电陶瓷驱动器疲劳特性对变形镜校正能力的影响[J]. 中国激光, 2018, 45(9): 0905002. doi: 0905002 Luo Shuai, Wang Jiaqiu, Zhang Bin. Influence of fatigue characteristics of piezoelectric ceramic actuator on deformable mirror correction ability [J]. Chinese Journal of Lasers, 2018, 45(9): 0905002. (in Chinese) doi: 0905002 [10] 谢晓钢, 张建柱, 岳玉芳, 等. 激光系统组件化仿真软件EasyLaser[J]. 强激光与粒子束, 2013, 25(10): 2536-2540. doi: 10.3788/HPLPB20132510.2536 Xie Xiaogang, Zhang Jianzhu, Yue Yufang, et al. Component simulation software EasyLaser for laser system [J]. High Power Laser and Particle Beam, 2013, 25(10): 2536-2540. (in Chinese) doi: 10.3788/HPLPB20132510.2536 [11] Betanzos-Torres M A, Castillo -Mixcoatl J, Munoz-Aguirre S, et al. Adaptive optics system simulator [J]. Optics & Laser Technology, 2018, 105: 118-28. [12] 辛建波, 康琛, 翁新林, 等. 基于聚类和时间序列分析的变压器状态评价方法[J]. 电力系统保护与控制, 2019, 47(3): 64-70. Xin Jianbo, Kang Chen, Weng Xinlin, et al. Transformer condition evaluation method based on clustering and time series analysis [J]. Power System Protection and Control, 2019, 47(3): 64-70. (in Chinese) [13] 郭巳秋, 张涛, 苗锡奎. 引入样本删除机制的TLD粒子群目标跟踪[J]. 光学 精密工程, 2019, 27(5): 1206-1217. Guo Siqiu, Zhang Tao, Miao Xikui. TLD particle swarm optimization target tracking with sample deletion mechanism [J]. Optics and Precision Engineering, 2019, 27(5): 1206-1217. (in Chinese) [14] 多丽娅, 张丽杰. 北斗卫星导航系统接收机测量误差建模及估计[J]. 红外与激光工程, 2015, 44(S1): 137-142. Doria, Zhang Lijie. Modeling and estimation of measurement error of Beidou satellite navigation system receiver [J]. Infrared and Laser Engineering, 2015, 44(S1): 137-142. (in Chinese) -







 下载:
下载: