-
近几十年来,传感器技术在快速发展,传感器的种类也越来越多。所获得的信息只包含角度信息的传感器被称为纯角度传感器,常见的纯角度传感器包括红外传感器[1]、光学传感器[2]、被动雷达传感器等[3-6]。在各类跟踪场景中,基于纯角度传感器的目标跟踪被称之为纯角度跟踪(bearings-only tracking,BOT)[7]。长期以来,由于纯角度传感器的广泛应用,BOT都是目标跟踪领域的重要课题,因为其在被动场景中能够发挥重要作用[8-9]。但是,由于不能获得目标的距离信息,与有距离信息的传感器相比,根据纯角度传感器获得的数据来估计目标的状态,其估计的精度往往不高[10]。要提升纯角度传感器的跟踪精度,有两种可行的方法。第一种方法是增加信息输入,由其他传感器给其提供目标的距离信息,以提升对目标的跟踪性能;但是这种方法需要其他传感器配合纯角度传感器工作,所需代价太大,在很多场合并不适用。另一种方法是通过信号处理的方法,充分利用纯角度传感器自身获得的数据提升跟踪性能;这种方法硬件成本低,是很多场合下的理想方法,但是也给信号处理算法带来了很大的挑战。
伯努利滤波器(Bernoulli filter,BF)[11-12],是由Mahler在2007年提出的用于单目标跟踪的滤波器。研究表明,在存在目标随机出现和消失且目标检测不确定的情况下,伯努利滤波器是贝叶斯框架内的最优单目标滤波器[12]。在滤波过程中,伯努利滤波器可以求得目标的存在概率和完整的后验概率密度函数,在单目标跟踪场景中能发挥重要作用,且能更好地判断目标出现和消失。由于其优良的单目标跟踪性能,有关伯努利滤波器的研究已经涉及到单目标跟踪的许多方面[13-18],有大量研究成果。
但是,当前针对纯角度跟踪的伯努利滤波器还很缺乏,Ristic等人提出了一种用于纯角度跟踪的伯努利滤波器[19],但是其在建模目标运动过程时,仍然采用了目标的位置信息,因此实际获得的性能还有不足。文中着眼于解决纯角度跟踪问题,基于伯努利滤波器,提出纯角度跟踪伯努利滤波器,并给出其粒子滤波(particle filter,PF)实现。仿真结果显示文中提出的滤波器在纯角度跟踪中能够更好地判断目标的存在与否并能够更精确地估计目标状态。
-
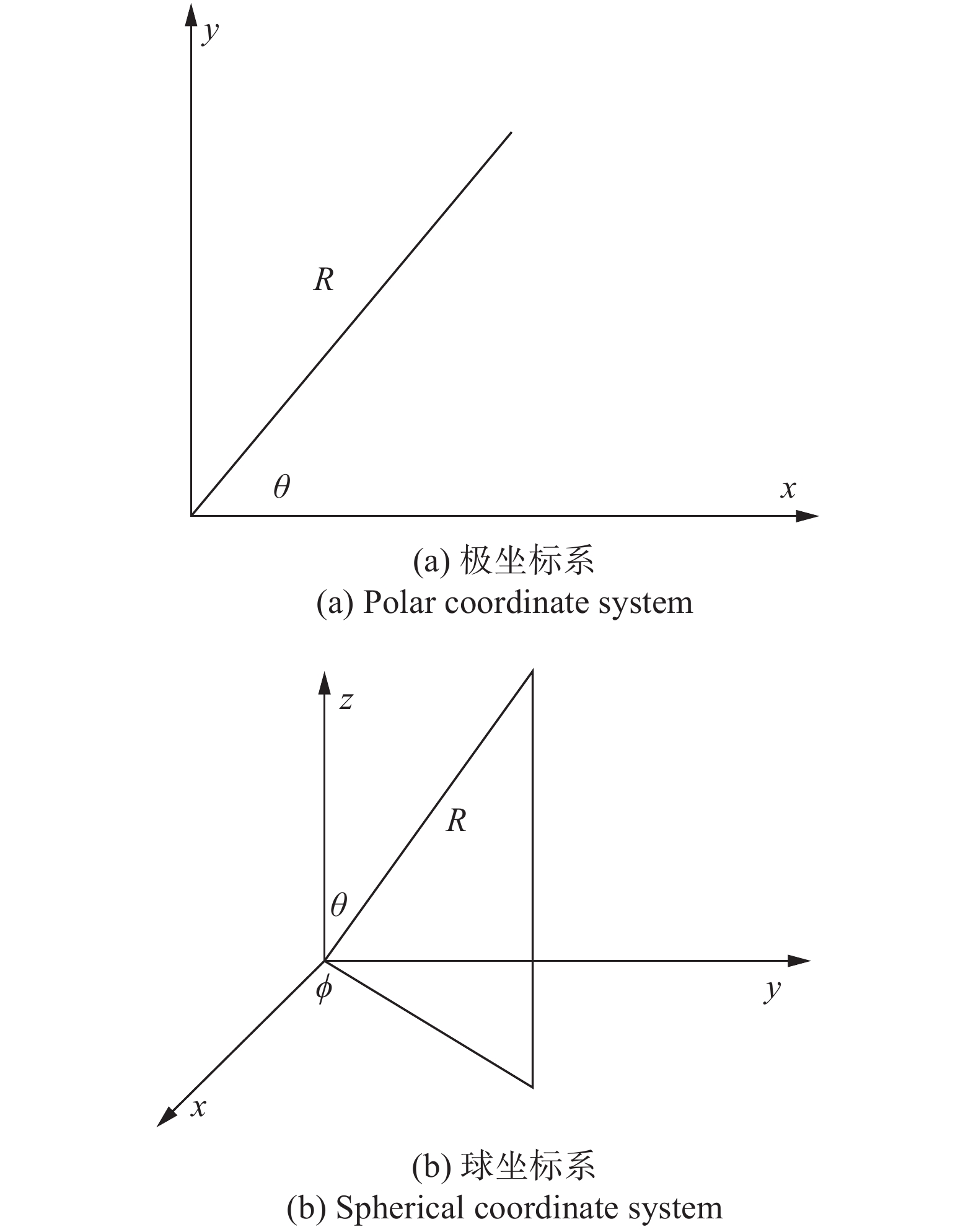
在常见的直角坐标系中,有关角度的量并不会直接出现在坐标系中,而需要通过一定的公式计算获得。与之相对应,极坐标系以及球坐标系中,角度信息分别被用于直接描述二维平面和三维空间中目标的位置。极坐标系和球坐标系如图1所示。极坐标中,目标的位置用
$(R,\theta )$ 表示,其中$\theta $ 表示方位角;而在球坐标系中,目标位置用$(R,\theta ,\phi )$ 表示,$\theta $ 和$\phi $ 分别表示俯仰角和方位角。
图 1 极坐标系与球坐标系示意图
Figure 1. Schematic diagram of polar coordinate system and spherical coordinate system
极坐标系
$(R,\theta )$ 与直角坐标系$(x,y)$ 的转换关系如下所示:$$\left\{ \begin{array}{l} x = R\cos \theta \\ y = R\sin \theta \end{array} \right.$$ (1) 球坐标系
$(R,\theta ,\phi )$ 与直角坐标系$(x,y,{\textit{z}})$ 的转换关系如下所示:$$\left\{ \begin{array}{l} x = R\sin \theta \cos \phi \\ y = R\sin \theta \sin \phi \\ {\textit{z}} = R\cos \theta \end{array} \right.$$ (2) 从公式(1)和(2)中可以看出,不管是在极坐标系中求解
$(x,y)$ 还是球坐标系中求解$(x,y,{\textit{z}})$ ,距离$R$ 都是必须给出的。但是在纯角度传感器中,距离信息无法给出。因此,当前纯角度传感器主要应用于两个方面:一是与其他能够测距的传感器协同工作,根据所得到的距离一起完成跟踪,这对应用背景有很大的限制;二是主要关注目标的有无问题,核心在于目标是否存在。纯角度跟踪问题,就需要在只获得了角度信息的前提下,完成目标跟踪。
-
伯努利滤波器首先由Mahler在2007年提出[11],也被称为联合目标检测跟踪(joint target detection and tracking,JOTT)滤波器,其理论基础是随机有限集(random finite set,RFS)。作为贝叶斯框架内的最优单目标滤波器,伯努利滤波器传递完整的概率密度函数,在递归过程中传递目标存在概率和目标后验概率密度函数。
伯努利滤波器与其他贝叶斯滤波器一致,滤波过程也分为预测步和更新步。在文中滤波器中,
$k$ 时刻为前一时刻,$k{\rm{ + }}1$ 时刻为当前时刻。滤波器滤波的过程,就是根据前一时刻的目标状态和当前时刻的观测估计当前时刻的目标状态。下标$k|k$ 表示前一时刻的后验信息,同时也是当前时刻的先验信息。$k{\rm{ + }}1|k$ 表示预测步的信息,而$k{\rm{ + }}1|k{\rm{ + }}1$ 表示当前时刻的后验信息,在下一时刻的滤波中,这又是先验信息。滤波器具体如下[11]:预测步为:
$${p_{k{\rm{ + 1}}|k}} = {p_b}(1 - {p_{k|k}}) + {p_s}{p_{k|k}}$$ (3) $${f_{k{\rm{ + 1}}|k}}({{x}})\! =\! \dfrac{{{p_b}{b_{k{\rm{ + 1}}|k}}({{x}})(1\! -\! {p_{k|k}})}}{{{p_{k{\rm{ + 1}}|k}}}}{\rm{ + }}\dfrac{{{p_s}{p_{k|k}} \displaystyle\int {{f_{k{\rm{ + 1}}|k}}({{x}}|{{x}}')} {f_{k|k}}({{x}}'){\rm d}{{x}}'}}{{{p_{k{\rm{ + 1}}|k}}}}$$ (4) 更新步为:
$${p_{k{\rm{ + 1}}|k + 1}} = \dfrac{{1 - {f_{k{\rm{ + 1}}|k}}[{p_D}] + \displaystyle\sum\limits_{{{{\textit{z}}}} \in {Z_{k{\rm{ + 1}}}}} {\frac{{\kappa ({Z_{k + 1}} - \left\{ {{{\textit{z}}}} \right\})}}{{\kappa ({Z_{k + 1}})}}{f_{k{\rm{ + 1}}|k}}[{p_D}{L_{{{\textit{z}}}}}]} }}{{\frac{{\rm{1}}}{{{p_{k{\rm{ + 1}}|k}}}} - {f_{k{\rm{ + 1}}|k}}[{p_D}] + \displaystyle\sum\limits_{{{\textit{z}}} \in {Z_{k + 1}}} {\dfrac{{\kappa ({Z_{k + 1}} - \left\{ {{\textit{z}}} \right\})}}{{\kappa ({Z_{k + 1}})}}{f_{k{\rm{ + 1}}|k}}[{p_D}{L_{{\textit{z}}}}]} }}$$ (5) $${f_{k{\rm{\! +\! 1}}|k \!+\! 1}}({{x}}) \!\!=\!\! {f_{k{\rm{ \!+\! \!1}}|k}}({{x}})\dfrac{{1 \!- \!{p_D}({{x}}) \!+\! {p_D}({{x}})\displaystyle\sum\limits_{{{\textit{z}}} \in {Z_{k \!+\! 1}}} {\dfrac{{\kappa ({Z_{k\! +\! 1}} \!-\! \left\{ {{\textit{z}}} \right\})}}{{\kappa ({Z_{k \!+\! 1}})}}{L_{{\textit{z}}}}({{x}})} }}{{1 \!-\! {f_{k{\rm{ + 1}}|k}}[{p_D}] \!+\! \displaystyle\sum\limits_{{{\textit{z}}} \in {Z_{k \!+ \!1}}} {\dfrac{{\kappa ({Z_{k\! + \!1}} \!-\! \left\{ {{\textit{z}}} \right\})}}{{\kappa ({Z_{k \!+\! 1}})}}{f_{k{\rm{\! +\! 1}}|k}}[{p_D}{L_{{\textit{z}}}}]} }}$$ (6) 其中用到的具体参数和符号说明如表1所示。
表 1 伯努利滤波器的符号说明
Table 1. Symbol description of the Bernoulli filter
Symbol Description ${p_b}$ The newborn probability of the target ${b_{k{\rm{ + 1}}|k}}({{x}})$ The probability density function of the newborn target ${p_s}$ The existence probability of the target (not related to the target state in this paper) ${f_{k{\rm{ + 1}}|k}}({{x}}|{{x}}')\;\;$ The Markov transition density of the target ${p_{k|k}}$ The priori probability of existence ${f_{k|k}}({{x}}')$ The priori probability density function $\kappa (Z)$ The probability density function of the clutter ${Z_{k{\rm{ + 1}}}}$ The current measurement set ${p_D}({{x}})$ The target detection probability ${L_{{\textit{z}}}}({{x}}) = f({{\textit{z}}}|{{x}})$ The measurement likelihood function 为了便于计算,研究人员提出了许多伯努利滤波器的改进形式。若杂波过程可由泊松RFS建模,且其均值为
$\lambda $ ,空间分布为$c({{\textit{z}}})$ ,即杂波概率密度函数为$\kappa (Z) = {{\rm e}^{ - \lambda }}\displaystyle\prod\limits_{{{\textit{z}}} \in Z} {\lambda c({{\textit{z}}})}$ ,因此有$$\frac{{\kappa ({Z_{k + 1}} - \left\{ {{\textit{z}}} \right\})}}{{\kappa ({Z_{k + 1}})}}{\rm{ = }}\frac{1}{{\lambda c({{\textit{z}}})}}$$ (7) 则更新步可以表示为:
$${p_{k{\rm{ + 1}}|k + 1}}{\rm{ = }}\frac{{{p_{k{\rm{ + 1}}|k}}\displaystyle\int {{l_{k + 1}}({Z_{k + 1}}|{{x}}){f_{k{\rm{ + 1}}|k}}({{x}}){\rm d}{{x}}} }}{{1 - {p_{k{\rm{ + 1}}|k}} + {p_{k{\rm{ + 1}}|k}}\displaystyle\int {{l_{k + 1}}({Z_{k + 1}}|{{x}}){f_{k{\rm{ + 1}}|k}}({{x}}){\rm d}{{x}}} }}$$ (8) $${f_{k{\rm{ + 1}}|k + 1}}({{x}}){\rm{ = }}\dfrac{{{l_{k + 1}}({Z_{k + 1}}|{{x}}){f_{k{\rm{ + 1}}|k}}({{x}})}}{{\displaystyle\int {{l_{k + 1}}({Z_{k + 1}}|{{x}}){f_{k{\rm{ + 1}}|k}}({{x}}){\rm d}{{x}}} }}$$ (9) 其中
${l_{k + 1}}({Z_{k + 1}}|{{x}}) = 1 - {p_D}({{x}}) + {p_D}({{x}})\displaystyle\sum\limits_{{{\textit{z}}} \in {Z_{k + 1}}} {\frac{{f({{\textit{z}}}|{{x}})}}{{\lambda c({{\textit{z}}})}}}$ 。 -
文中提出的纯角度跟踪伯努利滤波器,与参考文献[19]中所提出的用于纯角度跟踪的伯努利滤波器的区别,主要在于所使用的状态矢量不一致。参考文献[19]使用传统的目标坐标和速度作为状态矢量,文中直接使用目标相对于传感器的角度以及角度变化率作为状态矢量。因此,实际上文中的状态矢量是可求的,而参考文献[19]中的滤波器必须借助其他距离信息求解状态矢量。
-
为了计算简洁且不失一般性,文中用滤波器实现二维运动目标的跟踪,即所采用的坐标系为极坐标系。目标状态矢量为
${x_k} = {[\theta ,\dot \theta ]^{\rm T}}$ ,其中$\theta $ 表示方位角,$\dot \theta $ 表示方位角的变化率。若采样间隔为
$T$ ,则目标运动模型可表示如下:$${x_{k + 1}} = F{x_k} + G{w_k}$$ (10) 其中
$$F = \left[ {\begin{array}{*{20}{c}} 1&T \\ 0&1 \end{array}} \right]$$ (11) $$G = {\left[ {{{{T^2}} / 2}\;\;\;T} \right]^{\rm T}}$$ (12) 式中:
${w_k}$ 表示过程噪声。根据公式(10),可得此时的状态转移函数
${f_{k{\rm{ + 1}}|k}}({{x}}|{{x}}')$ ,然后根据伯努利滤波器的预测步计算预测概率密度函数和预测目标存在概率。 -
传感器获得的观测量只有角度信息,因此观测矢量可以表示为
${{\textit{z}}_k} = \theta $ 。此时的观测过程可以表示为:$${{\textit{z}}_k} = {x_k}(1) + {w_\theta }$$ (13) 式中:
${w_\theta }$ 表示角度上零均值高斯白噪声。根据公式(13)可得此时的观测似然
${L_{{\textit{z}}}}({{x}}) = $ $ f({{\textit{z}}}|{{x}})$ ,然后根据伯努利滤波器的更新步计算后验概率密度函数。 -
伯努利滤波器中包含了集积分,在具体执行过程中,需要计算不可积函数的高维积分,计算复杂且一般难以获取其解析形式。目前解决此类问题主要包括两种方法:一是高斯混合(Gaussian mixture,GM)实现方法;二是粒子滤波实现方法。文中采用粒子滤波实现方法近似实现纯角度跟踪伯努利滤波器。伯努利滤波器的粒子滤波实现在2012年首先由Ba-Tuong Vo等人提出[20]。
粒子滤波实现的核心工作是使用带有权重的粒子集
$\{ {{x}}_k^n,w_k^n\} _{n = 1}^{{N_S}}$ 近似概率密度函数,相应的近似可以表示为:$${f_{k|k}}({{x}}) \approx \sum\limits_{n = 1}^{{N_S}} {w_k^n{\delta _{{{x}}_k^n}}({{x}})} $$ (14) 伯努利滤波器的粒子滤波实现形式主要包括状态预测、观测更新、粒子重采样及目标状态估计四个部分。具体实现过程如下所示。
1)预测步
预测概率密度函数可以通过粒子近似表示为:
$${f_{k{\rm{ + 1}}|k}}({{x}}) \approx \sum\limits_{n = 1}^{{N_S} + {N_B}} {w_{k{\rm{ + 1}}|k}^n{\delta _{{{x}}_{k{\rm{ + 1}}|k}^n}}({{x}})} $$ (15) 其中,
$${{x}}_{k{\rm{ + 1}}|k}^n \sim \left\{ \begin{array}{l} {f_{k{\rm{ + 1}}|k}}({{x}}|{{x}}_k^n)\;\;\;\;\;\;\;\;\;\;n = 1, \cdots ,{N_S} \\ {b_{k{\rm{ + 1}}|k}}({{x}})\;\;\;\;\;n = {N_s} + 1, \cdots ,{N_S} + {N_B} \end{array} \right.$$ (16) 预测权重为:
$$w_{k{\rm{ + 1}}|k}^n = \left\{ \begin{array}{l} \dfrac{{{p_s}{p_{k|k}}}}{{{p_{k + 1|k}}{N_S}}}\;\;\;\;\;\;\;\;\;\;\;\;n = 1, \cdots ,{N_S} \\ \dfrac{{{p_b}(1 - {p_{k|k}})}}{{{p_{k + 1|k}}{N_B}}}\;\;\;\;\;n = {N_s} + 1, \cdots ,{N_S} + {N_B} \end{array} \right.$$ (17) 2)更新步
若杂波过程为泊松分布,则更新步可由公式(8))和(9)表示。其中对于每一个粒子
${{x}}_{k + 1|k}^n$ ,似然比${l_{k + 1}}({Z_{k + 1}}|{{x}}_{k + 1|k}^n)$ 为:$${l_{k + 1}}({Z_{k + 1}}|{{x}}_{k + 1|k}^n) = 1 - {p_D}({{x}}) + \sum\limits_{{{\textit{z}}} \in {Z_{k + 1}}} {\dfrac{{{p_D}({{x}}){f_p}({{\textit{z}}}|{{x}}_{k + 1|k}^n)}}{{\lambda c({{\textit{z}}})}}} $$ (18) 根据公式(15)所示的预测概率密度函数的粒子近似,后验存在概率可以近似表示为:
$${p_{k{\rm{ + 1}}|k + 1}} \approx \frac{{{p_{k{\rm{ + 1}}|k}} \displaystyle\sum\limits_{n = 1}^{{N_S} + {N_B}} {{l_{k + 1}}({Z_{k + 1}}|{{x}}_{k{\rm{ + 1}}|k}^n)w_{k{\rm{ + 1}}|k}^n} }}{{1 - {p_{k{\rm{ + 1}}|k}} + {p_{k{\rm{ + 1}}|k}} \displaystyle\sum\limits_{n = 1}^{{N_S} + {N_B}} {{l_{k + 1}}({Z_{k + 1}}|{{x}}_{k{\rm{ + 1}}|k}^n)w_{k{\rm{ + 1}}|k}^n} }}$$ (19) 后验概率密度函数可以近似表示为:
$${f_{k{\rm{ + 1}}|k + 1}}({{x}}) \approx \frac{{ \displaystyle\sum\limits_{n = 1}^{{N_S} + {N_B}} {{l_{k + 1}}({Z_{k + 1}}|{{x}}_{k{\rm{ + 1}}|k}^n)w_{k{\rm{ + 1}}|k}^n{\delta _{{{x}}_{k{\rm{ + 1}}|k}^n}}({{x}})} }}{{ \displaystyle\sum\limits_{n = 1}^{{N_S} + {N_B}} {{l_{k + 1}}({Z_{k + 1}}|{{x}}_{k{\rm{ + 1}}|k}^n)w_{k{\rm{ + 1}}|k}^n} }}$$ (20) 若将
$k + 1$ 时刻的后验概率密度函数通过粒子近似表示为:$${f_{k{\rm{ + 1}}|k + 1}}({{x}}) \approx \sum\limits_{n = 1}^{{N_S} + {N_B}} {w_{k{\rm{ + }}1}^{'n}{\delta _{{{x}}_{k{\rm{ + }}1|k}^n}}({{x}})}$$ (21) 则权重可以近似表示为:
$$w_{k{\rm{ + }}1}^{'n} \approx \frac{{{l_{k + 1}}({Z_{k + 1}}|{{x}}_{k{\rm{ + 1}}|k}^n)w_{k{\rm{ + 1}}|k}^n}}{{ \displaystyle\sum\limits_{n = 1}^{{N_S} + {N_B}} {{l_{k + 1}}({Z_{k + 1}}|{{x}}_{k{\rm{ + 1}}|k}^n)w_{k{\rm{ + 1}}|k}^n} }}$$ (22) 对权重进行归一化,可得带权重粒子集
$\{ {{x}}_{k{\rm{ + 1}}|k}^n,\bar w_{k{\rm{ + }}1}^n\} _{n = 1}^{{N_S} + {N_B}}$ 。3)重采样
采用经典方法完成重采样,从粒子集
$\{ {{x}}_{k{\rm{ + 1}}|k}^n,\bar w_{k{\rm{ + }}1}^n\} _{n = 1}^{{N_S} + {N_B}}$ 获得$k + 1$ 时刻的后验概率密度函数近似粒子集$\{ {{x}}_{k + 1}^n,w_{k + 1}^n\} _{n = 1}^{{N_S}}$ 。后验概率密度函数近似表示为:$${f_{k{\rm{ + 1}}|k + 1}}({{x}}) \approx \sum\limits_{n = 1}^{{N_s}} {w_{k{\rm{ + }}1}^n{\delta _{{{x}}_{k{\rm{ + }}1}^n}}({{x}})} $$ (23) 这一后验概率密度函数也就是
$k + 2$ 时刻的先验概率密度函数。伯努利滤波器是一个递归滤波器,每一步的后验概率密度函数都作为下一步的先验概率密度函数,按时间顺序完成每一时刻的目标状态估计。4)状态估计
如果后验存在概率大于0.5,则认为目标存在,对获得的后验概率密度函数近似粒子集中的所有粒子求平均获得目标状态
${{\hat{ x}}_{k + 1}}$ 。纯角度跟踪伯努利滤波器的PF实现伪代码如表2所示。
表 2 算法1
Table 2. Algorithm 1
Algorithm 1. PF implementation of the bearings-only tracking Bernoulli filter (1) Input: The priori probability of existence ${p_{k|k}}$, particle set $\{ {{x}}_k^n,w_k^n\} _{n = 1}^{{N_S}}$, measurement set ${Z_{k + 1}}$ (2) Calculate the predicted probability of existence by (3). (3) Draw a sample for the particle set by (16), and calculate the predicted weights by (17) (4) Compute the likelihood ratio using (18) (5) Compute the posterior probability density function using (19) (6) Compute the posterior weights using (20) and normalize the weights (7) Resample and target state estimation (8) Output: The posterior probability of existence ${p_{k{\rm{ + }}1|k{\rm{ + }}1}}$, particle set $\{ {{x}}_{k + 1}^n,w_{k + 1}^n\} _{n = 1}^{{N_S}}$, target state ${{\hat{ x}}_{k + 1}}$ -
这一部分给出了纯角度跟踪伯努利滤波器的仿真实现结果,证明了所提出滤波器在纯角度跟踪场景中的有效性。
-
传感器位于坐标系原点,为纯角度传感器,只能获得角度信息,监视区域为
$[ - \pi /2,\pi /2]$ 范围。传感器输入模型采用参考文献[18]所示的检测器输出模型。在每一时刻,传感器都能有可能得到许多个观测信息输入,其中有可能包含目标产生的观测,也有可能是杂波引起的虚警。传感器观测过程中的噪声为白高斯噪声,标准差为${\sigma _{{w_\theta }}} = \pi /36\;\;{\rm{rad}} = 5^\circ $ 。目标在监视区域内运动,为了方便描述目标运动,先建立直角坐标系。传感器采样周期为
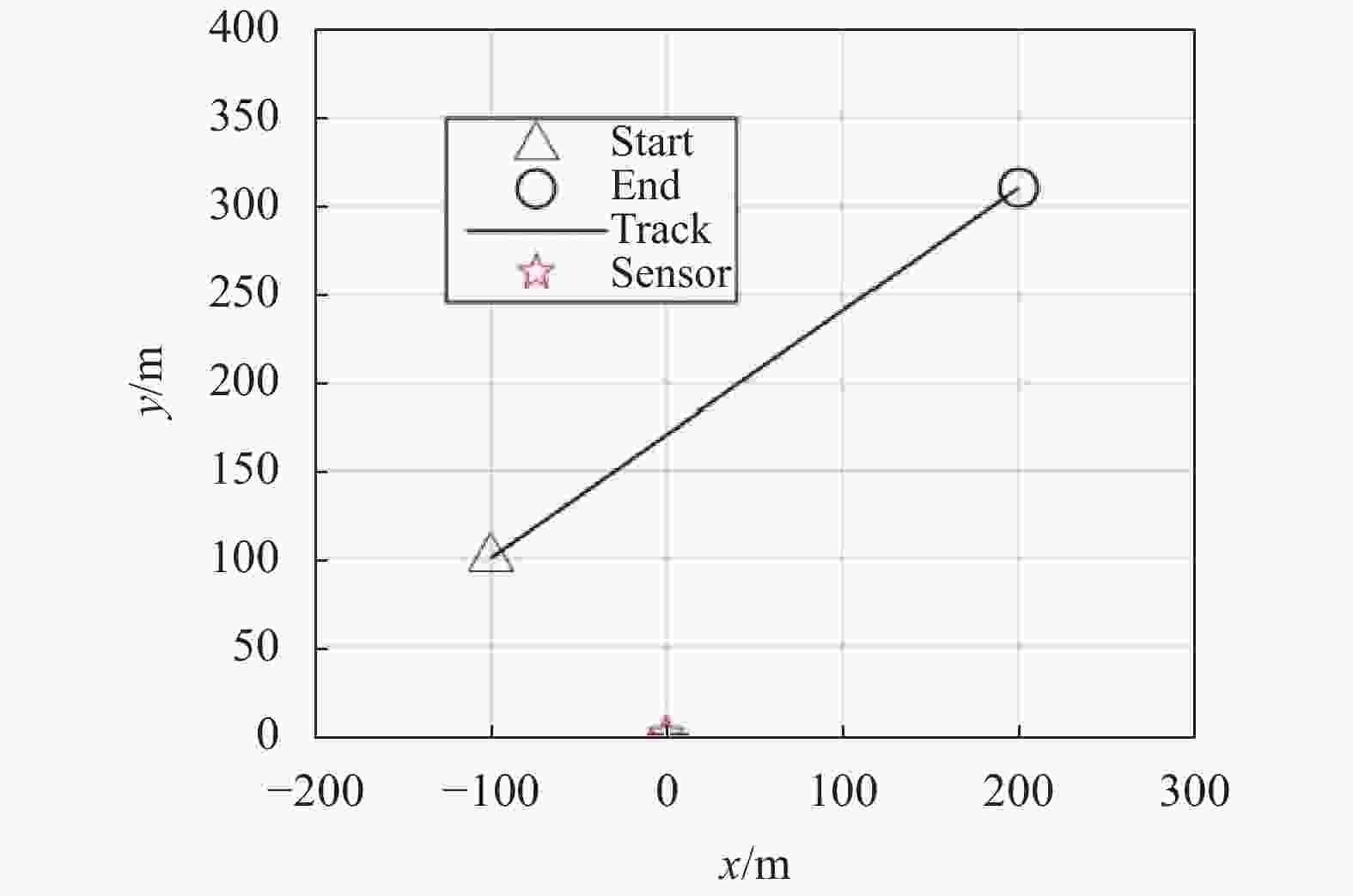
$T = 1\;{\rm s}$ ,仿真持续时间为50个周期,即50 s。目标初始位置为$[ - 100,100]\;{\rm m}$ ,从第10时刻开始进行匀速直线运动,到第40时刻目标消失。x方向速度为$10\;{\rm m/s}$ ,y方向速度为$7\;{\rm m/s}$ 。目标运动轨迹如图2所示。图中,传感器所在位置为五角星所示原点,三角形为目标运动的初始位置,圆形为目标运动的终点,实线所示为目标轨迹。实际上,传感器接收到的只有目标的角度信息,因此文中还需在相同原点建立极坐标系,可以看出目标初始角度为
$ - \pi /4$ 。在观测过程中,假定每一时刻的杂波数目服从泊松分布,数目均值为10,且均匀分布于感兴趣区间内。在传感器中,目标检测概率为${p_D}({{x}}) = 0.95$ 。可以得到目标和杂波形成的观测集,如图3所示。图中实线所示为目标轨迹,纵坐标为目标的角度,横坐标为采样时刻。小x形状表示纯角度传感器获得的观测,其中既包括目标的观测,也包括杂波。从图中可以看出,此时杂波比较密集,目标观测被杂波淹没。在滤波过程中,文中假设目标新生概率为
${p_b} = $ $ 0.1$ ,目标存活概率为${p_s} = 0.99$ ,用于存活目标的粒子数为3000个,新生粒子数目为1000个且均匀分布于场景中。 -
为了说明文中提出算法的有效性,笔者用Ristic等人提出的伯努利滤波器[19]作为对比。在Ristic等人提出的伯努利滤波器中,虽然也用于的角度。由于其关注的重点有偏差,其在计算角度时,又会带来更大的误差,因此性能不如文中提出的滤波器。
文中算法与Ristic等人的普通伯努利滤波器的对比示意图如图4所示。图中,实线仍然表示目标真实轨迹,小x形状仍然表示纯角度传感器获得的观测,黑点表示文中提出的纯角度跟踪伯努利滤波器的跟踪结果,圆形所示为普通伯努利滤波器的跟踪结果。从图中可以看出,文中提出的纯角度跟踪伯努利滤波器得到的跟踪结果更加接近目标的真实轨迹,而普通伯努利滤波器的跟踪结果与真实轨迹的差距较大。这是因为文中将状态矢量建模为目标方位角和方位角的变化率,能够更加精确地估计目标的角度信息。
-
为了充分说明文中算法的有效性,笔者继续采用Ristic等人提出的伯努利滤波器作为比较算法。在伯努利滤波器中,可以得到目标的存在概率和目标的状态。而衡量伯努利滤波器跟踪性能主要通过两个参数。一是目标存在概率:若实际没有目标,则目标存在概率应该无限接近0;若存在目标,则目标存在概率应该接近1。而滤波器的估计误差,即滤波器获得的目标状态与实际目标的误差大小。文中采用一种与最优子模式分配(optimal subpattern assignment, OSPA)度量[21]类似的误差衡量方法,即设置一个最大误差
$c$ ,若计算得到的误差小于$c$ ,则用计算得到的误差;若计算得到的误差大于$c$ ,则误差值为最大误差$c$ ;同时,若估计得到的目标数目与真实目标数目不一致,误差值也为最大误差$c$ 。考虑到单次的仿真结果不一定是稳定的结果,因此文中采用500次蒙特卡洛仿真得到平均结果以对比两种滤波器的跟踪性能。
纯角度跟踪伯努利滤波器与普通伯努利滤波器获得的目标存在概率对比如图5所示。从图中可以看出,在目标不存在时,文中提出的纯角度跟踪伯努利滤波器的目标存在概率更加接近0;在目标存在时,文中提出的纯角度跟踪伯努利滤波器的目标存在概率更加接近1;而且在目标出现时,文中提出的纯角度跟踪伯努利滤波器的目标存在概率更加快速接近1;在目标消失后,文中提出的纯角度跟踪伯努利滤波器的目标存在概率更加快速接近0。这说明文中提出的算法对于目标数目的估计更加准确,对于目标的出现消失反应更加迅速。

图 5 纯角度跟踪伯努利滤波器与伯努利滤波器估计的目标存在概率对比(500次蒙特卡洛平均)
Figure 5. Comparison of the estimated target existence probability of the BOT Bernoulli filter and the Bernoulli filter (500 Monte Carlo runs)
纯角度跟踪伯努利滤波器与普通伯努利滤波器获得的角度估计误差对比如图6所示。从图中可以看出,在目标不存在时,两种滤波器基本上都不会判断出错误结果;在目标存在时,文中提出的纯角度跟踪伯努利滤波器的角度估计误差更小。而且在目标出现和消失时,文中提出的纯角度跟踪伯努利滤波器的角度估计误差只有在目标出现和目标消失的一两个时刻比较大,然后迅速收敛;而普通伯努利滤波器的收敛时间明显大于文中提出的滤波器。这说明文中提出的算法对于目标数目的角度估计更加准确。
-
文中着眼于纯角度跟踪场景中的单目标跟踪问题,基于RFS理论,在Mahler提出的伯努利滤波器的基础上,提出了一种纯角度跟踪伯努利滤波器,同时给出了其PF实现方法。所提滤波器将目标相对于传感器的角度以及角度的变化率作为目标状态矢量,用于判断目标是否存在并估计其状态信息。仿真结果显示,文中提出的滤波器能够更好地判断目标的存在与否,同时对于目标估计的误差比普通伯努利滤波器更小。这充分说明了文中提出的纯角度跟踪伯努利滤波器具有较好的跟踪性能,能够有效应用于纯角度跟踪场景中并获得更准确的目标状态信息。在接下来的研究中,可以通过常见的纯角度传感器如红外传感器、光学传感器以及被动雷达传感器采集相应的数据用于验证所提出滤波器的跟踪性能。
Application of Bernoulli filter in bearings-only tracking scenarios
-
摘要: 所获得信息只包含角度信息的传感器被称为纯角度传感器,基于纯角度传感器的目标跟踪被称之为纯角度跟踪(Bearings-only Tracking,BOT)。BOT是目标跟踪领域的重要课题,在被动目标跟踪场景中能够发挥重要作用。伯努利滤波器(Bernoulli Filter,BF)是贝叶斯框架内的最优单目标滤波器,可以求得目标的存在概率和完整的后验概率密度函数,并判断目标出现和消失。作者将伯努利滤波器应用于纯角度跟踪场景下的单目标跟踪问题,提出了一种纯角度跟踪伯努利滤波器。在所提出的滤波器中,将目标相对于传感器的角度及其变化率作为状态矢量,用于估计目标是否存在;若目标存在,估计其状态信息。同时,还给出了所提出滤波器的粒子滤波(Particle Filter,PF)实现方法。仿真结果显示,与普通伯努利滤波器相比,所提出的纯角度跟踪伯努利滤波器能够更好地判断目标是否存在,同时滤波器对于目标估计的误差也更小。因此,所提出的滤波器具有更好的跟踪性能和更高的跟踪精度,能够有效应用于被动跟踪场景中。Abstract: The sensor whose information only contains angle information is called bearings-only sensor, and the target tracking based on bearings-only sensor is called bearings-only tracking (BOT). BOT is an important topic in the field of target tracking and will play an important role in passive target tracking surveillance. Bernoulli filter (BF) is the best single target filter within the Bayesian framework. It can obtain the existence probability of the target and the complete posterior probability density function, and judge the appearance and disappearance of the target. The Bernoulli filter was applied to single target tracking in the bearings-only tracking surveillance, and a bearings-only tracking Bernoulli filter was proposed. In the proposed filter, the angle of the target relative to the sensor and its change rate were used as the state vectors to estimate the existence of the target as well as the target state. At the same time, the particle filter (PF) implementation was proposed, too. The simulation results show that, compared with the ordinary Bernoulli filter, the proposed bearings-only tracking Bernoulli filter can judge the existence of the target better, and the error of the target estimation generated by the filter is smaller. Thus, the proposed filter has better tracking performance and higher tracking accuracy, which can be effectively applied to the passive tracking scenarios.
-
Key words:
- bearings-only sensor /
- bearings-only tracking /
- Bernoulli filter /
- particle filter
-
表 1 伯努利滤波器的符号说明
Table 1. Symbol description of the Bernoulli filter
Symbol Description ${p_b}$ The newborn probability of the target ${b_{k{\rm{ + 1}}|k}}({{x}})$ The probability density function of the newborn target ${p_s}$ The existence probability of the target (not related to the target state in this paper) ${f_{k{\rm{ + 1}}|k}}({{x}}|{{x}}')\;\;$ The Markov transition density of the target ${p_{k|k}}$ The priori probability of existence ${f_{k|k}}({{x}}')$ The priori probability density function $\kappa (Z)$ The probability density function of the clutter ${Z_{k{\rm{ + 1}}}}$ The current measurement set ${p_D}({{x}})$ The target detection probability ${L_{{\textit{z}}}}({{x}}) = f({{\textit{z}}}|{{x}})$ The measurement likelihood function 表 2 算法1
Table 2. Algorithm 1
Algorithm 1. PF implementation of the bearings-only tracking Bernoulli filter (1) Input: The priori probability of existence ${p_{k|k}}$ , particle set$\{ {{x}}_k^n,w_k^n\} _{n = 1}^{{N_S}}$ , measurement set${Z_{k + 1}}$ (2) Calculate the predicted probability of existence by (3). (3) Draw a sample for the particle set by (16), and calculate the predicted weights by (17) (4) Compute the likelihood ratio using (18) (5) Compute the posterior probability density function using (19) (6) Compute the posterior weights using (20) and normalize the weights (7) Resample and target state estimation (8) Output: The posterior probability of existence ${p_{k{\rm{ + }}1|k{\rm{ + }}1}}$ , particle set$\{ {{x}}_{k + 1}^n,w_{k + 1}^n\} _{n = 1}^{{N_S}}$ , target state${{\hat{ x}}_{k + 1}}$ -
[1] 房胜男, 谷小婧, 顾幸生. 基于自适应响应融合的相关滤波红外目标跟踪[J]. 红外与激光工程, 2019, 48(6): 0626003. Fang Shengnan, Gu Xiaojing, Gu Xingsheng. Infrared target tracking with correlation filter based on adaptive fusion of responses [J]. Infrared and Laser Engineering, 2019, 48(6): 0626003. (in Chinese) [2] 曲蕴杰, 莫宏伟, 王常虹. 一种用于无人机的目标颜色核相关跟踪算法研究[J]. 红外与激光工程, 2018, 47(3): 0326001. Qu Yunjie, Mo Hongwei, Wang Changhong. A target color kernel correlation tracking algorithm for UAVs [J]. Infrared and Laser Engineering, 2018, 47(3): 0326001. (in Chinese) [3] 欧阳成. 基于随机集理论的被动多传感器多目标跟踪[D]. 西安: 西安电子科技大学, 2012. Ouyang Cheng. Multi-target tracking based on random finite set theory for passive multi-sensor systems[D]. Xi’an: Xidian University, 2012. (in Chinese) [4] 刘娜, 岳琪琪, 陈加宏, 等. 搜索区域和目标尺度自适应的无人艇海面目标跟踪[J]. 光学 精密工程, 2020, 28(3): 671-685. doi: 10.3788/OPE.20202803.0671 Liu Na, Yue Qiqi, Chen Jiahong, et al. Search area and target scale adaptive sea surface object tracking for unmanned surface vessel [J]. Optics and Precision Engineering, 2020, 28(3): 671-685. (in Chinese) doi: 10.3788/OPE.20202803.0671 [5] 罗秀娟, 刘辉, 张羽, 等. 地球同步轨道暗弱目标地基光学成像技术综述[J]. 中国光学, 2019, 12(4): 753-766. doi: 10.3788/co.20191204.0753 Luo Xiujuan, Liu Hui, Zhang Yu, et al. Review of ground-based optical imaging techniques for dim GEO objects [J]. Chinese Optics, 2019, 12(4): 753-766. (in Chinese) doi: 10.3788/co.20191204.0753 [6] 王博, 董登峰, 周维虎, 等. 面向激光跟踪仪跟踪恢复的合作目标视觉检测[J]. 光学 精密工程, 2020, 28(2): 271-282. Wang Bo, Dong Dengfeng, Zhou Weihu, et al. Visual detection of targetball for laser tracker target tracking recovery [J]. Optics and Precision Engineering, 2020, 28(2): 271-282. (in Chinese) [7] 韩崇昭. 多源信息融合[M]. 北京: 清华大学出版社, 2006. Han Chongzhao. Multi-Source Information Fusion[M]. Beijing: Tsinghua University Press, 2006. (in Chinese) [8] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991. Zhou Hongren, Jing Zhongliang, Wang Peide. Tracking of Maneuvering Targets[M]. Beijing: National Defense Industry Press, 1991. (in Chinese) [9] 潘泉, 梁彦, 杨峰, 等. 现代目标跟踪与信息融合[M]. 北京: 国防工业出版社, 2009. Pan Quan, Liang Yan, Yang Feng, et. al. Modern Target Tracking and Information Fusion[M]. Beijing: National Defense Industry Press, 2009. (in Chinese) [10] 胡剑虹, 宁飞, 沈湘衡, 等. 目标表面发射率对红外热像仪测温精度的影响[J]. 中国光学与应用光学, 2010, 3(2): 152-156. Hu Jianhong, Ning Fei, Shen Xiangheng, et al. Influence of surface emissivity of objects on measuring accuracy of infrared thermal imagers [J]. Chinese Journal of Optics and Applied Optics, 2010, 3(2): 152-156. (in Chinese) [11] Mahler R. Statistical Multisource Multitarget Information Fusion[M]. Norwood, MA, USA: Artech House, 2007. [12] Mahler R, Advances in Statistical Multisource-Multitarget Information Fusion[M]. Norwood, MA, USA: Artech House, 2014. [13] Luo Xiaobo, Fan Hongqi, Song Zhiyong, et al. Passive target tracking with intermittent measurement based on random finite set [J]. Journal of Central South University, 2014, 21(6): 2282-2291. doi: 10.1007/s11771-014-2179-x [14] Guldogan M B. Consensus Bernoulli filter for distributed detection and tracking using multi-static Doppler shifts [J]. IEEE Signal Processing Letters, 2014, 21(6): 672-676. doi: 10.1109/LSP.2014.2313177 [15] Baser E, Mcdonald M, Kirubarajan T, et al. A joint multitarget estimator for the joint target detection and tracking filter [J]. IEEE Transactions on Signal Processing, 2015, 63(15): 3857-3871. doi: 10.1109/TSP.2015.2434321 [16] Gunes A, Guldogan M B. Joint underwater target detection and tracking with the Bernoulli filter using an acoustic vector sensor [J]. Digital Signal Processing, 2016, 48: 246-258. doi: 10.1016/j.dsp.2015.09.020 [17] Ristic B, Sherrah J. Bernoulli filter for joint detection and tracking of an extended object in clutter [J]. IET Radar, Sonar & Navigation, 2013, 7(1): 26-35. [18] Ristic B, Vo B T, Vo B N, et al. A tutorial on Bernoulli filters: theory, implementation and applications [J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3406-3430. doi: 10.1109/TSP.2013.2257765 [19] Ristic B, Arulampalam S. Bernoulli particle filter with observer control for bearings-only tracking in clutter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2405-2415. doi: 10.1109/TAES.2012.6237599 [20] Vo B T, See C M, Ma N, et al. Multi-sensor joint detection and tracking with the Bernoulli filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1385-1402. doi: 10.1109/TAES.2012.6178069 [21] Schuhmacher D, Vo B T, Vo B N. A consistent metric for performance evaluation of multi-object filters [J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457. doi: 10.1109/TSP.2008.920469 -






 下载:
下载: