-
激光器通常由三要素构成:谐振腔、泵浦源以及增益介质。谐振腔的作用是提供轴向光波模的正反馈及保证激光器的单模(或少数轴向模)振荡,它决定了激光的众多关键特性,如光谱和空间模结构、方向、频率、偏振等输出光束的其他参数。在随机激光器中,没有传统的谐振腔结构,出射光的性质是由光子在增益介质中的随机多次散射决定的,即随机激光的产生只依赖于增益介质和无序散射介质,从而获得反馈和光放大。因此,增益和散射材料的特性对随机激光尤为重要。根据反馈机制的不同,可将随机激光分为两种:(1)非相干的能量反馈;(2)相干的场或振幅反馈。
1967年,前苏联科学家Ambartsumyan等人将F-P腔中的一个反射镜换成一个散射表面,制成一种没有谐振反馈的激光腔。增加泵浦能量时,这种激光腔的发射谱会向着增益谱中心窄化,其窄化过程远远慢于传统激光器[1]。腔中的众多模式均与增益介质相互作用,使产生的激光与传统激光器相比有完全不同的统计特征[2]。
1968年,Letokhov从理论上预测了随机激光的出现,提出临界体积Vcr的概念:当散射介质的体积V大于临界体积且增益大于损耗时,光子的能量密度就会随时间累积呈指数增加[3]。即达到阈值后,随机激光的发射光谱会窄化,在最大增益波长处有最大强度。这个过程存在一个链式反应,类似原子弹中的中子倍增,一个光子产生两个光子,两个产生四个,被称为“光子弹”。
20世纪80年代,科学家们对激光晶体粉末的光发射现象进行了研究。他们无法确定这种发射的物理本质:这是激光发射还是超辐射光?“腔体”是由单个激光晶体粒子的内部反射还是它们之间的散射形成的?
直到1994年,N. M. Lawandy等人在掺杂罗丹明640激光染料和TiO2纳米颗粒的甲醇溶液中观察到强度高且谱线窄的发射峰,与激光类似[4]。由于粒子的尺寸非常小,排除了单粒子内部共振产生激光的可能性,证明了激光反馈是粒子间散射带来的;而且增益存在于散射粒子之外,也表明这不是单粒子激光器。
1995年,Wiersma, D. S和Lagendijk, A正式提出随机激光的概念[5]。
1996年,Wiersma, D. S等人根据Letokhov等人的理论,在扩散模型中发现了弛豫振荡和激光尖峰[6]。用扩散理论解释了非相干随机激光的产生过程,借助具有四能级系统的平板型增益介质,将临界体积简化为临界厚度Lcr,提出振荡平衡条件。
1998年,H. Cao等人观察到相干随机激光[7]。用脉冲激光器泵浦ZnO粉末和多晶薄膜,泵浦光强度超过阈值后,观察到各项异性的随机激光发射谱。这证明了相干共振反馈即干涉的存在,表明确实需要考虑光场的相位。次年,H. Cao等人对这种现象做出解释[8]。由于散射平均自由程ls(即光在连续两次散射之间所走的平均路程)较小,发射光强烈散射,以至于在不同区域形成闭合环形腔,进而形成干涉。并且在不同区域泵浦或在不同区域接收,会观察到不同的激光发射峰。
如图1所示,可以从不同散射体系中得到随机激光,比如聚合物[9]、波导[10-11]、量子点[12]、掺杂激光染料和纳米颗粒的悬浊液[13]、半导体粉末[14]、液晶[15]、稀土[16]等。
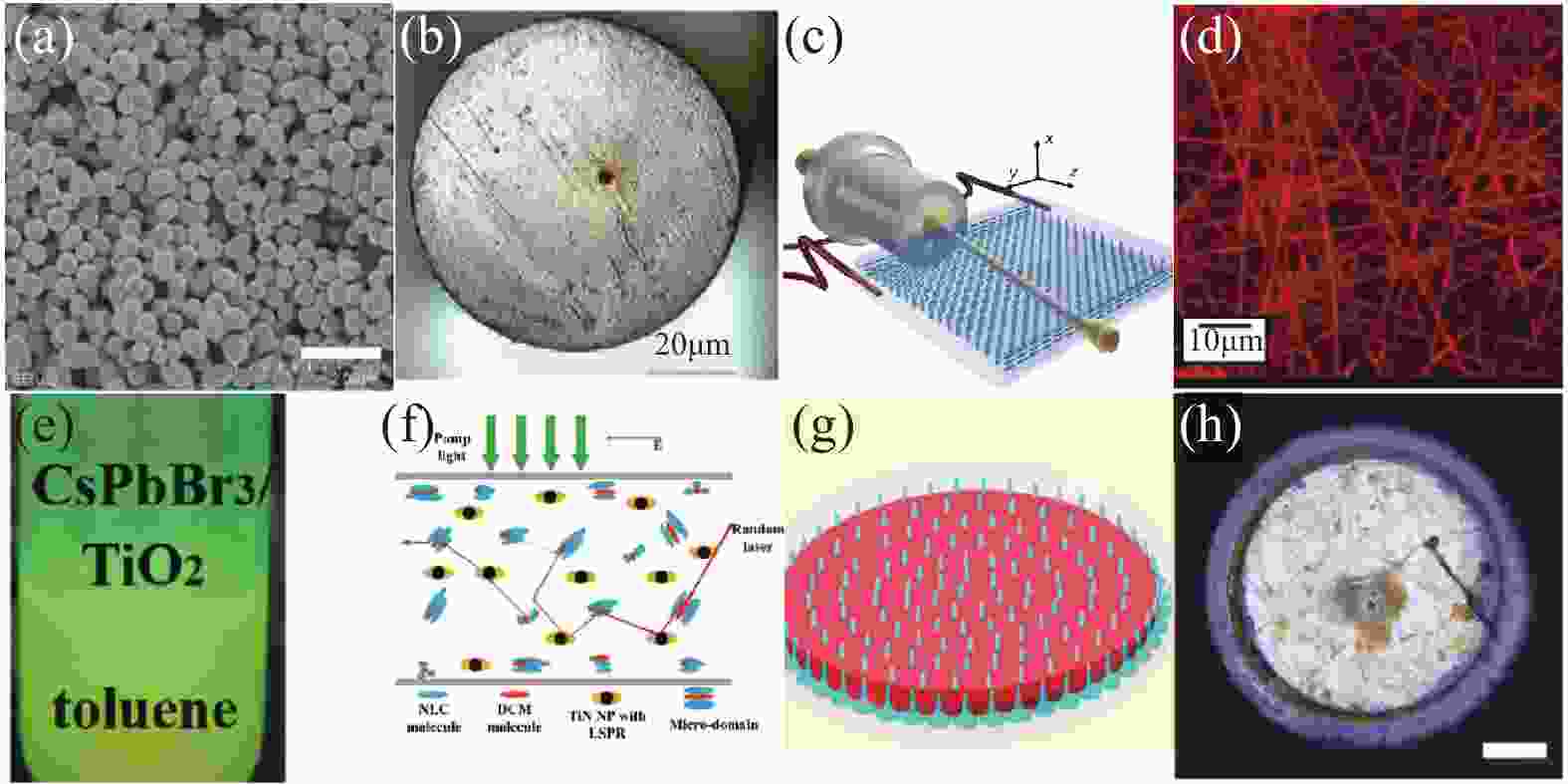
图 1 各种随机激光体系:(a) ZnO粒子[17]; (b)聚合物光纤[18]; (c)光孤子[19]; (d)静电纺丝纤维[20]; (e)量子点[21]; (f)液晶[15]; (g)荷叶[22]; (h)钙钛矿[23]
Figure 1. Different kinds of RL systerms: (a) ZnO particles[17]; (b) Polymer optical fiber[18]; (c) Soliton[19]; (d) Electrospun nanofibers[20]; (e) Quantum dots[21]; (f) Liquid crystals[15]; (g) Lotus-leaf[22]; (h) Perovskitec[23]
聚合物散射体系有聚合物溶液、聚合物光纤、聚合物薄膜、聚合物波导等,聚合物体系中可以掺杂金属纳米颗粒以增强散射,激光染料或者活性有机聚合物容易渗透或掺杂在许多不同的材料中。Yuchen Wang等人[9]利用
$\pi $ 共轭聚合物凝聚引起折射率波动,使随机激光模式在空间上扩展,这些模式在溶液与比色皿交界面上被放大。基于液晶(LC)的散射体系既可以产生非相干随机激光又可以产生相干随机激光,由于液晶优异的光电性质,有利于实现随机激光的调谐。液晶有着部分有序的分子排列,所以具有部分有序的光学特性,易于获得高Q值的随机激光。当随机激光器中的散射介质达到最佳无序程度时,输出激光模式的 Q 值最大[24]。根据液晶分子排列的有序性,可将液晶分为向列相(一维有序且各向异性)、近晶相(二维有序)、胆甾相(手性向列)等类型。由于液晶分子的排列及光轴方向对温度和电场有着很强的依赖性,通过控制温度和电场可以有效地调控液晶随机激光的输出特性[25-26]。
直接带隙半导体材料也广泛应用在随机激光中,ZnO粒子是应用最为广泛的无序半导体材料之一。随机激光中的ZnO有着各种形式,比如粉末、薄膜、纳米线、纳米棒等。由ZnO纳米棒和TiO2纳米粒子组成的复合材料可以使激光阈值比纯ZnO纳米棒的激光阈值降低近两倍[27]。这是通过激发电子空穴对的共振导致边带发射,将荧光能量从二氧化钛纳米粒子转移到氧化锌纳米棒上实现的。
金属纳米颗粒的局域表面等离子共振效应可以提高散射效率,增强随机激光的性能,使随机激光的阈值更低,谱线更窄。常用的金属纳米颗粒有金、银等,通常与激光染料一起掺杂在其他散射体系中,比如掺杂在聚合物薄膜[28]或半导体材料[29]中。
基于量子点的随机激光是近几年的研究热点之一,近年来核壳结构的胶体量子点结构得到不断改进。Claudia Gollner等人[12]利用CdSe/CdS胶体量子点薄膜获得了重复性高稳定性好的随机激光体系。樊海波等人[30]用电子束泵浦CsPbBr3钙钛矿薄膜,证明高能电子束具有很强的随机散射特性,更易产生随机激光。
2019年,F. Lahoz等人在小鼠脑组织中观察到随机激光[31]。同年,Zhen-zhen Zhang等人发现[32]POSS(polyhedral oligomeric silsesquio-xanes:多面体低聚倍半硅氧烷)纳米颗粒通过共价键连接到DPP (perylene diimide:苝二酰亚胺)的两端,可以产生NFSE (near-field sca-ttering enhancement:近场散射增强),这种苝基聚集体的NFSE可以产生相干随机激光。2020年,中国台湾的Yun-Tzu Hsu等人[33]利用3D打印技术制作出结构灵活多样并且应用广泛的随机激光器。
由于缺少谐振腔束缚,随机激光的性质与传统激光器产生的激光有很大的不同。随机激光没有规则的模结构,没有等间距的纵向模式,输出光束也没有明确定义的波前结构。但二者也有相似之处,就像传统激光器一样,随机激光器也需要满足增益大于损耗的阈值条件,受激辐射仍是随机激光的关键。
传统激光器中的精密谐振腔结构可以产生具有相干性、方向性、单色性和高强度的激光,而随机激光器会产生多种模式、各向异性的激光,并且这种激光的空间相干性和时间相干性都很低。低相干性对很多激光应用来说都是一个不利条件,但这个特点在激光散斑抑制方面和宽谱激光应用等方面有很大的优势。
由于不需要精密微腔,随机激光器可以制作得小巧紧凑,制造起来也相对简单。阻碍随机激光发展的主要是其高阈值和无方向性的特点。为了解决这两个难题,研究者们想到利用光纤波导的一维束缚来控制随机激光的阈值和方向。现在随机激光的研究重点在于对随机激光调控,包括波长、偏振、阈值、输出功率等,同时寻找新的应用场景。
-
随机激光器的工作原理与传统激光器类似,存在一个阈值,当系统的总增益大于损耗时就会出射激光。但随机激光的模式与传统激光器也有很大不同,它是由多次散射而不是由激光腔决定的。随机激光在弱散射系统和强散射系统中都能产生。当
$$\lambda < {l_s} < L$$ (1) 时,光子做扩散运动,整个散射体系被称作一个扩散体系。式中:L为散射体系的尺度;
$\lambda $ 为光波长。当$${l_s} \geqslant L$$ (2) 时,散射体系被称作亚平均自由程体系或者弹性体系。弱散射体系一般出现在以上两种类型中,基于能量密度或能量反馈的非相干随机激光往往在弱散射体系中产生。当
$${l_s} \leqslant \lambda $$ (3) 时,散射体系被称为局域化体系。强散射一般会在这种体系中产生,散射光波能够产生场或振幅反馈,形成干涉。根据Letokhov等人的理论,要使光在散射过程中产生受激辐射,需要满足
$$ V\geqslant {V}_{cr}{\text{且}}{L}_{pat}\geqslant {L}_{gen}$$ (4) 式中:V为散射体系的体积;Lpat为
光子的路径平均自由程,即受激发射光子在散射体系中所走的平均路程;Lgen为光子产生自由程,即入射光子使增益体系产生受激辐射光子前所走的平均路程,其值可用增益自由程lg (发射光强被放大e倍所走的路程)来估计。这样,散射介质中就会发生一个“链式反应”,使光子数目剧增,即上文提到的“光子弹”现象。2016年,Leicheng Yin等人[34]发现ls和lg的差值 $$\Delta l = {l_s} - {l_g}$$ (5) 也会制约随机激光的产生。
随机激光峰代表了激光模式,H. Cao等人[35]测量了弱散射系统中激光模式的相关光谱以及强度统计,与放大自发辐射峰(ASE)进行了比较:由于ASE的峰值来源于独立的自发辐射,这些峰值的频率互不相关;而弱散射系统中的激光峰值(peaks)强度比ASE的峰值(spikes)大50倍左右;数值模拟结果表明,增益区域内散射体反馈的选择性放大可以显著地改变激光模的轮廓。
在强散射介质中,多重散射与光放大的结合可以产生随机激光。通过不断增加散射粒子的密度,多重散射为激光出射提供共振反馈,H. Cao的团队观察到ASE到激光峰值的转变[36]。他们通过基于麦克斯韦方程组的数值模拟,清晰地展示了转变发生的时间。在多模重叠的情况下[37],用时域有限差分(FDTD)法求解Maxwell-Bloch方程,能够重现ASE到受激辐射的跃迁;在同一随机体系中,噪声不会影响模式的频率,但增益内的所有模式都不断被噪声激发放大,导致稳定的发射谱中总是出现多种激光模式。另外,共振谱的重叠程度越小,噪声对激光的影响就越小。
1966年,Ambartsumyan这样解释非相干激光现象:光在散射体系中多次散射,光的传播方向在每次散射时都会改变,因此,散射介质中的光无法回到它原来的位置;或者用模式理论解释:散射光造成大量低Q值的谐振,这些低Q值的谐振在频谱上重叠,形成一个连续的光谱,即非谐振反馈的随机激光[24]。
显然,非相干随机激光的理论模型无法解释相干反馈的产生。因为在这些模型中,仅针对光强进行计算,并没有考虑电磁场和相位。于是研究者们提出了一系列模型,尝试定量分析随机激光的干涉现象,包括混沌激光理论[38-44]:混沌激光器的形状不规则,散射粒子处于腔中随机位置处;量子理论:从量子统计特性角度来理解离散的随机激光[45];对于未超过激光阈值的线性介质,可以用随机散射相关的统计学理论解释[46-47];半经典理论[48-52]:结合极化率密度方程、麦克斯韦方程和粒子数反转速率方程,得到随机体系中的电磁场分布和时间演化特征;环型波导理论[8, 53]:将随机共振区域看做介电常数比周围环境大的环型区域;时间理论[54]:将麦克斯韦方程与电子密度的速率方程相结合;数值解析理论[55-56]:用解析方法推导了随机介质中相干稳态激光振荡的条件。
Diederik S. Wiersma认为扩散随机激光和相干随机激光不是两种对立的随机激光[57]。随机材料中的光散射是弹性的,理应存在干涉效应,区别在于我们是否能从一个适当的实验中观察到干涉带来的影响。他认为相干反馈对随机激光来说不是必须的,一阶相干是对光场波动的度量,二阶相干性解释了强度的涨落。如果光满足一阶和二阶相干,那么产生的随机激光就具有相干性。
-
局域化的概念最先由安德森提出[58],他描述了掺杂介质中的自旋扩散和传导过程,从本质上引入了随机性,说明了扩散对密度的依赖性:弹性散射后,电子的相位改变。随着传播距离的增加,当系统的无序性强到一定程度时,波函数的包络会呈指数衰减,即波函数是局域的。后来Abrahams等人发现无序电子系统的电导率与系统尺度有关[59]。在无限一维系统和二维系统中,较小的随机性就能产生局域化。而在三维系统中局域化的出现需要满足Ioffe-Rrgel判据[60],即
$$k{l_s} < 1$$ (6) 式中:k为波矢。该判据与局域化体系的分类条件相比,相差1/2π的系数。从本质来说,电子的局域化来源于电子的波动特性,那么对同样具有波动特性的光波[61-62]和声波[63]来说也应存在这种现象。在大多数随机材料中,光会在整个样品中扩散,模态会扩展。在局域化散射体系中,强烈的干涉会使光波在前进的方向上干涉相消,散射光会被禁锢在一定的区域内,这就是光子的局域化。相干背向散射被称为一种弱局域化现象,也叫预局域化。当入射光在散射介质中散射后,在其反方向可以观察到一个强度大于散射背景光的光斑,类似于无序介质中的后向散射[64-65]。这是因为在介质中传播路径相同但方向相反的两束光具有完全相同的相位,会发生干涉。
在不同介质中可以观察到局域化现象,比如截断的一维[66]和二维[67]无序光子晶体晶格的边界上、无序光纤中[68]等,也可以通过研究样品的反射[69-70]、透射[71-72]、背向散射[73]以及随机激光[74-76]等特性来研究局域化在不同样品中的特点。
近几年,研究者们对随机激光局域化的研究取得了新进展:Giancarlo Ruocco等人[77]展示了无序光纤中单横模局域态,这要求系统在传输方向是均匀的,而在横截面方向的折射率分布要具有无序性;合肥工业大学的Lei Hu等人[78]在氧化铝陶瓷柱的半径上引入缺陷,观察到Dirac频率处的峰值,展示了二维光子晶体微腔中的局域化现象。Behnam Abaie等人[79]在实验中观察到安德森局域光纤中M2<2的高质量波前,不需要对输入光进行复杂的空间调制就可以产生单模激光输出。Walter Schirmacher等人[80]设计实验探寻了描述安德森局域化的两种理论:一种理论认为局域长度对入射波长有着强烈的依赖性;另一种理论认为根据电模量的空间波动,局域长度不受光波长的影响。实验结果和基于非线性sigma模型的理论分析都证明了第二种理论的正确性。图2表明第一种理论是错误的,从图2(b)中可以看出局域化长度不随波长变化。

图 2 (a)平均局域化长度与沿光纤传输距离z的函数;(b)测量了横向无序光纤的平均局域化长度与入射激光波长(圆)的函数关系,并与(a) (三角形)进行了比较[80]
Figure 2. (a) Average localization length as a function of the distance z along the fiber for the two light wavelengths; (b) Measured averaged localization length of fibers with transverse disorder as a function of the incident-laser wavelength (full circles) compared with (a) (full triangles)[80]
光在随机介质中的局域态也被称作准态,当随机介质的结构确定后,准态模就基本确定下来,当散射介质受到不同方式泵浦就会激发不同的模式谐振。根据随机散射介质的边界条件,随机介质内部和外部的准态会发生能量交换。这个过程中,光子从边界逃逸和交换会造成光子损耗,这种损耗可以用准态频率的虚部来描述。
-
随机激光的模式来源于无序系统的本征态,具体来源于哪一种本征态主要取决于模式的质量因子以及各模式的相互作用。到目前为止,还没有一套公认的、完备的理论或模型能系统地解释随机激光的各项特点。这个模型至少应包括对增益产生的解释、对是否产生干涉及多种模式相互作用的解释,还要包括噪声对散射系统的影响。C. W. J. Beenakker在1998年预测了随机激光放大自发辐射过程中的过量噪声,将光统计分布与散射矩阵联系起来,计算出辐射混沌散射系统的热发射统计量[44]。V. M. Apalkov等人利用折射率波动的薄膜制作了一个无序引发的谐振器,忽略增益对空间分布的影响,计算出谐振器的面密度,得到“谐振腔”的Q值和散射平均自由程[53]。H. Cao[81]等人证明了随机激光模的空间重叠和相互耦合,但没有从理论上分析这些现象产生的物理本质。Karen L. vander Molen等人进行定量实验并从理论上分析了随机激光发射谱的强度涨落,在纳秒或皮秒脉冲泵浦下,设计了一个预测随机激光输出功率波动的模型[82]。Johannes Fallert等人提出一种直接提取模式局域区域的方法,用脉冲泵浦ZnO粉末,观察到强局域随机激光模式与其他空间扩展的模式共存:扩散模式主要出现在增益最高的光谱区域,而强局域模式出现在增益较低的区域[83]。Peter Stano和Philippe Jacquod认为强散射体系中的每一个激光模式都来自一个安德森局域模。他们证明干涉导致的安德森局域化不受非线性的影响,空间烧孔效应导致的非线性决定了发射模式、阈值和强度[84]。
-
20世纪70年代,研究者们开始研究激光的统计力学特点[85]。例如均匀腔内激光的统计特性,包括激光锁模过程的相变[86-88]、非线性光学中的模式形成与竞争[89-90]以及激光脉冲的量子行为[91]等。随机激光涉及热力学、非线性光学、量子光学等众多领域,统计力学在无序物质中也有广泛的应用。例如Lucia Florescu和Sajeev John[92]展示了随机多重散射介质中出射光子的光子数概率分布。另外,自旋玻璃理论和随机激光动力学的结合也是典型的例子。
2006年,Angelani等人利用无序系统的统计物理方法研究了多模激光的非线性动力学,展示了光在随机非线性介质中传播时表现出的玻璃化行为,将副本对称性破缺(Replica Symmetry Breaking,RSB)相变预测为泵浦强度的函数[93]。对称性破缺是一个跨学科的概念,是指对称性良好的系统中出现了不对称的元素。副本对称性破缺是指相同的系统在相同条件下可以处在不同的状态。同年[94],Angelani等人通过理论分析预测随机激光的锁模变化会以无序系统相变的形式展现出来,副本对称性破缺会出现在随机激光系统中。2015年,他们提出一个研究多模随机激光的模型,从非线性和无序的角度描绘了闭腔到开腔转换的完整相位图,并预测对称破缺相变能在有荧光淬灭缺陷的随机激光系统中出现[95]。同年,F. Antenucci等人提出了一种适用于开放和不规则腔的多模激光无序平均场模型,预测了阈值下的副本对称性破缺相变[96]。N. Ghofraniha等人[97]在非晶形固体中加入低聚物染料,给出了副本对称性破缺的第一个实验证明并提出一种新的方法来描述随机性。为了识别副本对称性破缺的发生,用一定频率下的光谱强度波动
${\Delta _\alpha }\left( k \right)$ 来表征不同副本强度起伏之间的重叠${q_{\alpha \beta }}$ 。$${\Delta _\alpha }\left( k \right) = {I_\alpha }\left( k \right) - \bar I\left( k \right)$$ (7) 其中,
${I_\alpha }\left( k \right)$ 是副本指数为$\alpha $ 、数据采集指数为k的光模式的强度;$\bar I\left( k \right)$ 是各光模式强度的平均值:$$\bar I\left( k \right) = \frac{1}{{{N_s}}}\sum\limits_{\alpha = 1}^{{N_s}} {{I_\alpha }\left( k \right)} $$ (8) 式中:
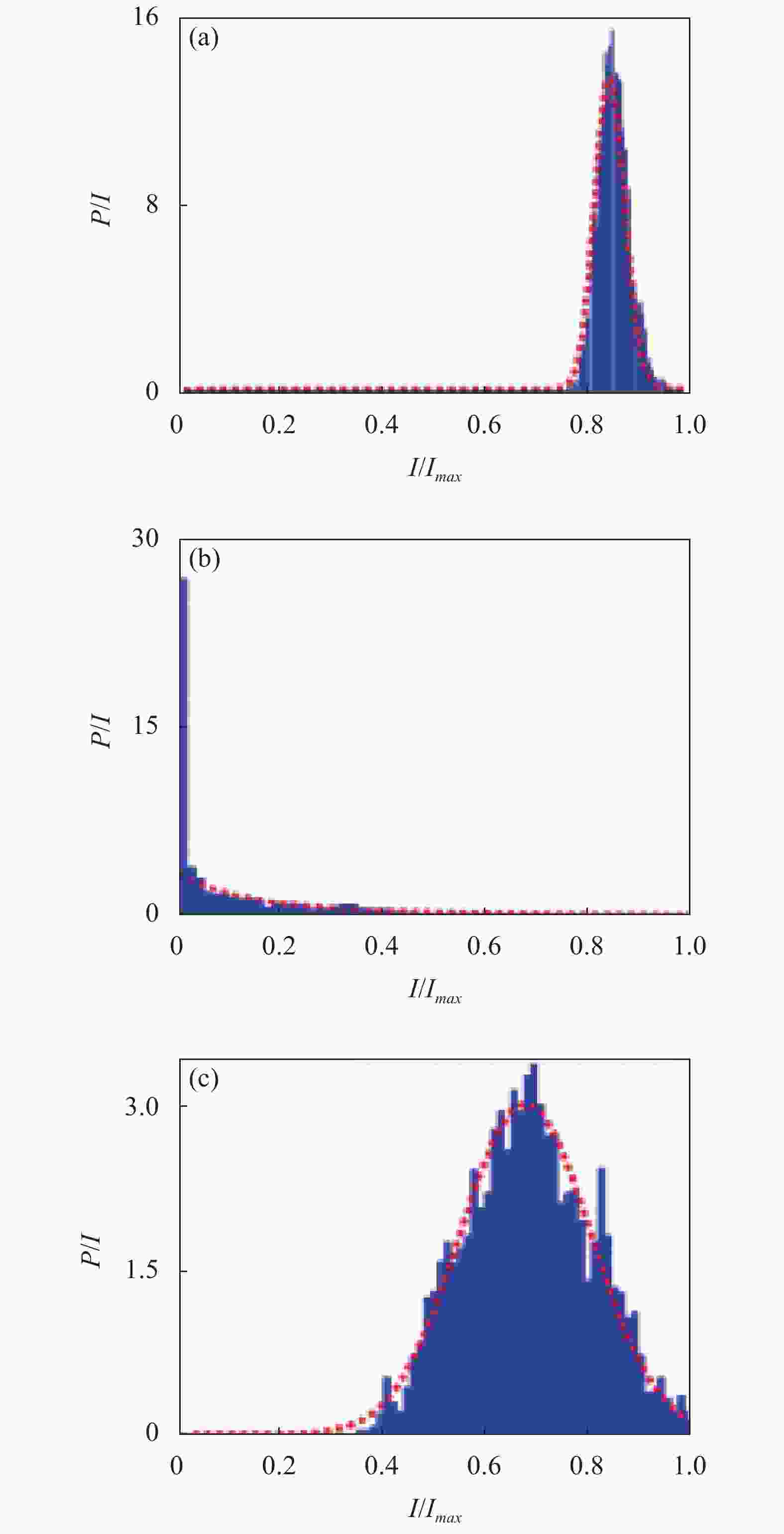
${N_s}$ 为副本数。$${q_{\alpha \beta }} = \dfrac{{ \displaystyle\sum\limits_{k = 1}^N {{\Delta _\alpha }\left( k \right){\Delta _\beta }\left( k \right)} }}{{\sqrt { \displaystyle\sum\limits_{k = 1}^N {\Delta _\alpha ^2\left( k \right)} } \sqrt {\sum\limits_{k = 1}^N {\Delta _\beta ^2\left( k \right)} } }}$$ (9) 式中:N为获取的光谱数;β为副本指数。根据测得的光谱,计算出不同泵浦能量下共Ns(Ns−1)/2个qαβ的值q,得出q的分布函数P(q)。他们发现在泵浦能量较低时,光谱强度波动重叠参数q集中在0附近,各模式在顺磁相的状态下不发生相互作用。而在高能泵浦下,光谱强度波动重叠参数会分散在[−1,1]之间,各模式在自旋玻璃相的状态下发生相互作用并受到无序性的干扰。两种状态的临界点就是激光的阈值,这种转变也表明出现了副本对称性破缺现象。之后,Anderson S. L. Gomes等人也在一维连续掺铒光纤随机激光器[98]和掺杂YBO3的Nd3+晶体粉末的随机激光体系[99]中观察到了副本对称性破缺。Cid B. de Araújo等人[100]介绍了掺铒光纤随机激光器的强度统计行为。如图3所示,当泵浦能量从阈值以下增大到阈值之上时,随机激光出射强度会从 Gaussian 分布(正态分布)转变为 Lévy分布(“尖峰肥尾”),再回到Gaussian 分布。Jiangying Xia等人等人[101]利用静电纺丝技术制作了聚合物纤维随机激光器,在不同的泵浦能量下观察到明显的顺磁相和自旋玻璃相。同样的,当泵浦能量达到阈值时,相变产生,统计结果表明自旋玻璃理论可以用于描述随机激光体系的统计特性。
-
光纤随机激光具有以下特点:(1)光纤波导可以限制光的径向散射,将出射光约束在光纤轴向,有效缓解随机激光无方向性的缺陷;这种限制也促进了光场的相互作用,能产生许多非线性光学现象;(2)丰富的光纤种类能为激光的产生提供不同的增益机制和反馈类型,为随机激光的研究提供了广阔的平台。
根据反馈类型的不同,可以将光纤随机激光分为填充型光纤随机激光、基于光栅的光纤随机激光以及基于Rayleigh散射的分布式反馈光纤随机激光。根据增益机制的不同,可以将随机激光分为Raman型、Brillouin型、有源光纤型。根据输出光的不同,可以分为连续输出型和脉冲输出型。在随机增益体系中,纳米颗粒提供多重散射反馈,增益介质通常为荧光分子。增益介质和散射介质可以是同一物质,比如量子点散射体系;增益介质和散射介质也可以是不同物质,比如纳米颗粒混合激光染料的溶液体系。
-
① 填充型光纤随机激光
此类光纤随机激光是最早提出的一种类型,它基于纳米颗粒的散射获得随机激光。2007年,Christiano J. S. de Matos等人[102]将散射增益介质——TiO2悬浮物和罗丹明的乙二醇溶液注入空心光子晶体光纤的纤芯,得到第一个光纤随机激光器,实现了对随机激光出射方向的控制,通过侧向泵浦获得非相干的随机激光。填充后的光纤仍满足全反射条件,仍能限制并引导光的传输。但是这种光纤随机激光器的自发辐射因子[103]比之前的块状随机激光器低10倍左右。
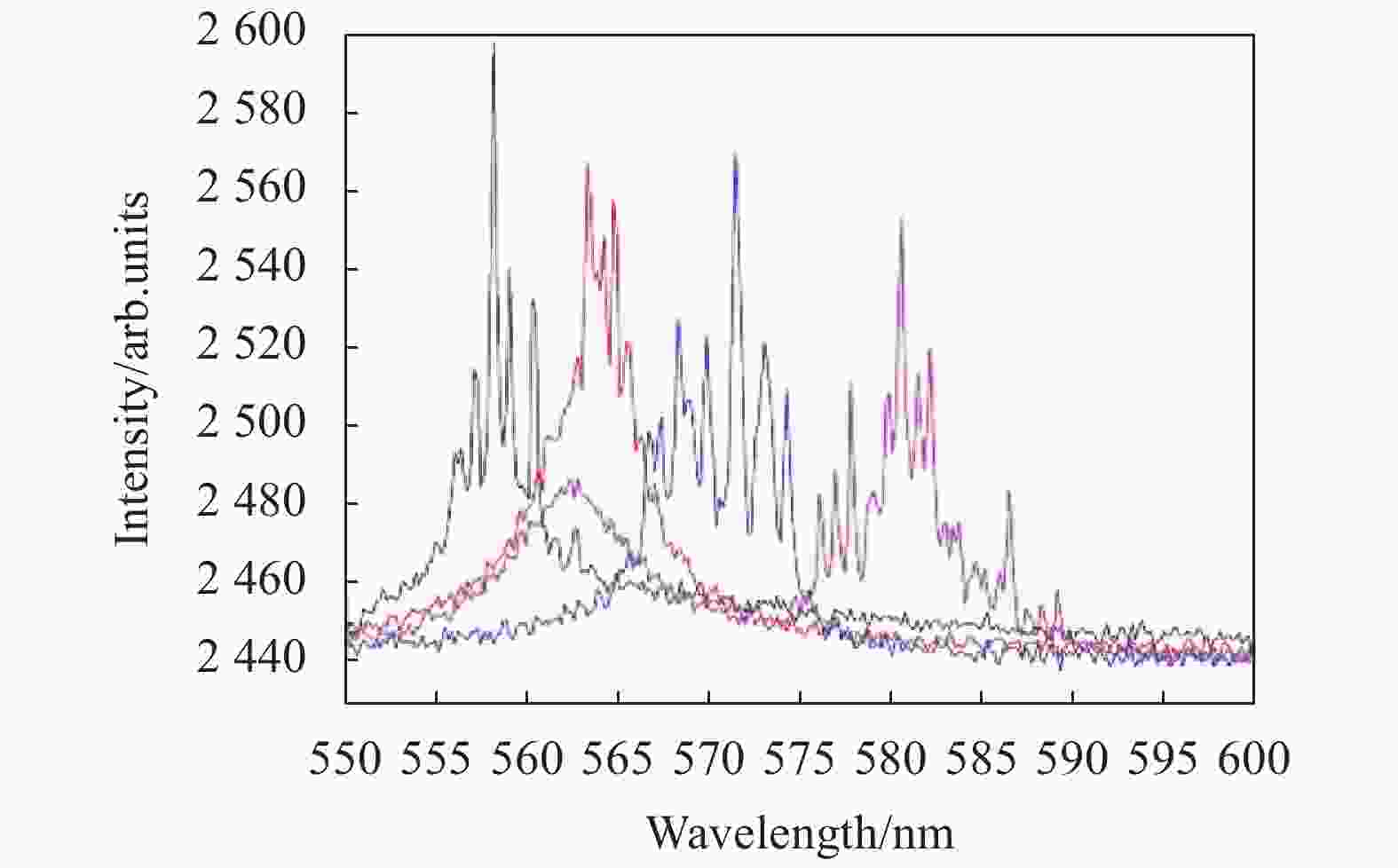
2012年,胡志家等人[13, 104]将POSS纳米颗粒和PM597激光染料的二硫化碳溶液注入空芯光纤中制成液芯光纤,实现了从非相干到相干随机激光的转换。图4(a)所示为非相干随机激光发射谱,图4(b)为相干随机激光发射谱。在光纤的束缚下,散射平均自由程ls很小,通过端面泵浦得到了相干随机激光,其阈值为0.41 mJ。从相干随机激光的发射谱中可以看出,在不同泵浦能量下,随机激光各峰值之间的波长间隔几乎相等,这预示着“谐振腔”的存在[73]。用Fabry-Perot腔的理论来解释这种现象。根据
$$\Delta \lambda = {{{\lambda ^2}}/{2{n_e}}}d$$ (10) 式中:波长间隔Δλ由腔长d决定;ne为随机散射增益体系的有效折射率。该体系的散射平均自由程ls远大于的d,根据上文中对强弱散射体系的分类,相干随机激光一般不会在弱散射体系中产生。因此,该散射体系中一定存在另一种反馈使光子回到增益介质中。这种反馈极有可能是光纤波导的全反射带来的。“散射-全反射-散射”效应既提高了散射概率,又增加了干涉概率,还有利于调控随机激光的出射方向。
2013年,他们又制作了聚合物光纤随机激光器[18]。聚合物光纤的纤芯材料是掺杂了PM597激光染料的POSS、甲基丙烯酸甲酯(MMA)和甲基丙烯酸苄酯(BzMA)的共聚物,包层材料是MMA和丙烯酸丁酯(BA)共聚物,这种聚合物光纤随机激光器的阈值进一步降低至54 μJ。2014年,他们制作了长程无序和短程无序两种聚合物光纤[105]。其中短程无序聚合物光纤的材料与上文相同;长程无序的聚合物光纤的纤芯材料是掺杂PM597的MMA和BzMA共聚物,包层材料与短程无序聚合物光纤相同。通过端面泵浦,在两种聚合物体系中都能观测到相干随机激光,通过调控散射强度控制随机激光输出波长,调谐范围为568.7 nm至580.7 nm。
2016年,Wei Li Zhang等人[106]在类似光纤的毛细管(内外直径分别为100 μm和170 μm)内表面涂覆一层厚度约为3 μm的TiO2薄膜作为包层,再将罗丹明溶液填充进毛细管中作为纤芯。包层的折射率大于纤芯,包层中的散射颗粒能将侧面泵浦的入射光散射到纤芯的增益介质中,进而产生随机激光。实验数据表明,出射激光的强度与纤芯染料的浓度呈指数关系,可以作为一种检测粒子浓度的新方法。
填充型光纤随机激光具有方向性良好和阈值较低等优点,但制作起来相对复杂,需要选用合适的特种光纤和散射增益介质。液芯结构存在纳米颗粒吸附聚集、激光染料失效的缺陷。在填充后需在光纤两端涂抹紫外胶固化,不利于与现有的商用光纤熔接,阻碍了填充型光纤随机激光在全光纤系统中的应用。
② 分布式反馈光纤随机激光
分布式反馈光纤随机激光可以看作随机激光和分布式反馈光纤激光的结合[107],它的构成非常简单,通常只包含一个泵浦激光器和一段光纤。其中,基于光栅的光纤随机激光是指在光纤上刻写空间随机分布的光纤Bragg光栅,2009年,N. Lizárraga等[108]用倍频氩离子激光器产生的紫外光,在铒锗共掺的单模光纤纤芯上刻写光栅阵列。每个光栅长5 mm,各光栅之间的间隔在4.2~5.8 mm间随机分布。在980 nm的激光泵浦下,在反射端观察到多个竞争模式的发射光谱。光栅阵列的随机反射使某些波长的光产生局域化[109],光在局域区域的强度比入射光的强度大6倍左右。将各局域区域前后的两个光栅看做Fabry-Perot腔的两个反射镜,在合适的泵浦下,当增益大于损耗时就能观测到随机激光的出射。
同年,Mathieu Gagné和Raman Kashyap 利用他们在2008年发表的一种在光栅结构中引入随机相位误差的方法[110]刻写了由大量不同长度、相互间存在随机相移的短光栅组成的光栅阵列,制成阈值约3 mW、线宽约0.5 pm的光纤随机激光器[111]。2015年,Lulu Wang等人[112]在铒镱共掺光纤上刻写仅25 mm长的多相移光纤光栅,制成超短光纤随机激光器,通过调节泵浦功率可获得单波长或双波长输出。2016年,S. R Abdullina等人[113]在掺铒保偏光纤上刻写4 cm长的FBG,这个光栅由10个相位和振幅随机变化的子光栅构成,获得了20 mW左右的单纵模随机激光输出。
基于光栅结构的光纤随机激光器具有阈值低、结构紧凑、加工简易等优点。但有时模间干涉会带来复杂的模式竞争,在丰富光子行为的同时会使输出光谱不稳定。2019年,胡志家等人[114]借助45°倾斜光栅的极弱反射(反射率为0.09%),基于拉曼和掺铒光纤的混合增益和单模光纤的极弱Rayleigh反馈制作了高保偏的光纤随机激光器,实现了1556.05 nm(1556.06 nm)的固定波长输出,消光比约为15.3 dB。
基于Rayleigh散射的光纤随机激光也是一种分布式反馈随机激光,其反馈机制是光纤本身折射率不均匀带来的Rayleigh散射。2010年,D. V. Churkin等人[115]提出基于分布式Rayleigh散射反馈和受激Raman增益的光纤随机激光器,在无镜的开放腔中获得类似高斯光束的随机激光窄谱线。由于普通单模光纤的背向瑞利散射系数很低(1550 nm处为4.5×10−5 km−1)[116],所以D. V. Churkin等人使用了41 km的超长单模光纤。同年,S. A. Babin在IEEE的光学全球会议上发表文章[117],分析了基于Rayleigh散射和Raman增益的分布式反馈光纤随机激光器的基本工作原理和实验结果。这种基于光纤本身瑞利散射的光纤随机激光器结构简单,有利于实现随机激光器的全光纤化。
-
从上文中可以看出,基于瑞利散射的光反馈需要借助增益实现光放大。这些增益包括Raman增益、Brillouin增益以及光纤中掺杂的稀土离子的增益。
① Raman增益与Brillouin增益
散射是指光束经过光学性质不均匀的介质时发生方向偏转,向四面八方散开的现象。也指在透明介质中,电子吸收入射电磁波的能量,向各个方向发出次波的现象。按照散射前后的能量关系,散射可以分为弹性散射:包括Rayleigh散射和Mie散射;非弹性散射:包括Raman散射和Brillouin散射。弹性散射的散射光频率不会发生改变,而非弹性散射的光波会在散射过程中发生能量交换,光波频率会改变,这是由与时间变化相关的介质不均匀起伏引起的。在非弹性散射过程中不同波长的光之间有着丰富的能量传递,是一种有效的增益机制。
瑞利散射一般存在于不导电、各向同性,由球形小质点构成的稀体系。散射光强与入射波长的四次方成反比,光波长越短,散射光强度越大;入射光与晶体晶格振动的声子相互作用,散射光频移在3×1010~3×1013 Hz称为Raman散射,散射光频移在3×107~3×1010 Hz称为Brillouin散射。光纤内的受激Raman散射(Stimulated Raman Scattering,SRS)包含两个能量变换过程:一是斯托克斯光通过受激拉曼散射获得拉曼增益,从泵浦获得能量而被放大;二是泵浦光通过受激拉曼散射将能量转移给斯托克斯光而衰减,两个过程在光纤内传输也会有能量损耗。在足够强的光学激发下,Brillouin散射的Stokes光和声学波可能被指数式放大,这个效应称为受激Brillouin散射。受激Brillouin散射(Stimulated Brillouin Scattering,SBS)是指当受到超过阈值的入射光泵浦时会激发产生超声波,该超声波反过来对入射激光本身进行散射。受激Brillouin散射来源于两种机制:电致伸缩效应和物质对光的吸收。在透明介质中,只有电致伸缩效应起作用;在吸收介质中,光吸收引起的局部温度变化将导致可传播的密度波,进而导致受激热布里渊散射(Stimulated Thermal Brillouin Scattering,STBS)。当以受激布里渊散射为增益机制时,只能采用后向泵浦方式,即信号光与泵浦光反向才能产生光放大[118-121]。
② 有源光纤的增益
在光纤中掺杂稀土离子作为增益介质的光纤被称作有源光纤,比如掺铒、掺镱、掺铋等。在光纤随机激光的报道中,最常见的就是EDF (Erbium-doped fiber)。分析EDF的理论模型有原子速率方程、功率传输方程以及在前两者基础上推出的Giles模型[122]。
2010年,Andrei A. Fotiadi[123]解释了分布式反馈光纤随机激光器的非线性原理。他认为当Raman增益抵消光纤中的损耗时,一些共振光子最先达到出射条件,使光谱中出现狭窄的随机成分,而产生的随机尖峰又会导致类似雪崩的Brillouin不稳定性。受激Brillouin散射中光子与声子的相互作用与Raman增益过程类似,只是放大程度不同。在1550 nm的泵浦下,Brillouin增益系数比Raman增益高三个数量级。当泵浦功率超过阈值时,交叉相位调制能够抑制布里渊不稳定性,使激光稳定输出。
2020年,国防科技大学的Jun Ye等人[124]从理论和实验中证明宽带泵浦可以实现更宽更平坦的多波长随机Raman光纤激光器。用带宽为40 nm的ASE光源泵浦2 km长的掺锗光纤,获得光谱范围从1116~1125 nm的随机激光出射谱,谱中有19条激光尖峰,间距约为0.47 nm,信噪比约为31 dB。如图5所示,JiangMing Xu等人[125]演示了光纤随机激光中的光学怪波[126]。用非相干ASE光源泵浦3.05 km长的无源光纤,由于光纤折射率不均匀和电致伸缩效应会引发受激布里渊散射,多普勒效应会激发频率减小的光子,使该光纤随机激光具有自脉冲现象,在阈值附近和远超阈值的泵浦下都可以观察到怪波的存在。O. A. Gorbunov等人[127]在分布式反馈光纤随机激光器的输出光谱中观察到怪波的泊松分布,发现怪波产生的概率与随机激光的输出波长有关。
-
自2007年Christiano等人设计出第一个光纤随机激光器以来,世界各国已有众多研究团队就这一领域开展了各方面的工作。在这些研究中,除了对随机激光相关原理的分析研究,还包括众多对随机激光器各参数进行调控的探索。随机激光的输出光谱蕴含着丰富的物理内涵,为随机激光的调控提供了广泛的空间和丰富的方法。下面针对随机激光器的输出波长、功率、阈值、线宽、模式、方向、偏振等参数的研究进展和最新成果进行简单的总结。
-
研究人员广泛开展了随机激光输出波长调控的研究,包括波长可调谐的随机激光器、多波长输出的随机激光器。
在可调谐随机激光的研究方面,2011年,英国Aston大学的Turitsyn团队[128]设计了一个调谐范围为1535~1570 nm的随机分布反馈光纤激光器,采用多个不同波长的 FBG 作为点式反馈来实现多波长输出,具有输出功率平坦和效率高的优良特性,不亚于传统的拉曼光纤激光器。2016年,中国科学院上海光学精密机械研究所的Lei Zhang等人[129]用掺镱激光器泵浦掺镱双包层保偏光纤,将瑞利反馈的宽谱特性与受激拉曼散射相结合,通过不断调整泵浦波长、增加泵浦功率激发高阶拉曼斯托克斯随机激光,实现了1070~1370 nm的输出调谐。随机分布反馈拉曼光纤激光器在任意波长均可获得受激拉曼散射增益和瑞利散射反馈,具有超宽的波长调谐范围。2017年,他们利用相似的结构实现了1~1.9 μm的连续调谐随机激光输出[130]。同年,胡志家等人[131]利用掺杂纳米粒子和激光染料的聚合物光纤制作了三种不同材料的实时温控可调谐光纤随机激光器。由于所使用的聚合物材料具有较大的负热光系数,通过改变温度来调节纤芯材料的折射率,进而改变平均散射自由程ls。当温度从25 ℃升高到70 ℃时,光谱红移,发射波长的调谐范围分别为18.5、17.9、12.3 nm。2020年,他们从蚕丝中提取真丝蛋白与激光染料混合,利用静电纺丝工艺制成无序纤维,通过改变泵浦位置获得调谐范围为33 nm的相干随机激光[132],如图6所示。
2016年,Sreekanth Perumbilavil等人[133]制作了光孤子辅助的光泵浦液晶随机激光器。将激光染料掺杂在向列相液晶中,基于近红外光束发射的空间孤子实现对随机激光的增强和限制,获得波长和线宽可调的随机激光。有孤子辅助的随机激光与无孤子辅助的随机激光相比具有更窄的线宽、更低的阈值、更高的激光效率。
在多波长输出的随机激光器方面,有多种方案可实现随机激光的多波长输出:比如基于拉曼增益的方法,包括采用保偏光纤环型镜[134]、法布里-珀罗干涉仪[135]、Lyot滤波器[136]等。还有基于级联布里渊散射的方法:比如多波长布里渊-掺铒光纤随机激光器[137-138]、多波长布里渊-拉曼光纤随机激光器[139-141]等。2020年,国防科技大学的Yang Zhang等人[142]用两个带宽可调滤光片来调节斯托克斯光的中心波长和线宽,用自制的线偏功率放大器泵浦800 m长的掺锗保偏光纤,获得波长、线宽、功率比都可调的双波长随机分布反馈光纤激光器。其中,波长间隔能从2.5 nm连续调至13 nm、3 dB线宽范围为1.01~2.20 nm、斯托克斯线的功率比可在0~100%间调节。同年,N. Mohd Yusoff等人[143]用两根间隔200 μm的光纤制成外置空腔,两根光纤的端面切平,其作用相当于一对反射镜。采用功率为2 W的双向泵浦,在1552.5 nm和1557.7 nm处实现了双波长随机激光输出。
瑞利散射反馈的光谱为宽带反射谱,因此光纤随机激光器的激射带宽一般比传统激光器更宽。目前的研究已经从最初的1500 nm附近的近红外光拓展到了中红外波段和可见光范围,E. I. Dontsova等人[144]制作了一种随机分布反馈的拉曼光纤激光器,输出光照射在非线性晶体上,使1308 nm的近红外光纤随机激光倍频到654 nm,将光纤随机激光拓展到可见光范围。
-
起初,随机激光的输出功率不到1 W[145]。近年来,研究者们设计了众多方法实现高功率[146-153]、高效率[154-155]的随机激光输出:比如采用高功率泵浦源[156]、缩短光纤长度[157]或腔长[149,158]、利用高阶Stokes光[159-161]、采用锥形光纤[162-163]等方法。2015年,Yulong Tang和Jiangqiu Xu[164]基于受激Brillouin散射和光纤纤芯中的瑞利散射制作了调Q随机激光器。瑞利散射诱导产生随机共振,受激Brillouin散射使光纤中“谐振腔”的Q值增大,从而产生高亮度、高功率的随机激光,其峰值功率达到2 kW以上。2019年,Jun Ye等人[165]用宽带ASE光源泵浦375 m长的无源光纤,获得超过99 W的随机激光输出功率。发现宽带泵浦在抑制光谱展宽的同时还能保持超高的光谱纯度(约99.96%),利用无源光纤提供随机分布反馈,光纤光栅提供点反馈,得到非相干随机激光。
基于拉曼和掺铒的混合增益还可以获得低阈值的随机激光。2018年,电子科技大学的Han Wu等人[166]提出一种低阈值、高效率的光纤随机激光器。将10 km长的单模光纤与12 m长的掺铒光纤相连,在掺铒光纤后面接一个光纤布拉格光栅以形成双向泵浦,阈值低至75 mW,光光转换效率达65.5%。
2014年,东南大学的Lihua Ye等人[167]实验研究了染料掺杂液晶随机激光的电磁调控。液晶的排列方式会影响随机激光的阈值,增大外加电场时,部分液晶分子呈均匀排列,随机激光的响应时间会减小甚至无激光出射。当外加电场被移除时,液晶分子的无序度增加。光子在无序的LCs中再次形成多次散射,从而恢复了随机激光。2020年,Zhiwen Wang等人[168]用紫外固化的方法制备含 ZnCdSeS/ZnS合金的量子点掺杂聚合物分散液晶,通过改变液晶和量子点的掺杂浓度,可以改变液晶滴的密度和形态,进而改变随机激光的阈值、线宽和稳定性,实现了50 μJ的低阈值随机激光。
-
窄线宽随机激光的研究对随机激光在传感领域的应用具有十分重要的意义。实现随机激光的窄线宽输出主要有以下几种方法,如使用窄线宽的反射或透射器件压缩随机激光的带宽。2013年,Meng Pang等人[169]用连续波光纤激光器作为泵浦源,在相干布里渊光纤随机激光器中观测到窄线宽激光脉冲。以一段25 km长的普通单模光纤中的受激布里渊散射为增益机制,而另一段非均匀光纤中的瑞利散射提供了随机分布反馈,实现了线宽约为7.5 Hz的相干随机激光输出。同年,D. V. Churkin团队的研究者们[170]用窄带光纤Bragg光栅和光纤法布里-珀罗干涉滤波片进行滤波选模,使随机激光的出射线宽降至0.05 nm,获得了多波长窄带分布式反馈光纤随机激光。2015年,Daniel Leandro等人[171]用相移光纤Bragg光栅和普通光纤Bragg光栅组合作为反射镜和滤波元件,限制了受激Raman增益的宽增益谱和瑞利散射的宽谱反射,获得线宽为3.2 pm的窄带随机激光发射谱。
另一种方法是用受激布里渊增益和随机瑞利反馈或随机光栅压窄线宽。2016年,Yanping Xu等人[172]设计了一种基于随机光栅的布里渊光纤随机激光器,随机光栅使随机反馈显著增强,超过了瑞利后向散射的强度,使随机激光获得布里渊增益并降低了阈值,获得约45.8 Hz的相干随机激光输出。2017年,同组的Liang Zhang等人将布里渊放大与光纤中随机分布的瑞利反馈相结合,获得线宽1 kHz的相干随机激光。2020年,俄罗斯的S. M. Popov等人[173]报道了一种5 m长的掺铒光纤随机激光器。在掺铒光纤纤芯上刻蚀随机分布的弱反射光纤Bragg光栅,使随机激光输出的洛伦兹线宽缩小到290 Hz,高斯线宽控制在4 kHz以下。
2006年,复旦大学的Qinghai Song等人[10]制造了一种平面随机微腔激光器,该结构由传统的平面微腔和随机增益层组成,由于随机空腔和平面微空腔提供了双重光学约束,具有相同衰减率的模数可以显著减少,产生线宽极窄、超低阈值和单向发射的随机激光,随机激光阈值为2.5 μW/cm2,发散角为1.68°。
2002年,Diederik S. Wiersma等人[174]将液晶和激光染料与烧结的玻璃粉末混合,通过调节外界温度的变化来控制随机激光的发射带宽和强度。扩散常数取决于液晶与玻璃粉末的折射率差,当温度变化时,扩散常数改变进而影响随机激光的辐射特性。液晶在42.8 ℃从向列相变为各向同性,扩散常数在该温度下最大,随机激光也在该温度下达到阈值。
-
对于传统激光器来说,激光的模式频率和空间分布与偏振无关,只与边界条件即腔的结构有关。只要确定了谐振腔的结构,就确定了激光模式。要使输出的激光带有偏振特性,则需要在激光腔内加入偏振器件才能获得线偏的相干光。而在随机激光器中没有传统的谐振腔结构,多重散射提供反馈,散射情况决定了随机激光的模式频率和空间分布。2005年,华中科技大学的王春等人[175]用数值分析方法研究随机激光的偏振特性,基于半经典激光理论和麦克斯韦方程组,用时域有限差分法求解方程组,得出二维随机激光系统中TM和TE波的演化情况,证明偏振会影响随机激光模式的频率和空间分布,也会影响随机激光的阈值[176]。2013年,德国Sebastian Knitter等人[177]介绍了一种测量强散射介质中随机激光偏振模式的方法。设计了一种微观随机激光,证明了该随机激光的偏振态是随机分布的,并且对泵浦光的偏振态有很强的依赖性。实验结果表明不同频率的随机激光模式具有不同的偏振态,随机激光的模式和偏振可能是由随机介质中泵浦光的干涉与模场空间随机分布的重叠决定。同年,他们利用麦克斯韦方程组的时域有限差分积分和带增益的速率方程对三维随机激光进行模拟[178]。在弱散射的条件下,用各向同性的泵浦光泵浦可以得到随机的模式偏振态,用各向异性的泵浦光泵浦可以得到线性的模式偏振态。而在强散射介质中,随机激光模式的偏振是完全随机的,不受泵浦光的影响。
在传统激光器中,通过卷绕光纤、使用正交光栅或设计特殊结构来实现激光的线偏输出[179-180]。比如光纤的卷绕技术可以抑制高阶模,利用快轴与慢轴的弯曲损耗差异来实现单偏振的输出。这些方法也可以用在随机激光中。2015年,国防科技大学的周朴等人[181]设计了一种输出波长为1178 nm、基于拉曼增益和瑞利反馈的线偏随机分布式反馈光纤激光器。他们用泵浦源连接一个保偏光纤Bragg光栅,后面接一根0.5 km长的保偏光纤作为无序介质,构成半开腔结构,将保偏光纤绕在外径为2.9 cm的圆柱体上,以保证输出光的线偏特性,再用一个二向色分束器从泵浦光中提取随机激光。同年,俄罗斯的E. A. Zlobina等人[155]将500 m长的保偏光纤与保偏光纤环型镜相连,并用线偏光泵浦,制成全保偏光纤结构的光纤随机激光器,实现了1.11 μm的线偏随机激光输出,偏振消光比大于25 dB,光光转换效率高达87%。
研究人员们针对其他体系中随机激光中的偏振控制也开展了一系列研究。2006年,Eunice S. P. Leong等人[182]制作了ZnO波导随机激光器,实现了强TE模式紫外随机激光输出。波导宽度限制了闭环光路的形成,从而减少了激光峰的数量。2012年,Sebastian Knitter等人[183]在有机染料溶液中观察到具有高度偏振性的相干随机激光。通过选择不同吸收程度的激光染料和粘性溶剂,并用线偏光泵浦,可以使随机激光出射的所有波长都是线性偏振的。2013年,哈尔滨工业大学的Fengfeng Yao等人[184]在掺杂激光染料的向列相液晶中观察到线性偏振的随机激光输出,线偏方向大约在最大散射偏振方向和向列指向中间。这种线偏随机激光是由各向异性散射和染料分子吸附共同作用产生的,通过旋转样品可以控制随机激光输出的线偏方向。2015年,电子科技大学的饶云江[185]等人制作了基于石墨烯的带宽可调单偏振光纤随机激光器,能够产生消光比为41 dB的脉冲随机激光。同年,Victor Lisinetskii等人[186]将掺罗丹明激光染料的液晶材料与多孔聚丙烯混合制成复合材料的聚合物薄膜,在紫外光的照射下,液晶分子从向列相转变为各向同性,获得近红外范围的线偏随机激光,偏振方向与薄膜拉伸方向(液晶分子方向)相同。2017年,东南大学的Lihua Ye等人[187]和中国台湾国立中山大学的Chun-Wei Chen等人[188]都在向列相液晶中观察到双向的线偏振随机激光输出。
-
传统激光器的主要优点是具有良好的方向性、单色性和相干性,含有多纵模及多橫模的激光束单色性和相干性差。在精密干涉测量、光通信及大面积全息照相等应用中,要求激光既是单横模又是单纵模输出的。在随机激光器领域,研究者们也设计了一系列调控随机激光模式的方法。2010年,J. Andreasen和H. Cao等人[189]从数值和理论上阐述了无序介质中有增益的激光模式的性质,重点研究了阈值附近的单模随机激光输出,讨论了阈值附近随机激光模式与无增益的无源系统共振的联系。同年,新加坡南洋理工大学的H. K. Liang等人[190]在ZnO随机激光二极管阵列中实现了高功率的稳定单模激光输出,如图7所示。他们选取Al2O3作为介电绝缘体,以实现相邻随机腔之间的电隔离和光耦合。2013年,日本北海道大学的Hideki Fujiwara等人[17]在亚微米级的均匀ZnO球形粒子薄膜中引入聚合物粒子缺陷,在缺陷点激发了单模低阈值的随机激光。

图 7 ZnO随机激光二极管阵列的电压电流曲线、光电流曲线和Q值与注入电流的关系。插图绘制了不同偏压条件下从激光二极管阵列边缘测量的电致发光光谱[190]
Figure 7. Voltage-current curve, light-current curve, and Q-factor vs injection current of the ZnO random laser diode array. The insert plots the EL spectra measured from the edge of the laser diode array at different bias conditions[190]
随机激光的选模操控主要通过改变泵浦位置来实现。如图8所示,N. Bachelard等人[191]使用局部泵浦的方法,通过改变泵浦位置显著提高其他模式的阈值,以牺牲其他模式为代价来选择所需的激光模式。次年,Thomas Hisch等人[192]通过主动控制空间泵浦的轮廓,使所期望的模式具有最低的激光阈值,来控制随机激光出射模式。锁模技术可以使光束中不同振荡的纵模具有确定的相位关系,从而使各个模式相干叠加得到超短脉冲。2009年,L. Leuzzi等人[193]对无序结构中的激光锁模进行了全面的理论分析。2011年,Marco Leonetti等人[194]设计了一个由二氧化钛纳米颗粒自组装簇形成的随机激光器,通过增大泵浦光的角度范围,产生了一个有许多共振的平滑发射光谱,并且具有高度的相关性和更短的寿命。这可能是无序谐振自发锁模的第一个实验证据。2016年,R. Ma等人[195]将一个点反射镜与一个随机分布的光纤Bragg光栅阵列相连,构成一个具有相干反馈的光纤随机激光器。随机分布的FBG和石墨烯可饱和吸收体的结合,能使高频到低频集体共振,产生高重复率的脉冲,为随机激光的锁模和脉冲调控提供了新的可能性。同年,该团队的W. L. Zhang等人[196]设计了一种通过加热无序光纤Bragg光栅阵列特定位置来控制随机激光模式的方法。
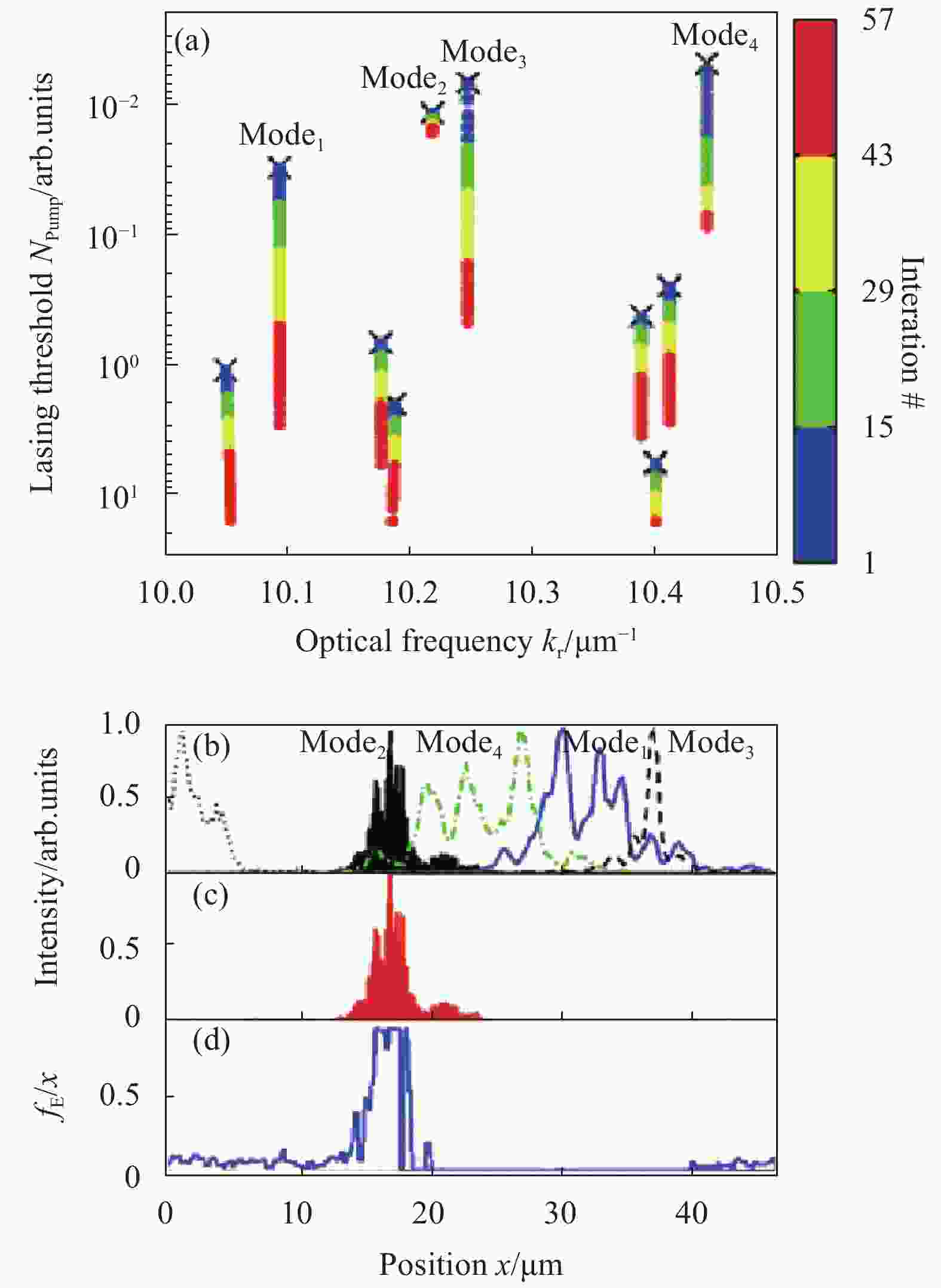
图 8 局域随机激光示例。(a)当优化程序用于选择模式2时,连续迭代中激光模式的频率与阈值的关系,十字表示均匀泵送的初始位置;(b)五种局域激光模式的空间分布,左边缘的模式轮廓对应于泄漏模式,其阈值最高;(c)优化后模式2的空间轮廓;(d)得到优化的空间泵型[191]
Figure 8. Localized random laser case. (a) Frequency vs threshold of the lasing modes at successive iterations, when the optimization routine is applied to select Mode 2. Crosses represent initial positions for uniform pumping;(b) Spatial profile of five localized lasing modes. The mode profile on the left edge corresponds to the leaky mode with the highest threshold;(c) Spatial profile of Mode 2 after optimization;(d) Resulting optimized spatial pump profile[191]
自从1910年Lord Rayleigh[197]提出回音壁现象以来,研究者们开展了大量有关回音壁现象的研究。光学中的回音壁模式(Wispering Gallery Modes,WGM)是指光沿着弯曲介质分界面传播的现象。当光在两介质分界面发生全反射,如果介质为圆形,某些频率的光可以发生多次全反射。当形成一个环形回路时就会发生干涉,从而产生WGM共振。2013年,香港理工大学的Hai Zhu等人[198]将ZnS包裹在光纤表面形成环形微腔,构成波导和增益区,产生了回音壁模式,实现了定向单模的随机激光输出。2020年,北京科技大学的Zhiyang Xu等人[199]设计了一种能同时产生回音壁模式和随机激光的环形复合腔,将喷墨打印技术与金属辅助的化学腐蚀相结合,将聚合物薄膜附着在腔上构成随机激光器。通过改变腔体直径,可以控制随机激光的模间距。
-
随机激光器有着独特的输出特性和灵活简单的结构,自提出随机激光这一概念以来,随机激光器的应用研究也在同步开展。近年来,研究者们就随机激光传感、远距离光传输、无散斑成像、超连续光源等多个领域设计了一系列新颖有效的方法与应用。
① 传感领域
随机激光可以检测气体及溶液的浓度、应变、温度、PH等。2016年,Emilio Ignesti等人[200]将随机激光作为检测生物样本的方法,克服了传统检测方法需要向样品中注入有毒物质,改变了样本理化成分的缺陷。将生物活性介质与无序介质分隔开,细胞的透明壁可以让自发辐射光传输到外部无序介质中,经过无序介质散射后部分光回到细胞内,在细胞内产生受激辐射光放大。增大样本浓度时,随机激光输出光谱会发生红移。2020年,北京科技大学的Xiaoyu Shi等人[201]设计了基于等离子随机激光器的生物传感器,利用银纳米粒子和聚合物薄膜的自组装等离子体散射产生随机激光。如图9所示,将该传感器与蛋白A特异性结合可以检测人类免疫球蛋白,监测免疫球蛋白的浓度。2017年,Michele Gaio等人[202]研制了一种基于随机激光的PH传感方法。随机激光的增益会与生物化学环境相互作用进而影响随机激光的阈值,在中性溶液中能观察到随机激光出射,而在碱性溶液中随机激光会被抑制。2019年,Shuaijie Miao等人[203]提出了一种基于光纤随机激光器的高精度静态应变传感器。随机分布的光栅和相移光纤Bragg光栅环形镜组成光纤随机激光器,将两个光纤随机激光器作为探针,一个作为传感探针用于应变检测,另一个作为参考探针用于补偿温度和频率漂移。今年,Shuaije Miao等人[204]制作了一种基于光纤随机激光器的高分辨光纤声发射传感器,光纤随机激光器中的窄线宽光纤Bragg光栅是滤波和传感元件,掺铒光纤提供增益,在基于3×3耦合器的相位解调下,声发射分辨率约为
${{280 \; f\varepsilon }/{\sqrt {{\rm{H}}{\text{z}}} }}$ ,而底噪仅为3.4×10−7 pm/$ {\sqrt {{\rm{H}}{\text{z}}}}$ 。此外,如图10所示,由于癌细胞比正常细胞更大、折射率更高,所以散射更强,可以用随机激光来区分正常细胞和癌细胞[205]。
图 9 (a)免疫捕获法检测IgG示意图;(b)基于RL的传感器在蛋白A功能化前(红线)和IgG溶液中培养15min (红线)后的相应光谱;(c)研究了34 μM浓度IgG对生物传感器波长漂移的影响;(d)不同浓度IgG溶液对波长漂移的影响[201]
Figure 9. (a) Schematic diagram of capture immunoassay employed for IgG detection; (b) Corresponding spectra of the RL-based sensor before functionalization with protein A (red line) and after being cultivated in IgG solution for 15 min (red line); (c) Temporal behavior of wavelength shift for the biosensors exposed to IgG with the concentrations of 34 μM; (d) Variation of wavelengh shift as a function of IgG solution with different concentrations[201]

图 10 基于随机激光的癌细胞鉴别。(a)正常乳腺上皮细胞(MCF-10A)和乳腺癌细胞的图像;(b)正常乳腺上皮细胞与乳腺癌细胞的直径差异;(c)相同功率泵浦时,填充三种细胞与未填充细胞时的生物流体随机激光发射谱;(d)填充了三种细胞的激光强度与泵浦功率关系图[205]
Figure 10. Identification of cancer cells based on RL. (a) Optical images of MCF-10A, MCF-7, and MDA-MB-231 cells; (b) Diameters of MCF-10A, MCF-7, and MDA-MB-231 cells; (c) Emission spectra of the BFRL with three different cells and without cells at the same pump power; (d) Lasing intensity as a function of pump power for BFRL filled with three different cells[205]
② 无散斑成像
无散斑成像是随机激光的典型应用,2012年,Hui Cao[206]等人利用随机激光器的低空间相干性展示了强光散射背景下的无斑点全场成像,非常适合用在全场显微镜和数字光投影系统中。由于随机激光光源具有易激发、可以产生超短脉冲、相干性低和亮度高等优点,德国Alexandre Mermillod-Blondin等人将随机激光用作时间分辨显微镜的频闪光源[207]。2019年,Yilin Liu等人[208]将钙钛矿多晶硅薄膜夹在两个Bragg反射器之间,光在该结构中多次散射。由于垂直方向上对光的严格限制,可以产生发散角在3°~5°之间、具有低空间相干性的多模随机激光。如图11所示,用产生的随机激光直接照射图像,可以显著去除散斑,这也证明随机激光是光学成像照明的理想光源。同年,电子科技大学的Yunjiang Rao团队[209]将光纤随机激光作为近红外光源用于牙科成像。由于牙釉质、牙本质、龋齿等结构具有不同的反射率,用随机激光照射牙齿,不同的部位会表现出不同的强度,病变区域与正常牙齿间会有明显的明暗对比。如图12所示,他们也将随机激光光源与自发辐射放大光源以及窄线宽激光光源照明下的牙齿图像进行对比,在随机激光照明下,图像最清晰、对比度最高。
2020年,电子科技大学的马瑞[210]等人将全光纤随机激光作为具有低相干性和中等带宽的光源,在不透明的毛玻璃后面获取到物体的像。通过扫描散斑模式,用相位检索算法重建出物体。他们提出的局部照明方式能够准确的识别物体的方位,将光源波长扩展到近红外波段并简化了照明方案。
③ 鬼影成像(ghost imaging)
近几年,鬼影成像引发研究热潮,时域鬼成像为超快波的发展提供了新的可能性。鬼成像存在的前提是光源具有随机的强度波动,即成像各瞬间的光源强度完全不相关。2020年,Han Wu等人[211]证明随机激光是时域瞬态鬼成像的理想光源,如图13所示,能够避免传统多模激光器造成的波形失真。
④ 长距离传感
随机激光在长距离传感中也有着丰富的应用,包括长距离点式传感[212-213]和长距离分布式传感[214-215]以及光传输过程中随机激光的放大[216-217]。2012年,Z. N. Wang等人[218]提出用光纤随机激光器实现远距离传感的方法,由于光纤随机激光器具有良好的温度稳定性,可以利用随机激光提供高保真的传感信号。2016年,西班牙的Daniel Leandro等人[219]利用准分布式光纤随机激光器结合波分复用和时分复用,实现200 km的传感监测。2019年,Yun Fu等人[220]利用高阶随机激光放大,实现了175 km的无重复布里渊光学时域分析(Brillouin optical time-domain analysis,BOTDA),空间分辨率为8 m。
⑤ 超分辨光谱
随机激光还可以产生超分辨光谱。通过频域稀疏采样,随机激光的发射光谱会在不相关的频率上出现稀疏的尖峰,可用于探测样品的光谱响应,并且能以超高分辨率重建样品[221]。随机激光也能用来产生真正的随机数,Song Gao等人[222]用双向泵浦的光纤随机激光器实现了比特率约为71 Mbps的随机数,显著突破了通信光纤中的固有Brillouin带宽限制。
-
从随机激光的发展历史和基本理论出发,综述了随机激光的调控方式和新近应用,重点介绍了光纤随机激光的反馈类型与增益机制。到目前为止,对随机激光物理本质的探究还处于研究阶段,在这个领域中仍会产生许多新结构、新想法。未来会出现较完善的、不同层次(经典、半经典和量子论)的随机激光模型,能解释各种不同的实验现象。周期结构在光子学中的应用已有很长的历史,是当今各种光学方法、技术、器件的固有组成部分。而无序的随机光学结构很可能被应用到这些已经发展成熟的光子器件中。在不久的将来,这一课题会有更多的工程应用并实现随机激光器的商业化生产。随机光学结构的新兴将为未来光学技术的发展焕发新活力。
Review of random laser research (Invited)
-
摘要: 随机激光器由于其独特的结构和低相干性,在无散斑成像、传感、光治疗等领域中得到广泛应用。随机激光器的反馈机制是无序介质引入的光散射,高阈值和无方向性是其主要缺点。为解决这些问题,研究者们利用光纤的一维束缚获得低阈值并有一定方向性的光纤随机激光。近十年来,随机激光的发展经历了从非相干反馈到相干反馈、从完全无序到输出参数可控的过程。大量研究尝试用量子理论、混沌激光理论和数值分析等方法来解释随机激光的物理本质。回顾了随机激光和光纤随机激光的起源和发展历史,介绍了随机激光的分类和相关原理,总结了调控随机激光输出参数的方法并展示了随机激光的新近典型应用,分析了光纤随机激光的反馈类型和增益机制,并在最后展望了随机激光未来的发展趋势。Abstract: Due to its unique structure and low coherence, random lasers are widely used in fields such as speckle-free imaging, sensing, and light therapy. The feedback mechanism of random lasers is light scattering introduced by disordered media. High threshold and non-directionality are its main disadvantages. In order to solve these problems, researchers used the one-dimensional confinement of optical fibers to obtain random fiber lasers with a low threshold and a certain directionality. In the past ten years, the development of random lasers has experienced a process from incoherent feedback to coherent feedback, from complete disorder to controllable output parameters. A large number of studies have tried to explain the physical nature of random lasers using quantum theory, chaotic laser theory, and numerical analysis. The origin and development history of random lasers and random fiber lasers were reviewed, the classification and related principles of random lasers were introduced, the methods of controlling random laser output parameters were summarized, the recent typical applications of random lasers were demonstrated, fiber random lasers feedback types and gain mechanisms were analyzed, and finally the future of random lasers development was prospected.
-
Key words:
- random lasers /
- random fiber lasers /
- multiple scattering /
- disorder structure /
- localization
-
图 1 各种随机激光体系:(a) ZnO粒子[17]; (b)聚合物光纤[18]; (c)光孤子[19]; (d)静电纺丝纤维[20]; (e)量子点[21]; (f)液晶[15]; (g)荷叶[22]; (h)钙钛矿[23]
Figure 1. Different kinds of RL systerms: (a) ZnO particles[17]; (b) Polymer optical fiber[18]; (c) Soliton[19]; (d) Electrospun nanofibers[20]; (e) Quantum dots[21]; (f) Liquid crystals[15]; (g) Lotus-leaf[22]; (h) Perovskitec[23]
图 2 (a)平均局域化长度与沿光纤传输距离z的函数;(b)测量了横向无序光纤的平均局域化长度与入射激光波长(圆)的函数关系,并与(a) (三角形)进行了比较[80]
Figure 2. (a) Average localization length as a function of the distance z along the fiber for the two light wavelengths; (b) Measured averaged localization length of fibers with transverse disorder as a function of the incident-laser wavelength (full circles) compared with (a) (full triangles)[80]
图 7 ZnO随机激光二极管阵列的电压电流曲线、光电流曲线和Q值与注入电流的关系。插图绘制了不同偏压条件下从激光二极管阵列边缘测量的电致发光光谱[190]
Figure 7. Voltage-current curve, light-current curve, and Q-factor vs injection current of the ZnO random laser diode array. The insert plots the EL spectra measured from the edge of the laser diode array at different bias conditions[190]
图 8 局域随机激光示例。(a)当优化程序用于选择模式2时,连续迭代中激光模式的频率与阈值的关系,十字表示均匀泵送的初始位置;(b)五种局域激光模式的空间分布,左边缘的模式轮廓对应于泄漏模式,其阈值最高;(c)优化后模式2的空间轮廓;(d)得到优化的空间泵型[191]
Figure 8. Localized random laser case. (a) Frequency vs threshold of the lasing modes at successive iterations, when the optimization routine is applied to select Mode 2. Crosses represent initial positions for uniform pumping;(b) Spatial profile of five localized lasing modes. The mode profile on the left edge corresponds to the leaky mode with the highest threshold;(c) Spatial profile of Mode 2 after optimization;(d) Resulting optimized spatial pump profile[191]
图 9 (a)免疫捕获法检测IgG示意图;(b)基于RL的传感器在蛋白A功能化前(红线)和IgG溶液中培养15min (红线)后的相应光谱;(c)研究了34 μM浓度IgG对生物传感器波长漂移的影响;(d)不同浓度IgG溶液对波长漂移的影响[201]
Figure 9. (a) Schematic diagram of capture immunoassay employed for IgG detection; (b) Corresponding spectra of the RL-based sensor before functionalization with protein A (red line) and after being cultivated in IgG solution for 15 min (red line); (c) Temporal behavior of wavelength shift for the biosensors exposed to IgG with the concentrations of 34 μM; (d) Variation of wavelengh shift as a function of IgG solution with different concentrations[201]
图 10 基于随机激光的癌细胞鉴别。(a)正常乳腺上皮细胞(MCF-10A)和乳腺癌细胞的图像;(b)正常乳腺上皮细胞与乳腺癌细胞的直径差异;(c)相同功率泵浦时,填充三种细胞与未填充细胞时的生物流体随机激光发射谱;(d)填充了三种细胞的激光强度与泵浦功率关系图[205]
Figure 10. Identification of cancer cells based on RL. (a) Optical images of MCF-10A, MCF-7, and MDA-MB-231 cells; (b) Diameters of MCF-10A, MCF-7, and MDA-MB-231 cells; (c) Emission spectra of the BFRL with three different cells and without cells at the same pump power; (d) Lasing intensity as a function of pump power for BFRL filled with three different cells[205]
-
[1] Ambartsumyan R V, Kryukov P G, Letokhov V C. Dynamics of emission line narrowing for a laser with nonresonant feedback [J]. Journal of Experimental and Theoretical Physics, 1967, 6(24): 1129-1134. [2] Ambartsumyan R V, Kryukov P G, Letokhov V C, et al. Statistical emission properties of a nonresonant Feedback laser [J]. Journal of Experimental and Theoretical Physics, 1968, 6(26): 1109-1114. [3] Letokhov V S. Generation of light by a scattering medium with negative resonance absorption [J]. Journal of Experimental and Theoretical Physics, 1968, 4(26): 835-840. [4] Lawandy N M, Balachandran R M, Gomes A S L, et al. Laser action in strongly scattering media [J]. Nature, 1994, 368: 436-438. doi: 10.1038/368436a0 [5] Wiersma D S, Van-Albada M P, Lagendijk A. Random laser? [J]. Nature, 1995, 373: 203-204. [6] Wiersma D S, Lagendijk A. Light diffusion with gain and random lasers [J]. Physical Review E, 1996, 54(4): 4256-4265. doi: 10.1103/PhysRevE.54.4256 [7] Cao H, Zhao Y G, Ong H C, et al. Ultraviolet lasing in resonators formed by scattering in semiconductor polycrystalline films [J]. Applied Physics Letters, 1998, 73(25): 3656-3658. doi: 10.1063/1.122853 [8] Cao H, Zhao Y G, Ho S T, et al. Random laser action in semiconductor powder [J]. Physical Review Letters, 1999, 82(11): 2278-2281. doi: 10.1103/PhysRevLett.82.2278 [9] Wang Y, Yang X, Li H, et al. Bright single-mode random laser from a concentrated solution of π-conjugated polymers [J]. Optics Letters, 2016, 41(2): 269-272. doi: 10.1364/OL.41.000269 [10] Song Q, Liu L, Xiao S, et al. Unidirectional high intensity narrow-linewidth lasing from a planar random microcavity laser [J]. Physical Review Letters, 2006, 96(3): 033902. doi: 10.1103/PhysRevLett.96.033902 [11] Xia J, Xie K, Ma J, et al. The transition from incoherent to coherent random laser in defect waveguide based on organic/inorganic hybrid laser dye [J]. Nanophotonics, 2018, 7(7): 1341-1350. doi: 10.1515/nanoph-2018-0034 [12] Gollner C, Ziegler J, Protesescu L, et al. Random lasing with systematic threshold behavior in films of CdSe/CdS core/thick-shell colloidal quantum dots [J]. ACS Nano, 2015, 9(10): 9792-9801. doi: 10.1021/acsnano.5b02739 [13] Hu Z, Zhang Q, Miao B, et al. Coherent random fiber laser based on nanoparticles scattering in the extremely weakly scattering regime [J]. Physical Review Letters, 2012, 109(25): 253901. doi: 10.1103/PhysRevLett.109.253901 [14] Fujiwara H, Suzuki T, Niyuki R, et al. ZnO nanorod array random lasers fabricated by a laser-induced hydrothermal synthesis [J]. New Journal of Physics, 2016, 18(10): 103046. doi: 10.1088/1367-2630/18/10/103046 [15] Wan Y, Deng L. Pump-controlled plasmonic random lasers from dye-doped nematic liquid crystals with TiN nanoparticles in non-oriented cells [J]. Applied Sciences, 2020, 10(1): 199. [16] Azkargorta J, Bettinelli M, Iparraguirre I, et al. Random lasing in Nd:LuVO4 crystal powder [J]. Optics Express, 2011, 19(20): 19591-19599. doi: 10.1364/OE.19.019591 [17] Fujiwara H, Niyuki R, Ishikawa Y, et al. Low-threshold and quasi-single-mode random laser within a submicrometer-sized ZnO spherical particle film [J]. Applied Physics Letters, 2013, 102(6): 061110. doi: 10.1063/1.4792349 [18] Hu Z, Miao B, Wang T, et al. Disordered microstructure polymer optical fiber for stabilized coherent random fiber laser [J]. Optics Letters, 2013, 38(22): 4644-4647. doi: 10.1364/OL.38.004644 [19] Perumbilavil S, Piccardi A, Barboza R, et al. Beaming random lasers with soliton control [J]. Nature communications, 2018, 9(1): 1-7. doi: 10.1038/s41467-017-02088-w [20] Chen W C, Shiao J H, Tsai T L, et al. Multiple scattering from electrospun nanofibers with embedded silver nanoparticles of tunable shape for random lasers and white-light-emitting diodes [J]. ACS Applied Materials & Interfaces, 2019, 12(2): 2783-2792. [21] Tang X, Bian Y, Liu Z, et al. Room-temperature up-conversion random lasing from CsPbBr3 quantum dots with TiO2 nanotubes [J]. Optics Letters, 2019, 44(19): 4706-4709. doi: 10.1364/OL.44.004706 [22] Li X, Liu H, Xu X, et al. Lotus-leaf-inspired flexible and tunable random laser [J]. ACS Applied Materials & Interfaces, 2020, 12(8): 10050-10057. [23] Zhang X, Yan S, Tong J, et al. Perovskite random lasers on fiber facet [J]. Nanophotonics, 2020, 9(4): 935-941. doi: 10.1515/nanoph-2019-0552 [24] Cao H. Lasing in random media [J]. Waves in Random Media, 2003, 13(3): R1-R39. doi: 10.1088/0959-7174/13/3/201 [25] Lu H, Wei C, Zhang Q, et al. Wide tunable laser based on electrically regulated bandwidth broadening in polymer-stabilized cholesteric liquid crystal [J]. Photonics Research, 2019, 7(2): 137-143. doi: 10.1364/PRJ.7.000137 [26] Lu H, Yang L, Xia L, et al. Band-edge-enhanced tunable random laser using a polymer-stabilised cholesteric liquid crystal [J]. Liquid Crystals, 2020(2): 1-8. [27] Firdaus K, Nakamura T, Adachi S. Improved lasing characteristics of ZnO/organic-dye random laser [J]. Applied Physics Letters, 2012, 100(17): 171101. doi: 10.1063/1.4705471 [28] Popov O, Zilbershtein A, Davidov D. Random lasing from dye-gold nanoparticles in polymer films: enhanced gain at the surface-plasmon-resonance wavelength [J]. Applied Physics Letters, 2006, 89(19): 191116. doi: 10.1063/1.2364857 [29] Wang C S, Lin H Y, Lin J M, et al. Surface-plasmon-enhanced ultraviolet random lasing from ZnO nanowires assisted by Pt nanoparticles [J]. Applied Physics Express, 2012, 5(6): 062003. doi: 10.1143/APEX.5.062003 [30] Fan H, Mu Y, Liu C, et al. Random lasing of CsPbBr3 perovskite thin films pumped by modulated electron beam [J]. Chinese Optics Letters, 2020, 18(1): 011403. doi: 10.3788/COL202018.011403 [31] Lahoz F, Acebes A, González-Hernández T, et al. Random lasing in brain tissues [J]. Organic Electronics, 2019, 75: 105389. doi: 10.1016/j.orgel.2019.105389 [32] Zhang Z Z, Yin L C, Xu X L, et al. Near-field scattering enhancement of Perylene based aggregates for random lasing [J]. Chinese Journal of Chemical Physics, 2019, 32(6): 739-746. doi: 10.1063/1674-0068/cjcp1807167 [33] Hsu Y T, Lin Y Y, Chen Y Z, et al. 3D printed random lasers [J]. Advanced Materials Technologies, 2020, 5(1): 1900742. doi: 10.1002/admt.201900742 [34] Yin L, Liang Y, Yu B, et al. Quantitative analysis of “Δl=ls−lg” to coherent random lasing in solution systems with a series of solvents ordered by refractive index [J]. RSC Advances, 2016, 6(100): 98066-98070. doi: 10.1039/C6RA19029D [35] Wu X, Cao H. Statistical studies of random-lasing modes and amplified spontaneous-emission spikes in weakly scattering systems [J]. Physical Review A, 2008, 77(1): 013832. doi: 10.1103/PhysRevA.77.013832 [36] Cao H, Xu J Y, Chang S H, et al. Transition from amplified spontaneous emission to laser action in strongly scattering media [J]. Physical Review E, 2000, 61(2): 1985. doi: 10.1103/PhysRevE.61.1985 [37] Andreasen J, Cao H. Numerical study of amplified spontaneous emission and lasing in random media [J]. Physical Review A, 2010, 82(6): 063835. doi: 10.1103/PhysRevA.82.063835 [38] Dingjan J, Altewischer E, van Exter M P, et al. Experimental observation of wave chaos in a conventional optical resonator [J]. Physical Review Letters, 2002, 88(6): 064101. doi: 10.1103/PhysRevLett.88.064101 [39] Frahm K M, Schomerus H, Patra M, et al. Large Petermann factor in chaotic cavities with many scattering channels [J]. EPL (Europhysics Letters), 2000, 49(1): 48-54. doi: 10.1209/epl/i2000-00118-y [40] Misirpashaev T S, Beenakker C W J. Lasing threshold and mode competition in chaotic cavities [J]. Physical Review A, 1998, 57(3): 2041-2045. doi: 10.1103/PhysRevA.57.2041 [41] Hackenbroich G, Viviescas C, Elattari B, et al. Photocount statistics of chaotic lasers [J]. Physical Review Letters, 2001, 86(23): 5262-5265. doi: 10.1103/PhysRevLett.86.5262 [42] Patra M, Schomerus H, Beenakker C W J. Quantum-limited linewidth of a chaotic laser cavity [J]. Physical Review A, 2000, 61(2): 023810. doi: 10.1103/PhysRevA.61.023810 [43] Patra M. Theory for photon statistics of random lasers [J]. Physical Review A, 2002, 65(4): 043809. doi: 10.1103/PhysRevA.65.043809 [44] Beenakker C W J. Thermal radiation and amplified spontaneous emission from a random medium [J]. Physical Review Letters, 1998, 81(9): 1829-1832. doi: 10.1103/PhysRevLett.81.1829 [45] Hackenbroich G, Viviescas C, Haake F. Field quantization for chaotic resonators with overlapping modes [J]. Physical Review Letters, 2002, 89(8): 083902. doi: 10.1103/PhysRevLett.89.083902 [46] Patra M, Beenakker C W J. Excess noise for coherent radiation propagating through amplifying random media [J]. Physical Review A, 1999, 60(5): 4059-4066. doi: 10.1103/PhysRevA.60.4059 [47] Patra M, Beenakker C W J. Propagation of squeezed radiation through amplifying or absorbing random media [J]. Physical Review A, 2000, 61(6): 063805. doi: 10.1103/PhysRevA.61.063805 [48] Soukoulis C M, Jiang X, Xu J Y, et al. Dynamic response and relaxation oscillations in random lasers [J]. Physical Review B, 2002, 65(4): 041103. [49] Ling Y, Cao H, Burin A L, et al. Investigation of random lasers with resonant feedback [J]. Physical Review A, 2001, 64(6): 063808. doi: 10.1103/PhysRevA.64.063808 [50] Jiang X, Soukoulis C M. Localized random lasing modes and a path for observing localization [J]. Physical Review E, 2002, 65(2): 025601. [51] Sebbah P, Vanneste C. Random laser in the localized regime [J]. Physical Review B, 2002, 66(14): 144202. doi: 10.1103/PhysRevB.66.144202 [52] Vanneste C, Sebbah P. Selective excitation of localized modes in active random media [J]. Physical Review Letters, 2001, 87(18): 183903. doi: 10.1103/PhysRevLett.87.183903 [53] Apalkov V M, Raikh M E, Shapiro B. Random resonators and prelocalized modes in disordered dielectric films [J]. Physical Review Letters, 2002, 89(1): 016802. doi: 10.1103/PhysRevLett.89.016802 [54] Jiang X, Soukoulis C M. Time dependent theory for random lasers [J]. Physical Review Letters, 2000, 85(1): 70-73. doi: 10.1103/PhysRevLett.85.70 [55] Herrmann J, Wilhelmi B. Mirrorless laser action by randomly distributed feedback in amplifying disordered media with scattering centers [J]. Applied Physics B: Lasers & Optics, 1998, 66(3): 305-312. [56] Burin A L, Ratner M A, Cao H, et al. Random laser in one dimension [J]. Physical Review Letters, 2002, 88(9): 093904. doi: 10.1103/PhysRevLett.88.093904 [57] Wiersma D S. The physics and applications of random lasers [J]. Nature Physics, 2008, 4(5): 359-367. doi: 10.1038/nphys971 [58] Anderson P W. Absence of diffusion in certain random lattices [J]. Physical Review, 1958, 109(5): 1492-1505. doi: 10.1103/PhysRev.109.1492 [59] Abrahams E, Anderson P W, Licciardello D C, et al. Scaling theory of localization: Absence of quantum diffusion in two dimensions [J]. Physical Review Letters, 1979, 42(10): 673-676. doi: 10.1103/PhysRevLett.42.673 [60] Ioffe A F, Regel A R. Non-crystalline, amorphous and liquid electronic semiconductors [J]. Prog Semicond, 1960, 4(89): 237-291. [61] Keller O. On the theory of spatial localization of photons [J]. Physics Reports, 2005, 411(1-3): 1-232. [62] John S. Localization of light [J]. Phys Today, 1991, 44(5): 32-40. doi: 10.1063/1.881300 [63] He S, Maynard J D. Detailed measurements of inelastic scattering in Anderson localization [J]. Physical Review Letters, 1986, 57(25): 3171-3174. doi: 10.1103/PhysRevLett.57.3171 [64] Crosignani B, Sa’ar A, Yariv A. Coherent backscattering and localization in a single-mode fiber with random imperfections [J]. Physical Review A, 1991, 43(6): 3168. doi: 10.1103/PhysRevA.43.3168 [65] Zhang Z Q, Sheng P. Wave localization in random networks [J]. Physical Review B, 1994, 49(1): 83. doi: 10.1103/PhysRevB.49.83 [66] Szameit A, Zeil P, Dreisow F, et al. Wave localization at the boundary of disordered photonic lattices [J]. Optics Letters, 2010, 35(8): 1172-1174. doi: 10.1364/OL.35.001172 [67] Jović D M, Kivshar Y S, Denz C, et al. Anderson localization of light near boundaries of disordered photonic lattices [J]. Physical Review A, 2011, 83(3): 033813. doi: 10.1103/PhysRevA.83.033813 [68] Karbasi S, Mirr C R, Yarandi P G, et al. Observation of transverse Anderson localization in an optical fiber [J]. Optics Letters, 2012, 37(12): 2304-2306. doi: 10.1364/OL.37.002304 [69] Pradhan P, Kumar N. Localization of light in coherently amplifying random media [J]. Physical Review B, 1994, 50(13): 9644. doi: 10.1103/PhysRevB.50.9644 [70] Kumar N, Pradhan P, Jayannavar A M. Coherently amplifying random medium: Statistics of super-reflection [J]. Superlattices and Microstructures, 1998, 23(3-4): 853-858. doi: 10.1006/spmi.1997.0546 [71] Störzer M, Gross P, Aegerter C M, et al. Observation of the critical regime near Anderson localization of light [J]. Physical Review Letters, 2006, 96(6): 063904. doi: 10.1103/PhysRevLett.96.063904 [72] Illarramendi M A, Cascales C, Aramburu I, et al. Characterization of light propagation in NdxY1-xAl(BO3)4 laser crystal powders [J]. Optical Materials, 2007, 30(1): 126-128. doi: 10.1016/j.optmat.2006.11.038 [73] Wu X, Fang W, Yamilov A, et al. Random lasing in weakly scattering systems [J]. Physical Review A, 2006, 74(5): 053812. doi: 10.1103/PhysRevA.74.053812 [74] Li S, Wang Z J, Chen L S, et al. Collective behavior and disorder-induced resonator of random lasers [J]. Applied Physics Letters, 2005, 86(17): 171109. doi: 10.1063/1.1920409 [75] Ferjani S, Sorriso-Valvo L, De Luca A, et al. Statistical analysis of random lasing emission properties in nematic liquid crystals [J]. Physical Review E, 2008, 78(1): 011707. doi: 10.1103/PhysRevE.78.011707 [76] Conti C, Leonetti M, Fratalocchi A, et al. Condensation in disordered lasers: Theory, 3D+1 simulations, and experiments [J]. Physical Review Letters, 2008, 101(14): 143901. doi: 10.1103/PhysRevLett.101.143901 [77] Ruocco G, Abaie B, Schirmacher W, et al. Disorder-induced single-mode transmission [J]. Nature Communications, 2017, 8(1): 1-6. doi: 10.1038/s41467-016-0009-6 [78] Hu L, Xie K, Hu Z, et al. Experimental observation of wave localization at the Dirac frequency in a two-dimensional photonic crystal microcavity [J]. Optics Express, 2018, 26(7): 8213-8223. doi: 10.1364/OE.26.008213 [79] Abaie B, Peysokhan M, Zhao J, et al. Disorder-induced high-quality wavefront in an Anderson localizing optical fiber [J]. Optica, 2018, 5(8): 984-987. doi: 10.1364/OPTICA.5.000984 [80] Schirmacher W, Abaie B, Mafi A, et al. What is the right theory for Anderson localization of light? An experimental test [J]. Physical Review Letters, 2018, 120(6): 067401. doi: 10.1103/PhysRevLett.120.067401 [81] Cao H, Jiang X, Ling Y, et al. Mode repulsion and mode coupling in random lasers [J]. Physical Review B, 2003, 67(16): 161101. doi: 10.1103/PhysRevB.67.161101 [82] van der Molen K L, Mosk A P, Lagendijk A. Intrinsic intensity fluctuations in random lasers [J]. Physical Review A, 2006, 74(5): 053808. doi: 10.1103/PhysRevA.74.053808 [83] Fallert J, Dietz R J B, Sartor J, et al. Co-existence of strongly and weakly localized random laser modes [J]. Nature Photonics, 2009, 3(5): 279-282. doi: 10.1038/nphoton.2009.67 [84] Stano P, Jacquod P. Suppression of interactions in multimode random lasers in the Anderson localized regime [J]. Nature Photonics, 2013, 7(1): 66-71. doi: 10.1038/nphoton.2012.298 [85] Synergetics H H. Self-Organizing Systems[M]// Boston, MA: Springer, 1987: 417-434. [86] Gordon A, Vodonos B, Smulakovski V, et al. Melting and freezing of light pulses and modes in mode-locked lasers [J]. Optics Express, 2003, 11(25): 3418-3424. doi: 10.1364/OE.11.003418 [87] Gordon A, Fischer B. Phase transition theory of pulse formation in passively mode-locked lasers with dispersion and Kerr nonlinearity [J]. Optics Communications, 2003, 223(1-3): 151-156. doi: 10.1016/S0030-4018(03)01622-5 [88] Weill R, Rosen A, Gordon A, et al. Critical behavior of light in mode-locked lasers [J]. Physical Review Letters, 2005, 95(1): 013903. doi: 10.1103/PhysRevLett.95.013903 [89] Arecchi F T. Optical morphogenesis: pattern formation and competition in nonlinear optics [J]. Physica D: Nonlinear Phenomena, 1995, 86(1-2): 297-322. doi: 10.1016/0167-2789(95)00110-P [90] Arecchi F T, Boccaletti S, Ramazza P L. Pattern formation and competition in nonlinear optics [J]. Physics Reports, 1999, 318(1-2): 1-83. doi: 10.1016/S0370-1573(99)00007-1 [91] Vodonos B, Weill R, Gordon A, et al. Formation and annihilation of laser light pulse quanta in a thermodynamic-like pathway [J]. Physical Review Letters, 2004, 93(15): 153901. doi: 10.1103/PhysRevLett.93.153901 [92] Florescu L, John S. Photon statistics and coherence in light emission from a random laser [J]. Physical Review Letters, 2004, 93(1): 013602. doi: 10.1103/PhysRevLett.93.013602 [93] Angelani L, Conti C, Ruocco G, et al. Glassy behavior of light [J]. Physical Review Letters, 2006, 96(6): 065702. doi: 10.1103/PhysRevLett.96.065702 [94] Angelani L, Conti C, Ruocco G, et al. Glassy behavior of light in random lasers [J]. Physical Review B, 2006, 74(10): 104207. doi: 10.1103/PhysRevB.74.104207 [95] Antenucci F, Conti C, Crisanti A, et al. General phase diagram of multimodal ordered and disordered lasers in closed and open cavities [J]. Physical Review Letters, 2015, 114(4): 043901. doi: 10.1103/PhysRevLett.114.043901 [96] Antenucci F, Crisanti A, Leuzzi L. Complex spherical 2+4 spin glass: A model for nonlinear optics in random media [J]. Physical Review A, 2015, 91(5): 053816. doi: 10.1103/PhysRevA.91.053816 [97] Ghofraniha N, Viola I, Di Maria F, et al. Experimental evidence of replica symmetry breaking in random lasers [J]. Nature Communications, 2015, 6(1): 1-8. [98] Gomes A S L, Lima B C, Pincheira P I R, et al. Glassy behavior in a one-dimensional continuous-wave erbium-doped random fiber laser [J]. Physical Review A, 2016, 94(1): 011801. doi: 10.1103/PhysRevA.94.011801 [99] Gomes A S L, Raposo E P, Moura A L, et al. Observation of Lévy distribution and replica symmetry breaking in random lasers from a single set of measurements [J]. Scientific Reports, 2016, 6: 27987. doi: 10.1038/srep27987 [100] Araújo C B, Gomes A S L, Raposo E P. Lévy statistics and the glassy behavior of light in random fiber lasers [J]. Applied Sciences, 2017, 7(7): 644. doi: 10.3390/app7070644 [101] Xia J, He J, Xie K, et al. Replica symmetry breaking in FRET‐assisted random laser based on electrospun polymer fiber [J]. Annalen Der Physik, 2019, 531(9): 1900066. doi: 10.1002/andp.201900066 [102] de Matos C J S, Menezes L S, Brito-Silva A M, et al. Random fiber laser [J]. Physical Review Letters, 2007, 99(15): 153903. doi: 10.1103/PhysRevLett.99.153903 [103] Van Exter M P, Nienhuis G, Woerdman J P. Two simple expressions for the spontaneous emission factor β [J]. Physical Review A, 1996, 54(4): 3553. doi: 10.1103/PhysRevA.54.3553 [104] Hu Z, Zheng H, Wang L, et al. Random fiber laser of POSS solution-filled hollow optical fiber by end pumping [J]. Optics Communications, 2012, 285(19): 3967-3970. doi: 10.1016/j.optcom.2012.05.048 [105] Hu Z, Gao P, Xie K, et al. Wavelength control of random polymer fiber laser based on adaptive disorder [J]. Optics Letters, 2014, 39(24): 6911-6914. doi: 10.1364/OL.39.006911 [106] Zhang W L, Zheng M Y, Ma R, et al. Fiber-type random laser based on a cylindrical waveguide with a disordered cladding layer [J]. Scientific Reports, 2016, 6: 26473. doi: 10.1038/srep26473 [107] Turitsyn S K, Babin S A, Churkin D V, et al. Random distributed feedback fibre lasers [J]. Physics Reports, 2014, 542(2): 133-193. doi: 10.1016/j.physrep.2014.02.011 [108] Lizárraga N, Puente N P, Chaikina E I, et al. Single-mode Er-doped fiber random laser with distributed Bragg grating feedback [J]. Optics Express, 2009, 17(2): 395-404. doi: 10.1364/OE.17.000395 [109] Shapira O, Fischer B. Localization of light in a random-grating array in a single-mode fiber [J]. JOSA B, 2005, 22(12): 2542-2552. doi: 10.1364/JOSAB.22.002542 [110] Gagné M, Bojor L, Maciejko R, et al. Novel custom fiber Bragg grating fabrication technique based on push-pull phase shifting interferometry [J]. Optics Express, 2008, 16(26): 21550-21557. doi: 10.1364/OE.16.021550 [111] Gagné M, Kashyap R. Random fiber Bragg grating Raman fiber laser [J]. Optics Letters, 2014, 39(9): 2755-2758. doi: 10.1364/OL.39.002755 [112] Wang L, Dong X, Shum P P, et al. Random laser with multiphase-shifted Bragg grating in Er/Yb-codoped fiber [J]. Journal of Lightwave Technology, 2015, 33(1): 95-99. doi: 10.1109/JLT.2014.2374216 [113] Abdullina S R, Vlasov A A, Lobach I A, et al. Single-frequency Yb-doped fiber laser with distributed feedback based on a random FBG [J]. Laser Physics Letters, 2016, 13(7): 075104. doi: 10.1088/1612-2011/13/7/075104 [114] Hu Z, Ma R, Zhang X, et al. Weak feedback assisted random fiber laser from 45°-tilted fiber Bragg grating [J]. Optics Express, 2019, 27(3): 3255-3263. doi: 10.1364/OE.27.003255 [115] Churkin D V, Babin S A, El-Taher A E, et al. Raman fiber lasers with a random distributed feedback based on Rayleigh scattering [J]. Physical Review A, 2010, 82(3): 033828. doi: 10.1103/PhysRevA.82.033828 [116] Agrawal G P. Fiber-Optic Communication Systems[M]. US: John Wiley & Sons, 2012. [117] Babin S A. Random fiber laser based on Rayleigh scattering: Basic principles and experimental results[C]//Photonics Global Conference, IEEE, 2010: 1-5. [118] Hulst H C, Hulst H C. Light Scattering by Small Particles[M]. US: Courier Corporation, 1981. [119] Cardona M. 固体中的光散射[M]. 北京: 科学出版社, 1986. [120] Boyd R W. Nonlinear Optics[M]. 3rd ed. US: Elsevier, 2008. [121] Agrawal G. 非线性光纤光学[M]. 第5版. 贾东方, 葛春风, 等译. 北京: 电子工业出版社, 2014. Agrawal G. Nonlinear Fiber Optics [M]. 5th ed. Jia Dongfang, Ge Chunfeng, et al. translated. Beijing: Publishing House of Electronics Industry, 2014. (in Chinese) [122] Giles C R, Desurvire E. Modeling erbium-doped fiber amplifiers [J]. Journal of Lightwave Technology, 1991, 9(2): 271-283. doi: 10.1109/50.65886 [123] Fotiadi A A. An incoherent fibre laser [J]. Nature Photonics, 2010, 4(4): 204-205. doi: 10.1038/nphoton.2010.76 [124] Ye J, Zhang Y, Xu J, et al. Broadband pumping enabled flat-amplitude multi-wavelength random Raman fiber laser [J]. Optics Letters, 2020, 45(7): 1786-1789. doi: 10.1364/OL.389071 [125] Xu J, Wu J, Ye J, et al. Optical rogue wave in random fiber laser [J]. Photonics Research, 2020, 8(1): 1-7. doi: 10.1364/PRJ.8.000001 [126] Kharif C, Pelinovsky E. Physical mechanisms of the rogue wave phenomenon [J]. European Journal of Mechanics B/Fluids, 2003, 22: 603-634. [127] Gorbunov O A, Sugavanam S, Vatnik I D, et al. Poisson distribution of extreme events in radiation of random distributed feedback fiber laser [J]. Optics Letters, 2020, 45(8): 2375-2378. doi: 10.1364/OL.390492 [128] Babin S A, El-Taher A E, Harper P, et al. Tunable random fiber laser [J]. Physical Review A, 2011, 84(2): 021805. doi: 10.1103/PhysRevA.84.021805 [129] Zhang L, Jiang H, Yang X, et al. Ultra-wide wavelength tuning of a cascaded Raman random fiber laser [J]. Optics Letters, 2016, 41(2): 215-218. doi: 10.1364/OL.41.000215 [130] Zhang L, Jiang H, Yang X, et al. Nearly-octave wavelength tuning of a continuous wave fiber laser [J]. Scientific Reports, 2017, 7: 42611. doi: 10.1038/srep42611 [131] Hu Z, Xia J, Liang Y, et al. Tunable random polymer fiber laser [J]. Optics Express, 2017, 25(15): 18421-18430. doi: 10.1364/OE.25.018421 [132] Xie Z, Xie K, Hu T, et al. Multi-wavelength coherent random laser in bio-microfibers [J]. Optics Express, 2020, 28(4): 5179-5188. doi: 10.1364/OE.384105 [133] Perumbilavil S, Piccardi A, Buchnev O, et al. Soliton-assisted random lasing in optically-pumped liquid crystals [J]. Applied Physics Letters, 2016, 109(16): 161105. doi: 10.1063/1.4965852 [134] Du X, Zhang H, Wang X, et al. Multiwavelength Raman fiber laser based on polarization maintaining fiber loop mirror and random distributed feedback [J]. Laser Physics Letters, 2015, 12(4): 045106. doi: 10.1088/1612-2011/12/4/045106 [135] Zhu Y Y, Zhang W L, Jiang Y. Tunable multi-wavelength fiber laser based on random Rayleigh back-scattering [J]. IEEE Photonics Technology Letters, 2013, 25(16): 1559-1561. doi: 10.1109/LPT.2013.2271044 [136] Sugavanam S, Yan Z, Kamynin V, et al. Multiwavelength generation in a random distributed feedback fiber laser using an all fiber Lyot filter [J]. Optics Express, 2014, 22(3): 2839-2844. doi: 10.1364/OE.22.002839 [137] Huang C, Dong X, Zhang N, et al. Multiwavelength Brillouin-erbium random fiber laser incorporating a chirped fiber Bragg grating [J]. IEEE Journal of Selected Topics in Quantum Electronics, 2014, 20(5): 294-298. doi: 10.1109/JSTQE.2014.2301018 [138] Huang C, Dong X, Zhang S, et al. Cascaded random fiber laser based on hybrid Brillouin-erbium fiber gains [J]. IEEE Photonics Technology Letters, 2014, 26(13): 1287-1290. doi: 10.1109/LPT.2014.2321386 [139] Wang Z, Wu H, Fan M, et al. Broadband flat-amplitude multiwavelength Brillouin-Raman fiber laser with spectral reshaping by Rayleigh scattering [J]. Optics Express, 2013, 21(24): 29358-29363. doi: 10.1364/OE.21.029358 [140] Wu H, Wang Z, Jia X, et al. Flat amplitude multiwavelength Brillouin–Raman random fiber laser with a half-open cavity [J]. Applied Physics B, 2013, 112(4): 467-471. doi: 10.1007/s00340-013-5569-0 [141] Ahmad H, Zulkifli M Z, Jemangin M H, et al. Distributed feedback multimode Brillouin–Raman random fiber laser in the S-band [J]. Laser Physics Letters, 2013, 10(5): 055102. doi: 10.1088/1612-2011/10/5/055102 [142] Zhang Y, Ye J, Xu J, et al. Dual-wavelength random distributed feedback fiber laser with wavelength, linewidth, and power ratio tunability [J]. Optics Express, 2020, 28(7): 10515-10523. doi: 10.1364/OE.390796 [143] Yusoff N M, Lau K Y, Abidin N H Z, et al. Dual-wavelength random fiber laser incorporating micro-air cavity [J]. Journal of Optics, 2020, 22(3): 035603. doi: 10.1088/2040-8986/ab68f1 [144] Dontsova E I, Kablukov S I, Vatnik I D, et al. Frequency doubling of Raman fiber lasers with random distributed feedback [J]. Optics Letters, 2016, 41(7): 1439-1442. doi: 10.1364/OL.41.001439 [145] Turitsyn S K, Babin S A, El-Taher A E, et al. Random distributed feedback fibre laser [J]. Nature Photonics, 2010, 4(4): 231-235. doi: 10.1038/nphoton.2010.4 [146] Wang Z, Wu H, Fan M, et al. Random fiber laser: simpler and brighter [J]. Opt Photon News, 2014, 25(12): 30. [147] Zhang H, Huang L, Zhou P, et al. More than 400 W random fiber laser with excellent beam quality [J]. Optics Letters, 2017, 42(17): 3347-3350. doi: 10.1364/OL.42.003347 [148] Xu J, Lou Z, Ye J, et al. Incoherently pumped high-power linearly-polarized single-mode random fiber laser: experimental investigations and theoretical prospects [J]. Optics Express, 2017, 25(5): 5609-5617. doi: 10.1364/OE.25.005609 [149] Du X, Zhang H, Xiao H, et al. High‐power random distributed feedback fiber laser: From science to application [J]. Annalen der Physik, 2016, 528(9-10): 649-662. doi: 10.1002/andp.201600099 [150] Zhang H, Zhou P, Wang X, et al. Hundred-watt-level high power random distributed feedback Raman fiber laser at 1150 nm and its application in mid-infrared laser generation [J]. Optics Express, 2015, 23(13): 17138-17144. doi: 10.1364/OE.23.017138 [151] Du X, Zhang H, Ma P, et al. Kilowatt-level fiber amplifier with spectral-broadening-free property, seeded by a random fiber laser [J]. Optics letters, 2015, 40(22): 5311-5314. doi: 10.1364/OL.40.005311 [152] Xu J, Huang L, Jiang M, et al. Near-diffraction-limited linearly polarized narrow-linewidth random fiber laser with record kilowatt output [J]. Photonics Research, 2017, 5(4): 350-354. doi: 10.1364/PRJ.5.000350 [153] Zhang J, Bai G, Li X, et al. 1.36-kW spectral-narrowing fiber laser seeded by random fiber laser [J]. IEEE Photonics Technology Letters, 2019, 31(16): 1343-1346. doi: 10.1109/LPT.2019.2916610 [154] Zhang H, Zhou P, Xiao H, et al. Efficient Raman fiber laser based on random Rayleigh distributed feedback with record high power [J]. Laser Physics Letters, 2014, 11(7): 075104. doi: 10.1088/1612-2011/11/7/075104 [155] Zlobina E A, Kablukov S I, Babin S A. Linearly polarized random fiber laser with ultimate efficiency [J]. Optics Letters, 2015, 40(17): 4074-4077. doi: 10.1364/OL.40.004074 [156] Babin S A, Dontsova E I, Kablukov S I. Random fiber laser directly pumped by a high-power laser diode [J]. Optics Letters, 2013, 38(17): 3301-3303. doi: 10.1364/OL.38.003301 [157] Vatnik I D, Churkin D V, Podivilov E V, et al. High-efficiency generation in a short random fiber laser [J]. Laser Physics Letters, 2014, 11(7): 075101. doi: 10.1088/1612-2011/11/7/075101 [158] Du X, Zhang H, Wang X, et al. Short cavity-length random fiber laser with record power and ultrahigh efficiency [J]. Optics Letters, 2016, 41(3): 571-574. doi: 10.1364/OL.41.000571 [159] Babin S A, Zlobina E A, Kablukov S I, et al. High-order random Raman lasing in a PM fiber with ultimate efficiency and narrow bandwidth [J]. Scientific Reports, 2016, 6: 22625. doi: 10.1038/srep22625 [160] Lou Z, Jin X, Zhang H, et al. High power, high-order random Raman fiber laser based on tapered fiber [J]. IEEE Photonics Journal, 2017, 9(1): 1-6. [161] Evmenova E A, Kuznetsov A G, Nemov I N, et al. 2nd-order random lasing in a multimode diode-pumped graded-index fiber [J]. Scientific Reports, 2018, 8(1): 1-7. doi: 10.1038/s41598-017-17765-5 [162] Zhang H, Du X, Zhou P, et al. Tapered fiber based high power random laser [J]. Optics Express, 2016, 24(8): 9112-9118. doi: 10.1364/OE.24.009112 [163] Zhang H, Ye J, Zhou P, et al. Tapered-fiber-enabled high-power, high-spectral-purity random fiber lasing [J]. Optics Letters, 2018, 43(17): 4152-4155. doi: 10.1364/OL.43.004152 [164] Tang Y, Xu J. A random Q-switched fiber laser [J]. Scientific Reports, 2015, 5(1): 1-5. doi: 10.9734/JSRR/2015/14076 [165] Ye J, Xu J, Song J, et al. Pump scheme optimization of an incoherently pumped high-power random fiber laser [J]. Photonics Research, 2019, 7(9): 977-983. doi: 10.1364/PRJ.7.000977 [166] Wu H, Wang Z, Sun W, et al. 1.5 μm low threshold, high efficiency random fiber laser with hybrid erbium–raman gain [J]. Journal of Lightwave Technology, 2017, 36(4): 844-849. [167] Ye L, Liu B, Zhao C, et al. The electrically and magnetically controllable random laser from dye-doped liquid crystals [J]. Journal of Applied Physics, 2014, 116(5): 053103. doi: 10.1063/1.4891683 [168] Wang Z, Cao M, Shao G, et al. Coherent random lasing in colloidal quantum dot-doped polymer-dispersed liquid crystal with low threshold and high stability [J]. The Journal of Physical Chemistry Letters, 2020, 11(3): 767-774. doi: 10.1021/acs.jpclett.9b03409 [169] Pang M, Bao X, Chen L. Observation of narrow linewidth spikes in the coherent Brillouin random fiber laser [J]. Optics Letters, 2013, 38(11): 1866-1868. doi: 10.1364/OL.38.001866 [170] Sugavanam S, Tarasov N, Shu X, et al. Narrow-band generation in random distributed feedback fiber laser [J]. Optics Express, 2013, 21(14): 16466-16472. doi: 10.1364/OE.21.016466 [171] Leandro D, Rota-Rodrigo S, Ardanaz D, et al. Narrow-linewidth multi-wavelength random distributed feedback laser [J]. Journal of Lightwave Technology, 2015, 33(17): 3591-3596. doi: 10.1109/JLT.2015.2445377 [172] Xu Y, Gao S, Lu P, et al. Low-noise Brillouin random fiber laser with a random grating-based resonator [J]. Optics Letters, 2016, 41(14): 3197-3200. doi: 10.1364/OL.41.003197 [173] Popov S M, Butov O V, Bazakutsa A P, et al. Random lasing in a short Er-doped artificial Rayleigh fiber [J]. Results in Physics, 2020, 16: 102868. doi: 10.1016/j.rinp.2019.102868 [174] Wiersma D S, Cavalieri S. Temperature-controlled random laser action in liquid crystal infiltrated systems[J]. Physical Review E, 2002, 66(5): 056612. [175] Wang C, Liu J, Liu H. Characteristic of polarization of random laser[C]//Proceedings of SPIE, International Society for Optics and Photonics, 2005, 5644: 714-722. [176] Liu J S, Xiong Z, Chun W. Theoretical investigation on polarization-dependent laser action in two-dimensional random media [J]. Journal of Optics A: Pure and Applied Optics, 2007, 9(7): 658. doi: 10.1088/1464-4258/9/7/016 [177] Knitter S, Kues M, Fallnich C. Spectro-polarimetric signature of a random laser [J]. Physical Review A, 2013, 88(1): 013839. doi: 10.1103/PhysRevA.88.013839 [178] Knitter S, Kues M, Haidl M, et al. Linearly polarized emission from random lasers with anisotropically amplifying media [J]. Optics Express, 2013, 21(25): 31591-31603. doi: 10.1364/OE.21.031591 [179] Niay P, Bernage P, Taunay T, et al. Polarization selectivity of gratings written in Hi-Bi fibers by the external method [J]. IEEE photonics technology letters, 1995, 7(4): 391-393. doi: 10.1109/68.376812 [180] Loh W H, Samson B N, Dong L, et al. High performance single frequency fiber grating-based erbium: ytterbium-codoped fiber lasers [J]. Journal of Lightwave Technology, 1998, 16(1): 114. doi: 10.1109/50.654992 [181] Du X, Zhang H, Wang X, et al. Investigation on random distributed feedback Raman fiber laser with linear polarized output [J]. Photonics Research, 2015, 3(2): 28-31. doi: 10.1364/PRJ.3.000028 [182] Leong E S P, Yu S F, Abiyasa A P, et al. Polarization characteristics of ZnO rib waveguide random lasers [J]. Applied Physics Letters, 2006, 88(9): 091116. doi: 10.1063/1.2181634 [183] Knitter S, Kues M, Fallnich C. Emission polarization of random lasers in organic dye solutions [J]. Optics Letters, 2012, 37(17): 3621-3623. doi: 10.1364/OL.37.003621 [184] Yao F, Zhou W, Bian H, et al. Polarization and polarization control of random lasers from dye-doped nematic liquid crystals [J]. Optics Letters, 2013, 38(9): 1557-1559. doi: 10.1364/OL.38.001557 [185] Yao B C, Rao Y J, Wang Z N, et al. Graphene based widely-tunable and singly-polarized pulse generation with random fiber lasers [J]. Scientific Reports, 2015, 5: 18526. [186] Lisinetskii V, Ryabchun A, Bobrovsky A, et al. Photochromic composite for random lasing based on porous polypropylene infiltrated with azobenzene-containing liquid crystalline mixture [J]. ACS Applied Materials & Interfaces, 2015, 7(48): 26595-26602. [187] Ye L, Zhao C, Feng Y, et al. Study on the polarization of random lasers from dye-doped nematic liquid crystals [J]. Nanoscale Research Letters, 2017, 12(1): 1-8. doi: 10.1186/s11671-016-1773-2 [188] Chen C W, Huang H P, Jau H C, et al. Polarization-asymmetric bidirectional random laser emission from a twisted nematic liquid crystal [J]. Journal of Applied Physics, 2017, 121(3): 033102. doi: 10.1063/1.4974476 [189] Andreasen J, Asatryan A A, Botten L C, et al. Modes of random lasers [J]. Advances in Optics and Photonics, 2011, 3(1): 88-127. doi: 10.1364/AOP.3.000088 [190] Liang H K, Yu S F, Yang H Y. ZnO random laser diode arrays for stable single-mode operation at high power [J]. Applied Physics Letters, 2010, 97(24): 241107. doi: 10.1063/1.3527922 [191] Bachelard N, Andreasen J, Gigan S, et al. Taming random lasers through active spatial control of the pump [J]. Physical Review Letters, 2012, 109(3): 033903. doi: 10.1103/PhysRevLett.109.033903 [192] Hisch T, Liertzer M, Pogany D, et al. Pump-controlled directional light emission from random lasers [J]. Physical Review Letters, 2013, 111(2): 023902. doi: 10.1103/PhysRevLett.111.023902 [193] Leuzzi L, Conti C, Folli V, et al. Phase diagram and complexity of mode-locked lasers: from order to disorder [J]. Physical Review Letters, 2009, 102(8): 083901. doi: 10.1103/PhysRevLett.102.083901 [194] Leonetti M, Conti C, Lopez C. The mode-locking transition of random lasers [J]. Nature Photonics, 2011, 5(10): 615-617. doi: 10.1038/nphoton.2011.217 [195] Ma R, Zhang W L, Zeng X P, et al. Quasi mode-locking of coherent feedback random fiber laser [J]. Scientific Reports, 2016, 6: 39703. doi: 10.1038/srep39703 [196] Zhang W L, Song Y B, Zeng X P, et al. Temperature-controlled mode selection of Er-doped random fiber laser with disordered Bragg gratings [J]. Photonics Research, 2016, 4(3): 102-105. doi: 10.1364/PRJ.4.000102 [197] Rayleigh L. CXII. The problem of the whispering gallery [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1910, 20(120): 1001-1004. doi: 10.1080/14786441008636993 [198] Zhu H, Yu S F, Wang Q J, et al. Directional single-mode emission from coupled whispering gallery resonators realized by using ZnS microbelts [J]. Optics Letters, 2013, 38(9): 1527-1529. doi: 10.1364/OL.38.001527 [199] Xu Z, Tong J, Shi X, et al. Tailoring whispering gallery lasing and random lasing in a compound cavity [J]. Polymers, 2020, 12(3): 656. doi: 10.3390/polym12030656 [200] Ignesti E, Tommasi F, Fini L, et al. A new class of optical sensors: a random laser based device [J]. Scientific Reports, 2016, 6(1): 1-6. doi: 10.1038/s41598-016-0001-8 [201] Shi X, Ge K, Tong J H, et al. Low-cost biosensors based on a plasmonic random laser on fiber facet [J]. Optics Express, 2020, 28(8): 12233-12242. doi: 10.1364/OE.392661 [202] Gaio M, Caixeiro S, Marelli B, et al. Gain-based mechanism for pH sensing based on random lasing [J]. Physical Review Applied, 2017, 7(3): 034005. doi: 10.1103/PhysRevApplied.7.034005 [203] Miao S, Zhang W, Huang W, et al. High-resolution static strain sensor based on random fiber laser and beat frequency interrogation [J]. IEEE Photonics Technology Letters, 2019, 31(18): 1530-1533. doi: 10.1109/LPT.2019.2937009 [204] Miao S, Zhang W, Song Y, et al. High-resolution random fiber laser acoustic emission sensor [J]. Optics Express, 2020, 28(9): 12699-12708. doi: 10.1364/OE.389135 [205] He J, Hu S, Ren J, et al. Biofluidic random laser cytometer for biophysical phenotyping of cell suspensions [J]. ACS Sensors, 2019, 4(4): 832-840. doi: 10.1021/acssensors.8b01188 [206] Redding B, Choma M A, Cao H. Speckle-free laser imaging using random laser illumination [J]. Nature Photonics, 2012, 6(6): 355-359. doi: 10.1038/nphoton.2012.90 [207] Mermillod-Blondin A, Mentzel H, Rosenfeld A. Time-resolved microscopy with random lasers [J]. Optics Letters, 2013, 38(20): 4112-4115. doi: 10.1364/OL.38.004112 [208] Liu Y, Yang W, Xiao S, et al. Surface-emitting perovskite random lasers for speckle-free imaging [J]. ACS Nano, 2019, 13(9): 10653-10661. doi: 10.1021/acsnano.9b04925 [209] Guo J, Rao Y, Zhang W, et al. Dental imaging with near-infrared transillumination using random fiber laser [J]. Photonic Sensors, 2020, 10: 333-339. doi: 10.1007/s13320-020-0582-5 [210] Ma R, Wang Z, Zhang H H, et al. Imaging through opacity using a near-infrared low-spatial-coherence fiber light source [J]. Optics Letters, 2020, 45(13): 3816-3819. doi: 10.1364/OL.397152 [211] Wu H, Han B, Wang Z, et al. Temporal ghost imaging with random fiber lasers [J]. Optics Express, 2020, 28(7): 9957-9964. doi: 10.1364/OE.387762 [212] Fernandez-Vallejo M, Bravo M, Lopez-Amo M. Ultra-long laser systems for remote fiber Bragg gratings arrays interrogation [J]. IEEE Photonics Technology Letters, 2013, 25(14): 1362-1364. doi: 10.1109/LPT.2013.2265916 [213] Wang Z, Sun W, Wu H, et al. Long-distance random fiber laser point sensing system incorporating active fiber [J]. Optics Express, 2016, 24(20): 22448-22453. doi: 10.1364/OE.24.022448 [214] Tan M, Rosa P, Le S T, et al. Transmission performance improvement using random DFB laser based Raman amplification and bidirectional second-order pumping [J]. Optics Express, 2016, 24(3): 2215-2221. doi: 10.1364/OE.24.002215 [215] Leandro D, deMiguel-Soto V, López-Amo M. High-resolution sensor system using a random distributed feedback fiber laser [J]. Journal of Lightwave Technology, 2016, 34(19): 4596-4602. doi: 10.1109/JLT.2016.2536650 [216] Wang Z N, Zeng J J, Li J, et al. Ultra-long phase-sensitive OTDR with hybrid distributed amplification [J]. Optics Letters, 2014, 39(20): 5866-5869. doi: 10.1364/OL.39.005866 [217] Rosa P, Rizzelli G, Tan M, et al. Characterisation of random DFB Raman laser amplifier for WDM transmission [J]. Optics Express, 2015, 23(22): 28634-28639. doi: 10.1364/OE.23.028634 [218] Wang Z N, Rao Y J, Wu H, et al. Long-distance fiber-optic point-sensing systems based on random fiber lasers [J]. Optics Express, 2012, 20(16): 17695-17700. doi: 10.1364/OE.20.017695 [219] Leandro D, Soto V M, Perez-Herrera R A, et al. Random DFB fiber laser for remote (200 km) sensor monitoring using hybrid WDM/TDM [J]. Journal of Lightwave Technology, 2016, 34(19): 4430-4436. doi: 10.1109/JLT.2016.2547868 [220] Fu Y, Zhu R, Han B, et al. 175-km repeaterless BOTDA with hybrid high-order random fiber laser amplification [J]. Journal of Lightwave Technology, 2019, 37(18): 4680-4686. doi: 10.1109/JLT.2019.2916413 [221] Boschetti A, Taschin A, Bartolini P, et al. Spectral super-resolution spectroscopy using a random laser [J]. Nature Photonics, 2020, 14(3): 177-182. doi: 10.1038/s41566-019-0558-4 [222] Gao S, Zhang L, Xu Y, et al. High-speed random bit generation via brillouin random fiber laser with non-uniform fibers [J]. IEEE Photonics Technology Letters, 2017, 29(16): 1352-1355. doi: 10.1109/LPT.2017.2722381 -






 下载:
下载: