-
High power laser device requires that laser beam can achieve precision target after long optical path transmission[1-3], in which laser system and mirror group are used to achieve laser amplification and guidance. In addition, with the wide promotion of laser technology in fields of material processing and precision measurement[4-6], strict requirements are put forward for laser beam quality, beam pointing stability and output power stability. In order to achieve stable beam pointing in high-power laser device and stable laser output power[7-9], optical mount is required to have excellent structural stability. The mount also needs to be adjustable to achieve excellent alignment. Compared with the non-adjustable optical mount, the adjustable structure leads in fit clearance while introducing adjustability. The clearance will inevitably lead to structural instability and deterioration of the laser beam quality. Therefore, it is of great significance to study and design an optical mount with high stability in laser system.
Researchers have carried out extensive research and design work about high-stability optical mount. Bullock[10] et al. compared the stability of several kinds of commercial and custom-built optical mounts by utilizing thermal shocking test. However the results did not mention the factors affecting the structural stability. Jacobs[11] and Baskaran[12] introduced and studied the stability of common materials for optical mounts and optical parts from the aspect of materials. In terms of structural improvement design, Zachary[13] and Pijnenburg[14] et al. have designed an a-thermal support structure for optical parts from the material thermal matching. Dewitt[15] and Kvamme[16] utilized the same material to improve the design of an adjustable optical mount from the overall structure to reduce the effect of thermal mismatch. Kautz[17] improved the locking structure of adjusting mechanism in the optical mount.
At present, the design and research of high stability optical mount mainly focus on the material selection and matching between the mount and optical parts, as well as the locking mechanism of the adjustability in the mount. However, there are few literatures about the design of the adjustment mechanism which is an important causes for the structure instability of the mounts. In this paper, a novel structure design was put forward aiming at the instability caused by the grease in the adjustment screw structure of the mount. The stability comparison experiment was carried out on the improved structure and the common structure.
-
Figure 1(a) shows a kind of optical mount structure commonly used in laser system. The mount adopts two adjustment screws with spherical tips (the red circle in Fig.1) and a steel ball to make point contact with the tetrahedron surface, Vee surface and flat surface on the front plate respectively. The totally six point contacts constrain the six degrees of freedom of the front plate and achieve complete degree of freedom constraint. In order to ensure that the front plate is always against the spherical tip and steel ball, two wire springs are used to pull the front plate to the base plate. By driving adjustment screw structure at different position, yaw or pitch position of the optical parts mounted on the front plate can be adjusted. The adjustment screw plays the role of precise driving and maintaining the position stability of optical parts.
The adjustment screw in Fig.2(a) is a common precision displacement driving structure, which consists of a nut and a driving rod. When driving the driving rod, the spherical tip of the rod produces axial micro-displacement through thread pair, thereby achieving precise orientation adjustment of the front plate. The structure is widely used in optical three-dimensional adjustment platform. Designers often use fine thread and limit fitting tolerance to achieve precision adjustment. On the other hand, they always add grease in thread pair to achieve smooth adjustment and repeatability. Due to inevitable straightness machining error of the driving rod and nut and the unsmooth surface of the screw tooth, many partially sealed small spaces are formed on the entire thread mating surface and filled with grease. Under the unidirectional preload of the spring, the grease squeezed on the pressure side of thread mating surface forms hydraulic pressure, leading to a flexible state of non-rigid contact and forming the so-called "piston effect". This phenomenon directly hinders tight fit of the screw tooth surface between the driving rod and the nut (refer to the schematic diagram of the thread pair in Fig.2(b)). This non-rigid contact piston effect is susceptible to environmental micro-vibration and temperature changes, and changes slowly with the creep of grease. Obviously, this slow creep directly causes a slow axial shift of the spherical tips of the driving rod, which in turn causes a slight position shift of the front plate and then changes the precise position of the optical parts.

Figure 2. Cross-sectional view of a common adjustment screw for precision displacement driving. (a) Common adjustment screw; (b) Schematic diagram of the thread pair
Figure 3 illustrates the effect of the axial shift of adjustment screw on the angular position of optical part. Structural deformation caused by stress is not within the scope of this work. Due to micro-vibration and temperature fluctuation, the spherical tip of adjustment screw 1 moves from point B to point B1 and produces a small displacement
$\Delta $ z1. While the spherical tip of adjustment screw 2 moves from point C to point C1 and produces a small displacement$\Delta $ z2. If the steel ball and the spherical tips of the adjustment screws are all simplified to one point, the optical surface can be considered to be formed by plane A-B-C. Take point A as the origin, parallel to the base plate and pointing to the adjustment screw 2 as the x-axis to establish Cartesian coordinate system. Figure 3(b) is a schematic diagram of the position change of optical surface. The coordinates of A, B and C are (0, 0, 0), (0, l, z1) and (L, 0, z2) respectively. The plane A-B-C equation and normal vector before optical surface change are:
Figure 3. Effect of the axial shift of the adjustment screw structure on the position of the optical part. (a) Schematic diagram of optical mount disassembly; (b) Position change of optical part
$$\left| {\begin{array}{*{20}{c}} x&y&{\textit{z}} \\ 0&{{L}}&{{{\textit{z}}_1}} \\ {{L}}&0&{{\textit{z}}_2} \end{array}} \right| = 0$$ (1) $$ \overrightarrow{n}={[{{L\textit{z}}}_{2},{{L\textit{z}}}_{\rm{1}}, {{-L}}^{2}]}^{\rm{T}}$$ (2) The coordinates of B1 and C1 points are (0, l, z1+
$\Delta $ z1) and (L, 0, z2 +$\Delta $ z2) respectively. The optical surface after axial shift of adjustment screw structure is plane A-B1-C1, and its equation and normal vector are$$\begin{split} &\\ \left| {\begin{array}{*{20}{c}} x&y&{\textit{z}} \\ 0&{{L}}&{\textit{z}_1 + \Delta {{\textit{z}}_1}} \\ {{L}}&0&{\textit{z}_2 + \Delta {{\textit{z}}_2}} \end{array}} \right| = 0 \end{split}$$ (3) $$ {\overrightarrow{n}}_{1}={[{L(\textit{z}}{}_{1}+\Delta {z}_{1}),{L(\textit{z}}{}_{2}+\Delta {\textit{z}}_{2}{)}, {{-L}}^{2}]}^{{{\rm{T}}}}$$ (4) This work mainly focuses on the change of the angular position of optical parts. According to the normal vectors before and after optical surface change, the cosine angle in the direction of horizontal yaw and vertical pitch are:
$$\cos {\theta _{{\rm{yaw}}}} = \cos {\theta _{{{y - {\rm{rotate}}}}}} = \dfrac{{\left| {\overrightarrow {{n_{{{y\textit{z}}}}}} \cdot \overrightarrow {{n_{{{1y\textit{z}}}}}} } \right|}}{{\left\| {\overrightarrow {{n_{{{y\textit{z}}}}}} } \right\|\cdot \left\| {\overrightarrow {{n_{{{1y\textit{z}}}}}} } \right\|}}$$ (5) $$\cos {\theta _{{\rm{pitch}}}} = \cos {\theta _{{{x - {\rm{rotate}}}}}} = \dfrac{{\left| {\overrightarrow {{n_{{{x\textit{z}}}}}} \cdot \overrightarrow {{n_{{{1x\textit{z}}}}}} } \right|}}{{\left\| {\overrightarrow {{n_{{{x\textit{z}}}}}} } \right\|\cdot \left\| {\overrightarrow {{n_{{{1x\textit{z}}}}}} } \right\|}}$$ (6) Among them,
$\overrightarrow {{n_{{{y\textit{z}}}}}} $ ,$\overrightarrow {{n_{{{x\textit{z}}}}}} $ is the projection vector of the vector$\overrightarrow n $ on the yz plane and xz plane respectively, and$\overrightarrow {{n_{1{{y\textit{z}}}}}} $ ,$\overrightarrow {{n_{1{{x\textit{z}}}}}} $ is the projection vector of the vector$\overrightarrow {{n_1}} $ on yz plane and xz plane respectively. Since the values of the two angles are tiny, the angular changes of the optical surface in yaw and pitch can be written as:$${\theta _{{\rm{yaw}}}} \approx \sin {\theta _{{\rm{yaw}}}} = \sqrt {1{\rm{ - co}}{{\rm{s}}^{\rm{2}}}({\theta _{{\rm{yaw}}}})} $$ (7) $${\theta _{{\rm{pitch}}}} \approx \sin {\theta _{{\rm{pitch}}}} = \sqrt {1{\rm{ - co}}{{\rm{s}}^{\rm{2}}}({\theta _{{\rm{pitch}}}})} $$ (8) From equations (2) and (4), we can get
$$\overrightarrow {{n_{{{y\textit{z}}}}}} = {\left( {{{L}}{{{\textit{z}}}_1}, - {{{L}}^2}} \right)^{\rm{T}}}$$ (9) $$\overrightarrow {{n_{{{x\textit{z}}}}}} = {\left( {{{L}}{{{\textit{z}}}_2}, - {{{L}}^2}} \right)^{\rm{T}}}$$ (10) $$\overrightarrow {{n_{{{1y\textit{z}}}}}} = {\left( {{{L(}}{{{\textit{z}}}_1} + \Delta {{\textit{z}}_1}), - {{{L}}^2}} \right)^{\rm{T}}}$$ (11) $$\overrightarrow {{n_{{{1x\textit{z}}}}}} = {\left( {{{L(}}{{\textit{z}}_2} + \Delta {{\textit{z}}_2}), - {{{L}}^2}} \right)^{\rm{T}}}$$ (12) By introducing equations (5)-(6) and (9)-(12) into equations (7)-(8), it can be obtained that:
$${\theta _{{\rm{yaw}}}} \approx \dfrac{{{{10}^6}}}{{\sqrt {{{\left( {\dfrac{{{{{\textit{z}}}_2}}}{{{L}}}} \right)}^2} + 1} \times \sqrt {{{\left( {\dfrac{{{{{\textit{z}}}_2}}}{{\Delta {{\textit{z}}_2}}} + 1} \right)}^2} + {{\left( {\dfrac{{{L}}}{{\Delta {{\textit{z}}_2}}}} \right)}^2}} }}$$ (13) $${\theta _{{\rm{pitch}}}} \approx \dfrac{{{{10}^6}}}{{\sqrt {{{\left( {\dfrac{{{{{\textit{z}}}_1}}}{{{L}}}} \right)}^2} + 1} \times \sqrt {{{\left( {\dfrac{{{{{\textit{z}}}_1}}}{{\Delta {{\textit{z}}_1}}} + 1} \right)}^2} + {{\left( {\dfrac{{{L}}}{{\Delta {{\textit{z}}_1}}}} \right)}^2}} }}$$ (14) The unit of z1, z2,
$\Delta $ z1,$\Delta $ z1 and L is mm, and the unit of θyaw and θpitch is μrad. It can be seen from equations (13) and (14) that the tilt instability of optical parts is not only related to the axial shift of the adjustment screw structure, but also related to the design dimension L of the mount itself and the initial position of the adjustment screw relative to the mount. The adjustment screw 1 only affects the instability of the pitch direction, and does not affect that of the yaw direction, and vice versa. Take adjustment screw 1 as the research object, and take L=40 mm as the fixed value. The relationship between the angular shift of the optical part and the axial shift$\Delta $ z1 and the initial position z1 of the adjustment screw 1 can be drawn by using MATLAB software, as shown in Fig.4. It can be seen that the angular shift of the mount only has an impact when the axial shift of the screw is large, and the impact is small. However, this value increases rapidly with the increase of the axial shift of the screw. The micron-level axial shift will be amplified to millimeter level after long optical path transmission. The position stability of adjustment screw structure directly affects the stability of the optical mount, and then affects the beam quality and stable power output in the laser system. It is of great significance to design a high-stability adjustment screw structure to relieve the long-term creep of grease and improve the long-term stability of optical mount. -
Some manufacturers may design a grease-free adjustment screw structure by selecting wear-resistant materials and controlling the thread clearance of the thread pair and the roughness of the thread surface to achieve the smoothness and precision of adjustment. However, this kind of structure still wears out after working for a period of time, and the material requirements and processing are relatively strict, and the price is also relatively costly. Furse[18] proposed an improved structure for adjustment screw structure. The main method was to split the nut into two parts, and removed part of the screw teeth on the two halves of the nut respectively. The screw teeth could achieve tight fitting under the radial and axial pressure. This paper proposed an improved design of adjustment screw structure which could improve the stability of optical mount.
Figure 5 shows an improved adjustment screw structure which process n (n≥3) axial slots on the inner thread surface of the nut. The axial slots are uniformly distributed along the circumference of the thread surface, and its maximum radial depth H is greater than the major diameter radius D/2 of the thread. The width of slot is slightly larger than the minimum machine width of WEDM (electrical discharge wire-cutting). The cross-sectional shape of the slot in this work is U-shaped, and the design parameters are shown in Tab.1. In practical use, the number and size of axial slots should be determined according to the amount of grease that can be filled in the thread pair. The cross-sectional shape is mainly convenient for processing.

Figure 5. An improved adjustment screw structure. (a) Exploded view of the structure; (b) Thread fit; (c) The cross section of A-A
Table 1. Design parameters of the axial slots of adjustment screw structure
Parameters Numbers of slots D/mm D1/mm H/mm Value 3-6 7 6.65 0.5 Under the action of unidirectional preload of the springs, most of grease filled in the mating surfaces of the screw teeth flows into the axial slots for storage. Since the slots run through the entire thread surface, the amount of small space that is partially sealed in thread pair is greatly reduced. This behavior reduces the hydraulic pressure and makes the screw tooth surface rigid contact as well, alleviating the piston effect. Each time the driving rod is adjusted, the screw tooth surface carries grease from the axial slots into the thread pair to realize the lubrication of the adjustment. When the driving is over, most of the grease will quickly flow into the axial slots, and only a small amount of grease is chemically adsorbed on the screw tooth surface. This achieves close fitting of the screw tooth surface and improves the support stability of the optical mount. It should be noted that the axial slot depth should be as small as possible when it is greater than the major diameter of the thread. This is to avoid excessive grease attached to the bottom of the groove, which cannot be carried by the screw tooth surface into the thread pair to play a lubricating role.
-
The purpose of the experiment was to verify the effectiveness of the slotted adjustment screw proposed in this paper compared to the un-slotted adjustment screw. Firstly, a test platform was set up to measure the axial micro-displacement of the two adjustment screw structures under the action of unidirectional preload. Secondly, the two adjustment screws were installed on the two optical mounts with same specification, and the structural stability comparison test was carried out. Both tests evaluated the stability change by observing the position changes under several thermal shockings.
-
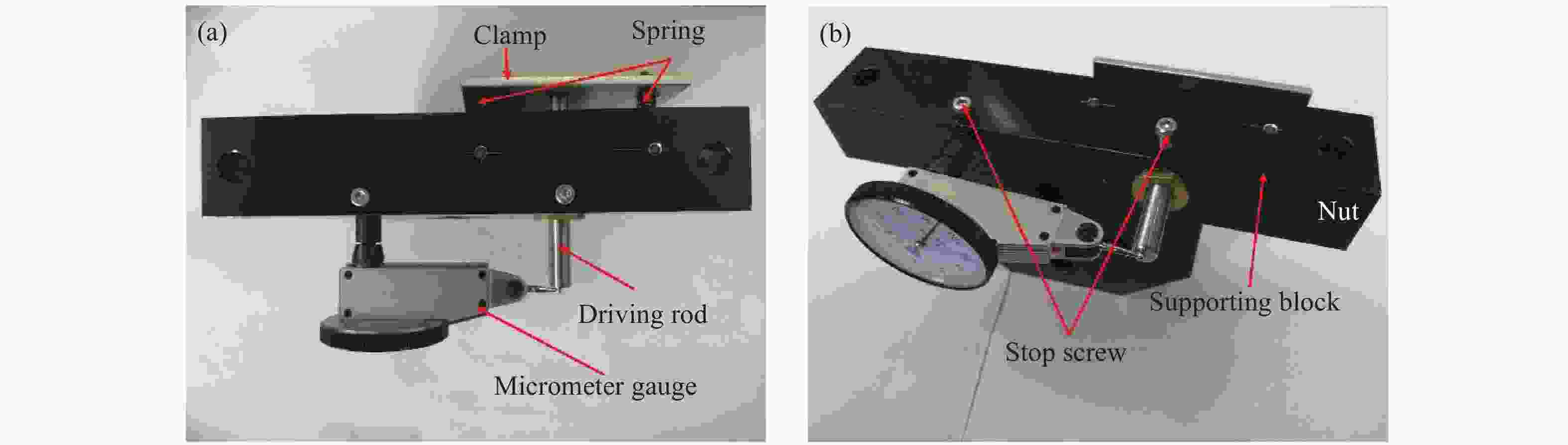
Figure 6 is the schematic diagram of two different adjustment structures. The two structures have the same specifications of the driving rod (Fig.6(a)) and the two nuts have the same external dimension and the same specification of thread size. The specific design parameters of slotted nut (Fig.6(b)) refer to Tab.1. The internal thread surface of the un-slotted nut has no axial groove (Fig.6(c)). With reference to the force of the adjustment structure in optical mount, a test device (shown in Fig.7) was built to compare the stability of the two adjustment structures. The device adopted two wire springs to press clamp against one end of the driving rod to achieve unidirectional preload. The other end of the driving rod was pressed against the contact of the micrometer gauge to record the change of the axial clearance in the adjustment screw. The smallest scale of the micrometer gauge is 1 μm. In the test, an adjustable temperature heating lamp (not shown) was installed on the top of the device to carry out thermal shocking. When heating the structures, the heating temperature, heating time and heating direction were kept same to ensure that the temperature changes have the same influence on the micrometer gauge.

Figure 6. Diagram of adjustment screw and nuts. (a) Adjustment screw; (b) Slotted nut; (c) Un-slotted nut
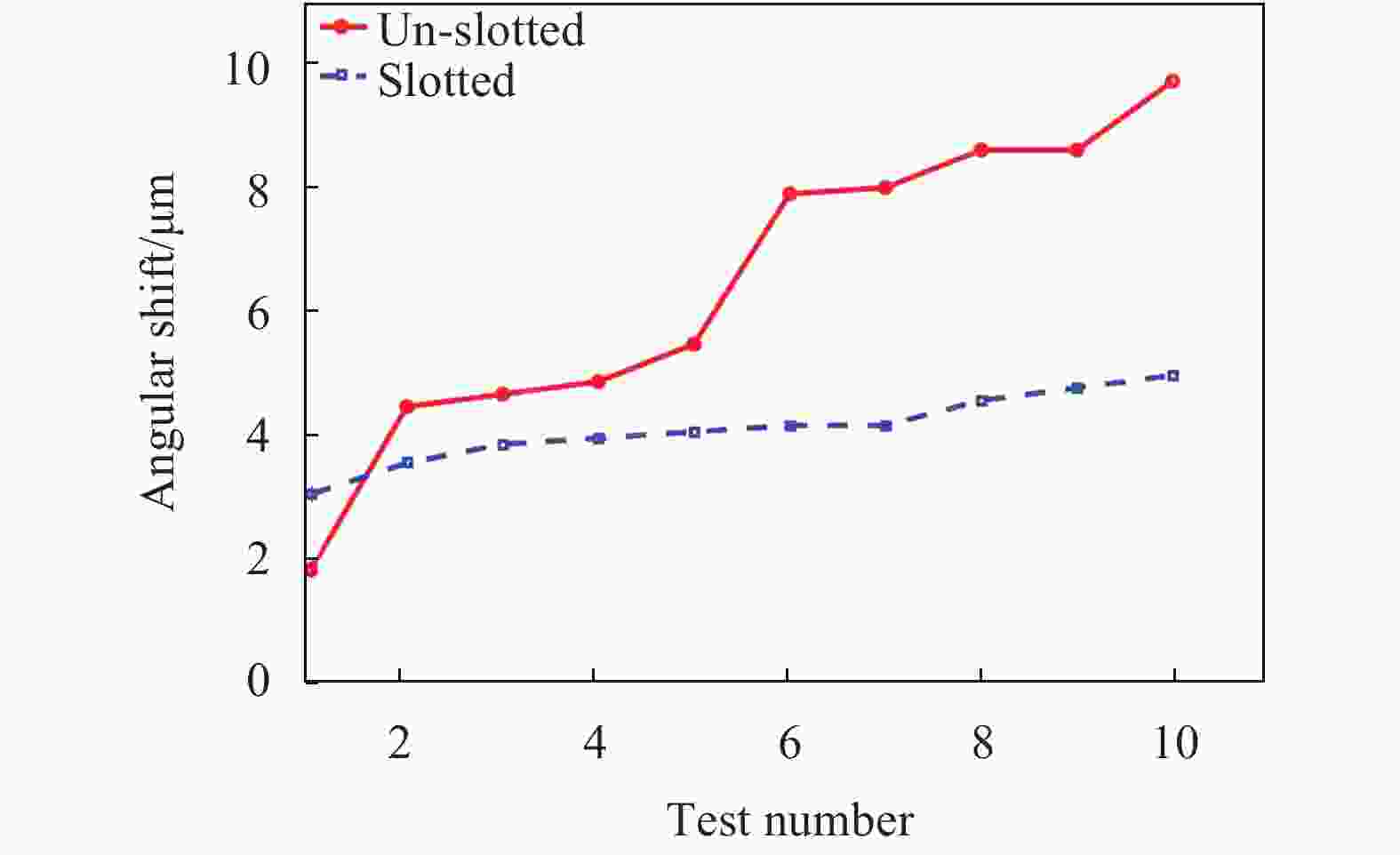
After filling with the same amount of grease, the two adjustment screws (the slotted and the un-slotted) were installed in the same way as shown in Fig.7 for the same number of thermal shocking tests. A single thermal shocking was to heat the structure with a maximum temperature of 35-40 ℃ for 1 h, and then record the dial indicator before heating and after cooling. Figure 8 plots the change of micrometer gauge values of the two structures under several thermal shocking tests. In 9 thermal shockings, the axial shift (7.7 μm) of the un-slotted structure was larger than that of the slotted structure (2 μm), and it was still increasing. While the position of the slotted structure tended to be stable.
In the slotted adjustment screw structure, the grease on the squeezed side flows into the axial slots under the action of the unidirectional preload and the screw tooth surface produces a large area of tight fit. In the un-slotted structure, the hydraulic pressure formed by the many partially sealed small spaces hindered the close fit of the screw tooth surface. With the action of the thermal shockings, the grease squeezed in the thread pair was further reduced. Since the internal screw tooth surface had produced large contact, the axial clearance of the slotted structure changed little, and the micrometer gauge changed little too. While in the thermal shocking tests of the un-slotted structure, the grease squeezed in the pressure side gradually flowed into the non-pressure side under the effect of temperature change and unidirectional preload, resulting in a large change in the axial clearance. The results show that the existence of axial slots could improve the stability of adjustment screw structure under unidirectional preload.
-
The effect of two different adjustment screws on the stability of the optical mount was tested. In the experiment, two optical mounts with same specification were installed with the slotted and un-slotted adjustment screw at the same position respectively. It can be seen from the analysis in Section 2.2 that the axial shift of the adjustment screw 1 only affects the pitch position, but has no effect on the yaw position. In order to enhance the contrast, the mounts both installed the adjustment screw at point B, and the rest of the adjustment positions were replaced by stainless steel balls, as shown in Fig.9. The driving rod only affected the pitch position of the optical part.
The current methods of measuring the stability of optical mounts are mainly developed for a single mount. Tapply[19] used an autocollimator to measure the stability of a single optical mount. Wang Dahui[20] et al. compared the angular shifts before and after the splitting of the spectroscope installed on the test mount to evaluate the stability. In this work, using a similar optical path to measure the stability of two different structures at different time periods will lead to large environmental variations. In addition, the stability of the mount is usually judged by applying a thermal shocking and observing the angular shift of the mount after it returns to normal temperature[10, 19]. Therefore, a stability measurement scheme was proposed as shown in Fig.10 and the mounts were also imposed thermal shockings. The detailed scheme was referred to Ref. [21].

Figure 9. Optical mounts with different adjustment screw structure. (a) The un-slotted; (b) The slotted

Figure 10. Light path diagram for stability comparison[20]
Figure 11 shows the change of angular position of the two mounts after two consecutive thermal shockings. Before and after the first thermal shocking, a certain amount of angular shift both occurred in the pitch position of the two mounts. After the second thermal shocking, the pitch value of the slotted structure had little change while that of the un-slotted structure still had a certain shift. Within the two thermal shockings, the yaw values of the two mounts both changed little, so they were no longer used as the measurement index for comparison in this paper. In addition, the angular position of the two-dimensional direction (yaw and pitch) of the slotted structure was stable with the change of temperature, and the spot was not disturbed. However, that of the un-slotted structure produced a large disturbance with the change of temperature. This was due to the fact that there was more grease on the pressure side of the thread pair in the un-slotted structure than in the slotted grooved structure. When the temperature changed, the creep of grease squeezed on the pressure side could easily cause the driving rod to be unstable relative to the nut.
Several thermal shocking tests were carried out continuously on two optical mounts. For each thermal shocking test, the data one hour before thermal shocking and the data one hour after cooling to room temperature were extracted respectively, and the average value were taken as the angular position before and after each thermal shocking test. Figure 12 plots the change of pitch position of the two mounts in several thermal shocking tests, in which the temperature was the normal temperature value of the corresponding mount after each thermal shocking. After several thermal shocking tests, the environmental temperature deviation of the two mounts didn’t exceed 0.3 ℃. In the 1-4 thermal shocking tests, the angular shift of the un-slotted structure had larger fluctuations than that of the slotted structure. Since the fifth thermal shocking test, the angular shift of the two structures kept the same. Compared with the un-slotted structure, the angular shift of the slotted structure was slightly reduced, but there was still a tendency to continue to increase.
To quickly achieve stable distribution of the grease and reduce the distribution of grease in the squeezed side of the thread pair, the slotted optical mount was put into the incubator for sufficient time baking. In order to compare the effect of high-temperature baking on the two mounts, the un-slotted structure was also put into the same incubator for the same baking. The baking process was to bake the two mounts for eight hours a day (80 ℃) for several days. The baking temperature must not be higher than the dropping point of the grease. The baking time should be as long as possible. In this experiment, the baking duration in this work was one week, which has achieved the desired effect. The purpose of shutting down and cooling after baking was to achieve a stable state of the grease distribution in the thread fit. Then the two mounts was taken out and the stability comparison test was carried out again. In addition, the experiment added a comparative test between the heat-treated slotted mount and the grease-free mount to compare the effect of heat treatment on the stability of the slotted mount.
The angular position of the heat-treated slotted structure only changed slightly in the first two thermal shocking tests, and maintained a stable state under thermal shocking tests (Fig.13(a)). However, the angular position of the un-slotted structure always changed greatly after each thermal shocking test. The angular position of the grease-free optical mount was always in a stable state under several thermal shocking tests, while that of the heat-treated slotted structure only fluctuated slightly during the 5th-6th thermal shocking test, and then returned to a stable state (Fig.13(b)).

Figure 13. Angular shift of different optical mounts under thermal shocking. (a) The slotted (grease+heat treatment) versus the un-slotted (grease+heat treatment); (b) the slotted (grease +heat treatment) versus the structure (no grease)
Further, it could be seen from Tab.2 that the angular shift of the heat-treated slotted structure in two comparative experiments was only 14-15 μrad, which was close to the angular shift of the grease-free structure (8 μrad), and far less than that of the un-slotted structure (34 μrad). The results show that the stability of the heat-treated slotted structure was close to that of the grease-free structure, and was better than that of the un-slotted structure.
Table 2. Angular shift of different optical mounts after baking
Slotted 1-8 tests Un-slotted 1-8 tests No-grease 1-8 tests Angular shift (pitch)/μrad 14-15 34 11 -
This paper studied and analyzed an instability factor of optical mount in laser system. The effect of the axial shift of the adjustment screw caused by the creep of grease on the position of the optical part was analyzed theoretically. It was concluded that the axial shift of the adjustment screw was an important factor for the position instability of the optical mount. An improved thread adjustment structure was proposed. A number of axial slots evenly distributed in the circumferential direction were machined on the inner thread surface of the nut. The maximum radial depth of the axial slot was larger than the major diameter depth of the thread. The structure combined with heat treatment process greatly improved the stability of optical mount. The experiment tested the change of internal axial clearance of two different adjustment screws (the slotted and the un-slotted) under thermal shocking tests. The results showed that the slotted structure could reach stable quickly under the thermal shockings. Secondly, two optical mounts with same specification were used to install the two adjustment screws to carry out the stability comparison test. The results showed that under several thermal shocking tests, the angular shift of the slotted mount was slightly reduced compared to that of the un-slotted structure, but there was still a tendency to increase. Furthermore, in order to achieve a stable internal grease distribution, a long time high-temperature baking for heat treatment process was carried out on two mounts. The stability comparison experiment was built again, and the stability of the slotted heat-treated mount was compared with that of the un-slotted mount and that of the grease-free mount respectively. The results showed that the stability of the heat-treated structure was close to that of the grease-free, while was better than that of the un-slotted structure. The optical mount with slotted heat-treated adjustment screw combined with baking heat treatment process shows more excellent stability. This adjustment screw structure can be used in the optical mechanisms with high stability requirements.
-
摘要: 激光系统要求光束经长光程传输后具有优异的指向稳定性,而光束指向稳定性直接由支撑光学件的支撑镜架结构稳定性决定。为了实现光束的指向稳定性和准直性,常常要求光学镜架既具有优异的结构稳定性又具有良好的可调节性。可调节性由于引入了间隙配合,将引入不稳定性。针对支撑镜架中螺纹微调结构由于存在润滑脂而引入的不稳定性,提出了一种结构改进设计。在微调结构的螺母内螺纹面加工轴向槽,结合该结构进一步提出了一种热处理工艺,可以极大地减小润滑脂所引入的不稳定性。实验测试了两种结构的螺纹轴向间隙变化情况。进一步,对安装有槽结构的支撑镜架在热处理前后分别与无槽结构的支撑镜架进行稳定性对比实验,结果表明经热处理后的有槽微调结构可以极大地提升支撑镜架结构的稳定性。Abstract: Laser system requires that optical beam has excellent pointing stability after long optical path transmission, which is directly determined by the structural stability of optical mounts. In order to achieve beam pointing stability and alignment, optical mount is often required to have excellent structural stability and adjustability. Due to the existence of clearance fit, the adjustability will lead to instability. Aiming at the instability caused by grease in adjustment screw structure of the mount, a structure improvement design was proposed. Axial slots were machined on the internal thread surface of the nut in the adjustment structure. Combined with the proposed structure, a heat treatment process was further proposed, which can greatly reduce the instability introduced by grease. Change of axial clearance of two adjustment structures were tested. Structure stability of optical mount with slotted adjustment structure was compared with the un-slotted mount before and after heat treatment. The results show that the slotted adjustment structure after heat treatment can greatly improve the stability of optical mount.
-
Figure 10. Light path diagram for stability comparison[20]
Table 1. Design parameters of the axial slots of adjustment screw structure
Parameters Numbers of slots D/mm D1/mm H/mm Value 3-6 7 6.65 0.5 Table 2. Angular shift of different optical mounts after baking
Slotted 1-8 tests Un-slotted 1-8 tests No-grease 1-8 tests Angular shift (pitch)/μrad 14-15 34 11 -
[1] Danson C N, Haefner C, Bromage J, et al. Petawatt and exawatt class lasers worldwide [J]. High Power Laser Science and Engineering, 2019, 7(3): e54. [2] Bagnoud V, Hornung J, Afshari M, et al. Implementation of a phase plate for the generation of homogeneous focal-spot intensity distributions at the high-energy short-pulse laser facility PHELIX [J]. High Power Laser Science and Engineering, 2019, 7(4): e62. [3] Galletti M, Oliveira P, Galimberti M, et al. Ultra-broadband all-OPCPA petawatt facility fully based on LBO [J]. High Power Laser Science and Engineering, 2020, 8(4): e31. [4] Jiang T, Gao S, Tian Z N, et al. Fabrication of diamond ultra-fine structures by femtosecond laser [J]. Chinese Optics Letters, 2020, 18(10): 101402. doi: 10.3788/COL202018.101402 [5] Cheng Y, Liu X, Tan C Y, et al. Research and development of spaceborne solid state laser technology for laser altimeter [J]. Infrared and Laser Engineering, 2020, 49(11): 20201046. (in Chinese) [6] Shu R, Huang G H, Kong W. Development and review of space-based laser altimetry technology [J]. Infrared and Laser Engineering, 2020, 49(11): 20201047. (in Chinese) [7] Huang J C, Wang L K, Duan Y F, et al. All-fiber-based laser with 200 mHz linewidth [J]. Chinese Optics Letters, 2019, 17(7): 071407. doi: 10.3788/COL201917.071407 [8] Jia Y C, Chen F. Compact solid-state waveguide lasers operating in the pulsed regime: a review [J]. Chinese Optics Letters, 2019, 17(1): 012302. doi: 10.3788/COL201917.012302 [9] Wang J L, Zhao K Q, Feng T, et al. 1.5 J high-beam-quality Nd: LuAG ceramic active mirror laser amplifier [J]. Chinese Optics Letters, 2020, 18(2): 021401. [10] Bullock K T, DeYoung R J, Sandford S P. Angular alignment testing of laser mirror mounts under temperature cycling [J]. NASA Technical Reports Server, 1997, 3661: 1-17. [11] Jacobs S F. Variable invariables: dimensional instability with time and temperature [C]//Critical Review Collection, 2017. [12] Baskaran R, Sivakumar P, Arivuoli D. Dimensional stability of mirror materials for opto-mechanical reference systems [J]. International Journal of Physical Sciences, 2013, 8(19): 997-1004. doi: 10.5897/IJPS2013.3810 [13] Leahy Z N, Magner A J, Hatheway A E. Athermal mounting of optics in metallic housings [C]//Proceedings of SPIE-Optomechanical Engineering, 2013, 8836: 88360P. [14] Pijnenburg J, Voert M J A T, Vreugd J D, et al. Ultra-stable isostatic bonded optical mount design for harsh environments [C]//Proceedings of SPIE-The International Society for Optical Engineering, 2012, 8450: 27. [15] Dewitt F. A novel mirror-mount design suitable for laboratory and OEM applications [C]//Proceedings of SPIE, 2018, 10747: 107470D. [16] Kvamme E T, Sullivan M T. A small low-stress stable 3-DOF mirror mount with one arc-second tip/tilt resolution [C]//Proceedings of SPIE-The International Society for Optical Engineering, 2004, 5528: 264-271. [17] Kautz M, Close L M, Males J R. A locking clamp that enables high thermal and vibrational stability for kinematic optical mounts [C]//Proceedings of SPIE, 2018, 10703: 107032Q. [18] Furse J E. Kinematic design of fine mechanisms in instruments [J]. Journal of Physics E Scientific Instruments, 1981, 14(3): 264. doi: 10.1088/0022-3735/14/3/001 [19] Tapply J K. Optical testing technique for the evaluation of mechanical mount thermal stability [C]//Proceedings of SPIE, 1999, 3786: 386-394. [20] Wang D H, Zhao J, Zhao X Q, et al. Measurement and analysis on structure stability of optical mirror mounts with small aperture [J]. Chinese Journal of Lasers, 2010, 37(S1): 308-311. (in Chinese) [21] Zhang C, Tang G X, Liu Z G, et al. Research on structural stability of adjustable support mount in laser system [J]. Chinese Journal of Lasers, 2020, 47(10): 1001002. (in Chinese) doi: 10.3788/CJL202047.1001002 -







 下载:
下载: