-
相位式激光测距技术在中近程距离测量领域具有重要应用,是航空航天、高端智能制造、高精度测绘等领域的通用关键技术。相位式激光测距系统中,测量精度和测量速度是表征测距系统性能的重要指标和主要突破方向[1]。提高测量精度主要通过提高测尺频率和鉴相精度来实现;提高测量速度主要通过提高鉴相信号处理电路的计算速度来实现[2]。以上性能的提高对鉴相信号处理电路的带宽和复杂度提出更高要求[3]。针对上述问题,采用高速采样结合数字鉴相法,将待测信号直接转换为数字信号进行鉴相处理,可降低鉴相电路的复杂性,减小信号处理过程中引入的鉴相误差,具有硬件集成度高、鉴相精度高等优点。同时,对鉴相算法进行优化,能够提高鉴相速度,提高相位式激光测距系统的测量速度[4]。
目前常用的数字鉴相方法包括数字相关法、数字同步解调法、数字频域鉴相法(Discrete Fourier Transform, DFT)和矢量内积法等[5-6]。2013年,王心遥等人通过仿真分析了白噪声、频率偏移等因素对数字相关法、数字同步解调法及数字频域鉴相法的鉴相精度影响,仿真结果表明数字频域鉴相法的相位误差最小,鉴相精度最高[7]。2019年,中北大学杨佳敏对数字相关法、数字同步解调法及数字频域法进行分析比较,提出了一种改进后的数字相关法,实现了相位误差0.374°[8]。2009年,贾秀方等人基于数字同步解调法结合模拟混频快速鉴相,利用Matlab仿真实现了最大鉴相误差0.25°误差标准方差为0.09°[9]。2017年,周翔等人针对数字同步解调法中通道信号不平衡存在误差和不匹配的情况提出了补偿算法,经过仿真验证,有效提高了系统性能[10]。2012年,王选钢等人基于数字频域鉴相法引入希尔伯特变换进行预处理,经仿真和实验验证鉴相无相位偏差,调制频率为100 MHz时,测距精度为0.4 mm[11]。2019年,郭天茂等人为解决传统数字频域鉴相法的频谱泄露问题,采用全相位数字频域鉴相法,仿真结果表明测量距离大于50 m时,测距误差小于0.3 mm[12]。2002年,黄正英等人提出了基于矢量内积原理,验证矢量内积法在相位测距系统中鉴相的可行性,指出了该方法相较于数字频域鉴相法的计算量更小[13]。2004年,田桂平等人提出了矢量内积法不仅可以消除鉴相系统中幅值变化的影响,而且可以实现实时鉴相处理[14]。2016年,朱珏颖等人将矢量内积法应用于动不平衡检测中相位的测量中,相位差测量的相对误差为−0.05% [15]。
以上研究表明,数字频域鉴相法作为相位式激光测距系统中常采用的方法之一,具有较高的测量精度,但其计算过程较为复杂,鉴相速度有待进一步提升。与数字频域鉴相法相比,矢量内积(Vector Inner Product, VIP)法的计算过程简单,具有鉴相速度快的优点,但基于该方法的鉴相性能未有对比分析和实验测试研究。
文中从鉴相精度及鉴相速度两方面研究了VIP法的鉴相性能,并与传统DFT法进行了性能对比。仿真及实验均表明,VIP法具更高的鉴相速度和鉴相精度,是一种适用于高速相位式激光测距系统的鉴相测量方法。
-
二维平面中,两个矢量利用三角变换可以求得两者之间夹角的余弦值,如图1所示。以此类推,可将二维空间的两个矢量推广到n维空间,同理可得n维空间两个矢量的夹角。
基于矢量内积法进行正弦信号相位计算时,待测信号需满足实数序列[10]。将相位测距中出射、测量信号作为n维矢量,矢量维度取决于采集的数据量,将两路采集后的离散信号分别表示为矢量X、Y。两路信号数量积的值由矢量X、Y的长度及X、Y的夹角的余弦确定,可表示为:
$$ X \cdot Y = \left\| X \right\| \cdot \left\| Y \right\|\cos \varphi $$ (1) n维空间的内积可表示为:
$$ X \cdot Y = \left( {{x_1},{x_2}, \cdots {x_n}} \right) \cdot \left( {{y_1},{y_2}, \cdots {y_n}} \right) = \sum\limits_{i = 1}^n {{x_i}} {y_i} $$ (2) 矢量X、Y的长度可表示为:
$$ \left\| X \right\| = \sqrt {\sum\limits_{i = 1}^n {{x_i}^2} } \text{,}\left\| Y \right\| = \sqrt {\sum\limits_{i = 1}^n {{y_i}^2} } $$ (3) 则n维矢量X、Y的夹角即待求相位差可表示为:
$$ \varphi = \arccos \frac{{X \cdot Y}}{{\left\| X \right\| \cdot \left\| Y \right\|}} $$ (4) -
VIP法求解相位时,出射和反射两路信号均为实数序列,根据反余弦函数
$\arccos x$ 的取值范围推导出一路信号的鉴相范围为[0, π/2],因此VIP法的鉴相范围为[0, π],相较于VIP法,DFT法求解相位差时,信号幅度最大谱线对应的位置对应的实部虚部有正负之分,根据反正切函数$\arctan x$ 的取值范围可以推导出一路信号的相位范围为(−π/2,π/2),因此DFT法的鉴相范围为(−π,π)。当所求距离超过一个测尺长度时,VIP法和DFT法求解的相位值为真实相位差的“小数部分”,因此所求真实相位差值可表示为:
$$ \Delta {\varphi _{{\rm{VIP}}}} = N \cdot {\text{π}} + {\varphi _{{\rm{VIP}}}} $$ (5) $$ \Delta {\varphi _{{\rm{DFT}}}} = N \cdot 2{\text{π}} + {\varphi _{{\rm{DFT}}}} $$ (6) 其中,N的取值由测距系统的粗测确定。
-
在实际测量系统中,鉴相方法的计算速度影响系统的测量速度。连续信号经过采样后为有限长离散信号,对于带有相位信息的N点的有限测量数据,利用VIP法和DFT法进行相位求解的速度主要取决于两类算法的计算复杂度。上述鉴相方法硬件一般采用FPGA实现。针对N点的有限序列的DFT算法可以表示为:
$$ X(k) = \sum\limits_{n = 0}^{N - 1} {x(n)} W_N^{kn},k = 0,\;1, \cdots \;,N - 1 $$ (7) N点DFT的计算量为N2次复数乘法以及N×(N−1)次复数加法。基于旋转因子的周期性和对称性,将N点DFT分解为较短的DFT进行计算,可以大幅减少计算量,N点的DFT法的计算量可降低为:复数乘法共
$ N/2 \times {\text{log}_2}N $ 次,复数加法共$ N \times {\text{log}_2}N $ 次[16]。相较于DFT法,由公式(4)可得,基于FPGA实现VIP法所需的计算量为3N次乘法、3(N−1)次加法以及2次开方实数运算,则在同等数据量运算下,VIP法均为实数运算且运算量更小,所占用内存资源更小。
为直观地进行比较,以N=1024为例,计算两种方法的计算量。DFT法的计算量为:复数乘法共
$ 1024/2 \times {\text{log}_2}1\;024 = 5\;120 $ 次,复数加法共$ 1\;024 \times {\text{log}_2} $ $ 1\;024 = 10\;240 $ 次。VIP法的计算量为:实数乘法共3×1024=3072次,实数加法共3×(1024−1)=3069次,以及2次实数开方运算。从上述示例中可以看出,在同等数据量时,VIP算法的计算量约为DFT算法的1/3,在实际测量中能够实现更快的鉴相计算。
-
为了进一步分析VIP法的鉴相性能,设置初始相位不同的两路正弦调制信号,参考信号与测量信号均设置为50 MHz,采样率设置为1 GHz,从鉴相精度和鉴相速度两方面分析比较VIP法和DFT法的鉴相性能。
-
参考信号和测量信号的相位差依次设置为30°、90°、150°、210°、270°及330°时,计算点数设置400~8000个,分析不同计算点数时VIP法和DFT法的鉴相精度。
不同计算点数的鉴相稳定度如图2所示,所求的相位差值与预设相位差值偏差量如图3所示。图2表明,VIP法和DFT法的稳定度数量级均可达到10−9。图3表明,采用VIP法进行鉴相时,不同计算点数所求相位差值与预设相位差值偏差均很小;而采用DFT法进行鉴相时,当计算点数少于1200个时,所求相位差值与预设相位差值偏差较大,多于1200个点后与预设相位值偏差趋于稳定。与DFT法相比,VIP法中的相位差偏差值受计算点数变化的影响更小,采用更少的采样点数进行计算即达到较高的鉴相稳定度,鉴相计算时间更短,有利于提高鉴相速度。
-
参考信号和测量信号的相位差值设置为0°~360°,计算点数设置为4000,分析在相同计算点数、不同相位差情况下两种方法的鉴相精度。为便于与预设相位差值进行比较,根据前述VIP法和DFT法的鉴相范围,对两种鉴相方法所求的相位差值进行修正。
VIP法和DFT法在不同相位差下的鉴相精度如图4所示。从图4可以看出,在固定计算点数、不同预设相位差的情况下,VIP法的鉴相精度优于DFT法,且在不同预设相位差的情况下,VIP法的鉴相稳定度波动范围小于DFT法。

图 4 固定计算点数不同相位差VIP法和DFT法鉴相精度
Figure 4. Detection accuracy of VIP method and DFT method with different phase differences and fixed calculation points
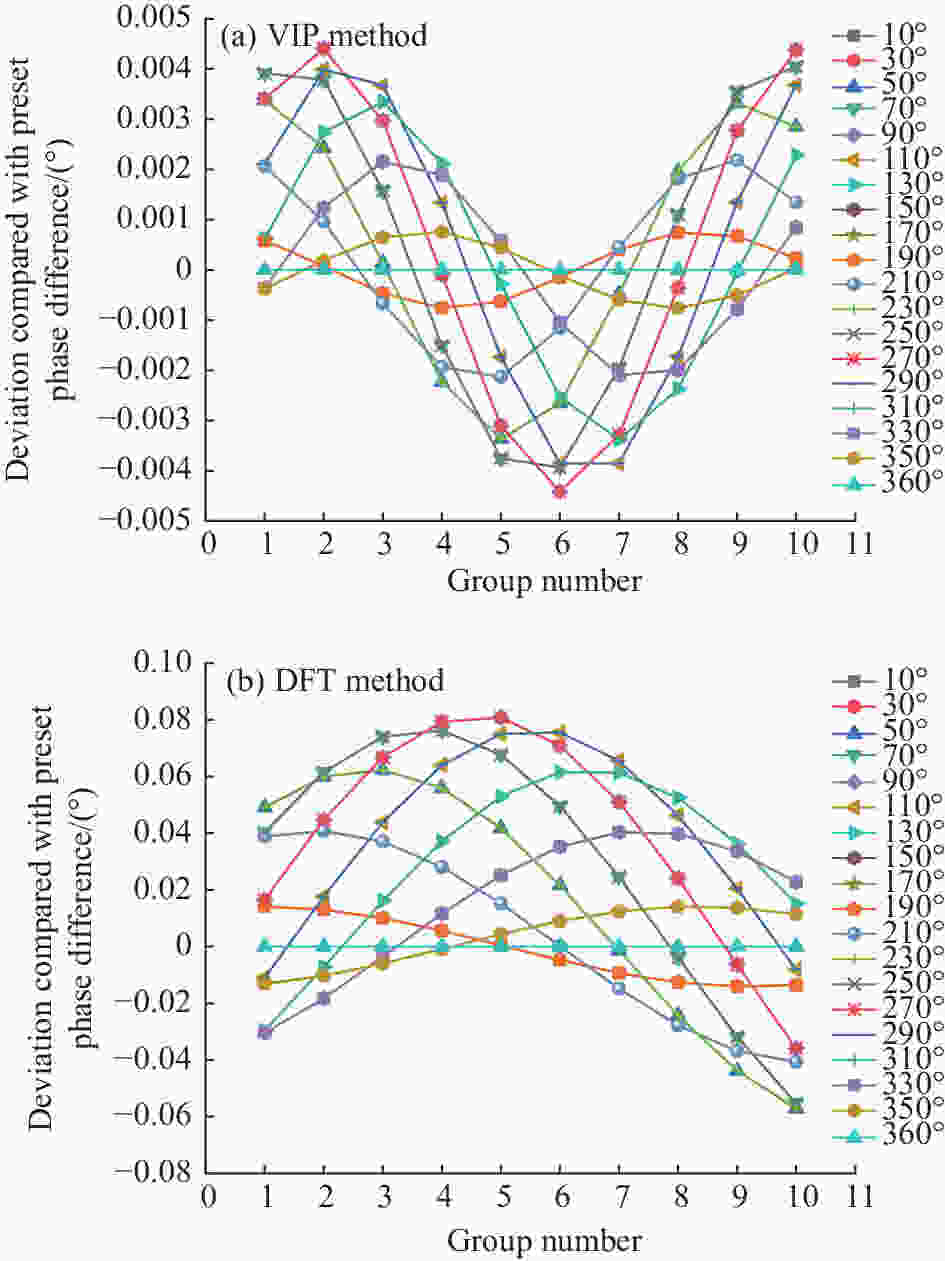
VIP法及DFT法鉴相相位值与预设相位值偏差如图5所示,仿真结果表明,在固定计算点数鉴相情况下,VIP法鉴相相位差值与预设相位差偏差更小。
-
使用信号发生器(安捷伦81150 A)产生两路具有不同相位值的正弦信号,信号频率设为50 MHz,不同相位差等效为不同测量距离。使用采样频率为1 GHz的高速采样板卡对两路信号进行同步采样,从鉴相精度及鉴相速度两方面对VIP法和DFT法的鉴相性能进行测试分析。
-
使用高速采样板卡对两路信号进行采集,基于不同计算点数对VIP法和DFT法的鉴相性能进行计算测试。
VIP法和DFT法在不同计算点数时的鉴相精度如图6所示。采样点数对DFT法的鉴相稳定度影响较大,要达到稳定的鉴相精度需1200个点以上。采样点数对VIP法的鉴相精度稳定度影响较小,且计算点数在1200个点以下时鉴相精度优于DFT法。因此,基于高速采样板卡采样时,鉴相计算数据量对VIP法影响小于DFT法,实测结果与仿真结果一致。
-
使用采样板卡采集4000个数据点,共10组,参考信号和测量信号相位差值同样设置为 0°~360°,分别利用DFT法和VIP法进行鉴相计算。
VIP法和DFT法在不同预设相位差下的鉴相精度如图7所示。基于高速采样板卡鉴相时,采集同等数据量的情况下, VIP法求解的鉴相精度优于DFT法,实测结果与仿真结果一致。

图 7 固定计算点数不同相位差下VIP法和DFT法鉴相精度
Figure 7. Phase detection accuracy of VIP method and DFT method with different phase differences and fixed calculation points
利用同轴线缆传输参考信号和测量信号进行采样时,两路线缆的长度不能保证完全相等,因此预设相位差并不是待测相位差的真值,为了对照不同鉴相方法的相位差偏移量,将10组信号取均值与预设相位做差,分析VIP法和DFT法预设不同相位时系统固有相位差的波动情况。如图8所示,当预设相位差在0°~360°范围内变化时,VIP法的固有相位差波动范围比DFT法小。
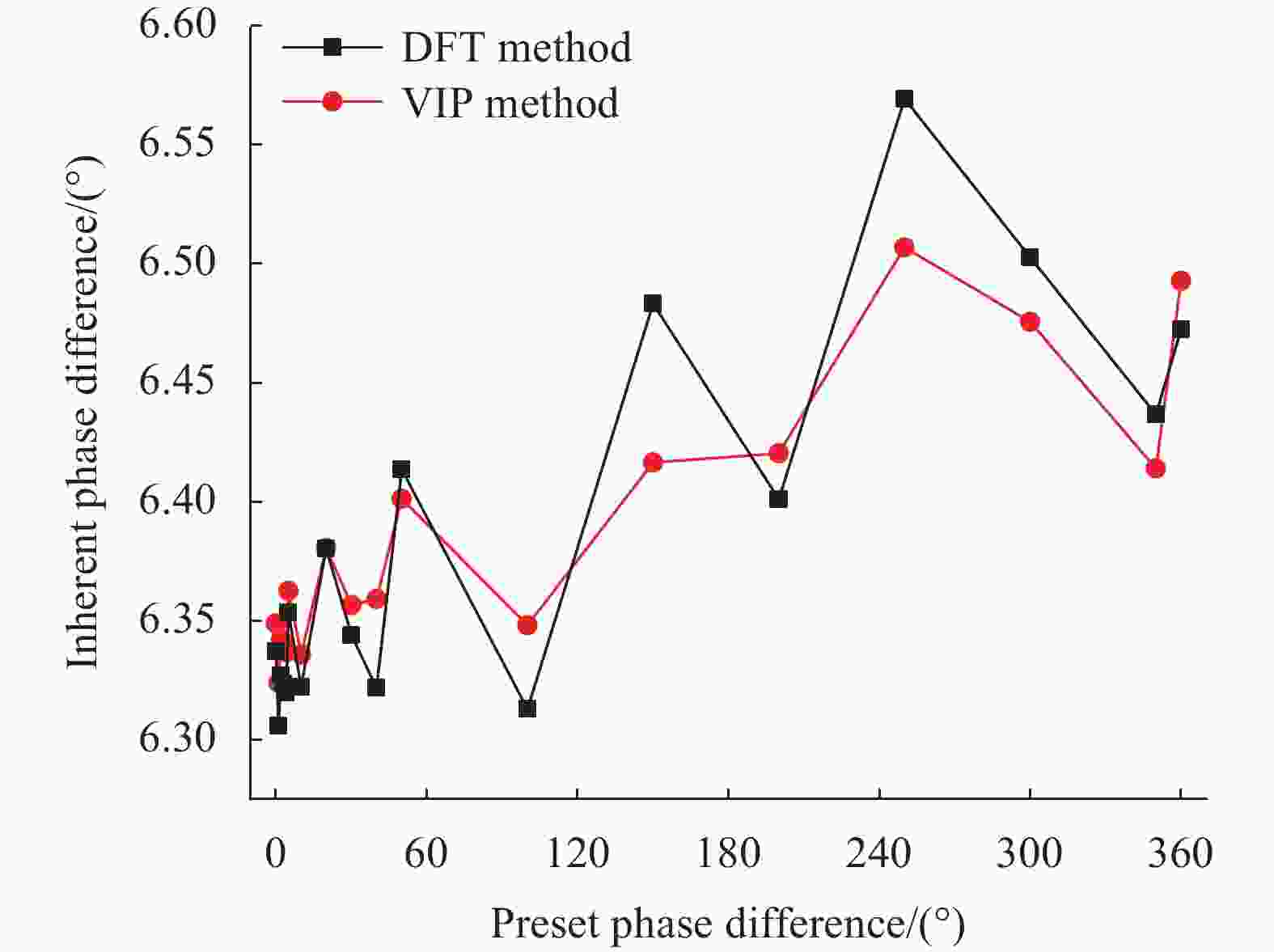
图 8 不同预设相位差VIP法和DFT法系统固有相位差波动图
Figure 8. Inherent phase difference fluctuation diagram of VIP method and DFT method system with different phase differences
以上实测结果表明,当待测信号调制频率为50 MHz、测相计算点数为4000个点时,VIP法的鉴相精度优于0.1°,测距精度优于0.2 mm。
为了确定VIP法和DFT法的实时计算速度,使用Xilinx公司XC7K325T型号的FPGA板卡进行DFT法和VIP法的鉴相计算测试。测试结果表明,完成一次4000个点的鉴相计算,VIP法的计算时间为32 μs,DFT法的计算时间为78 μs,VIP法具有更快的鉴相计算速度。
综上所述,针对相位式激光测距系统对鉴相速度和鉴相精度的需求,与DFT法相比,VIP法具有鉴相速度快和鉴相精度高的优点。
-
首先介绍了相位式激光测距系统中采用的数字鉴相方法,分析了不同鉴相方法的特点和研究进展。针对测距系统中对测量速度和测量精度的需求,从鉴相计算所需点数和相同点数的鉴相精度等方面,对VIP法和DFT法进行仿真和实验研究。结果证明,计算点数对VIP法鉴相稳定度影响更小;相同计算点数时,VIP法的鉴相精度更高,鉴相速度更快。根据实测结果,当待测信号调制频率设置为50 MHz、计算点数为4000个时,VIP法所求鉴相精度优于0.1°,测距精度为0.2 mm以内。针对相位式激光测距系统对鉴相速度和精度的需求, VIP法具有更快的鉴相速度和更高的鉴相精度,对提高相位式激光测距系统的测量速度和测量精度具有重要的研究意义和应用价值。
-
摘要: 测量速度和测量精度是相位式激光测距系统的两个重要指标。针对高速高精度测距需求,研究了基于矢量内积(Vector Inner Product, VIP)法的高速数字鉴相方法,从鉴相计算的点数、鉴相计算速度和鉴相精度等方面对VIP法的鉴相性能进行了仿真分析和实验测试,并与传统的数字频域鉴相法(Discrete Fourier Transform, DFT)进行了性能对比。仿真和实验结果表明,VIP法具有更高的鉴相速度和鉴相精度,当信号调制频率为50 MHz时,基于高速采样板卡实测得到的鉴相精度优于0.1°,测距精度0.2 mm以内,相同计算点数VIP法的鉴相处理速度是DFT法的3倍。研究结果表明,VIP法具有鉴相精度高、鉴相速度快的优点,适用于高速高精度激光测距系统。Abstract: Measurement speed and measurement accuracy are two important indicators of the phase laser ranging system. Aiming to the needs of high-speed and high-precision ranging system, a high-speed digital phase detection method based on the Vector Inner Product (VIP) method was studied. The phase detection performance of the VIP method was simulated and tested in terms of the number of phase detection calculation points, phase detection calculation speed, and phase detection accuracy. The simulation and experimental results were compared with the traditional digital frequency domain phase detection method (Discrete Fourier Transform (DFT) method), which show that the VIP method has higher phase detection speed and phase detection accuracy. When the signal modulation frequency is set as 50 MHz, based on high-speed sampling board, the measured phase detection accuracy is better than 0.1°, the ranging accuracy is within 0.2 mm, the phase detection processing speed of the VIP method is 3 times faster than that of the DFT method under the circumstance with the same number of calculation points. Referring to the high phase detection accuracy and fast phase detection speed, all the analysis data show that the VIP method has the significant advantages, which is suitable for the high-speed and high-precision laser ranging systems.
-
-
[1] Li Guicun, Fang Yahao, Zhang Hao, et al. Correction of power-to-phase conversion for distance measurement using synthetic wavelength method of a femtosecond laser [J]. Chinese Journal of Lasers, 2021, 48(1): 0104002. (in Chinese) [2] Tan Xiaorui, Zhang Pizhuang, Fan Yuanyuan. Design of new type phase laser ranging system circuit [J]. Laser & Infrared, 2016, 46(3): 279-283. (in Chinese) doi: 10.3969/j.issn.1001-5078.2016.03.007 [3] Xu Xianze, Weng Mingjie, Xu Fengqiu, et al. Phase laser ranger based on quadrature modem and frequency reduction [J]. Optics and Precision Engineering, 2017, 25(8): 1979-1986. (in Chinese) doi: 10.3788/OPE.20172508.1979 [4] Zhang Shilei, Cui Yu, Xing Muzeng, et al. Light field imaging target ranging technology [J]. Chinese Journal of Optics, 2020, 13(6): 1332-1342. (in Chinese) doi: 10.37188/CO.2020-0043 [5] Hu Qi, Wang Zhe, Liu Hongshun, et al. Step diffraction algorithm based on single fast Fourier transform algorithm [J]. Chinese Optics, 2018, 11(4): 568-575. (in Chinese) doi: 10.3788/co.20181104.0568 [6] Xu Yongyao, Zhang Tieli, Gao Xiaoqiang, et al. Review of digital processing techniques for phase signal in absolute distance measurement [J]. Journal of Astronautic Metrology and Measurement, 2020, 40(6): 1-6. (in Chinese) [7] 王心遥, 张珂殊. 基于欠采样的激光测距数字鉴相方法[J]. 红外与激光工程, 2013, (5): 1330-1337. Wang Xinyao, Zhang Keshu. Digital phase-shift measuring methods based on sub-sampling in laser range finder[J]. Infrared and Laser Engineering, 2013, 42(5): 1330-1337. (in Chinese) [8] 杨佳敏. 基于连续波相移的实时测量及触发技术研究[D]. 山西: 中北大学, 2019. Yang Jiamin. Research on real-time measurement and trigger technology based on continuous wave phase shift [D]. Taiyuan: North University of China, 2019. (in Chinese) [9] Jia Fangxiu, Ding Zhenliang, Yuan Feng. New phase difference measurement based on digital synchronous demodulation [J]. Instrument Technique and Sensor, 2009(4): 78-80. (in Chinese) doi: 10.3969/j.issn.1002-1841.2009.04.028 [10] Zhou Xiang, Lv Youxin. Research on estimation and compensation of I/Q imbalance in orthogonal channels [J]. Radar Science and Technology, 2017, 15(1): 8-12. (in Chinese) doi: 10.3969/j.issn.1672-2337.2017.01.002 [11] Wang Xuangang, Gou Ningyi, Zhang Keshu. Unbiased improvement of spectrum analysis phase discrimination for phase-shift laser range finder [J]. Optics and Precision Engineering, 2012, 20(4): 888-895. (in Chinese) doi: 10.3788/OPE.20122004.0888 [12] Guo Tianmao, Liu Ke, Miao Yinxiao, et al. Application of all phase FFT frequency measurement in FMCW laser ranging technology [J]. Journal of Astronautic Metrology and Measurement, 2019, 39(2): 45-50. (in Chinese) doi: 10.12060/j.issn.1000-7202.2019.02.10 [13] Huang Zhengying, Li Ji, Chen Jiexiang, et al. The phase difference detector by inner product applied in laser phase distance measurement system [J]. Optoelectronic Technology & Information, 2002, 15(6): 31-34. (in Chinese) [14] 田桂平, 万钧力, 陈滟涛. 基于矢量内积法的高精度数字相位差计[J]. 电测与仪表, 2004, 41(10): 16-18. Tian G P, Wan J L, Chen Y T. High precision digital phase detector based on inner product theory [J]. Electrical Measurement & Instrumentation, 2004, 41(10): 16-18. (in Chinese) [15] Zhu Jueying, Yang Jue, Fang Xiang, et al. Phase difference measurement based on vector inner product method and its application [J]. Measurement Technique, 2016(12): 35-37. (in Chinese) [16] Wang Linquan, Pi Yiming, Chen Xiaoning, et al. Realization of high-speed FFT by FPGA [J]. Journal of University of Electronic Science and Technology of China, 2005, 34(2): 152-155. (in Chinese) doi: 10.3969/j.issn.1001-0548.2005.02.003 -







 下载:
下载: