-
同步泵浦光参量振荡器（OPO）广泛地应用于中红外宽带光频梳与超短脉冲的产生。双谐振光参量振荡器（DRO）是一类信号光与闲频光均在腔内振荡的OPO，具有低阈值、大增益带宽等特点[1]。当信号光波长与闲频光波长相等时，DRO又称为简并DRO（DOPO）。在简并以及简并附近的DRO，相比于单谐振光参量振荡器（SRO）以及远离简并的DRO，其增益带宽更宽，是目前研究的热门方向之一[2-8]。
2013年，Haakestad等人基于0.8 mm长的PPLN晶体，在3 μm波段，产生了半高全宽为51 fs脉冲[8]。2016年，Wolf等报道了基于1 mm长的PPLN晶体的DOPO，产生了35 fs的2 μm的飞秒脉冲[9]。在2016年，Smolski等人使用OP-GaAs晶体，产生了瞬时带宽覆盖2.6~7.5 μm的中红外频率梳；并在2018年，利用该频率梳对多种分子的中红外吸收谱进行了精准的测量[10-11]。
飞秒DRO呈现出很多同飞秒SRO不同的性质。2012年，Rudy等人对DOPO在简并腔长附近进行腔长调谐，发现将标准的DOPO的腔长调短时，DOPO将不再简并，信号光与闲频光的中心波长不再相等。同时他们也在实验中发现，DRO的输出功率同腔长存在周期性的调谐关系，调谐的周期刚好为泵浦光的中心波长[3]。2018年，Jankowski等人提出了通过将DOPO的腔长由刚好满足信号光与泵浦光同步的情况，进一步调长，可以使DOPO输出孤子脉冲[4]。
笔者所在的课题组也对飞秒DRO进行了相关研究。在参考文献[12]中，课题组首次报道了简并DRO的多孤子输出，成功地在实验中产生了飞秒的双孤子与三孤子的输出。在参考文献[13]中，课题组利用非简并DRO的调谐特性，通过结合使用级间调谐和级内调谐，首次在DRO中获得了中心波长可连续调谐的飞秒激光输出，信号光与闲频光的调谐范围分别为1 910~2070 nm和2140~2340 nm。
腔长调谐特性是DRO中非常具有代表性的特点。随着腔长的改变，DRO将会在非简并、近似简并以及完全简并态之间切换状态。目前大部分针对简并附近DRO工作特点的研究一般局限于某一特定的工作状态。文中将基于数值仿真模型，对常规的泵浦条件下的简并附近DRO的腔长调谐特性进行系统的研究分析。文中将对腔长无调谐、负调谐以及正调谐三种情况进行分析，同时对比已有的实验结果，总结出简并附近DRO的腔长调谐特性。
-
可以利用耦合波方程建立光参量过程的仿真计算模型。在信号光的移动坐标系下，包含色散效应的DRO两波耦合波方程可以写为：
$$\frac{{\partial {A_1}}}{{\partial {\textit{z}}}} - i\sum\limits_{m \geqslant 2} {\frac{{{i^m}\beta _{\omega 1}^{(m)}}}{{m!}}\frac{{{\partial ^m}{A_1}}}{{\partial {\eta ^m}}}} = \frac{{2i{\omega _{\rm{1}}}{d_{eff}}}}{{{n_1}c}}{A_2}A_1^*$$ (1) $$\frac{{\partial {A_{\rm{2}}}}}{{\partial {\textit{z}}}} + \nu \frac{{\partial {A_{\rm{2}}}}}{{\partial \eta }} - i\sum\limits_{m \geqslant 2} {\frac{{{i^m}\beta _{\omega 2}^{(m)}}}{{m!}}\frac{{{\partial ^m}{A_{\rm{2}}}}}{{\partial {\eta ^m}}}} = \frac{{i{\omega _2}{d_{eff}}}}{{{n_2}c}}A_1^2$$ (2) 式中：A为脉冲的包络；ω为脉冲的中心频率；v为信号光和泵浦光的群时延差；n为折射率；deff为有效非线性系数；角标1，2分别代表信号和泵浦光。对激光器的腔长调谐，可以等效为对信号脉冲时延的改变，因此可在迭代中按照公式(3)引入仿真模型：
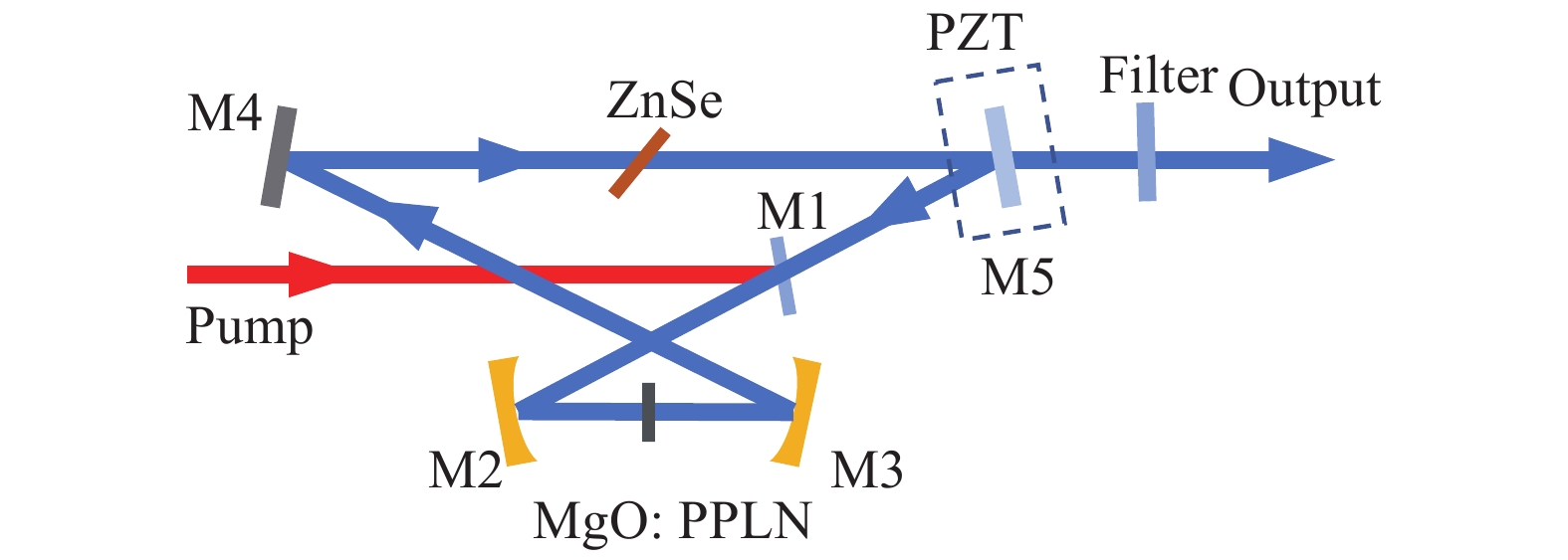
$${A_1}^{N + 1}(t) = {F^{ - 1}}\{ {{\rm e}^{i\Delta T\omega }}F[A_1^N(t)]\} $$ (3) 式中：ΔT为腔长调谐所对应的时延。基于上述数学模型，可以对简并及其附近的DRO进行数值仿真。所仿真的DRO结构如图1所示。
图 1 数值仿真中使用的DRO结构
Figure 1. Schematic of the DRO structure in numerical simulation
图中，M1为泵浦耦合镜，对泵浦光增反，信号光和闲频光增透，通过反射将泵浦光注入光参量振荡器中。M2~M5为光参量振荡器的四个腔镜，其中，M2和M3为曲率半径为−100 mm的镀金平凹透镜，M4为平面银镜，M5为宽带宽的输出耦合镜，其对信号光和闲频光的反射率为80%。仿真所使用的参数如表1所示。所选用的SiO2与ZnSe窗口片用于色散补偿，保证在简并波长即2070 nm处的二阶群速度色散为0。在不进行腔长调谐下，DRO的阈值约为30 mW。
表 1 DRO数值仿真中所使用的各项参数
Table 1. Parameters used in the numerical simulation of the DRO
Symbol Parameter Value λp Central wavelength of the pump light/nm 1035 frep Pump repetition/MHz 80 tp Duration of the pump pulses/fs 180 Lc Length of the PPLN crystal/mm 3 Lz Thickness of the ZnSe plate/mm 1.8 Ls Thickness of the SiO2 plate/mm 3 Λ Poling period of the PPLN crystal/μm 31.4 deff 2nd order nonlinear optical coefficient/pm·V−1 25[14] R Reflection of the output coupling mirror 60% -
仿真所使用的移动参考坐标系的波长设置为2070 nm，即简并时的信号光波长。因此，0腔长调谐代表简并波长同泵浦光完全同步时的腔长。笔者将泵浦功率设置为120 mW（4倍阈值），在−4.5~2.15 μm范围内进行腔长调谐，记为Δz，调谐的分辨率为0.05 μm。记录DRO的输出光谱与输出功率随Δz的变化，如图2所示。
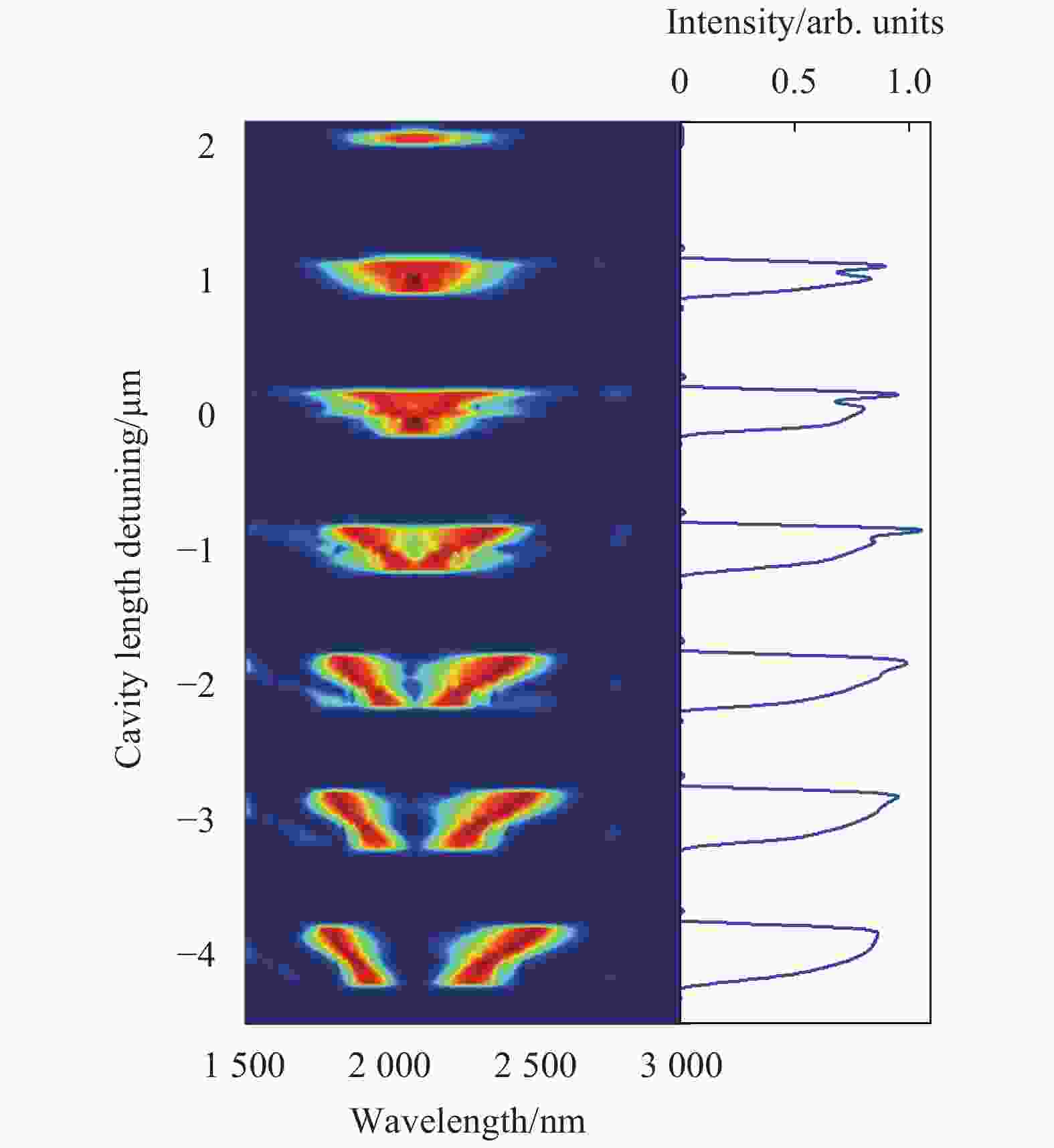
图 2 简并附近DRO输出光谱与输出功率随腔长的变化
Figure 2. Output spectrum and output power vs cavity length detuning in the DRO
图2右侧的功率曲线由孤立的谐振峰构成，类似于一个一个孤立的级次，每一个谐振峰的间隔为1.03 μm，即λp。关于这种现象，可以通过如下理论分析进行解释。
在OPO中，为保证能量由泵浦光转化到信号光与闲频光，有公式(4)所示的相位关系[13]：
$${\varphi _{\rm p}} = {\varphi _{\rm s}} + {\varphi _{\rm i}} + \frac{\pi }{2}$$ (4) 式中：ϕp，ϕs和ϕi分别为泵浦、信号和闲频光的相位。在文中的数值仿真中，默认了当Δz=0时，上述关系成立。当Δz≠0时，将使信号光与闲频光在每次往返中增加额外相位。为保持上述的相位关系仍然成立，需要
$$\Delta {\varphi _{{\rm s}}} + \Delta {\varphi _{\rm i}} = 2\pi \Delta {\textit{z}}\left(\dfrac{1}{{{\lambda _{\rm s}}}} + \dfrac{1}{{{\lambda _{\rm i}}}}\right) = 2N\pi $$ (5) 式中：N为整数。由能量守恒公式
$1/{\lambda _{\rm s}} + 1/{\lambda _{\rm i}} = 1/{\lambda _{\rm p}}$ ，可以得出：$$\Delta {\textit{z}} = N{\lambda _{\rm p}}$$ (6) 由公式(6)可知，当Δz为泵浦波长整数倍时，DRO可以获得最大的参量转换效率，这同图2中的功率曲线一致。关于上述的输出功率特性，笔者的仿真结果与参考文献[4, 13]中的实验测试非常吻合。
为方便表示，以N的值来表示各个级次，则图2左侧的七个谐振峰由下至上依次为−4，−3，−2，−1，0，1，2级次，下面笔者分别对零级次（N=0），负调谐腔长（N<0）以及正调谐腔长（N>0）时DRO的工作特性进行分析。
-
零级次属于简并与非简态交界的状态，因此，在零级次内简并与非简并两种状态均存在。关于这一级次，以往的文献对其研究已非常丰富[3, 15-16]。总结来说，当腔长为0时，DRO工作于完全简并状态，当泵浦功率足够时，其输出的简并态时域宽度基本与泵浦光相当，通过降低泵浦功率至阈值附近，可以一定程度上压缩输出脉冲宽度。在零级次内微调腔长，可以使信号与闲频光产生分裂，而其是否分裂受腔内二阶色散符号的影响。值得注意的是，当信号光与闲频光的频率差较小时，DRO将输出近似简并的光谱。此时信号与闲频光的光谱仍有重叠，形成宽带的频率梳输出。如图3所示，在零级次内将腔长调谐至0.1 μm时，输出即为近似简并的光谱。
可以看到此时信号光与闲频光的中心波长分别为1 962 nm和2197 nm，光谱的−10 dB带宽为1 911~2256 nm。类似的近似简并状态在宽谱频率梳产生方面应用广泛，参见参考文献[17]。
图 3 DRO的近似简并光谱输出
Figure 3. Near-degenerate optical spectrum generated by the DRO
-
如图2所示，当Δz<0时，DRO处于非简并状态（N=−1, −2, −3, −4）。使用
$\Delta \omega = {\omega _{\rm s}} - {\omega _{\rm i}}$ 表示信号光与闲频光的频率差。由图2中可以看到，在某一级次之内，存在连续的输出波长调谐过程，具体为Δω随着Δz的减小而减小。为分析其中的原因，笔者再次从公式(1)出发，考虑当Δz≠Nλp的情况。由公式(5)可知，此时信号光与闲频光在DRO内每振荡一次，将引入额外相位Δϕ，此相位将导致原先振荡的信号与闲频光波长的增益下降。由于腔内色散的存在，当信号光与闲频光发生波长偏移时，将改变其往返的相位，具体计算如公式(7)所示：$$\Delta \varphi = {{{L}}_{\rm c}}({\rm d}{k_{\rm s}} + {\rm d}{k_{\rm i}}) = {{{L}}_{\rm c}}\left(\frac{{{\rm d}{k_{\rm s}}}}{{{\rm d}{\omega _{\rm s}}}} - \frac{{{\rm d}{k_{\rm i}}}}{{{\rm d}{\omega _{\rm i}}}}\right){\rm d}\omega $$ (7) 式中：Lc为腔内色散晶体的长度；ks和ki分别为信号光和闲频光的波矢；dω为信号光的频率变化量（闲频光为−dω），式中采用了一阶近似。其中
${{{L}}_{\rm c}}\left(\dfrac{{{\rm d}{k_{\rm s}}}}{{{\rm d}{\omega _{\rm s}}}} - \dfrac{{{\rm d}{k_{\rm i}}}}{{{\rm d}{\omega _{\rm i}}}}\right)$ 即为信号光与闲频光在色散晶体中的群时延差。当上述频率变化引入的额外相位能够补偿由于Δz≠Nλp所引入的相位时，DRO的增益将重新提升，从而在DRO中自发地发生这种频率变化。此时由公式(5)，(7)可以给出频率变化量dω同Δz的关系，如公式(8)所示：$${\rm d}\omega = \frac{{ - 2\pi \Delta {\textit{z}}}}{{{\lambda _{\rm p}}{L_{\rm c}}\left(\dfrac{{{\rm d}{k_{\rm s}}}}{{{\rm d}{\omega _{\rm s}}}} - \dfrac{{{\rm d}{k_{\rm i}}}}{{{\rm d}{\omega _{\rm i}}}}\right)}}$$ (8) 为进一步同仿真结果做验证，仿真中DRO的腔内总相对群时延曲线绘制在图4中（包含腔内非线性晶体与窗口片的材料色散）。
图 4 DRO的腔内相对群时延曲线
Figure 4. Calculated relative intra-cavity group delay (GD) curve of DRO
通过上述群时延曲线可以计算出，在该仿真所使用的参数下，
${{{L}}_{\rm c}}\left(\dfrac{{{\rm d}{k_s}}}{{{\rm d}{\omega _{\rm s}}}} - \dfrac{{{\rm d}{k_{\rm i}}}}{{{\rm d}{\omega _{\rm i}}}}\right) < 0$ 。因此由公式(8)可知，dω与dz的符号相同。即腔长调长，信号光频率增大；腔长调小，信号光频率减小。同图2对比可以看出理论分析同数值仿真结果一致。上述的级次内调谐在参考文献[3-4,13]的实验中均观察到。除每个级次之内的调谐，可以看到不同级次之间，其输出的波长范围亦不相同。为方便分析不同级次之间的波长调谐，选取每个级次的中心（Δz=Nλp）作为分析对象。腔长调谐将在腔内引入额外的时延
$\Delta \tau = \Delta {\textit{z}}/c$ 。记录每个级次中心对应的信号光中心波长以及该级次引入的时延，如图5中蓝色圆圈所示，为方便对比，将各个时延下把与泵浦光同步的波长同时绘制在图5中，如黑色曲线所示。由图5可以看到，两个曲线几乎重叠。因此可以得知，各个级次中心的工作波长为同泵浦光同步较好的波长，通过调节不同级次引入额外的时延，可以对每个级次中心工作的波长进行调谐。
图 5 不同腔长调谐时，每个级次中心对应的信号光中心波长及腔内相对群时延（蓝色圆圈），黑色实线为腔内相对群时延曲线
Figure 5. Signal light central wavelength correspondings to each level center at different cavity length detuning and the calculated relative intra-cavity GD (blue circle)，the black solid line is the relative group delay curve
结合DRO中级次内与不同级次之间的波长调谐，笔者可以较好地预测DRO的调谐特性。在实际应用中，可以通过设置腔内的群时延曲线来获得需要的调谐性质。
-
下面分析当N为正整数时，DRO的工作特性。同N≤0时情况不同，当N>0时，即使腔长未处于级次的中心，信号光与闲频光仍不会产生分裂[4]。在参考文献[4]中，Jankowski等人忽略色散，得出了N为正整数时，DRO输出为孤子脉冲，且泵浦功率增大，脉冲变窄。在实际情况中，即使完全补偿二阶色散，三阶色散仍然难以补偿，因此在此节中，笔者将通过数值仿真，研究在存在三阶色散（TOD）时，DRO的输出情况。通过设置不同的ZnSe与SiO2窗中片厚度的组合，可以在保持2070 nm处二阶色散为0的同时组合出不同的三阶色散值。为防止多孤子的产生，泵浦功率被降低至90 mW[12]。Δz=1.035 μm，在表1的仿真中，总的三阶色散约为4500 fs3，此时输出的脉冲时域和光谱图分别如图6(a)、(b)所示。
图 6 正调腔下DRO输出的时域(a) 和光谱(b)
Figure 6. The temporal (a) and spectral intensities (b) of the DRO under positive cavity length detuning
此时输出脉冲的半高全宽为51.7 fs，光谱半高全宽为115 nm。在保持腔内2070 nm处二阶色散为0的条件下，笔者使用SiO2与ZnSe窗口片组合出了一系列不同的腔内三阶色散值，如表2所示，并分别记录对应DRO所输出的脉冲宽度。结果如图7所示。
表 2 不同厚度的SiO2与ZnSe窗口片组合时的腔内三阶色散值
Table 2. Intra-cavity TODs under different thickness of the SiO2 and ZnSe plates
SiO2 /mm ZnSe/mm TOD/fs3 0 0.55 2424 3 1.8 4500 6 3.15 6576 9 4.4 8634 
图 7 不同腔内三阶色散下DRO输出孤子的半高全宽
Figure 7. FWHM of the DRO output soliton with different intra-cavity TODs
可以看出，随着三阶色散的不断增大，输出信号脉冲的半高全宽在不断加宽。基于3 mm长的MgO:PPLN晶体所能产生的最短脉冲宽度为42.6 fs。若要进一步产生更短的飞秒脉冲输出，可以使用更短的非线性晶体。例如，在仿真中使用1 mm长的非线性晶体，在仅补偿二阶色散的情况下，可以产生的最短脉冲宽度为29 fs的脉冲（400 mW泵浦功率，0.17 mm ZnSe窗口片补偿二阶色散）。
-
文中基于数值仿真，在低色散、适中的泵浦功率下，围绕简并附近的DRO在腔长调谐中出现的各个工作状态的输出光谱、时域信号等进行了模拟与分析。总结来说，相对于简并波长同泵浦脉冲完全同步的腔长，调小腔长可以使DRO工作于非简并状态，而增大腔长则可以使DRO工作于完全简并态，并输出孤子。基于同步泵浦OPO的特性，可以对此现象做出解释。在同步泵浦的OPO中，只有当信号光与泵浦光在时间上重叠比较好时，才能获得比较高的增益。在此仿真中，腔内的零色散点为2070 nm（简并波长），腔内的相对群时延曲线如图4所示。由于泵浦光的重复频率固定，因此当腔长调小时，非简并态同泵浦光同步更好，因此，此时DRO工作于非简并态；而当腔长调长时，由于简并波长为腔内群时延最小的波长，因此，简并状态将同泵浦光同步最好，故此时DRO工作于完全简并态。
对于非简并状态的DRO，通过改变腔长，其输出激光的中心波长将会随之改变。通过理论分析结合仿真结果，文中对非简并DRO中的波长调谐的机理进行了解释。在级次内，波长随腔长的改变受到相位匹配条件的控制。较小的腔长调谐在信号光和闲频光中引入了额外的相位，导致原波长的增益下降，由于腔内色散的存在，通过波长的偏移，可以补偿上述额外色散，从而恢复增益。对于不同级次之间的调谐，笔者分析了各个级次中心处的信号光波长的变化，结合腔内的群时延曲线，可以看到在不受相位匹配条件影响时，DRO将输出与泵浦脉冲有较好的同步特性的波长的脉冲。对于将DRO的腔长调长的情况，笔者分析了不同色散补偿情况下，输出孤子脉冲宽度的变化，在仿真中可以得出，随着腔内TOD的增加，信号脉冲的半高全宽将不断增大。为获得更窄的脉冲输出，需要尽可能减小腔内TOD的数值。必要时可以通过减小所使用的非线性晶体的厚度来获得更窄的信号脉冲输出。同时，需要指出的是，此仿真是基于低色散、飞秒泵浦的DRO所进行，对于大色散，皮秒或更长脉冲泵浦的DRO，将会呈现出不同的性质[18-19]。超短脉冲DRO中蕴含着丰富的脉冲形成机制，对其进一步的研究和探索在超短脉冲、宽带激光频率梳以及可调谐飞秒激光的产生领域都具有较高的价值。
Cavity-length detuning of mid-infrared femtosecond doubly resonant optical parametric oscillators (Invited)
-
摘要: 超快双谐振光参量振荡器（DRO）在宽带中红外频率梳产生、中红外超短脉冲产生等领域有较大的应用前景。由于信号光与闲频光均在腔内振荡，DRO呈现出很多同单谐振光参量振荡器（SRO）所不同的工作特性。其中，在简并附近的腔长调谐特性是DRO中最具有代表性的特点。随着腔长的改变，DRO会在非简并、近似简并以及完全简并态之间切换状态。为具体分析腔长调谐对简并附近DRO工作状态的作用，文中基于数值仿真，对常用泵浦条件下，低色散飞秒泵浦DRO的腔长调谐特性进行了系统的研究与总结，并对相关特性的产生原因进行了理论分析。
-
关键词:
- 宽谱中红外激光 /
- 同步泵浦光学参量振荡器 /
- 双谐振光参量振荡器
Abstract: Ultrafast doubly resonant optical parametric oscillators (DRO) are widely used in the generation of mid-infrared broadband optical combs and mid-infrared ultrashort pulses. Because the signal and idler lights both oscillate in the optical cavity, DROs exhibit many different features against singly resonant optical parametric oscillators (SRO). One typical feature is the cavity length detuning in degenerate DRO. The DRO would work in non-degenerate, near-degenerate, and totally degenerately states with cavity length detuning. In order to analyze the effect of cavity length detuning on the work state of degeneracy DRO, the cavity length detuning characteristics of DRO pumped with low dispersion femtosecond laser were systematically studied and summarized based on numerical simulation and usual pumping condition. The production reason of the correlation characteristic was analyzed in theory. -
图 2 简并附近DRO输出光谱与输出功率随腔长的变化
Figure 2. Output spectrum and output power vs cavity length detuning in the DRO
图 4 DRO的腔内相对群时延曲线
Figure 4. Calculated relative intra-cavity group delay (GD) curve of DRO
图 5 不同腔长调谐时，每个级次中心对应的信号光中心波长及腔内相对群时延（蓝色圆圈），黑色实线为腔内相对群时延曲线
Figure 5. Signal light central wavelength correspondings to each level center at different cavity length detuning and the calculated relative intra-cavity GD (blue circle)，the black solid line is the relative group delay curve
图 6 正调腔下DRO输出的时域(a) 和光谱(b)
Figure 6. The temporal (a) and spectral intensities (b) of the DRO under positive cavity length detuning
图 7 不同腔内三阶色散下DRO输出孤子的半高全宽
Figure 7. FWHM of the DRO output soliton with different intra-cavity TODs
表 1 DRO数值仿真中所使用的各项参数
Table 1. Parameters used in the numerical simulation of the DRO
Symbol Parameter Value λp Central wavelength of the pump light/nm 1035 frep Pump repetition/MHz 80 tp Duration of the pump pulses/fs 180 Lc Length of the PPLN crystal/mm 3 Lz Thickness of the ZnSe plate/mm 1.8 Ls Thickness of the SiO2 plate/mm 3 Λ Poling period of the PPLN crystal/μm 31.4 deff 2nd order nonlinear optical coefficient/pm·V−1 25[14] R Reflection of the output coupling mirror 60% 
下载: 导出CSV
表 2 不同厚度的SiO2与ZnSe窗口片组合时的腔内三阶色散值
Table 2. Intra-cavity TODs under different thickness of the SiO2 and ZnSe plates
SiO2 /mm ZnSe/mm TOD/fs3 0 0.55 2424 3 1.8 4500 6 3.15 6576 9 4.4 8634
下载: 导出CSV
-
[1] Newell A. Nonlinear Optics[M]. Boca Raton: CRC Press, 2018. [2] Leindecker N, Marandi A, Byer R L, et al. Broadband degenerate OPO for mid-infrared frequency comb generation [J]. Optics Express, 2011, 19(7): 6296-6302. doi: 10.1364/OE.19.006296 [3] Rudy C W, Marandi A, Ingold K A, et al. Sub-50 fs pulses around 2070 nm from a synchronously-pumped, degenerate OPO [J]. Optics Express, 2012, 20(25): 27589-27595. doi: 10.1364/OE.20.027589 [4] Jankowski M, Marandi A, Phillips C R, et al. Temporal simultons in optical parametric oscillators [J]. Physical Review Letters, 2018, 120(5): 053904. doi: 10.1103/PhysRevLett.120.053904 [5] Vainio M, Merimaa M, Halonen L, et al. Degenerate 1 GHz repetition rate femtosecond optical parametric oscillator [J]. Optics Letters, 2012, 37(21): 4561-4563. doi: 10.1364/OL.37.004561 [6] McCracken R A, Reid D T. Few-cycle near-infrared pulses from a degenerate 1 GHz optical parametric oscillator [J]. Optics Letters, 2015, 40(17): 4102-4105. doi: 10.1364/OL.40.004102 [7] Leindecker N, Marandi A, Byer R L, et al. Octave-spanning ultrafast OPO with 2.6-6.1 µm instantaneous bandwidth pumped by femtosecond Tm-fiber laser [J]. Optics Express, 2012, 20(7): 7046-7053. doi: 10.1364/OE.20.007046 [8] Haakestad M W, Marandi A, Leindecker N, et al. Five-cycle pulses near λ = 3 μm produced in a subharmonic optical parametric oscillator via fine dispersion management [J]. Laser & Photonics Reviews, 2013, 7(6): L93-L97. [9] Wolf S, Marandi A, Leedle K, et al. 19-nJ five-cycle pulses from a 2-μm degenerate optical parametric oscillator[C]//Advanced Solid State Lasers, Optical Society of America, 2016: AW4A. 5. [10] Smolski V O, Yang H, Gorelov S D, et al. Coherence properties of a 2.6–7.5 μm frequency comb produced as a subharmonic of a Tm-fiber laser [J]. Optics Letters, 2016, 41(7): 1388-1391. doi: 10.1364/OL.41.001388 [11] Muraviev A V, Smolski V O, Loparo Z E, et al. Massively parallel sensing of trace molecules and their isotopologues with broadband subharmonic mid-infrared frequency combs [J]. Nature Photonics, 2018, 12(4): 209-214. doi: 10.1038/s41566-018-0135-2 [12] Ning C, Zhang Z. Multi-soliton formation in femtosecond degenerate optical parametric oscillators [J]. Optics Letters, 2020, 45(3): 734-737. doi: 10.1364/OL.383974 [13] Ning C, Liu P, Qin Y, et al. Continuous wavelength tuning of nondegenerate femtosecond doubly resonant optical parametric oscillators [J]. Optics Letters, 2020, 45(9): 2551-2554. doi: 10.1364/OL.390380 [14] Shoji I, Kondo T, Kitamoto A, et al. Absolute scale of second-order nonlinear-optical coefficients [J]. JOSA B, 1997, 14(9): 2268-2294. doi: 10.1364/JOSAB.14.002268 [15] Smith A V, Armstrong D J, Phillips M C, et al. Degenerate type I nanosecond optical parametric oscillators [J]. JOSA B, 2003, 20(11): 2319-2328. doi: 10.1364/JOSAB.20.002319 [16] Wolf S J, Phillips C R, Marandi A, et al. Dynamical behavior of an ultrafast OPO near degeneracy[C]//CLEO: Science and Innovations. Optical Society of America, 2013: CW1B. 1. [17] Loparo Z E, Ninnemann E, Ru Q, et al. Broadband mid-infrared optical parametric oscillator for dynamic high-temperature multi-species measurements in reacting systems [J]. Optics Letters, 2020, 45(2): 491-494. doi: 10.1364/OL.382308 [18] Koch P, Ruebel F, Nittman M, et al. Narrow-band, tunable 2 μm optical parametric oscillator based on MgO: PPLN at degeneracy with a volume Bragg grating output coupler [J]. Applied Physics B, 2011, 105(4): 715-720. doi: 10.1007/s00340-011-4795-6 [19] Bjorkholm J. Analysis of the doubly resonant optical parametric oscillator without power-dependent reflections [J]. IEEE Journal of Quantum Electronics, 1969, 5(6): 293-295. doi: 10.1109/JQE.1969.1081950 -
点击查看大图
计量
- 文章访问数: 223
- HTML全文浏览量: 90
- PDF下载量: 54
- 被引次数: 0
