-
调制传递函数(传函)是评价成像系统成像性能的一个通用而重要的技术指标。对于空间光学遥感器(以下简称相机),传函表征了相机在不同空间频率下对目标对比度传输或分辨的能力。传函测试是相机研制过程中一个重要环节[1] ,进行传函测试的目的通常包括确定相机焦面位置和判定相机成像质量。相机研制过程中,通常利用平行光管进行相机系统传函测试。
随着空间相机分辨率要求越来越高,相机焦距越来越长,口径也越来越大,超大口径相机相继问世[2-4]。按照传统的传函测试方法,需要口径巨大的平行光管对其进行测试,测试设备非常复杂。利用大口径平面镜和激光干涉仪配合使用的镜头装调方法在相机装调中得到广泛应用,大口径的平面镜已经成为相机装调的常用设备。
文中提出了一种基于自准直方法的传函测试方案,这种方案不需要平行光管,只需要一块能够覆盖相机口径的平面镜即可完成测试,大大简化了对测试设备的要求,使大口径空间相机传函测试变得容易。
-
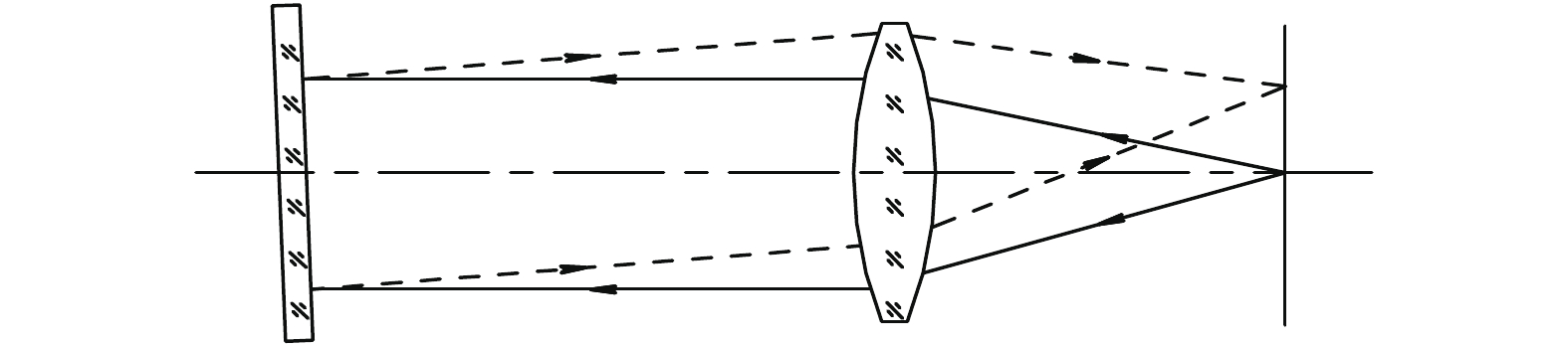
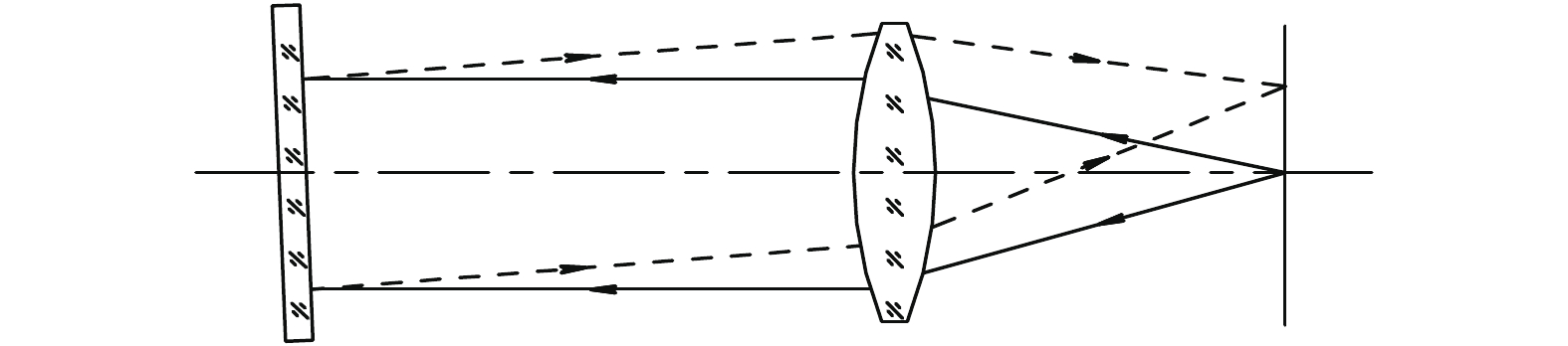
自准直原理是指当发光点(物)处在光学系统的焦平面时,它发出的光线通过光学系统后将成为一束平行光,若在光学系统前放置一与光轴垂直的平面镜,则该平面镜会将出射的平行光反射回去,反射光再次通过光学系统后仍汇聚于系统焦平面上 [5-8],如图1所示。
自准直传函测试系统需要在相机焦面位置放置传函测试用的矩形条纹靶标,在靶标背后设置照亮靶标的光源,在相机入光口前方放置平面反射镜。测试时,点亮光源,从焦面靶标处发出的光线通过相机后成为一束带有靶标信息的平行光,这束平行光经过平面镜反射后又返回相机,到达焦面探测器,形成靶标像。平面反射镜绕相机光轴小范围旋转、倾斜,靶标像将被反射至相机焦面不同视场。利用该靶标像即可计算相机系统传函。以某空间相机为例,搭建自准直传函检测系统如图2所示。
自准直传函检测系统了解决了相机传函测试需要依赖平行光管的问题。特别是对于利用激光干涉仪装调的相机,由于平面镜本身也是镜头装调的必须设备,搭配自准直传函测试方案能够实现相机的原工位装调与检测,大大减少相机在工位间的转运。
-
工程上进行相机镜头组件与焦面组件对接时,通常利用传函值判定相机焦面组件是否位于最佳位置。对于平行光管测传函方案,通过在平行光管无穷远焦面位置附近前后挪动靶标实现“走过焦”,利用过焦曲线判定相机焦面位置。通过相机与光管的焦距换算关系计算相机焦面与无穷远焦面位置的差值,最终保证焦面组件位于正确位置。
自准直原理进行系统传函测试时,由于靶标已经与探测器事先拼接在一起,无法向调节平行光管靶标一样方便地调节位置,若想判定焦面组件位置是否位于系统最佳焦面,则需要利用相机调焦机构改变系统光路,实现“走过焦”。若调焦机构位于0位(镜头装调完成时确定的位置)时,相机传函值最大,则表征焦面组件位于正确位置。
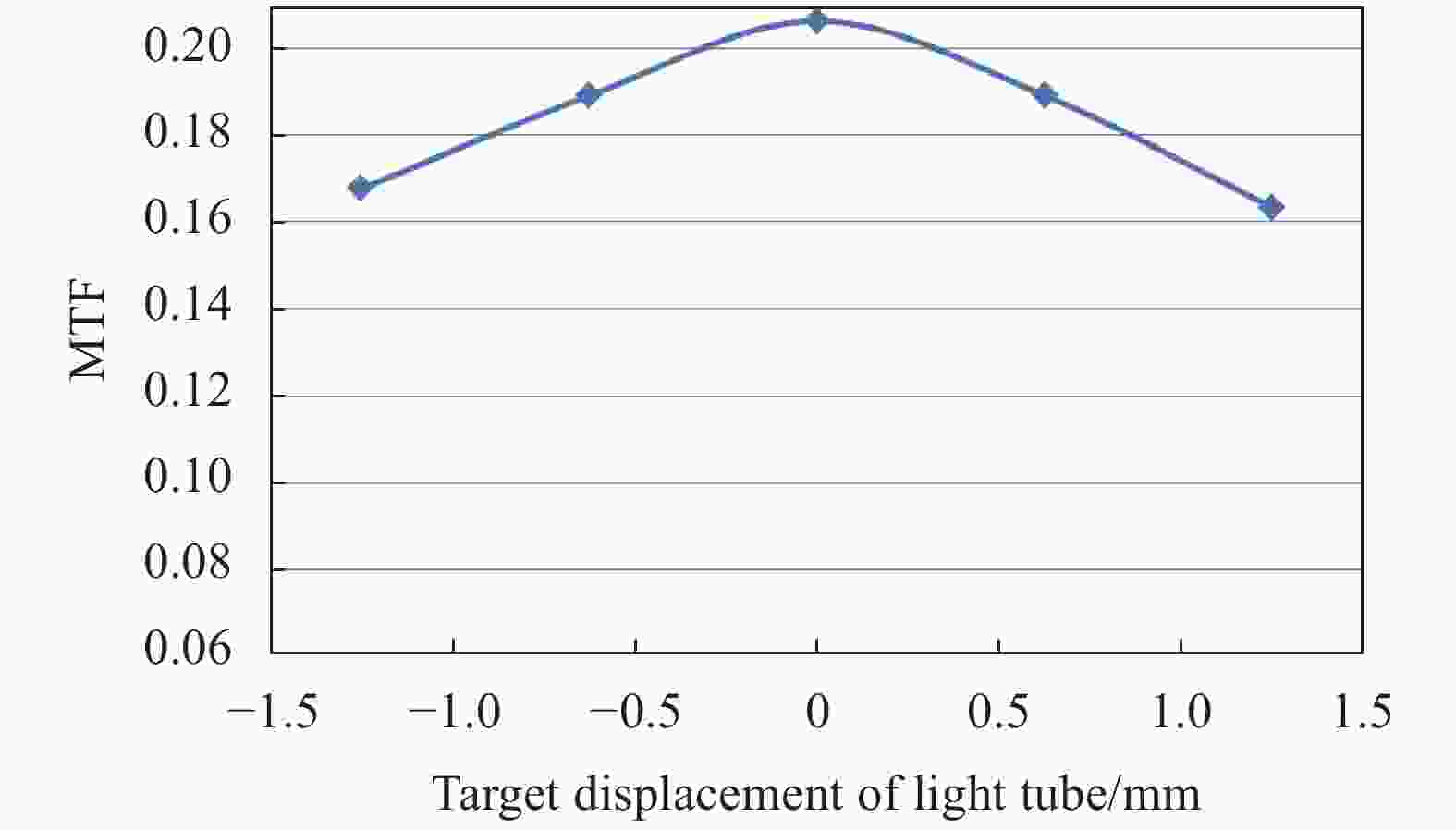
图3为某空间相机利用平行光管测试的过焦曲线。横坐标为测试时靶标相对平行光管无穷远位置的偏移量。对于该测试系统,平行光管靶标位置变化0.625 mm对应相机半焦深,即图示传函过焦曲线为分别前后走2×半焦深的结果。
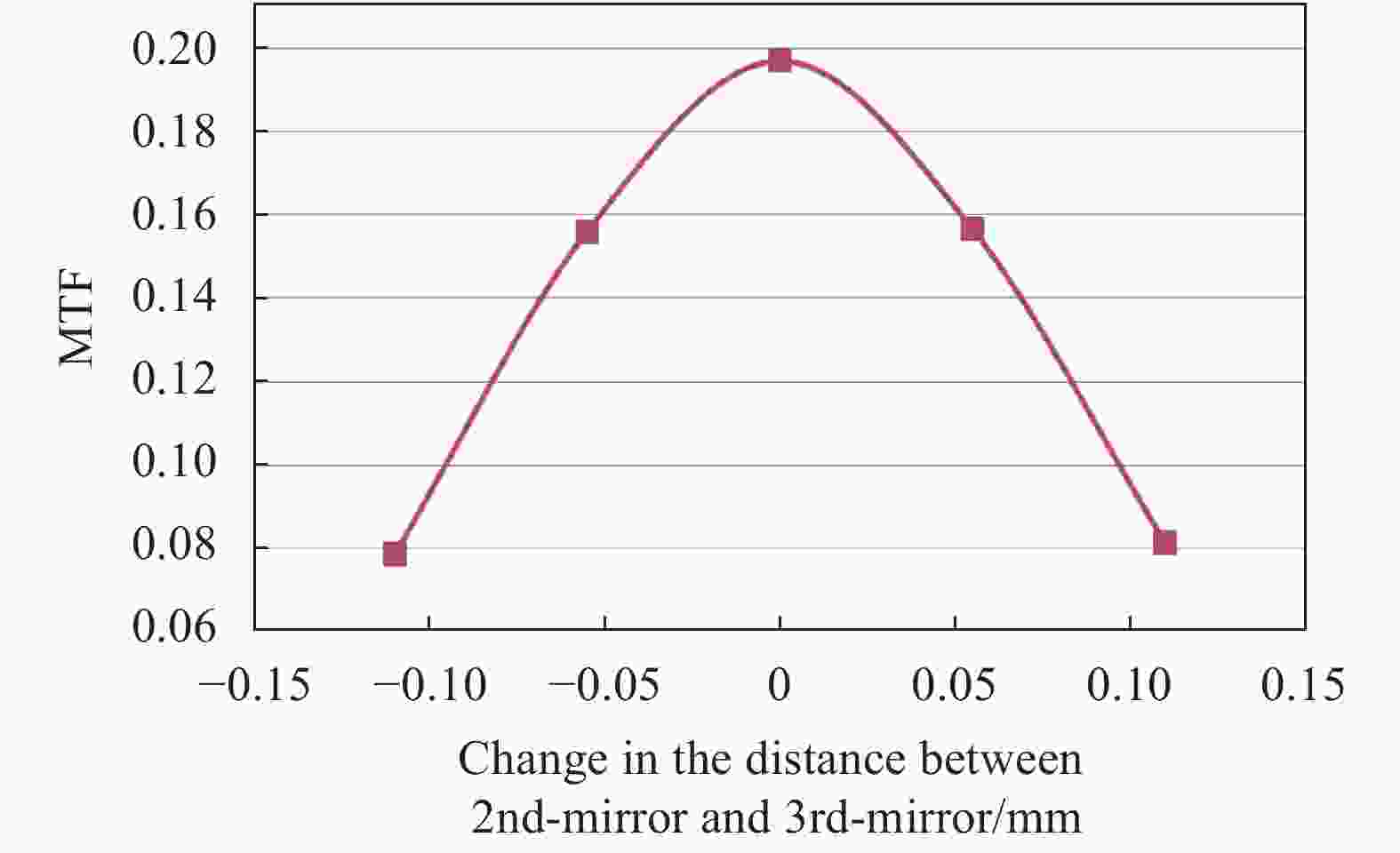
为分析自准直法传函测试对焦面离焦的敏感程度,将该相机参数代入光学仿真软件中,预估自准直法测试过焦曲线如图4所示。该相机采用三镜调焦形式,因此仿真时固定焦面位置,调整次三镜间距“走过焦”,计算不同离焦情况下的系统传函。为方便比较,仿真时亦选取前后2×半焦深的点计算传函。图4横坐标为次三镜间距相对设计值(0位)的偏离量,其中次三镜间距变化0.055 mm对应相机半焦深。
通过对比两条曲线(图5)可以发现,自准直传函测试系统对焦面离焦敏感程度不亚于传统平行光管,可以用于判定焦面位置正确性。在大范围离焦时,由于直接改变系统成像光路,导致传函值下降明显。由于两次通过相机光路,自准直法测试得到传函结果通常会略低于平行光管测试结果。
-
利用平行光管进行系统传函测试时,要求光管靶标夹具具备旋转调整能力,能够保证测试时条纹方向与相机探测器积分方向平行,避免由于条纹与积分方向不平行带来的传函值下降。
利用自准直原理测试传函的相机,需要在焦面位置预先设置靶标,该靶标需要位于相机有效视场内。为了设置和测试方便,通常需要在合适的边缘视场设置一块或两块矩形靶标(条纹靶标),通过拼接保证靶标与相机探测器光敏面共焦。
由于镜面反射的特性,当利用位于边缘视场的靶标测试相机中心视场系统传函时,靶标条纹会产生一定的偏转。当空间相机选用的探测器为TDI(时间延迟积分)型探测器时,反射后的靶标条纹将与探测器积分方向成一定角度。偏转角过大时会导致系统测试结果降低,进而影响对相机成像质量是否满足指标要求的判断。
下文对这一偏转角对自准直传函测试结果的影响进行分析。
-
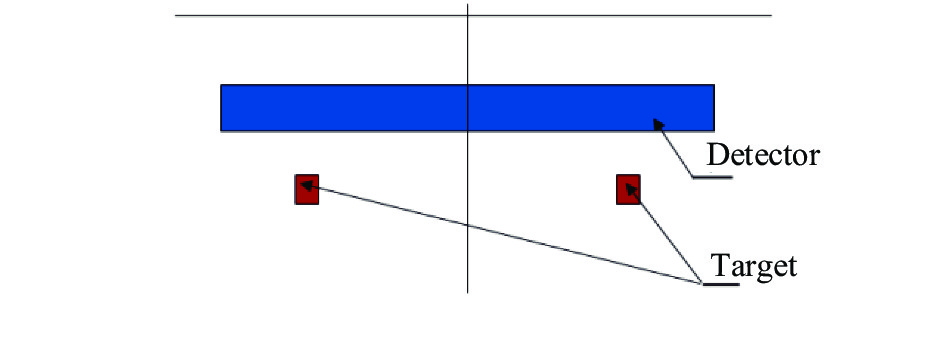
某典型TDI线阵相机焦面靶标布局方案如图6所示。
空间相机入射光线为平行光,到焦面汇聚,因此从焦面打光,镜头出射光线也为平行光。位于镜头上方的平面镜对平行光进行反射。因此自准直传函测试系统搭建和分析时不需要限制平面镜与镜头的距离。为方便分析,自准直传函检测系统光路可以简化成图7。平面镜初始位置位于光学系统主面,探测器和靶标分别位于焦面不同位置(仅选取一处靶标,另一处与之对称)。
定义X为沿线阵方向,Y为垂直线阵方向,Z为光轴方向,相机线阵位于偏场位置。O为相机主面与光轴焦点,f为相机焦距。D0为靶标条纹中心位置,D为反射后靶标像的中心位置,D和D0均位于相机焦面上。欲将位于D0位置的靶标“反射”到位于线阵最小偏场中心的D位置,需要绕O旋转平面镜。已知相机线阵最小偏场角α(Y向),靶标中心沿线阵方向偏场角γ(X向),垂直于线阵方向偏场角β(Y向)。
已知靶标中心位置D0坐标为
$(-\mathrm{tan}\gamma \cdot f,\; -\mathrm{tan}\beta \cdot f,\; -f)$ ,靶标像中心位置D点坐标为$ (0,\;-\mathrm{tan}\alpha \cdot f,\;-f) $ 。定义从O点出发指向D0点的向量为${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over D}_{0}}$ ,从O点出发指向D点的向量为$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over D} $ ,将它们转化为列向量并单位化,则:$$ \displaystyle {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over {{D}_{0}}}=\left[\begin{array}{c}-\dfrac{ \mathrm{tan}\gamma }{\sqrt{{( \mathrm{tan}\gamma )}^{ 2} \displaystyle +{( \mathrm{tan}\beta )}^{ 2} \displaystyle + \displaystyle 1}}\\ -\dfrac{ \mathrm{tan}\beta }{\sqrt{{( \mathrm{tan}\gamma )}^{ 2} \displaystyle +{( \mathrm{tan}\beta )}^{ 2} \displaystyle + \displaystyle 1}}\\ -\dfrac{ \displaystyle 1}{\sqrt{{( \mathrm{tan}\gamma )}^{ 2} \displaystyle +{( \mathrm{tan}\beta )}^{ 2} \displaystyle + \displaystyle 1}}\end{array}\right]=\left[\begin{array}{c}{D}_{0X}\\ {D}_{0Y}\\ {D}_{0Z}\end{array}\right]} $$ (1) $$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over D}=\left[\begin{array}{c} \displaystyle 0\\\\ -\dfrac{ \mathrm{tan}\alpha }{\sqrt{{( \mathrm{tan}\alpha )}^{ 2}+ \displaystyle 1}}\\\\ -\dfrac{ \displaystyle 1}{\sqrt{{(\displaystyle \mathrm{tan}\alpha )}^{ 2}+ \displaystyle 1}}\end{array}\right]=\left[\begin{array}{c}0\\\\ {D}_{Y}\\\\ {D}_{Z}\end{array}\right] $$ (2) 由镜面反射原理,可知单位化的
$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n}= \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over {{D}_{0}}}$ 与$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over D} $ 关于旋转后的镜面法向量$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} $ 对称,且$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n}=\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over {{D}_{0}}}+\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over D} $ ,则:$$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over N}=\left[\begin{array}{c}{D}_{0X}\\\\ {D}_{0Y}+{D}_{Y}\\\\ {D}_{0Z}+{D}_{Z}\end{array}\right] $$ (3) 将
$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over N} $ 单位化,得到单位镜面法向量$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} $ ,即:$$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n}=\left[\begin{array}{c}\begin{array}{c}\dfrac{{D}_{0 X}}{\sqrt{{{(D}_{0 X})}^{2}+{\left({D}_{0 Y}+{D}_{Y}\right)}^{2}+{\left({D}_{0 Z}+{D}_{Z}\right)}^{2}}}\\ \dfrac{{D}_{0 Y}+{D}_{Y}}{\sqrt{{{(D}_{0 X})}^{2}+{\left({D}_{0 Y}+{D}_{Y}\right)}^{2}+{\left({D}_{0 Z}+{D}_{Z}\right)}^{2}}}\end{array}\\ \dfrac{{D}_{0 Z}+{D}_{Z}}{\sqrt{{{(D}_{0 X})}^{2}+{\left({D}_{0 Y}+{D}_{Y}\right)}^{2}+{\left({D}_{0 Z}+{D}_{Z}\right)}^{2}}}\end{array}\right]=\left[\begin{array}{c}{n}_{X}\\ {n}_{Y}\\ {n}_{Z}\end{array}\right]$$ (4) 已知靶标上刻蚀的条纹方向为
$ \mathop {DN}\limits^ \rightharpoonup $ ,与探测器积分方向平行,即$ \mathop {DN}\limits^ \rightharpoonup $ 位于焦平面内,且平行于Y轴。将其单位化,有:$$ \mathop {DN}\limits^ \rightharpoonup =\left[\begin{array}{c}0 \\ 1 \\ 0\end{array}\right] $$ (5) 靶标条纹经过单位镜面法向量为
$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} $ 的平面镜反射后的向量为$ {\mathop {DN}\limits^ \rightharpoonup }' $ ,由镜面反射原理有:$ \mathop {DN}\limits^ \rightharpoonup + {\mathop {DN}\limits^ \rightharpoonup} ' = 2 k\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} $ ,其中$ k $ 为$ \mathop {DN}\limits^ \rightharpoonup $ 在单位向量$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} $ 上的投影长度,即:$${\mathop {DN}\limits^ \rightharpoonup} ' =2k\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n}-\mathop {DN}\limits^ \rightharpoonup =2\left(\mathop {DN}\limits^ \rightharpoonup \cdot \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n}\right)\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n}-\mathop {DN}\limits^ \rightharpoonup $$ (6) 将公式(4)、(5)代入,则有:
$${ \mathop {DN}\limits^ \rightharpoonup} '=\left[\begin{array}{c}2{n}_{Y}{n}_{X}\\\\ 2{n}_{Y}^{2}-1\\\\ 2{n}_{Y}{n}_{Z}\end{array}\right] $$ (7) 反射后,向量
$ {\mathop {DN}\limits^ \rightharpoonup} ' $ 在XY平面的投影与Y轴的夹角$ \eta $ 即为$ \mathrm{反}\mathrm{射}\mathrm{后}\mathrm{靶}\mathrm{标}\mathrm{条}\mathrm{纹}\mathrm{与}\mathrm{积}\mathrm{分}\mathrm{方}\mathrm{向}\mathrm{的}\mathrm{夹}\mathrm{角}, $ 则有:$$ \eta ={{{\rm{arcsin}}}}\left(\dfrac{2{n}_{Y}{n}_{X}}{\sqrt{1-{\left(2{n}_{Y}{n}_{Z}\right)}^{2}}}\right) $$ (8) -
靶标像条纹与积分方向的偏转对传函的影响可以简化成利用
${\rm{sinc}}$ 函数求解[9]。已知探测器像元尺寸为
$ d $ ,探测器积分级数为$ k $ ,反射后的靶标偏离原位置与像元尺寸的比为$ m $ ,则有:$$ m=\dfrac{{{\rm{tan}}}\eta \cdot kd}{d}={{\rm{tan}}}\eta \cdot k $$ (9) 计算其对传函的影响,则有:
$$ {{\rm{sinc}}}\left(m\right)=\dfrac{{{\rm{sin}}}\left(m\times \dfrac{\pi }{2}\right)}{m\times \dfrac{\pi }{2}} $$ (10) -
分析3.1节公式可以发现:靶标偏转角与系统焦距无关,仅与靶标和探测器在像面上的位置有关;Y向偏场α、β越大,偏转角
${\eta}$ 越大;靶标X向偏场γ越大,偏转角${\eta}$ 越大。分析3.2节公式可以发现:偏转角引起的传函值下降与探测器像元尺寸大小无关;靶标偏转角越大,对传函值影响越大;探测器积分级数越高,传函值下降越多。
将上述公式代入不同空间相机系统进行比较计算,得到如下结果:
代入某离轴TDI线阵相机,其α=5°、β=5.8°、γ=2.6°,依次代入公式(1)、(2)、(4) 、(8),得到
$ {\eta }_{离轴} $ =0.248°。代入某同轴TDI线阵相机,其α=0.5°、β=1.75°、γ=0.8°,得到$ {\eta }_{同轴} $ =0.011°。分别将上述偏转角度代入公式(9) 、(10),在不同积分级数下得到曲线,如图8所示。
比对两条曲线可以发现:(1) 对于某典型离轴系统,α、β、γ均较大,导致偏转角较大。随着探测器积分级数增大,偏转角对系统传函的影响急剧增加。当积分级数为128级时,测试传函将为系统实际传函值的87.9%。(2) 对于某典型同轴系统,α、β、γ均较大小,导致偏转角小。系统传函对积分级数高低不敏感,偏转角对系统传函的影响不明显,测试传函与系统实际传函接近。
-
由于自准直传函测试靶标为预先拼接在相机焦面组件内,为了保证严格的共焦,通常粘接(或其他固连)安装,无法方便地调整靶标角度。
为避免自准直传函测试时靶标经反射后的偏转角对系统传函值造成影响,应首先利用3.1节、3.2节公式进行计算预估,判断系统传函下降情况。当传函下降量不能接受时,可以采用在一块靶标上刻划多组不同角度条纹靶标的方法。即:首先计算偏转角
$ \eta $ ,然后在靶标光刻面设计两组条纹靶标,一组为正常方向靶标,一组为偏转$ \eta $ 角的预置倾斜靶标。测试时,根据不同被测视场选择不同靶标。同样,当视场偏场过大,两组靶标无法满足需求时,可以设计多组不同偏转角靶标,多组靶标条纹互为补充,满足全视场传函测试需求。 -
自准直传函测试方案要求靶标与探测器严格共焦。自准直传函检测系统实际焦面拼接时,可以利用拼接仪实现靶标刻画面与探测器光敏面“共焦面”[10-12]。同时利用拼接仪也可以实现靶标条纹与探测器积分方向的精确配准。
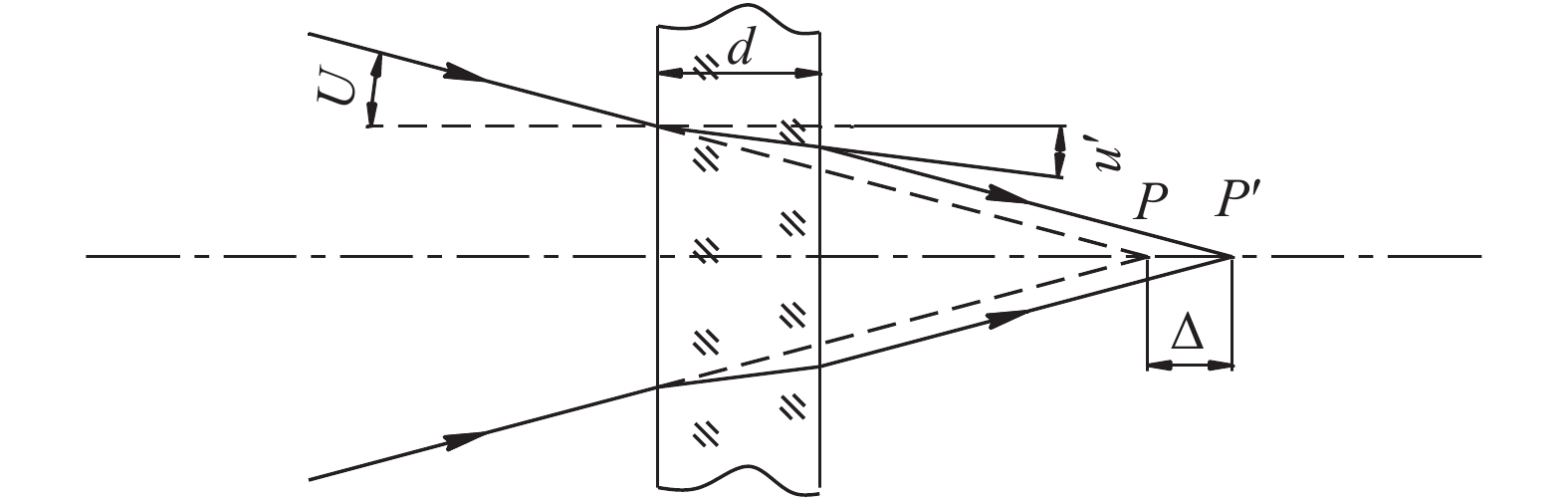
探测器表面常设有滤光片,用来控制探测器接收到的光谱范围。该滤光片可以看做光学平行平板。由Snell定律可知,插入平板不会改变光学系统的焦距和像的大小,但是会将光程拉长,从而影响焦点的物理位置,即造成像的纵向位移[4-5],如图9所示。可以得到纵向位移量
$\Delta $ 的精确计算公式:$$ \Delta =d\left(1-\dfrac{{\rm{tan}}{U}^{\text{'}}}{{\rm{tan}}U}\right)=\dfrac{d}{n}(n-\dfrac{{\rm{cos}}U}{{\rm{cos}}{U}^{\text{'}}}) $$ (11) 因此,对于利用自准直原理进行传函测试的相机,结构设计时应区分直通焦面位置和加入滤光片后的焦面位置,按照两个位置分别布放靶标和探测器,不能简单地将其放置在同一平面。
对于普通同种探测器的焦面拼接,它们在拼接仪上共焦且等光程。即在给定一片基准探测器的理论位置时,利用等光程原理,将其余探测器拼接到同一焦深方向位置即可实现共焦。
但是对于这种探测器与靶标混合拼接的系统,“共焦”并不意味着“等光程”。这是由于在拼接仪上拼靶标时,拼接光路中没有滤光片,可以称作“直通光路”,如图10所示的左侧光路。当拼接仪镜头“平移”(保证共焦)到有滤光片的探测器上时,由于滤光片的影响,光程会伸长,焦点位置将后移,如图10所示的右侧光路。
综合上述分析可以发现,对于自准直法传函测试靶标的共焦面拼接,首先应在三维结构设计软件中得到没有滤光片的直通焦面到结构基准的距离。然后利用拼接仪按照此距离将靶标放置在设计位置。最后通过平移拼接仪镜头进行探测器拼接,保证探测器与靶标“共焦面”。
-
将自准直传函测试方法应用在某空间相机上。该相机采用三反同轴光学系统,搭载TDI线阵焦面组件,调焦方案为三镜调焦。
相机设计时,将靶标布放在边缘视场位置,设计靶标托框及安装结构,并预留空间供光源打光。按照3.1节和3.2节公式,代入该相机实际参数,计算靶标条纹偏转角
$ \eta $ =0.023°,得到该偏转引起的传函下降量约为0.1%,该量级在传函测试时可以忽略不计。因此,靶标仅需设计与积分方向平行的条纹。焦面组装时,利用拼接仪保证探测器光敏面与靶标刻画面共焦,保证TDI方向与靶标条纹平行。
测试时,在焦面位置利用直流发光二极管(LED)光源将靶标照亮,调整架设在相机入光口前方的平面镜的角度,使靶标像投射在相机探测器上。利用三镜调焦机构“走过焦”,得到实测过焦曲线如图11所示。其中横坐标为三镜位置调整量,0 mm对应调焦机构位于0位(镜头装调完成时确定的位置),各个测试点间隔半焦深。

图 11 某空间相机自准直传函测试过焦曲线
Figure 11. Test over focal curve of self-collimating test system on a space camera
对比该相机平行光管测试的过焦曲线(图3)、自准直传函测试的过焦曲线(图11)及仿真的自准直传函曲线(图4),可以发现:在确定焦面位置方面,自准直传函测试方法对焦面离焦的灵敏度与平行光管测试相当,实测结果实际曲线比仿真曲线更平缓。系统传函值方面,自准直传函测试结果略低于平行光管测试结果,实测传函最大值与仿真结果相当。
-
文中提出了一种应用于空间相机的自准直传函测试方法,介绍了自准直传函测试系统的原理和搭建方案及实际应用中需要注意的问题。
自准直传函测试方案不依赖于平行光管,特别是对于利用激光干涉仪自准直法装调的相机,由于平面镜本身也是镜头装调的必需设备,搭配自准直传函测试方案能够实现相机的原工位装调与检测,大大减少相机在工位间的转运,节省转运后等待静置时间,缩短相机测试周期。
通过与平行光管测试结果比较,准直传函测试方案对焦面离焦敏感程度不亚于传统平行光管,可以用于判定焦面位置正确性。
自准直测试靶标与焦面探测器高精度共面拼接,保证靶标光刻面与探测器光敏面严格共焦面,且靶标条纹方向与探测器积分方向平行,避免后期人工调节,可以保证传函测试精度。针对条纹偏转引起的传函结果下降问题,给出了数值计算公式和靶标设计方案。该方案可以将靶标条纹偏转引起的传函测试误差降至可以忽略的量级。
相信随着大口径空间相机的进一步发展,更多与传统中小口径相机不同的测试方法将会得到应用,自准直原理在大口径空间相机测试上的应用将会更加广泛。
Self-collimating MTF test method and application of space camera
-
摘要: 调制传递函数(传函)测试是空间相机研制过程的重要环节,常规传函测试需要用到平行光管。自准直传函测试方法是一种不依赖于平行光管的系统传函测试方案。首先介绍了自准直传函测试系统的原理和搭建方案。其次对比了平行光管测试的过焦曲线和自准直传函测试的过焦曲线,发现该系统对焦面离焦敏感程度不亚于平行光管,得到该系统可以用于判定焦面位置正确性的结论。再次分析了自准直靶标条纹经过平面镜反射后偏转的现象,该现象将引入测试误差。给出了偏转角的数值计算公式和条纹偏转对传函值影响的计算公式。针对离轴系统对偏转角敏感的问题,给出自准直靶标的设计方法。利用该方法可以将靶标条纹偏转造成的传函测试误差降至可以忽略的量级。然后讨论了采用自准直传函测试方案时相机探测器与测试靶标的拼接,分析了探测器滤光片对焦面位置的影响,提出了探测器与靶标共焦面的设计及拼接方案。最后总结了该测试方法在某型号相机的实际应用,为自准直传函测试方法在后续系统的应用打下基础。Abstract: MTF test is an important part of the camera manufacture process. General practice of MTF test needs to use the parallel light tube. Self-collimating MTF test method does not rely on the parallel light tube. Firstly, the principle and construction plan of the self-collimating MTF test system were introduced. Secondly, the curve measured by parallel light tube and self-collimating MTF test were compared. It is obtained that the self-collimating MTF test system has high sensitivity to the off-focus, this method can be used to determine the focal plane position. Thirdly, the phenomenon of the deflection of the self-collimating target fringe were analyzed, which will affect the MTF test result. The formula of the deflection angle of target fringe and the formula of the influence of fringe deflection on MTF test result were given. Design method of the self-collimating target of off-axis system were given. With this method, the deviation of MTF caused by the deflection of the target fringe can be reduced to a negligible level. Splicing relationship between the detector and the test target of self-collimating MTF test system were discussed, influence of detector's filter on focal plane position was analyzed, and design and splicing program of the detector and the target were proposed. Finally, the application of self-collimating MTF test on a camera were summarized. The result obtained by this study can be used to other camera in the future.
-
Key words:
- space camera /
- self-collimating /
- MTF test /
- focal plane position /
- plane mirror /
- target
-
[1] 张孝弘, 王宇. 面阵CCD相机的MTF测试技术 [C]//中国空间科学学会空间探测专业委员会第十九次学术会议论文集(上册), 2006: 359-366. [2] Yue Tao. The achievements and future prospects of chinese space optical remote sensing technology [J]. Spacecraft Recovery & Remote Sensing, 2008, 29(3): 10-19. (in Chinese) doi: 10.3969/j.issn.1009-8518.2008.03.004 [3] Wang Xiaoyong. Development and prospect of space optical technology [J]. Spacecraft Recovery & Remote Sensing, 2018, 39(4): 79-86. (in Chinese) doi: 10.3969/j.issn.1009-8518.2018.04.010 [4] Li Shengyang, Liu Zhiwen, Liu Kang, et al. Advances in application of space hyperspectral remote sensing (Invited) [J]. Infrared and Laser Engineering, 2019, 48(3): 0303001. (in Chinese) [5] Yoder P R Jr. 光机系统设计[M]. 北京: 机械工业出版社. 2008.1. Yoder P R Jr. Opto-Mechanical Systems Design [M]. 3rd ed. Zhou Haixian, Cheng Yunfang, translated. Beijing: China Machine Press, 2008. (in Chinese) [6] 沃伦J. 史密斯. 现代光学工程[M]. 北京: 化学工业出版社. 2017.1. Smith W J. Modern Optical Engineering [M]. 4th ed. Zhou Haixian, Cheng Yunfang, translated. Beijing: Chemical Industry Press, 2011. (in Chinese) [7] Shi Lei, Jin Guang, Tian Haiying, et al. Autofocusing method with automatic calibration for aerial camera [J]. Optics and Precision Engineering, 2008, 16(12): 2460-2464. (in Chinese) doi: 10.3321/j.issn:1004-924X.2008.12.023 [8] Zhu He, Liang Wei, Gao Xiaodong. Autofocusing system with opto-electronic auto-collimation method for aerial camera [J]. Opto-Electronic Engineering, 2011, 38(3): 35-39. (in Chinese) [9] Xiao Zhanquan, Zhai Linpei, Ding Yalin, et al. Research of optical assembly errors effects on TDI-CCD camera [J]. Semiconductor Optoelectronics, 2008, 29(5): 795-798. (in Chinese) [10] Yong Chaoliang, Lin Jianchun, Zhao Ming, et al. Mosaic of spatial large scale CMOS focal plane array [J]. Infrared and Laser Engineering, 2012, 41(10): 2562-2566. (in Chinese) [11] Zhou Huaide, Liu Jinguo, Zhang Liping, et al. Development of focal plane module for three-line LMCCD mapping cameras [J]. Optics and Precision Engineering, 2012, 20(7): 1492-1499. (in Chinese) doi: 10.3788/OPE.20122007.1492 [12] Meng Qinghua. Structure design of stitching instrument for area CCD [J]. OME Information, 2010, 27(11): 32-35. (in Chinese) -






 下载:
下载: