-
大气透过率和背景辐射(包括散射的太阳辐射和热辐射)是影响空间目标观测的重要大气光学参数,在光学工程中具有重要的应用。根据大气辐射传输理论和测量的大气参数,建立精确而快速的辐射传输计算模式和软件,快速获得大气光谱透过率和环境背景辐射,是工程上特别关注的问题。自2006年开始,笔者研制了通用大气辐射传输软件 (CombinedAtmospheric Radition Transfer, CART)[1-2],可以根据大气参数计算可见光到远红外波段的大气透过率和背景辐射。该软件在不断更新中,2020年发布了CART2.0版[3]。文中主要介绍在CART2.0基础上新增加的关于大气传输特性的二维场景快速计算功能。
在CART中[1−4],提出了基于逐线积分的中高分辨率的大气分子吸收算法[1,3],基于大气吸收和散射组合重排的离散坐标快速计算算法[5],考虑大气分子和气溶胶粒子的吸收[1,6]、散射、热辐射效应以及地表的反射和辐射效应,建立了CART软件[2-4],可用来快速计算空间任意两点之间的大气光谱透过率、散射和透射以及地表反射的太阳辐射、地表和大气的热辐射等,光谱波段为可见光到远红外波段 (1~25 000 cm−1或0.4~10000 μm),光谱分辨率分为中分辨率1 cm−1和高分辨率0.1 cm−1,并且带有我国若干个地区的逐月平均的大气模式。
大气透过率和背景辐射具有强烈的空间分布,在给定大气参数廓线和波段范围的情况下,这些量随仰角、方位、距离、高度的变化而变化。对于一些应用场景来说,需要计算不同方向(仰角、方位、距离、高度等)的矩阵参数,称之为场景计算。目前,CART计算一次给定路径、可见光到远红外波段的大气光谱透过率和背景辐射视不同情况需要数百毫秒到百秒量级的计算时间。对于具体应用场景,上述组合计算的一幅场景有时需要高达104~106次路径和方向的计算量,按照逐点逐方向计算,需要几十分钟到百小时的计算时间(在Win10的64位操作系统,i7-12700K 3.61 GHz CPU的个人计算机上,下同),计算速度远远不能满足工程上的需要。因此,如何能快速计算一幅场景的大气传输和背景辐射特性在工程上具有现实意义。
一些计算机视觉图像场景生成系统也需要天空背景光和颜色的数字场景图。目前采用的方法多数是在数字场景图中按照一定的公式以函数形式生成不同位置的背景值和RGB颜色,从而形成纹理,使图像“看”起来逼真[7-8]。目前天空背景模型的渲染方式主要采用该方法加载静态图片纹理的结果。
在物理仿真方面,黄建余[9]采用倍加法仿真计算了白天天空背景亮度的方法,分析了不同太阳天项角、观测方向以及不同大气光学厚度条件下天空背景亮度;杨春平等[10]利用混合修正的delta~Eddington近似计算出二维天空亮度数组,基于云的边缘特征和天空亮度分布特征、二次随机法和分形几何算法设计云纹理生成算法,实现了云场景的动态仿真。广泛使用的美国前空军地球物理实验室研制的中分辨率大气透过率计算软件MODTRAN[11]提供了可连续计算不同路径的串行计算功能,对于多路径计算量非常大,也非常耗时。这些物理仿真方法的计算速度远远不能满足实时动态的要求。因此,建立一个基于物理基础的多维场景仿真的快速大气辐射传输计算模式软件在工程应用中具有特别重要的意义。
文中先分析了满足精度的多次散射辐射传输求解时的耗时问题,讨论了散射相函数勒让德(Lengdre)展开流数对散射辐射强度计算精度的影响。然后根据离散坐标法和大气传输及背景辐射的空间分布特征,设计了快速计算二维场景的大气辐射传输和背景辐射算法,实现了利用CART进行二维场景大气透过率和背景辐射(包括散射太阳辐射和热辐射)的快速计算功能。
-
离散坐标法(DISORT)[12]是目前可以精确求解介质中包含多次散射的辐射传输问题的方法之一。在研制的CART中采用基于DISORT多次散射快速求解算法[5]。DISORT[12]将天顶角积分用有限求和公式代替,将辐射传输方程转化为一阶微分线性方程组,根据对应的边界条件解出散射辐射的空间分布。给定每层大气介质的散射相函数,DISORT按光学厚度坐标计算空间不同位置的光辐射强度和通量。DISORT用2N个节点的高斯(Gauss)求积公式代替辐射传输方程中的天顶角积分,可以得到方程的离散坐标近似解[13]:
$$\begin{split} {\mu }_{i}\dfrac{{\rm{d}}{I}^{m}(\tau ,{\mu }_{i})}{{\rm{d}}\tau }=&{I}^{m}(\tau ,{\mu }_{i})-{\displaystyle \sum _{\begin{array}{l}j=-N\\ J\ne 0\end{array}}^{N}{w}_{j}{D}^{m}(\tau ,{\mu }_{i},{\mu }_{j}){I}^{m}(\tau ,{\mu }_{j})-}\\ &{{Q}^{m}(\tau ,{\mu }_{i})}\\ &(i=\pm 1,\cdot \cdot \cdot ,\pm N,m=0,1,\cdot \cdot \cdot ,2N-1) \end{split} $$ 式中:
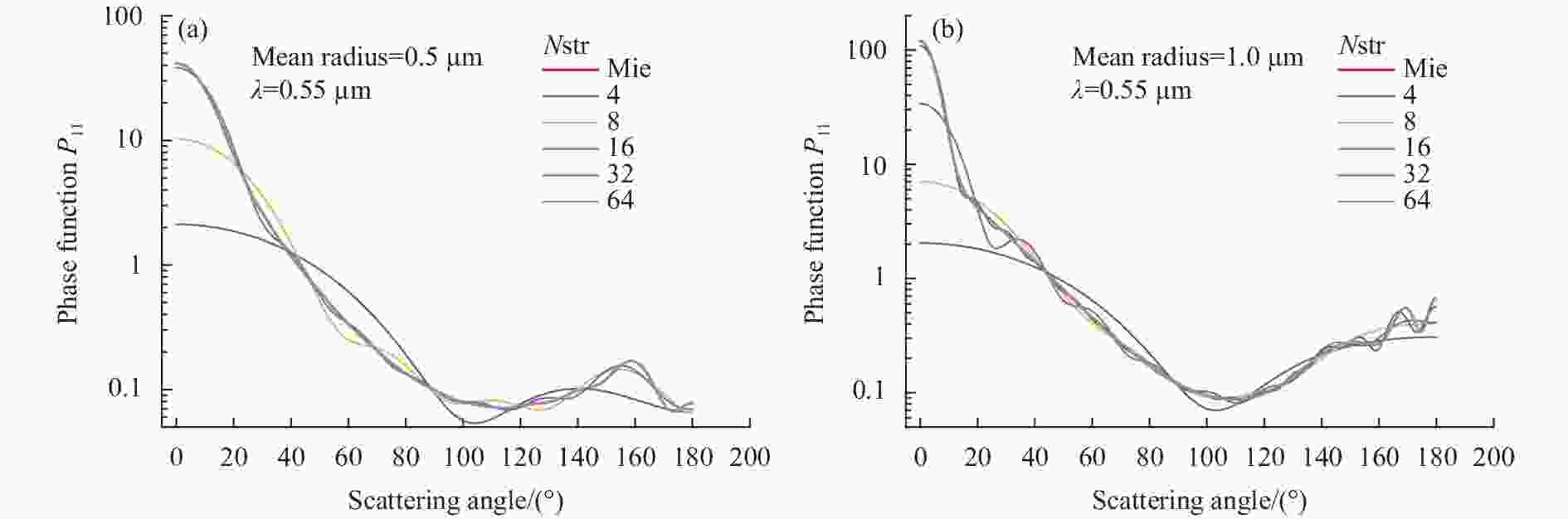
${\mu _i}$ 和${w_i}$ 为求积节点和权重;${D^m}(\tau ,{\mu _i},{\mu _j})$ 为相函数离散化后的矩阵形式。在DISORT求解时,通常将散射相函数展开成2N阶 Legendre多项式,2N通常被称为流数Nstr。由于大粒子前向散射尖锐,需要较高阶Legendre多项式逼近,收敛慢,计算效率低,为此,Wiscombe提出$ \delta - M $ 的相函数截断处理方法[14],即将前向一定角度内散射相函数截断,假定前向这一小角度内相函数为$ \delta $ 函数,这样相函数展开可能只要较少项就能较好地描述散射问题。即使采用$ \delta - M $ 方法,对于前向比较尖锐的相函数(如冰晶云之类的大粒子的散射),展开甚至需要数百项才能收敛[15]。段民征等[16]讨论了在流数有限下相函数截断导致的相函数展开的虚假振荡问题,并给出了两种用较少流数达到较高计算精度的高效计算方法。对于该问题,Hu等人[17]提出了$ \delta - fit $ (非线性加权拟合) 法来展开相函数。该方法的原理与段民征等提出的方法相同。笔者发现用Hu等的$ \delta - fit $ 展开方法展开式收敛快,计算所需要的流数少,因此在CART中采用$ \delta - fit $ 展开进行散射相函数的展开。Yin等[18]设计了一套大气散射相函数近似处理软件G-delta-L,可以将任意散射相函数展开成包括$ \delta - M $ 方法在内的Lengdre多项式。一般来说,采用的流数多,计算精度高,但计算时间随流数呈指数增加。计算半球辐射通量一般采用4~8流就够了,但计算不同方向的散射强度时,对气溶胶粒子尺度较大的散射相函数,8流可能不能满足要求。从Lengdre多项式展开的近似散射相函数与实际相函数的符合程度就可以判断计算流数是否满足要求。假定气溶胶粒子谱分布满足伽马分布,采用米氏(Mie)散射计算程序计算了平均半径分别为0.5 μm和1 μm的球形水滴粒子的散射在0.55 μm波长(折射率实部和虚部分别为1.33和1.96E-9)处的散射相函数。将这个计算的Mie散射相函数作为实际相函数,采用
$ \delta - fit $ 方法[17]分别用4、8、16、32和64流勒让德多项式展开得到近似的散射相函数(DISORT计算时利用这个散射相函数的展开系数PMOM计算光散射强度),如图1 (a)和1(b)所示。可以看出,低流数(4和8流)Lengdre多项式展开的近似散射相函数与实际Mie散射相函数相差甚远,特别是前向,低流数展开的近似相函数前向很宽,散射角内平缓弥散,而实际计算的Mie散射相函数前向尖锐,前向小角度内散射能量集中。采用8流展开,实际散射相函数前向比展开的相函数大4倍,采用16流展开,展开的近似散射相函数与实际相函数基本一致。通常来说,粒子尺度越小,Mie散射计算的前向越平缓。所以,从DISORT求解散射辐射的相函数展开符合度来看,对于半径小于0.5 μm的气溶胶粒子,取16流展开足以精确地描述气溶胶的散射相函数,而对于半径大于1 μm粒径的大粒子气溶胶,则可能需要32流以上才可以满足要求。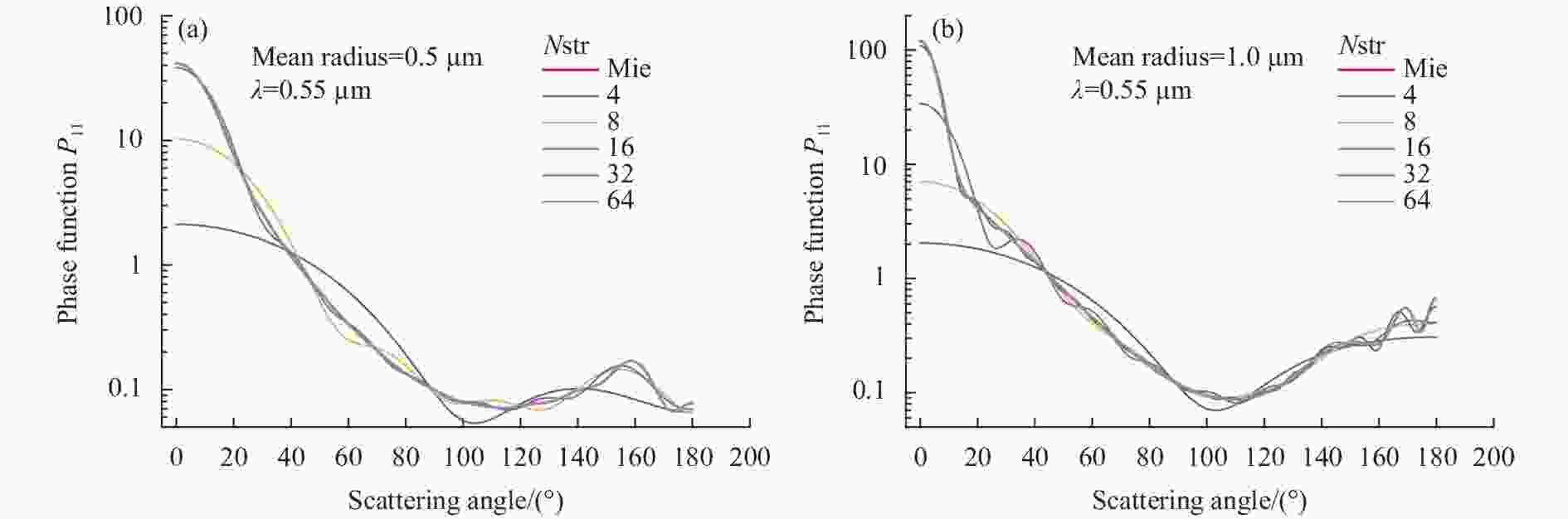
图 1 用不同流数(Nstr=4,8,16,32,64)的勒让德多项式展开的Mie散射相函数。(a) 粒子平均半径0.5 μm;(b) 粒子平均半径1.0 μm
Figure 1. Mie phase function and Lengdre extension with different
Nstr=4,8,16,32,64. (a) Particle mean radius=0.5 μm; (b) Particle mean radius=1.0 μm 根据以上散射相函数展开的流数,假设太阳的天顶角30°、方位角90°,利用修改后的CART分别用4、8、16和32流计算了地对空观测方向,观测天顶角0°~88°,方位角0°~360°,大气散射的二维场景辐亮度。计算时假定乡村型气溶胶模式,Mie散射相函数,地面能见度23 km。计算可见光到近红外400~1100 nm (9090~25000 cm−1)波段,光谱分辨率1 cm−1,积分得到天空散射辐亮度分布如图2所示。从图中可以看出,当采用较低的流数(Nstr=4)时(见图2(a)),在前向散射方向,多次散射弥散在较大的角度范围内,而在散射正前向(90°方位角,30°天顶角)处看不出明显的散射的太阳像,前向散射光强度随角度变化很平缓,这与在太阳方向附近很强的散射光的实际情况不符,这是因为图1左边Nstr=4时Lengdre展开的近似散射相函数前向平滑与实际散射相函数相差较大造成的,说明用4流Lengdre级数展开流数显然不够。对于图2(b)的Nstr=8的情况有所改善,散射的能量比Nstr=4时显著地向前向集中了,能看出明显的太阳前向散射像。但是,太阳前向散射光仍然弥散在前向方位角15°~165°的较大范围内,说明采用8流展开也不足以描述平均半径0.5 μm气溶胶的散射问题。对于图2(c)中Nstr=16时,散射光主要集中在前向±15°范围内,并且其峰值位置散射光强达到了208 W·m-2·sr-1 ,与图2(d)中Nstr=32时的结果一致,说明DISORT计算时,对平均半径小于0.5 μm气溶胶的散射,采用
$ \delta - fit $ 方法的Lengdre相函数展开取Nstr=16流足以精确地描述大气气溶胶的多次散射,不需要使用更高的流数。
图 2 CART用不同流数(Nstr依次为: 4,8,16,32)相函数展开计算的天空散射辐亮度
Figure 2. Sky radiance calculated using CART with the different
Nstr of 4, 8, 16, and 32 工程和理论计算常用基于不对称因子g参数化的Henyey-Greenstain解析式(简称H-G散射相函数)来描述一般粒子的散射相函数。g介于−1~1之间。分别取g=0.8(代表通常情况的气溶胶粒子)和g=0.95(代表大的气溶胶粒子或云粒子)的H-G散射相函数,采用
$ \delta - fit $ 方法分别用4~64流勒让德多项式展开的近似散射与实际的H-G散射相函数比较,如图3所示。可以看出,对于g=0.8时,用16流展开的近似散射相函数基本上与实际的H-G相函数非常接近。但对于g=0.95,即使用32流,前向小角度内展开的近似散射相函数与真实的H-G相函数仍有差别。
图 3 不同流数 Nstr(4,8,16,32,64)勒让德多项式展开的散射相函数与H-G相函数的比较。 (a) g=0.8;(b) g=0.95
Figure 3. Comparisons of Lengdre extension with different Nstr(4,8,16,32,64) and the H-G phase function. (a) g=0.8; (b) g=0.95
同样,g=0.95时,相函数的展开分别用4、8、16和32流勒让德多项式,用CART计算了地对空观测不同方向的天空散射光的辐亮度分布,如图4所示,结果与图2类似。不同的是对于图4(d),当Nstr=32时,太阳散射光主要集中在前向±5°很小的角度范围内,并且峰值散射辐亮度是图4(c) Nstr=16的5倍以上,即散射强度主要集中在前向很小的角度范围内。原因是当g=0.95时(见图3 (b)),散射相函数前向非常尖锐,此时必须使用32流以上的Lengdre展开,才能较精确地模拟实际相函数,进而准确地计算大气的多次散射辐亮度。即对于较大的散射粒子,不对称因子大,前向散射强,多次散射计算时相函数展开需要32流以上才能得到满意的精度。
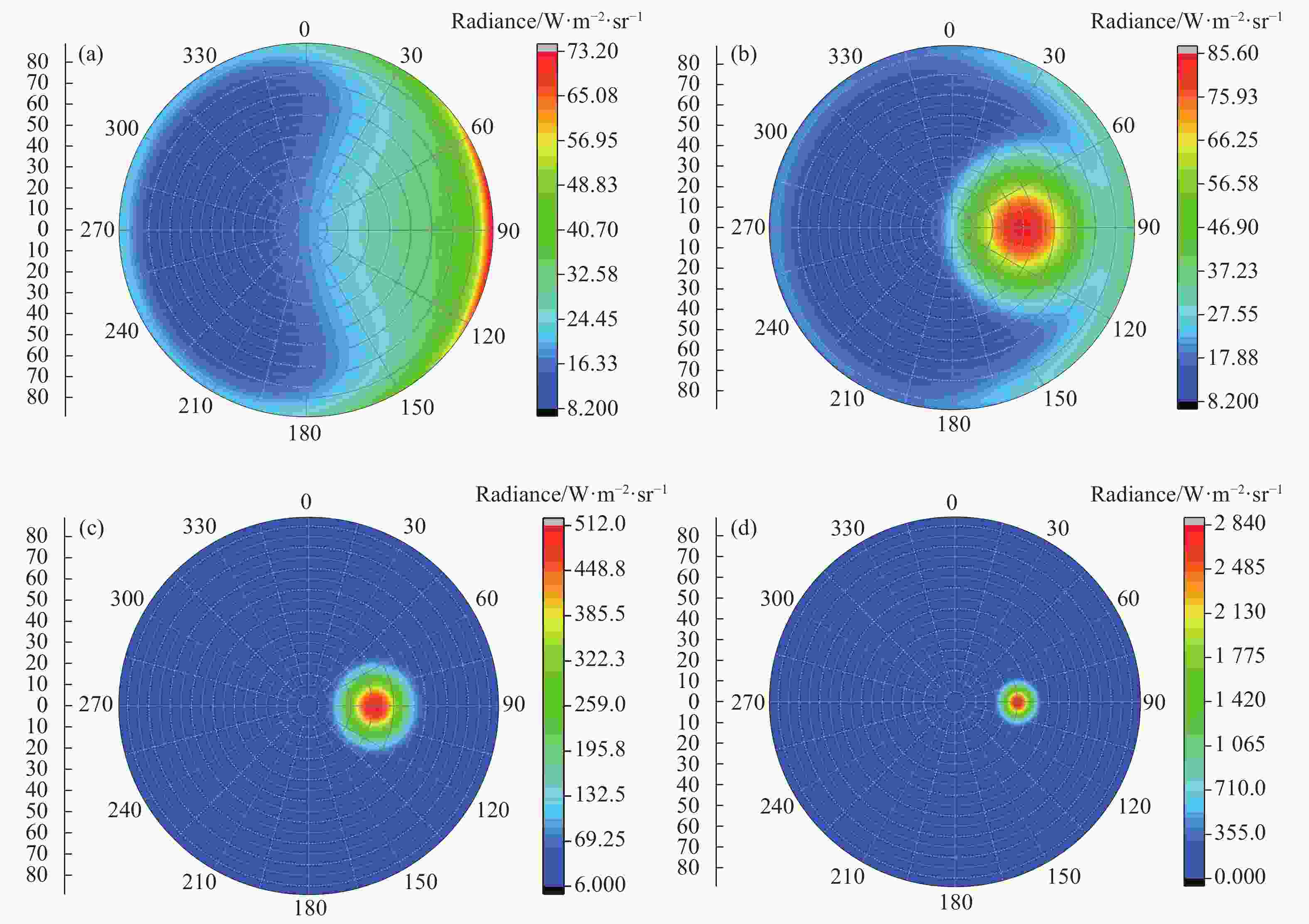
图 4 CART计算H-G 相函数不对称因子为0.95时的气溶胶粒子散射天空辐亮度(Nstr:4,8,16,32)
Figure 4. Aerosol scattered sky radiance calculated by using of CART with the Nstr of 4, 8, 16, and 32 for the case of H-G phase fucntion with g=0.95
计算大气多次散射的耗时与展开阶数的关系。图5为用CART的多次散射快速算法计算的大气向下的多次散射场景所需要的时间与勒让德多项式展开流数的关系。图中的时间扣除了分子吸收计算所需要的时间。大气分成50层,波段 400~1100 nm(9090~25000 cm−1),光谱分辨率1 cm−1。可以看出,计算耗时随展开流数几乎成指数增长。CART采用16流相函数展开,一次计算一个方向多次散射的时间约为18.1 s,计算场景(比如100×100点阵)时耗时将超过50 h,在工程上因计算时间太长而无法使用较高的流数。若要计算不同方向散射的一幅场景的散射光强,必须寻求更快的场景计算方法。
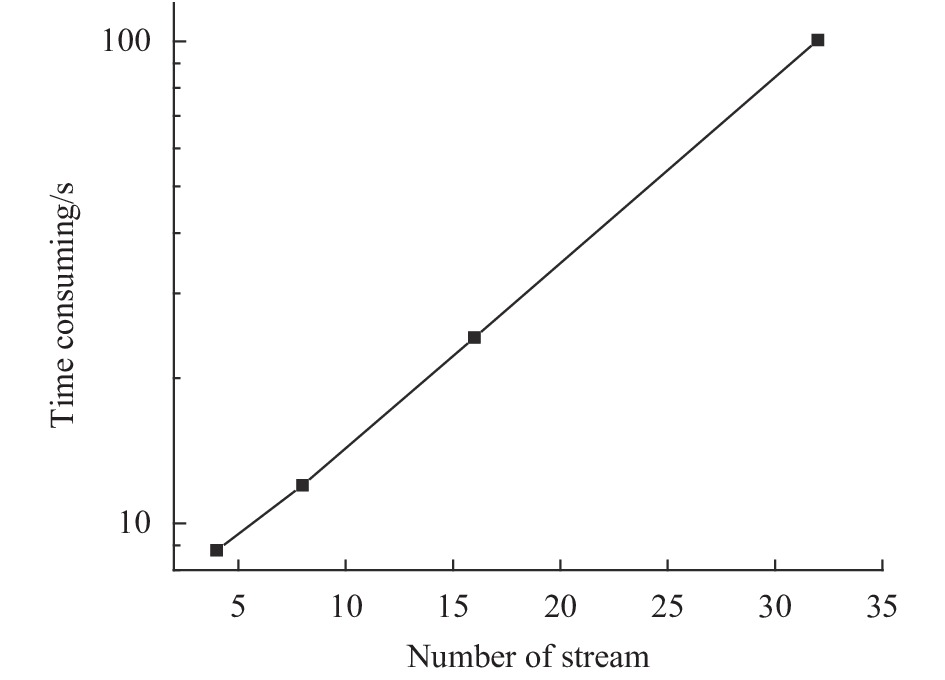
图 5 CART多次散射计算耗时与散射相函数勒让德多项式展开流数的关系
Figure 5. Relationship between the time-consuming of CART multiple scattering calculation and the Nstr of Lengendre extension
通常情况下,大气气溶胶的粒子平均尺度一般介于几百纳米到微米之间,大粒子有可能达到1 μm以上,不对称因子有可能达到0.8以上,所以在用DISORT计算大气气溶胶多次散射时,建议采用16流Lendgre多项式展开气溶胶散射相函数。MODTRAN也采用2流近似或DISORT计算多次散射,折中考虑计算时间开销和计算精度,MODTRAN推荐用使用8流。从文中的内容来看,对于不对称因子大于0.8的大粒子散射(图3(a)),8流并不能满足计算精度要求,需要采用较高的流数计算。
-
对于一些工程应用场景来说,需要计算不同方向(仰角、方位、距离、高度等)的背景辐射。可见光到近红外波段,背景辐射主要为大气和地表散射的太阳辐射;长波红外至远红外波段,背景辐射主要是大气和地表的热辐射。下文讨论大气散射背景辐射和热辐射的快速场景计算。
-
因为大气散射是波长的慢变函数,为了加快多次散射的计算速度,在散射计算的光谱维度,CART将可见光到中红外波段分成11个波段,即2000~5000 cm−1波段,每隔1000 cm−1分成一段;5000~25000 cm−1,每隔2500 cm−1分成一段。在每一个波段采用DISORT计算其中8个波长处的散射强度,然后基于大气吸收、散射光学厚度和地表反照率组合重排,拟合得到该波段的其他波长处的散射强度,拟合时考虑了吸收、散射、地表反射和散射相函数的波长分布,与每个波长DISORT积分相比,误差一般小于2%,计算速度提高两个量级[5]。即使这样,上节的结果表明,采用16流相函数展开,计算可见光到近红外波段的一条光谱也需要24.3 s,32流需要约102 s。对于上万个空间方向的场景计算来说,需要超过50 h的时间,因此计算速度不能满足工程上的需要。
DISORT计算时,可以同时输出不同天顶角和方位角方向的辐亮度以及半球方向的辐射通量[12]。修改源程序,在CART多次散射算法中的每一个波段,Numu设定为需要计算的天顶角个数,按天顶角的余玄等间隔划分,Nphi设定为需要设定的方位角个数,按方位角等间隔划分,每次计算同时输出Numu×Nphi个方向的二维空间分布,按参考方向像元将该二维分布归一化后平均。对每一个子波段,该二维分布乘以参考方向的积分辐亮度得到各个子波段的散射辐亮度分布,然后各个子波段的累加就得到了需要计算的各个方位角和天顶角方向的辐亮度的二维分布。
经测试,在400~1100 nm范围内,CART计算单一方向的多次散射耗时18.1 s,而一次计算同时输出Numu×Nphi=101×101=10201个方向,耗时24.3 s,只比计算单一方向的时间略多一点,平均速度提高了7600倍。图2和图4即为采用修改后CART计算的结果。原先逐方向、逐像元计算一幅图需要耗时2天多,而修改后的CART可以在不到半分钟内就可以计算一幅场景的大气多次散射背景辐射,给工程计算带来了极大的便利。程序中规定Numu和Nphi的最大输出个数为201,即一幅场景一次可以计算不超过40401个方向的背景辐射值。
-
环境热辐射也是高度和天顶角的函数(CART采用球面平行大气,即热辐射与方位无关)。因为波段积分热辐射随高度和天顶角平滑缓慢地变化,所以把目标高度方向从起始高度到终止高度按对数等间隔从低到高分成10段,计算从观测高度到10个目标高度处的大气热辐射,然后采用样条插值得到其他目标高度的计算值。同样,对天顶角,按天顶角的余弦cos(θ)按从大到小的顺序等分成10段,计算10个天顶角下的环境热辐射,然后用样条插值法得到其他天顶角下的计算值。这样,对于任意天顶角方向和目标高度的环境热辐射计算可以简化成10×10次的计算量,而插值得到环境热辐射精度与逐点计算相对差别小于1%。
图6为假定观测者在地面(H1=0 km),用CART模拟计算的8~12 μm波段(833~1250 cm−1)大气向下的热辐射随天顶角θ和目标高度H2的变化。方块点是抽样的格点上计算的值,实线是拟合的值。可见10个计算格点可以较好地拟合出环境热辐射随高度或天顶角的变化。
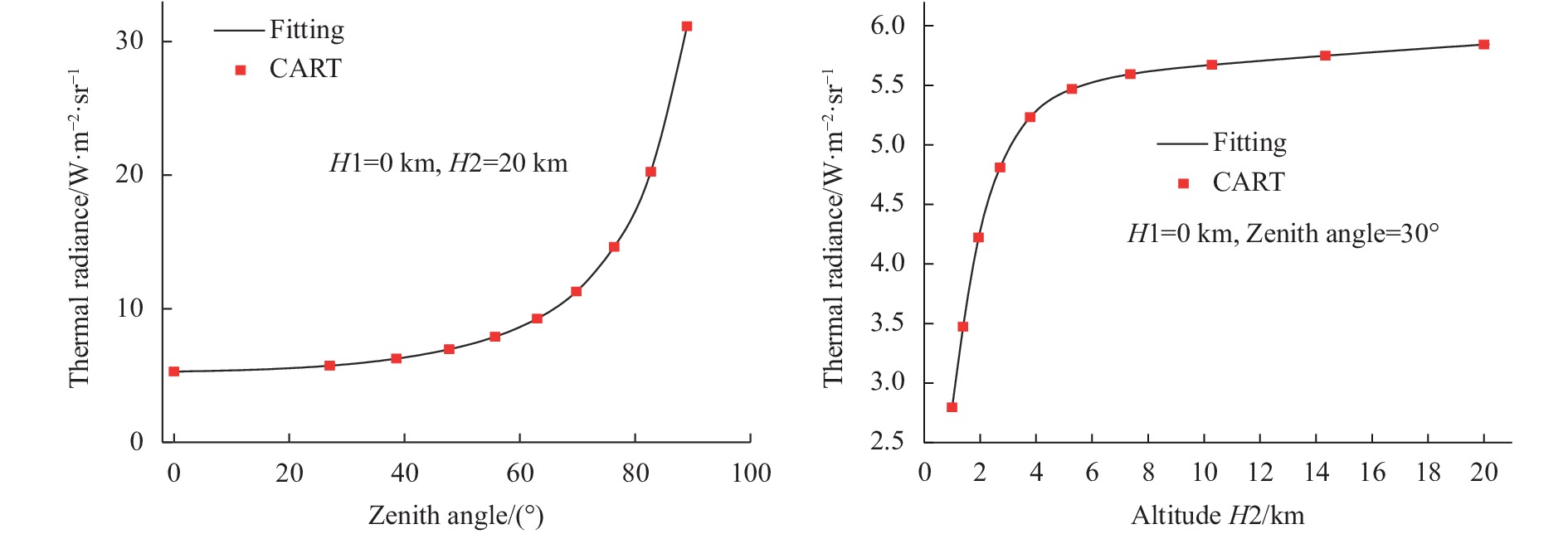
图 6 CART计算的大气热辐射随天顶角和目标高度的变化及其与拟合结果的比较
Figure 6. Comparisons of atmospheric thermal radiation vs. zenith angle and target altitude between CART calculations and fittings
图7是用CART的快速场景功能计算的833~1250 cm−1(8~12 μm)波段的大气向下的热辐射随天顶角和目标高度的二维变化,高度范围0.1~20 km,天顶角范围0°~89°,网格点100×100,计算时间18.1 s,而单个方向计算时间0.22 s,计算速度提高了约120倍。
-
在给定大气参数廓线的情况下,某一波段的大气平均透过率是光传输距离和天顶角的函数,即大气透过率是目标高度和观测天顶角的函数。很多场合下,如空间目标观测,随着目标的移动需要计算不同仰角和目标高度的大气透过率。
图8为CART计算的斜程8~12 μm波段(833~1250 cm−1)大气平均透过率分别随天顶角和目标高度的变化。可以看出,大气平均透过率随天顶角和高度平缓、光滑地变化,只有在天顶角接近90°时和高度接近地表时变化较为迅速。因此,在一幅场景的计算中,只需要计算有限个高度和天顶角下的透过率,其他情况采用插值的方法,可以大大节约计算时间。将高度方向从起始高度到终止高度按等对数、等间隔从低到高分成10段,计算10个高度处的大气透过率,然后用样条插值得到其他高度的计算值;同样,对天顶角,按天顶角的余弦cos(θ)从大到小的顺序等分成10段,计算10个天顶角下的大气透过率,然后用样条插值法得到其他天顶角下的计算值。从图8中可以看出,插值结果和实际计算结果非常接近,一般误差小于1%。这样对于任意天顶角方向和目标高度的大气透过率场景计算,可以简化成不超过10×10次的计算量,而插值得到大气透过率精度与逐点计算相对差别小于1%。
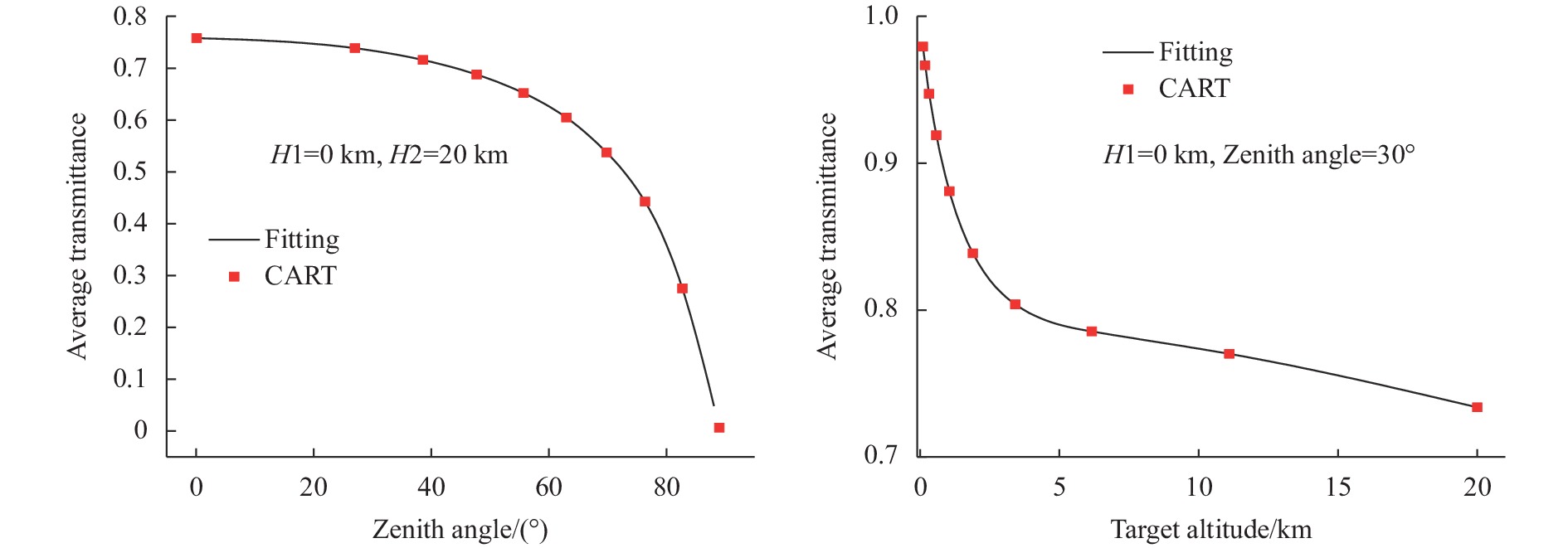
图 8 CART计算的大气平均透过率随天顶角和目标高度的变化与拟合结果的比较
Figure 8. Comparisons of atmospheric average transmittance vs. zenith angle and target altitude between CART calculations and fittings
对于目标高度0.1~100 km,0°~89°天顶角的101×101=10201个方向的计算,在1~25000 cm−1(0.4~10000 μm)波段耗时1′38″,而单独计算一次耗时2.15″。比逐点计算每个方向的速度大约提高了220倍。
图9为用CART的快速场景功能计算的833~10000 cm−1(1~12 μm)波段的大气平均透过率随天顶角和目标高度的二维变化,高度范围1~20 km,天顶角范围0°~89°,网格点101×101,计算时间53.0 s。
-
在CART中,对于大气透过率、热辐射、太阳直射辐射计算,除了原先的高度和天顶角输入参数外,还分别增加了高度和天顶角的起始、终止和步长值的输入项,当步长值大于0时,进行二位场景快速计算,若高度或天顶角的步长值只有一个大于0,则按步长设置的一维连续计算。对于多次散射计算,分别增加了观测天顶角和方位角起始、终止和步长值的输入项,当步长值大于0时,进行天空辐亮度二维场景快速计算。计算得到的二维或一维光谱背景辐射或大气光谱透过率的波长积分值的数组矩阵分别以SceneRad.dat和SceneTrans.dat文件名存于目录\output\中。同时,每次计算的光谱透过率或光谱辐亮度也以文件SpecScTrans.dat和SpecScThermal.dat存于目录\output\中。参考点的光谱背景辐射或光谱透过率如原先一样保存在\output\子目录中。
-
在所研制的大气通用辐射传输软件CART的基础上,增加了针对空间(天顶角、方位角、目标高度等)的一维或二维连续场景快速计算功能。根据计算大气多次散射的离散坐标法可以同时输出不同天顶角和方位角的辐亮度的特点,设计程序,一次计算同时得到各方位和俯仰角的多次散射辐射强度,对于大气透过率和热辐射随空间位置的变化缓慢的特点,采用抽样计算、样条插值的方法,在保持计算精度基本不变的情况下,大大节省了计算时间。在小于2 min内,CART可以完成可见光到远红外波段大气透过率和背景辐射在不同方向的二维场景计算,在实际工程应用的场景计算中将有重要的应用。
Applications of scene calculations of atmopsheric radiative transfer by using of CART (Invited)
-
摘要: 研制了通用大气辐射传输软件CART,可以根据大气参数计算可见光到远红外波段的大气光谱透过率和背景辐射(包括环境散射太阳辐射和热辐射)。光学工程特别关注某一波段的大气透过率随天顶角、距离等参数的多维变化,需要快速计算这些场景变化的大气光学特性。介绍了CART新增的大气辐射传输二维场景计算功能。引入离散坐标法(DISORT)模块,一次计算可同时得到各方位角和天顶角的多次散射辐射强度,大大提高了计算效率。对于大气透过率和热辐射随空间位置的变化缓慢的特点,采用抽样计算、样条插值的方法,在保持计算精度基本不变的情况下,大大节省了计算时间。对于场景计算,相对于逐点串行计算,速度提高了2~3个量级。这在实际工程应用的大气辐射传输场景计算中将有重要的应用。Abstract: A Combined Atmospheric Radiation Transfer (CART) software was developed, which could be used to calculate the spectral transmittance and background radiation (including ambient scattered solar radiation and thermal radiation) of the atmosphere from visible to far infrared wavelength bands based on atmospheric parameters. The multi-dimensional variations of atmospheric transmittance and background radiation in a certain wavelength-band with zenith angle and distance were paid special attention by researches in optical engineering area. Thus, it was necessary to quickly calculate the scene atmospheric optical characteristics. The newly two-dimensional scene fast computing function of atmospheric radiative transfer by using CART was mainly introduced. According to the characteristics of discrete coordinate method (DISORT) which could simutaniously output the radiance at various zenith angles and azimuth angles, the program to calculate the multiple-scattered atmospheric radiance was designed at each direction (azimuth and zenith angles) simultaneously, which greatly improved the calculation efficiency. As the atmospheric transmittance and heat radiation change slowly with space position, sampling calculation and spline interpolation were adopted to save the calculation time greatly while keeping the calculation accuracy. For a scene with more than 10000 times calculations, the speed was 2-3 orders of magnitude faster than before. It will be usefull in the calculation of atmospheric radiative transfer scenarios in practical engineering applications.
-
-
[1] Wei Heli, Chen Xiuhong, Rao Ruizhong, et al. A moderate-spectral-resolution transmittance model based on fitting the line-by-line calculation [J]. Optics Express, 2007, 15(13): 8360-8370. doi: 10.1364/OE.15.008360 [2] Wei Heli, Chen Xiuhong, Rao Ruizhong, et al. Introduction to the combined atmospheric radiative transfer software (CART) [J]. Journal of Atmospheric and Environmental Optics, 2007, 2(6): 446-450. (in Chinese) [3] Wei Heli, Dai Congming, Wu Pengfei, et al. An upgraded combined atmospheric radiative transfer CART2(Invited) [J]. Infrared and Laser Engineering, 2020, 49(7): 20201024. (in Chinese) doi: 10.3788/IRLA20201024 [4] Wei Heli, Chen Xiuhong, Dai Congming. Combined atmospheric radiative transfer (CART) model and its applications [J]. Infrared and Laser Engineering, 2012, 41(12): 3360-3366. (in Chinese) [5] Chen Xiuhong, Wei Heli, Yang Ping, et al. An efficient method for computing atmospheric radiances in clear-sky and cloudy conditions [J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2011, 112(1): 109-118. [6] Chen Xiuhong, Wei Heli, Li Xuebin, et al. Calculating model for aerosol extinction from visible to far infrared wavelength [J]. High Power Laser and Particle Beams, 2009, 21(2): 183-189. (in Chinese) [7] Zhou Y, Li Jing, Xu Wenzhuo, et al. A real-time beach scene simulation based on Poisson fusion [J]. Engineering Journal of Wuhan University, 2018, 51(4): 363-370. (in Chinese) [8] Gu Daquan, Fan Yin, Gong ling, et al. Simulation algorithm for creating sky scene [J]. Meteorological Science and Technology, 2007, 35(2): 292-294. (in Chinese) [9] Huang Jianyu. Background brightness simulation of daytime sky [J]. Journal of Aircraft Measurement and Control, 2008, 27(1): 61-64. (in Chinese) [10] Yang Chunping, Wu Jian, Wei Ling, et al. Cloud scene simulation based on radiative transfer theory and fractal theory [J]. High Power Laser and Particle Beams, 2007, 19(7): 1085-1088. (in Chinese) [11] Berk A, Anderson G P, Acharya P K, et al. MODTRAN5: A reformulated atmospheric band model with auxilary species and practical multiple scattering options [C]//Proceedings of SPIE, 2005, 5655: 88-95. [12] Stamnes K, Tsay S C, Wiscombe W J, et al. Numerically stable algorithmfor discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media [J]. Appl Opt, 1988, 27: 2502-2509. [13] Shi Guangyu. Atmospheric Radiation[M]. Beijing: Science Press, 2007: 148-151. (in Chinese) [14] Wiscombe W. The Delta-m method: Rapid yet accurate radiative flux calculations [J]. J Atmos Sci, 1977, 34: 1408-1422. [15] Chen Xiuhong, Liu Qiang, Wei Heli, et al. The treatment of scattering phase function in the multi-scattering radiative transfer calculation [J]. Journal of Light Scattering, 2007, 19(3): 283-289. (in Chinese) [16] Duan Minzheng, Lv Daren. Rapid yet accurate radiative transfer algorithm for remote sensing [J]. Journal of Remote Sensing, 2007, 11(3): 359-366. (in Chinese) [17] Hu Y X, Wielicki B, Lin B, et al. A fast and accurate treatment of particle scattering phase functions with weighted singular-value decomposition least-squares fitting [J]. J Quant Spectrosc Radiat Trans, 2000, 68: 681-690. [18] Yin Qiu, Song Ci. G-delta-L approximation software and its application tests for atmospheric scattering phase function [J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2020, 258(1): 107398. -






 下载:
下载: