-
早在1931年,Dirac在关于磁单极子的研究中,在场内发现了相位奇点线,开始了人们对相位奇点的研究[1]。1974年,人们在电磁波领域发现了相位奇点的存在,该点处信号强度为零,相位变化2π[2]。1979年,Willetts等人通过实验生成了拉盖尔-高斯光束,并发现其中心轴线上强度为零,存在着相位奇点[3]。同年,Berry等人报道了在多光束干涉中关于相位奇点线的研究[4]。1981年,Baranova等人在激光的光斑中发现了波前的错位[5]。1989年,Collet等人发现了菲尼尔数值较大的激光腔内存在着类似超流体的涡旋,推导出这个涡旋的公式带有螺旋项的解,并且提出“光学涡旋”这一术语[6]。1992年,Allen等人从光学涡旋的传播过程中意识到,相位项为
${\rm e}^{im\varphi }$ 的光束中,每个光子携带了$ m\hslash $ 的轨道角动量,并且远大于自旋角动量[7]。此后,研究者们相继提出了计算全息法[8-10]、双柱透镜相位转换器[11-13]、螺旋相位板[14-16]、可编程空间光调制器[17-19]、模式分离器[20]、激光器直接输出[21-23]等多种方法生成光学涡旋。涡旋光场具有螺旋形的波前相位、并且每个光子携带轨道角动量,使其在光镊[24-25]、光通信[26-30]、高分辨率显微镜[31-32]、光刻[33]、量子纠缠[34-35]等领域都有应用。涡旋光场在形成的过程中要求输入光具有很好的相干性,也就是说只有相干光才可以转换成涡旋光,利用这一特点,涡旋光场被用来区分相干光和散射光,具有空间滤波的作用。
文中将分析涡旋光场空间滤波作用的原理,介绍涡旋光场在强散射环境中的空间滤波作用的研究进展,并通过水下强散射环境中的激光雷达测距实验分析涡旋光场对雷达测距精度的提高。
-
涡旋光场是一种具有螺旋形波前的光场,携带轨道角动量,并且具有相位奇点;它的模场呈环形分布,在光束传播方向上的轴向强度为零,也被称为暗中空光束。涡旋光束的光场表达式为:
$$ E\left(x,y\right)=u\left(r,{\textit{z}}\right){\rm e}^{il\theta }{\rm e}^{-ik{\textit{z}}} $$ (1) 式中:
$ u\left(r,{\textit{z}}\right) $ 为光场振幅表达式;${\rm e}^{il\theta }$ 为相位因子,其中$ l $ 为拓扑荷数;$ k $ 为波数。从公式中可以看出,涡旋光波前随着空间旋转角作周期性变化,呈螺旋分布,绕轴旋转一周相位前进$ 2\pi l $ 。涡旋光束的特殊性质正是由相位因子引起的,相位分布由${\rm e}^{il\theta }$ 决定。具有螺旋形波前和特殊相位结构的涡旋光束,需要光束具有空间相干性。空间相干性的减弱会破坏涡旋光束轴上的相位奇点,不再保持暗中空的环状光强分布[36-39]。因此,涡旋光束可分辨并分离空间相干光与空间非相干光,作为空间滤波的窗口。
涡旋光束与粒子的散射特性早有研究[40-45],而涡旋光场在散射环境中的空间滤波作用也引起了人们的注意。
2002年,David等人就利用涡旋光的空间滤波作用,以涡旋光的中心作为窗口,在明亮的相干源眩光中区分并检测到微弱的非相干信号[46]。以螺旋相位板作为高斯光生成涡旋光的转换元件,进入螺旋相位板的光束中的空间相干光可以生成暗中空的涡旋光,而空间非相干的散射光无法生成涡旋光,因此分布在涡旋中心的光大部分是散射光,使得在明亮的相干光源掩盖的背景场显露出来,从而实现消除了空间相干的非散射光的影响,并测量沿光轴方向的不具有空间相干性的散射光。以涡旋光场作为空间滤波的窗口测量弱的散射信号,可以实现至少7个数量级的信噪比增强[47]。因而可以作为新型的光学日冕仪[48-50],得到强光源附近微弱星体的信息。
与高斯光束相比,涡旋光束通过海水这一散射介质后的透过率更高。实验表明,以水作为散射体,高斯光与具有不同拓扑荷数的涡旋光,在水中的衰减与光束的拓扑荷数有关[51]。在海水浑浊程度不大时,高斯光和涡旋光的透过率相差不多;而海水浑浊程度较大时,涡旋光束的透过率比高斯光束高,且拓扑荷数越高的涡旋光通过强散射的水体后透过率越高[52-55]。有研究认为,这是由于涡旋光束拓扑荷数的增大,入射涡旋光束的暗中空的面积将增大,与海水中散射粒子的作用面积随之将减少。并且最佳透过率对应的涡旋光的拓扑荷数是由散射介质中的光束传播距离决定的[56]。孙存志等人还研究了高斯光束与不同拓扑荷数的涡旋光强聚焦后透过散射介质的透过率,实验结果同样表明,拓扑荷数越大的聚焦光束透过散射介质后的透过率越高[57]。
此外,与高斯光束相比,涡旋光束经过散射介质后的散斑尺寸更小;并且涡旋光束的拓扑荷数越大,散斑尺寸越小[58-60]。这一特性在恒星强度干涉测量、热重影成像上都有应用[61-62]。
涡旋光束在散射环境中除了具有与高斯光不同的透过率,还具有在强散射环境中在空间上区分出目标和散射的能力,在激光雷达的探测中有很好的效果。在白天的激光雷达探测中,明亮的太阳光散射使得雷达探测器饱和,而无法探测到明亮表面(如陆地、雪和厚云)的回波信号,对气溶胶和超薄云等光学稀薄大气成分也无法准确探测。2016年,Sun等人在机载激光雷达中使用涡旋光作为“窗口”,将涡旋光场与光子筛结合,在空间上把较强的太阳杂散光和微弱激光雷达回波信号分离,实现了系统中的散射背景光的抑制[63]。
涡旋光场也可以在水下探测雷达中用于减少海水散射噪声的干扰。2017年,Brandon的研究团队使用涡旋光作为空间滤波器,探测浸没在强散射海水环境中的物体。通过把回波中分布在环形涡旋光内部的散射光作为背景光,从而提高了探测的对比度,在强散射环境中区分出微弱的目标回波[64]。涡旋光滤波窗口的使用成功实现了在弹道目标回波振幅比后向散射杂波低两到三个数量级时,把目标回波提取出来,在水下雷达中抑制了散射噪声的干扰。
2018年,Linda等人在水下测距雷达中使用涡旋光提高测距精度。利用涡旋光对空间相干性的要求,在空间分布上区分出了空间相干弹道目标回波与空间非相干散射光。使用条纹相机作为探测设备在空间上只探测回波中分布在涡旋圆环上的信号,从而减少分布在涡旋中心和涡旋外的散射光的干扰,提升测距准确性[65]。实验证明涡旋光场的空间滤波效果可以提高强散射环境下测距精度,利用涡旋光的空间滤波作用,实现了在8个衰减长度下将18 cm的测距误差降低到3 cm以下。
-
涡旋光场可作为空间滤波器件分辨并分开不具有空间相干性的散射光和具有空间相干性的目标反射光。因此,其在高散射环境中可以作为窗口,减少散射光的对探测的干扰。具体来说,具有高度空间相干性的高斯激光入射到散射介质中,在物体表面发生反射,回波中包含散射光和目标反射光。回波探测器前置螺旋相位板作为将高斯光束转换成涡旋光束的光学元件,回波中只有具有良好空间相干的目标反射弹道光子可以在通过螺旋相位板后生成环形分布的涡旋光,而多次散射的光子空间相干性较差,通过螺旋相位板后不能形成涡旋场,仍为按原有空间状态分布。因此,分布在环形涡旋场内的光大部分是散射光。并且,按照散射原理,入射光为高斯光束,那么前向散射和后向散射在光束的中心分布最多。因此,在探测器前使用遮光片将涡旋中心的部分遮挡,在空间上不接收涡旋中心的散射光,只接收涡旋圆环上的光。该方法可以在不影响对目标反射光子接收的前提下,减少对散射光的接收,从而提升探测的信噪比。
实验中,如图1所示,使用准直连续激光作为光源,出射光为高斯光,功率为1 W。用电光调制器对激光器进行强度调制,频率为300 MHz。目标表面具有0.7的反射率,浸没在散射介质中。散射介质设置为水,充满了直径0.5 m、长3 m的圆柱形水箱。介质中的散射强度通过添加不同浓度的Mg(OH)2粉末调节。以衰减长度,即散射介质中的总衰减系数和介质中目标物理距离的乘积,作为衡量散射介质中散射强弱的标准。回波经过一个16阶的螺旋相位板,并使用遮光片遮挡生成的涡旋光的中心。探测器为PMT,接收到被遮挡后的光子,转换成电信号并传递给示波器,再由计算机计算测距结果。测距方法为相位测距法,通过求回波和参考信号的相位差间接求出光经过的距离。在该实验中,参考信号设置为信号发生器向电光调制器发出的射频电信号。因此,测距之前需要将目标放置在水箱边缘,求出此时的距离作为测距的原点。目标放置在水箱内的测距结果,减去该原点的结果,为目标真正被测的距离。

图 1 涡旋光场在强散射环境探测雷达中空间滤波作用示意图
Figure 1. Schematic diagram of spatial filtering of vortex light field in detection lidar in strong scattering environment
在实验中,将物体放置在1 m、1.5 m、2 m位置处。每个位置处在水箱中加入不同浓度的Mg(OH)2粉末,调整水箱中散射介质的衰减系数。测量在散射介质处于不同浑浊程度下的有无涡旋场对测距结果的影响,测距误差如图2所示。可以看出,物体位置在1 m、介质浑浊程度低于7 m−1时,涡旋光场的有无对探测的影响不大,测距结果误差很小。介质衰减系数超过7 m−1,测距误差增大,使用涡旋光场可以矫正测距的误差。而物体位置在1.5 m和2 m、衰减系数为4 m−1时测距误差基本相同,此后涡旋光场可以明显降低散射光带来的测距误差。并且散射越强,涡旋光场对误差的降低效果越明显。这是因为在物体位置较近、介质较清澈时,介质中散射强度不大,散射光子在回波中占比不大,散射带来的误差也不大。因此遮挡涡旋中心的散射光子对测距没有很大影响。而介质的浑浊和物体位置的挪动都会使得光束在介质中发生更多的散射,散射光子增多的同时弹道目标反射光子减少,为测距带来更大的误差,从而使用涡旋光场后,涡旋中心的散射光子在回波中占比更多,被遮挡后可以有效降低这部分散射光带来的误差,使得测距的结果变得更加准确。

图 2 在目标位于(a) 1 m、(b) 1.5 m和(c) 2 m位置处,散射介质不同浑浊程度时,使用涡旋光场测距误差与没有使用涡旋光场测距误差的比较
Figure 2. Comparison of with vortex light field ranging error and without vortex light field ranging error when the target is at (a) 1 m, (b) 1.5 m and (c) 2 m locations and the scattering medium is of varying turbidity
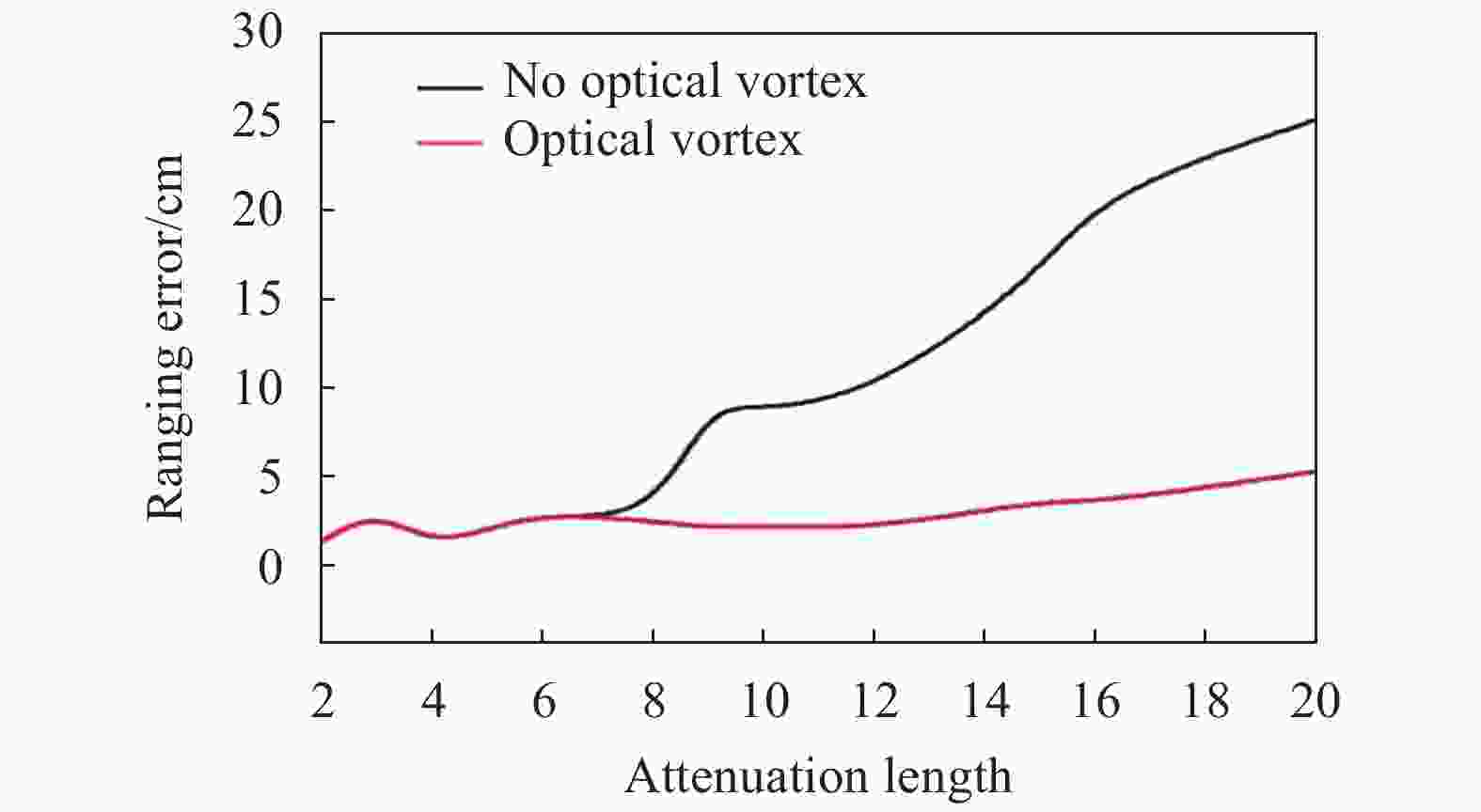
从衰减长度的角度直观分析涡旋光场对测距误差的改善作用,如图3所示。可以看出,在衰减长度较低时,涡旋光场对测距误差没有很大影响,测距误差整体不大。而衰减长度增大,测距误差明显增大,而使用涡旋光场可以有效减小测距的误差,提升测距的准确性。
-
涡旋光场独特的波前特性使其在强散射环境中具有与普通高斯光束截然不同的表现。涡旋光场通过强散射介质后的透过率比高斯光束更高,并且涡旋光场具有在空间上区分散射光与反射光的滤波能力,使其在行星探测上可用于提取被明亮相干光源掩盖的背景信息,从而作为新型的日冕仪,得到强光源附近的微弱星体的信息。反之,也可以利用空间滤波能力滤除散射光的干扰,在星载雷达中降低太阳背景光影响,在海水高散射环境中提高探测对比度等方面都有应用。
通过激光雷达测距实验证明了涡旋光场的空间滤波作用。在强散射环境中,涡旋光场可以把目标回波和散射光在空间中分辨并分离,通过减少区分出的散射光的接收,可以提升激光雷达探测效果。在强散射环境中,使用涡旋光场可以减小散射光带来的测距误差,并且在越强的散射环境下对误差的减小就越明显。
Application of vortex light field in strong scattering environment
-
摘要:
涡旋光场具有螺旋形的波前和相位奇点,光场中的每个光子都携带轨道角动量。其独特的性质使得涡旋光场可以在空间上区分不具有空间相干性的散射光与具有空间相干性的非散射光,从而可以作为系统中的空间滤波器件使用,并且在强散射环境里这种空间滤波效果尤为显著。分析了涡旋光场所具有的空间滤波作用的原理,并介绍了近年来利用涡旋光场在强散射环境中进行空间滤波的研究。设计了使用涡旋光场的水下激光雷达测距实验,从而证明涡旋光场在强散射环境中可以通过其空间滤波作用提高激光雷达水下测距的精度,并且散射越强,这种空间滤波作用对测距精度的提高越明显。
Abstract:The vortex light field has helically shaped wavefront and phase singularities where each photon carries orbital angular momentum (OAM). Its unique properties allow the vortex light field to spatially distinguish incoherent scattered light from coherent non-scattered light, which thus can therefore be used as a spatial filter element. And in the strong scattering environment, this spatial filtering effect is particularly remarkable. The principle of spatial filtering was analyzed and studies of vortex light field in strong scattering environment were introduced. The underwater lidar ranging experiment using the vortex light field was designed to prove that the vortex light field can improve the accuracy of the underwater lidar through its spatial filtering in strong scattering environment. And with strong scattering, this spatial filtering improves the range accuracy more significantly.
-
Key words:
- lidar /
- vortex light field /
- underwater ranging /
- strong scattering
-
-
[1] Dirac P A M. Quantised singularities in the electromagnetic field [J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 1931, 133(821): 60-72. [2] Nye J F, Berry M V. Dislocations in wave trains [J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 1974, 336(1605): 165-190 [3] Vaughan J M, Willetts D V. Interference properties of a light beam having a helical wave surface [J]. Optics Communications, 1979, 30(3): 263-267. doi: 10.1016/0030-4018(79)90350-X [4] Berry M V, Nye J F, Wright F J. The elliptic umbilic diffraction catastrophe [J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1979, 291(1382): 453-484. [5] Baranova N B, Zel’Dovich B Y, Mamaev A V, et al. Dislocations of the wavefront of a speckle-inhomogeneous field (theory and experiment) [J]. Jetp Letters, 1981, 33: 206B. [6] Coullet P, Gil L, Rocca F. Optical vortices [J]. Optics Communications, 1989, 73(5): 403-408. doi: 10.1016/0030-4018(89)90180-6 [7] Allen L, Beijersbergen M W, Spreeuw R, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes [J]. Phys Rev A, 1992, 45(11): 8185. doi: 10.1103/PhysRevA.45.8185 [8] Heckenberg N R, Mcduff R, Smith C P, et al. Generation of optical phase singularities by computer-generated holograms [J]. Optics Letters, 1992, 17(3): 221. doi: 10.1364/OL.17.000221 [9] Bekshaev A, Orlinska O, Vasnetsov M. Optical vortex generation with a "fork" hologram under conditions of high-angle diffraction [J]. Optics Communications, 2010, 283(10): 2006-2016. doi: 10.1016/j.optcom.2010.01.012 [10] Bekshaev A Y, Sviridova S V, Popov A Y, et al. Generation of optical vortex light beams by volume holograms with embedded phase singularity [J]. Optics Communications, 2012, 285(20): 4005-4014. doi: 10.1016/j.optcom.2012.06.010 [11] Lin Y C, Lu T H, Huang K F, et al. Generation of optical vortex array with transformation of standing-wave laguerre-gaussian mode [J]. Optics Express, 2011, 19(11): 10293-10303. doi: 10.1364/OE.19.010293 [12] Chu S C, Ohtomo T, Otsuka K. Generation of doughnutlike vortex beam with tunable orbital angular momentum from lasers with controlled hermite-gaussian modes [J]. Applied Optics, 2008, 47(14): 2583-2591. doi: 10.1364/AO.47.002583 [13] Chu S C, Otsuka K. Doughnut-like beam generation of laguerre-gaussian mode with extremely high mode purity [J]. Optics Communications, 2008, 281(6): 1647-1653. doi: 10.1016/j.optcom.2007.11.023 [14] Beijersbergen M W, Coerwinkel R, Kristensen M, et al. Helical-wavefront laser beams produced with a spiral phaseplate [J]. Optics Communications, 1994, 112(5-6): 321-327. doi: 10.1016/0030-4018(94)90638-6 [15] Kotlyar V V, Almazov A A, Khonina S N, et al. Generation of phase singularity through diffracting a plane or gaussian beam by a spiral phase plate [J]. Journal of the Optical Society of America A Optics Image Science & Vision, 2005, 22(5): 849-861. [16] Turnbull G A, Robertson D A, Smith G M, et al. The generation of free-space laguerre-gaussian modes at millimetre-wave frequencies by use of a spiral phaseplate [J]. Optics Communications, 1996, 127(4-6): 183-188. [17] Walde M, Jost A, Wicker K, et al. Engineering an achromatic Bessel beam using a phase-only spatial light modulator and an iterative Fourier transformation algorithm [J]. Optics Communications, 2017, 383: 64-68. doi: 10.1016/j.optcom.2016.08.050 [18] Ostrovsky A S, Rickenstorff-Parrao C, Arrizón V. Generation of the "perfect" optical vortex using a liquid-crystal spatial light modulator [J]. Optics Letters, 2013, 38(4): 534-536. doi: 10.1364/OL.38.000534 [19] Yuan G, Wang Q, Yuan X. Dynamic generation of plasmonic Moiré fringes using phase-engineered optical vortex beam [J]. Optics Letters, 2012, 37(13): 2715-2717. [20] Abramochkin E, Losevsky N, Volostnikov V. Generation of spiral-type laser beams [J]. Optics Communications, 1997, 141(1-2): 59-64. doi: 10.1016/S0030-4018(97)00215-0 [21] Oron R, Blit S, Davidson N, et al. The formation of laser beams with pure azimuthal or radial polarization [J]. Appl Phys Lett, 2000, 77(21): 3322-3324. doi: 10.1063/1.1327271 [22] Oron R, Davidson N, Friesem A A, et al. Efficient formation of pure helical laser beams [J]. Optics Communications, 2000, 182(1-3): 205-208. doi: 10.1016/S0030-4018(00)00804-X [23] Litvin I A, Ngcobo S, Naidoo D, et al. Doughnut laser beam as an incoherent superposition of two petal beams [J]. Opt Lett, 2014, 39(3): 704-707. doi: 10.1364/OL.39.000704 [24] Wright E M, Arlt J, Dholakia K. Toroidal optical dipole traps for atomic Bose-Einstein condensates using Laguerre-Gaussian beams [J]. Physical Review A, 2000, 63(1): 013608. [25] Zhang D W, Yuan X C. Optical doughnut for optical tweezers [J]. Opt Lett, 2003, 28: 740-742. doi: 10.1364/OL.28.000740 [26] Vetter C, Steinkopf R, Bergner K, et al. Realization of free-space long-distance self-healing bessel beams [J]. Laser & Photonics Reviews, 2019: 1900103. [27] Wang J, Yang J Y, Fazal I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing [J]. Nature Photonics, 2012, 6(7): 488-496. doi: 10.1038/nphoton.2012.138 [28] Bozinovic N, Yue Y, Ren Y, et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers [J]. Science, 2013, 340(6140): 1545-1548. doi: 10.1126/science.1237861 [29] Gao Chunqing, Zhang Shikun, Fu Shiyao, et al. Adaptive optics wavefront correction techniques of vortex beams [J]. Infrared and Laser Engineering, 2017, 46(2): 0201001. (in Chinese) doi: 10.3788/IRLA201746.0201001 [30] Ke Xizheng, Ning Chuan, Wang Jiao. Crosstalk analysis of orbital angular momentum-multiplexed state under atmospheric turbulence [J]. Infrared and Laser Engineering, 2018, 47(11): 1122002. (in Chinese) doi: 10.3788/IRLA201847.1122002 [31] Westphal V, Hell S W. Nanoscale resolution in the focal plane of an optical microscope [J]. Physical Review Letters, 2005, 94(14): 143903. doi: 10.1103/PhysRevLett.94.143903 [32] Maurer C, Jesacher A, Fürhapter S, et al. Upgrading a microscope with a spiral phase plate [J]. Journal of Microscopy, 2010, 230(1): 134-142. [33] Levenson M D, Morikawa Y, Hayashi N, et al. Vortex viaprocess: analysis and mask fabrication for contact CDs <80 nm [C]//SPIE, 2003, 5040: 344-370. [34] Dutra S M, Eliel E R, Nienhuis G, et al. Comment on "orbital and intrinsic angular momentum of single photons and entangled pairs of photons generated by parametric down-conversion" [J]. Physical Review Letters, 2001, 86(22): 5208-5216. doi: 10.1103/PhysRevLett.86.5208 [35] Mair A, Vaziri Al, Weihs G, et al. Entanglement of the orbital angular momentum states of photons [J]. Nature, 2001, 412(6844): 313-316. [36] Maleev I D, Marathay A S, Swartzlander G A, et al. Spatial correlation singularity of a vortex field [J]. Physical Review Letters, 2004, 92(14): 143905. doi: 10.1103/PhysRevLett.92.143905 [37] Wei Gongxiang, Liu Xiaojuan, Liu Yunyan, et al. Spin and orbital angular momentum of light [J]. Laser & Optoelectronics Progress, 2014, 51(10): 30-37. (in Chinese) [38] Gbur G, Visser T D. Coherence vortices in partially coherent beams [J]. Optics Communications, 2003, 222(1-6): 117-125. doi: 10.1016/S0030-4018(03)01606-7 [39] Schouten H F, Gbur G, Visser T D, et al. Phase singularities of the coherence functions in Young's interference pattern [J]. Optics Letters, 2003, 28(12): 968-970. doi: 10.1364/OL.28.000968 [40] Nes A, Trk P. Rigorous analysis of spheres in gauss-laguerre beams [J]. Optics Express, 2007, 15(20): 13360. doi: 10.1364/OE.15.013360 [41] Zambrana-Puyalto X, Vidal X, Molina-Terriza G. Excitation of single multipolar modes with engineered cylindrically symmetric fields [J]. Optics Express, 2012, 20(22): 24536-24544. doi: 10.1364/OE.20.024536 [42] Rury A S, Freeling R. Mie scattering of purely azimuthal laguerre-gauss beams: angular-momentum-induced transparency [J]. Physical Review A, 2012, 86(5): 11781. [43] Kiselev A D, Plutenko D O. Mie scattering of laguerre-gaussian beams: photonic nanojets and near-field optical vortices [J]. Physical Review A, 2014, 89(4): 043803. doi: 10.1103/PhysRevA.89.043803 [44] Sun Wenbo, Hu Yongxiang, Weimer C, et al. A FDTD solution of scattering of laser beam with orbital angular momentum by dielectric particles: far-field characteristics [J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2017, 188: 200-213. [45] Ou Jun, Jiang Yuesong, Shao Yuwei, et al. Scattering of the Laguerre-Gaussian beam by a homogeneous spheroid [J]. Acta Physica Sinica, 2013(11): 241-248. (in Chinese) [46] Palacios D, Rozas D, Swartzlander G A. Observed scattering into a dark optical vortex core [J]. Phys Rev Lett, 2002, 88(10): 103902-103904. doi: 10.1103/PhysRevLett.88.103902 [47] Swartzlander G. Peering into darkness with a vortex spatial filter [J]. Optics Letters, 2001, 26(8): 497-505. doi: 10.1364/OL.26.000497 [48] Foo G, Palacios D, Swartzlander G. Optical vortex coronagraph [J]. Opt Lett, 2005, 30(24): 3308-3310. doi: 10.1364/OL.30.003308 [49] Swartzlander G, Ford E, Abdul-Malik R, et al. Astronomical demonstration of an optical vortex coronagraph [J]. Opt Express, 2008, 16(14): 10200-10207. doi: 10.1364/OE.16.010200 [50] Lee J H, Foo G, Johnson E G, et al. Experimental verification of an optical vortex coronagraph [J]. Physical Review Letters, 2006, 97: 053901. [51] Cochenour B, Morgan K, Miller K, et al. Propagation of modulated optical beams carrying orbital angular momentum in turbid water [J]. Appl Opt, 2016, 55(31): C34. doi: 10.1364/AO.55.000C34 [52] Wang W B, Gozali R, Shi L, et al. Deep transmission of Laguerre–Gaussian vortex beams through turbid scattering media [J]. Opt Lett, 2016, 41(9): 2069-2072. doi: 10.1364/OL.41.002069 [53] Wang W B, Gozali R, Nguyen T A, et al. Propagation and transmission of optical vortex beams through turbid scatteringwall with orbital angular momentums [C]//Conference onOptical Biopsy XIII, International Society for Optics andPhotonics, 2015: 931805. [54] Morgan K S, Johnson E G, Cochenour B M. Attenuation of beams with orbital angular momentum for underwater communication systems [C]//Oceans, IEEE, 2016: 1-3. [55] Jantzi A W, Cockrell M G, Rumbaugh L K, et al. Mixed numerical and analytical method for investigating orbital angular momentum beam scattering in turbid water [J]. Optical Engineering, 2019, 58(4): 043104. [56] Peng Bo, Zhong Kun, Li Zhongyun. Influence of topological charge on turbid underwater propagation of Laguerre-Gaussian vortex beams [J]. Acta Optica Sinica, 2017, 37(6): 0601005. (in Chinese) [57] Sun Cunzhi, Chen Ziyang, Pu Jixiong. Experimental study of tightly focused vortex beams through turbid media [J]. Acta Optica Sinica, 2014, 34(6): 0601002. (in Chinese) [58] Gangireddy S, Prabhakar S, Kumar A, et al. Higher order optical vortices and formation of speckles [J]. Optics Letters, 2014, 39(15): 4364-4367. [59] Liu Jilin, Huang Huiling, Chen Ziyang, et al. Investigation on the speckle produced by vortex beams through a scattering medium [J]. Journal of Optoelectronics · Laser, 2015, 26(8): 1626-1632. (in Chinese) [60] Reddy S G, Kumar A, Prabhakar S, et al. Experimental generation of ring-shaped beams with random sources [J]. Optics Letters, 2013, 38(21): 4441-4444. doi: 10.1364/OL.38.004441 [61] Gilead Y, Silberberg Y. Effect of second-order coupling on photon-pair statistics in waveguide structures [J]. Phys Rev A, 2017, 96(5): 053803. doi: 10.1103/PhysRevA.96.053803 [62] Chan K W C, O’Sullivan M N, Boyd R W. Optimization of thermal ghost imaging: high-order correlations vs background subtraction [J]. Optics Express, 2010, 18(6): 5562-5573. [63] Sun W, Hu Y, MacDonnell D G, et al. Technique to separate lidar signal and sunlight [J]. Optics Express, 2016, 24(12): 12949. [64] Cochenour B, Rodgers L, Laux A, et al. The detection of objectsin a turbid underwater medium using orbital angular momentum(OAM) [C]//SPIE, 2017, 10186: 1018603. [65] Jantzi A, Jemison W, Laux A, et al. Enhanced underwater ranging using an optical vortex [J]. Optics Express, 2018, 26(3): 2668-2674. -

 点击查看大图
点击查看大图
计量
- 文章访问数: 656
- HTML全文浏览量: 300
- 被引次数: 0





 下载:
下载: