-
光学显微成像技术在各个领域有着非常重要的应用[1-2],其中相衬显微镜[3-4]通过相衬作用将人眼无法观察的相移转化为可被识别的振幅差,常被用来观测透明的物体,如活细胞或未染色的生物标本等。光学非线性测量是研究非线性光学材料的关键技术之一[5],Georges Boudebs等利用相衬显微镜原理提出了一种基于4f相干成像系统单脉冲测量材料三阶非线性折射率的方法[6],用于材料光学非线性系数的测量。与测量材料光学非线性的Z扫描技术[7]相比,该方法最主要的优点是单脉冲测量,没有样品的移动[8]。4f相位相干成像测量系统的关键器件为相位物体(Phase object, PO)。为了提高4f相位相干成像系统的测量灵敏度,人们对PO进行了多种改进[9-10],这些改进都是为了提高系统测量的灵敏度。然而,这些PO存在着一个明显的缺陷,其厚度固定不变,对于不同波长的激光,PO的相位大小会发生改变,而相位大小对整个系统测量灵敏度有很大的影响[10],甚至在光程差接近半个波长时无法测出信号,对于不同波长的光源,需要更换对应规格的PO,以保证系统测量的灵敏度。
另外,平顶光束经常被应用光束整形及光学非线性测量技术中[11-12],以提高光学非线性测量系统的灵敏度,例如Z扫描技术及4f相位相干成像系统,平顶光束比高斯光束的灵敏度提高2.5倍左右。但是不足之处是,在实际测量过程中,平顶光会损失大部分激光能量(与限制光阑的面积成反比),激光能量的利用率较低。由于大部分情况下入射光不是理想的高斯光束,这些将影响测量结果的可靠性,在激光能量较低时,一般采用近平顶光束(即采用一定直径大小的光阑使大部分激光光束通过),这样既可以提高系统测量灵敏度和可靠性,还提高了激光能量的利用率。
文中利用迈克尔逊干涉结构设计了一种相位可调的PO,用来解决现有PO存在的不足。通过调整迈克尔逊干涉仪两个反射镜的距离来改变两束光的光程差,从而达到调节相位大小的目的,使不同波长和不同形状光束下的测量都能达到最优状态。该系统可测量样品非线性折射率、折射率谱、热光系数等物理量。理论上给出了入射激光波长对PO相移大小的影响,详细讨论了在近平顶光束下,PO的相移大小、PO与小孔光阑的半径比值等因素对4f相位相干测量系统灵敏度的影响,并详细解释了产生该影响的主要原因。并给出近平顶光束下,PO的最优参数,使得系统测量可以达到最佳灵敏度。另外,实验中为了验证迈克尔逊干涉结构代替PO的可行性,利用硫酸铜水溶液样产生的热透镜效应[13-14]形成非线性光斑图像,通过对实验图像的分析,获得不同情况下迈克尔逊干涉仪相位物体(Michelson interferometer phase object,MIPO)的相位大小。
-
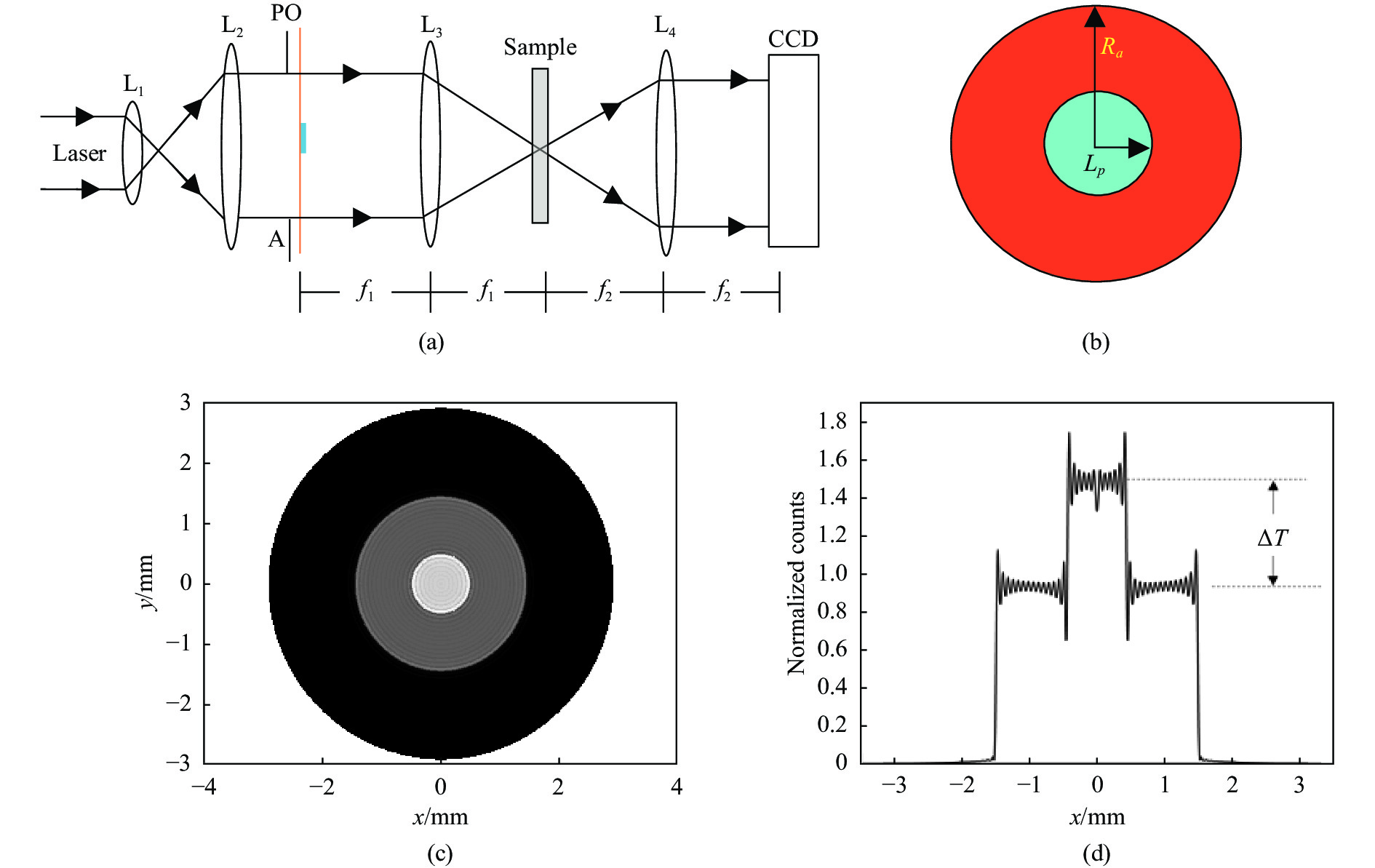
4f相位相干成像测量实际上是相衬原理的逆应用[6]:传统4f相位相干成像测量系统如图1所示,即在4f 系统的入射面上放置PO,而将非线性样品放置在傅里叶平面上,强激光作用下非线性样品产生非线性相移对入射光进行滤波,其结果是将PO 的相位延迟转化为透射光非线性图像上的振幅变化。图1(a)为4f相位相干成像系统示意图,一束激光经扩束准直系统L1、L2后,经过半径为Ra的小孔A后进入与小孔贴近的PO。传统的PO是通过在玻璃板上镀一定厚度的透明介质薄膜而形成的,其只改变透过光束的相位而不改变其振幅,如图1(b)所示,圆形PO处于玻璃板中心处,半径为Lp,薄膜的厚度为
${d_{po}}$ ,折射率为${n_d}$ ,其会对波长为$\lambda $ 的光波产生一个相位差${\varphi _L} = 2\pi ({n_d} - 1){d_{po}}/\lambda $ 。PO的位置处于透镜L3及L4组成的4f系统的入射面上,非线性样品Sample放置在4f系统的频谱面上,采集图像的CCD处于系统的出射面上。图1(c)为4f相位相干成像系统的光强分布数值模拟图,图1(d)为图1(c)的剖面图,归一化透射率变化∆T定义为PO区域的内部归一化光强与外部归一化光强的差值。需要特别指出的是,从相位延迟的公式可以看出,相位差的大小与入射激光的波长相关,会随着入射波长的变化而变化。而PO的相位变化对系统的测量灵敏度有着较大的影响,因此不同波长激光下的测量需要更换对应相位差的PO。显然现有及改进的PO不适用于4f相位相干成像系统在不同波长下材料非线性折射率的测量,需要设计一种相移能随波长变化的PO。文中利用迈克尔逊干涉结构实现了一种相移能随波长变化的PO (即MIPO)。改进后的实验装置如图2所示,M0为反射镜,BS为分束镜,反射镜M1和M2中分别放置小孔和圆形挡板。主光路结构与经典的4f相位相干成像系统相似,激光束经扩束准直后,经半径为Ra的小孔后,形成近平顶光束,经过反射镜M0反射后进入迈克尔逊干涉仪,并形成相移连续可调的两束光合成一束光,用来替代4f相位相干成像测量系统中的关键器件—相位物体。具体设计方案如图3所示,在迈克尔逊干涉仪的反射镜M1前放置一个半径为Lp 的小圆孔,小圆孔的透射率为t=1(r<Lp) ,t=0(r>Lp)。在反射镜M2前放置一个半径为Lp的圆形遮板,遮板的透射率为t=1(r>Lp)。圆孔和遮板形状互补,经过分光镜BS后两束光合并为一束,在合成光束的中间和边缘将形成一个相移,相当于形成了一个相位可调、大小为Lp的PO。在4f相位相干成像系统中合成光束的相位差与传统PO产生的相移效果相同。然而,通过迈克尔逊干涉装置可以灵活地改变相移的大小,便于在不同波长的激光作用下进行材料光学性质的测量,而且还可以保持系统测量的最佳灵敏度。实验中使用的半导体连续激光器产生波长为655 nm的光源,激光功率为5.0 mW,经过扩束准直系统及小孔A后,激光的光斑半径为4.5 mm,小圆孔的半径约为0.7 mm,样品前的凸透镜L3焦距为f1=300 mm,样品后凸透镜L4的焦距为f2=200 mm,CCD为荷兰Adimec-4 020 m,分辨率为2 048×2 048,像元尺寸为7.4 μm。实验中使用的样品放置在厚度为2 mm比色皿中的硫酸铜水溶液,线性透射率为60%,水溶液的热光系数
$\dfrac{{{\rm{d}}n}}{{{\rm{d}}T}}$ 取−1.0×10−4(K−1)[15]。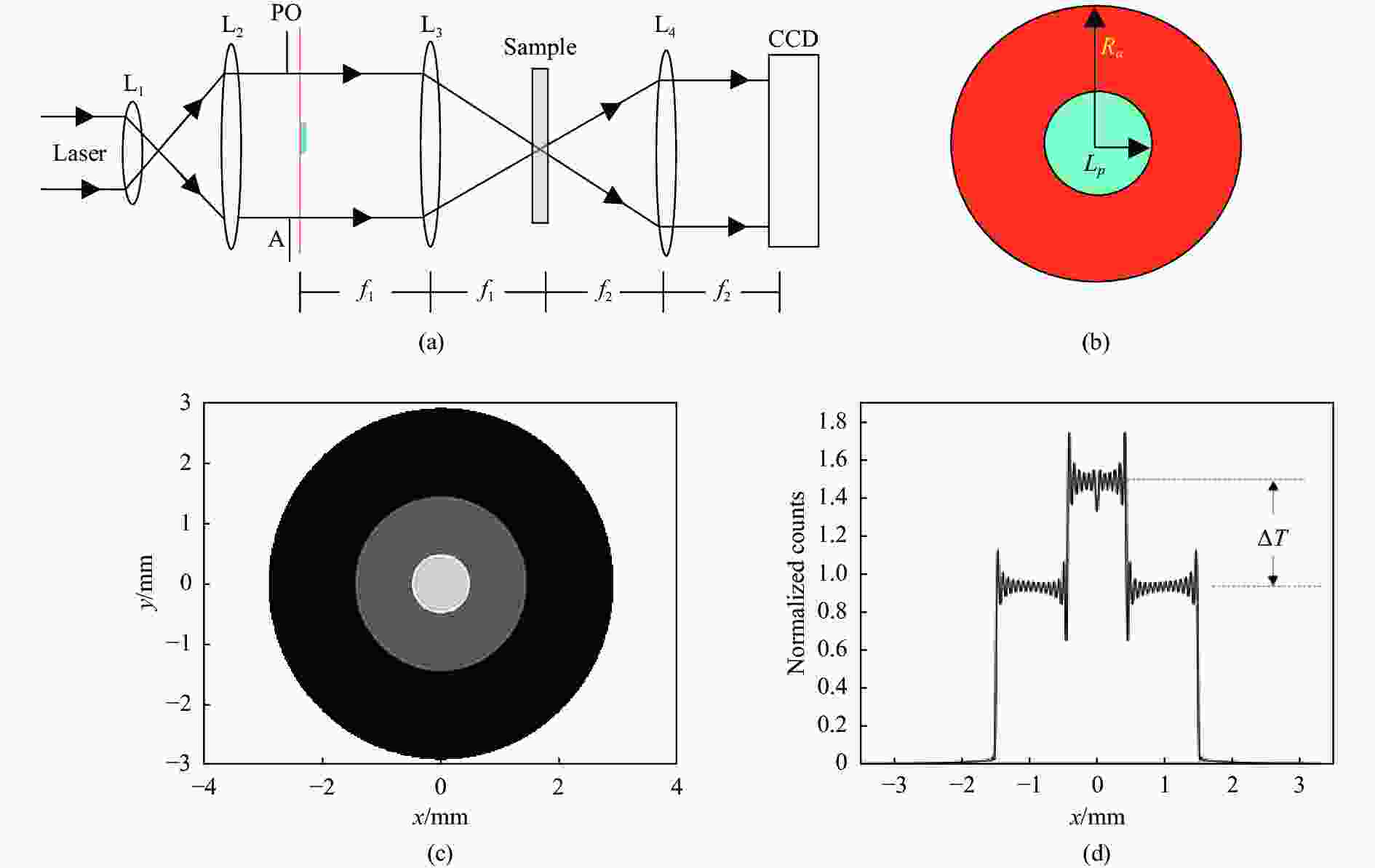
图 1 传统4f相干成像测量系统示意图及理论拟合结果图。(a) 4f相干成像系统实验装置图;(b) 传统相位物体示意图;(c) 4 f系统出射面上的光强空间分布图;(d) 图(c)的剖面图
Figure 1. Schematic of a conventional 4f coherent imaging measurement system and results of theoretical fitting. (a) Experimental setup diagram of the 4f coherent imaging system; (b) Schematic of the diaphragm with phase object; (c) Spatial distribution of intensity in the output plane of the 4f system; (d) Profile of Fig. (c)
-
设入射光是束腰半径为
$\omega $ 的线偏振高斯光束,横向光场分布可以写成:$$ E(x,y) = {E_0}{\text{ }}{\rm{exp}}\left(\frac{{ - r{{(x,y)}^2}}}{{{\omega ^2}}}\right) $$ (1) 式中:
$ {E_0} $ 为轴上峰值场强。半径为Ra的小孔A的透射函数为:
$$ {t_\alpha }(x,y) = circ(\sqrt {{x^2} + {y^2}} /{R_\alpha }) $$ (2) 圆形函数
${{circ}}(r)$ 定义为当$r(x,y)$ 小于1时为1,其余地方为0。通过小孔A后的光场分为:$$ {E_1}(x,y) = E(x,y){t_\alpha }(x,y) $$ (3) 经过小孔后的近平顶光束进入图3所示的迈克尔逊干涉仪中,合成的两束光相位差为
$ {\varphi _L} = 2\pi d/\lambda $ ,d为M1和M2两个反射镜之间产生的光程差。通过迈克尔逊干涉仪后光场的分布为:
图 2 含改进后的迈克尔逊干涉结构相位物体4f相干成像测量系统示意图
Figure 2. Schematic diagram of the 4f coherent imaging measurement system with an improved MIPO
$$ \begin{split} {E_2}(x,y) =& {E_1}(x,y){t_p} \\ {t_p}(x,y) =& \exp \left\{ {j{\varphi _L}circ\left[ {\sqrt {{x^2} + {y^2}} /{L_p}} \right]} \right\} \end{split} $$ (4) 经傅里叶变换后频谱处的光场分布为:
$$ s\left( {u,v} \right) = \frac{1}{{\lambda {f_1}}}FT\left[ {{E_2}\left( {x,y} \right)} \right] $$ (5) 式中:FT代表傅里叶变换。
当激光作用到样品上,在慢变振幅近似和薄溶液近似下,样品中的光强I和相位的变化
$ {\varphi _{NL}} $ 可以用下面的一对耦合方程来表示:$$ \begin{split} \frac{{{\text{d}}I}}{{{\text{d}}z'}} =& - {\alpha _0}I \\ \frac{{{\text{d}}{\varphi _{NL}}}}{{{\text{d}}z'}} =& \Delta n(I)k \end{split} $$ (6) 式中:
$ z' $ 为样品中的传播深度;${\alpha _0}$ 为线性吸收系数;$ \Delta n $ 为样品中非线性折射率的变化。通过对公式(6)的求解,可以得到经过溶液后的光场分布:$$ {S_L}\left( {u,v} \right) = S\left( {u,v} \right)\exp \left[ {j{\varphi _{NL}}\left( {u,v} \right)} \right] $$ (7) 最后经由傅里叶逆变换可得到CCD探测到的光强分布:
$$ {I_{im}}\left( {x,y} \right) = {\left| {U\left( {x,y} \right)} \right|^2} = {\left| {\lambda {f_2}F{T^{ - 1}}\left[ {{S_L}\left( {u,v} \right)} \right]} \right|^2} $$ (8) 式中:FT-1代表逆傅里叶变换。
利用公式(1)~(8)能够计算出4f系统出射面上的图像,将理论图像和实验图像进行拟合对比,可获得材料的光学非线性参数,或在已知实验条件及材料非线性折射率的情况下获得相位物体的相移大小。
-
在测量过程中,入射光的形状及PO大小与相移大小对系统灵敏度有非常大的影响,同时对于一个固定厚度的相位物体,入射光的波长将会对系统测量灵敏产生较大的影响。文中将给出入射激光波长对PO相移大小的影响,即设计MIPO的原因。给出了在近平顶光束下,PO的相移大小及其与小孔光阑半径的比值等因素对系统测量信号的影响,以及产生影响的主要原因。
利用公式(1)~(8)可以进行数值模拟。模拟中所用的主要参数包括,入射激光波长
$\lambda = 650 \;{\rm{nm}}$ ,小孔半径${R_a} = 4 \;{\rm{mm}}$ ,入射功率为$ 1.25 \times {10^9}\;{\rm{W}} $ ,系统中透镜L1及L2的焦距$ {f_{1}} = {f_2} = 400\;{\rm{mm}} $ ,材料非线性折射率$ {n_2} $ 分别为$ 0.7 \times {10^{ - 18}}\;{{\rm{m}}^2}/{\rm{W}} $ 和$ 3.2 \times {10^{ - 18}}\;{{\rm{m}}^2}/{\rm{W}} $ 。图4 (a)所示为PO的相移随入射激光波长变化的曲线图,其中PO的厚度为600 nm,由此可以看出,随着波长的增加,PO的相移
${\varphi _L}$ 变小。然而,从图4(b)可以看出,相位物体相移${\varphi _L}$ 对归一化透射率变化$\Delta T$ 影响非常大。在模拟中${L_p}/{R_a} = 0.1$ ,准直后的束腰半径$\omega = 4\; {\rm{mm}}$ ,等于小孔A的半径Ra,该取值也为实际应用较多的情况。从图中可以看到$ \Delta T $ 随${\varphi _L}$ 成周期性变化,在${\varphi _L} = 0.5\pi $ 附近,$\Delta T$ 达到了正的最大值,而在${\varphi _L} = 1.5\pi $ 的地方达到了负的最大值。在图4(b)中,当非线性折射率较小时,PO内的光场在经过样品后产生的非线性相移非常小,非线性透射率变化∆T在PO变化一个周期内呈近对称状态,在PO相移为$\pi $ 处,∆T接近0。然而当样品非线性折射率较大时,使PO内的光场在经过样品后也会产生一定的非线性相移,从而导致在PO相移为$\pi $ 处的∆T不为0。同时由于小于0的∆T最小为接近−1,而大于0的∆T理论上没有上限,当非线性相移较大时,大于0的∆T随PO变化的值要比小于0的∆T大,从而导致透射率随PO相移变化曲线不对称。结合图4(a),显然要使测量系统在不同波长的入射激光获得最佳灵敏度,则需要改变PO的光程差,使其在对应波长下的相移保持在$0.5\pi $ 附近,这正是文中设计可调相移PO的原因所在。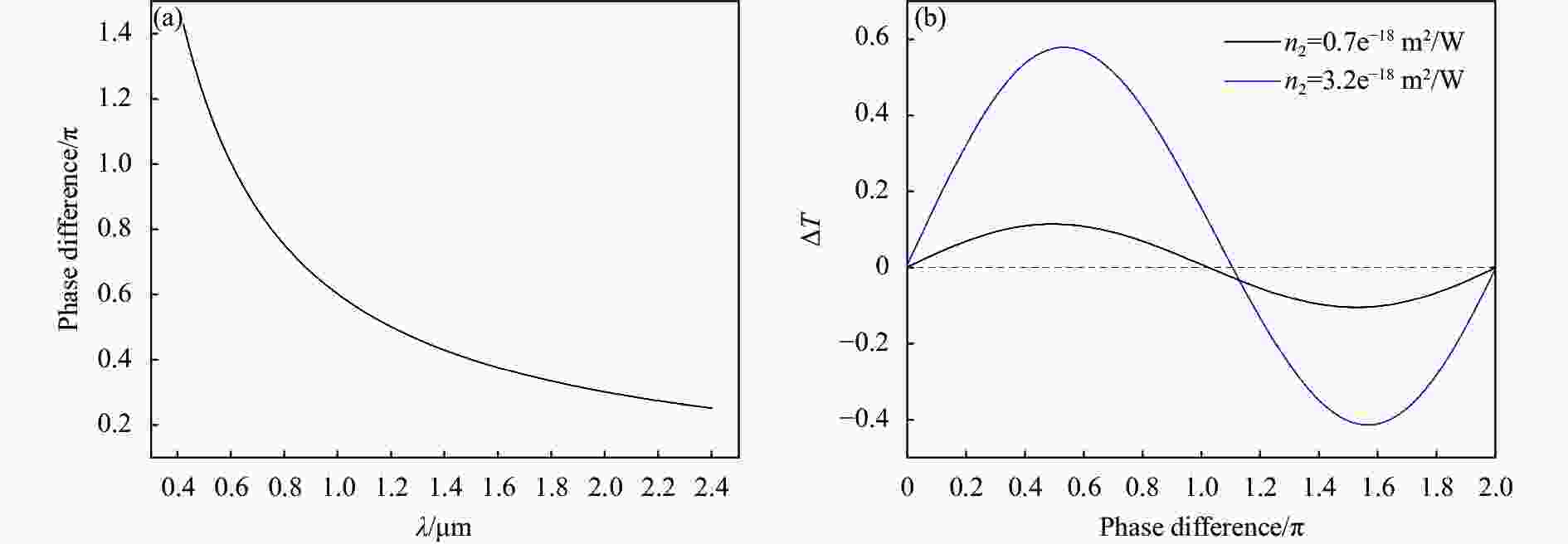
图 4 (a) PO相移随入射波长变化曲线;(b) 当Lp/Ra=0.1时,∆T随
${\varphi _L}$ 的变化曲线Figure 4. (a) Phase shift of PO as a function of laser wavelength; (b) ∆T as a function of
${\varphi _L}$ when Lp/Ra=0.1图5(a)给出了
${\varphi _L} = 0.5\pi $ 时,不同束腰半径的激光经过小孔A后,归一化透射率变化$\Delta T$ 随Lp/Ra的变化图,从图5 (a)中可以看到∆T随着Lp/Ra的减小而增大,但近平顶光束和平顶光束的结果存在一定的差别。虽然入射光强一样,但越接近平顶光束,灵敏度越高,这是因为相同入射能量的情况下,平顶光束在频谱面上的光强最强。事实上在使用近平顶光束时,只要增加入射光的能量即可,且所需增加的能量要比截取平顶光束所损失的能量小得多。从图5(a)可以看出,当入射激光光束的束腰半径为小孔A半径的2倍时,与平顶光束的结果相差较小,因此在实际实验中,不需要将激光扩束到远大于小孔A的半径。图5(b)给出了频谱面上的峰值光强I0随Lp/Ra的变化曲线,可以清楚地看出光强I0随Lp/Ra变化规律和图5(a)中的∆T随着Lp/Ra变化规律非常相似,说明Lp/Ra对测量结果的影响主要是Lp/Ra的大小改变了频谱面上的光强分布,在相移一定的情况下,测量信号的大小主要与频谱面上的峰值光强有关。从图4(b)和图5(a)中可以看出当入射光束为
$\omega = {R_a}$ 的近平顶光束时,Lp/Ra越小,${\varphi _L} = 0.5\pi $ 附近时,系统的灵敏度达到最大值。在实际测量中Lp/Ra的值正常取0.1~0.3,此时系统灵敏度与其最高灵敏度相差并不是很大。需要指出的是,不同形状的光束,PO的最优参数有一定的变化,因此需要能实时实现最优测量的PO、MIPO能很好地满足该要求。综上所述,入射激光的光束形状、入射波长、
Lp/Ra 的大小及相移 ${\varphi _L}$ 都会对系统的测量结果产生直接的影响,如果采用传统镀膜方法的PO,则只适用于某个形状的光束和某个激光波长的最优测量,不适用于任意形状光束及多波段入射光的光学非线性测量。文中采用MIPO,不仅可适用于不同波长下的测量,还可以方便调整Lp/Ra的大小,获得在近平顶光束下PO的最优参数,使得系统测量可以达到最优测量状态,因此文中的设计的MIPO对于4f相位相干成像技术的发展和改进具有一定的意义。
图 5 (a)
${\varphi _L} = 0.5\pi $ 时,不同形状的光束作用下,$\Delta T$ 随Lp/Ra的变化曲线;(b)${\varphi _L} = 0.5\pi $ 时,不同形状的光束作用下,频谱面上峰值光强I0随Lp/Ra的变化曲线Figure 5. (a) Variation curves of
$\Delta T$ with Lp/Ra under the action of beams of different shapes when${\varphi _L} = 0.5\pi $ ; (b) Variation curves of peak light intensity I0 on the spectral plane with Lp/Ra under the action of beams of different shapes when${\varphi _L} = 0.5\pi $ -
该实验采用近平顶光束及连续激光作为入射光作用在频谱面上的样品上,样品吸收一部分热量,产生热透镜效应,即材料的折射率发生改变,所产生的效果与三阶非线性折射率变化后所产生的结果基本保持一致。焦点附近的激光分布大多为类高斯分布的光束,因此溶液吸收部分激光能量的分布也为非均匀分布,从而使溶液局域的温度分布不均匀,引起溶液不同位置的折射率变化
$ \Delta n $ 也是不同的,折射率变化为[15]:$$ \Delta n(r)=\frac{{\rm{d}}n}{{\rm{d}}T}{\alpha }_{0}{\omega }^{2}I(r)/4K $$ (9) 式中:
$\dfrac{{{\rm{d}}n}}{{{\rm{d}}T}}$ 为热光系数;K为热传导率;$ \omega $ 为样品处激光光斑的束腰半径;I为样品中的激光光强。将公式(9)代入到公式(6)中,通过对实验结果的拟合,可获得材料的非线性折射系数或热光系数。当材料热光系数及光路实验条件已知的情况下,可获得迈克尔逊干涉仪相位物体的准确相位差的大小,最终可以应用于其他样品光学物理量的测量。按照图2及图3搭建光路。实验中对于迈克尔逊干涉仪中两镜子的要求为相互垂直,且迈克尔逊干涉仪两个镜面反射的光斑在成像面不能发生重合。调节步骤为:(1)调节迈克尔逊干涉仪前的反射镜M0,使入射光水平入射(借助小孔光阑),粗调使入射到分光镜BS的入射角为45°;(2)挡住定镜M1并移开动镜M2,调节干涉仪的底盘3个螺丝高度,使分光镜BS反射后的反射光水平;(3)挡住定镜M1,放置动镜M2,调节M2上的螺丝,使M2的反射光经BS反射后水平,前后移动M2,观察反射光是否存在移动。如移动,调节反射镜M0,最终使入射到BS上的入射角度为45°,此时反射光线完全进入小孔A;(4)挡住动镜M2,仔细调节定镜M1上的螺丝,使M1表面与入射光垂直,反射光线也应完全进入小孔A。(5)经过前两步调节后,两个反射最亮的激光点在BS上重合,M1和M2垂直。放置–短焦距的透镜,则在光屏上形成圆形干涉条纹,如在眼睛不同位置观察时,没有条纹的涌出或陷入即为M1和M2严格垂直。缓慢调节旋钮,移动动镜M2,使迈克尔逊干涉仪两臂处在等光程的位置。
将样品放置在4f系统焦点位置,缓慢调节迈克尔逊干涉仪两臂的距离,改变光程差,观察CCD探测到的光强变化,直到观察到圆孔位置呈现最大光强或最小光强,记录此图像为非线性图像,将样品放置于远离焦平面位置,记录此图像为线性图像。将实验条件代入拟合程序中,通过对实验图像进行数值模拟取值就可以获得此时MIPO的相位大小,从而用于其他材料的热光系数等光学非线性参数的测量。
实验结果如图6所示,图6(a)为线性光斑图像,将样品放置在远离焦平面的位置,热透镜效应非常弱。图6(b)为样品放置在焦平面位置,经过缓慢调节迈克尔逊干涉仪的动镜,而得到的非线性光斑图像,通过数值模拟可以获得MIPO的相位大小为2kπ-0.43π,实验中在确定了两臂等光程后,微调动镜距离,光斑中心经过两个亮斑后,进行了实验测量,因此k=3。图6(c) 样品位置和图6(b)中一样,继续缓慢调节迈克尔逊干涉仪的动镜,就可以得到图6(c)中的非线性光斑图像,通过数值模拟可以获得此时MIPO的相位大小为2kπ+0.46π (k=3)。需要指出的是,在获得图6(b)和图6(c)中的光斑图像时,样品的位置没有发生改变,只调节了迈克尔逊干涉仪的动镜位置,可以观察到圆孔中光强分布发生了明显相反的变化,这是因为MIPO的相位大小发生了变化,如图4(b)所示。该系统中,小孔和圆形挡板的接缝处会导致远场出现衍射条纹,然而当光路系统严格符合4f成像条件时,该接缝处的衍射条纹会比较小,如图6所示。但在该实验中截取近平顶光束时,由于小孔A的位置没有严格处于系统的入射面位置,因此在成像面上,光斑边缘会产生衍射条纹。但这些衍射条纹对材料非线性折射率的测量影响比较小,因为非线性折射率的测量主要取决于PO内光强与PO外光强的差值。
数值模拟的结果如图7所示,其中虚线为实验结果曲线,实线为通过线性光斑图像拟合的数值拟合曲线, 可以看出两种情况下实验曲线和理论曲线吻合得较好。该实验说明通过迈克尔逊干涉仪作为相位大小可调的PO是可行的。
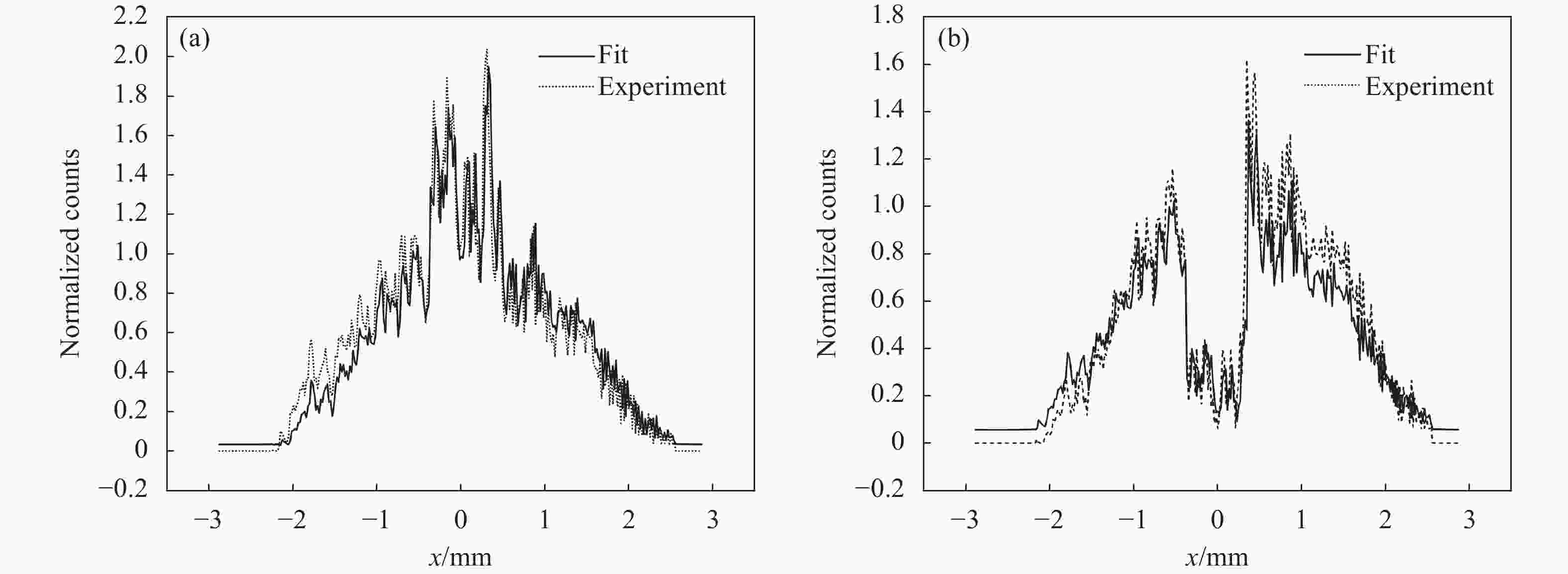
图 7 利用两种相移的相位物体所测得的硫酸铜水溶液的光学非线性图像的剖面拟合图。(a) 相移为2kπ−0.43π时的非线性光斑图像拟合图;(b) 相移为2kπ+0.46π时的非线性光斑图像拟合图
Figure 7. Profile fitting of optical nonlinear image of copper sulfate aqueous solution measured using two phase objects with phase different. (a) Fitted plot of the nonlinear spot image with the phase difference of 2kπ−0.43π; (b) Fitted plot of the nonlinear spot image with the phase difference of 2kπ+0.46π
-
文中对4f相位相干成像测量技术中的PO进行了改进,弥补了普通PO相位大小不可调节的缺点。理论上详细分析了不同形状光束下PO的半径和相移的大小对4f相位相干成像系统灵敏度的影响。发现系统的灵敏度与入射光束的波长及形状有关,且随着PO半径与光阑半径的比值Lp/Ra的减小而增大。当比值Lp/Ra一定时,系统灵敏度最大值的位置在相移约为0.5π处,具体值与光束形状相关。将迈克尔逊干涉结构应用到相位相干成像测量中,利用迈克尔逊干涉仪实现了PO的相位大小连续可调,且可灵活改变比值Lp/Ra的大小,使系统的测量灵敏度达到最优状态,适用于不同形状光束及激光波长下样品非线性折射率及热光系数等物理量的测量。对改进后的PO进行了测量,实验结果与理论分析吻合,为进一步优化4f相位相干成像测量技术提供了可行性的方案。
Application of Michelson interferometer in phase coherent imaging measurement system
-
摘要: 传统4f相位相干成像测量技术中,利用相位物体使测量材料产生的相位变化转换为可直接观察的振幅变化,实现材料光学非线性折射率的测量。然而相位物体的厚度是固定不变的,相位延迟会随激光波长的改变而改变,测量中需要更换合适的相位物体。理论分析了不同激光波长对相位物体相移大小的影响,详细讨论了不同形状光束下相位物体的半径和相移的大小对4f相位相干成像系统灵敏度的影响。利用了迈克尔逊干涉仪中两束光的相位延迟替代传统相位物体的功能,实现了一种相位可调的相位物体。因为迈克尔逊干涉仪两束光的相位延迟连续可调,使得在不同形状光束及不同波长激光下的测量灵敏度达到最优。该方法进一步完善了4f相位相干成像测量技术,不仅解决了传统相位物体的不足,而且提高了系统测量的精度。Abstract: In the conventional 4f phase coherent imaging measurement technology, phase objects were used to convert the phase change generated by the measured material into a directly observable amplitude change to achieve the measurement of the nonlinear refractive index of the material. However, the thickness of the phase object was fixed, and the phase delay changes with the laser wavelength, and a suitable phase object needs to be replaced in the measurement. The influence of different laser wavelength on the phase shift of the phase object was theoretically analyzed, and the influence of the radius of the phase object and the phase shift on the sensitivity of the 4f phase coherent imaging system was discussed in detail. A phase-adjustable phase object was realized by using the phase delay of two beams in Michelson interferometer instead of the conventional phase object. Because the phase delay of the two beams of Michelson interferometer was continuously adjustable, it makes the sensitivity of measurement at different shapes and different wavelengths of laser optimal. This method further improves the 4f phase coherent imaging measurement technology, not only solves the deficiencies of the conventional phase object, but also improves the accuracy of the measurement.
-
Key words:
- Michelson interferometer /
- phase object /
- laser /
- refractive index /
- near top-hat beams
-
图 1 传统4f相干成像测量系统示意图及理论拟合结果图。(a) 4f相干成像系统实验装置图;(b) 传统相位物体示意图;(c) 4 f系统出射面上的光强空间分布图;(d) 图(c)的剖面图
Figure 1. Schematic of a conventional 4f coherent imaging measurement system and results of theoretical fitting. (a) Experimental setup diagram of the 4f coherent imaging system; (b) Schematic of the diaphragm with phase object; (c) Spatial distribution of intensity in the output plane of the 4f system; (d) Profile of Fig. (c)
图 5 (a)
${\varphi _L} = 0.5\pi $ 时,不同形状的光束作用下,$\Delta T$ 随Lp/Ra的变化曲线;(b)${\varphi _L} = 0.5\pi $ 时,不同形状的光束作用下,频谱面上峰值光强I0随Lp/Ra的变化曲线Figure 5. (a) Variation curves of
$\Delta T$ with Lp/Ra under the action of beams of different shapes when${\varphi _L} = 0.5\pi $ ; (b) Variation curves of peak light intensity I0 on the spectral plane with Lp/Ra under the action of beams of different shapes when${\varphi _L} = 0.5\pi $ 图 7 利用两种相移的相位物体所测得的硫酸铜水溶液的光学非线性图像的剖面拟合图。(a) 相移为2kπ−0.43π时的非线性光斑图像拟合图;(b) 相移为2kπ+0.46π时的非线性光斑图像拟合图
Figure 7. Profile fitting of optical nonlinear image of copper sulfate aqueous solution measured using two phase objects with phase different. (a) Fitted plot of the nonlinear spot image with the phase difference of 2kπ−0.43π; (b) Fitted plot of the nonlinear spot image with the phase difference of 2kπ+0.46π
-
[1] Zong Haotian, Zhang Yunhai, Wang Famin, et al. Large field of view line-scanning confocal holographic microscopy [J]. Optics and Precision Engineering, 2021, 29(1): 1-9. (in Chinese) doi: 10.37188/OPE.20212901.0001 [2] Cao Binghua, Zhang Yumeng, Fan Mengbao, et al. Research progress of terahertz super-resolution imaging [J]. Chinese Optics, 2022, 15(3): 405-417. doi: 10.37188/CO.2021-0198 [3] Fan Yao, Chen Qian, Sun Jiasong, et al. Review of the development of differential phase contrast microscopy [J]. Infrared and Laser Engineering, 2019, 48(6): 0603014. (in Chinese) doi: 10.3788/IRLA201948.0603014 [4] Koppell S, Kasevich M. Information transfer as a framework for optimized phase imaging [J]. Optica, 2021, 8(4): 493-501. doi: 10.1364/OPTICA.412129 [5] Lv Ze, Fang You, Feng Tiao, et al. The principle, performance characterization and research progress of optical limiting of nonlinear materials [J]. Chinese Optics, 2022, 15(4): 625-639. (in Chinese) doi: 10.37188/CO.2021-0195 [6] Boudebs G, Cherukulappurath S. Nonlinear optical measure-ments using a 4f coherent imaging system with phase objects [J]. Phys Rev A, 2004, 69(5): 053813. doi: 10.1103/PhysRevA.69.053813 [7] Zeng Xi, Qi Pengfei, Li Mengdi, et al. Nonlinear optical properties of human cornea measured by spectral domain Z-scan method [J]. Optics Express, 2021, 29(23): 38870-38878. doi: 10.1364/OE.441731 [8] Zong Jie, Wu Xingzhi, Xin Jian, et al. Ultrafast third-order nonlinear optical properties of self-assembled PCPDTPhSO3 Na/C-70-(EDA)(8) periodically overlapping film [J]. Journal of Modern Optics, 2022, 69(1): 41-46. doi: 10.1080/09500340.2021.1994048 [9] Yang Yong, Yang Junyi, Li Zhongguo, et al. Sensitive measurement of optical nonlinearity using absorptive phase object [J]. Appl Phys B, 2017, 123(248): 1-5. [10] Li Yunbo, Song Yinglin, Wang Yu. Improvement of the diaphragm with phase object in the 4 f coherent imaging system [J]. Infrared and Laser Engineering, 2008, 37(5): 830-833. (in Chinese) [11] Li Dangjuan, Wang Jiachao, Chen Yang, et al. Design of high power long-coke deep-Gaussian beam shaping system [J]. Optics and Precision Engineering, 2020, 28(10): 2129-2137. (in Chinese) doi: 10.37188/OPE.20202810.2129 [12] Serna, Lin H T, Alonso-Ramos C, et al. Engineering third-order optical nonlinearities in hybrid chalcogenide-on-silicon platform [J]. Optics Letters, 2019, 44(20): 5009-5012. doi: 10.1364/OL.44.005009 [13] Ghanem A, Zidan M D, EL-Daher M S, et al. Thermal lens investigation of the Acid Blue 29 using dual beam z-scan technique [J]. Optik, 2022, 252: 168499. doi: 10.1016/j.ijleo.2021.168499 [14] Li Long, Zhang Qiujuan, Zhang Chunlin, et al. Transient thermal effect of Nd: YAG ceramics with pulsed laser diode bar side-pumped [J]. Infrared and Laser Engineering, 2021, 50(11): 20200495. (in Chinese) doi: 10.3788/IRLA20200495 [15] Brochard P, Grolier-Mazza V, Cabanel R. Thermal nonlinear refraction in dye solutions: A study of the transient regime [J]. J Opt Soc Am B, 1997, 14(2): 405-414. doi: 10.1364/JOSAB.14.000405 -






 下载:
下载: