-
光学成像是人类感知和获取信息的最基本手段之一,在生物医学、天文观测、智能制造、城市智能感知和国防安全等领域发挥重要作用。以光作为信息载体的光学成像,其实质是一种构建光学图像信息在(可感知的)“像空间”与(不可感知的)“物空间”之间一一对应关系。从微观角度而言,携带物质信息的光场作为一种随机过程,可以通过各阶联合矩(即光场的各阶关联函数)来描述。而光学成像则通过光场的各阶(一阶、二阶、更高阶)关联函数建立起光场图像信息在“像空间”与“物空间”之间的一一对应关系,从而提取物体的光学图像信息。
以几何光学成像和波动光学成像为代表的传统光学成像,其本质上均是对包含有透镜、相位板、全息板等光学器件的光学系统进行设计,使得物体图像信息包含在光场的一阶关联函数(光场自关联/光强、光场互关联/互强度)中。20世纪中叶,Hanbury Brown和Twiss为了解决传统Michelson星体干涉仪等被大气扰动的难题,提出并完成了HBT强度干涉成像实验[1-2],在人类历史上第一次实现了从光场的二阶关联函数中提取物体图像信息的光学成像。20世纪八九十年代,随着量子纠缠光源技术的不断发展,基于纠缠光子对的鬼成像开启了从光场的二阶互关联函数中提取物体图像信息的光学成像新时代[3-4]。2002年,美国的Bennink等人首次利用非量子纠缠光源演示了“鬼成像”实验[5]。随后,中国科学院上海光学精密机械研究所(下面简称中科院上海光机所)韩申生课题组[6]和意大利A. Gatti等人[7]分别从经典的统计光学和量子相干性理论出发,理论上完成了经典热光的“鬼成像”理论分析。至此,鬼成像摆脱了量子纠缠光源的局限,其从光场的二阶关联函数获取物体图像信息的物理本质逐渐被学术界厘清。
相比传统光学成像技术,鬼成像利用光场的时空涨落将物体的高维光场信息调制或编码到低维探测空间,不仅实现了光场各个维度信息的互相转换和压缩感知,而且具有超像素分辨[8-9]、超衍射极限分辨[10-13]的潜力,在雷达[14-16]、三维成像[17]、光谱成像[18-21]、偏振成像[22-27]、X光成像[28-31]、电子成像[32]、原子成像[33]、中子成像[34-35]、荧光显微[36-37]以及声学探测[38]等应用领域大放异彩。然而,随着鬼成像在技术应用及系统优化方面的进一步深入发展,对鬼成像理论提出了新的挑战和要求。鬼成像与传统成像的物理层面上的不同是什么?如何定量分析鬼成像的成像性能?鬼成像系统优化的理论判据和理论极限是什么?文中抛砖引玉,从鬼成像的物理本质、图像信息获取理论研究及理论分辨率研究三方面介绍中科院上海光机所所鬼成像近期的一些理论工作,并对今后的鬼成像的理论研究进行了探讨与展望。
-
根据随机过程理论,数学上可以通过光场的样本函数及其概率完备地描述作为随机过程的光场。一般来说,光场可看作一个统计平稳过程,其统计性质(例如一阶概率密度函数)不依赖于域原点的选择。由概率论中的特征函数理论可知,其概率密度函数可通过相应的联合矩来表征。因此,可以通过光场各阶联合矩(即光场的各阶关联函数)来描述光场的随机过程。
对于物空间和像空间之间直接“点到点一一映射”的传统光学成像,由于探测时间远大于光场涨落的特征时间,因此,探测的光场强度为平均光场强度,即:
$$ \begin{array}{c}I\left(\boldsymbol{r}\right)={\left\langle{I\left(\boldsymbol{r},t\right)}\right\rangle}_{t}={\left\langle{{E}^{*}\left(\boldsymbol{r},t\right)E\left(\boldsymbol{r},t\right)}\right\rangle}_{t} \end{array} $$ (1) 此时,物体图像信息
$ I\left(\boldsymbol{r}\right) $ 是通过光场$ E\left(\boldsymbol{r},t\right) $ 的一阶自关联函数表征的。此外,对于全息成像,全息图记录的光强分布为:$$ \begin{split} I\left(\boldsymbol{r}\right)=&{\left\langle{{E}_{o}^{*}\left(\boldsymbol{r},t\right){E}_{o}\left(\boldsymbol{r},t\right)}\right\rangle}_{t}+{\left\langle{{E}_{r}^{*}\left(\boldsymbol{r},t\right){E}_{r}\left(\boldsymbol{r},t\right)}\right\rangle}_{t}+\\ &{\left\langle{{E}_{o}^{*}\left(\boldsymbol{r},t\right){E}_{r}\left(\boldsymbol{r},t\right)}\right\rangle}_{t}+{\left\langle{{E}_{r}^{*}\left(\boldsymbol{r},t\right){E}_{o}\left(\boldsymbol{r},t\right)}\right\rangle}_{t} \end{split} $$ (2) 式中:
$ {E}_{o}\left(\boldsymbol{r},t\right) $ 为物光;$ {E}_{r}\left(\boldsymbol{r},t\right) $ 为参考光,再通过与参考光相同或共轭的光照明全息图再现物体的图像信息。此时,物体图像信息是通过物光$ {E}_{o}\left(\boldsymbol{r},t\right) $ 或参考光$ {E}_{r}\left(\boldsymbol{r},t\right) $ 的一阶关联函数(互强度,公式(2)的第三项、第四项)来获取。因此,从统计光学的角度来看,传统光学成像均是通过设计光学系统将物体图像信息包含在光场的一阶关联函数(自关联/强度、互关联/互强度)中。1956年,Hanbury Brown与Twiss提出了著名的HBT强度干涉成像实验[1],首次实现了利用物体光场的二阶自关联函数(强度自关联)获取物体图像信息。如图1所示,来自遥远星体的光被半透半反镜分为两路,分别用光电倍增管接收记录随时间起伏的光强,即有:
$$\begin{split} &\qquad \quad{I}_{1}\left({\boldsymbol{r}}_{1},t\right)={E}_{1}^{*}\left({\boldsymbol{r}}_{1},t\right){E}_{1}\left({\boldsymbol{r}}_{1},t\right) \\ &{I}_{2}\left({\boldsymbol{r}}_{2},t+\Delta t\right)={E}_{2}^{*}\left({\boldsymbol{r}}_{2},t+\Delta t\right){E}_{2}\left({\boldsymbol{r}}_{2},t+\Delta t\right) \end{split} $$ (3) $ \Delta t $ 为两路探测的时间差,两者的强度涨落关联函数为:$$ \begin{split}\left\langle{\Delta {I}_{1}\left({\boldsymbol{r}}_{1},t\right)\Delta {I}_{2}\left({\boldsymbol{r}}_{2},t+\Delta t\right)}\right\rangle={\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2};\Delta t\right)\right|}^{2} \end{split} $$ (4) 式中:
$ \Delta {I}_{i}={I}_{i}-\left\langle{{I}_{i}}\right\rangle $ ($ i=\mathrm{1,2} $ )为光场强度的涨落,$$ \begin{split}{{\varGamma }}_{E}\left({\boldsymbol{r}}_{1},{\boldsymbol{r}}_{2};\Delta t\right)=\left\langle{{E}_{1}^{*}\left({\boldsymbol{r}}_{1},t\right){E}_{2}\left({\boldsymbol{r}}_{2},t+\Delta t\right)}\right\rangle \end{split} $$ (5) 为光场的互强度。公式(4)表明,通过计算时间域光强涨落的自关联函数可以知道探测处的光场互强度的模。由范希特-泽尼克(Van Cittert-Zernike)定理可知,探测光场互强度分布反比于非相干光源的角直径,从而可以利用公式(4)计算星体角直径。该方法不仅被广泛应用于天文学,而且用于在高能物理领域开展基本粒子的量子关联特性研究等[39-40]。
1995年,Pittman和Abouraddy等人利用参量下转换产生的动量纠缠光源,通过对经过物体的“信号光”与没有经过物体的“参考光”进行符合计数计算两路光场的二阶互关联函数(强度互关联),实现了“鬼衍射”[3]和“鬼成像”[4]。早期,人们将这种成像能力归因于纠缠光源的量子纠缠特性,认为量子纠缠光源必不可少。2002年,美国的Bennink等人首次利用具有互关联的经典光源在相同的光路结构中演示了“鬼成像”实验[5]。随后,中科院上海光机所韩申生课题组[6]和意大利A. Gatti等人[7]分别从经典的统计光学和量子相干性理论出发,理论上完成了经典热光的“鬼成像”理论分析。
图2是经典的双臂鬼成像示意图,双臂光强涨落的关联函数为:
$$\begin{split} \left\langle{\Delta {I}_{t}\left({\boldsymbol{r}}_{t}\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle\propto &{\left|\displaystyle\iint {\rm d}{\boldsymbol{r}}_{0}{\rm d}{\boldsymbol{r}}_{0}^{\text{'}}{h}_{t}^{*}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{0}\right){h}_{r}\left({\boldsymbol{r}}_{r},{\boldsymbol{r}}_{0}^{\text{'}}\right)\right.}\cdot\\ &{\left.\left\langle{{E}_{0}^{*}\left({\boldsymbol{r}}_{0}\right){E}_{0}\left({\boldsymbol{r}}_{0}^{\text{'}}\right)}\right\rangle\right|}^{2} \end{split}$$ (6) 式中:
$ {h}_{t}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{0}\right) $ 为包含物体图像信息的物光路的点扩散函数;$ {h}_{r}\left({\boldsymbol{r}}_{r},{\boldsymbol{r}}_{0}^{\text{'}}\right) $ 为参考光路的点扩散函数;$ {E}_{0}\left({\boldsymbol{r}}_{0}^{\text{'}}\right) $ 为光源处的光场。因此,通过设计点扩散函数,可利用双臂光强涨落的关联函数$ \left\langle{\Delta {I}_{t}\left({\boldsymbol{r}}_{t}\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle $ 提取物体的图像信息。总的来说,在光场相干性理论的视角下,传统成像通过光学系统设计将物体图像信息包含在光场的一阶关联函数中,而鬼成像则是通过光学系统设计将物体图像信息包含在光场的二阶关联函数中。考虑到光场的时空涨落特性,根据光场二阶关联函数的统计系综域的不同,可以将鬼成像分为基于时域系综统计的鬼成像和基于空域系综统计的鬼成像。
-
基于时域系综统计的鬼成像主要利用光场强度在时间域的涨落,通过物光和参考光在时间域光强涨落的关联函数获取物体的图像信息。一种典型的基于时域系综统计的鬼成像示意图如图3所示,光源发出的光经过分束器分为两路,不经过物体的参考光自由传播
$ z $ 距离后的光场强度的时空起伏被一个具有空间分辨的探测器探测,物光路先自由传播$ {z}_{1} $ 后经过物体再传播$ {z}_{2} $ ,由一个没有空间分辨率的点探测器记录经过物体的光强信息。对于热光场,有$ \left\langle{{E}_{0}^{*}\left({\boldsymbol{r}}_{0}\right){E}_{0}\left({\boldsymbol{r}}_{0}^{\text{'}}\right)}\right\rangle\propto $ $ \delta \left({\boldsymbol{r}}_{0}-{\boldsymbol{r}}_{0}^{\text{'}}\right) $ ,因此,代入公式(6),可得两路在时域系综统计的强度关联函数为:$$ \begin{split} {\left\langle{\Delta {I}_{t}\left({\boldsymbol{r}}_{t},t\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{r},t\right)}\right\rangle}_{t}\propto {\left|\int {\rm d}{\boldsymbol{r}}_{0}{h}_{t}^{*}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{0}\right){h}_{r}\left({\boldsymbol{r}}_{r},{\boldsymbol{r}}_{0}^{\text{'}}\right)\right|}^{2} \end{split} $$ (7) 式中:
$ {\left\langle{\cdots }\right\rangle}_{t} $ 表示对时间域$ t $ 做系综统计。 -
当
$ z={z}_{1} $ 时,物光路由一个没有空间分辨的桶探测器收集所有透过物体的总光强,即$ {I}_{t}\left({\boldsymbol{r}}_{t},t\right)={I}_{t}\left(t\right) $ ,此时:$$ \begin{split} {\left\langle{\Delta {I}_{t}\left(t\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{r},t\right)}\right\rangle}_{t}\propto {\left|T\left({\boldsymbol{r}}_{r}\right)\right|}^{2} \end{split} $$ (8) 式中:
$ T\left(\cdots \right) $ 为物体的空间分布函数。公式(8)表明,在此光路结构下,可以通过两路光强关联在时间域的系综统计获得物体的空间分布信息。 -
当
$ z={z}_{1}+{z}_{2} $ 时,物光路由一个没有空间分辨的点探测器获取经过物体的衍射光强[6],有:$$ \begin{split} {\left\langle{\Delta {I}_{t}\left({\boldsymbol{r}}_{t},t\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{r},t\right)}\right\rangle}_{t}\propto {\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{2} \end{split} $$ (9) 式中:
$ \mathfrak{F} $ 表示傅里叶变换;$ T $ 为物体的空间复分布函数;$ \lambda $ 为波长。上述公式表明,可以通过两路强度在时间域上涨落的关联函数获得物体的Fraunhofer衍射像,即物体空间复分布函数的傅里叶变换的模平方。再结合相位恢复算法[42],可获得物体的空间复分布信息。基于时域系综统计的鬼成像需要探测光场在时间域的强度涨落,因此要求探测器的时间分辨率高于光场的相干时间。对于自然光和物体自发辐射等热光场,其相干时间往往在飞秒量级,难以实时探测。为了实现基于时域系综统计的鬼成像,研究人员提出光场强度涨落可控的赝热光来模拟热光场,从而大大降低鬼成像对探测器的要求。赝热光通常利用旋转的毛玻璃[43]、空间光调制器[44-45]、数字微透镜阵列(DMD)[46]等随机调制激光的相位或幅度,产生光强随时间涨落的光场。20世纪60年代,Arecchi等人证明赝热光能够完全模拟真实热光的统计特性[47]。为了研究探测时间对鬼成像的影响并对探测时间给出一个合理的估计,刘红林等人通过理论和实验分析了赝热光源在近场和远场衍射的交叉谱特性[48]。相比真热光极短的相干时间,赝热光相干时间取决于调制器件的刷新特征时间,便于控制,大大推动了鬼成像在主动照明成像领域中的应用。而在光源无法控制的被动光学成像中,则可以通过光谱滤波的方式将光场的相干时间增大到探测器的时间分辨率之内。中国科学院物理研究所的吴令安课题组利用极窄的滤波、高时间分辨率和高灵敏度的光强探测手段,于2005年实现了真热光鬼成像[49],并在2014年完成了太阳光鬼成像演示[50]。然而,极窄带滤波片、高时间分辨率和高探测灵敏度探测器的制备成本高,而且滤波导致能量利用率低,大大限制了其在实际场景中的应用。
-
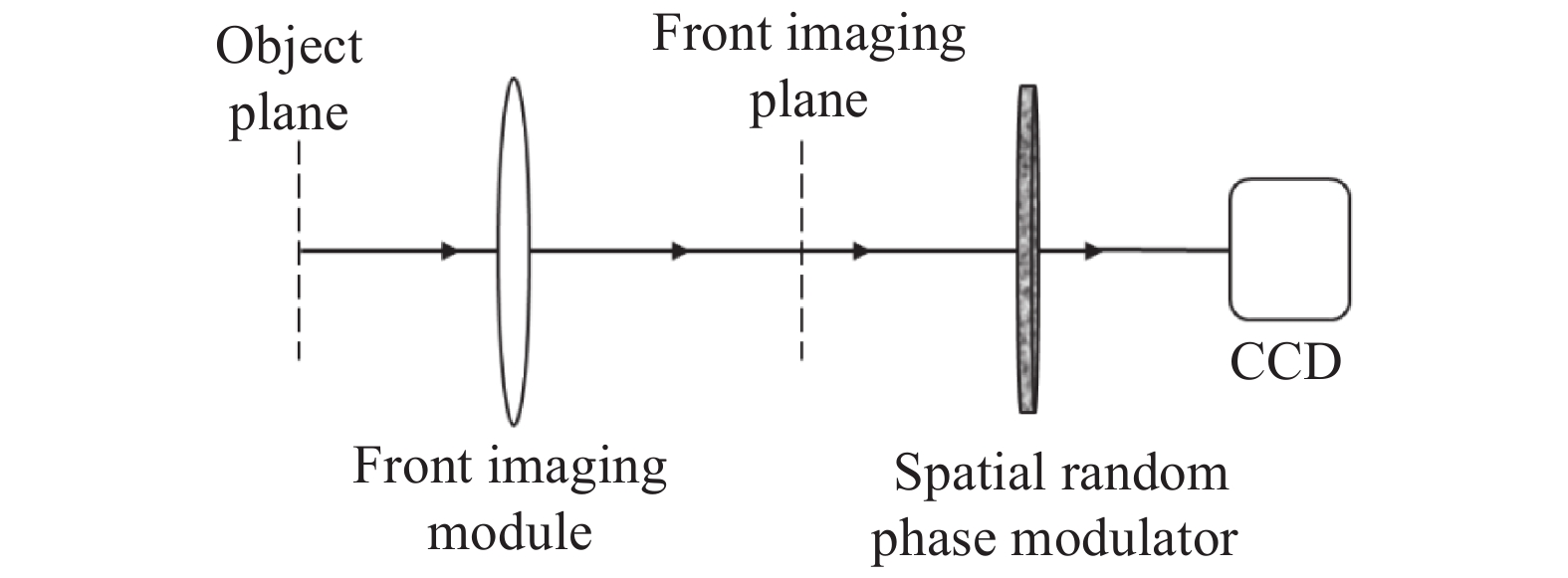
为了克服基于时域系综统计的鬼成像方案在一些实际应用中所受到的原理性限制,研究人员又发展了基于空域系综统计的鬼成像。它利用光场的遍历特性,通过物光和参考光在空间域光强涨落的关联函数获取物体的图像信息。研究人员从近场衍射产生散斑场的理论和实验现象[51-52]受到启发,提出热光场经过空间随机相位调制可衍射产生光强在空间随机分布的光场,利用该光场强度在空间域的涨落,通过计算没有物体时的光场强度涨落与有物体时的光场强度涨落在空间域下的系综关联函数获取物体的信息,进而提出了一种实用化的被动鬼成像方案——鬼成像相机[18]。作为一种典型的基于空域系综统计的鬼成像,鬼成像相机系统示意图如图4所示,前置成像系统将远处的待成像物体成像到前置成像面上,再经过一个空间随机相位调制板,所产生的空间涨落光强被面阵探测器CCD探测记录下来。
由理论推导可得,没有物体时的光场强度涨落与有物体时的光场强度涨落在空间域下的系综关联函数为[18]:
$$\begin{split} {\left\langle{\Delta {I}_{t}\left({\boldsymbol{r}}_{t}\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{t};{\boldsymbol{r}}_{0},{k}\right)}\right\rangle}_{{\boldsymbol{r}}_{t}}\propto T\left({\boldsymbol{r}}_{0},{k}\right) \end{split} $$ (10) 式中:
$ {\left\langle{\cdots }\right\rangle}_{{\boldsymbol{r}}_{t}} $ 表示对空间域$ {\boldsymbol{r}}_{t} $ 做系综统计;${k}=1/\lambda$ 为波数;$T\left({\boldsymbol{r}}_{0},{k}\right)$ 为物体的空间-光谱分布函数;$ {I}_{t}\left({\boldsymbol{r}}_{t}\right) $ 为探测面的光强空间分布;${I}_{r}\left({\boldsymbol{r}}_{t};{\boldsymbol{r}}_{0},{k}\right)$ 为成像系统物面$\left({\boldsymbol{r}}_{0},{k}\right)$ 在探测面上对应的空间光强点扩散函数。公式(10)表明,通过计算有无物体时的光场强度涨落在空间域系综统计下的关联函数可以获得物体的空间-光谱信息。不同于基于时域系综统计的鬼成像在时间域上光场调控和多次测量,基于空域系综统计的鬼成像相机只需在传统被动成像光路上引入光场调制模块,并在对物体成像时只需单次测量探测面在空间域的光强分布,使得单次曝光获取动态场景的空间-光谱信息成为可能。近些年来,这类利用光场空间域强度随机涨落的计算成像方案也获得国内外研究人员越来越多的关注和研究[53-58]。此外,在傅里叶变换衍射鬼成像方面,也提出通过探测面上多个点探测器的空间复用探测,将时域系综和空域系综相结合来实现傅里叶谱重构[59]。
-
作为一种光学成像体制,鬼成像系统的图像信息获取能力的定量描述其不可或缺的组成部分。早期的相关研究着重于描述成像的对比度、分辨率与光源面积、相干尺寸等的关系[60-62],其内容更偏重于定性的分析。之后,研究人员通过关联运算重构图像的信噪比[63-64]或衬噪比[65]来描述图像信息的获取能力。不同于面向关联运算重构结果的分析研究,针对结合信号处理理论而使用优化算法来进行图像重构的鬼成像机制,对其进行不依赖于具体重构结果的图像信息获取能力的定量描述工作很少。国防科技大学的刘吉英[66]将鬼成像系统中的光场特性转化为测量矩阵的特性,分析了“近似消息传递”(approximate message passing, AMP)算法应用于鬼成像中的重构条件,为误差界分析提供了可能。Jialali、袁鑫[67-68]等人使用统计学中的“集中性度量”(concentration measure)分析了模型结构较为特殊的“单次曝光压缩成像”(snapshot compressive imaging)系统中的图像重构误差限。下面分别从概率统计理论和Cramér-Rao Bound(CRB)理论出发,以实空间鬼成像和傅里叶衍射鬼成像为例,理论上给出关联运算的统计重构误差及与鬼成像重构算法无关的统计重构误差下界,并通过Fisher信息理论[69-70]研究鬼成像中光场涨落大小与所含物体图像信息量之间的理论关系。
-
在鬼成像的理论中,物体的图像信息是通过参考臂光强信号和物臂光强信号的涨落关联得到的。然而,在实际的探测采样过程中,无法得到无穷次的采样数据来计算上面的系综平均,只能对有限次采样的数据进行处理。在这种情况下,通过有限次数据的关联运算得到的结果与系综平均的理论值之间会有偏差。通过概率统计的方法能够给出一个统一的思路探索鬼成像系统通过关联运算重构结果的误差特性与采样次数、探测信噪比等参量的定量关系。
目前,基于关联计算来重构图像的方法,在采样次数有限的条件下,实际的计算公式为:
$$ \begin{array}{c}\widehat{x}=\dfrac{1}{N}\displaystyle\sum _{i=1}^{N}\left({I}_{t}^{\left(i\right)}-\overline{{I}_{t}}\right)\left({I}_{r}^{\left(i\right)}\left({\boldsymbol{r}}_{r}\right)-\overline{{I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right) \end{array} $$ (11) 式中:
$ {\left\{{I}_{t}^{\left(i\right)}\right\}}_{i=1}^{N} $ 、$ {\left\{{I}_{r}^{\left(i\right)}\right\}}_{i=1}^{N} $ 分别是$ N $ 次采样得到的物臂和参考臂的探测光强;$\overline{{I}_{t}}=\dfrac{1}{N}\displaystyle\sum _{i=1}^{N}{I}_{t}^{\left(i\right)}$ 、$\overline{{I}_{r}}=\dfrac{1}{N}\displaystyle\sum _{i=1}^{N}{I}_{r}^{\left(i\right)}$ 分别是物臂和参考臂的探测光强的均值。当采样次数足够大时,可近似有$ \overline{{I}_{t}}\approx \left\langle{{I}_{t}}\right\rangle $ 、$ \overline{{I}_{r}}\approx \left\langle{{I}_{r}}\right\rangle $ ,因而有:$$ \begin{split} \widehat{x}\approx \frac{1}{N}\sum _{i=1}^{N}\left({I}_{t}^{\left(i\right)}-\left\langle{{I}_{t}}\right\rangle\right)\left({I}_{r}^{\left(i\right)}\left({\boldsymbol{r}}_{r}\right)-\left\langle{{I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle\right)\triangleq \frac{1}{N}\sum _{i=1}^{N}{x}^{\left(i\right)} \\[-10pt] \end{split} $$ (12) 上式表明,实际中关联运算重构的结果
$ \widehat{x} $ 可以近似看做是一系列独立同分布随机变量$ {\left\{{x}^{\left(i\right)}\right\}}_{i=1}^{N} $ 的平均值。因而,$\widehat{x}$ 也可以看作一个随机变量,其期望为:$$ \begin{split} \mathbb{E}\left\{\widehat{x}\right\}=\mathbb{E}\left\{x\right\} \end{split} $$ (13) 其方差为:
$$ \begin{split} \mathbb{V}\left\{\widehat{x}\right\}=\frac{1}{N}\sum _{i=1}^{N}\mathbb{V}\left\{x\right\} \end{split} $$ (14) 在此基础上,通过定量分析
$ \widehat{x} $ 的期望和方差可以给出关联重构结果$ \widehat{x} $ 的误差特性。下面分别以典型的实空间鬼成像和傅里叶衍射鬼成像为例,分析两者的关联运算重构误差特性。 -
在实空间鬼成像系统中,每次物臂的探测是一个将所有通过物体的光强度收集起来的过程,即:
$$ \begin{split} {I}_{t}=\alpha \int {\rm d}{\boldsymbol{r}}_{0}{I}_{r}\left({\boldsymbol{r}}_{0}\right)T\left({\boldsymbol{r}}_{0}\right)+n \end{split} $$ (15) 式中:
$ \mathrm{\alpha } $ 为物臂照射到物体表面的光强分布与参考臂探测光强分布$ {I}_{r}\left({\boldsymbol{r}}_{0}\right) $ 的比值;$ n $ 表示加性的外界噪声,这里将其简单建模为一般的零均值高斯随机噪声。假设:
(1)参考臂的光场和物臂照明物体的光场都是均匀的散斑场,即:
$$\begin{split} \left\langle{{I}_{r}\left({\boldsymbol{r}}_{0}\right)}\right\rangle\approx \left\langle{{I}_{r}}\right\rangle \end{split} $$ (16) (2)物臂的外界噪声与参考臂光强是独立的,即:
$$\begin{split} \left\langle{\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)\Delta n}\right\rangle=\left\langle{\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle\left\langle{\Delta n}\right\rangle=0 \end{split} $$ (17) (3)物面光场的相干尺度小于物体变化的特征尺寸,因此,
$ x $ 的期望为:$$ \begin{split} \mathbb{E}\left\{x\right\}=\mathbb{E}\left\{\Delta {I}_{t}\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)\right\}\approx \alpha {\left\langle{{I}_{r}}\right\rangle}^{2}{S}_{c}T\left({\boldsymbol{r}}_{r}\right) \end{split} $$ (18) 式中:
$ {S}_{c} $ 为物面照射光场的相干面积。而$ x $ 的方差为:$$ \begin{split} \mathbb{V}\left\{x\right\}&=\mathbb{E}\left\{{x}^{2}\right\}-{\mathbb{E}\left\{x\right\}}^{2}\approx \\ &{\mathrm{\alpha }}^{2}{\left\langle{{I}_{r}}\right\rangle}^{4}\left[{S}_{c}\int {\rm d}{\boldsymbol{r}}_{0}{T}^{2}\left({\boldsymbol{r}}_{0}\right)+7{S}_{c}^{2}{T}^{2}\left({\boldsymbol{r}}_{r}\right)+\frac{{\sigma }_{n}^{2}}{{\alpha }^{2}{\left\langle{{I}_{r}}\right\rangle}^{2}}\right] \\[-15pt] \end{split} $$ (19) 将公式(18)和(19)分别代入公式(13)和(14),并归一化后,可得实空间鬼成像关联运算重构结果
$ \widehat{x} $ 的误差特性为:$$ \begin{split} \mathbb{E}\left\{\widehat{x}\right\}\propto T\left({\boldsymbol{r}}_{r}\right) \end{split} $$ (20) $$ \begin{split} \mathbb{V}\left\{\widehat{x}\right\}\propto &\frac{1}{N}\left[\frac{1}{{S}_{c}}\int {\rm d}{\boldsymbol{r}}_{0}{T}^{2}\left({\boldsymbol{r}}_{0}\right)+7{T}^{2}\left({\boldsymbol{r}}_{r}\right)+\frac{{\sigma }_{n}^{2}}{{\alpha }^{2}{S}_{c}^{2}{\left\langle{{I}_{r}}\right\rangle}^{2}}\right] =\\ &\frac{1}{N}\left[\frac{1}{{S}_{c}}\int {\rm d}{\boldsymbol{r}}_{0}{T}^{2}\left({\boldsymbol{r}}_{0}\right)+7{T}^{2}\left({\boldsymbol{r}}_{r}\right)+\frac{{\varsigma }^{2}}{{\mathrm{S}\mathrm{N}\mathrm{R}}^{2}}\right] \\[-18pt] \end{split} $$ (21) 式中:
$\mathrm{S}\mathrm{N}\mathrm{R}=\left\langle{{I}_{t}}\right\rangle/{\sigma }_{n}=\alpha \left\langle{{I}_{r}}\right\rangle{S}_{T}\overline{T}/{\sigma }_{n}$ ,$\overline{T}=\dfrac{1}{{S}_{T}}\displaystyle\int {\rm d}{\boldsymbol{r}}_{0}T\left({\boldsymbol{r}}_{0}\right)$ 为物体的空间平均强度透射/反射率,$ {S}_{T} $ 为成像物体面积;$\varsigma =\overline{T}{S}_{T}/{S}_{c}$ 。公式(20)表明,实空间鬼成像关联运算重构结果$ \widehat{x} $ 是物体图像信息的无偏估计。而从公式(21)可以看出,关联运算重构结果$ \widehat{x} $ 的重构误差与物体的总体强度(公式(21)第一项)、物体图像分布(公式(21)第二项)、桶探测时的外界噪声情况(公式(21)第三项)有关。选取一个圆斑(如图5所示)作为成像目标,仿真生成了100000次采样的参考光路光场强度分布和桶探测信号。图6展示了无噪声(
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ )和信噪比为$\sqrt{\text{10}} $ ($ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{\text{10}}$ )两种情况下仿真成像结果与理论推导的结果对比。可以看出,两种信噪比下的仿真数据的方差分布均与理论方差分布相符,即重构方差分布呈现为在本底误差项(公式(21)第一项和第三项)叠加一个与物体图像分布相关的误差项(公式(21)第二项)。当信噪比不高时,可以看出本底误差项远高于与物体图像分布相关的误差项,此时重构方差主要取决于本底误差项。
图 6 不同物光路探测信噪比下,实空间鬼成像关联结果的仿真方差分布与理论比较。(a)信噪比
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ;(b)信噪比$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{\text{10}}$ Figure 6. Comparison of variance distribution of simulated results in real-space ghost imaging with theoretical results at different SNRs in object light path. (a)
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ; (b)$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{\text{10}}$ -
在傅里叶衍射鬼成像中,考虑到物臂信号的零均值高斯随机噪声时,即
$$ \begin{split} {I}_{t}\left({\boldsymbol{r}}_{t}\right)={I}_{t}^{\left(0\right)}\left({\boldsymbol{r}}_{t}\right)+n \end{split} $$ (22) 此时,可得:
$$ \begin{split} \mathbb{E}\left\{x\right\}&=\left\langle{\Delta \left[{I}_{t}^{\left(0\right)}\left({\boldsymbol{r}}_{t}\right)+n\right]\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle=\\&\left\langle{\Delta {I}_{t}^{\left(0\right)}\left({\boldsymbol{r}}_{t}\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle+\left\langle{\Delta n\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle \end{split} $$ (23) 考虑到物臂的噪声与参考臂光场相互独立,且假定参考臂和物臂的光场服从联合的圆复高斯分布,可得:
$$ \begin{split} \mathbb{E}\left\{x\right\}&=\left\langle{\Delta {I}_{t}^{\left(0\right)}\left({\boldsymbol{r}}_{t}\right)\Delta {I}_{r}\left({\boldsymbol{r}}_{r}\right)}\right\rangle=\\ &\left\langle{{I}_{t}^{\left(0\right)}}\right\rangle\left\langle{{I}_{r}}\right\rangle{\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{2}\\ &\propto {\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{2} \end{split} $$ (24) 此式与公式(9)相一致。其中,
$$ \begin{split} {\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{2}=\frac{{z}^{2}}{{z}_{2}^{2}{S}_{T}{S}_{s}}{\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{2} \end{split} $$ (25) 式中:
$ {S}_{s} $ 为光源面面积。而$ x $ 的方差为:$$ \begin{split} \mathbb{V}\left\{x\right\}&\approx {\left\langle{{I}_{t}^{\left(0\right)}}\right\rangle}^{2}{\left\langle{{I}_{r}}\right\rangle}^{2}\cdot\\&\left[1+3{\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{4}+4{\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{2}+\frac{{\sigma }_{n}^{2}}{{\left\langle{{I}_{t}^{\left(0\right)}}\right\rangle}^{2}}\right] \end{split} $$ (26) 分别将公式(24)和(26)代入公式(13)和(14)中,并归一化后,可得傅里叶衍射鬼成像关联运算重构结果
$ \widehat{x} $ 的误差特性为:$$\begin{split} \mathbb{E}\left\{\widehat{x}\right\}\propto {\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{2} \end{split} $$ (27) $$ \begin{split} \mathbb{V}\left\{\widehat{x}\right\}&\propto \frac{1}{N}\left[1+3{\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{4}+4{\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{2}+\frac{{\sigma }_{n}^{2}}{{\left\langle{{I}_{t}^{\left(0\right)}}\right\rangle}^{2}}\right]=\\ &\frac{1}{N}\left[1+3{\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{4}+4{\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{2}+\frac{1}{{\mathrm{S}\mathrm{N}\mathrm{R}}^{2}}\right]\\[-15pt] \end{split} $$ (28) 从公式(27)可以看出,傅里叶衍射鬼成像关联运算重构结果
$ \widehat{x} $ 也是物体傅里叶变换强度谱图像信息的无偏估计。而公式(28)表明,不同空间频率的傅里叶幅度谱分量的重构误差也分别与常数本底项(公式(28)第一项)、幅度谱的四次方和平方项(公式(28)第二、三项)、物光路点探测时的外界噪声均匀本底项(公式(28)第四项)有关。选取一个纯振幅的数字‘5’(如图7(a)所示)作为仿真物体,它的衍射谱图样如图7(b)所示。图8展示了无噪声(
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ )和信噪比为$ \sqrt{\text{10}} $ ($ \mathrm{S}\mathrm{N}\mathrm{R}= \sqrt{\text{10}}$ )两种情况下仿真成像结果与理论推导的结果对比。可以看出,两种信噪比下的仿真数据的方差分布均与理论的方差分布相符。
图 7 傅里叶衍射鬼成像的仿真目标(a)及其傅里叶衍射谱图像(b)
Figure 7. Simulated target in Fourier diffraction ghost imaging (a) and its Fourier spectrum (b)

图 8 不同物光路探测信噪比下,傅里叶衍射鬼成像关联结果的仿真方差分布与理论比较。 (a)信噪比
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ;(b)信噪比$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{10}$ Figure 8. Comparison of variance distribution of simulated results in Fourier diffraction ghost imaging with theoretical results at different SNRs. (a)
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ;(b)$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{\text{10}}$ -
2.1节分析了鬼成像关联算法的重构误差的统计特性。然而,结合压缩感知重构算法进行鬼成像图像恢复[71-73]比关联运算具有更好的重构质量,也是目前常用的鬼成像重构算法。因此,与重构算法无关的图像重构理论精度极限亟待研究。
一般来说,Cramér-Rao Bound理论是分析图像重构结果统计误差的理论极限的一种重要手段。通过CRB进行重构误差下界分析时,一般需要给出相应的观测模型及其观测量的概率密度分布函数。对于鬼成像系统来说,就是需要给出物臂和参考臂光强的联合概率密度分布函数。然而,目前针对光场二阶关联函数的理论研究还不充分,难以直接从双臂光路的视角给出相应的联合概率密度分布函数。因此,当前只能通过各种方法将二阶关联函数的估计问题转换为一阶关联函数(即光强)的估计问题[74],即变为如下求解问题模型
$$ \begin{split} \boldsymbol{y}=\boldsymbol{\varPhi} \boldsymbol{x} \end{split} $$ (29) 式中:
$ \boldsymbol{x}\in {\mathbb{R}}^{M} $ 是待恢复的图像信号;$ \boldsymbol{\varPhi }\in {\mathbb{R}}^{N\times M} $ 是采样矩阵;$ \boldsymbol{y}\in {\mathbb{R}}^{N} $ 是探测信号。下面分别以实空间鬼成像和傅里叶衍射鬼成像为例,先将其转化为公式(29)形式的观测模型,再通过分析对应观测量的概率密度分布函数,最终使用CRB理论分析其相应的重构误差的统计下界。 -
在实空间鬼成像中,将公式(15)离散化,在采样N次下,物臂探测光强可表示为:
$$ \begin{split} \boldsymbol{y}={\mathrm{\beta }}_{0}\boldsymbol{A}\boldsymbol{x}+\boldsymbol{n} \end{split} $$ (30) 式中:
${ \mathrm {\; \beta}}_{0}=\mathrm{\alpha }{\kappa }_{0}$ ,$ {\kappa }_{0} $ 是量纲为长度平方的常量,考虑到物体离散化的最小尺寸为相干面积$ {S}_{c} $ ,则有$ {\kappa }_{0}={S}_{c} $ 。探测噪声$ \boldsymbol{n} \sim \mathcal{N}\left(0,{\sigma }_{n}^{2}\right) $ ,测量矩阵$ \boldsymbol{A}=\left[{\boldsymbol{a}}_{1},{\boldsymbol{a}}_{2},\cdots ,{\boldsymbol{a}}_{j},\cdots ,{\boldsymbol{a}}_{M}\right] $ ,且$$ \begin{split} &{\boldsymbol{a}}_{j}={\left[{I}_{r}\left({\boldsymbol{r}}_{0,j},{t}_{1}\right),{I}_{r}\left({\boldsymbol{r}}_{0,j},{t}_{2}\right),\cdots ,{I}_{r}\left({\boldsymbol{r}}_{0,j},{t}_{i}\right),\cdots ,{I}_{r}\left({\boldsymbol{r}}_{0,j},{t}_{N}\right)\right]}^{\mathrm{T}} \\ & \boldsymbol{x}={\left[ T\left({\boldsymbol{r}}_{\mathrm{0,1}}\right),T\left({\boldsymbol{r}}_{\mathrm{0,2}}\right),\cdots ,T\left({\boldsymbol{r}}_{0,j}\right),\cdots ,T\left({\boldsymbol{r}}_{0,M}\right)\right]}^{\mathrm{T}},j=1,\cdots,M \\& \boldsymbol{y}={\left[{I}_{t}\left({t}_{1}\right),{I}_{t}\left({t}_{2}\right),\cdots ,{I}_{t}\left({t}_{i}\right),\cdots ,{I}_{t}\left({t}_{N}\right)\right]}^{\mathrm{T}},i=1,\cdots ,N \\[-8pt] \end{split} $$ (31) 式中:
$ {I}_{r}\left({\boldsymbol{r}}_{0,j},{t}_{i}\right) $ 表示第$ i $ 次参考臂$ {\boldsymbol{r}}_{0,j} $ 坐标的光强;$ T\left({\boldsymbol{r}}_{0,j}\right) $ 表示按照参考臂坐标离散化的物体图像$ \boldsymbol{x} $ 在$ {\boldsymbol{r}}_{0,j} $ 坐标的图像信息;$ {I}_{t}\left({t}_{i}\right) $ 表示第$ i $ 次物臂探测光强。由于各次探测之间相互独立且满足同样的分布
$ \boldsymbol{n}\sim \mathcal{N}\left(0,{\sigma }_{n}^{2}\right) $ ,$ \boldsymbol{y} $ 和$ \boldsymbol{A} $ 在待估计参量$ \boldsymbol{x} $ 下的联合概率密度分布为:$$ \begin{split} &p\left(\boldsymbol{y},\boldsymbol{A};\boldsymbol{x}\right)=p\left(\boldsymbol{y}|\boldsymbol{A};\boldsymbol{x}\right)p\left(\boldsymbol{A}\right)=\\ &\frac{1}{{\left(\sqrt{2\pi }{\sigma }_{n}\right)}^{N}}{\rm exp}\left\{-\frac{1}{2{\sigma }_{n}^{2}}{\left(\boldsymbol{y}-{\mathrm{\beta }}_{0}\boldsymbol{A}\boldsymbol{x}\right)}^{\mathrm{T}}\left(\boldsymbol{y}-{\mathrm{\beta }}_{0}\boldsymbol{A}\boldsymbol{x}\right)\right\}p\left(\boldsymbol{A}\right) \end{split} $$ (32) 对上式取对数,可得:
$$\begin{split} &\mathrm{ln}p\left(\boldsymbol{y},\boldsymbol{A};\boldsymbol{x}\right)=\\&-N\mathrm{ln}\sqrt{2\pi }{\sigma }_{n}-\frac{1}{2{\sigma }_{n}^{2}}{\left(\boldsymbol{y}-{\mathrm{\beta }}_{0}\boldsymbol{A}\boldsymbol{x}\right)}^{\mathrm{T}}\left(\boldsymbol{y}-{\mathrm{\beta }}_{0}\boldsymbol{A}\boldsymbol{x}\right)+\mathrm{ln}p\left(\boldsymbol{A}\right) \end{split} $$ (33) 此时,
$ \mathrm{ln}p\left(\boldsymbol{y},\boldsymbol{A};\boldsymbol{x}\right) $ 对$ \boldsymbol{x} $ 的一阶偏导数分量为:$$ \begin{split} \frac{\partial \mathrm{ln}p\left(\boldsymbol{y},\boldsymbol{A};\boldsymbol{x}\right)}{\partial {\boldsymbol{x}}_{i}}=\frac{{\mathrm{\beta }}_{0}}{{\sigma }_{n}^{2}}{\left[{\boldsymbol{A}}^{\mathrm{T}}\left(\boldsymbol{y}-{\mathrm{\beta }}_{0}\boldsymbol{A}\boldsymbol{x}\right)\right]}_{i} \end{split} $$ (34) $ \mathrm{ln}p\left(\boldsymbol{y},\boldsymbol{A};\boldsymbol{x}\right) $ 对$ \boldsymbol{x} $ 的二阶偏导数分量为:$$\begin{split} \frac{\partial \mathrm{ln}p\left(\boldsymbol{y},\boldsymbol{A};\boldsymbol{x}\right)}{\partial {\boldsymbol{x}}_{i}\partial {\boldsymbol{x}}_{j}}=-\frac{{\mathrm{\beta }}_{0}^{2}}{{\sigma }_{n}^{2}}{\left[{\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{A}\right]}_{ij} \end{split} $$ (35) 因此,关于
$ \boldsymbol{x} $ 的Fisher信息矩阵为:$$ \begin{split} {\left[{I}\left(\boldsymbol{x}\right)\right]}_{ij}={\mathbb{E}}_{\boldsymbol{y},\boldsymbol{A}}\left\{-\frac{\partial \mathrm{ln}p\left(\boldsymbol{y},\boldsymbol{A};\boldsymbol{x}\right)}{\partial {\boldsymbol{x}}_{i}\partial {\boldsymbol{x}}_{j}}\right\}=\frac{{\mathrm{\beta }}_{0}^{2}}{{\sigma }_{n}^{2}}{\mathbb{E}}_{\boldsymbol{A}}{\left[{\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{A}\right]}_{ij} \end{split} $$ (36) 假定参考光整体均匀且不同位置处的光场相互独立,则有:
$$ \begin{split} {\mathbb{E}}_{\boldsymbol{A}}{\left[{\boldsymbol{A}}^{\mathrm{T}}\boldsymbol{A}\right]}_{ij}\approx N{\left\langle{{I}_{r}}\right\rangle}^{2}\left(1+{\delta }_{ij}\right) \end{split} $$ (37) $$ \begin{split} {\left[{I}\left(\boldsymbol{x}\right)\right]}_{ij}\approx \frac{{\mathrm{\beta }}_{0}^{2}{N\left\langle{{I}_{r}}\right\rangle}^{2}}{{\sigma }_{n}^{2}}\left(1+{\delta }_{ij}\right) \end{split} $$ (38) 因此,对
$ {\boldsymbol{x}}_{i} $ 估计的CRB为:$$ \begin{split} \mathbb{V}\left\{{\boldsymbol{x}}_{i}\right\}={\left[{{I}}^{-1}\left(\boldsymbol{x}\right)\right]}_{ii}\approx \frac{{\sigma }_{n}^{2}}{{\mathrm{\beta }}_{0}^{2}{N\left\langle{{I}_{r}}\right\rangle}^{2}}\frac{M}{M+1} \end{split}$$ (39) 当重构图像
$ \boldsymbol{x} $ 的像素数$ M $ 较大时,则$ \dfrac{M}{M+1}\approx 1 $ ,因此$$ \begin{split} \mathbb{V}\left\{{\boldsymbol{x}}_{i}\right\}\approx \frac{{\sigma }_{n}^{2}}{{\mathrm{\beta }}_{0}^{2}{N\left\langle{{I}_{r}}\right\rangle}^{2}}={\left(\frac{{S}_{T}}{{S}_{c}}\right)}^{2}\frac{{\overline{T}}^{2}}{N\cdot {\mathrm{S}\mathrm{N}\mathrm{R}}^{2}}=\frac{{\varsigma }^{2}}{N\cdot {\mathrm{S}\mathrm{N}\mathrm{R}}^{2}} \end{split} $$ (40) -
对于傅里叶衍射鬼成像,通过参考臂的光场
$ {E}_{r}\left({\boldsymbol{r}}_{r}\right) $ 逆传播到物臂探测面,对应的光场强度为:$$ \begin{split} {I}_{t}\left({\boldsymbol{r}}_{t}\right)=&{E}_{t}^{*}\left({\boldsymbol{r}}_{t}\right){E}_{t}\left({\boldsymbol{r}}_{t}\right)=\\&\frac{\alpha }{{\lambda }^{4}{z}_{2}^{4}}\iint {\rm d}{\boldsymbol{r}}_{r}{\rm d}{\boldsymbol{r}}_{r}^{\text{'}}{E}_{r}^{*}\left({\boldsymbol{r}}_{r}\right){E}_{r}\left({\boldsymbol{r}}_{r}^{\text{'}}\right)\times\\&\mathrm{e}\mathrm{x}\mathrm{p}\left\{\frac{j\pi }{\lambda {z}_{2}}\left({\boldsymbol{r}}_{r}^{2}-{{\boldsymbol{r}}_{r}^{\text{'}}}^{2}\right)\right\}{{\mathfrak{F}}^{\mathfrak{*}}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}^{\text{'}}}{\lambda {z}_{2}}} \end{split} $$ (41) 然而,对于参考臂来说,可探测的仅为光场强度,即:
$$\begin{split} {I}_{r}\left({\boldsymbol{r}}_{r}\right)={E}_{r}^{*}\left({\boldsymbol{r}}_{r}\right){E}_{r}\left({\boldsymbol{r}}_{r}^{\text{'}}\right){\kappa }_{1}\delta \left({\boldsymbol{r}}_{r}-{\boldsymbol{r}}_{r}^{\text{'}}\right) \end{split} $$ (42) 式中:
$ {\kappa }_{1} $ 是量纲为长度平方的常量。将公式(42)代入公式(41),可得一个“虚拟”的物臂光场强度为:$$ \begin{split} {I}_{t}^{\text{'}}\left({\boldsymbol{r}}_{t}\right)=\frac{\alpha {\kappa }_{1}}{{\lambda }^{4}{z}_{2}^{4}}\int {\rm d}{\boldsymbol{r}}_{r}{I}_{r}\left({\boldsymbol{r}}_{r}\right){\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{2} \end{split} $$ (43) 且当常数
$ {\kappa }_{1}={\lambda }^{2}{z}^{2}/{S}_{s}={S}_{c} $ 时,有:$$\begin{split} \mathbb{E}\left\{{I}_{t}^{\text{'}}\left({\boldsymbol{r}}_{t}\right)\right\}=E\left\{{I}_{t}\left({\boldsymbol{r}}_{t}\right)\right\} \end{split} $$ (44) 即该“虚拟”物臂信号与真实物臂信号有相同的系综平均值。因此,
$$ \begin{split} {I}_{t}\left({\boldsymbol{r}}_{t}\right)&={I}_{t}^{\text{'}}\left({\boldsymbol{r}}_{t}\right)+\mathrm{\Delta }=\frac{\alpha {\kappa }_{1}}{{\lambda }^{4}{z}_{2}^{4}}\int {\rm d}{\boldsymbol{r}}_{r}{I}_{r}\left({\boldsymbol{r}}_{r}\right){\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{2}+\mathrm{\Delta }=\\&\frac{\alpha {S}_{T}}{{\lambda }^{2}{z}_{2}^{2}}\int {\rm d}{\boldsymbol{r}}_{r}{I}_{r}\left({\boldsymbol{r}}_{r}\right){\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r}\right)\right|}^{2}+\Delta \end{split} $$ (45) 其中,
$$ \begin{split} \Delta ={I}_{t}\left({\boldsymbol{r}}_{t}\right)-{I}_{t}^{\text{'}}\left({\boldsymbol{r}}_{t}\right) \end{split} $$ (46) 假定
$ \mathfrak{F}\left\{T\right\} $ 的相位随机分布,根据中心极限定理,可得$ \mathrm{\Delta } $ 服从高斯分布,其期望为:$$ \begin{split} \mathbb{E}\left\{\mathrm{\Delta }\right\}=0 \end{split} $$ (47) 方差为:
$$ \begin{split} \mathbb{V}\left\{\mathrm{\Delta }\right\}&=\mathbb{E}\left\{{\mathrm{\Delta }}^{2}\right\}-{\mathbb{E}\left\{\mathrm{\Delta }\right\}}^{2}=\\ &\mathbb{E}\left\{{I}_{t}^{2}\left({\boldsymbol{r}}_{t}\right)\right\}+\mathbb{E}\left\{{{I}_{t}^{\text{'}}}^{2}\left({\boldsymbol{r}}_{t}\right)\right\}-2\mathbb{E}\left\{{I}_{t}\left({\boldsymbol{r}}_{t}\right){I}_{t}^{\text{'}}\left({\boldsymbol{r}}_{t}\right)\right\}=\\ &{\left\langle{{I}_{t}}\right\rangle}^{2}\left\{1-{\kappa }_{1}\frac{\int {\rm d}{\boldsymbol{r}}_{r}{\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{4}}{{\left[\int {\rm d}{\boldsymbol{r}}_{r}{\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{2}\right]}^{2}}\right\} \end{split} $$ (48) 忽略量纲时,近似有:
$$ \begin{split} \int {\rm d}{\boldsymbol{r}}_{r}{\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{4}\ll {\left[\int {\rm d}{\boldsymbol{r}}_{r}{\left|{\mathfrak{F}\left\{T\right\}}_{\frac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}}}\right|}^{2}\right]}^{2} \end{split} $$ (49) 因此,公式(48)有:
$$\begin{split} \mathbb{V}\left\{\mathrm{\Delta }\right\}\approx {\left\langle{{I}_{t}}\right\rangle}^{2} \end{split} $$ (50) 同时,考虑到探测噪声
$\boldsymbol{n}\sim \mathcal{N}\left(0,{\sigma }_{n}^{2}\right)$ 时,对公式(45)离散化,可得:$$ \boldsymbol{y}=\beta \boldsymbol{Ax}+{\boldsymbol{\varepsilon}} $$ (51) 式中:
$\mathrm{ \;\beta }=\left\langle{{I}_{t}}\right\rangle/\left\langle{{I}_{r}}\right\rangle$ 是无量纲的常量;$\boldsymbol{x}= {[{x}_{1},{x}_{2},\cdots ,} $ $ {{x}_{j},\cdots ,{x}_{M}]}^{\mathrm{T}}$ ;$\boldsymbol{y}= {[{y}_{1},{y}_{2},\cdots ,} {{y}_{i},\cdots ,{y}_{N}]}^{\mathrm{T}}$ ;$\boldsymbol{A}=[{\boldsymbol{a}}_{1},{\boldsymbol{a}}_{2},\cdots , $ $ {\boldsymbol{a}}_{j},\cdots , {\boldsymbol{a}}_{M}]$ ,其中,$$ \begin{split} &{x}_{j}={\left|{{\varGamma }}_{E}\left({\boldsymbol{r}}_{t},{\boldsymbol{r}}_{r,j}\right)\right|}^{2},j=1,\cdots ,M \\& {y}_{i}={I}_{t}\left({\boldsymbol{r}}_{t},{t}_{i}\right),i=1,\cdots ,N \\& {\boldsymbol{a}}_{j}=\left[{I}_{r}\left({\boldsymbol{r}}_{r,j},{t}_{1}\right),{I}_{r}\left({\boldsymbol{r}}_{r,j},{t}_{2}\right),\cdots ,{I}_{r}\left({\boldsymbol{r}}_{r,j},{t}_{i}\right),\cdots ,{I}_{r}\left({\boldsymbol{r}}_{r,j},{t}_{N}\right)\right] \\[-10pt] \end{split} $$ (52) 且,
$$ \boldsymbol{\varepsilon} =\left\{\boldsymbol{n}+\mathrm{\Delta }\right\} \sim N\left(0,{\sigma }^{2}\right),\\ {\sigma }^{2}=\mathbb{V}\left\{\boldsymbol{n}\right\}+\mathbb{V}\left\{\mathrm{\Delta }\right\} ={\sigma }_{n}^{2}+\mathbb{V}\left\{\mathrm{\Delta }\right\}$$ (53) 与实空间鬼成像类似,傅里叶衍射鬼成像对
${\boldsymbol{x}}_{i}$ 估计的CRB为:$$ \begin{array}{c}\mathbb{V}\left\{{\boldsymbol{x}}_{i}\right\}\approx \dfrac{{\sigma }^{2}}{{\mathrm{\beta }}^{2}{N\left\langle{{I}_{r}}\right\rangle}^{2}}\dfrac{M}{M+1} \end{array} $$ (54) 代入公式(50)和(53),可得:
$$ \begin{split} \mathbb{V}\left\{{\boldsymbol{x}}_{i}\right\}\approx \frac{{\sigma }_{n}^{2}+{\left\langle{{I}_{t}}\right\rangle}^{2}}{{\mathrm{\beta }}^{2}{N\left\langle{{I}_{r}}\right\rangle}^{2}}\frac{M}{M+1} \end{split} $$ (55) 当重构图像
$ \boldsymbol{x} $ 的像素数$ M $ 较大时,则有:$$ \begin{split} \mathbb{V}\left\{{\boldsymbol{x}}_{i}\right\}\approx \frac{{\sigma }_{n}^{2}+{\left\langle{{I}_{t}}\right\rangle}^{2}}{{\mathrm{\beta }}^{2}{N\left\langle{{I}_{r}}\right\rangle}^{2}}=\frac{1}{N}\left(1+\frac{1}{{\mathrm{S}\mathrm{N}\mathrm{R}}^{2}}\right) \end{split}$$ (56) 理论上,任何一个无偏估计量的重构误差都不会低于CRB给出的重构误差下界。由于在鬼成像中,强度关联运算本身就是目标图像的一个无偏估计,因而它的统计重构误差理论上应该高于CRB。公式(40)和(56)与关联计算重构结果误差(公式(21)和(28))的对比也验证这一点。需要指出的是,CRB给出的只是一个不能超过的统计重构误差下界,而实际上是否能达到CRB的无偏估计量则需要视具体的模型而定。
-
光学成像系统本质上类似于一个通信系统,因此,可以从信息理论的方法对光学成像系统进行研究。通过对于鬼成像系统的信息理论研究,不仅可以用于评价鬼成像系统的成像能力,还能够为鬼成像系统的信息获取效率优化提供方向。按照经典的Shannon信息论中的理论方法,中科院上海光机所李恩荣等人分析了在预先给定的参考光路探测光场条件下,物光路探测信号与成像物体的互信息[75]。北京大学李俊晖等人通过基于概率论的互信息分析,半定量地解释了实验上观测到的强度涨落关联得到的图像与真实图像之间的互信息随探测次数的负指数变化关系[76]。而与互信息不同,Fisher信息[69-70]是一种能够反映观测系统中探测信号携带的关于目标的信息量多少的信息度量方法。下面以傅里叶衍射鬼成像为例,通过Fisher信息理论分析成像系统,并在此基础上给出了一种用于衍射鬼成像系统目标衍射谱图像重构的条件平均方法[77]。
在傅里叶衍射鬼成像中,成像目标的不同空间频率的傅里叶分量是各自独立地被重构得到的。具体地说,假设固定物臂的探测空间坐标
$ {\boldsymbol{r}}_{t} $ ,关联运算重构空间频率为$ \dfrac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}} $ 的分量只依赖于参考臂坐标$ {\boldsymbol{r}}_{r} $ 的对应的光强$ {I}_{r}\left({\boldsymbol{r}}_{r}\right) $ ,而与其他位置的参考臂探测强度无关。因此,其观测模型可以被简化为:多次采样得到的若干组双臂的两点光强$ \left\{{I}_{r}\left({\boldsymbol{r}}_{r}\right),{I}_{t}\left({\boldsymbol{r}}_{t}\right)\right\} $ 是系统的观测量,成像目标上对应空间频率$ \dfrac{{\boldsymbol{r}}_{t}-{\boldsymbol{r}}_{r}}{\lambda {z}_{2}} $ 的傅里叶分量的模方$ {\mu }^{2} $ 是待估计的参数。已知热光场服从联合圆复高斯分布,可得:观测量
$ \left\{{I}_{r}\left({\boldsymbol{r}}_{r}\right),{I}_{t}\left({\boldsymbol{r}}_{t}\right)\right\} $ 的含参数联合概率密度分布(probability distribution function, PDF)为[77]:$$ \begin{split} & p\left({I}_{r},{I}_{t};{\mu }^{2}\right)=\frac{1}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle\left(1-{\mu }^{2}\right)}\times\\ &{\rm exp}\left\{-\frac{\left\langle{{I}_{r}}\right\rangle{I}_{t}+\left\langle{{I}_{t}}\right\rangle{I}_{r}}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle\left(1-{\mu }^{2}\right)}\right\}{{J}}_{0}\left\{\frac{2\mu }{1-{\mu }^{2}}\sqrt{\frac{{I}_{r}{I}_{t}}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle}}\right\} \end{split} $$ (57) 式中:
${{J}}_{0}\left\{\cdots \right\}$ 是零阶第一类修正Bessel函数。在理论推导得到联合PDF后,进行衍射鬼成像系统的条件Fisher信息研究。考虑到物臂探测信号
$ {I}_{t} $ 是直接包含物体图像信息的,因此将其作为Fisher信息的“条件”。将$ {I}_{t} $ 的取值范围$ \left.\left[0,\infty \right.\right) $ 用不同的上下界系数划分成了多个彼此相邻但不重叠的间隔,使得落在每个区间部分的概率都相同。选取其中的一个区间$ \;{\rho }_{1}\left\langle{{I}_{t}}\right\rangle < {I}_{t} < {\rho }_{2}\left\langle{{I}_{t}}\right\rangle $ ($ {\rho }_{1} < {\rho }_{2} $ 均为常数),对应的条件联合概率密度为:$$ \begin{split} &p\left({I}_{r},{I}_{t}|{\rho }_{1}\left\langle{{I}_{t}}\right\rangle < {I}_{t} < {\rho }_{2}\left\langle{{I}_{t}}\right\rangle\right) = \frac{1}{{\rm e}^{-{\rho }_{1}}-{\rm e}^{-{\rho }_{2}}}\frac{1}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle\left(1-{\mu }^{2}\right)} \\ & \times{\rm exp}\left\{-\frac{\left\langle{{I}_{r}}\right\rangle{I}_{t}+\left\langle{{I}_{t}}\right\rangle{I}_{r}}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle\left(1-{\mu }^{2}\right)}\right\}{{J}}_{0}\left\{\frac{2\mu }{1-{\mu }^{2}}\sqrt{\frac{{I}_{r}{I}_{t}}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle}}\right\} \end{split} $$ (58) 因此,条件Fisher信息为:
$$ \begin{split} &\mathcal{I}\left({\mu }^{2}|{\rho }_{1}\left\langle{{I}_{t}}\right\rangle < {I}_{t} < {\rho }_{2}\left\langle{{I}_{t}}\right\rangle\right)=\\&\underset{{\rho }_{1}\left\langle{{I}_{t}}\right\rangle}{\overset{{\rho }_{2}\left\langle{{I}_{t}}\right\rangle}{\int }}{\rm d}{I}_{t}\underset{0}{\overset{\infty }{\int }}{\rm d}{I}_{r}p\left({I}_{r},{I}_{t}|{\rho }_{1}\left\langle{{I}_{t}}\right\rangle < {I}_{t} < {\rho }_{2}\left\langle{{I}_{t}}\right\rangle\right) \times\\ &{\left[\frac{\partial \mathrm{ln}p\left({I}_{r},{I}_{t}|{\rho }_{1}\left\langle{{I}_{t}}\right\rangle < {I}_{t} < {\rho }_{2}\left\langle{{I}_{t}}\right\rangle\right)}{\partial {\mu }^{2}}\right]}^{2} \end{split} $$ (59) 其中,
$$ \begin{split} &\dfrac{\partial \mathrm{ln}p\left({I}_{r},{I}_{t}|{\rho }_{1}\left\langle{{I}_{t}}\right\rangle < {I}_{t} < {\rho }_{2}\left\langle{{I}_{t}}\right\rangle\right)}{\partial {\mu }^{2}}=\\& \dfrac{1}{1-{\mu }^{2}}-\left(\dfrac{{I}_{r}}{\left\langle{{I}_{r}}\right\rangle}+\dfrac{{I}_{t}}{\left\langle{{I}_{t}}\right\rangle}\right)\dfrac{1}{1-{\mu }^{2}}+\\& \dfrac{{{J}}_{1}\left\{\dfrac{2\mu }{1-{\mu }^{2}}\sqrt{\dfrac{{I}_{r}{I}_{t}}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle}}\right\}}{{{J}}_{0}\left\{\dfrac{2\mu }{1-{\mu }^{2}}\sqrt{\dfrac{{I}_{r}{I}_{t}}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle}}\right\}}\sqrt{\dfrac{{I}_{r}{I}_{t}}{\left\langle{{I}_{r}}\right\rangle\left\langle{{I}_{t}}\right\rangle}}\dfrac{\mu +\dfrac{1}{\mu }}{{\left(1-{\mu }^{2}\right)}^{2}} \end{split} $$ (60) 式中:
${{J}}_{1}\left\{\cdots \right\}$ 是一阶第一类修正Bessel函数。根据公式(59)和(60),通过数值计算的方式计算得到的Fisher信息与相对强度系数
$ \rho ={I}_{t}/\left\langle{{I}_{t}}\right\rangle $ 的关系曲线如图9所示,图中展示了三个不同取值的$ \;{\mu }^{2} $ 对应的曲线。可以看出,随着相对强度系数$\; \rho $ 的增大,Fisher信息呈现先下降后上升的趋势。这个结果表明,将$ {I}_{t} $ 中包含小涨落的观测量滤除的选择性探测方式,能够有助于提高采样效率。该理论结果与实空间鬼成像的条件平均方法[78-79]提升采样效率相似。在此基础上,可以给出基于条件平均的傅里叶衍射鬼成像方法。不同于通常的傅里叶衍射鬼成像利用物臂和探测臂所有涨落的光强关联获取物体的衍射谱信息,基于条件平均的傅里叶衍射鬼成像利用涨落较大的物臂光强相对应的参考臂光强的平均运算获取物体的衍射谱信息。假定此时物臂光强
$ {I}_{t} > {\rho }_{i}\left\langle{{I}_{t}}\right\rangle $ ($ {\rho }_{i} $ 为某一常数),此时参考臂光强服从的条件概率分布为:$$ \begin{split} p\left({I}_{r}|{I}_{t} > {\rho }_{i}\left\langle{{I}_{t}}\right\rangle\right)&= \underset{{\rho }_{i}\left\langle{{I}_{t}}\right\rangle}{\overset{\infty }{\int }}{\rm d}I_{t}\frac{p\left({I}_{r},{I}_{t}\right)}{p\left({I}_{t} > {\rho }_{i}\left\langle{{I}_{t}}\right\rangle\right)}=\\ &{\rm e}^{{\rho }_{i}}\underset{{\rho }_{i}\left\langle{{I}_{t}}\right\rangle}{\overset{\infty }{\int }}{\rm d}{I}_{t}p\left({I}_{r},{I}_{t}\right) \end{split} $$ (61) 对此时的
$ {I}_{r} $ 进行平均运算,可得:$$ \begin{split} {R}_+=\underset{0}{\overset{\infty }{\int }}{\rm d}{I}_{r}p\left({I}_{r}|{I}_{t} > {\rho }_{i}\left\langle{{I}_{t}}\right\rangle\right){I}_{r}=\left\langle{{I}_{r}}\right\rangle\left(1+{\rho }_{i}{\mu }^{2}\right) \end{split} $$ (62) 从公式(62)可以看出,此条件下的平均能够重构出带有均匀本底的正物体衍射谱图样。类似计算,当物臂光强
$ {I}_{t} < {\rho }_{j}\left\langle{{I}_{t}}\right\rangle $ ($ {\rho }_{j} $ 为某一常数)时,对应的参考臂光强$ {I}_{r} $ 的平均运算结果为:$$ \begin{split} {R}_-=\underset{0}{\overset{\infty }{\int }}{\rm d}{I}_{r}p\left({I}_{r}|{I}_{t} < {\rho }_{j}\left\langle{{I}_{t}}\right\rangle\right){I}_{r}=\left\langle{{I}_{r}}\right\rangle\left(1-\frac{{\rm e}^{-{\rho }_{j}}{\rho }_{j}}{1-{\rm e}^{-{\rho }_{j}}}{\mu }^{2}\right)\\[-20pt] \end{split} $$ (63) 此时得到是带有均匀本底的负物体衍射谱图样。对公式(62)和(63)作差,可得:
$$ \begin{split} \Delta R={R}_+-{R}_-=\left\langle{{I}_{r}}\right\rangle\frac{{\rho }_{i}-\left({\rho }_{i}-{\rho }_{j}\right){\rm e}^{-{\rho }_{j}}}{1-{\rm e}^{-{\rho }_{j}}}{\mu }^{2} \end{split} $$ (64) 从而消除均匀本底,获得正比于物体衍射谱信息的图像。特别地,当
${\;\rho }_{i}={\rho }_{j}=\rho$ 时,则有:$$ \begin{split} \Delta R=\left\langle{{I}_{r}}\right\rangle\frac{\rho }{1-{\rm e}^{-\rho }}{\mu }^{2} \end{split} $$ (65) 为了保证
$ {R}_{+} $ 和$ {R}_{-} $ 所用的数据量大致相当,选取$\;\rho =\mathrm{ln}2$ 处理2.1.2中的仿真数据$ {I}_{t} $ ,图10显示了去除均匀本底的正、负图像以及相减图像,能够初步重构物体的衍射图像信息。考虑到公式(59)及图9中不同$\;\rho$ 取值所包含物体图像信息量的不同,通过选取不同的${\;\rho }_{i}$ 和${\;\rho }_{j}$ ,只利用包含较大涨落的$ {I}_{t} $ 对应的参考臂光强信息进行平均运算,有望进一步提升重构质量。图11(a)显示了选取${\;\rho }_{i}=\mathrm{ln}\dfrac{\text{8}}{\text{7}}$ 、${\;\rho }_{j}=\mathrm{ln}\text{8}$ 条件平均相减运算的仿真和实验重构结果,与利用所有光强涨落的强度关联运算重构结果(如图11(b))相比,利用较大涨落的条件平均运算的重构结果更好。同时,针对实验数据的重构结果(如图12所示)也证明了上述条件平均方法提升衍射图样质量的有效性。
图 10 两等分的仿真数据条件平均得到的衍射谱图样。(a) 正图像;(b) 负图像;(c) 正负图像相减图像;(d) 参考的物体衍射谱图样[77]
Figure 10. Diffraction spectrum images obtained via conditional averaging on two equally-divided parts. (a) Positive image; (b) Negative image; (c) Subtraction image of positive images and negative images; (d) Diffraction spectrum image of reference object[77]
-
在压缩感知理论中,通常用测量矩阵的互相干度来分析利用稀疏重构算法进行图像重构时所能达到的性能[80]。测量矩阵
$ \boldsymbol{\varPhi } $ 的互相干度的定义为:$$ \begin{split} \mu \left(\boldsymbol{\varPhi }\right):=\underset{1 \leqslant i < j \leqslant M}{\mathrm{max}}\dfrac{\left|\boldsymbol{\varPhi }_{i}^{\rm T}\boldsymbol{\varPhi }_{j}\right|}{{‖\boldsymbol{\varPhi }_{i}‖}_{2}{‖\boldsymbol{\varPhi }_{j}‖}_{2}} \end{split} $$ (66) 式中:
$ \left\| {\cdots } \right\|_{2} $ 表示$ {l}_{2} $ 范数;向量${\boldsymbol\varPhi }_{i}$ 表示矩阵$\boldsymbol{\varPhi }$ 的第$ i $ 列。当无限采样时,测量矩阵互相干度与归一化二阶关联函数$ {\text{g}}^{\left(2\right)}\left(i,j\right) $ 之间有如下关系[10]:$$ \begin{split} \mu \left(\boldsymbol{\varPhi }\right)=\underset{1 \leqslant i < j \leqslant M}{\mathrm{max}}\left|{\text{g}}^{\left(2\right)}\left(i,j\right)\right| \end{split} $$ (67) 即测量矩阵互相干度等于归一化二阶关联函数的最大值。此时,测量矩阵的互相干度决定了鬼成像的统计分辨率。对于正交匹配追踪算法(OMP)[81],在无噪声条件下,当测量矩阵的互相干度满足
$\; \mathrm{\mu }\left(\boldsymbol{\varPhi }\right) < $ $ \dfrac{1}{2 K-1} $ 时,可以保证任意$ K $ -稀疏信号准确重构[82]。代入公式(67),则鬼成像的统计分辨率受限于如下公式[10]:$$ \begin{split} \underset{1 \leqslant i < j \leqslant M}{\mathrm{max}}\left|{{g}}^{\left(2\right)}\left(i,j\right)\right| < \frac{1}{2K-1} \end{split} $$ (68) 特别地,对于鬼成像相机,能保证任意
$ K $ -稀疏信号准确重构时,对应的光场高维空间中的最小距离$ (\Delta {\boldsymbol{r}}_{\mathrm{m}\mathrm{i}\mathrm{n}}, $ $ \Delta {\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}) $ 为[10]:$$ \begin{split} {\rm exp}\left[-{\left(\dfrac{2\pi \left({n}_{p}-1\right)\omega \Delta {\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\stackrel-{\lambda }}^{2}}\right)}^{2}\right]{\left[\frac{2{J}_{1}\left(\dfrac{\pi D{\left|\Delta {\boldsymbol{r}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right|}^{2}}{\stackrel-{\lambda }f}\right)}{\dfrac{\pi D{\left|\Delta {\boldsymbol{r}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right|}^{2}}{\stackrel-{\lambda }f}}\right]}^{2} < \dfrac{1}{2K-1} \end{split} $$ (69) 式中:
$ {n}_{p} $ 和$ \omega $ 分别为空间随机相位调制板的折射率及高度起伏的均方差;$ D $ 和$ f $ 为前置成像系统的口径和焦距。公式(69)表明,鬼成像相机的分辨率极限不仅受限于成像系统参数,还与目标的稀疏度有关。图13展示了不同目标稀疏度下鬼成像相机在光场高维空间( x , λ )的分辨率极限。可以发现,稀疏目标重构的分辨率高于传统瑞利极限分辨率,而且,鬼成像相机的空间分辨率随着目标在光谱维度差异性的增加而提升,这为打破传统光学成像系统的空间衍射受限提供了新的可能[10]。
图 13 鬼成像相机在高维空间(x , λ)中的统计分辨率极限[10],其中
$ \Delta {\boldsymbol{r}}_{\mathrm{m}\mathrm{i}\mathrm{n}} $ 和$ \Delta {\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}} $ 分别为在高维空间中$ K $ 个点能分辨的最近空间距离和光谱距离,分别取$ K $ =2,3,5,7。$\Delta {\boldsymbol{r}}_{s}$ 为空间分辨率瑞利判据,$ \Delta {\mathit{\lambda }}_{\mathit{s}} $ 为鬼成像相机的光谱分辨率Figure 13. Statistical resolution limit of ghost imaging camera in (x, λ) light-field space[10],
$\Delta {\boldsymbol{r}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and$ \Delta {\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}} $ are the nearest resolved spatial distance and spectral distance among K points, respectively, with K=2,3,5,7.$\Delta {\boldsymbol{r}}_{s}$ is Rayleigh’s spatial resolution criterion, and$ \Delta {\mathit{\lambda }}_{\mathit{s}} $ is the spectral resolution of ghost imaging camera -
由Mandel光电探测理论[83]可知,现有探测技术的光强探测值服从泊松分布。当光强较强时,光强探测值相对涨落较小,近似为光场的期望值,即为光场的一阶关联;而当光强较弱时,光强探测值涨落较大,难以反映光场的一阶关联。针对弱光探测,一方面可以通过增大增益、长时间探测趋近光场的一阶关联,另一方面则可利用探测值的先验分布特性(例如极大似然估计)和物体先验约束来估计光场的一阶关联[84-85]。总的来说,现有光电探测技术可直接获得光场一阶关联的相关信息。而鬼成像基于光场的二阶关联获取物体图像信息,无法由现有光电探测技术直接得到。早期鬼成像技术通过弱光下的双臂光子符合计数[4-5]、或通过光场的宏观涨落模拟光场微观涨落产生多个独立同分布的光强信号[86-89],再数值计算这些样本数据关联度的均值来估计真实期望值(即光场的二阶关联函数),最终实现对物体成像。然而,受限于实际应用条件,当样本数据不足时,上述方法样本均值估计结果与真实期望值之间的偏差较大,导致成像质量较差。为了降低估计偏差,研究人员利用光场的统计性质提出了差分鬼成像(differential ghost imaing)[63, 90]、归一化鬼成像(normalized ghost imaging)[91]、伪逆鬼成像(pseudo-inverse ghost imaging)[92-93]、奇异值分解鬼成像(SVD ghost imaging)[94]、预处理鬼成像(precon-ditioning ghost imaging)[95]等改进真实期望值的估计方法,提升鬼成像成像质量。此外,与弱光估计光场一阶关联的方法类似,大批研究人员关注和持续研究鬼成像中结合信号处理理论估计物体的图像信息。2009年,Katz等人[71]首次将压缩感知[96-97]框架结合进使用赝热光的实空间鬼成像系统中,提出通过基于目标先验的重构算法来求解获得目标图像。从目标的稀疏性出发,中科院上海光机所韩申生课题组提出了基于稀疏约束的鬼成像技术[14, 74],并在雷达[14, 98]、X光衍射成像[28, 99]、光谱成像[18, 100]、荧光显微[36]等领域开展应用研究。然而,目前针对光场二阶关联函数分布的理论研究还不充分,难以像传统弱光探测那样直接给出其先验分布约束。为了能够有效地结合信号处理理论,目前只能通过各种方法将二阶关联函数的估计问题转换为一阶关联函数(即光强)的估计问题[74]。
因此,一方面,针对各种鬼成像方案如何实现这种转换、转换误差的理论分析、以及在“一阶模型”下的重构误差理论分析,是结合信号处理理论的鬼成像应用亟待解决的理论问题。现阶段的统计重构误差下界没有考虑到物体的先验特性,只给出了鬼成像无偏估计下的重构误差下界,对于结合信息理论的鬼成像的重构误差描述还不够准确。Bayesian CRB[101]可以将物体的先验约束纳入重构误差下界中,还可以给出任意估计(不论是无偏估计还是有偏估计)下的重构误差下界,是开展结合信息理论的鬼成像重构误差理论研究的重要手段。此外,不同于利用CRB给出统计误差下界来理论分析鬼成像的重构误差,通过Bootstrap[102]分析重构结果的置信区间、利用马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo,MCMC)[103-104]开展重构结果的不确定度分析等方法也是理论分析鬼成像重构结果的重要研究内容。另一方面,还可以直接针对光场二阶关联模型构建鬼成像信号处理理论。例如,利用有限估计的二阶关联函数与物体图像的理论关系,考虑物体图像的先验约束,可以尝试结合双线性方程理论[105],同时估计物体图像和误差。
在鬼成像的Fisher信息理论研究方面,目前所考虑的联合概率密度分布只是简单的两点的探测信号,如何考虑所有像素的探测信号的联合概率密度分布及目标本身的先验特性开展鬼成像的Fisher信息理论分析,不仅能够为鬼成像系统优化[75]及数据后处理[77-78]提供理论依据,而且也对定量描述鬼成像系统的性能、评估该系统所能传递的信息量理论极限具有重要意义。
此外,信息理论也是研究成像分辨率的重要手段。1964年,Helstrom[106]首次从信号探测统计理论角度研究成像分辨率,通过计算CRB来估计单个或多个非相干点源位置参量误差的下界来衡量成像系统的分辨率。1990年,Kosarev[107]从信息论的角度研究了成像分辨率的问题,定量给出超分辨能力与探测信噪比的关系。1992年,Lucy等人[108-109]分析了解卷积图像分辨率的统计极限,认为解卷积图像分辨率与收集到光子数的密切相关。1997年,Dekker等人[110]系统性分析了成像系统的分辨率问题,包括传统成像分辨率、信噪比限制分辨率、基于参量统计估计理论分析成像系统分辨率下界,以及基于奇异性理论分析分辨率等。2006年,Smith[111]首次提出统计分辨率(statistical resolution)的概念,并分别从参数估计理论、检测理论分析统计分辨率。近年来,Tsang[112-113]和陆晓铭等人[114]分别从参数估计理论和检测理论出发,给出了分辨率的量子极限。在鬼成像领域,中科院上海光机所韩申生课题组基于压缩感知理论中准确重构稀疏信号的充分条件,初步探索了鬼成像的统计分辨率极限[10],并提出了基于正则化预处理的超分辨成像技术[95]及基于光场高维空间可辨识度的超分辨成像技术[10]。北京邮电大学的韩哲等人[115]则从压缩感知的凸优化几何理论出发,探究了光场涨落预处理提高成像分辨率的理论解释。然而,目前的鬼成像统计分辨率极限[10]对应于系综统计下的无限次采样,而实际成像的分辨率不仅与重建算法密切相关,而且受到探测噪声的影响。因此,从信息理论出发,通过约束CRB[116]等理论开展实际应用场景(有限次采样、信噪比有限)下考虑目标先验信息的鬼成像分辨率极限分析,也是鬼成像有待进一步开展的理论研究工作。
总的来说,鬼成像相比传统成像引入了基于光场涨落的成像信息调制及重构过程,不仅提升了图像信息获取方式的灵活性,可以具备传统成像所不具备的成像性能,而且利用目标的先验特性优化设计光场调制,相比传统成像系统能够具有更高的信息获取效率和抗噪性能。随着信号处理算法的广泛引入,越来越多的信号处理理论及信息论研究工作得到鬼成像领域的关注,为鬼成像提供了全新的研究手段和认知视角。在此基础上,基于现代信号处理和信息理论的鬼成像理论研究,不仅能够定量分析和评价鬼成像的成像性能,而且也为优化鬼成像系统提供理论支撑,从而有望大大推动鬼成像的学科发展和技术应用。
Some research progress on the theoretical study of ghost imaging in Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences (Invited)
-
摘要: 相比利用光场的一阶关联实现物空间与像空间一一对应的传统成像,鬼成像基于光场的二阶关联实现物空间与像空间的一一对应,从而获取物体图像信息。通过引入光场涨落调制和计算重构,鬼成像不仅可以具有更高的信息获取效率,而且提升了图像信息获取方式的灵活性,能够具备传统成像所不具备的成像能力。随着鬼成像在系统优化及技术应用方面的进一步发展,对鬼成像理论也提出了新的要求和挑战。文中分别从鬼成像的物理本质、图像信息获取理论及理论分辨率研究三方面介绍了中国科学院上海光学精密机械研究所近期在鬼成像理论上的若干研究工作,并对今后鬼成像的理论研究工作进行了展望。Abstract: Compared with traditional imaging that uses the first-order correlation of light fields to realize the one-to-one correspondence between the object and image spaces, ghost imaging realizes the correspondence based on the second-order correlation of light fields and thereby obtains object’s image information. By introducing light field fluctuation modulation and computational reconstruction, ghost imaging not only has higher information acquisition efficiency, but also improves the flexibility of image information acquisition modes, thus having imaging capabilities that traditional imaging does not have. The further developments of ghost imaging in system optimization and technical applications bring new demands and challenges to ghost imaging theory. In this paper, the recent research progress of ghost imaging theory in Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences was introduced from three aspects: the physical nature, the image information acquisition theory and theoretical resolution. And the future theoretical research on ghost imaging was prospected.
-
图 6 不同物光路探测信噪比下,实空间鬼成像关联结果的仿真方差分布与理论比较。(a)信噪比
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ;(b)信噪比$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{\text{10}}$ Figure 6. Comparison of variance distribution of simulated results in real-space ghost imaging with theoretical results at different SNRs in object light path. (a)
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ; (b)$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{\text{10}}$ 图 8 不同物光路探测信噪比下,傅里叶衍射鬼成像关联结果的仿真方差分布与理论比较。 (a)信噪比
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ;(b)信噪比$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{10}$ Figure 8. Comparison of variance distribution of simulated results in Fourier diffraction ghost imaging with theoretical results at different SNRs. (a)
$ \mathrm{S}\mathrm{N}\mathrm{R}=\mathrm{\infty } $ ;(b)$ \mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{\text{10}}$ 图 10 两等分的仿真数据条件平均得到的衍射谱图样。(a) 正图像;(b) 负图像;(c) 正负图像相减图像;(d) 参考的物体衍射谱图样[77]
Figure 10. Diffraction spectrum images obtained via conditional averaging on two equally-divided parts. (a) Positive image; (b) Negative image; (c) Subtraction image of positive images and negative images; (d) Diffraction spectrum image of reference object[77]
图 13 鬼成像相机在高维空间(x , λ)中的统计分辨率极限[10],其中
$ \Delta {\boldsymbol{r}}_{\mathrm{m}\mathrm{i}\mathrm{n}} $ 和$ \Delta {\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}} $ 分别为在高维空间中$ K $ 个点能分辨的最近空间距离和光谱距离,分别取$ K $ =2,3,5,7。$\Delta {\boldsymbol{r}}_{s}$ 为空间分辨率瑞利判据,$ \Delta {\mathit{\lambda }}_{\mathit{s}} $ 为鬼成像相机的光谱分辨率Figure 13. Statistical resolution limit of ghost imaging camera in (x, λ) light-field space[10],
$\Delta {\boldsymbol{r}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and$ \Delta {\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}} $ are the nearest resolved spatial distance and spectral distance among K points, respectively, with K=2,3,5,7.$\Delta {\boldsymbol{r}}_{s}$ is Rayleigh’s spatial resolution criterion, and$ \Delta {\mathit{\lambda }}_{\mathit{s}} $ is the spectral resolution of ghost imaging camera -
[1] Brown R H, Twiss R Q. Correlation between photons in two coherent beams of light [J]. Nature, 1956, 177(4497): 27-29. doi: 10.1038/177027a0 [2] Hanbury Brown R, Twiss R Q. The question of correlation between photons in coherent light rays [J]. Nature, 1956, 178(4548): 1447-1448. doi: 10.1038/1781447a0 [3] Strekalov D V, Sergienko A V, Klyshko D N, et al. Observation of two-photon "ghost'' interference and diffraction [J]. Physical Review Letters, 1995, 74(18): 3600-3603. doi: 10.1103/PhysRevLett.74.3600 [4] Pittman T B, Shih Y H, Strekalov D V, et al. Optical imaging by means of two-photon quantum entanglement [J]. Physical Review A, 1995, 52(5): R3429-R3432. doi: 10.1103/PhysRevA.52.R3429 [5] Bennink R S, Bentley S J, Boyd R W. "Two-photon'' coincidence imaging with a classical source [J]. Physical Review Letters, 2002, 89(11): 113601. doi: 10.1103/PhysRevLett.89.113601 [6] Cheng J, Han S. Incoherent coincidence imaging and its applicability in X-ray diffraction [J]. Physical Review Letters, 2004, 92(9): 093903. doi: 10.1103/PhysRevLett.92.093903 [7] Gatti A, Brambilla E, Bache M, et al. Ghost imaging with thermal light: Comparing entanglement and classicalcorrelation [J]. Physical Review Letters, 2004, 93(9): 093602. doi: 10.1103/PhysRevLett.93.093602 [8] Chen Huaijin, Asif M S, Sankaranarayanan A C, et al. FPA-CS: Focal plane array-based compressive imaging in short-wave infrared[C]//Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015. [9] Duarte M F, Davenport M A, Takhar D, et al. Single-pixel imaging via compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 83-91. doi: 10.1109/MSP.2007.914730 [10] Tong Z, Liu Z, Wang J, et al. Breaking Rayleigh’s criterion via discernibility in high-dimensional light-field space with snapshot ghost imaging [J]. arXiv, 2020: 2004.00135. [11] Gong W, Han S. Experimental investigation of the quality of lenslesssuper-resolution ghost imaging via sparsity constraints [J]. Physics Letters A, 2012, 376(17): 1519-1522. doi: 10.1016/j.physleta.2012.03.027 [12] Li Longzhen, Yao Xuri, Liu Xuefeng, et al. Super-resolution ghost imaging via compressed sensing [J]. Acta Physica Sinica, 2014, 63(22): 224201. (in Chinese) doi: 10.7498/aps.63.224201 [13] Chen Z, Shi J, Li Y, et al. Super-resolution thermal ghost imaging based on deconvolution [J]. The European Physical Journal - Applied Physics, 2014, 67(1): 10501. doi: 10.1051/epjap/2014140122 [14] Zhao C, Gong W, Chen M, et al. Ghost imaging lidar via sparsity constraints [J]. Applied Physics Letters, 2012, 101(14): 141123. doi: 10.1063/1.4757874 [15] Erkmen B I. Computational ghost imaging for remote sensing [J]. J Opt Soc Am A, 2012, 29(5): 782-789. doi: 10.1364/JOSAA.29.000782 [16] Hardy N D, Shapiro J H. Computational ghost imaging versus imaging laser radar for three-dimensional imaging [J]. Physical Review A, 2013, 87(2): 023820. doi: 10.1103/PhysRevA.87.023820 [17] Sun B, Edgar M P, Bowman R, et al. 3D computational imaging with single-pixel detectors [J]. Science, 2013, 340(6134): 844-847. doi: 10.1126/science.1234454 [18] Liu Z, Tan S, Wu J, et al. Spectral camera based on ghost imaging via sparsity constraints [J]. Scientific Reports, 2016, 6(1): 25718. doi: 10.1038/srep25718 [19] Wang Y, Suo J, Fan J, et al. Hyperspectral computational ghost imaging via temporal multiplexing [J]. IEEE Photonics Technology Letters, 2016, 28(3): 288-291. doi: 10.1109/LPT.2015.2494878 [20] Li Meixuan, Zhang Siqi, Li Hong, et al. Research on the bandpass filter used for single-exposure multi-spectral ghost imaging system [J]. Infrared and Laser Engineering, 2020, 49(9): 20200169. (in Chinese) doi: 10.3788/IRLA20200169 [21] Huang Jian, Shi Dongfeng, Meng Wenwen, et al. Study on spectral encoded computational ghost imaging [J]. Infrared and Laser Engineering, 2021, 50(1): 20200120. (in Chinese) doi: 10.3788/IRLA20200120 [22] Chu C, Liu S, Liu Z, et al. Spectral polarization camera based on ghost imaging via sparsity constraints [J]. Appl Opt, 2021, 60(16): 4632-4638. doi: 10.1364/AO.417022 [23] Shi D, Hu S, Wang Y. Polarimetric ghost imaging [J]. Opt Lett, 2014, 39(5): 1231-1234. doi: 10.1364/OL.39.001231 [24] Zhu Y, Shi J, Yang Y, et al. Polarization difference ghost imaging [J]. Appl Opt, 2015, 54(6): 1279-84. doi: 10.1364/AO.54.001279 [25] Liu Y, Shi J, Zeng G. Single-photon-counting polarization ghost imaging [J]. Appl Opt, 2016, 55(36): 10347-10351. doi: 10.1364/AO.55.010347 [26] Kobata T, Nomura T. Digital holographic three-dimensional Mueller matrix imaging [J]. Appl Opt, 2015, 54(17): 5591-5596. doi: 10.1364/AO.54.005591 [27] Ye Z, Xiong J, Liu H C. Ghost difference imaging using one single-pixel detector [J]. Physical Review Applied, 2021, 15(3): 034035. doi: 10.1103/PhysRevApplied.15.034035 [28] Yu H, Lu R, Han S, et al. Fourier-transform ghost imaging with hard X rays [J]. Physical Review Letters, 2016, 117(11): 113901. doi: 10.1103/PhysRevLett.117.113901 [29] Pelliccia D, Rack A, Scheel M, et al. Experimental X-Ray Ghost Imaging [J]. Physical Review Letters, 2016, 117(11): 113902. doi: 10.1103/PhysRevLett.117.113902 [30] Klein Y, Schori A, Dolbnya I P, et al. X-ray computational ghost imaging with single-pixel detector [J]. Opt Express, 2019, 27(3): 3284-3293. doi: 10.1364/OE.27.003284 [31] Zhang A X, He Y H, Wu L A, et al. Tabletop x-ray ghost imaging with ultra-low radiation [J]. Optica, 2018, 5(4): 374-377. doi: 10.1364/OPTICA.5.000374 [32] Li S, Cropp F, Kabra K, et al. Electron ghost imaging [J]. Physical Review Letters, 2018, 121(11): 114801. doi: 10.1103/PhysRevLett.121.114801 [33] Khakimov R I, Henson B M, Shin D K, et al. Ghost imaging with atoms [J]. Nature, 2016, 540(7631): 100-103. doi: 10.1038/nature20154 [34] He Y H, Huang Y Y, Zeng Z R, et al. Single-pixel imaging with neutrons [J]. Science Bulletin, 2021, 66(2): 133-138. doi: 10.1016/j.scib.2020.09.030 [35] Kingston A M, Myers G R, Pelliccia D, et al. Neutron ghost imaging [J]. Physical Review A, 2020, 101(5): 053844. doi: 10.1103/PhysRevA.101.053844 [36] Li W, Tong Z, Xiao K, et al. Single-frame wide-field nanoscopy based on ghost imaging via sparsity constraints [J]. Optica, 2019, 6(12): 1515-1523. doi: 10.1364/OPTICA.6.001515 [37] Tian N, Guo Q, Wang A, et al. Fluorescence ghost imaging with pseudothermal light [J]. Opt Lett, 2011, 36(16): 3302-3304. doi: 10.1364/OL.36.003302 [38] Tian Y, Ge H, Zhang X J, et al. Acoustic ghost imaging in the time domain [J]. Physical Review Applied, 2020, 13(6): 064044. doi: 10.1103/PhysRevApplied.13.064044 [39] Collaboration N A, Bøggild H, Boissevain J, et al. Two-kaon correlations in central Pb+Pb collisions at 158 A GeV/c [J]. Physical Review Letters, 2001, 87(11): 112301. doi: 10.1103/PhysRevLett.87.112301 [40] Adler S S, Afanasiev S, Aidala C, et al. Bose-Einstein correlations of charged pion pairs in Au+Au collisions at $\scriptsize{\sqrt {{\rm{sNN}}}} $ =200 GeV [J]. Physical Review Letters, 2004, 93(15): 152302. doi: 10.1103/PhysRevLett.93.152302[41] Gatti A, Brambilla E, Bache M, et al. Correlated imaging, quantum and classical [J]. Physical Review A, 2004, 70(1): 013802. doi: 10.1103/PhysRevA.70.013802 [42] Shechtman Y, Eldar Y C, Cohen O, et al. Phase retrieval with application to optical imaging: A contemporary overview [J]. IEEE Signal Processing Magazine, 2015, 32(3): 87-109. doi: 10.1109/MSP.2014.2352673 [43] Martienssen W, Spiller E. Coherence and fluctuations in light beams [J]. American Journal of Physics, 1964, 32(12): 919-926. doi: 10.1119/1.1970023 [44] Bromberg Y, Katz O, Silberberg Y. Ghost imaging with a single detector [J]. Physical Review A, 2009, 79(5): 053840. doi: 10.1103/PhysRevA.79.053840 [45] Shapiro J H. Computational ghost imaging[C]//Proceedings of the Conference on Lasers and Electro-Optics/International Quantum Electronics Conference, 2009. [46] Lu Minghai, Shen Xia, Han Shensheng. Ghost imaging via compressive sampling based on digital micromirror device [J]. Acta Optica Sinica, 2011, 31(7): 0711002. (in Chinese) doi: 10.3788/AOS201131.0711002 [47] Arecchi F T. Measurement of the statistical distribution of gaussian and laser sources [J]. Physical Review Letters, 1965, 15(24): 912-916. doi: 10.1103/PhysRevLett.15.912 [48] Liu H, Cheng J, Han S. Cross spectral purity and its influence on ghost imaging experiments [J]. Optics Communications, 2007, 273(1): 50-53. doi: 10.1016/j.optcom.2006.12.025 [49] Zhang D, Zhai Y H, Wu L A, et al. Correlated two-photon imaging with true thermal light [J]. Opt Lett, 2005, 30(18): 2354-2356. doi: 10.1364/OL.30.002354 [50] Liu X F, Chen X H, Yao X R, et al. Lensless ghost imaging with sunlight [J]. Opt Lett, 2014, 39(8): 2314-2317. doi: 10.1364/OL.39.002314 [51] Giglio M, Carpineti M, Vailati A. Space intensity correlations in the near field of the scattered light: A direct measurement of the density correlation function g(r) [J]. Physical Review Letters, 2000, 85(7): 1416-1419. doi: 10.1103/PhysRevLett.85.1416 [52] Cerbino R, Peverini L, Potenza M A C, et al. X-ray-scattering information obtained from near-field speckle [J]. Nature Physics, 2008, 4(3): 238-243. doi: 10.1038/nphys837 [53] Arce G R, Brady D J, Carin L, et al. Compressive coded aperture spectral imaging: An introduction [J]. IEEE Signal Processing Magazine, 2014, 31(1): 105-115. doi: 10.1109/MSP.2013.2278763 [54] Antipa N, Kuo G, Heckel R, et al. DiffuserCam: lensless single-exposure 3 D imaging [J]. Optica, 2018, 5(1): 1-9. doi: 10.1364/OPTICA.5.000001 [55] Sahoo S K, Tang D, Dang C. Single-shot multispectral imaging with a monochromatic camera [J]. Optica, 2017, 4(10): 1209-1213. doi: 10.1364/OPTICA.4.001209 [56] Kwon H, Arbabi E, Kamali S M, et al. Computational complex optical field imaging using a designed metasurface diffuser [J]. Optica, 2018, 5(8): 924-931. doi: 10.1364/OPTICA.5.000924 [57] Li X, Greenberg J A, Gehm M E. Single-shot multispectral imaging through a thin scatterer [J]. Optica, 2019, 6(7): 864-871. doi: 10.1364/OPTICA.6.000864 [58] Monakhova K, Yanny K, Aggarwal N, et al. Spectral DiffuserCam: Lensless snapshot hyperspectral imaging with a spectral filter array [J]. Optica, 2020, 7(10): 1298-1307. doi: 10.1364/OPTICA.397214 [59] Zhu R, Yu H, Lu R, et al. Spatial multiplexing reconstruction for Fourier-transform ghost imaging via sparsity constraints [J]. Opt Express, 2018, 26(3): 2181-2190. doi: 10.1364/OE.26.002181 [60] Cai Y, Zhu S Y. Ghost imaging with incoherent and partially coherent light radiation [J]. Physical Review E, 2005, 71(5): 056607. doi: 10.1103/PhysRevE.71.056607 [61] Liu H, Cheng J, Han S. Ghost imaging in Fourier space [J]. Journal of Applied Physics, 2007, 102(10): 103102. doi: 10.1063/1.2812597 [62] Shen Xia, Bai Yanfeng, Qin Tao, et al. Experimental investigation of quality of lensless ghost imaging with pseudo-thermal light [J]. Chinese Physics Letters, 2008, 25(11): 3968-3971. doi: 10.1088/0256-307X/25/11/036 [63] Ferri F, Magatti D, Lugiato L A, et al. Differential ghost imaging [J]. Physical Review Letters, 2010, 104(25): 253603. doi: 10.1103/PhysRevLett.104.253603 [64] Erkmen B I, Shapiro J H. Signal-to-noise ratio of Gaussian-state ghost imaging [J]. Physical Review A, 2009, 79(2): 023833. doi: 10.1103/PhysRevA.79.023833 [65] Chan K W C, O’Sullivan M N, Boyd R W. Optimization of thermal ghost imaging: high-order correlations vs. background subtraction [J]. Opt Express, 2010, 18(6): 5562-5573. doi: 10.1364/OE.18.005562 [66] Liu J. On the recovery conditions for practical ghost imaging with AMP algorithm [J]. Opt Express, 2018, 26(16): 20519-20533. doi: 10.1364/OE.26.020519 [67] Jalali S, Yuan X. Snapshot compressed sensing: Performance bounds and algorithms [J]. IEEE Transactions on Information Theory, 2019, 65(12): 8005-8024. doi: 10.1109/TIT.2019.2940666 [68] Yuan X, Brady D J, Katsaggelos A K. Snapshot compressive imaging: Theory, algorithms, and applications [J]. IEEE Signal Processing Magazine, 2021, 38(2): 65-88. doi: 10.1109/MSP.2020.3023869 [69] Fisher R A, Russell E J. On the mathematical foundations of theoretical statistics [J]. Philosophical Transactions of the Royal Society of London Series A, Containing Papers of a Mathematical or Physical Character, 1922, 222(594-604): 309-368. doi: 10.1098/rsta.1922.0009 [70] Kay S M. Fundamentals of Statistical Signal Processing [M]. NJ: Prentice Hall, 2001. [71] Katz O, Bromberg Y, Silberberg Y, et al. Compressive ghost imaging [J]. Applied Physics Letters, 2009, 95(13): 131110. doi: 10.1063/1.3238296 [72] Jiying L, Jubo Z, Chuan L, et al. High-quality quantum-imaging algorithm and experiment based on compressive sensing [J]. Opt Lett, 2010, 35(8): 1206-1208. doi: 10.1364/OL.35.001206 [73] Katkovnik V, Astola J. Compressive sensing computational ghost imaging [J]. J Opt Soc Am A, 2012, 29(8): 1556-1567. doi: 10.1364/JOSAA.29.001556 [74] Han S, Yu H, Shen X, et al. A review of ghost imaging via sparsity constraints [J]. Applied Sciences, 2018, 8(8): 1379. doi: 10.3390/app8081379 [75] Li Enrong, Chen Mingliang, Gong Wenlin, et al. Ghost imaging via compressive sampling based on digital micromirror device [J]. Acta Optica Sinica, 2013, 33(12): 1211003. (in Chinese) doi: 10.3788/AOS201333.1211003 [76] Li J, Luo B, Yang D, et al. Negative exponential behavior of image mutual information for pseudo-thermal light ghost imaging: observation, modeling, and verification [J]. Science Bulletin, 2017, 62(10): 717-723. doi: 10.1016/j.scib.2017.04.008 [77] Hu C, Zhu R, Yu H, et al. Correspondence Fourier-transform ghost imaging [J]. Physical Review A, 2021, 103(4): 043717. doi: 10.1103/PhysRevA.103.043717 [78] Luo Kaihong, Huang Boqiang, Zheng Weimou, et al. Nonlocal imaging by conditional averaging of random reference measurements [J]. Chin Phys Lett, 2012, 29(7): 074216. doi: 10.1088/0256-307X/29/7/074216 [79] Li M-F, Zhang Y-R, Luo K-H, et al. Time-correspondence differential ghost imaging [J]. Physical Review A, 2013, 87(3): 033813. doi: 10.1103/PhysRevA.87.033813 [80] Donoho D L, Huo X. Uncertainty principles and ideal atomic decomposition [J]. IEEE Transactions on Information Theory, 2001, 47(7): 2845-2862. doi: 10.1109/18.959265 [81] Davenport M A, Wakin M B. Analysis of orthogonal matching pursuit using the restricted isometry property [J]. IEEE Transactions on Information Theory, 2010, 56(9): 4395-4401. doi: 10.1109/TIT.2010.2054653 [82] Tropp J A. Greed is good: Algorithmic results for sparse approximation [J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. doi: 10.1109/TIT.2004.834793 [83] Mandel L, Sudarshan E C G, Wolf E. Theory of photoelectric detection of light fluctuations [J]. Proceedings of the Physical Society, 1964, 84(3): 435-444. doi: 10.1088/0370-1328/84/3/313 [84] Kolaczyk E D, Nowak R D. Multiscale likelihood analysis and complexity penalized estimation [J]. The Annals of Statistics, 2004, 32(2): 500-527. [85] Makitalo M, Foi A. Optimal inversion of the anscombe transformation in low-count poisson image denoising [J]. IEEE Transactions on Image Processing, 2011, 20(1): 99-109. doi: 10.1109/TIP.2010.2056693 [86] Ferri F, Magatti D, Gatti A, et al. High-resolution ghost image and ghost diffraction experiments with thermal light [J]. Physical Review Letters, 2005, 94(18): 183602. doi: 10.1103/PhysRevLett.94.183602 [87] Zhang M, Wei Q, Shen X, et al. Lensless Fourier-transform ghost imaging with classical incoherent light [J]. Physical Review A, 2007, 75(2): 021803. doi: 10.1103/PhysRevA.75.021803 [88] Bache M, Magatti D, Ferri F, et al. Coherent imaging of a pure phase object with classical incoherent light [J]. Physical Review A, 2006, 73(5): 053802. doi: 10.1103/PhysRevA.73.053802 [89] Gatti A, Bache M, Magatti D, et al. Coherent imaging with pseudo-thermal incoherent light [J]. Journal of Modern Optics, 2006, 53(5-6): 739-760. doi: 10.1080/09500340500147240 [90] Gong W, Han S. A method to improve the visibility of ghost images obtained by thermal light [J]. Physics Letters A, 2010, 374(8): 1005-1008. doi: 10.1016/j.physleta.2009.12.030 [91] Sun B, Welsh S S, Edgar M P, et al. Normalized ghost imaging [J]. Opt Express, 2012, 20(15): 16892-16901. doi: 10.1364/OE.20.016892 [92] Zhang C, Guo S, Cao J, et al. Object reconstitution using pseudo-inverse for ghost imaging [J]. Opt Express, 2014, 22(24): 30063-30073. doi: 10.1364/OE.22.030063 [93] Gong W. High-resolution pseudo-inverse ghost imaging [J]. Photon Res, 2015, 3(5): 234-237. doi: 10.1364/PRJ.3.000234 [94] Zhang X, Meng X, Yang X, et al. Singular value decomposition ghost imaging [J]. Opt Express, 2018, 26(10): 12948-12958. doi: 10.1364/OE.26.012948 [95] Tong Z, Liu Z, Hu C, et al. Preconditioned deconvolution method for high-resolution ghost imaging [J]. Photon Res, 2021, 9(6): 1069-1077. doi: 10.1364/PRJ.420326 [96] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. doi: 10.1109/TIT.2006.871582 [97] Candes E J, Tao T. Near-optimal signal recovery from random projections: Universal Encoding Strategies? [J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425. doi: 10.1109/TIT.2006.885507 [98] Gong W, Zhao C, Yu H, et al. Three-dimensional ghost imaging lidar via sparsity constraint [J]. Scientific Reports, 2016, 6(1): 26133. doi: 10.1038/srep26133 [99] Wang H, Han S. Coherent ghost imaging based on sparsity constraint without phase-sensitive detection [J]. EPL (Europhysics Letters), 2012, 98(2): 24003. doi: 10.1209/0295-5075/98/24003 [100] Liu S, Liu Z, Wu J, et al. Hyperspectral ghost imaging camera based on a flat-field grating [J]. Opt Express, 2018, 26(13): 17705-17716. doi: 10.1364/OE.26.017705 [101] Gill R D, Levit B Y. Applications of the van trees inequality: A Bayesian Cramér-Rao bound [J]. Bernoulli, 1995, 1(1-2): 59-79. [102] Davison A C, Hinkley D V. Bootstrap Methods and Their Application [M]. New York: Cambridge University Press, 1997. [103] Tenorio L, Andersson F, de Hoop M, et al. Data analysis tools for uncertainty quantification of inverse problems [J]. Inverse Problems, 2011, 27(4): 045001. doi: 10.1088/0266-5611/27/4/045001 [104] Xu J, Li Q, Wang J. Multiple norms and boundary constraint enforced image deblurring via efficient MCMC algorithm [J]. IEEE Signal Processing Letters, 2020, 27: 41-45. doi: 10.1109/LSP.2019.2954001 [105] Cohen S, Tomasi C. Systems of Bilinear Equations [R]. California: Stanford University, 1997. [106] Helstrom C. The detection and resolution of optical signals [J]. IEEE Transactions on Information Theory, 1964, 10(4): 275-287. doi: 10.1109/TIT.1964.1053702 [107] Kosarev E L. Shannon's superresolution limit for signal recovery [J]. Inverse Problems, 1990, 6(1): 55-76. doi: 10.1088/0266-5611/6/1/007 [108] Lucy L B. Resolution limits for deconvolved images [J]. The Astronomical Journal, 1992, 104: 1260. doi: 10.1086/116315 [109] Lucy L B. Statistical limits to super resolution [J]. Astronomy and Astrophysics, 1992, 261: 706. [110] den Dekker A J, van den Bos A. Resolution: A survey [J]. J Opt Soc Am A, 1997, 14(3): 547-557. doi: 10.1364/JOSAA.14.000547 [111] Smith S T. Statistical resolution limits and the complexified Crame/spl acute/r-Rao bound [J]. IEEE Transactions on Signal Processing, 2005, 53(5): 1597-1609. doi: 10.1109/TSP.2005.845426 [112] Tsang M. Quantum limits to optical point-source localization [J]. Optica, 2015, 2(7): 646-653. doi: 10.1364/OPTICA.2.000646 [113] Tsang M, Nair R, Lu X-M. Quantum theory of superresolution for two incoherent optical point sources [J]. Physical Review X, 2016, 6(3): 031033. doi: 10.1103/PhysRevX.6.031033 [114] Lu X-M, Krovi H, Nair R, et al. Quantum-optimal detection of one-versus-two incoherent optical sources with arbitrary separation [J]. NPJ Quantum Information, 2018, 4(1): 64. doi: 10.1038/s41534-018-0114-y [115] 韩哲. 敏感性分析和凸优化理论在鬼成像中的应用研究 [D]; 北京邮电大学, 2020. Han Zhe. Research on application of sensitivity analysis and convex optimization theory in ghost imaging[D]. Beijing: Beijing University of Posts and Telecommunications, 2020. (in Chinese) [116] Ben-Haim Z, Eldar Y C. On the constrained CramÉr–Rao bound with a singular fisher information matrix [J]. IEEE Signal Processing Letters, 2009, 16(6): 453-456. doi: 10.1109/LSP.2009.2016831 -







 下载:
下载: